杯形件二次拉深的应力分析

引用本文

郭哲锋, 汤文成. 杯形件二次拉深的应力分析.吉林大学学报:工学版, 2016, 46(2): 494-499
GUO Zhe-feng, TANG Wen-cheng. Stress analysis of cup-shaped parts in secondary deep drawing. Journal of Jilin University Engineering and Technology Edition, 2016, 46(2): 494-499 复制到剪切板

Permissions

杯形件二次拉深的应力分析

郭哲锋, 汤文成

东南大学机械工程学院,南京 211189

通讯作者:汤文成(1958-),男,教授,博士生导师.研究方向:CAD/CAE/CAM/PPM/ERP.E-mail:tangwc@seu.edu.cn

作者简介:郭哲锋(1983-),男,博士研究生.研究方向:机械结构动态分析,优化与控制.E-mail:gdxtfj@163.com

基金:国家重大科技专项项目(2012ZX0401031)

摘要

为了研究二次拉深成形理论,提出了二次拉深拉应力的理论模型.首先,通过理论分析得到了拉应力的计算公式,应用Swift失稳理论建立了极限二次拉深系数的计算方法.然后,通过二次拉深成形模拟检验了计算模型的精度,并通过成功的二次拉深成形实验对计算模型的适用性进行了检验.检验结果表明:拉深力和极限二次拉深系数的理论模型具有较高的计算精度.

关键词: 机械制造工艺与设备; 二次拉深; 拉应力; 拉深系数

中图分类号:TG386 文献标志码:A 文章编号:1671-5497(2016)02-0494-06

Stress analysis of cup-shaped parts in secondary deep drawing

GUO Zhe-feng, TANG Wen-cheng

School of Mechanical Engineering, Southeast University, Nanjing 211189, China

Abstract

In order to study the secondary deep drawing forming theory, the tensile stress theoretical model of secondary deep drawing is proposed. First, by theoretical analysis, the calculation formula of tensile stress is deduced, and the calculation method of the limited secondary deep drawing coefficient is established based on the Swift instability theory. Second, the accuracy of the calculation model is examined by secondary deep drawing simulation, and the applicability of the calculation model is verified by means of successful secondary deep drawing forming experiment. The results show that the theoretical model of the tensile stress and the limited secondary deep drawing coefficient has high precision.

Keyword: machinery manufacturing technology and equipment; secondary deep drawing; tensile stress; deep drawing coefficient

Show Figures

0 引言

目前, 对于拉深成形的理论研究主要集中在一次拉深成形方面, 对于二次及多次拉深成形, 由于工艺过程的复杂性, 现阶段的研究方法主要以各种虚拟或实体试验为主.Zein等^[1]对拉深成形进行了有限元模拟, 通过研究凹模圆角半径, 凸模圆角半径, 摩擦因数, 压边力和拉深间隙等因素对回弹和壁厚变薄的影响, 得到了可以明显减少回弹和变薄的工艺参数.Tamasco等^[2]主要通过有限元法对单次和多次拉深成形进行了全程模拟, 通过梯度法进行了工艺参数的优化, 效果良好.Kang等^[3]对多次拉深矩形杯零件时的影响因素进行了分析, 主要进行了中间工步拉深工具形状的分析和修改, 修整后可以顺利成形.Ku等^[4]应用有限元软件对难成形的深矩形件进行了多次拉深的成形模拟, 对影响成形质量的因素进行了分析, 并应用实物拉深实验检验了有限元模拟的正确性.Liu等^[5]对高强度钢板多次拉深成形矩形杯时的凸耳现象进行了研究, 对初始的拉深平板的形状进行了改进, 改进后的拉深零件不仅获得了良好的拉深形状, 而且也明显节省了材料消耗.Harada等^[6]进行了镁合金板在多次拉深成形工艺中成形能力的研究, 通过不同的拉深温度进行多次拉深, 最后得出了在较低温度下镁合金板可以通过多次拉深提高成形能力的结论.汪超等^[7]对影响多次拉深成形质量的因素进行了分析和优化, 应用优化后的工艺参数对开水煲外壳分别进行虚拟和实物拉深实验, 实验结果吻合较好.于鸣等^[8]对筒形件的正反复合拉深成形工艺进行了成形模拟, 分析了压边力, 压边间隙和摩擦因数等主要工艺参数对正反复合拉深成形质量的影响, 对工艺参数进行合理的设置后完成了正反复合成形的模拟, 并对模拟结果进行了实物拉深实验检验, 效果良好.通过这些研究成果可以看出, 当前在多次拉深成形方面还缺少必要而准确的理论研究成果.本文以深杯形件的二次拉深作为研究对象, 讨论径向应力与拉深行程之间的关系, 得到了简洁而准确的拉应力计算模型, 并在此基础上提出了极限二次拉深系数的计算方法, 最后通过二次拉深成形的有限元模拟和实验检验了计算模型的正确性.

1 凸缘变形区的变形抗力分析

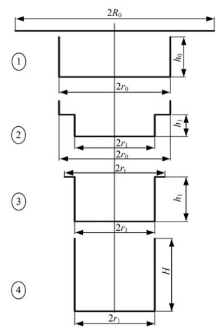
二次拉深时, 板料可分为如图1所示的4个位置状态, 半径为 $\begin{matrix} R_{0} \end{matrix}$ 的原始圆形板料经过一次拉深成形得到半径为 $\begin{matrix} r_{0} 、 \end{matrix}$ 高度为 $\begin{matrix} h_{0} \end{matrix}$ 的杯形件, 对应图1中的① 位置; ① 位置的半成品杯形件经过二次拉深变形为② 位置的阶梯杯形件, 其中小端底面半径为 $\begin{matrix} r_{1}, \end{matrix}$ 高度为 $\begin{matrix} h_{1}; \end{matrix}$ 随着拉深的继续进行, ② 位置的阶梯杯形件变形为③ 位置的带凸缘的杯形件; ③ 位置的半成品继续拉深最终成形为④ 位置的深杯形件.

	Figure Option View Download New Window
	图1 二次拉深过程位置图Fig.1 Secondary deep drawing process location diagram

为了对二次拉深过程中的应力状态进行分析, 首先进行如下假设:a.在拉深过程中板料的厚度认为不变化, 只在计算承载能力时考虑厚度的变化.b.板料的法向应力相对于径向和切向应力是一个微小量, 可以忽略不计.c.法兰变形抗力分析的过程中不考虑摩擦作用, 只在计算单位径向拉应力时考虑摩擦.

对于① 位置的应力状态, 在文献^[9]中已经进行了详细的论述.本文重点分析二次拉深时板料处于中间状态② 位置和③ 位置时的应力状态.

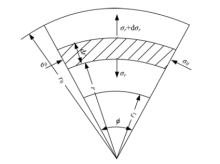
随着拉深的进行, 处于② 位置的阶梯杯形件大端直壁部分的板料持续进入法兰部分, 然后进入小端直壁部分, 在这一过程中变形只发生在法兰部分, 对法兰部分取一微小扇形体进行分析, 如图2所示.

	Figure Option View Download New Window
	图2 法兰应力状态图Fig.2 Flange stress state diagram

因为微体处于平衡状态, 其径向合力为零, 即:

$\begin{matrix} \begin{matrix} (σ_{r} + d σ_{r}) φ (r + dr) t - σ_{r} φrt + 2 σ_{θ} dr \cdot tsin \frac{φ}{2} = 0 \end{matrix} \end{matrix}$ (1)

当 $\begin{matrix} φ \end{matrix}$ 角很小时, $\begin{matrix} \sin \frac{φ}{2} \approx \frac{φ}{2} 。 \end{matrix}$ 略去高阶项, 可化简为:

$\begin{matrix} d σ_{r} = - (σ_{r} + σ_{θ}) \frac{dr}{r} \end{matrix}$ (2)

式(2)即为微分平衡方程.

引入塑性条件 $\begin{matrix} σ_{r} + σ_{θ} = β σ_{i} (σ_{i} \end{matrix}$ 为应力强度).为了简化计算, 按照文献[9]的方法用平均值 $\begin{matrix} \bar{σ_{i}} \end{matrix}$ 代替 $\begin{matrix} σ_{i}, \end{matrix}$ 对式(2)积分可得:

$\begin{matrix} σ_{r} = - β \bar{σ_{i}} lnr + C \end{matrix}$ (3)

在法兰边缘 $\begin{matrix} r_{0} \end{matrix}$ 处, 阶梯杯形件大端的板料在进入法兰区之前已经变形为直壁部分, 直壁部分对于法兰边缘 $\begin{matrix} r_{0} \end{matrix}$ 处的径向作用力为0, 若再忽略模具对直壁的摩擦力, 可以认为法兰边缘 $\begin{matrix} r_{0} \end{matrix}$ 处的径向应力 $\begin{matrix} σ_{r_{0}} = 0, \end{matrix}$ 代入式(2)可得 $\begin{matrix} C = βln r_{0}, \end{matrix}$ 式(3)化为:

$\begin{matrix} σ_{r} = β \bar{σ_{i}} \ln \frac{r_{0}}{r} \end{matrix}$

假设在② 位置的半径为 $\begin{matrix} r_{0} \end{matrix}$ 的变形体在未拉深以前处于原始圆形板料上的位置为半径 $\begin{matrix} R, \end{matrix}$ 拉深过程中体积不变化, 即零件的表面积不变, 可以计算出 $\begin{matrix} R = \sqrt[]{r_{0}^{2} + 2 r_{1} h_{1}}, \end{matrix}$ 所以 $\begin{matrix} r_{0} \end{matrix}$ 处的周向应变为:

$\begin{matrix} \begin{matrix} ε_{θ r_{0}} = \ln \frac{r_{0}}{R} = \ln \frac{r_{0}}{\sqrt[]{r_{0}^{2} + 2 r_{1} h_{1}}} = - \frac{1}{2} \ln (1 + \frac{2 r_{1} h_{1}}{r_{0}^{2}}) \end{matrix} \end{matrix}$

同理可得 $\begin{matrix} r_{1} \end{matrix}$ 处的周向应变为:

$\begin{matrix} ε_{θ r_{1}} = - \frac{1}{2} \ln (1 + \frac{2 h_{1}}{r_{1}}) \end{matrix}$

所以法兰上的平均周向应变为:

$\begin{matrix} \begin{matrix} \bar{ε_{θ}} = |\frac{1}{2} (ε_{θ r_{0}} + ε_{θ r_{1}})| = \frac{1}{4} \ln [1 + 2 h_{1} (\frac{r_{1}}{r_{0}^{2}} + \frac{1}{r_{1}}) + \frac{4 h_{1}^{2}}{r_{0}^{2}}] \end{matrix} \end{matrix}$

根据拉深前, 后表面积不变的条件, 零件处于② 位置时的拉深高度应满足 $\begin{matrix} h_{1} < \frac{R_{0}^{2} - r_{0}^{2}}{2 r_{1}} 。 \end{matrix}$ 因为 $\begin{matrix} \bar{ε_{θ}} \end{matrix}$ 为最大主应变, 所以可以假设 $\begin{matrix} \bar{ε_{i}} \approx \bar{ε_{θ}} \end{matrix}$ , $\begin{matrix} \bar{ε_{i}} \end{matrix}$ 为平均应变强度, 根据Hollomon流动应力模型可知 $\begin{matrix} \bar{σ_{i}} = K {\bar{ε_{i}}}^{n}, \end{matrix}$ 代入式(3)可得:

$\begin{matrix} σ_{r} = βK {\{\frac{1}{4} \ln [1 + 2 h_{1} (\frac{r_{1}}{r_{0}^{2}} + \frac{1}{r_{1}}) + \frac{4 h_{1}^{2}}{r_{0}^{2}}]\}}^{n} \ln \frac{r_{0}}{r} \end{matrix}$ (4)

因为 $\begin{matrix} \bar{σ_{i}} \end{matrix}$ 恒为增函数, 通过式(4)可知, 法兰上最大的径向应力出现在 $\begin{matrix} h_{1} \end{matrix}$ 取最大值时, 即坯料即将从图1中② 位置进入③ 位置的时刻, 而且出现在法兰的 $\begin{matrix} r_{1} \end{matrix}$ 处, 此时 $\begin{matrix} h_{1} = \frac{R_{0}^{2} - r_{0}^{2}}{2 r_{1}}, \end{matrix}$ 所以有:

$\begin{matrix} \max (σ_{r}) = βK {\{\frac{1}{4} \ln [R_{0}^{2} (\frac{R_{0}^{2}}{r_{0}^{2} r_{1}^{2}} + \frac{1}{r_{0}^{2}} - \frac{1}{r_{1}^{2}})]\}}^{n} \ln \frac{r_{0}}{r_{1}} \end{matrix}$ (5)

对于③ 位置也可以按照② 位置的分析方法得到径向应力的表达式为:

$σ_{r} = β \bar{σ_{i}} \ln \frac{r_{t}}{r}$ (6)

$σ_{r} = βK {[\frac{1}{4} \ln (\frac{1 + \frac{2 h_{1}}{r_{1}}}{1 - \frac{2 h_{1} r_{1}}{R_{0}^{2}}})]}^{n} \ln \frac{\sqrt[]{R_{0}^{2} - 2 h_{1} r_{1}}}{r}$ (7)

r_t为毛坯处于③ 位置时坯料法兰部分的外边缘半径, $\begin{matrix} r_{t} = \sqrt[]{R_{0}^{2} - 2 h_{1} r_{1}} 。 \end{matrix}$ 此时 $\begin{matrix} \frac{R_{0}^{2} - r_{0}^{2}}{2 r_{1}} < h_{1} < \frac{R_{0}^{2} - r_{1}^{2}}{2 r_{1}}, σ_{r} \end{matrix}$ 的最大值仍然在 $\begin{matrix} r_{1} \end{matrix}$ 处.由于③ 位置的坯料已经处于变形的后期, 随着 $\begin{matrix} h_{1} \end{matrix}$ 的增加, $\begin{matrix} {[\frac{1}{4} \ln (1 + \frac{2 h_{1}}{r_{1}}) / (1 - \frac{2 h_{1} r_{1}}{R_{0}^{2}}))]}^{n} \end{matrix}$ 部分的增大趋势相比较 $\begin{matrix} \ln (\sqrt[]{R_{0}^{2} - 2 h_{1} r_{1}} / r) \end{matrix}$ 部分的减小处于劣势, 因此, 主要由 $\begin{matrix} \ln (\sqrt[]{R_{0}^{2} - 2 h_{1} r_{1}} / r) \end{matrix}$ 部分决定 $\begin{matrix} σ_{r} \end{matrix}$ 的大小, 可以认为当 $\begin{matrix} r_{t} = r_{0} \end{matrix}$ 时, $\begin{matrix} r_{1} \end{matrix}$ 处的径向应力取得最大值.此时 $\begin{matrix} h_{1} = (R_{0}^{2} - r_{0}^{2}) / (2 r_{1}), \end{matrix}$ 可得到与式(5)相同的最大径向应力表达式.令 $\begin{matrix} m_{0} = r_{0} / R_{0} 、 m_{1} = r_{1} / r_{0}, \end{matrix}$ 则式(5)化为:

$\begin{matrix} \begin{matrix} \max (σ_{r}) = βK \{\frac{1}{4} \ln [\frac{1}{m_{0}^{2}} (\frac{1}{m_{0}^{2} m_{1}^{2}} + {1 - \frac{1}{m_{1}^{2}})]\}}^{n} \ln \frac{1}{m_{1}} \end{matrix} \end{matrix}$ (8)

由式(8)可以看出:二次拉深时最大径向应力 $\begin{matrix} \max (σ_{r}) \end{matrix}$ 与材料参数K、n、第一次拉深系数m₀ 、第二次拉深系数m₁都有关系.

随着拉深继续进行, r₀处的径向应力 $\begin{matrix} σ_{r} \end{matrix}$ 持续减小, 直到法兰上的坯料被完全拉入杯形直壁部分, 此时 $\begin{matrix} h_{1} = (R_{0}^{2} - r_{1}^{2}) / (2 r_{1}), \end{matrix}$ 进入④ 位置, 此后径向应力恒为0.综上, 可以整理出二次拉深时 $\begin{matrix} r_{1} \end{matrix}$ 处的径向应力 $\begin{matrix} σ_{r_{1}} \end{matrix}$ 随拉深行程 $\begin{matrix} h_{1} \end{matrix}$ 变化的函数关系:

$\begin{matrix} σ_{r_{1}} = \{\begin{matrix} βK {\{\frac{1}{4} \ln [1 + 2 h_{1} (\frac{r_{1}}{r_{0}^{2}} + \frac{1}{r_{1}}) + \frac{4 h_{1}^{2}}{r_{0}^{2}}]\}}^{n} \ln \frac{r_{0}}{r_{1}}, \\ h_{1} < \frac{R_{0}^{2} - r_{0}^{2}}{2 r_{1}} \\ βK {[\frac{1}{4} \ln (\frac{1 + \frac{2 h_{1}}{r_{1}}}{1 - \frac{2 h_{1} r_{1}}{R_{0}^{2}}})]}^{n} \ln \frac{\sqrt[]{R_{0}^{2} - 2 h_{1} r_{1}}}{r_{1}}, \\ \frac{R_{0}^{2} - r_{0}^{2}}{2 r_{1}} \leq h_{1} < \frac{R_{0}^{2} - r_{1}^{2}}{2 r_{1}} \\ 0, h_{1} \geq \frac{R_{0}^{2} - r_{1}^{2}}{2 r_{1}} \end{matrix} \end{matrix}$ (9)

2 凸模拉力和极限拉深系数

法兰变形区的变形抗力是直壁传力区(半径为 $\begin{matrix} r_{1} \end{matrix}$ )拉应力的主要组成部分, 除此之外直壁传力区还包括模具对法兰的摩擦力, 材料绕过模具圆角时的弯曲抗力和摩擦阻力.计算公式如下^[9]:

摩擦力: $\begin{matrix} σ_{m} = \frac{μQ}{π r_{1} t} \end{matrix}$

绕过压边圈圆角的弯曲抗力: $\begin{matrix} σ_{wu} = \frac{σ_{b}}{2 \frac{r_{u}}{t} + 1} \end{matrix}$

绕过凹模圆角的弯曲抗力: $\begin{matrix} σ_{wd} = \frac{σ_{b}}{2 \frac{r_{d}}{t} + 1} \end{matrix}$

式中: $\begin{matrix} t \end{matrix}$ 为板料厚度; $\begin{matrix} σ_{b} \end{matrix}$ 为板料的抗拉强度; $\begin{matrix} r_{u} \end{matrix}$ 为压边圈圆角半径; $\begin{matrix} r_{d} \end{matrix}$ 为凹模圆角半径; $\begin{matrix} μ \end{matrix}$ 为摩擦因数; $\begin{matrix} Q \end{matrix}$ 为压边力.

绕过凹模圆角需要克服圆角区的摩擦阻力, 相当于皮带绕过圆柱^[9].可以整理出直壁传力区处的单位拉应力为:

$\begin{matrix} p = (σ_{r_{1}} + σ_{m} + σ_{wu}) (1 + 1.6 μ) + σ_{wd} \end{matrix}$ (10)

与之对应的凸模拉力为:

$\begin{matrix} F = p \cdot 2 π r_{1} t \end{matrix}$ (11)

通过式(10)可知直壁传力区最大单位拉应力为:

$\begin{matrix} p_{\max} = [\max (σ_{r_{1}}) + σ_{m} + σ_{wu}] (1 + 1.6 μ) + σ_{wd} \end{matrix}$ (12)

板料拉深过程中, 凸模圆角与直壁相切处一般最先出现拉裂现象.此处材料的收缩变形量很小, 可以认为属于平面应变性质, 即 $\begin{matrix} ε_{θ} = 0, ε_{r} = - ε_{t}, \end{matrix}$ 又因为 $\begin{matrix} σ_{t} = 0, \end{matrix}$ 根据塑性应力应变的关系可得 $\begin{matrix} σ_{θ} = \frac{r}{1 + r} σ_{r}, r \end{matrix}$ 为厚向异性系数, 继而可得此处的应力强度为 $\begin{matrix} σ_{i} = \sqrt[]{σ_{r}^{2} - \frac{2 r}{1 + r} σ_{r} σ_{θ} + σ_{θ}^{2}}, \end{matrix}$ 即:

$\begin{matrix} σ_{r} = \frac{1 + r}{\sqrt[]{1 + 2 r}} σ_{i} \end{matrix}$ (13)

根据Swift失稳理论可知, 处于平面应变状态下的材料发生失稳时的极限应变强度为^{[9, 10]}:

$\begin{matrix} ε_{i} = \frac{1 + r}{\sqrt[]{1 + 2 r}} n \end{matrix}$

因为 $\begin{matrix} σ_{i} = K {ε_{i}}^{n}, \end{matrix}$ 代入式(13)可得失稳拉应力为:

$\begin{matrix} σ_{r}^{*} = \frac{1 + r}{\sqrt[]{1 + 2 r}} \cdot K {(\frac{1 + r}{\sqrt[]{1 + 2 r}} n)}^{n} \end{matrix}$ (14)

为了防止拉深过程中出现拉裂现象, 最大单位拉应力 $\begin{matrix} p_{\max} \end{matrix}$ 应小于极限径向拉应力 $\begin{matrix} σ_{r}^{*} 。 \end{matrix}$ 当 $\begin{matrix} p_{\max} = σ_{r}^{*} \end{matrix}$ 时为临界状态, 若已知 $\begin{matrix} m_{0}, \end{matrix}$ 则此时对应的 $\begin{matrix} m_{1} \end{matrix}$ 即为二次拉深时的最小极限拉深系数.

3 有限元拉深模拟的结果对比

为了检验上述计算模型的正确性, 应用有限元分析软件dynaform进行二次拉深的成形模拟.软件模拟相对于实体实验, 在缩短研究周期的同时, 也能得到与实体实验相类似的结果, 是被广泛采用的研究方法.

在二次拉深工步, 需要导入一次拉深后生成的dynain文件作为拉深坯料, 这样即可同步导入一次拉深成形后的半成品杯形件的应力应变状态.

参数设置如下:材料为DQSK37, r=1.653mm, K=520.4MPa, n=0.231 979; R₀=80mm, t=1mm, r₀=50mm, r₁=35mm, μ =0.125, Q=8000N, r_d=6mm, r_u=2mm, σ _b=269.43MPa.将上述参数作为毛坯和模具内壁尺寸设计拉深模具, 一次拉深时凹模圆角设置为 $\begin{matrix} r_{d_{1}} = 10 mm, \end{matrix}$ 两次拉深凸模圆角半径都设置为2 mm, 拉深速度都设置为2000 mm/s, 两次拉深成形模拟后的FLD图如图3和图4所示.从图中可以看出:拉深过程中并未出现拉裂缺陷, 但在杯形件口部都出现了很少的起皱现象, 这是因为在凹模圆角处板料无法被压边圈作用而导致的, 这种微小缺陷无法避免.

图5为二次拉深时的杯形件壁厚分布情况图.从图中可以看出:最小壁厚为0.801 mm, 此处位于二次拉深开始时的凹模圆角位置附近, 最大壁厚为1.399 mm, 位于杯形件的口部起皱处, 即一次拉深开始时的法兰边缘处, 壁厚的变化与模具, 板料, 压边力和拉深速度等都有关系, 通常很难获得准确的解析解.

	Figure Option View Download New Window
	图3 杯形件一次拉深FLDFig.3 Cup-shaped parts first deep drawing FLD

	Figure Option View Download New Window
	图4 杯形件二次拉深FLDFig.4 Cup-shaped parts secondary deep drawing FLD

	Figure Option View Download New Window
	图5 杯形件二次拉深壁厚分布Fig.5 Cup-shaped parts secondary deep drawing thickness distribution

由于板料厚度的变化会使得用本文计算模型计算的极限二次拉深系数偏小.取 $\begin{matrix} β = 1.1, \end{matrix}$ 按照式(11)计算得到的凸模拉力与有限元模拟得到的凸模拉力对比如图6所示.可以看出:通过理论计算和有限元模拟得到的凸模拉力曲线随拉深行程的变化趋势基本相同, 而且最大拉力出现的位置也比较一致, 说明理论模型是正确的.成形后期较为吻合, 但在前期偏差较大, 这是因为理论模型比较理想化, 与拉深模拟不完全一致.最大拉力位置附近产生较大偏差的原因, 是因为一次拉深时杯形件口部有少量起皱和增厚现象, 在此处板料进入压边圈时产生额外的附加作用力导致了凸模拉深力的急剧增大.

	Figure Option View Download New Window
	图6 拉深力计算和模拟对比图Fig.6 Comparison figure of deep drawing force calculation and simulation

重新设计二次拉深, 取阶梯杯形件小端底面半径r'₁=33 mm, 其他参数不变, 二次拉深尚未完成即出现拉裂现象, 如图7所示.

	Figure Option View Download New Window
	图7 杯形件二次拉深失败FLDFig.7 Failure FLD for cup-shaped parts secondary deep drawing

考察各次拉深成形的拉深系数m₀=r₀/R₀=0.625, m₁=r₁/r₀=0.7, m'₁=r'₁/r₀=0.66.在一次拉深 $\begin{matrix} m_{0} = 0.625 \end{matrix}$ 的前提下, 二次拉深 $\begin{matrix} m_{1} = 0.7 \end{matrix}$ 时顺利完成成形, 而 $\begin{matrix} m'_{1} = 0.66 \end{matrix}$ 时无法完成成形, 说明本次拉深成形模拟的极限二次拉深系数介于0.66~0.7, 取平均值0.68.通过本文理论分析计算得到的最小极限二次拉深系数为 $\begin{matrix} m_{1} = 0.616, \end{matrix}$ 理论计算结果与模拟结果的相对误差为9.4%, 说明极限二次拉深系数的理论模型也是比较准确的.出现误差的原因是因为理论分析中忽略了拉深对板料的削弱作用和板料厚度的变化等因素.

4 实验检验

文献^[7]中通过二次拉深成形实验成功拉深出杯形零件, 并未出现破裂等缺陷.通过本文的计算模型可以得到其极限二次拉深系数为0.41, 实验模型中的二次拉深系数为0.78, 满足顺利成形时二次拉深系数大于极限二次拉深系数的要求, 所以顺利完成了拉深成形.本文计算模型的适用性通过实验得到了很好的印证.

5 结束语

通过理论分析方法获得了二次拉深成形时径向拉应力随拉深行程变化的函数关系式, 指出最大径向拉应力出现在由阶梯杯形件过渡到凸缘杯形件时刻的小端直壁处, 并结合Swift失稳理论, 提出了极限二次拉深系数的计算方法, 弥补了二次拉深成形理论研究方面的不足.通过有限元软件进行了二次拉深的成形模拟来检验理论模型的计算准确度.结果显示拉深力的计算值和模拟结果的变化趋势基本相同, 而且最大拉深力出现的位置也比较吻合, 极限二次拉深系数的理论计算值和软件模拟结果也比较一致, 相对误差为9.4%.对文献^[7]的实验数据进行了计算检验, 计算结果表明, 实验模型满足顺利拉深成形时的二次拉深系数要求, 所以可以顺利拉深成形, 本文计算模型的适用性得到实验印证.这说明本文推导的理论模型具有很高的应用价值, 能够适用于二次拉深成形的工程应用和理论解析.本文的研究方法同样可以扩展应用到三次以上的拉深成形中, 只需把每次拉深完成的杯形件(图1中④ 位置)作为一次拉深的成形件(图1中① 位置)即可.

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Zein H, EI Sherbiny M, Abd-Rabou M, et al. Thinning and spring back prediction of sheet metal in the deep drawing process[J]. Materials and Design, 2014, 53: 797-808. [本文引用:1]
[2]	Tamasco C M, Rais-Rohani M, Buijk A. Coupled finite element simulation and optimization of single- and multi-stage sheet-forming processes[J]. Engineering Optimization, 2013, 45(3): 357-373. [本文引用:1]
[3]	Kang B S, Ku T W. Experimental study on multi-stage deep drawing for rectangular cup with high aspect ratio[J]. International Journal for Advanced Manufacturing Technology, 2011, 53(4): 131-143. [本文引用:1]
[4]	Ku T W, Ha B K, Song W J, et al. Finite element analysis of multi-stage deep drawing process for high-precision rectangular case with extreme aspect ratio[J]. Journal of Materials Processing Technology, 2002, 130: 128-134. [本文引用:1]
[5]	Liu P, Ku T W, Kang B S. A study on initial blank design to minimize earing in multi-stage deep drawing process for rectangular cup using high strength steel material[J]. 3rd International Conference on Advances in Materials Manufacturing, 2013, 652: 1971-1975. [本文引用:1]
[6]	Harada Y, Yamamoto A, Goto T, et al. Formability of magnesium-lithium alloy sheet by multi-stage deep drawing[J]. 7th International Conference on Processing and Manufacturing of Advanced Materials, 2012, 706: 1164-1169. [本文引用:1]
[7]	汪超, 胡道春. 基于数值模拟的筒形件多道次拉深工艺与实验研究[J]. 机械设计与制造, 2011(11): 119-121. Wang Chao, Hu Dao-chun. Study on multi-stage drawing process and test of tubular parts based on mumerical simulation[J]. Machinery Design & Manufacture, 2011(11): 119-121. [本文引用:3]
[8]	于鸣, 陆春林, 乔广, 等. 基于数值模拟的筒形件正反拉深复合成形[J]. 吉林大学学报: 工学版, 2009, 39(2): 296-300. Yu Ming, Lu Chun-lin, Qiao Guang, et al. Complex drawing and reverse drawing forming of cylinder part basing on numerical simulation[J]. Journal of Jilin University(Engineering and Technology Edition), 2009, 39(2): 296-300. [本文引用:1]
[9]	胡世光, 陈鹤峥, 李东升, 等. 钣料冷压成形的工程解析[M]. 2版. 北京: 北京航空航天大学出版社, 2009. [本文引用:4]
[10]	Swift H W. Plastic instability under plane stress[J]. Phys Solids, 1952, 1(1): 1-18. [本文引用:1]

2014

0.0

... Zein等^[1]对拉深成形进行了有限元模拟,通过研究凹模圆角半径,凸模圆角半径,摩擦因数,压边力和拉深间隙等因素对回弹和壁厚变薄的影响,得到了可以明显减少回弹和变薄的工艺参数 ...

2013

0.0

... Tamasco等^[2]主要通过有限元法对单次和多次拉深成形进行了全程模拟,通过梯度法进行了工艺参数的优化,效果良好 ...

2011

0.0

... Kang等^[3]对多次拉深矩形杯零件时的影响因素进行了分析,主要进行了中间工步拉深工具形状的分析和修改,修整后可以顺利成形 ...

2002

0.0

... Ku等^[4]应用有限元软件对难成形的深矩形件进行了多次拉深的成形模拟,对影响成形质量的因素进行了分析,并应用实物拉深实验检验了有限元模拟的正确性 ...

2013

0.0

... Liu等^[5]对高强度钢板多次拉深成形矩形杯时的凸耳现象进行了研究,对初始的拉深平板的形状进行了改进,改进后的拉深零件不仅获得了良好的拉深形状,而且也明显节省了材料消耗 ...

2012

0.0

... Harada等^[6]进行了镁合金板在多次拉深成形工艺中成形能力的研究,通过不同的拉深温度进行多次拉深,最后得出了在较低温度下镁合金板可以通过多次拉深提高成形能力的结论 ...

2011

0.0

. 2011, (11):119-121 DOI:doi:10.3969/j.issn.1001-3997.2011.11.047

Study on multi-stage drawing process and test of tubular parts based on mumerical simulation

Wang Chao , Hu Dao-chun.

汪超, 胡道春

摘　要：分析了开水煲外壳零件成形的工艺特点,采用有限元分析软件Dynaform对其多道次拉深成形过程进行了数值模拟。首先确定出该零件合理的拉深系数分配,并在此基础上,选取影响最终成形质量的主要因素压边力、摩擦系数、模具圆角半径等为优化变量,通过正交试验,分析了零件关键位置的最大变薄率及表面质量情况,对上述工艺参数进行了优化。通过实践生产验证,经工艺优化后的成形零件质量得到一定程度的提高,取得了满意的结果。

... 汪超等^[7]对影响多次拉深成形质量的因素进行了分析和优化,应用优化后的工艺参数对开水煲外壳分别进行虚拟和实物拉深实验,实验结果吻合较好 ...

... 4 实验检验文献^[7]中通过二次拉深成形实验成功拉深出杯形零件,并未出现破裂等缺陷 ...

... 对文献^[7]的实验数据进行了计算检验,计算结果表明,实验模型满足顺利拉深成形时的二次拉深系数要求,所以可以顺利拉深成形,本文计算模型的适用性得到实验印证 ...

2009

0.0

. 2009, 39(2):296-300

Complex drawing and reverse drawing forming of cylinder part basing on numerical simulation

基于数值模拟的筒形件正反拉深复合成形

Yu Ming , Lu Chun-lin , Qiao Guang

于鸣, 陆春林, 乔广

摘　要：通过对筒形件正反拉深一次复合成形的有限元数值模拟,分析了主要工艺参数对筒形件正反拉深一次复合成形的影响。依据数值模拟设计了某一型号的机油滤清器壳体正反拉深复合成形模具并进行了工艺调试,既验证了数值模拟的可靠性又将正反拉深一次复合成形工艺用于了机油滤清器壳体的实际生产,获得了较为理想的效果。

... 于鸣等^[8]对筒形件的正反复合拉深成形工艺进行了成形模拟,分析了压边力,压边间隙和摩擦因数等主要工艺参数对正反复合拉深成形质量的影响,对工艺参数进行合理的设置后完成了正反复合成形的模拟,并对模拟结果进行了实物拉深实验检验,效果良好 ...

2009

0.0

... 位置的应力状态,在文献^[9]中已经进行了详细的论述 ...

... 计算公式如下^[9]: ...

... 绕过凹模圆角需要克服圆角区的摩擦阻力,相当于皮带绕过圆柱^[9] ...

... 根据Swift失稳理论可知,处于平面应变状态下的材料发生失稳时的极限应变强度为^[9,10]: ...

1952

0.0

... 根据Swift失稳理论可知,处于平面应变状态下的材料发生失稳时的极限应变强度为^[9,10]: ...