基于滑动窗口的量子秘钥管理算法

引用本文

韩家伟, 刘衍珩, 孙鑫, 宋立军. 基于滑动窗口的量子秘钥管理算法.吉林大学学报:工学版, 2016, 46(2): 535-541
HAN Jia-wei, LIU Yan-heng, SUN Xin, SONG Li-jun. Quantum key management algorithm based on sliding window. Journal of Jilin University Engineering and Technology Edition, 2016, 46(2): 535-541 复制到剪切板

Permissions

基于滑动窗口的量子秘钥管理算法

韩家伟^1,², 刘衍珩¹, 孙鑫³, 宋立军²

1.吉林大学计算机科学与技术学院,长春 130012

2.长春大学量子通信技术实验室,长春 130022

3.吉林大学符号计算与知识工程教育部重点实验室,长春 130012

通讯作者:刘衍珩(1958-),男,教授,博士生导师.研究方向:移动网络,网络安全.E-mail:lyh_lb_lk@hotmail.com

作者简介:韩家伟(1978-),男,博士研究生,副教授.研究方向:网络安全,量子保密通信.E-mail:Jason.hjw@gmail.com

基金:国家自然科学基金项目(61373123,61401413); 吉林省科技发展计划项目(20150414004GH,20140101187JC, 20140101206JC-18); 长春市科技计划项目(2014217)

摘要

针对量子秘钥分发(QKD)技术应用在经典网络加密时量子秘钥管理的问题,提出了一种基于滑动窗口的量子秘钥管理算法(RSQKW).算法首先引入滑动窗口机制控制量子秘钥的消耗;然后通过探测到的量子网络的状态和量子秘钥生成速率协商滑动窗口的控制参数;最后利用量子秘钥本身的随机特性计算滑动窗口的滑动步长,滑动窗口中的量子秘钥序列作为新生成的用于经典加密算法的秘钥.与传统方法相比,该算法能够在应用量子加密到经典网络环境时更好的动态管理量子秘钥.在真实的量子秘钥分发网络中的实验结果证明了该算法的可行性和有效性.

关键词: 计算机应用; 量子密钥分发; 滑动窗口; 秘钥管理; QKD协议

中图分类号:TP393 文献标志码:A 文章编号:1671-5497(2016)02-0535-07

Quantum key management algorithm based on sliding window

HAN Jia-wei^1,², LIU Yan-heng¹, SUN Xin³, SONG Li-jun²

1. College of Computer Science and Technology, Jilin University, Changchun 130012,China

2. Quantum Cryptography Laboratory, Changchun University, Changchun 130022,China

3.Key Laboratory of Symbolic Computation and Knowledge Engineering of Ministry of Education, Jilin University, Changchun 130012,China

Abstract

A Random Sliding Quantum Key Window (RSQKW) management algorithm is proposed in order to handle the problem of applying Quantum Key Distribution (QKD) in classical network encryption. First, a sliding window mechanism is introduced to control quantum key consumption. Then, the algorithm negotiates the control parameters of the sliding window by detecting the status of the quantum communication network and the final quantum key generated rate. Finally, using the stochastic characteristics of the quantum key to calculate the sliding step width, the quantum key series in the sliding window can be used as a new secret key for classical encryption algorithm. Comparing with traditional method, the RSQKW algorithm can better dynamically manage the quantum key and enhance the efficiency and effectiveness of quantum key distribution and management. Experimental results in a real quantum key distribution network demonstrate the feasibility and effectiveness of the proposed algorithm.

Keyword: computer application; quantum key distribution; sliding window; key management; QKD protocol

Show Figures

0 引言

量子保密通信技术是依据量子态的物理特性以及量子物理理论进行加密通信的技术, 是当今世界上公认的可证安全的保密通信技术^[1].量子秘钥管理是量子保密通信技术应用到实际网络环境中的重要研究内容, 量子秘钥对于安全加密传输具有显著优势.与传统秘钥相比, 量子秘钥依赖于量子物理学作为安全模式的关键方面, 而不是数学计算的复杂性."量子态不可克隆定理"保证了量子信道传递的信息不可复制, "海森堡测不准原理"使攻击者在窃听时会破坏传输的信息, 从而及时检测到攻击^[2].因此即使攻击者拥有超强的计算能力或者高效的算法, 也不会对量子秘钥造成威胁.目前, 除了在安全需求极高的各种低带宽网络信道中采用基于比特"一次一密"的方案^{[2, 3, 4]}, 实际的量子网络通常采用量子秘钥分发(Quantum key distribution, QKD)与经典加密算法组合进行加密的方案.例如欧洲的SECOQC网络^[5], 瑞士的SwissQuantum网络^[6], 日本TokyoQKD网络^[7]和中国芜湖量子政务网^[8]等.这些方案一般采用QKD层, 秘钥管理层和应用层的三层结构模型.其中量子秘钥的生成和量子信息传递均由QKD层物理设备在独立的量子链路中实现, 秘钥管理层对已生成的量子秘钥的存储和使用进行管理, 应用层面向具体需要加密的应用.量子秘钥的管理主要可以分为定时更新和定量更新两类.SECOQC等^{[5, 6, 7, 8]}网络采用固定间隔时间为AES和IPSEC-VPN更新秘钥的定时更新方案.Neppach^[9]等人提出改进的量子秘钥交换QIKE方案, 可以更方便快速的定时更新秘钥.Allé aume^[10]等人提出使用量子秘钥和AES算法组合进行加密时, 可采取每加密固定数量数据块后更新一次秘钥的定量更新方案.此外Fujiwara^[11]等人提出将量子秘钥作为哈希函数种子再次生成秘钥, 实现对每个数据包更新秘钥的"一次一密".虽然各项研究对于组合加密的量子秘钥管理提供了比较可行的方案, 但是没有根据量子网络的状态和量子秘钥生成速率等因素的变化动态管理量子秘钥.因此, 本文提出了一种基于滑动窗口机制可动态进行量子秘钥管理的算法(Random sliding quantum key window management algorithm, RSQKW), 算法引入滑动窗口机制, 根据量子网络中量子密钥生成速率及与其相关的QBER等量子网络状态, 协商控制窗口移动速度, 利用量子密钥本身的随机特性控制窗口的随机滑动, 动态管理量子密钥的分发, 实现基于数据块量子加密的"一次一密", 从而充分利用量子加密提高现有网络安全性.

1 问题分析及相关定义

1.1 影响量子密钥生成速率的因素分析

QKD层主要的量子秘钥分发协议有基于量子态的BB84协议, B92协议, 还有基于量子纠缠的EPR协议等^[8].BB84协议是以量子秘钥分发为核心的量子保密通信技术中比较成熟的协议, 也是进入实际应用阶段的量子秘钥分发协议.BB84协议采用两组共轭基, 每个共轭基包含两个互相正交的量子态, 通过四个量子态作为量子信息的载体, 发送者将要传输的光子调制到一种偏振态, 接收者选择相应的测量基来测量接收到的光子的偏振态, 并将其转化成对应的二进制序列.GLLP公式^[12]是对于实际常用的弱相干光源给出的BB84协议安全秘钥率公式.

$\begin{matrix} R \geq q \{- Q_{u} f (E_{u})\} H_{2} (E_{u}) + Q_{1} [1- H_{2} (e_{1})] \end{matrix}$ (1)

式中:q表示对基效率, BB84为50%; Q_u表示平均光子数为u的光脉冲在接收端被探测到的几率; E_u是总的量子误码率; f(E_u)表示纠错效率; Q₁表示发送单光子脉冲且被接收端探测到的几率; e₁表示单光子脉冲引起的误码率.

1.2 随机滑动的量子秘钥窗口的定义

本文提出了RSQKW算法, 引入滑动窗口机制用于量子密钥的分发管理, 重新定义量子秘钥滑动窗口, 通过量子秘钥自身物理特性驱动滑动窗口随机移动, 每次移动后, 生成新的量子秘钥串, 提供给经典加密算法进行加密.

定义1 量子秘钥序列.基于QKD层量子秘钥协议得到的发送方量子秘钥|C_T> ={|s₁s₂, , et al., s_i, et al.s_n> }, (i=1, 2, , et al., n), 二进制序列表示为T={t₁, t₂, , et al., t_i, , et al., t_n}, t_i∈ {0, 1}, (i=1, 2, , et al., n); 接收方量子秘钥|C_R> ={|q₁q₂, et al.q_i, et al.q_n> }, (i=1, 2, , et al., n), 二进制序列表示为R={r₁, r₂, , et al., r_i, , et al., r_n}, r_i∈ {0, 1}, (i=1, 2, , et al., n).T和R分别称为发送方和接收方的量子秘钥序列, 其中n为目前生成的量子秘钥末位的位数.

根据量子网络秘钥分发协议, 若采用共享量子秘钥技术, 发送方和接收方通过量子网络得到相同的量子秘钥, 相应的双方量子秘钥二进制序列也相同, 即R=T.

定义2 量子秘钥滑动窗口.定义发送方量子秘钥滑动窗口W_t={t_i, t_i+₁, t_i+₂, , et al., t_k}, t_i∈ {0, 1}, (i< k< n); 相应的定义接收方量子秘钥滑动窗口W_r={r_i, r_i+₁, r_i+₂, , et al., r_k}, r_i∈ {0, 1}, (i< k< n); 其中有W_t∈ T, W_r∈ R, 且发送窗口与接收窗口等大.

定义3 量子秘钥滑动窗口的大小.采用量子秘钥与经典加密算法组合加密时, 经过发送方和接收方协商, 取经典加密算法所需秘钥长度作为量子秘钥滑动窗口的大小, W_width=k-i+1.

通信双方根据组合加密采用的加密算法的秘钥长度初始化量子秘钥滑动窗口, 一般根据不同的经典加密算法的秘钥长度, 量子秘钥窗口大小为W_width∈ {56, 128, 256, 512, 768, 1024}, 量子秘钥窗口初始化后, 若未更换加密算法则窗口大小W_width不再改变.

定义4 当前量子秘钥.序列T中位于发送窗口范围内的比特组合作为当前加密秘钥Key_cryp={t_i, t_i+₁, t_i+₂, , et al.t_k}, t_i∈ {0, 1}, (i< k< n); 量子秘钥序列R中位于接收窗口范围内的比特组合作为当前解密秘钥Key_dec={r_i, r_i+₁, r_i+₂, , et al.r_k}, r_i∈ {0, 1}, (i< k< n), 且Key_cryp=Key_dec.

量子秘钥滑动窗口的功能是控制量子秘钥的使用速率和再生成用于组合加密的秘钥.滑动窗口中的比特组合即为当前要组合加密的量子秘钥, 因使用BB84或B92等基于共享秘钥的QKD层协议, 所以Key_cryp=Key_dec, 通信双方滑动窗口等大且同步移动.每次滑动窗口移动后, 当前秘钥都会发生改变, 完成一个重新组合生成秘钥, 分发给加密算法使用的过程.

定义5 基于组合加密的"一次一密".通过量子秘钥随机滑动窗口控制分发的量子密钥集为σ ={K₁, K₂, , et al., K_j, , et al., K_m}, (j=1, 2, , et al., m), 通过量子秘钥与AES等经典加密算法组合加密的"一次一密"可表示为:

$\begin{matrix} ρ_{c} = S_{σ} (M) \end{matrix}$ (2)

式中:ρ _c为加密后的密文, S_σ为利用量子秘钥加密的AES等加密算法, M为分组加密的数据块明文.对于每一个数据块进行分组加密时采用不同的量子秘钥, 如公式3所示.

$\begin{matrix} ρ_{cj} = S_{Kj} (M_{j}) \end{matrix}$ (3)

式中:K_j表示每次用于组合加密的秘钥, 在本算法中对应于当前量子秘钥Key_cryp, 由滑动窗口在量子秘钥序列中随机滑动获取.虽存在一定重复比特, 但与现有量子秘钥组合加密方法在秘钥更新周期内使用完全重复的量子秘钥相比, 本算法每次的量子秘钥均由窗口随机滑动重新生成, 对于每个要加密的单位数据块均使用不同的秘钥, 从而进行基于数据块的"一次一密", 实现对现有实用量子加密技术的增强.

1.3 窗口的随机滑动方法

量子秘钥滑动窗口根据收发双方的量子秘钥生成情况进行随机滑动, 随机滑动的步长依赖于量子秘钥本身的随机特性, 通过经典信道与发送方协商用于控制窗口随机移动的步长控制位数η , 窗口中的随机比特组合即为新产生的用于经典算法加密的量子秘钥串.

定义6 窗口随机滑动控制位数η .定义滑动窗口中比特组合的η 位为窗口随机滑动控制位数, 即滑动窗口中量子密钥的前η 位二进制数用于控制每次窗口的滑动.通信双方根据量子密钥分发链路的状态和最终量子密钥的生成速率, 协商η 的值(0< η ≤ log₂W_width).

根据量子链路量子密钥生成速率, 或者影响量子密钥生成速率的QBER等因素, 通信双方可以根据量子链路的状态协商η 值, 从而在一定概率范围内控制量子密钥消耗的速率.当量子密钥生成速率较高时可以取较大的η 值, 窗口以一定的概率较大幅度的移动; 当量子密钥生成速率变低时, 可以取较低的η 值, 窗口以一定的概率较小幅度的移动.

性质1 量子秘钥通过BB84或其他量子秘钥协议生成, 具有随机物理特性, 因此收发双方窗口中的比特位数具有随机性, 并且收发双方一致.通信双方协商确定η 的值后, 即可以同时得到η 位的随机比特组合, 用于计算窗口本轮随机滑动的位数λ .

定义7 滑动窗口的随机移动步长λ , 窗口随机滑动控制位数η 确定后, 在滑动窗口前端取出η 位比特组合, 将其转换为十进制计算得到移动步长λ =[t_i, t_i+₁, t_i+₂, , et al., t_{i+η -}₁]₁₀, 发送窗口和接收窗口同步向前移动λ 位, 称λ 为滑动窗口的随机移动步长.

性质2 由于η 的取值范围为0< η ≤ log₂W_width, 可根据实际量子网络环境进行定义.而λ 是根据η 位的随机比特组合计算的结果, 在η 位的比特全为0时, 视为进位后的结果, 此时λ =2^η, 因此有1≤ λ ≤ 2^η.计算可得λ _min=1和λ _max= $\begin{matrix} 2^{w_{widt h}} \end{matrix}$ , 即窗口以1至 $\begin{matrix} 2^{w_{widt h}} \end{matrix}$ 比特的速度随机向前滑动.

2 基于滑动窗口的量子秘钥管理算法

2.1 算法描述

根据量子秘钥滑动窗口的定义和窗口的随机滑动策略, 在量子网络开始产生秘钥后, 收发双方开始初始化滑动窗口.

RSQKW算法描述如下.

输入:由QKD设备生成的量子秘钥序列T={t₁, t₂, , et al.t_i, , et al., t_n}和R={r₁, r₂, , et al., r_i, , et al., r_n}; 缓冲区中量子秘钥量KEY_BUFFER; 量子秘钥生成速率KEYRATE.

输出:多个新组合生成的秘钥Key_cryp和Key_dec.

算法步骤:

Step 1 发送方和接收方根据采用的组合加密算法的量子秘钥长度, 确定窗口大小W_width;

Step 2 初始化发送方量子秘钥窗口W_t={t_i, t_i+1, t_i+2, , et al., t_k}, i=1, k=W_width;

Step 3 初始化接收方量子秘钥窗口W_r={r_i, r_i+1, r_i+2, , et al., r_k}, i=1, k=W_width;

Step 4 While(KEY_BUFFER≥ 2W_width){

Step 5 从发送窗口中取出量子秘钥Key_cryp={t_i, t_i+1, t_i+2, , et al., t_k};

Step 6 将取出的量子秘钥作为量子组合加密的秘钥, ρ _cj=S_Kj(Μ _j), 消耗量子秘钥;

Step 7 从接收窗口中取出共享量子秘钥Key_dec={r_i, r_i+1, r_i+2, , et al., r_k}, 作为解密秘钥;

Step 8 根据量子秘钥生成速率KEYRATE协商滑动窗口控制位数η ;

Step 9 计算位于滑动窗口中前η 位随机比特组合, 计算本轮窗口滑动步长λ =[t_i, t_i+1, t_i+2, , et al., t_{i+η -1}]₁₀;

Step10 通信双方滑动窗口同步向前移动λ 位.}

量子保密通信开始时, 根据定义3, 确定滑动窗口大小W_width.针对具体量子网络性能确定η 值的协商策略.在量子秘钥缓冲区中的量子秘钥量达到2倍W_width长度时, 随机滑动窗口启动工作.

2.2 量子秘钥管理过程

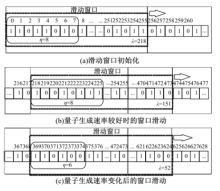
RSQKW算法对量子秘钥串的再生成以及为经典加密算法更新和分发量子秘钥的管理过程是通过动态控制滑动窗口的滑动实现的.由于采用共享量子秘钥的QKD协议, 收发双方已经同步拥有了由QKD物理设备生成的量子秘钥序列, 根据RSQKW算法, 将量子秘钥组合生成W_width位用于提供给传统算法进行消耗的新的秘钥串, 进行分发使用, 具体过程如图1.RSQKW算法首先初始化发送窗口和接收窗口, 发送方和接收方确定使用量子秘钥和AES-256组合进行加密后, 根据定义3确定窗口大小W_width的值为256, 通信双方根据量子秘钥生成速率KEYRATE的变化情况, 协商滑动窗口控制位数η , 量子秘钥滑动窗口开始同步滑动.

	Figure Option View Download New Window
	图1 随机滑动的量子秘钥滑动窗口Fig.1 Random sliding quantum key window

根据共享秘钥量子通信协议的特点, 发送方和接收方共享的量子秘钥是依据量子的物理特性生成的随机比特组合, 因此在协商得到η 后, 即可根据定义7计算每次窗口随机移动的步长λ .如图1(a), 协商确定η =8, 窗口中左侧8位的比特组合为11011010, 可计算λ =218, 即发送窗口和接收窗口同步向前滑动218位, 窗口大小W_width的值为256保持不变.每次窗口滑动后窗口范围内新的W_width位比特组合即为新生成的用于分发给经典加算法进行加密消耗的量子秘钥.发送方得到本轮加密秘钥Key_cryp, 接收方相应得到解密秘钥Key_dec, 发送方将新组合的秘钥Key_cryp分发给AES等经典加密算法完成本轮数据块的加密, 接收方使用相应的解密秘钥Key_dec进行解密, 完成一轮组合量子秘钥的生成, 分发和消耗的管理过程.图1(b)中所示在量子网络状态比较平稳, 量子秘钥生成速率稳定的情况下, 通信双方协商后的η 仍为8, 但是λ =(10010111)₁₀=151, 双方的量子秘钥滑动窗口均向前滑动151位; 而在量子网络状态受到影响, 量子秘钥生成速率降低时, 图1(c)中再次协商后的η 降为6, λ =(110100)₁₀₌52, 在η =6时, 根据性质2, 窗口移动λ 的最大值为64, 与η =8时移动λ 最大为256相比, 减小了每轮加密使用新鲜量子秘钥的数量规模, 相当于增加了量子秘钥的数量, 在量子网络状态不稳定, 量子秘钥生成速率低时可以有效地保障量子加密安全顺利地进行.

3 实验与分析

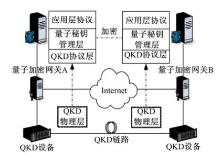
为验证随机滑动的量子秘钥滑动窗口RSQKW算法的可行性和有效性, 搭建了实际的量子秘钥管理网络实验环境, 如图2所示.发送方和接收方在量子加密网关上进行基于随机滑动窗口的量子秘钥分发管理, 在实验中采用AES-256作为组合加密的算法进行测试, 每次加密数据块大小为64字节, 量子组合加密网关系统采用机架嵌入式网络开发设备, 配置为至强P2865, 4 G内存, 1T硬盘, RSQKW算法在Centos6.5系统中通过C语言编程实现.QKD层的量子秘钥生成设备采用Quantum-CTEK QGW-A型设备, 设备的基本参数为:工作频率40 MHz, 信号光波长1550.12 nm, 信号光脉宽200, 探测器暗计数≤ 5× 10^-6.量子秘钥分发链路传输距离为10 km, 采用1550 nm单模光纤, 光路衰减为11.8 dB.

	Figure Option View Download New Window
	图2 RSQKW量子秘钥管理实验网络Fig.2 RSQKW quantum key management experimental network

本文进行了两个实验, 分别用于验证RSQKW算法的有效性和比较RSQKW算法与现有的量子秘钥管理方案在反映量子链路状态的QBER参数改变时, 量子秘钥的消耗情况.

3.1 η 对量子秘钥窗口滑动的影响

首先, 在实际量子网络环境中采用随机滑动量子秘钥滑动窗口算法RSQKW进行实验, 记录了5000次随机滑动的结果, 在本轮实验中, 量子秘钥与AES-256组合加密, 实验参数如表1.其中KEYRATE为当前时段量子秘钥生成速率, $\begin{matrix} \bar{r} \end{matrix}$ 为多轮实验统计的平均量子秘钥生成速率, 实验中滑动控制位数η 是以KEYRATE的变化与 $\begin{matrix} \bar{r} \end{matrix}$ 的关系作为协商依据.

表1 随机滑动量子秘钥管理算法RSQKW实验参数 Table 1 Random sliding quantum key window algorithm experiment parameters

KEYRATE与 $\begin{matrix} \bar{r} \end{matrix}$ 的关系	滑动控制位数η /bit	随机滑动步长λ /bit	量子秘钥倍增倍数
KEYRATE/ $\begin{matrix} \bar{r} \end{matrix}$ ≥ 1	8	1~256	2⁰~2⁸
KEYRATE/ $\begin{matrix} \bar{r} \end{matrix}$ ∈ [0.9, 1)	7	1~128	2¹~2⁸
KEYRATE/ $\begin{matrix} \bar{r} \end{matrix}$ ∈ [0.8, 0.9)	6	1~64	2²~2⁸
KEYRATE/ $\begin{matrix} \bar{r} \end{matrix}$ ∈ [0.7, 0.8)	5	1~32	2³~2⁸
KEYRATE/ $\begin{matrix} \bar{r} \end{matrix}$ ∈ [0.6, 0.7)	4	1~16	2⁴~2⁸
KEYRATE/ $\begin{matrix} \bar{r} \end{matrix}$ < 0.6	4	1~16	2⁴~2⁸

表1 随机滑动量子秘钥管理算法RSQKW实验参数 Table 1 Random sliding quantum key window algorithm experiment parameters

如图3所示, 在量子秘钥生成速率接近或高于统计平均速率 $\begin{matrix} \bar{r} \end{matrix}$ 时, 协商的η 的值较高, 从而随机计算出的量子秘钥分发窗口滑动步长λ 较大.

	Figure Option View Download New Window
	图3 随机滑动窗口滑动步长与滑动控制位Fig.3 Random sliding quantum key window step width and sliding control bits

	Figure Option View Download New Window
	图4 QBER对量子秘钥消耗算法的影响Fig.4 Effect of QBER on quantum key consumption rate

滑动步长λ 利用量子秘钥自身的随机特性以概率P_i=1/2^η随机分布, 此时量子秘钥消耗速度较快.当量子秘钥生成速率KEYRATE降低时, 协商得到的η 的值较低, 并且滑动速度降低, 量子秘钥消耗速度同时降低, 秘钥倍增倍数增加.通过实验验证RSQKW算法可以有效根据量子秘钥生成情况, 控制随机窗口滑动速度, 从而实现量子秘钥分发性能与网络传输的动态匹配.

3.2 QBER对量子秘钥消耗速率的影响

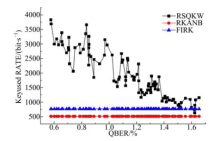
接下来的实验通过将RSQKW算法与文献^{[5, 6, 7, 8, 9]}定时更新量子秘钥方案和文献^[10]中加密固定数量数据块后更新量子秘钥的方案进行比较, 验证了RSQKW算法的动态量子秘钥管理符合量子网络中QBER等状态的变化.如图4所示, 图形FIRK表示定时更新量子秘钥方案, 图形RKANB表示按照加密数据量更新量子秘钥方案.在确定了更新秘钥的时间间隔或者使用相同秘钥加密的数据块个数后, 量子秘钥的消耗速率不根据QBER以及量子秘钥产生速率等量子网络的状态进行变化.在量子秘钥分发过程中, 由于量子网络距离, 灰尘污染和强光以及各节点插入等外界情况的变化对量子链路状态有一定影响, 这些因素都会最终反映在QBER值的变化上, 间接影响量子秘钥生成速率.现有更新量子秘钥的方案, 不能够根据量子网络状态进行动态调整, 因此导致在量子秘钥生成速率较高时, 量子秘钥利用率很低, 没有充分利用量子秘钥的安全性进行"一次一密"; 而在传输距离较远, 量子链路衰减较大, 量子秘钥生成率较低的环境中, 因消耗量子秘钥速率不能动态调整又容易出现量子秘钥严重不足影响通信的情况.而RSQKW算法根据量子秘钥生成速率动态调节量子秘钥分发速度, 在量子链路的QBER值较低时, 量子链路状态较好, 此时量子秘钥生成速率较高, 而RSQKW算法通过滑动窗口的控制机制, 动态调节量子秘钥的消耗速率, 量子秘钥的消耗速率相应升高, 在量子秘钥充足时量子秘钥利用率较高; 在量子链路状态QBER值较大时, 量子秘钥生成速率较低, 而RSQKW算法通过协商滑动窗口的η 值, 控制了量子秘钥的总体消耗速率, 确保能够有充足的量子秘钥进行后续的"一次一密".在通过窗口滑动控制位数η 的值控制量子秘钥消耗速率时, 通过缩小窗口滑动步长λ 的值的范围, 从而整体上降低窗口滑动速度, 控制量子秘钥消耗速率, 增大量子秘钥倍增的倍数.根据性质2, 当η =4时, λ _min=1, λ _max=16, W_width=256, 每次随机滑动量子秘钥窗口以P_i=1/16的概率确定λ 的值, 即使每次λ 值都为16, 仍需16次能完全滑出窗口, 即放大倍数为最小16倍, 最大是每次滑动λ 值均为1, 则需要256次完全滑出, 放大倍数为256倍.若采用定时更新秘钥方案, 量子秘钥的消耗与量子链路的状态以及网络负载无关, 若在秘钥更换周期内无数据传送也会将未用的秘钥进行更新, 浪费量子秘钥.若采用加密一定数量数据块更新一次量子秘钥的方法, 不根据量子链路状态进行调整, 在网络流量较小的时候, 会出现长时间使用同一秘钥加密的情况, 导致安全风险增加.RSQKW算法根据量子链路状态动态的调整量子秘钥消耗速率, 与现有的方案相比能够更好地适应量子秘钥与经典算法组合加密的网络环境, 实现基于数据块的量子加密传输"一次一密".

3.3 安全性的分析与比较

根据文献^[10]使用量子秘钥与AES组合加密时, 若使用秘钥长度为keylength的同一量子秘钥加密的数据块数量小于2^keylength, 可以实现组合加密的安全性, 数据块的定量越少, 安全性越高.RSQKW算法每1个数据块发送的会话中都使用随机滑动生成的一个量子秘钥, 实现了基于数据块会话的"一次一密".与现有的定时更新秘钥和定量更新秘钥在更新周期内使用完全相同的秘钥对数据进行加密相比有着更高的安全性.

采用RSQKW算法在整个通信过程中, 收发双方不传输任何量子秘钥信息, 确保通过量子链路分发的秘钥安全性, 收发双方通过协商量子秘钥滑动窗口的滑动控制位η 的值, 而后通过利用对称量子秘钥的绝对随机性, 双方分别计算窗口滑动的位数λ , 驱动窗口同步滑动, 每次滑动即生成1个新的256位秘钥, 提供给AES等算法进行加密, 每次会话中均使用新的256位比特组合作为新秘钥进行加密, 实现了基于组合加密的"一次一密".虽然每一次产生的秘钥中有部分比特组合属于原有秘钥, 但是由于窗口随机滑动后, 位置已经随机地进行了改变, 因此与原来在秘钥更换周期内多次使用同一秘钥进行加密的方法相比具有更好的安全性和实用性.

实验证明通过随机滑动量子秘钥窗口管理量子秘钥的方法, 可以更充分地利用量子秘钥进行加密, 提高量子秘钥利用率, 增强加密传输的安全性.并且通过与AES等传统加密算法结合的方式, 可以在兼顾网络吞吐率的情况下, 提高量子秘钥加密的安全性, 与经典量子秘钥组合加密方案相比较, 适合在实际的量子组合加密网络环境中应用.并且可以将RSQKW算法很好地与IPSEC-VPN, SSL-VPN等多种VPN技术结合, 通过IKE等技术进行量子秘钥管理, 将基于滑动窗口的量子秘钥管理机制应用到VPN网络中, 有效地提高了实际量子加密网络的安全性.

4 结束语

给出了一种基于随机滑动窗口的量子秘钥管理算法, 根据量子网络中的状态协商滑动窗口中的控制位的大小η , 利用量子的物理特性生成的量子秘钥具有很好的随机性, 算法通过滑动控制位中的随机比特组合计算得到每次随机滑动的步长λ , 量子秘钥滑动窗口中每次滑动后得到的比特组合作为与AES等传统加密算法组合加密的秘钥.结果表明, 算法在实际量子网络中, 能够根据量子秘钥的生成速率以及QBER等状态, 动态管理量子秘钥, 实现量子组合加密的"一次一密", 充分利用了量子秘钥加密的安全性, 实现量子秘钥加密与网络传输的性能匹配, 极大地提高了量子加密技术的实用性和现有网络的安全性.

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	吴华, 赵于康, 赵勇, 等. 实用化光纤量子加密电话网络和高速数据传输系统----现场应用与安全管理[J]. 中国科学: 信息科学, 2014, 44(3): 312-321. Wu Hua, Zhao Yu-kang, Zhao Yong, et al. Field application and security management of a telephone network and a high speed data transmission system with practical fiber quantum cryptography[J]. Scien-tia Sinica Informationis, 2014, 44(3): 312-321. [本文引用:1]
[2]	Fröhlich B, Dynes J F, Lucamarini M, et al. A quantum access network[J]. Nature, 2013, 501(7465): 69-72. [本文引用:2]
[3]	刘晓慧, 裴昌幸, 聂敏. 量子无线通信网络构建及性能分析[J]. 吉林大学学报: 工学版, 2014, 44(4): 1177-1181. Liu Xiao-hui, Pei Chang-xing, Nie Min. Quantum wireless communication network model and performance analysis[J]. Journal of Jilin University (Eng-ineering and Technology Edition), 2014, 44(4): 1177-1181. [本文引用:1]
[4]	Wang Qing-le, Gao Fei, Liu Bin, et al. Anonymous quantum communications using the quantum one-time pad[J]. Physica Scripta, 2015, 90(0151021): 1-6. [本文引用:1]
[5]	Peev M, Dynes J F, Fasel S, et al. The SECOQC quantum key distribution network in Vienna[J]. New Journal of Physics, 2009, 11(7): 75001-75037. [本文引用:3]
[6]	Stucki D, Legre M, Buntschu F, et al. Long-term performance of the Swiss quantum quantum key distribution network in a field environment[J]. New Journal of Physics, 2011, 13: 123001-123018. [本文引用:3]
[7]	Sasaki M, Fujiwara M, Ishizuka H, et al. Field test of quantum key distribution in the Tokyo QKD Net-work[J]. Optics Express, 2011, 19(11): 10387-10409. [本文引用:3]
[8]	吴华, 王向斌, 潘建伟. 量子通信现状与展望[J]. 中国科学: 信息科学, 2014, 44(3): 296-311. Wu Hua, Wang Xiang-bin, Pan Jian-wei. Quantum communication: status and prospects[J]. Scientia Sinica Informationis 2014, 44(3): 296-311. [本文引用:4]
[9]	Neppach A, Pfaffel-Janser C, Wimberger I, et al. Key management of quantum generated keys in IPsec[C]//Proceedings of the International Conference on Security and Cryptography, Porto, Portugal, 2008: 177-183. [本文引用:2]
[10]	Alléaume R, Branciard C, Bouda J, et al. Using quantum key distribution for cryptographic purposes: A survey[J]. Theoretical Computer Science, 2014, 560: 62-81. [本文引用:3]
[11]	Fujiwara M, Domeki T, Moriai S, et al. Highly secure network switches with quantum key distribution systems[J]. International Journal of Network Security, 2015, 17(1): 34-39. [本文引用:1]
[12]	Gottesman D, Lo H K, Lutkenhaus N, et al. Security of quantum key distribution with imperfect devices[J]. Quantum Information & Computation, 2004, 4(5): 325-360. [本文引用:1]

2014

0.0

. 2014, 44(3):312-321 DOI:10.1360/N112013-00168

Field application and security management of a telephone network and a high speed data transmission system with practical fiber quantum cryptography

实用化光纤量子加密电话网络和高速数据传输系统----现场应用与安全管理

Wu Hua , Zhao Yu-kang , Zhao Yong

吴华, 赵于康, 赵勇

1 The School of Public Affairs, University of Science and Technology of China, Hefei 230026, China; 2 Hefei National Laboratory for Physical Science at Microscale and Department of Modern Physics, University of Science and Technology of China, Hefei 230026, China; 3 Reseach Center for Quantum Technology and Application, Chinese Academy of Science, Jinan 250101, China; 4 Shandong Institute of Quantum Science & Technology Co., Ltd., Jinan 250101, China

To show how the introduction of quantum communication technology to traditional communication system can meet the demand of field application and security management, we explained in detail the design of a fiber quantum communication system, taking a telephone network and a high speed data transmission system as an example, both were encrypted with quantum cipher and were built on field fiber recently. The procedure of implement and long term operation result of this system were also briefly introduced. It has been veri ed that this system possessed good reliability and usability, while meeting the functional demand for various types of communication and high level security of critical events. We also made some proposals for introducing quantum communication system to public management.

本文以如何应用量子通信技术满足现场应用和安全管理需求为出发点，以国内最近完成的一个在现场光纤网络上搭建的多节点量子加密电话网络和高速数据传输系统为实例，具体分析了为满足现场应用和安全管理的需求，实用化光纤量子通信系统所采用设计方案，并简单介绍了该系统实施和长期运行情况. 该系统满足了重要事务对于不同应用形式及高安全等级通信的需求，并验证了实际应用环境下的可靠性和易用性，具有很好的代表性. 本文也对量子通信系统应用于公共管理提出了建议.

... 0 引言量子保密通信技术是依据量子态的物理特性以及量子物理理论进行加密通信的技术,是当今世界上公认的可证安全的保密通信技术^[1] ...

2013

0.0

... "量子态不可克隆定理"保证了量子信道传递的信息不可复制,"海森堡测不准原理"使攻击者在窃听时会破坏传输的信息,从而及时检测到攻击^[2] ...

... 目前,除了在安全需求极高的各种低带宽网络信道中采用基于比特"一次一密"的方案^[2,3,4],实际的量子网络通常采用量子秘钥分发(Quantum key distribution,QKD)与经典加密算法组合进行加密的方案 ...

2014

0.0

. 2014, 44(4):1177-1181 DOI:doi:10.13229/j.cnki.jdxbgxb201404042

Quantum wireless communication network model and performance analysis

量子无线通信网络构建及性能分析

Liu Xiao-hui , Pei Chang-xing , Nie Min.

刘晓慧, 裴昌幸, 聂敏

A quantum routing scheme is proposed to teleport a quantum state from one quantum device to another wirelessly, even though the two devices do not share EPR pairs mutually. The scheme is based on entanglement swapping and quantum teleportation. The model of quantum wireless communication network and correlative communication protocol is presented. In order to be compatible with the conventional wireless communication network, the network architecture of a two-tier database structure is proposed. In terms of qubit transmission time and security, performance analysis results show that the proposed scheme is superior to quantum relay routing scheme. The proposed scheme has high scalability and practicability.

提出了一种新的量子路由方案, 即使两个移动节点不共用EPR纠缠对, 仍可实现这两个移动节点之间的量子态无线远程传输。该量子路由方案可以被用来构建量子无线通信网络, 同时提出了相应的通信协议。为了实现与现有的经典无线通信网络的融合, 方案采用了两层数据库的量子无线通信网络结构。分析表明, 在量子信息传输时间和安全性两方面, 性能优于量子中继路由方案, 具有很高的可扩展性和实用价值。

2015

0.0

2009

0.0

... 例如欧洲的SECOQC网络^[5],瑞士的SwissQuantum网络^[6],日本TokyoQKD网络^[7]和中国芜湖量子政务网^[8]等 ...

... SECOQC等^[5,6,7,8]网络采用固定间隔时间为AES和IPSEC-VPN更新秘钥的定时更新方案 ...

... 2 QBER对量子秘钥消耗速率的影响接下来的实验通过将RSQKW算法与文献^[5,6,7,8,9]定时更新量子秘钥方案和文献^[10]中加密固定数量数据块后更新量子秘钥的方案进行比较,验证了RSQKW算法的动态量子秘钥管理符合量子网络中QBER等状态的变化 ...

2011

0.0

... 例如欧洲的SECOQC网络^[5],瑞士的SwissQuantum网络^[6],日本TokyoQKD网络^[7]和中国芜湖量子政务网^[8]等 ...

... SECOQC等^[5,6,7,8]网络采用固定间隔时间为AES和IPSEC-VPN更新秘钥的定时更新方案 ...

2011

0.0

... 例如欧洲的SECOQC网络^[5],瑞士的SwissQuantum网络^[6],日本TokyoQKD网络^[7]和中国芜湖量子政务网^[8]等 ...

... SECOQC等^[5,6,7,8]网络采用固定间隔时间为AES和IPSEC-VPN更新秘钥的定时更新方案 ...

2014

0.0

. 2014, 44(3):296-311 DOI:10.1360/N112013-00120

Quantum communication: status and prospects

量子通信现状与展望

Wu Hua , Wang Xiang-bin , Pan Jian-wei.

吴华, 王向斌, 潘建伟

1 School of Public Affairs, University of Science and Technology of China, Hefei 230026, China; 2 State Key Laboratory of Low-Dimensional Quantum Physics，Department of Physics, Tsinghua University, Beijing 100084, China; 3 Synergetic Innovation Center of Quantum Information and Quantum Physics, University of Science and Technology of China, Hefei 230026, China; 4 Jinan Institute of Quantum Technology, Jinan 250101, China

The paper overviews the fundamental principles, methods, technologies and applications of quantum communication. It introduces the basic protocol of secure quantum private communication, including the decoy method, quantum communication based on the entanglement distribution, quantum teleportation, manipulation of entangled photonspairs in polarization space. This review introduces recent status in quantum technology and applications, and attempts to discuss future directions in which the field is likely to develop.

本文综述量子通信基本原理、方法、技术手段与应用. 介绍量子保密通信基本协议和诱骗态方法，以及基于纠缠分发的量子通信，含基于纠缠光子对的量子保密通信、量子态隐性传输、纠缠光子对操控等. 介绍量子通信的技术与应用现状并对未来发展方向做展望.

... 例如欧洲的SECOQC网络^[5],瑞士的SwissQuantum网络^[6],日本TokyoQKD网络^[7]和中国芜湖量子政务网^[8]等 ...

... SECOQC等^[5,6,7,8]网络采用固定间隔时间为AES和IPSEC-VPN更新秘钥的定时更新方案 ...

... 1 影响量子密钥生成速率的因素分析QKD层主要的量子秘钥分发协议有基于量子态的BB84协议,B92协议,还有基于量子纠缠的EPR协议等^[8] ...

2008

0.0

... Neppach^[9]等人提出改进的量子秘钥交换QIKE方案,可以更方便快速的定时更新秘钥 ...

2014

0.0

... aume^[10]等人提出使用量子秘钥和AES算法组合进行加密时,可采取每加密固定数量数据块后更新一次秘钥的定量更新方案 ...

... 3 安全性的分析与比较根据文献^[10]使用量子秘钥与AES组合加密时,若使用秘钥长度为keylength的同一量子秘钥加密的数据块数量小于2^keylength,可以实现组合加密的安全性,数据块的定量越少,安全性越高 ...

2015

0.0

... 此外Fujiwara^[11]等人提出将量子秘钥作为哈希函数种子再次生成秘钥,实现对每个数据包更新秘钥的"一次一密" ...

2004

0.0

... GLLP公式^[12]是对于实际常用的弱相干光源给出的BB84协议安全秘钥率公式 ...