基于快速SIFT算法和模糊控制的人脸识别

引用本文

聂海涛, 龙科慧, 马军, 张雷, 马喜强. 基于快速SIFT算法和模糊控制的人脸识别.吉林大学学报:工学版, 2016, 46(2): 549-555
NIE Hai-tao, LONG Ke-hui, MA Jun, ZHANG Lei, MA Xi-qiang. Face recognition based on fast scale invariant feature transform algorithm and fuzzy control. Journal of Jilin University Engineering and Technology Edition, 2016, 46(2): 549-555 复制到剪切板

Permissions

基于快速SIFT算法和模糊控制的人脸识别

聂海涛^1,², 龙科慧¹, 马军¹, 张雷¹, 马喜强³

1.中国科学院长春光学精密机械与物理研究所, 长春130033

2.中国科学院大学, 北京 100039

3.河南科技大学河南省机械设计及传动系统重点实验室,河南洛阳 471003

通讯作者:龙科慧(1958-),女,研究员,博士生导师.研究方向:航天相机调焦系统.E-mail:long_kh@163.com

作者简介:聂海涛(1986-),男,博士研究生.研究方向:图像处理.E-mail:kelek2@126.com

基金:中科院长春光机所创新基金项目(Y2CX1SS125)

摘要

针对传统的人脸识别系统在复杂背景情况下不能实时准确进行人脸识别的问题,提出一种基于快速尺度不变特征变换(SIFT)算法结合模糊控制的人脸识别方法.首先,由SIFT特征点子区域方向直方图计算得到4个新角度,代表特征点方向信息.然后,在特征匹配阶段,根据SIFT特征点角度信息以及大小限制特征点匹配范围,简化算法复杂程度,得到快速SIFT算法.最后,引入闭环模糊控制系统,减少SIFT特征误匹配,提高人脸识别率.实验结果表明:基于快速SIFT算法的人脸识别方法平均识别时间提升了40%,在发生光照,姿态,表情等均有变化的复杂环境下人脸识别精度提高10%.

关键词: 计算机应用; 人脸识别; SIFT算法; 特征匹配; 模糊控制

中图分类号:TP391 文献标志码:A 文章编号:1671-5497(2016)02-0549-07

Face recognition based on fast scale invariant feature transform algorithm and fuzzy control

NIE Hai-tao^1,², LONG Ke-hui¹, MA Jun¹, ZHANG Lei¹, MA Xi-qiang³

1.Changchun Institute of Optics, Fine Mechanics and Physics, University of Chinese Academy of Science ,Changchun 130033,China

2. University of Chinese Academy of Sciences, Beijing 100039, China

3. He'nan Key Lab for Machinery Design & Transmission System, He'nan University of Technology and Science, Luoyang 471003, China

Abstract

Most traditional face recognition systems can not be implemented for fast and accurate face recognition under cluttered background. To solve this problem, an improved Scale Invariant Feature Transform (SIFT) method and a fuzzy control strategy are proposed. First, four new angles are computed from the sub-region orientation histogram, which represent the orientation information of each SIFT feature. Then, the progress of face recognition is limited in a range based on the new angles, meanwhile the SIFT features are split into two types according to the size; only the features of the same type are computed, leading to significant simplification of the algorithm, thus a fast SIFT algorithm is obtained. Finally, a fuzzy closed loop control system is applied to increase the accuracy of face recognition, which leads to a decrement of the incorrect matching. The results show that the computing speed of the improved SIFT method is raised more than 40% comparing with the original SIFT algorithm and the recognition rate is raised 10% even under the clutter conditions where the illumination, posture or expression are changing.

Keyword: computer application; face recognition; SIFT algorithm; feature matching; fuzzy control

Show Figures

0 引言

在过去的二十年间人脸识别技术取得了显着进步, 涌现出许多经典的人脸识别算法.麻省理工学院的Turk和Pentland^[1]在1991年提出了基于主成分分析(Principal component analysis, PCA)算法的"本征脸"(Eigenface)人脸识别方法, 成为FERET人脸库性能测试的基准算法, 它通过计算人脸图像的协方差矩阵获取其特征向量和特征值, 然后根据特征值从大到小选择一定数量的能代表人脸特征的主要分量, 舍弃次要分量, 从而实现了人脸图像降维和特征提取.Belhumeur等^[2]提出了基于线性判别分析(Linear discriminant analysis, LDA)算法的Fisherface人脸识别方法, 获得尽量大的类间离散度和尽量小的类内离散度, 有效提高了所提取特征的鉴别性能.在此基础上, Comon^[3]提出了基于独立成分分析(Independent component analysis, ICA)算法的人脸识别方法, 去除了二阶相关, 同时最大限度地去除了高阶相关, 某些情况下在FERET人脸库上取得了比PCA更好的识别效果.以上3种典型算法可以归纳为基于全局的人脸识别方法, 这类方法旨在将整个人脸区域作为系统输入并派生出一个显着的特征子空间, 用以分析不同人脸图像之间的相似性.但是当欲识别人脸在图像中发生局部遮挡, 旋转, 尺度变化以及光照变化等复杂背景干扰时, 这类算法鲁棒性降低, 人脸识别效果无法满足实际应用的要求.与此相对, 基于局部特征的人脸识别方法提取人脸局部区域特征并构建人脸特征描述符, 所提取的特征具有尺度, 旋转及照度不变特性, 对噪声干扰和局部遮挡具有较好的稳定性.典型的基于局部特征的人脸识别方法有:Gabor特征人脸识别方法^[4], Gabor特征能够获取人脸图像不同朝向与不同尺度的描述, 但Gabor特征的获得需要将图像与一组不同方向不同尺度的Gabor核进行卷积, 计算量庞大; 基于局部二值模式(Local binary pattern, LBP)算法的人脸识别方法^[5], 是一种有效的非参数化的图像局部纹理描述算法, LBP运算方法简单快速, 但是在发生较强非均匀光照噪声干扰下识别准确率降低.2004年, Lowe^[6]提出了尺度不变特性变换(Scale invariant feature transform, SIFT)算法, SIFT算法提取的特征点不仅对人脸图像缩放, 平移和旋转具有一定的不变性, 而且对光照变化以及仿射和投影具有鲁棒性, 复杂背景下基于SIFT算法的人脸识别方法应用前景广泛, 但是由于SIFT算法计算程度复杂, 使其很难满足人脸识别系统的实时性要求.

本文提出一种基于快速SIFT算法和模糊控制的人脸识别方法.① 扩展了人脸局部特征点:由SIFT特征点子区域方向直方图计算得到4个新角度, 代表特征点方向信息; ② 快速SIFT特征匹配:根据SIFT特征点角度信息以及大小限制特征点匹配范围, 简化算法复杂程度, 得到快速SIFT算法; ③ 引入闭环模糊控制系统:在快速SIFT算法基础上, 减少误匹配, 有效提高了复杂背景下的人脸识别精度.

1 SIFT算法

1999年Lowe首次提出了SIFT算法, 在此基础上于2004年完善总结.生成SIFT算子主要分为3个步骤:首先建立图像尺度空间并寻找极值点, 然后由图像局部特征计算特征点方向信息, 最终得到对尺度和方向无关的SIFT特征描述算子.

在SIFT特征点提取阶段, 建立尺度空间并从中寻找极值点.尺度空间 $\begin{matrix} L (x, y, σ) \end{matrix}$ 通过图像 $\begin{matrix} I (x, y) \end{matrix}$ 和高斯核卷积 $\begin{matrix} G \end{matrix}$ 得到, 为了提取稳定的具有尺度无关性的特征点, 提出高斯差分空间DoG(Different of Gaussian)检测局部极值点.DoG算子定义如下:

$\begin{matrix} \begin{matrix} D (x, y, σ) = \\ [G (x, y, kσ) - G (x, y, σ)] \times I (x, y) = \\ L (x, y, kσ) - L (x, y, σ) \end{matrix} \end{matrix}$ (1)

式中: $\begin{matrix} G (x, y, σ) = \frac{1}{2 π σ^{2}} e^{\frac{- (x^{2} + y^{2})}{2 σ^{2}}}; (x, y) \end{matrix}$ 为空间坐标; $\begin{matrix} σ \end{matrix}$ 为尺度空间因子.

在Lowe的算法中, 中间的检测点与它同尺度的8个相邻点和上下相邻尺度对应的9× 2个点共26个点比较, 以确保在尺度空间和二维图像空间都检测到极值点.如果一个点在DoG尺度空间本层以及上下两层的26个领域中是最大或最小值时, 就认为该点是图像在该尺度下的一个特征点.

传统SIFT算法利用图像的局部特征给SIFT特征点分配基准方向, 使SIFT描述符具有旋转不变性.使用图像梯度信息求取局部结构的稳定方向, 在高斯差分金字塔中检测出特征点, 采集其所在高斯金字塔图像3σ 邻域窗口内像素的梯度和方向分布特征.在完成特征点的梯度计算后, 使用直方图统计邻域内像素的梯度和方向.梯度直方图的范围是0° ~360° , 每10° 一个柱, 共36个柱, 方向直方图的峰值方向作为该特征点的方向, 一个特征点可能会被指定多个方向增强匹配的鲁棒性.最终建立特征点的特征描述符, 使用在特征点尺度空间内4× 4的窗口中计算8个方向的梯度信息, 共4× 4× 8=128维向量表征, 由此对每一个SIFT特征点构建一个128维的描述符.此时, SIFT特征向量已经去除了尺度, 旋转和几何变形因素的影响, 将这个向量归一化, 就可进一步去除光照的影响.

2 快速SIFT算法

传统SIFT算法的主要不足是高维数的SIFT特征描述符, 导致算法实时性较差.为此, 本文提出一种快速SIFT算法, 基于数学方法, 主要从SIFT特征点大小及角度两方面属性分类匹配提高算法速度.

2.1 分类SIFT特征点

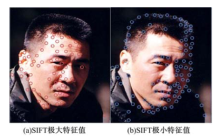
SIFT算法在图像尺度空间中寻找极值点, 文献^[7]统计大量图像, 提出一副图像中提取的SIFT极大特征值点与极小特征值点数目基本相等, 并且正确匹配的特征点全部来自同一类型的SIFT极值点.因此, 将提取的SIFT特征点分成极大特征值点组与极小特征值点组两组.在特征匹配阶段, 只将同一类型的特征点进行匹配, 这样, 在不损失正确匹配特征点的前提下, 有效提高了算法速度.图1为同一人脸图像提取的SIFT极大特征值点与极小特征值点.

	Figure Option View Download New Window
	图1 同一幅人脸图像提取的极大特征值点与极小特征值点Fig.1 The maxima and minima SIFT features extracted from the same facial image

2.2 扩展SIFT特征点角度

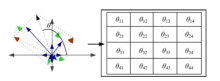
本节通过扩展SIFT特征点角度属性, 简化算法的计算复杂程度.由SIFT特征点子区域方向直方图计算得到4个两两相互独立的新角度, 依据角度信息限制匹配范围, 避免了比较大量的始终无法匹配的SIFT特征点, 能够有效提升算法速度, 具体方法如下:将特征点周围图像区域分成矩形小块的子区域, 为每一个子区域建立方向直方图, 根据梯度信息计算SIFT特征点角度^[8].计算特征点子区域内所有梯度方向的向量和, 将其与水平轴之间的夹角 $\begin{matrix} θ \end{matrix}$ 分配给对应的子区域, 假设由这一角度信息代表SIFT特征描述符的方向属性.在一个4× 4的窗口区域内计算得到16个角度, 如图2所示.

	Figure Option View Download New Window
	图2 由子区域直方图计算得到的角度Fig.2 Angles computed from sub orientation histogram

为了保证SIFT特征描述符具有旋转不变性, 所求得角度 $\begin{matrix} θ_{ij} \end{matrix}$ 必须满足两个条件:① 每一个角度平均分布在角度空间[-180° , +180° ]范围内; ② 这些角度两两相互独立.

首先, 检验角度θ _ij 是否满足均匀分布条件.角度{θ _ij; i, j=1, , et al., 4}由式(2)计算得到:

$\begin{matrix} θ_{ij} = \arctan (\frac{\overset{7}{\sum_{k = 0}} ma g_{ij} (k) \sin (or i_{ij} (k))}{\overset{7}{\sum_{k = 0}} ma g_{ij} (k) \cos (or i_{ij} (k))}) \end{matrix}$ (2)

式中:mag_ij (k)和ori_ij (k)分别为j^th 子区域直方图的k^th分量梯度的幅值和方向.

定义角度θ _ij 为随机变量Θ _ij^[9] .从800幅测试图像提取约10⁶个SIFT特征点估算每个角度的概率密度函数.将角度空间区域[-180° , +180° ]分为36子区域, 每10° 为一个子区域, 通过计算每个子区域的角度为 $\begin{matrix} θ_{ij} \end{matrix}$ 的SIFT特征点数目, 可以得到变量 $\begin{matrix} Θ_{ij} \end{matrix}$ 的概率密度函数.计算结果显示, 特征点中心附近的子区域角度集中分布在0° 附近; 而特征点边缘的子区域角度则在[-180° , +180° ]角度空间区域内呈现均匀分布.这一结果的主要原因为:一方面, 子区域方向直方图是在计算方向直方图的图像区域旋转后计算得出的, 因此, 每个中心子区域方向直方图的峰值角度方向趋于0° ; 另一方面, 对每个子区域方向直方图来说, 峰值角度方向和所有角度矢量和方位是相关的, 峰值角度方向是计算角度矢量和方向的主要影响因素.与此相反, 边界子区域方向直方图和方向直方图并不共享相同的梯度数据, 因此只有边界角度满足均匀分布条件.

然后, 验证所提出的角度θ _ij 是否满足两两相互独立条件, 采用皮尔逊积矩相关系数法^[10] 度量每两个角度之间的相关性.假设两个随机变量X, Y, 其期望值和方差分别为μ _x , μ _y , σ _x 及σ _y, 则这两个变量的皮尔逊积矩相关系数为:

$\begin{matrix} ρ_{xy} = E [(X - μ_{x}) (Y - μ_{y})] / σ_{x} σ_{y} \end{matrix}$ (3)

式中: $\begin{matrix} E [\cdot] \end{matrix}$ 为期望值算子.

每两个角度 $\begin{matrix} α 、 β \end{matrix}$ 之间的相关系数是由所测试图像中提取的10⁶个SIFT特征点计算得出的, 计算公式如下:

$\begin{matrix} ρ_{αβ} = 10^{6} \frac{\overset{10^{6}}{\sum_{i = 1}} [(α_{i} - μ_{α}) (β_{i} - μ_{β})]}{\sqrt[]{\overset{10^{6}}{\sum_{i = 1}} (α_{i} - μ_{α})^{2}} \sqrt[]{\overset{10^{6}}{\sum_{i = 1}} (β_{i} - μ_{β})^{2}}} \end{matrix}$ (4)

计算结果显示, 由相邻的子区域方向直方图计算得到的角度是高度相关的; 而由非邻近子区域方向直方图计算得到的角度没有或只有很低的相关性.造成这一结果的原因是由于梯度样本在相邻子区域方向直方图中的三线性插值导致的, 每一个样本梯度以1~d的权重加到每个子区域方向直方图中, 其中d为从相应子区域的中心到样本的距离.因此, 在16个角度中, 最多且只有4个角度能满足两两相互独立条件.

最终选定4个角度ϕ ₁=θ ₁₁, ϕ ₂=θ ₁₄, ϕ ₃=θ ₄₁ 及ϕ ₄=θ ₄₄作为扩展的SIFT特征点角度, 代表SIFT特征描述符方向属性.

2.3 快速SIFT算法

应用SIFT方法进行人脸识别, 实际上就是一个匹配原人脸图像特征点与欲识别图像特征点的过程.在所有可能的匹配特征之间, 只存在一定数量的正确匹配, 根据特征点角度属性对SIFT特征点进行分类, 只对两个角度差小于一个指定阈值的特征点进行比较, 避免比较所有可能的匹配特征点, 可有效简化算法计算的复杂程度.

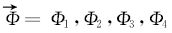
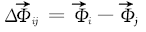
SIFT特征点的4个角度组成一个4维随机角度向量 , 对特征点之间每一个可能的特征匹配, 构造一个随机向量差:

(5)

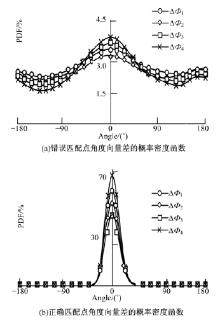
由此得到2个SIFT特征点之间的4个随机向量差 $\begin{matrix} {\vec{Δ Φ_{11}}, \vec{Δ Φ_{22}}, \vec{Δ Φ_{33}}, \vec{Δ Φ_{44}}} 。 \end{matrix}$

对2.2节800幅图像进行测试实验, 分别得到正确匹配和错误匹配的向量差 $\begin{matrix} Δ {\vec{Φ}}_{ij} \end{matrix}$ 的概率密度函数(PDF), 如图3所示.

	Figure Option View Download New Window
	图3 向量差概率密度函数Fig.3 Probability density function of angles difference

向量差根据匹配结果表现出不同的特性:错误的匹配时两个相关角度是独立的, 因此呈现均匀分布; 而正确的匹配的特征点具有相同的SIFT特征描述符, 向量差的概率密度函数集中在一个趋于的小范围附近.测试实验结果显示, 95%的正确匹配特征点的分布在[-36° , +36° ]⁴范围内, 而只有15%的错误匹配特征点分布在这一区间.因为可能的匹配是平均分布在4维的角度空间[-180° , +180° ]⁴中, 则在[-36° , +36° ]⁴范围内可能匹配概率等于(72/360)⁴× 100%.因此, 特征匹配阶段, SIFT特征点被存储在4维表格中, 每个单元格的SIFT特征点仅与特定单元格的特征点进行比较, 要求所选取的匹配特征点之间必须存在一个小于预设阈值36° 的角度向量差.这种方法有效简化了原SIFT算法的计算复杂程度, 保证了算法的实时性.

3 基于模糊控制的人脸识别优化策略

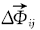
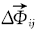
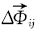
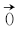
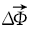
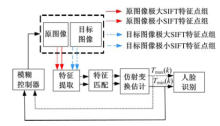
在应用快速SIFT算法进行人脸识别时, 当人脸发生光照, 姿态, 表情均有变化的复杂环境下, 误匹配数量增加, 识别准确率降低.为此, 在快速SIFT算法基础上, 提出基于扩展SIFT特征点的闭环模糊控制系统, 如图4所示.

	Figure Option View Download New Window
	图4 闭环模糊控制人脸识别系统Fig.4 Proposed fuzzy closed loop face recognition system

依据2.1节对SIFT特征点大小分类, 原人脸图像提取的特征点集合 $\begin{matrix} G F^{model} \end{matrix}$ 和目标人脸图像提取的特征点集合 $\begin{matrix} G F^{query} \end{matrix}$ 被分为两组子集:

$\begin{matrix} \{\begin{matrix} G F^{model} = G F_{\min}^{model} ⋃ G F_{\max}^{model} \\ G F^{query} = G F_{\min}^{query} ⋃ G F_{\max}^{query} \end{matrix} \end{matrix}$ (6)

SIFT特征匹配时只比较相同类型的特征点子集, 因此, 得到两组独立的正确匹配:

$\begin{matrix} \{\begin{matrix} G M_{\min} = match (G F_{\min}^{model}, G F_{m in}^{query}) \\ G M_{\max} = match (G F_{\max}^{model}, G F_{\max}^{query}) \end{matrix} \end{matrix}$ (7)

应用随机抽样一致算法(RANSAC)^[11], 估算这两组正确匹配之间的仿射变换:

$\begin{matrix} \{\begin{matrix} T_{\min} = RANSAC (G F_{\min}) \\ T_{\max} = RANSAC (G F_{\max}) \end{matrix} \end{matrix}$ (8)

根据两个仿射变换进行误匹配监测, 所估算的两组仿射变换均受到人脸在欲识别图像中产生噪声的干扰影响, 仿射变换之间的差异 $\begin{matrix} Dis (T_{1}, T_{2}) \end{matrix}$ 反映了输出匹配的好坏程度.

估算仿射变换矩阵需要两张图像之间至少3对非线性的匹配点, 为了计算两个仿射变换T₁ 和T₂, 假设p₁ (a, a), p₂ (a, -a), p₃ (-a, a)是xy坐标系内3个非线性点坐标, 这里a是一个随机值, 每一个变换后的点通过对应的仿射变换映射:

$\begin{matrix} \{\begin{matrix} P_{i}^{1} = T_{1} \cdot p_{1} \\ P_{i}^{2} = T_{2} \cdot p_{1} \end{matrix} \end{matrix}$ (9)

式中: $\begin{matrix} i = 1, 2, 3 。 \end{matrix}$

图像之间的差异 $\begin{matrix} Dis (T_{1}, T_{2}) \end{matrix}$ 由下面公式计算:

$\begin{matrix} Dis (T_{1}, T_{2}) = \frac{1}{3} \overset{3}{\sum_{i = 1}} (d (p_{i}^{1}, p_{i}^{2})) \end{matrix}$ (10)

式中:d(p₁, p₂)为两个点p₁ (x₁, y₁)和p₂ (x₂, y₂)之间的欧氏距离.

$\begin{matrix} d (p_{1}, p_{2}) = \sqrt[]{(x_{1} - x_{2}) + (y_{1} - y_{2})} \end{matrix}$ (11)

仿射变换之间的差异被用作一个指示匹配质量的参数.人脸识别系统难以建立精确数学模型, 因此, 结合模糊控制系统增强匹配的稳定性.将每一个仿射变换与单位矩阵的差异传递给模糊控制器, 用于改进匹配结果.模糊控制器的任务是选择最佳的变换, 并由此改进原图像, 用于下一次匹配过程.本文采用基于Mamdani模型的模糊控制方法^[12], Mamdani方法具有模糊理论处理复杂对象的优势, 不过度依赖于被控对象的精确数学模型, 对非线性不确定系统有较好的控制效果, 自适应能力强.Mamdani模糊控制规则如下:

$\begin{matrix} \begin{matrix} R^{i} : IF x_{1} is A_{1}^{i} ADN x_{2} is A_{2}^{i} \dots ADN x_{j} is A_{j}^{i} \\ THEN y^{i} = H^{i} \end{matrix} \end{matrix}$ (12)

式中:x_j 为第j个输入变量, j=1, 2, 3, , et al., k; A_jⁱ 为x_j 采用的模糊子集; yⁱ 为第i条规则对应的局域输出; Hⁱ 为yⁱ采用的模糊子集.

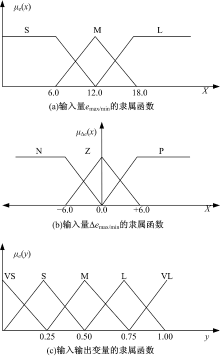
采用Mamdani模糊控制器时, 本文选取由式(10)计算的变换矩阵与单位矩阵之间的差异e_max/min和差异变化率Δ e_max/min作为模糊规则输入变量:

$\begin{matrix} \begin{matrix} e_{\max / \min} = Dis (T_{\max / \min}, I) \\ Δ e_{\max / \min} = e_{\max / \min} (k - 1) - e_{\max / \min} (k) \end{matrix} \end{matrix}$ (13)

式中: $\begin{matrix} I \end{matrix}$ 为单位变换矩阵:

$\begin{matrix} I = [\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \end{matrix}] \end{matrix}$ (14)

模糊规则中输出 $\begin{matrix} β \end{matrix}$ 定义为一个[0, 1]范围内的固定的质量指数, 代表估计仿射变换的正确性.

采用三角模型函数实现模糊化, 对于e_max/min和Δ e_max/min输入语言变量分别设置为{S(小), M(中), L(大)}和{Z(零), N(负), P(正)}, 输出语言变量设置为{VS(极小), S(小), M(中), L(大), VL(极大)}, 则输入和输出变量的隶属函数如图5所示.根据对2.2节统计的800幅测试图像进行处理, 总结得到较为合理的模糊规则控制表, 如表1所示.最后进行逆模糊化, 采用质心方法.寻找一个点, 这个点所在的垂直线能够将隶属函数分割成相等的两部分, 计算得到重力质心 $\begin{matrix} \bar{x} = 0.62 。 \end{matrix}$

基于模糊控制系统的人脸识别方法有效地增加了识别过程中正确匹配特征点数量, 提高了人脸识别在复杂背景下的抗干扰能力.

	Figure Option View Download New Window
	图5 输入输出变量的隶属函数Fig.5 Input and output membership function

表1 模糊控制规则表 Table 1 Fuzzy-expert rules in linguistic form

4 实验结果

4.1 快速SIFT算法与原SIFT算法比较实验

为了比较快速SIFT算法与原SIFT算法, 本文在CUHK Face Sketch database(CUFS)^[13]人脸画像库中进行SIFT特征点匹配实验.CUFS数据库主要用于原人脸图像与人脸素描图像的分析与识别, 由3部分组成:Chinese University of Hong Kong(CUHK)student database的188组人脸图像, AR database的123组人脸图像的和XM2VTS database的295组人脸图像, 共606组人脸图像.每一张人脸图像对应一张人脸正面姿势, 正常光照条件, 中性表情下的素描人脸图像.图6为3组CUFS数据库人脸图像.

	Figure Option View Download New Window
	图6 CUFS人脸数据库Fig.6 Examples of face photos and sketches from CUFS

分别应用快速SIFT算法与原SIFT算法进行人脸特征点匹配实验, 快速SIFT算法应用VC++语言编写, 通过Visual Studio 2012软件编译.实验计算机配置为:Intel Core2 CPU, 2.6 GHz, 2 G内存.表2为快速SIFT算法与原SIFT算法匹配时间比较.实验结果表明, 快速算法速度平均提升40%.

表2 快速SIFT算法与原SIFT算法人脸特征点匹配时间比较 Table 2 Comparison of feature matching speed for fast SIFT algorithm and original SIFT algorithm

4.2 基于快速SIFT算法和模糊控制的人脸识别实验

应用快速SIFT算法结合模糊控制方法在Georgia Tech face database^[14](GT)数据库上进行人脸识别实验, 库中有50人共750幅图像, 包括姿态, 表情, 光照, 采集时间等变化, 是一个相对复杂的人脸库.实验选取每人一幅共50幅图像作为采集样本, 剩余的700幅图像作为测试样本, 图7为GT人脸数据库正确匹配样本.

	Figure Option View Download New Window
	图7 GT人脸数据库正确匹配样本Fig.7 Correct matching sample in GT face database

实验结果表明, 快速SIFT算法结合模糊控制的人脸识别方法识别率较原SIFT算法平均提高了10%, 表3为识别率结果.

表3 改进方法与原SIFT方法用于GT人脸库的人脸识别率 Table 3 Comparison of recognition rate for improved method and original SIFT method in GT face database

5 结束语

提出了一种快速SIFT算法结合模糊控制的人脸识别方法, 根据SIFT特征点大小以及角度将特征点扩展分类, 简化了算法计算复杂程度, 提高了算法运算速度.引入闭环模糊控制系统, 有效减少了误匹配, 增强了人脸识别精度.实验结果表明, 改进方法与原SIFT算法相比, 算法速度平均提升40%, 人脸识别精度提升10%, 保证了在复杂背景下的人脸识别的效率和精度.

该方法还需要在以下几个方面进行改进:① 所提出的快速SIFT算法主要基于数学方法简化其计算复杂程度, 下一步工作将结合图形处理器设计人脸识别系统, 以达到更快速的人脸识别要求.② 应用模糊控制系统实现摄像机标定, 进一步提高人脸识别系统精度.

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Turk M A, Pentland A P. Face recognition using eigenfaces[C]//Proc IEEE Conf Computer Vision and Pattern Recognition, Maui, HI, 1991: 586-591. [本文引用:1]
[2]	Belhumeur P N, Hespanha J P, Kriegman D J. Eigenfaces vs. Fisherfaces: recognition using class specific linear projection[J]. IEEE Trans. Pattern Analysis and Machine Intelligence, 1997, 19(7): 711-720. [本文引用:1]
[3]	Comon P. Independent component analysis-a new concept[J]. Signal Processing, 1994, 36(2): 287-314. [本文引用:1]
[4]	聂海涛, 龙科慧, 马军, 等. 采用改进尺度不变特征变换在多变背景下实现快速目标识别[J]. 光学精密工程, 2015, 23(8): 2349-2356. Nie Hai-tao, Long Ke-hui, Ma Jun, et al. Fast object recognition under multiple varying background using improved SIFT method[J]. Optics and Precision Engineering, 2015, 23(8): 2349-2356. [本文引用:1]
[5]	Ahonen T, Hadid A, Pietikainen M. Face description with local binary patterns: application to face recognition[J]. IEEE Trans Pattern Analysis and Machine Intelligence, 2006, 28(12): 2037-2041. [本文引用:1]
[6]	Lowe D. Distinctive image features from scale-invariant keypoints, cascade filtering approach[J]. International Journal of Computer Vision, 2004, 60(2): 91-110. [本文引用:1]
[7]	聂海涛. 基于图像局部特征的康复机器人目标识别方法研究[D]. 北京: 中国科学院大学, 2015. Nie Hai-tao. Study of rehabilitative robtics object recognition method based on local image feature[D]. Beijing: University of Chinese Academy of Sciences, 2015. [本文引用:1]
[8]	Dalal N, Triggs B. Histograms of oriented gradients for human detection[C]//IEEE Computer Society Conference on Computer Society, San Diego, USA, 2005: 886-893. [本文引用:1]
[9]	Sabdi A, Hashemi H, Nader E S. On the PDF of the sum of rand om vectors[J]. IEEE Transaction on Communications, 2000, 48(1): 7-12. [本文引用:1]
[10]	Xu W T, Hung Y S, Niranjan M, et al. Asymptotic mean and variance of Gini correlation for Bivariate normal samples[J]. IEEE Transaction on Signal Processing, 2010, 58(2): 522-534. [本文引用:1]
[11]	Pappis C P, Mamdani Ehrahim H. A fuzzy logic controller for a trafc junction[J]. IEEE Transaction on Systems, Man and Cybernetics, 1977, 7(10): 707-717. [本文引用:1]
[12]	Chum O, Matas J. Optimal rand omized RANSAC[J]. IEEE Transaction on Pattern Analysis and Machine Intelligence, 2008, 30(8): 1472-1482. [本文引用:1]
[13]	Wang X, Tang X. Face photo-sketch synthesis and recognition[J]. Trans Pattern Analysis and Machine Intelligence, 2009, 31(11): 1955-1967. [本文引用:1]
[14]	Georgia Tech face database[DB/OL]. [2014-04-22]. http://www.anefian.com/research/face_reco.htm. [本文引用:1]

1991

0.0

... 麻省理工学院的Turk和Pentland^[1]在1991年提出了基于主成分分析(Principal component analysis,PCA)算法的"本征脸"(Eigenface)人脸识别方法,成为FERET人脸库性能测试的基准算法,它通过计算人脸图像的协方差矩阵获取其特征向量和特征值,然后根据特征值从大到小选择一定数量的能代表人脸特征的主要分量,舍弃次要分量,从而实现了人脸图像降维和特征提取 ...

1997

0.0

... Belhumeur等^[2]提出了基于线性判别分析(Linear discriminant analysis,LDA)算法的Fisherface人脸识别方法,获得尽量大的类间离散度和尽量小的类内离散度,有效提高了所提取特征的鉴别性能 ...

1994

0.0

... 在此基础上,Comon^[3]提出了基于独立成分分析(Independent component analysis,ICA)算法的人脸识别方法,去除了二阶相关,同时最大限度地去除了高阶相关,某些情况下在FERET人脸库上取得了比PCA更好的识别效果 ...

2015

0.0

. 2015, 23(8):2349-2356 DOI:doi:10.3788/OPE.20152308.2349

Fast object recognition under multiple varying background using improved SIFT method

采用改进尺度不变特征变换在多变背景下实现快速目标识别

Nie Hai-tao , Long Ke-hui , Ma Jun

聂海涛, 龙科慧, 马军

提出一种改进的尺度不变特征变换(SIFT)算法,用于实现多变背景下的快速目标识别。首先,构建目标图像尺度空间,提取SIFT特征点并将其按大小分类,目标识别时只需比较同一类型的特征点。然后,由SIFT特征点子区域方向直方图计算得到4个新角度用于代表特征点的方向信息,并且在目标识别时根据角度信息限制特征点匹配范围,从而提高SIFT算法的运算速度。最后,计算目标图像和待识别图像之间的尺度因子,在尺度因子约束条件下进行目标特征点匹配,从而有效地保证正确匹配数量,提高目标识别的鲁棒性。实验结果表明:当目标在待识别图像中发生局部遮挡、旋转、尺度变化或者弱光照等情况下,改进的SIFT算法能够完成多变背景下快速目标识别任务,平均识别速度提升了40%。

... 典型的基于局部特征的人脸识别方法有:Gabor特征人脸识别方法^[4],Gabor特征能够获取人脸图像不同朝向与不同尺度的描述,但Gabor特征的获得需要将图像与一组不同方向不同尺度的Gabor核进行卷积,计算量庞大 ...

2006

0.0

... 基于局部二值模式(Local binary pattern,LBP)算法的人脸识别方法^[5],是一种有效的非参数化的图像局部纹理描述算法,LBP运算方法简单快速,但是在发生较强非均匀光照噪声干扰下识别准确率降低 ...

2004

0.0

... 2004年,Lowe^[6]提出了尺度不变特性变换(Scale invariant feature transform,SIFT)算法,SIFT算法提取的特征点不仅对人脸图像缩放,平移和旋转具有一定的不变性,而且对光照变化以及仿射和投影具有鲁棒性,复杂背景下基于SIFT算法的人脸识别方法应用前景广泛,但是由于SIFT算法计算程度复杂,使其很难满足人脸识别系统的实时性要求 ...

2015

0.0

. 2015, :-

Study of rehabilitative robtics object recognition method based on local image feature[D].

基于图像局部特征的康复机器人目标识别方法研究[D]

Nie Hai-tao.

聂海涛

康复机器人通过视觉系统感知外部环境,将视觉信息反馈给控制系统,实现康复机器人导航定位以及机械手臂对任务目标的识别和操控,以辅助残疾人完成日常生活中的各种行为功能。康复机器人目标识别方法研究是实现机器人感知外部环境以及机器人操控的关键问题。目标特征提取与匹配是目标识别中的关键技术。提取对视角、尺度、旋转和光照具不变性的图像局部特征,对于复杂背景下目标识别的最终效果有着决定性的影响。同时,图像局部特征提取准确度直接影响康复机器人摄像机标定以及视觉系统对任务目标的姿态估计。针对康复机器人用户对象是残疾人,康复机器人目标识别的另一个主要工作是视觉系统对用户人脸信息的识别。本文根据康复机器人FRIENDⅢ研制需求,围绕基于图像局部特征的康复机器人目标识别方法关键问题展开研究,论文的主要研究工作如下:1研究了康复机器人目标识别的主要任务。概述了机器人视觉目标识别方法的关键问题。对比了基于全局信息和基于局部特征的目标识别图像处理算法,依次分析了典型的目标特征提取方法,特征描述符构建以及图像特征匹配策略。2提出了基于快速SIFT算法的目标识别方法。SIFT算法存在的主要不足是高维数的SIFT特征描述符计算复杂,造成算法实时性较差。为简化算法计算复杂程度,同时保证不损失正确匹配特征,首先构建目标图像尺度空间,提取SIFT特征点时将其按大小分类,然后扩展SIFT角度属性,由SIFT 特征点子区域方向直方图计算得到4个新角度,代表特征点方向信息,最后在特征匹配时,根据SIFT特征点角度信息以及大小来限制特征点匹配范围,简化算法复杂程度,得到快速SIFT算法。实验结果表明,应用快速SIFT算法有效提高了特征匹配效率。3为了实现复杂背景下目标识别的稳定性,在快速SIFT算法基础上,提出了基于图像尺度因子的SIFT特征匹配方法。康复机器人FRIENDⅢ的视觉系统主要任务之一在视觉传感器发生视角变化、目标局部遮挡、旋转、以及光照变化等复杂背景下进行目标识别,但是复杂背景下能够获取的SIFT特征点数目减少,识别准确率降低。通过计算目标图像和待识别图像之间的尺度因子,在尺度因子约束条件下进行目标特征匹配,有效的保证了正确匹配数量,同时将最近邻和次近邻特征点距离限定在一个特定范围查询,减小其比值,有效地恢复被错误排除的正确匹配,保证了复杂背景下目标识别的准确率。4提出了一个基于扩展SIFT特征点的闭环模糊控制方法。分别提取原目标图像与待识别目标图像的极大特征值点与极小特征值点,进行SIFT特征点匹配,将每一个仿射变换与单位矩阵的差异传递给模糊控制器,用于改进匹配结果。应用Mamdani模糊控制器,采用三角模型函数和梯形模型实现模糊化,通过康复机器人目标识别实验分析,构建合理的模糊规则表,采用质心逆模糊化方法,最终实现基于扩展 SIFT特征点的闭环模糊控制目标识别优化策略。5进行了康复机器人视觉系统目标姿态估计与摄像机标定研究。在闭环模糊控制策略的基础上,对机器人目标图像进行目标姿态估计实验,通过实验数据从图像信息中获取三维空间物体几何信息,通过计算摄像机成像几何模型参数实现康复机器人视觉系统摄像机标定。研究了基于图像的康复机器人视觉伺服方法。6提出了Adaboost算法与改进SIFT方法融合的机器人用户人脸信息识别方法。康复机器人FRIENDⅢ的视觉伺服系统需要实时采集用户人脸信息,通过基于Haar-like人脸特征的Adaboost机器学习算法进行人脸检测,再通过改进SIFT算法提取人脸局部特征,实现在光照、表情、姿态发生变化情况下的人脸识别。采用SIFT算法进行人脸识别不需要对人脸图像规范化,也不需要训练样本,同时改进SIFT算法,从速度和鲁棒性方面优化算法,满足视觉系统对用户人脸识别的要求。

... 1 分类SIFT特征点SIFT算法在图像尺度空间中寻找极值点,文献^[7]统计大量图像,提出一副图像中提取的SIFT极大特征值点与极小特征值点数目基本相等,并且正确匹配的特征点全部来自同一类型的SIFT极值点 ...

2005

0.0

... 由SIFT特征点子区域方向直方图计算得到4个两两相互独立的新角度,依据角度信息限制匹配范围,避免了比较大量的始终无法匹配的SIFT特征点,能够有效提升算法速度,具体方法如下:将特征点周围图像区域分成矩形小块的子区域,为每一个子区域建立方向直方图,根据梯度信息计算SIFT特征点角度^[8] ...

2000

0.0

... _ij^[9] ...

2010

0.0

... _ij 是否满足两两相互独立条件,采用皮尔逊积矩相关系数法^[10] 度量每两个角度之间的相关性 ...

1977

0.0

... 应用随机抽样一致算法(RANSAC)^[11],估算这两组正确匹配之间的仿射变换: ...

2008

0.0

... 本文采用基于Mamdani模型的模糊控制方法^[12],Mamdani方法具有模糊理论处理复杂对象的优势,不过度依赖于被控对象的精确数学模型,对非线性不确定系统有较好的控制效果,自适应能力强 ...

2009

0.0

... 1 快速SIFT算法与原SIFT算法比较实验为了比较快速SIFT算法与原SIFT算法,本文在CUHK Face Sketch database(CUFS)^[13]人脸画像库中进行SIFT特征点匹配实验 ...

2014

0.0

... 2 基于快速SIFT算法和模糊控制的人脸识别实验应用快速SIFT算法结合模糊控制方法在Georgia Tech face database^[14](GT)数据库上进行人脸识别实验,库中有50人共750幅图像,包括姿态,表情,光照,采集时间等变化,是一个相对复杂的人脸库 ...