基于云群的高维差分进化算法及其在网络安全态势预测上的应用

引用本文

胡冠宇, 乔佩利. 基于云群的高维差分进化算法及其在网络安全态势预测上的应用.吉林大学学报:工学版, 2016, 46(2): 568-577
HU Guan-yu, QIAO Pei-li. High dimensional differential evolutionary algorithm based on cloud population for network security prediction. Journal of Jilin University Engineering and Technology Edition, 2016, 46(2): 568-577 复制到剪切板

Permissions

基于云群的高维差分进化算法及其在网络安全态势预测上的应用

胡冠宇, 乔佩利

哈尔滨理工大学计算机科学与技术学院,哈尔滨 150080

通讯作者:乔佩利(1951-),男,教授,博士生导师.研究方向:智能计算,网络安全.E-mail:qiaopeili2014@163.com

作者简介:胡冠宇(1982-),男,博士研究生,讲师.研究方向:智能计算,网络安全.E-mail:huguanyu0708@163.com

基金:国家自然科学基金项目(61103149); 黑龙江省自然科学基金项目(QC2013C060)

摘要

提出了一种基于云群的高维差分进化算法(CPDE),并将其应用在网络安全态势预测领域.该算法所提出的云群和分布链概念增加了种群的多样性.算法中的入侵算子将获胜个体的分布植入给其他个体,使得在进化的过程中,个体的形态呈现多样性.协作算子在个体之间引入了合作机制并执行差分操作.局部搜索算子增加了算法的搜索精度.实验结果显示CPDE是一个有效的高维进化算法,它在优化网络安全态势预测模型中具有一定的优势.

关键词: 计算机应用技术; 差分进化算法; 云模型; 云群; 分布链; 网络安全态势预测

中图分类号:TP18 文献标志码:A 文章编号:1671-5497(2016)02-0568-10

High dimensional differential evolutionary algorithm based on cloud population for network security prediction

HU Guan-yu, QIAO Pei-li

School of Computer Science and Technology, Harbin University of Science and Technology, Harbin 150080, China

Abstract

A novel differential evolutionary algorithm based on could population (CPDE) is proposed to solve the network security situation prediction. The proposed concepts of cloud population and the distribution chain promote the diversity of the population. In this algorithm, first, the intrusion operator is employed to introduce the competition among the cloud populations, where the winners will implant their distribution into other cloud individuals. Then, cooperative operator is used to introduce the collaboration among the cloud individuals and perform the differential operation. Finally, the accuracy of the algorithm is improved using the local search operator. Experiment results show that the proposed CPDE is an efficient high-dimensional evolutionary algorithm and possesses certain advantages in optimizing the prediction model of the network security.

Keyword: computer application technology; differential evolutionary algorithm; cloud model; cloud population; distribution chain; network security situation prediction

Show Figures

0 引言

目前, 业界已经提出了很多改进的进化算法用于解决高维优化问题^{[1, 2, 3]}.文献^{[4, 5, 6]}利用云模型提出了一些新的进化算法, 例如Zhang等^[4]在2008年提出了基于云模型的进化算法(CBEA), 该算法利用正态云生成器生成种群, 并定义最优个体向量, 以最优向量中的个体为种子生成新的种群, 越优良的个体生成的种群越大.Dai等^[5]在2007年引入了基于云模型的遗传算法CGA, CGA采用正态云模型中的Y条件正态云发生器完成交叉操作.Dai等^[6]在2007年提出了云自适应遗传算法(CAGA).该算法以条件云发生器自适应调整交叉变异概率.以上这些算法都利用了云模型在统计学和模糊数学上的特点, 对传统的进化算法进行了改进, 得到了良好的效果, 为进化算法开辟了新的思路.但是这些算法在高维优化问题中容易陷入局部最优解.本文借鉴云模型提出了一种新的进化算法--基于云群的高维差分进化算法(以下简称CPDE).所提算法在高维优化中表现良好.该算法把利用云模型^[7]生成的小规模种群当做云个体, 在群体层面操作进化算子.

CPDE包含入侵算子, 协作算子和局部搜索算子三种基本操作.入侵算子体现了种群之间的竞争, 保证了算法的多样性.协作算子采用差分操作^{[8, 9]}体现了物种之间的合作, 保证了算法的启发性.局部算子保证了算法的精确性.CPDE具备了前述的三个必要特性, 具有很好的全局搜索能力, 在优化高维度多峰复杂函数时表现优异.因此, CPDE适用于解决网络安全态势预测这类高维复杂优化问题.

1 CPDE的基本概念

1.1 云模型的基本概念

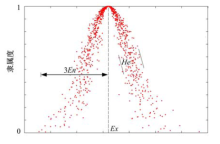
云模型是由李德毅^[7]提出的一种在定性与定量知识之间的不确定转换模型, 可以用来描述模糊的不确定的信息.一个云模型有很多云滴构成, 每个云滴都是某个概念的一次具体实现.云的外观形态由三个参数决定:期望值(Expected value)Ex, 熵(Entropy)En和超熵(Hyper entropy)He, 其中期望Ex是云模型中最能代表定性概念的取值, 处于云的形心, 决定了云的位置.熵En代表了概念可被接受的范围, 决定了云的延展度.超熵He是熵的不确定性度量, 它反映了云的厚度, 即云滴的离散程度.某个定性概念的一维正态云如图1所示.

	Figure Option View Download New Window
	图1 一维正态云模型Fig.1 One-dimensional normal cloud model

图1中的横轴代表概念的取值, 纵轴代表取值所对应的隶属度.

设I为论域U上的语言值, 映射CI(x):U→ [0, 1], 存在x∈ U, x→ CI(x), 则CI(x)在U上的分布称为I的隶属云, 当CI(x)满足正态分布时, 称为正态云模型, 记为C(Ex, En, He), 正态云模型可以由正态云发生器获得, 多维正态云模型的生成算法如下.

算法1:多维正态云生成算法

(1)确定云模型的云滴个数N和维度D;

(2)确定期望值(Ex₁, Ex₂, , et al., Ex_D);

(3)确定熵值(En₁, En₂, , et al., En_D);

(4)确定超熵值(He₁, He₂, , et al., He_D);

(5)进入循环:while I< N.

以(En₁, En₂, , et al., En_D)作为期望值, (He₁, He₂, , et al., He_D)作为标准差, 产生一个D维正态随机向量(En'₁, En'₂, , et al., En'_D).

以(Ex₁, Ex₂, , et al., Ex_D)作为期望值, (En'₁, En'₂, , et al., En'_D)作为标准差, 产生一个D维正态随机向量(x_i₁, x_i₂, , et al., x_iD), i∈ [1, N].

计算其隶属的u_i:

$\begin{matrix} u_{i} = \exp \overset{D}{\sum_{j = 1}} \frac{- (x_{ij} - E x_{j})}{2 (En'_{j})^{2}} \end{matrix}$

$\begin{matrix} I = I + 1 \end{matrix}$

End while

1.2 云个体的概念

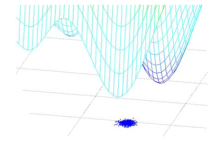
CPDE将云模型生成的种群当做个体.在进化过程中, 云个体的形态可以根据环境做出相应的调整, 一个二维的正态云个体如图2所示.

	Figure Option View Download New Window
	图2 二维正态云个体Fig.2 Two-dimensional normal cloud individual

图2描述了一个处于三维适应度景观中的二维云个体, 其形态由Ex、En、He以及构成云个体的解个数N共同决定.云个体本质上是一个围绕某个解生成的小种群.云个体是CPDE中的基本单元, 它们由不同的分布模型在解空间中采样而成, 所以云个体是由解构成的.我们扩展了正态云模型, 使用不同的分布产生云个体, 例如幂率分布, 柯西分布和泊松分布.不同的个体有不同的特点, 并且在搜索最优解时呈现了不同的特征.本文构造了如下云个体.

(1)正态分布云个体中的解x从正态分布取样:

$\begin{matrix} x ~N (μ, σ^{2}) \begin{matrix} \end{matrix} f (x) = \frac{1}{σ \sqrt[]{2 π}} \exp \frac{- {(x - μ)}^{2}}{2 σ^{2}} \end{matrix}$ (1)

式中: $\begin{matrix} μ \end{matrix}$ 代表均值; $\begin{matrix} σ \end{matrix}$ 代表标准差.

设云个体中心点(分布的期望)为 $\begin{matrix} μ = (μ_{1}, μ_{2}, \dots, μ_{D}), R_{N} (μ, σ) \end{matrix}$ 表示以 $\begin{matrix} μ \end{matrix}$ 为均值, $\begin{matrix} σ^{2} \end{matrix}$ 为方差的正态随机变量, 正态云个体中解 $\begin{matrix} x \end{matrix}$ 的某个维度 $\begin{matrix} x_{i} (i = 1, 2, \dots, D) \end{matrix}$ 可以通过下列方法计算^[10]:

$\begin{matrix} x_{i} = \{\begin{matrix} R_{N} (μ_{D}, σ), i = 1 \\ R_{N} (μ_{D - (i - 1)}, x_{i - 1}), 2 \leq i \leq D \end{matrix} \end{matrix}$ (2)

正态分布云个体大多数的解都集中在均值周围, 远离中心的解会越来越稀疏.正态分布云个体在探索和开采性能上比较均衡.

(2)柯西分布云个体中的解从柯西分布取样:

$\begin{matrix} x ~ C (θ, α) \begin{matrix} \end{matrix} f (x) = \frac{1}{π} [\frac{α}{{(x - θ)}^{2} + α^{2}}] \end{matrix}$ (3)

柯西分布没有均值和方差, $\begin{matrix} θ \end{matrix}$ 定义分布峰值位置的位置参数, $\begin{matrix} α \end{matrix}$ 是最大值一半处的一半宽度的尺度参数.柯西分布云个体比正态分布云个体具有更广的尾部, 可以产生更多不安分的解^[11], 但是只有在候选解远离最优点时才有利^{[12, 13]}.

(3)泊松分布云个体中的解是从泊松分布取样的:

$\begin{matrix} x ~ P (λ) \begin{matrix} \end{matrix} f (x) = \frac{e^{- λ} λ^{x}}{x!} (4) \end{matrix}$ (4)

泊松分布 $\begin{matrix} P (λ) \end{matrix}$ 中的参数 $\begin{matrix} λ \end{matrix}$ 既是均值也是方差, 泊松分布的云个体随机性较强, 其解的分布呈现出扩散的状态, 在进化过程中这样的分布有利于跳出局部最优解.

(4)幂律分布云个体中的解从幂律分布取样:

$\begin{matrix} x ~ P (r) \begin{matrix} \end{matrix} f (x) = c x^{- r} \end{matrix}$ (5)

幂律分布表现了一种很强的不平等性, 因此幂律分布具有更好的探索能力.

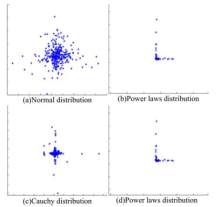
对上述云个体的特性可以总结为:正态分布云个体非常普通, 大多数的解都集中在中心点周围.越远离中心的位置被搜索的概率就越低.幂率分布云个体极端且不平等, 绝大多数的解都分散在中心点的周围, 呈现出良好的局部搜索能力.柯西分布云个体没有期望和方差, 它有一个良好的全局搜索能力.泊松分布云个体具有更强的随机性, 所以它们有很好的跳出局部最优解的能力.这些云个体的二维形态如图3所示.

	Figure Option View Download New Window
	图3 四种不同分布形态的云个体Fig.3 Four cloud individuals with different distributions

1.3 多态的混合云个体

云个体最初是由一种分布生成的, 这时它就属于该分布对应的云群(云群是指若干相同分布特性的云个体构成的种群).随着进化的深入, 云个体也可以由多种不同的分布共同生成, 我们赋予云群一个描述每种分布所占比例的分布链, 分布链的长度等于分布的种类数 $\begin{matrix} n, \end{matrix}$ 第 $\begin{matrix} i \end{matrix}$ 种云群的分布链为:

$\begin{matrix} L_{i} = (P_{i}^{1}, P_{i}^{2}, P_{i}^{3}, \dots, P_{i}^{n}) \end{matrix}$ (6)

式中:P表示云个体中的解服从某个分布的概率, P的上标表示分布的种类, 下标表示云群的编号, 第 $\begin{matrix} i \end{matrix}$ 种云群的初始分布链为:

$\begin{matrix} \begin{matrix} L_{i}^{int} = (P_{i}^{1} = 0, \dots, P_{i}^{i - 1} = 0, \\ P_{i}^{i} = 1, P_{i}^{i + 1} = 0, \dots, P_{i}^{n} = 0) \end{matrix} \end{matrix}$ (7)

随着进化的深入, 分布链也会发生变化, 每种分布的比例也会此消彼长, 按分布链生成的云个体会呈现多样化, 称之为多态的混合云个体.需要注意的是, 无论云个体最终由多少种分布构成, 它属于哪个云群是在初始时就确定了的.

多态的云个体使得种群具备多重特性, 并且增加了种群的多样性, 使得基于多态云个体的进化算法可以很大程度上避免个体早熟和种群进化的停滞.

分布链的想法来源于自然界中个体的基因链, 基因链生成生物体, 分布链构成云个体; 在进化的过程中, 基因链会发生改变, 导致生物体具备某个特性, 从而可以适应环境的变化.在接下来的进化操作算子中, 分布链也会发生变化.

2 CPDE的基本操作

2.1 入侵算子

入侵算子引入了竞争机制, 如果某个云个体找到了全局最优解, 那么它所属的云群就会将自己的分布扩散给其他云群, 扩散的程度取决于被入侵云群获得的惩罚度, 定义惩罚度为:

$\begin{matrix} φ_{i} = \frac{|gbest - pbes t_{i}|}{\overset{n}{\sum_{j = 1}} |gbest - pbes t_{j}|} \times a \end{matrix}$ (8)

式中: $\begin{matrix} φ_{i} \end{matrix}$ 代表第 $\begin{matrix} i \end{matrix}$ 种云群的惩罚度, $\begin{matrix} gbest \end{matrix}$ 代表全局最优值, $\begin{matrix} pbes t_{i} \end{matrix}$ 代表第 $\begin{matrix} i \end{matrix}$ 种云群中的最优解, $\begin{matrix} a \end{matrix}$ 代表缩小因子.如果云群中的最优解离全局最优解远, 则惩罚度大, 被入侵的程度就高, 被云群 $\begin{matrix} j \end{matrix}$ 入侵后的云群 $\begin{matrix} i \end{matrix}$ 的新分布链等于:

$\begin{matrix} \begin{matrix} L_{i}^{new} = (P_{i}^{1} = 0, \dots, P_{i} = P_{i} - φ_{i}, \\ \dots, P_{i}^{j} = P_{i}^{j} + φ_{i}, \dots, P_{i}^{n}) \end{matrix} \end{matrix}$ (9)

为了保证分布比例总和小于1, 新的分布链还要做归一化处理:

$\begin{matrix} P_{i}^{k} = \frac{P_{i}^{k}}{\overset{n}{\sum_{j = 1}} P_{i}^{j}} \end{matrix}$ (10)

被入侵后的云群分布链不再是只有一种分布存在, 经过多轮的入侵博弈, 云群中的云个体越来越多样化, 最终云个体会变成一种混合分布形式.例如, 当分布的种类为4个时, 分布链的长度n=4, 设p¹代表正态分布的云群; p²代表幂律分布的云群; p³代表柯西分布的云群; p⁴代表泊松分布的云群.那么4种云群的初始分布链分别为:

$\begin{matrix} L_{1} (t) = (P_{1}^{1}, P_{1}^{2}, P_{1}^{3}, P_{1}^{4}) = (1, 0, 0, 0), \end{matrix}$

$\begin{matrix} L_{2} (t) = (P_{2}^{1}, P_{2}^{2}, P_{2}^{3}, P_{2}^{4}) = (0, 1, 0, 0), \end{matrix}$

$\begin{matrix} L_{3} (t) = (P_{3}^{1}, P_{3}^{2}, P_{3}^{3}, P_{3}^{4}) = (0, 0, 1, 0), \end{matrix}$

$\begin{matrix} L_{4} (t) = (P_{4}^{1}, P_{4}^{2}, P_{4}^{3}, P_{4}^{4}) = (0, 0, 0, 1) 。 \end{matrix}$

假设在第一轮时, 云群1中的云个体找到了全局最优值1, 其他三种云群找到的本群中的最优值分别为0.4, 0.7, 0.5, 设 $\begin{matrix} a \end{matrix}$ =0.5, 则第4个云群的惩罚度 $\begin{matrix} φ_{4} \end{matrix}$ 等于:

$\begin{matrix} \begin{matrix} φ_{4} = (|1 - 0.5| \times 0.5) / (|1 - 0.4| + |1 - 0.7| + |1 - 0.5|) = 0.1786 \end{matrix} \end{matrix}$

其分布链更新为:

$\begin{matrix} \begin{matrix} L_{4} (t = 1) = (P_{4}^{1}, P_{4}^{2}, P_{4}^{3}, P_{4}^{4}) = (0.1786, 0, 0, 0.8214) \end{matrix} \end{matrix}$

可以看出第4个云群分布链中的正态分布增长了0.1786, 而自己原有分布减少了0.1786, 当按照此分布链生成云个体时, 其内部的解分布也会有17.86%是正态分布, 而余下的82.14%则是泊松分布.当运行到第 $\begin{matrix} n \end{matrix}$ 轮时, 云个体将会处于一种混合的状态, 第4个云群的云个体可能如图4所示.

	Figure Option View Download New Window
	图4 4种混合云个体Fig.4 Four hybrid cloud individuals

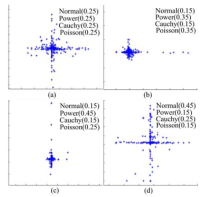
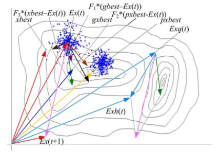
图4描述了4种具备不同分布链的混合云个体, 其中图4(a)的分布链为 $\begin{matrix} L_{4} (t = n) = (0.25, 0.25, 0.25, 0.25), \end{matrix}$ 云个体呈现平衡状态.图4(b)的分布链为 $\begin{matrix} L_{4} (t = n) = (0.15, 0.35, 0.15, 0.35) 。 \end{matrix}$ 图4(c)的分布链为 $\begin{matrix} L_{4} (t = n) = (0.15, 0.45, 0.15, 0.25), \end{matrix}$ 其中幂律分布占45%, 所以云个体呈现出长尾特性.图4(d)的分布链为 $\begin{matrix} L_{4} (t = n) = (0.45, 0.15, 0.25, 0.15), \end{matrix}$ 云个体结合了正态分布和柯西分布的特征.

2.2 协作算子

协作算子是一种变形的差分进化操作, 新的云个体期望等于旧期望与四种差值之和, 这4种差值分别是:① 云个体期望与云个体内部最优解的差值; ② 云个体期望与本种类云群最优解的差值; ③ 云个体期望与本代全局最优解的差值; ④ 任意两个云个体期望差值.假设在 $\begin{matrix} D \end{matrix}$ 维解空间中, 第 $\begin{matrix} i \end{matrix}$ 个云群中的第 $\begin{matrix} m \end{matrix}$ 个云个体的期望值为: $\begin{matrix} E x_{m} (t) = (x_{m}^{1}, x_{m}^{2}, x_{m}^{3}, \dots, x_{m}^{D}), \end{matrix}$ 那么在第 $\begin{matrix} t + 1 \end{matrix}$ 代, 期望的更新如公式(11)所示, 其中的 $\begin{matrix} F_{1} ~ F_{4} \end{matrix}$ 表示扩大因子, 调控各差分值的比例. $\begin{matrix} gxbest \end{matrix}$ 代表全局的最优解, $\begin{matrix} pxbes t_{i} \end{matrix}$ 代表第 $\begin{matrix} i \end{matrix}$ 种云群中的最优解, $\begin{matrix} xbes t_{m} \end{matrix}$ 代表第 $\begin{matrix} m \end{matrix}$ 个云个体中的最优解, $\begin{matrix} E x_{h} (t) \end{matrix}$ 和 $\begin{matrix} E x_{q} (t) \end{matrix}$ 分别代表在第 $\begin{matrix} t \end{matrix}$ 代中第 $\begin{matrix} h \end{matrix}$ 个云个体和第 $\begin{matrix} q \end{matrix}$ 个云个体.

$\begin{matrix} \begin{matrix} E x_{m} (t + 1) = \\ E x_{m} (t) + F_{1} \times (gxbest - E x_{m} (t)) + \\ F_{2} \times (pxbes t_{i} - E x_{m} (t)) + F_{3} \times (xbes t_{m} - \\ E x_{m} (t)) + F_{4} \times (E x_{h} (t) - E x_{q} (t)) \end{matrix} \end{matrix}$ (11)

如果全局最优解在某个云个体内部, 那么这个云个体将不执行公式(11), 而执行公式(12):

$\begin{matrix} E x_{m}^{t + 1} = gxbest \end{matrix}$ (12)

	Figure Option View Download New Window
	图5 协作算子的计算过程Fig.5 The computation process of the cooperative operator

公式(12)表示包含全局最优解的云个体不执行协作操作, 其新的期望将直接等于全局最优解.协作操作的细节如图5所示.图5描述了期望的更新步骤(从 $\begin{matrix} Ex (t) \end{matrix}$ 到 $\begin{matrix} Ex (t + 1)), \end{matrix}$ 红色的线表示期望的位置, 其他颜色的线表示差分计算的过程, 图5中的曲线代表解空间的等高线.

2.3 局部搜索算子

实验结果表明, 带有入侵和协作算子的CPDE算法具有良好的全局搜索能力, 即使在高维空间搜索时, 也能很快收敛到全局最优解附近, 但是由于云个体在小范围解空间内的结构松散, 并且云个体的解内部没有进化机制, 所以算法缺少很好的局部搜索能力.

本文提出了两种手段改善搜索精度, 一种是缩小最优解附近的云个体的熵, 使其结构更加紧密.另一种是让最优解执行局部搜索算法, 例如梯度下降算法, 单纯形优化算法, 粒子群算法和CMA-ES(Covariance matrix adaptation evolution strategy)^[14], CMA-ES是一个有效的局部搜索算法, 它被认为是目前最先进的进化算法, CMA-ES是协方差矩阵的适应进化策略.

选择CMA-ES作为CPDE的局部搜索算子, 只有每轮的最优解才会执行CMA-ES去寻找更精确的解, 局部搜索算子的执行次数为:

$\begin{matrix} Iteration s_{local} = K \times I \end{matrix}$ (13)

在公式(13)中, I代表CPDE的运行代数, K是一个系数, K的值不应该太大也不应该太小, 大的 $\begin{matrix} K \end{matrix}$ 值会增加计算代价, 小的K值会降低搜索精度, 我们选择K的取值为10, 这意味着每一轮的CPDE都要运行10× I次的CMA-ES算法.

3 算法流程

算法2:CPDE算法

(1)初始化输入:

确定进化代数G∈ N, 分布的种类数n∈ N, 云个体数目Cn∈ N;

初始化云个体参数;

解空间范围[R_min, R_max];

解的个数Sn∈ N;

熵的范围[En_min, En_max];

超熵的范围[He_min, He_max];

种群期望Ex∈ [R_min, R_max];

初始分布链L;

(2)根据初始参数产生云个体;

初始入侵操作的缩小因子a∈ [0, 1];

初始协作操作的扩大因子F₁~F₄∈ [0, 1];

初始局部搜索操作系数K∈ N;

(3)进入循环, WhileI≤ Gdo

1.计算每个云个体内部的解的适应度值;

2.找出全局最优解(gxbest);

3.找出每种云群的最优解(pxbest);

4.找出每个云个体中的最优解(xbest);

6.执行入侵操作;

6.计算每种云群的惩罚度, 更新云群分布链;

7.执行协作操作;

8.执行局部搜索操作;

9.用更新后期望和分布链产生新的云个体;

10.比较并更新全局解;

I=I+1))

满足条件结束循环, end While

(4)输出全局最优解.

整个算法的流程如图6所示.

	Figure Option View Download New Window
	图6 CPDE算法的流程图Fig.6 The flow diagram of the CPDE algorithm

4 比较实验

4.1 实验设计

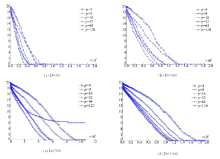
实验使用了一些高维的标准测试函数测试CPDE在高维优化问题上的性能.测试的维度取值为[50, 100, 500, 1000]维, 测试结果为运行30次的平均值.目标函数如表1所示, 其中 $\begin{matrix} D \end{matrix}$ 代表维度.另外, 实验还选择了一些主流的优化算法与CPDE进行比较, 这些算法的参数取值如表2所示.

4.2 CPDE的性能分析

为了测试CPDE在不同参数取值下的性能, 我们使用不同个体数目做测试。以Ackley函数为例, 图7表明了CPDE在不同个体数目和不同维度上的收敛性能, x轴代表函数的评价次数, y轴代表函数值, D代表维度, P代表个体数目。

表1 测试用目标函数 Table 1 Objective function for testing

取值范围:	Weierstrass Funciton[-0.5 0.5]^D
表达式:	$\begin{matrix} \begin{matrix} f (\vec{x}) = \overset{D}{\sum_{i = 1}} (\overset{kmax}{\sum_{k = 0}} [a^{k} \cos (2 π b^{k} (z_{i} + 0.5))]) - \\ D \overset{kmax}{\sum_{k = 0}} [a^{k} \cos (2 π b^{k} \times 0.5)] \end{matrix} \end{matrix}$
取值范围:	Schwefel's Problem 2.22[-10 10]^D
表达式:	$\begin{matrix} f (\vec{x}) = \overset{D}{\sum_{i = 1}} \|x_{i}\| + \overset{D}{\prod_{i = 1}} \|x_{i}\| \end{matrix}$
取值范围:	Powell Funciton [-5 5]^D
表达式:	$\begin{matrix} \begin{matrix} f (\vec{x}) = \overset{D / 4}{\sum_{i = 1}} [(x_{4 i - 3} + 10 x_{4 i - 2})^{2} + 5 (x_{4 i - 1} - x_{4 i})^{2} + \\ (x_{4 i - 2} - 2 x_{4 i - 1})^{4} + 10 (x_{4 i - 3} - x_{4 i})^{4}] \end{matrix} \end{matrix}$
取值范围:	Quartic Function i.e. Noise [-2 2]^D
表达式:	$\begin{matrix} f (\vec{x}) = \overset{D}{\sum_{i = 1}} i \times x_{i}^{4} + random [0, 1) \end{matrix}$
取值范围:	Ackley Function [-40 40]^D
表达式:	$\begin{matrix} \begin{matrix} f (\vec{x}) = - 20 \times \exp (- 0.2 \sqrt[]{\overset{D}{\sum_{i = 1}} \frac{x_{i}^{2}}{D}}) - \\ \exp (\overset{D}{\sum_{i = 1}} \frac{\cos (2 \times π \times x_{i})}{D}) + 20 + e \end{matrix} \end{matrix}$
取值范围:	Generalized Rastrigin [-5 5]^D
表达式:	$\begin{matrix} f (\vec{x}) = 10 D + \overset{D}{\sum_{i = 1}} [x_{i}^{2} - 10 \cos (2 π x_{i})] \end{matrix}$

表1 测试用目标函数 Table 1 Objective function for testing

表2 参与比较的优化算法参数取值 Table 2 The parameters of the optimization algorithms

图7阐述了随着维度的增加, 更多的个体数目将会获得更好的收敛性能.当维度为50时, 8个个体获得最好的收敛性能, 当维度为100时, 16个个体获得最好的收敛性能, 当维度是500时, 32个个体获得最好的收敛性能, 当维度是1000时, 32个个体获得最好的收敛性能, 其他函数的测试结果与图7相近, 不再赘述.

	Figure Option View Download New Window
	图7 CPDE在不同个体和不同维度上的收敛性能Fig.7 The convergence performance of CPDE

4.3 CPDE与其他优化算法的比较

CPDE与其他算法在高维度上的比较结果如表3~表5所示.选择CMA-ES^[14]算法, Standard Differential Evolutionary(SDE)^[15]和Particle Swarm Optimization(PSO)^[16]与CPDE算法比较.

表3 函数f1和f2的比较结果 Table 3 The comparison results for functions f1 and f2

表4 函数f3和f4的比较结果 Table 4 The comparison results for functions f3 and f4

表5 函数f5和f6的比较结果 Table 5 The comparison results for functions f5 and f6

测试实验运行30次, 结果取平均值.Dim表示维度, Mean Error表示搜索的平均精度值, FES代表平均函数评价次数.

表3~表5的结果显示CPDE的高维收敛性能优于传统算法.尤其是在某些难解函数中, CPDE的平均函数评价次数要低于其他算法, 甚至是在高达1000维时, 也能找到全局最优解.由于本文的目标主要是定位与解决网络安全态势预测问题, 所以并没有列出太多的标准测试函数.即使CPDE在个别测试函数中表现一般, 也并不影响它在实际工程中的应用.

5 网络安全态势预测案例

5.1 背景描述

网络安全态势是指对网络系统平台安全情况的整体描述^[17].网络安全态势预测是网络安全感知技术中的重要环节^[18], 通过准确预测网络安全态势值并预警, 网络管理员可以提前采取相应的防范措施, 真正做到主动防御.

网络安全态势的预测技术刚刚起步, 目前以神经网络预测模型为主.本文选取径向基神经网络(RBF)模型^[19]作为预测模型, 利用CPDE算法优化RBF模型的参数, 然后再用优化完的预测模型预测网络安全态势.

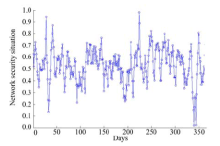
本文收集了2014年度某个真实网络平台上的攻击数据, 采用层次化加权平均的方法^[20]将这些数据整合成网络安全态势值, 并归一化, 得到如图8所示的态势值.

为了能够适合RBF神经网络模型的多维输入, 将图8所示的网络安全态势值通过设置滑动窗口的方法得到了362组样本, 每组样本中包含1个输入数据和1个输出数据(假定滑动窗口大小为k=3, 从收集到的网络安全态势的第1个值开始, 将前k个数值设为输入, 第k+1个数值设为输出, 然后依次移动窗口1个单位, 得到下一组样本).再将362组样本中的前262组作为训练数据, 后100组作为测试数据.

	Figure Option View Download New Window
	图8 某网络平台2014年度网络安全态势值Fig.8 The network security situation of a network platform in the 2014 year

5.2 网络安全态势预测结果比较

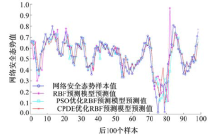
在预测结果的比较实验中, 选取了PSO算法和CPDE做比较, 预测模型采用RBF神经网络, 输入层神经元个数为3, 隐层神经元个数为8, 输出层神经元个数为1, 用上述的样本作为模型的训练数据和测试数据.预测的比较结果如图9和表6所示.可以看出, CPDE的优化结果精度要高于其他方法.

	Figure Option View Download New Window
	图9 不同优化算法的预测结果比较Fig.9 The comparison results of the network security situation Prediction

表6 网络安全态势预测误差 Table 6 The errors of the network security situation Prediction

6 结束语

本文结合云模型和差分进化的优点, 提出了一种基于云群的差分进化算法(CPDE), 该算法有良好的高维优化能力和天然的并行性, 它能有效地在高维复杂函数的优化中找到全局最优解.云模型是一种模糊化的方法, 并能够很好地处理复杂的问题.所提出的云群和分布链的概念增加了种群的多样性, 有效地避免了算法早熟.最后, 通过网络安全态势预测的案例验证了算法的有效性和实用性.

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	张晓伟, 刘三阳, 迟晓妮. 高效求解多峰值全局优化的区间-遗传算法[J]. 吉林大学学报: 工学版, 2008, 38(4): 876-879. Zhang Xiao-wei, Liu San-yang, Chi Xiao-ni. Efficient interval-genetic algorithm for multi-peak global optimization[J]. Journal of Jilin University (Engineering and Technology Edition), 2008, 38(4): 876-879. [本文引用:1]
[2]	朝勇, 郑建国. 用于高维函数优化的多智能体量子进化算法[J]. 自然科学进展, 2007, 18(2): 197-205. Chao Yong, Zheng Jian-guo. A multi-agent quantum evolutionary algorithm for the high dimensional function optimization[J]. Progress in Natural Science, 2007, 18(2): 197-205. [本文引用:1]
[3]	Noman N, Iba H. Enhancing differential evolution performance with local search for high dimensional function optimization[C]//Genetic and Evolutionary Computation Conference (GECCO), 2005: 967-974. [本文引用:1]
[4]	Zhang Wei-guang, He Rui, Liu Yu, , et al. An evolutionary algorithm based on cloud model[J]. Chinese Journal of Computers, 2008, 31(7): 1082-1091. [本文引用:2]
[5]	Dai Chao-hua, Zhu Yun-fang, Chen Wei-rong, et al. Cloud model based genetic algorithm and it's applications[J]. Acta Electronica Sinica, 2007, 35(7): 1419-1424. [本文引用:2]
[6]	Dai Chao-hua, Zhu Yun-fang, Chen Wei-rong. Adaptive genetic algorithm based on cloud theory[J]. Control Theory and Applications, 2007, 24(4): 646-650. [本文引用:2]
[7]	Li De-yi, Meng Hai-jun, Shi Xue-mei. Membership clouds and membership cloud generators[J]. Journal of Computer Research Development, 1995, 32(6): 15-20. [本文引用:2]
[8]	Storn R, Price K. Differential evolution-A simple and efficient adaptive scheme for global optimization over continuous spaces[R]. Berkeley: University of California , 2006. [本文引用:1]
[9]	Lampinen J. A bibliography of differential evolution algorithm[EB/OL]. http://www.lut.fi/~jlampine/debiblio.Htm, 2002-10-14. [本文引用:1]
[10]	李德毅, 杜鹢. 不确定性人工智能[M]. 北京: 国防工业出版社, 2005. [本文引用:1]
[11]	Andries P Engelbrecht. Computational Intelligence: An Introduction[M]. 2nd Edition. Beijing: Tsinghua University Press, 2010. [本文引用:1]
[12]	Yao X, Lin G, Liu Y. An analysis of evolutionary algorithms based on neighbourhood and step size[C]//Proceedings of the Sixth Annual Conference on Evolutionary Programming, 1997: 297-307. [本文引用:1]
[13]	Yao X, Liu Y, Lin G. Evolutionary programming made faster[J]. IEEE Transactions on Evolutionary Computation, 1999, 3(2): 82-102. [本文引用:1]
[14]	Nikolaus H. The CMA Evolution Strategy: A Comparing Review Towards a New Evolutionary Computation[M]. Berlin: Springer, 2006: 75-102. [本文引用:2]
[15]	Storn R, Price K. Differential evolution-a simple and efficient adaptive scheme for global optimization over continuous spaces[J]. Journal of Global Optimization, 1997, 11(4): 341-359. [本文引用:1]
[16]	Kennedy J, Eberhart R C. Particle swarm optimization[C]//Proceedings of the 1995 IEEE International Conference on Neural Networks, Piscataway, NJ: IEEE Service Center, 1995: 1942-1948. [本文引用:1]
[17]	BASS T. Intrusion detection system and multi-sensor data fusion: creating cyberspace situation awareness[J]. Communications of The ACM, 2000, 43(4): 99-105. [本文引用:1]
[18]	王慧强, 赖积保, 胡明明, 等. 网络安全态势感知关键技术研究[J]. 武汉大学学报: 信息科学版, 2008, 33(10): 995-998. Wang Hui-qiang, Lai Ji-bao, Hu Ming-ming, et al. Research on key technologies for implementing network security situation awareness[J]. Geomatics and Information Science of Wuhan University, 2008, 33(10): 995-998. [本文引用:1]
[19]	任伟, 蒋兴浩, 孙锬锋. 基于RBF神经网络的网络安全态势预测方法[J]. 计算机工程与应用, 2006, 31: 136-139. Ren Wei, Jiang Xing-hao, Sun Tan-feng. RBFNN-based prediction of network security situation[J]. Computer Engineering and Application, 2006, 31: 136-139. [本文引用:1]
[20]	陈秀真, 郑庆华, 管晓宏, 等. 层次化网络安全威胁态势量化评估方法[J]. 软件学报, 2006, 17(4): 885-897. Chen Xiu-zhen, Zheng Qing-hua, Guan Xiao-hong, et al. Quantitative hierarchical threat evaluation model for network security[J]. Journal of Software, 2006, 17(4): 885-897. [本文引用:1]

2008

0.0

. 2008, 38(4):876-879

Efficient interval-genetic algorithm for multi-peak global optimization

高效求解多峰值全局优化的区间-遗传算法

Zhang Xiao-wei , Liu San-yang , Chi Xiao-ni.

张晓伟, 刘三阳, 迟晓妮

针对传统区间优化算法求解高维问题耗时的缺点,将区间算法和遗传算法进行融合,提出了一种区间-遗传算法。该算法利用区间算法为遗传算法的搜索区域进行定界,同时采用拒绝指标可使包含全局最优解的区间更容易被选择,而且算法通过遗传算法提供的问题全局最优解的上界可对那些不包含全局最优解的区间进行删除。对一些多峰值全局优化问题进行了仿真实验,结果表明:该算法相比传统区间优化算法更加有效,而且随着问题维数的增大,算法的高效性更加明显。

... 0 引言目前,业界已经提出了很多改进的进化算法用于解决高维优化问题^[1,2,3] ...

2007

0.0

. 2007, 18(2):197-205 DOI:doi:10.3321/j.issn:1002-008X.2008.02.010

A multi-agent quantum evolutionary algorithm for the high dimensional function optimization

用于高维函数优化的多智能体量子进化算法

Chao Yong , Zheng Jian-guo.

朝勇, 郑建国

基于智能体的竞争和学习能力、量子计算理论及生物进化策略,提出了一种新的优化方法--多智能体量子进化算法.一个智能体代表优化问题的一个可能解,所有的智能体都以量子染色体表示.该算法将智能体分布于多智能体网络环境中,智能体之间通过量子进化来实现竞争及学习,以提高个体的竞争能力.理论证明该算法具有全局收敛性.实验结果表明,该算法具有强的全局寻优能力及快速搜索能力.

... 0 引言目前,业界已经提出了很多改进的进化算法用于解决高维优化问题^[1,2,3] ...

2005

0.0

... 0 引言目前,业界已经提出了很多改进的进化算法用于解决高维优化问题^[1,2,3] ...

2008

0.0

... 文献^[4,5,6]利用云模型提出了一些新的进化算法,例如Zhang等^[4]在2008年提出了基于云模型的进化算法(CBEA),该算法利用正态云生成器生成种群,并定义最优个体向量,以最优向量中的个体为种子生成新的种群,越优良的个体生成的种群越大 ...

2007

0.0

... Dai等^[5]在2007年引入了基于云模型的遗传算法CGA,CGA采用正态云模型中的Y条件正态云发生器完成交叉操作 ...

2007

0.0

... Dai等^[6]在2007年提出了云自适应遗传算法(CAGA) ...

1995

0.0

... 该算法把利用云模型^[7]生成的小规模种群当做云个体,在群体层面操作进化算子 ...

... 1 云模型的基本概念云模型是由李德毅^[7]提出的一种在定性与定量知识之间的不确定转换模型,可以用来描述模糊的不确定的信息 ...

2006

0.0

... 协作算子采用差分操作^[8,9]体现了物种之间的合作,保证了算法的启发性 ...

0.0

... 协作算子采用差分操作^[8,9]体现了物种之间的合作,保证了算法的启发性 ...

2005

0.0

. 2005, :-

李德毅, 杜鹢

本书回顾了人工智能50年以来对确定性人工智能研究的一些主要方法，分析其局限性，提出不确定性知识和智能研究的新领域。对不确定性智能的普遍性、数学基础、特征、表示、模型、推理机制、不确定性思维活动、云计算、语义计算等进行了深层次的研究，并讨论了它们在定性和定量相互转换、不确定性知识发现的物理学方法、智能控制，以及复杂网络中的不确定性计算等方面的实际应用，最后对不确定性人工智能研究的发展方向进行了展望。

... 设云个体中心点(分布的期望)为 μ=(μ1,μ2,…,μD),RNμ,σ表示以 μ为均值, σ2为方差的正态随机变量,正态云个体中解 x的某个维度 xi(i=1,2,…,D)可以通过下列方法计算^[10]: ...

2010

0.0

... 柯西分布云个体比正态分布云个体具有更广的尾部,可以产生更多不安分的解^[11],但是只有在候选解远离最优点时才有利^[12,13] ...

1997

0.0

... 柯西分布云个体比正态分布云个体具有更广的尾部,可以产生更多不安分的解^[11],但是只有在候选解远离最优点时才有利^[12,13] ...

1999

0.0

... 柯西分布云个体比正态分布云个体具有更广的尾部,可以产生更多不安分的解^[11],但是只有在候选解远离最优点时才有利^[12,13] ...

2006

0.0

... 另一种是让最优解执行局部搜索算法,例如梯度下降算法,单纯形优化算法,粒子群算法和CMA-ES(Covariance matrix adaptation evolution strategy)^[14],CMA-ES是一个有效的局部搜索算法,它被认为是目前最先进的进化算法,CMA-ES是协方差矩阵的适应进化策略 ...

... 选择CMA-ES^[14]算法,Standard Differential Evolutionary(SDE)^[15]和Particle Swarm Optimization(PSO)^[16]与CPDE算法比较 ...

1997

0.0

... 选择CMA-ES^[14]算法,Standard Differential Evolutionary(SDE)^[15]和Particle Swarm Optimization(PSO)^[16]与CPDE算法比较 ...

1995

0.0

... 选择CMA-ES^[14]算法,Standard Differential Evolutionary(SDE)^[15]和Particle Swarm Optimization(PSO)^[16]与CPDE算法比较 ...

2000

0.0

... 1 背景描述网络安全态势是指对网络系统平台安全情况的整体描述^[17] ...

2008

0.0

. 2008, 33(10):995-998 DOI:doi:10.7666/d.y1655593

Research on key technologies for implementing network security situation awareness

网络安全态势感知关键技术研究

Wang Hui-qiang , Lai Ji-bao , Hu Ming-ming

王慧强, 赖积保, 胡明明

近年来,Internet技术迅速发展,计算机网络在政治、经济、军事、社会生活等各个领域发挥着日益重要的作用。然而,网络中存在着大量黑客攻击、木马和病毒等威胁,使得网络安全状况日益严重。虽然防火墙、入侵检测、防病毒软件、身份认证、安全审计等安全防护和管理产品在网络中得到了广泛应用,但是这些设备往往仅限于对单点、单一的安全问题进行处理,不能相互支撑、协同工作,而且日志中存在大量的冗余、虚假警报,使得它们尚不能满足全局网络尤其是大规模网络安全状况的监控需求。因此,本文从态势感知的角度,对安全事件关联分析、网络威胁及宏观安全态势评估、态势预测等方面进行了相关研究,主要包括以下四个方面：首先,根据网络安全威胁态势评估指标的提取原则选取威胁评估指标。在此基础上,给出了评估指标的量化方法。针对灰色关联分析方法中分辨系数的选取意义不明确的问题,还提出了基于改进灰色关联分析的评估指标权重确定方法。该方法采用层次分析法对评价指标赋予归一化的重要性权重,对关联系数赋予比较序列与参考序列数值接近程度的量化权重,从而实现了对传统的灰色关联分析模型的修正,得到的指标权重更加客观、可信。其次,提出了基于层次式聚类的安全事件聚类方法。该方法采用层次方式结合不同的聚类方法对告警事件进行聚合,在充分体现不同聚类算法优点的同时避免了因方法单一而导致的聚类结果的单一性。此外,还提出了基于攻击图的安全事件关联方法。该方法借助网络攻击图提供的信息,得到弱点利用节点间距离(攻击图距离),通过攻击图距离来衡量安全事件间相关性,从而对多步攻击进行关联。再次,提出了基于灰色模糊权矩阵的网络威胁评估模型和基于自适应神经模糊推理系统的网络安全宏观态势评估模型。通过建立模糊权矩阵得到最终的网络威胁评估结果和网络威胁态势图,对网络威胁评估数据进行灰色关联分析,得到每种威胁类型的和各主机的威胁程度排序结果,进而发现哪些攻击类型更危险、哪些主机受到的威胁更严重。从入侵检测系统、漏洞扫描系统等多种设备提取能够反映网络安全性的指标,并采用自适应神经模糊推理技术对其进行融合、评估,最终以量化的形式显示宏观的网络安全态势演变趋势。最后,针对网络安全态势的预警问题,提出基于时间序列分析的网络安全态势预测技术。通过分析过去和当前的网络安全状况,结合ARMA (Auto-Regressive and Moving Average Model)时间序列分析模型对历史网络安全态势序列进行分析,得到了较为准确的网络安全态势的预测值。

... 网络安全态势预测是网络安全感知技术中的重要环节^[18],通过准确预测网络安全态势值并预警,网络管理员可以提前采取相应的防范措施,真正做到主动防御 ...

2006

0.0

. 2006, 31:136-139 DOI:doi:10.3321/j.issn:1002-8331.2006.31.041

RBFNN-based prediction of network security situation

基于RBF神经网络的网络安全态势预测方法

Ren Wei , Jiang Xing-hao , Sun Tan-feng.

任伟, 蒋兴浩, 孙锬锋

针对现有网络安全技术不能对网络未来安全态势进行预测的问题,利用网络安全态势值具有非线性时间序列的特点,借助神经网络处理混沌、非线性数据的优势,提出了一种基于RBF神经网络进行态势预测的方法.该方法通过训练RBF神经网络找出态势值的前N个数据和随后M个数据的非线性映射关系,进而利用该关系进行态势值预测.通过实验测试表明,该方法能够准确获得态势值预测结果,辅助网络管理者做出安全防护的决策.

... 本文选取径向基神经网络(RBF)模型^[19]作为预测模型,利用CPDE算法优化RBF模型的参数,然后再用优化完的预测模型预测网络安全态势 ...

2006

0.0

. 2006, 17(4):885-897

Quantitative hierarchical threat evaluation model for network security

层次化网络安全威胁态势量化评估方法

Chen Xiu-zhen , Zheng Qing-hua , Guan Xiao-hong

陈秀真, 郑庆华, 管晓宏

安全评估是贯穿信息系统生命周期的重要管理手段,是制定和调整安全策略的基础和前提.只有充分识别系统安全风险,才能有针对性地采取有效的安全防范措施.基于IDS(intrusion detection system)海量报警信息和网络性能指标,结合服务、主机本身的重要性及网络系统的组织结构,提出采用自下而上、先局部后整体评估策略的层次化安全威胁态势量化评估模型及其相应的计算方法.该方法在报警发生频率、报警严重性及其网络带宽耗用率的统计基础上,对服务、主机本身的重要性因子进行加权,计算服务、主机以及整个网络系统的威胁指数,进而评估分析安全威胁态势.实验表明,该系统减轻了管理员繁重的报警数据分析任务,能够提供服务、主机和网络系统3个层次的直观安全威胁态势,使其对系统的安全威胁状况有宏观的了解.而且,可以从安全态势曲线中发现安全规律,以便调整系统安全策略,更好地提高系统安全性能,为指导安全工程实践、设计相应安全风险评估和管理工具提供了有价值的模型和算法.

... 本文收集了2014年度某个真实网络平台上的攻击数据,采用层次化加权平均的方法^[20]将这些数据整合成网络安全态势值,并归一化,得到如图8所示的态势值 ...