引用本文
张贵军, 郝小虎, 周晓根, 秦传庆. 动态步长蛋白质构象空间搜索方法.吉林大学学报:工学版, 2016, 46(2): 585-594
ZHANG Gui-jun, HAO Xiao-hu, ZHOU Xiao-gen, QIN Chuan-qing. Ab-initio dynamic-step-size searching of protein conformational space. Journal of Jilin University Engineering and Technology Edition, 2016, 46(2): 585-594  
Permissions
Copyright©2016, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
动态步长蛋白质构象空间搜索方法
张贵军, 郝小虎, 周晓根, 秦传庆
浙江工业大学 信息工程学院, 杭州 310023

作者简介:张贵军(1974-),男,教授,博士.研究方向:智能信息处理,全局优化理论及算法设计,生物信息学.E-mail:zgj@zjut.edu.cn

基金:国家自然科学基金项目(61075062,61573317); 浙江省自然科学基金项目(LY13F030008); 浙江省科技厅公益项目(2014C33088); 浙江省重中之重学科开放基金项目(20120811); 杭州市产学研合作项目(20131631E31)
摘要

针对蛋白质构象空间采样问题,提出了一种基于能量引导树搜索框架的动态步长构象空间搜索方法.通过蛋白质构象特征提取,将高维二面角优化空间映射到低维结构特征向量空间,有效避免了维数灾难问题;根据能量和温度测度离散化特征空间为多个能量层和温度层,并系统划分为"构象室",减小构象空间搜索范围.在不同能量层,赋予相应的片段组装步长和蒙特卡洛扰动步长,在不同温度层,采用相应Metropolis准则接收当前构象;辅以副本交换方法,增强对构象空间中稳态结构的采样能力.12个蛋白质测试结果表明,该方法可以快速有效地采样得到近天然态构象.

关键词: 人工智能; 从头预测; 树搜索; 动态步长; 片段组装; 蒙特卡洛
中图分类号:TP301.6 文献标志码:A 文章编号:1671-5497(2016)02-0585-10
Ab-initio dynamic-step-size searching of protein conformational space
ZHANG Gui-jun, HAO Xiao-hu, ZHOU Xiao-gen, QIN Chuan-qing
College of Information Engineering, Zhejiang University of Technology, Hangzhou 310023, China
Abstract

To address the sampling problem of protein conformational space, an Ab-initio dynamic-step-size searching method of protein conformational space is proposed. This method is based on the energy tree-based searching framework. The high-dimensional optimization space of dihedral angle is projected to a low-dimensional space of feature vector with the protein conformation feature extraction, effectively avoiding the curse of dimensionality problem. The feature space is discretized according to the energy and temperature. Then the layers are systematically divided into cells to reduce the searching space. Relevant Fragment Assembly (FA) step-size and Monte Carlo disturbance step-size are set according to the specific energy layer, and the corresponding Metropolis criterion is employed to accept the conformation within different temperature layers. The replica-exchange method is used as auxiliary method to enhance the sampling of native-like protein conformation. Test results of 12 proteins show that their native-like protein conformations can be reached successfully and effectively by the proposed method.

Keyword: artificial intelligence; Ab-initio; tree-based searching; dynamic-step-size; fragment assembly; Monte Carlo
0 引 言

蛋白质分子只有折叠成特定三维结构, 才能表现出特有的生物学功能, 想要了解其功能, 进而理解并治愈多种由蛋白质结构改变而引起的疾病, 就必须获得其三维结构[1].根据Anfinsen原则[2], 以计算机为工具, 运用适当的算法, 从氨基酸序列出发, 直接预测蛋白质的三级结构, 是当前生物信息学中一个主要的研究课题和重要任务[3].由于蛋白质构象高维空间的复杂性, 使得通过计算得到蛋白质天然态构象成为一个极具挑战性的NP-Hard问题.设计有效的算法增强对构象空间的采样, 是解决蛋白质结构从头预测瓶颈问题的途径[4].

CASP 10(Critical assessment of techniques for protein structure prediction)将蛋白质结构预测方法分为两大类, 基于模板的方法[5]和不依赖模板的方法[6].从头预测(Ab-initio)作为不依赖模板的方法, 适用于同源性小于25%的大多数蛋白质[7], 仅从序列出发预测蛋白质结构, 对蛋白质分子设计及蛋白质折叠的研究等具有重要意义.在CASP的促进下相继提出了很多有效的构象空间采样方法, 如遗传算法[8, 9, 10, 11], 分子动力学模拟[12, 13, 14], Monte Carlo[15, 16, 17], 模拟退火[18, 19, 20], 副本交换[21, 22], 构象树指导搜索方法[23, 24, 25, 26, 27]等.基于低能量引导树搜索的框架, 本文提出了一种采用动态步长搜索蛋白质构象空间的方法(Dynamic step size method, DSSM):对构象空间按照能量和温度进行分层, 赋予不同能量层相应的片段组装(Fragment assembly, FA)步长和蒙特卡洛扰动(Monte Carlo, MC)步长; 通过蛋白质构象特征提取, 将构象由二面角空间投影到三维特征空间, 系统划分构象空间为"构象室"; 在不同的温度层采用相应的Metropolis准则接收当前构象; 并辅以副本交换方法.动态步长构象空间搜索方法提高了算法的收敛速度, 增强了对构象空间的采样能力, 改善了算法容易陷入局部极值点的缺陷, 能够快速有效采样得到近天然态构象.

1 理论分析

Rosetta基于蛋白质折叠问题的多尺度特性, 应用粗粒度蛋白质表达模型构建了基于知识的能量模型, 但是在这个能量模型下进行系统搜索仍然面临着高维复杂性的问题, 搜索过程极易陷入局部极小点.本文提出的动态步长构象空间搜索方法通过蛋白质构象特征提取, 将高维二面角优化空间映射到低维结构特征向量空间, 有效避免了维数灾难问题; 根据能量和温度测度离散化特征空间为多个能量层和温度层, 并系统划分为"构象室", 减小构象空间搜索范围; 基于片段组装的Monte Carlo扰动可以有效地缩小构象空间的搜索范围; 引入副本交换能够增强算法跳出局部极小点的能力; 设置动态搜索步长可以使算法更快的向低能量区域搜索, 并增强在低能量区域的采样能力.

1.1 粗粒度蛋白质能量模型

根据Anfinsen原则, 蛋白质的天然结构对应于其自由能最小的构象.利用数学和信息的手段, 根据所建立的能量模型确定能量函数, 设计有效的算法, 运用相关优化理论, 对能量模型施以优化, 通过求解能量模型, 得到全局最优解, 从而可以得到相应的蛋白质天然构象.这个能量模型能否正确区分蛋白质正确构象和其他构象是从头预测方法中关键性的一步, 理想的能量函数应该能精确地表达蛋白质所有原子的空间位置及其能量之间的关系, 通过能量极小化找到天然构象[28].但是, 在现有的技术水平条件下, 仍然有一些作用力没有被发现或者确认, 使得构建的能量模型不够精确, 这也是制约蛋白质结构预测精度的一个重要因素.而蛋白质折叠本质上是典型的多尺度问题.自2013年诺贝尔化学奖获得者Levitt及Warshel在1975年建立蛋白质分子粗粒度能量模型以来, 陆续有研究者建立了一系列从粗粒度到全原子尺度的多尺度能量模型[29, 30].这样, 在蛋白质构象空间优化过程中, 可以利用粗粒度能量模型快速优化得到"诱饵构象"; 然后, 进一步基于精度更高的全原子能量模型对"诱饵构象"进行修正.

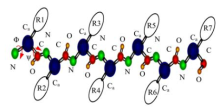
图1所示的粗粒度蛋白质表达模型只保留了主链骨干原子(N, Cα , C, O)及侧链替代原子, 用一系列设置为-120° 到120° 之间的二面角φ , ψ 来表示氨基酸链, 减少了空间自由度, 使计算简便.

图1 粗粒度蛋白质表达模型Fig.1 Coarse-grained protein representation

图1中用不同颜色的小球表示不同的原子, 圆柱体表示粒子键, 椭圆表示侧链.由N, Cα , C原子, 侧链替代原子和粒子键构成骨链, 分别用φ , ψ 表示二面角N-Cα , Cα -C, 其中φ , ψ ∈ [-120° 120° ].

应用上述粗粒度蛋白质表达模型构建如式(1)所示的Rosetta Score 3能量函数:

Eprotein=WrepullsionErepullsion+WattractionEattraction+WslovatinoEslovatino+Wbb-schbEbb-schb+Wbb-bbhbEbb-bbhb+Wsc-schbEsc-schbWpairEpair+WdunbrackEdunbrack+WramaErama+WreferenceEreference(1)

它是10种能量项独立加权计算的线性和.式中各能量项的具体能量函数表达式和参数请见参考文献[31, 32].这是一种基于知识的能量函数, 它利用蛋白质结构数据库(PDB)中已知结构数据作为学习样本, 计算得到具有统计性质的区分参数, 根据能量是按Boltzmann分布的原理反推得到.这种能量函数隐式体现了形成蛋白质天然结构的内在物理化学作用, 计算成本较低, 而且非常有效[33].

1.2 构象空间降维

蛋白质构象空间的高维特性和能量表面的崎岖性使得在构象空间中计算得到天然态构象过程中面临着巨大的困难.有效的降低构象空间的维数, 以规避维数灾难问题, 是解决所面临困难的途径.本文采取将高维二面角优化空间映射到低维结构特征向量空间, 离散化特征空间为多个能量层和温度层, 并系统划分为"构象室"的方法, 降低优化空间维度, 减小构象空间搜索范围, 以减少计算资源消耗.

超速形状识别[34](Ultrafast shape recognition, USR)方法基于蛋白质构象的特征向量, 将其空间结构投影变换到低维特征空间进行分析, 可以降低优化空间维度, 用于系统划分特征空间为"构象室", 并与实验室测定的蛋白质三维结构进行快速的比对得到相似度指标值.这种方法将分子看作是一个有界的离子, 分子的形状通过一系列包含蛋白质构象三维形状信息的一维分布来区别.使用骨架模型中所有原子相对于四种不同参考坐标系:质心(CTD), 离CTD最近的原子(CST), 离CTD最远的原子(FCT), 离FCT最远的原子(FTF), 计算蛋白质分子粗粒度骨架模型中所有原子与4个特征点的平均距离值, 平均距离的方差, 偏差值, 分别用μ 1, μ 2, μ 3表示, 将每个蛋白质抽象为12维的特征向量, 再通过归一化处理, 将蛋白质之间的相似度指标用一个分值Sqi表示, 如式(2):

Sqi=1/(1+1/12∑i=112Miq-Mii)Sqi∈[0, 1]M=(μ1ctd, μ2ctd, μ3ctd, μ1cst, μ2cst, μ3cst, μ1fct, μ2fct, μ3fct, μ1ftf, μ2ftf, μ3ftf)(2)

根据能量和温度测度离散化特征空间为多个能量层和温度层, 并系统划分为"构象室"以减小构象空间搜索范围.将特征空间按照能量和温度划分成一维网格, 能量值以δ E为间隔, 从最低能量到最高能量分层, 每层分配权重为ω (l), 如式(3):

ω(l)=Eavg2(l)(3)

式中:l表示温度层, Eavg2(l)表示该层平均能量值的平方, 这样, 每个能量层将以概率P(l)被选择, 如式(4):

P(l)=ω(χ)/∑l'∈GEω(l'), χ+l=n(4)

式中:n为所分能量层总数; 温度参数根据区间分半搜索方法[35]确定, 用于之后依玻尔兹曼概率P(Bol)接收构象, 如式(5):

P(Bol)=e(1/kBT)ΔE(5)

式中:Δ E为当前构象与前一构象之间的能量差, kB为玻尔兹曼常数, T为温度参数."构象室"以一定的概率P(cell)被选中, 用于构象的扩展, 如式(6):

P(cell)=1/(1+nsel)confs(6)

式中:nsel表示当前cell被选择的频次, confs表示当前cell中构象的数目.

采用上述降维方法, 有效地降低了构象空间维数, 减少了计算资源消耗, 同时可以避免对几何相似的构象过采样, 在一定程度上保证了算法的效率.

1.3 基于片段组装的Monte Carlo扰动

蒙特卡洛(Monte Carlo, MC)算法在蛋白质分子构象空间优化领域应用广泛.算法首先任意产生一个构象, 对其坐标做随机改变后生成新构象, 通过计算新旧构象能量差值, 按照给定温度T下的Boltzmann概率密度函数来接收新的构象, 该过程一直迭代直至得到能量最低构象.假定算法各态遍历, 产生的Markov过程将会收敛到正则分布[36].

基于片段组装的Monte Carlo扰动首先通过PISCES服务器[37]构建片段库:以sequence similarity≤ 30%, resolution≤ 3.0, R-factor≤ 0.3为参数, 从现有蛋白质PDB数据库得到14 071条蛋白质链的非冗余蛋白质子集, 将所得蛋白质子集中的氨基酸链分解成长度为L的片段, 根据Rosetta片段计分函数[38]从这些片段中挑选出一部分, 构成具有多样性的查询序列位置特定的结构片段库.

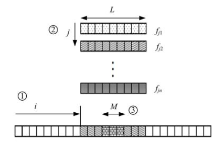
蛋白质构象空间高维特性, 模型的本质多尺度性及不精确性使得片段组装技术的应用成为从头预测蛋白质三维结构的一种重要手段.片段组装技术首先将预测序列划分成若干连续区段(Rosetta服务器区段长度为3和9个单体单元[39]), 然后通过序列比对寻找局部拟合已知蛋白质结构片段, 并组装成完整的目标结构.片段组装过程如图2所示.这里定义插入长度为M, 片段长度为L, M≤ L, 图示表明了片段组装的三个关键过程:① 选择开始插入的位置; ② 从片段库中选择用于该位置组装的片段; ③ 从选定的片段中选择插入长度M.

图2 片段组装过程示意图Fig.2 Fragment assembly process

通过片段组装, 一方面可以极大地减小搜索空间, 能够显著地提高计算速度; 另一方面, 由于蛋白质三维结构表现出一定的层次性和规律性, 许多序列同源性很低的远源蛋白质也存在相似的结构片段折叠模式, 因此, 通过该方法可以构建更为合理的蛋白质三维结构模型.一般来讲, 采用纯粹的优化技术, 目前只能得到序列长度为5~20个左右的多肽链公认稳定构象; 而引入片段组装, 则可以得到序列长度为150的高精度预测结构[17].

1.4 动态步长构象空间搜索过程

蛋白质片段组装技术的应用可以提高蛋白质结构预测的精度.现有的方法利用片段组装技术是在整个构象空间搜索过程中使用固定的片段组装次数(FA步长), 一般为N-2次(N为序列长度), 这样的设置很有可能由于步长偏大使得在构象空间中能量较低的地方忽略掉一些近天然态的构象, 而这些构象很有可能就是期望的构象.又由于蛋白质分子构象能量超曲面极其粗糙, 存在数目众多的构象能量势垒, 基本的蒙特卡洛算法往往存在某些不可达状态, 极易陷入局部极小值.为了实现各态遍历平衡条件, 现有的文献主要从采样方法和构象更新方法两个方面进行改进.在构象更新方面, 代表性的工作有能量极小化[40], 片段组装[41]及网格约束[18]等技术; 在采样方法改进方面, 基本思想是采用扩展的玻尔兹曼的权重进行采样, 对于不同的能量使用不同的温度子集, 以此来越过能量势垒.

本文由此提出了动态步长构象空间搜索方法.构象空间按温度分层, 在不同的温度层, 采用相应温度参数的Boltzmann准则接收当前构象, 在构象空间中搜索构象时采用动态步长.在构象空间能量较高的区域, 使用较大的FA步长和较小的MC步长, 迫使算法更快地向低能量区域搜索; 随着构象搜索逐步向低能量区域靠近, 在减小FA步长的同时增大MC步长, 以避免对天然态构象的采样不足导致算法有效性的降低.这里, FA, MC步长分别按照式(7)(8)计算:

M(N-2)ω(l)/∑l'∈GEω(l'(7)

Q(N-2)ω(χ)/∑l'∈GEω(l', χ+l=n(8)

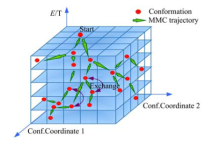
式中:N为序列长度, M, Q为常数.在构象搜索过程中, 同时引入了副本交换, 与常规的副本交换方法不同, 这里副本交换仅发生在前后两次产生的构象处于相邻的能量层时.采取这样的设计是因为随着不同构象间温度差值的增加, 副本交换接收的概率会急剧下降[21], 使副本交换只发生在前后两次产生的构象处于相邻的能量层的情况下, 一方面可以保留副本交换的优点, 即可以对构象空间有足够的采样点, 使得构象能够跳出局部极值点; 另一方面, 可以降低算法的复杂度.动态步长构象空间搜索过程如图3所示.

图3 动态步长搜索过程示意图Fig.3 The dynamic-step-size searching process

图3中红色的圆点表示构象, 绿色箭头表示构象更新MMC轨迹, 紫色双向箭头表示构象副本交换.搜索过程由初始点Start开始, 按动态步长逐步向低能量区域搜索, 当前构象和前一个构象处在相邻温度层时发生副本交换, 整个搜索过程形成了马尔科夫链, 这一搜索过程也称为马尔科夫过程.

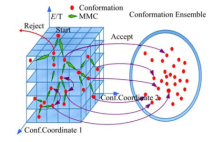
图4 构象系综更新过程示意图Fig.4 The update process of conformation ensemble

在构象搜索过程中, 需要将搜索得到的构象动态地保存下来, 用于进一步分析, 构象动态更新过程如图4所示, 图中红色的圆点表示构象, 绿色箭头表示构象更新的MMC轨迹, 右侧圆环表示构象系综.对给定的氨基酸序列随机扰动得到初始构象, 存入相应的cell, 并置入构象系综.此后, 由初始构象得到的每一个构象Cnew使用Metropolis准则判断是否接收:若拒绝, 则丢弃当前构象; 若接收, 则将其置入构象系综, 进行下一次迭代, 如此循环直至满足设定的终止条件.

2 动态步长构象空间搜索算法

动态步长构象空间搜索算法流程描述如下:

Step1 选择粗粒度能量模型(Rosetta Score3);

Step2 构象空间初始化:

① 对构象空间按能量和温度分层

② 对所分能量层赋权重

③ 设置温度参数列表

④ 划分能量层为"构象室"cell

⑤ 对"构象室"分配权重

⑥ 构象初始化Cinit

Step3 设置FA, MC步长, 终止条件为迭代次数达到10 000;

Step4 判断是否满足终止条件;

Step5 是, 转到Step12;

Step6 否, 依相应权重随机选择能量层, cell, Conf;

Step7 按所设动态步长对所选构象进行片段组装, 蒙特卡洛扰动生成新的构象;

Step8 判断是否进行副本交换;

Step9 是, 则进行副本交换, 更新cell, 构象系综ensemble;

Step10 否, 直接更新cell, 构象系综ensemble;

Step11 返回Step4;

Step12 结束.

3 实验结果分析
3.1 测试环境及测试蛋白选取

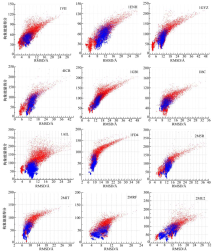
基于Rosetta生物分子建模软件, 在原有功能的基础上进行扩展, 采用Python语言实现动态步长构象空间搜索算法.运行环境为64位Linux系统, 内存40 G.迭代次数设置为10 000次; 动态步长FA和MC的参数M, Q分别设置为M=Q=[1, 2, 4]; 温度参数kBT列表为[32, 34, 36, 38, 40, 42, 44, 46, 48, 50, 52, 54, 56, 58, 60, 62, 64, 66].本文选取了12个蛋白质(1VII, 1ENH, 1GYZ, 4ICB, 1GB1, 1I6C, 1AIL, 1FD4, 2M5R, 2MIT, 2MRF, 2MU2)测试动态步长蛋白质构象空间搜索方法, 它们从蛋白质PDB库(http://www.rcsb.org)下载, 序列长度从26到80, 折叠类型有α , α /β , β 三种, 并与Shehu研究小组FeLTr方法进行比较.

3.2 测试结果分析

算法在各蛋白质上测试的结果如图5所示, 图中横坐标表示预测结构和实验方法测定结构的相似度指标RMSD值, 单位为Å ; 纵坐标表示构象能量得分, 红色为采用动态步长搜索方法得到的实验结果, 蓝色为根据参考文献[23, 24, 25, 26, 27]得到的实验结果.蛋白质预测结构和实验方法测定结构的三维相似性对比如图6所示, 图中绿色, 青色和粉色的结构分别为实验室测定结构, 动态步长搜索方法所得到的预测结构, 根据文献[23, 24, 25, 26, 27]实验得到的预测结构.测试蛋白信息及由不同算法计算得到的预测结构和实验方法测定的结构最小相似度指标RMSD值如表1所示.表1中DSSM为采用本文所提出的动态步长构象空间搜索方法得到的数据, Shehua为文献[23, 24, 25, 26, 27]中所列的数据(其中, 序号为9-12的4个蛋白质是2014年最新实验方法测定结构的蛋白质, 文献中没有相应的数据, 表中用* * * 表示), Shehub为根据文献[23, 24, 25, 26, 27]得到的实验数据.

图5 测试结果图Fig.5 Test results

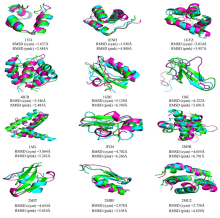图6 预测结构和实验方法测定结构的三维相似性对比图Fig.6 The 3D similarity comparison between predicted structures and experimental structures

表1 不同算法测试结果对比 Table 1 Comparison between Different Algorithms

图5表明, DSSM方法(红色)较FeLTr方法(蓝色)有更好的全局和局部搜索能力:DSSM方法能够在更为广阔的构象空间中采样, 并且逐步趋向能量更低的区域; 而FeLTr方法的搜索区域明显较小且对低能量区域的采样稍显不足.图6清晰地展示了采用DSSM方法和FeLTr方法得到的蛋白质三维结构与实验室测定的结构之间的相似程度:对于α 螺旋结构, 青色与绿色结构的重叠区域明显较粉色与绿色结构的重叠区域多, 但是对于β 折叠和loop结构, DSSM方法并没有表现出明显的优势.以上测试结果表明, 所提动态步长蛋白质构象空间搜索方法与预期一致:适当减少了在高能量区域的搜索次数, 降低了对高能量区域构象的采样频率, 使得算法能够快速地向天然态构象更可能处在的低能量区域搜索; 在低能量区域, 足够而又不过量的采样使得算法能够更好地搜索到近天然态构象; 副本交换的引入使得算法对整个构象空间的采样能力进一步增强; 构象空间按温度分层, 采用不同参数判断接受或拒绝构象的设计, 加强了算法跨越能量障碍, 跳出局部极值点的能力, 有效避免了算法"早熟"[42]的问题.从而, 使得算法能够快速有效的搜索得到蛋白质近天然态构象.就测试结果而言:对于多数测试蛋白, 如:1VII, 1ENH, 1GYZ, 4ICB, 1GB1, 1AIL, 1FD4, 2M5R, 2MRF, 2MU2, 本文提出的动态步长搜索方法较Shehu研究小组所设计的FeLTr方法有更强的采样能力, 能够对构象空间进行足够的采样, 对局部极小点的采样能力以及搜索得到的结构精度也优于FeLTr方法, 在跳出局部极值点, 避免算法早熟的问题上, 也较之有明显的优势, 算法的收敛速度也有一定的提升; 但是对于折叠类型为β 的蛋白质, 测试效果并不理想, 如1I6C, 2MIT, 其序列长度为26和32, 但是预测精度仅为4.322Å 和4.6564Å .可能造成这种结果的因素有很多:首先, 一个重要的原因是, 折叠类型为β 的蛋白质原子间作用力多为远距离作用, 这导致了力场模型可能不够精确, 进而使得所构建的能量函数不精确; 其次, 片段库的质量问题和选择的片段长度和插入长度可能是造成这种结果的又一原因; 最后, 构象空间的能量曲面的粗糙性也可能使得在搜索过程中陷入局部极小值.

4 结束语

本文提出的动态步长蛋白质构象空间搜索方法通过蛋白质构象特征提取, 将高维二面角优化空间映射到低维结构特征向量空间, 有效避免了维数灾难问题; 根据能量和温度测度离散化特征空间为多个能量层和温度层, 并系统划分为"构象室", 减小构象空间搜索范围; 赋予不同能量层相应的片段组装步长和蒙特卡洛扰动步长, 在不同的温度层采用相应的Metropolis准则来接收当前构象, 使用动态步长令算法更快地向低能量区域搜索, 温度分层使得构象空间中某些局部极小点更容易越过能量势垒, 避免陷入局部极小点, 从而更好地向全局极小点搜索; 副本交换进一步增强了算法对整个构象空间的采样能力.测试结果表明:动态步长构象空间搜索方法在所选取测试蛋白上取得了较好的测试效果, 是一种有效的构象空间采样方法.

在下一步的研究中, 将针对折叠类型为β 的蛋白质, 充分考虑原子远距离作用的影响, 建立更为合理的力场模型和相对精确的能量函数; 进一步构建兼具多样性和代表性的片段库, 合理设定片段长度和片段插入长度; 设计更为有效的构象空间优化算法, 以提高蛋白质结构预测的精度.

The authors have declared that no competing interests exist.

参考文献
[1] Ken A Dill, Justin L, Mac Callum. The protein folding problem, 50 years on[J]. Science, 2012, 338(11): 1042-1046. [本文引用:1]
[2] Anfinsen C. Principles that govern the folding of protein chains[J]. Science, 1973, 181(96): 223-230. [本文引用:1]
[3] 许忠能. 生物信息学[M]. 北京: 清华大学出版社, 2008. [本文引用:1]
[4] Kim D E, Blum B, Bradley P, et al. Sampling bottlenecks in de novo protein structure prediction[J]. Journal of Molecular Biology, 2009, 393(1): 249-260. [本文引用:1]
[5] 黄俊峰, 段鹏, 吴文言. 基于模板的蛋白质结构预测[J]. 生物物理学报, 2011, 27(1): 28-37.
Huang Jun-feng, Duan Peng, Wu Wen-yan. Protein structure prediction based on the template[J]. Acta Biophysica Sinica, 2011, 27(1): 28-37. [本文引用:1]
[6] Kryshtafovych A, Fidelis K, Moult J. CASP10 results compared to those of previous CASP experiments[J]. Proteins: Structure, Function, and Bioinformatics, 2014, 82(S2): 164-174. [本文引用:1]
[7] Beliakov G, Lim K F. Challenges of continuous global optimization in molecular structure prediction[J]. European Journal of Operational Research, 2007, 181(3): 1198-1213. [本文引用:1]
[8] Tantar A A, Melab N, Talbi E G, et al. A parallel hybrid genetic algorithm for protein structure prediction on the computational grid[J]. Future Generation Computer Systems, 2007, 23(3): 398-409. [本文引用:1]
[9] Hoque M T, Chetty M, Lewis A, et al. Twin removal in genetic algorithms for protein structure prediction using low-resolution model[J]. Computational Biology and Bioinformatics, IEEE/ACM Transactions on, 2011, 8(1): 234-245. [本文引用:1]
[10] Islam M K, Chetty M. Clustered memetic algorithm with local heuristics for Ab-initio protein structure prediction[J]. IEEE Transactions on Evolutionary Computation, 2013, 17(4): 558-576. [本文引用:1]
[11] Custódio F L, Barbosa H J C, Dardenne L E. A multiple minima genetic algorithm for protein structure prediction[J]. Applied Soft Computing, 2014, 15: 88-99. [本文引用:1]
[12] Duan Y, Kollman P A. Pathways to a protein folding intermediate observed in a 1-microsecond simulation in aqueous solution[J]. Science, 1998, 282(5389): 740-744. [本文引用:1]
[13] Scheraga H A, Khalili M, Liwo A. Protein folding dynamics: overview of molecular simulation techniques[J]. Annu Rev Phys Chem, 2007, 58: 57-83. [本文引用:1]
[14] Lindorff-Larsen K, Trbovic N, Maragakis P, et al. Structure and dynamics of an unfolded protein examined by molecular dynamics simulation[J]. Journal of the American Chemical Society, 2012, 134(8): 3787-3791. [本文引用:1]
[15] Zhang Y, Kihara D, Skolnick J. Local energy land scape flattening: parallel hyperbolic Monte Carlo sampling of protein folding[J]. Proteins: Structure, Function, and Bioinformatics, 2002, 48(2): 192-201. [本文引用:1]
[16] Shen Y, Picord G, Guyon F, et al. Detecting protein cand idate fragments using a structural alphabet profile comparison approach[J]. PloS One, 2013, 8(11): e80493. [本文引用:1]
[17] Xu D, Zhang Y. Toward optimal fragment generations for ab-initio protein structure assembly[J]. Proteins: Structure, Function, and Bioinformatics, 2013, 81(2): 229-239. [本文引用:2]
[18] Dotu I, Cebrian M, Van Hentenryck P, et al. On lattice protein structure prediction revisited[J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2011, 8(6): 1620-1632. [本文引用:2]
[19] Tyka M D, Jung K, Baker D. Efficient sampling of protein conformational space using fast loop building and batch minimization on highly parallel computers[J]. Journal of Computational Chemistry, 2012, 33(31): 2483-2491. [本文引用:1]
[20] Joo K, Lee J, Sim S, et al. Protein structure modeling for CASP10 by multiple layers of global optimization[J]. Proteins: Structure, Function, and Bioinformatics, 2014, 82(S2): 188-195. [本文引用:1]
[21] Sugita Y, Okamoto Y. Replicae-xchange molecular dynamics method for protein folding[J]. Chemical Physics Letters, 1999, 314(1): 141-151. [本文引用:2]
[22] Sugita Y, Okamoto Y. Replica-exchange multicanonical algorithm and multicanonical replica-exchange method for simulating systems with rough energy land scape[J]. Chemical Physics Letters, 2000, 329(3): 261-270. [本文引用:1]
[23] Shehu A. An Ab-initio tree-based exploration to enhance sampling of low-energy protein conformations[C]∥Robotics: Science and Systems, 2009: 241-248. [本文引用:5]
[24] Shehu A, Olson B. Guiding the search for native-like protein conformations with an Ab-inito tree-based exploration[J]. Robotics Research, 2010, 29(8): 1106-1127. [本文引用:5]
[25] Olson B, Molloy K, Shehu A. In search of the protein native state with a probabilistic sampling approach[J]. Journal of Bioinformatics and Computational Biology, 2011, 9(3): 383-398. [本文引用:5]
[26] Olson B, Shehu A. Evolutionary-inspired probabilistic search for enhancing sampling of local minima in the protein energy surface[J]. Proteome Sci, 2012, 10(Suppl 1): S5. [本文引用:5]
[27] Molloy K, Saleh S, Shehu A. Probabilistic search and energy guidance for biased decoy sampling in Ab initio protein structure prediction[J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics (TCBB), 2013, 10(5): 1162-1175. [本文引用:5]
[28] 周建红, 艾观华, 方慧生, 等. 蛋白质结构从头预测方法研究进展[J]. 生物信息学, 2011, 9(1): 1-5.
Zhou Jian-hong, Ai Guan-hua, Fang Hui-sheng, et al. Progress in ab initio protein structure prediction[J]. Bioinformatics, 2011, 9(1): 1-5. [本文引用:1]
[29] Bradley P, Misura K M, Baker D. Toward high-resolution de novo structure prediction for small proteins[J]. Science, 2005, 309(5742): 1868-1871. [本文引用:1]
[30] Liwo A, Khalili M, Scherage H A. Ab-initio simulations of protein-folding pathways by molecular dynamics with the united-residue model of polypeptide chains[J]. PNAS, 2005, 102(7): 2362-2367. [本文引用:1]
[31] Kuhlman B, Baker D. Native protein sequences are close to optimal for their structures[J]. Proceedings of the National Academy of Sciences of the Unitized States of America, 2000, 97(19): 10383-10388. [本文引用:1]
[32] Kortemme T, Morozov A V, Baker D. An orientation-dependent hydrogen bonding potential improves prediction of speci?city and structure for proteins and protein-protein complexes[J]. Journal of Molecular Biology, 2003, 326(4): 1239-1259. [本文引用:1]
[33] Enoch S Huang, Ram Samudrala, Britt H Park. Scoring functions for ab initio protein structure prediction[J]. Methods Mol Biol, 2000, 143(1): 223-245. [本文引用:1]
[34] Ballester P J, Richards W G. Ultrafast shape recognition for similarity search in molecular databases[J]. Proc R Soc A, 2007, 463(2081): 1307-1321. [本文引用:1]
[35] Lee J, Scheraga H A, Rackovsky S. New optimization method for conformational energy calculations on polypeptides: conformational space annealing[J]. Journal of Computational Chemistry, 1997, 18(9): 1222-1232. [本文引用:1]
[36] Berg B A, Neuhaus T. Multicanonical ensemble: a new approach to simulate first-order phase transitions[J]. Physical Review Letters, 1992, 68(1): 9-12. [本文引用:1]
[37] Wang G, Dunbrack R L. PISCES: a protein sequence culling server[J]. Bioinformatics, 2003, 19(12): 1589-1591. [本文引用:1]
[38] Gront D, Kulp D W, Vernon R M, et al. Generalized fragment picking in Rosetta: design, protocols and applications[J]. PLoS One, 2011, 6(8): e23294. [本文引用:1]
[39] Keaver-Fay A, Tyka M, Lewis S M, et al. ROSETTA3: an object-oriented software suite for the simulation and design of macromolecules[J]. Methods in Enzymology, 2011, 487: 545-574. [本文引用:1]
[40] Li Z, Scheraga H A. Monte Carlo-minimization approach to the multiple-minima problem in protein folding[J]. PNAS, 1987, 84(19): 6611-6615. [本文引用:1]
[41] Lee J Y, Lee J Y, Sasaki T N, et al. De novo protein structure prediction by dynamic fragment assembly and conformational space annealing[J]. Proteins, 2011, 79(8): 2403-2417. [本文引用:1]
[42] Stoean C, Preuss M, Stoean R, et al. Multimodal optimization by means of a topological species conservation algorithm[J]. Evolutionary Computation, 2010, 14(6): 842-864. [本文引用:1]