防潜在死锁的整体式自动物料搬运系统调度方法

引用本文

周炳海, 周琪. 防潜在死锁的整体式自动物料搬运系统调度方法.吉林大学学报:工学版, 2016, 46(2): 595-601
ZHOU Bing-hai, ZHOU Qi. Impending deadlock-free scheduling method for unified AMHS in semiconductor FABs. Journal of Jilin University Engineering and Technology Edition, 2016, 46(2): 595-601 复制到剪切板

Permissions

防潜在死锁的整体式自动物料搬运系统调度方法

周炳海, 周琪

同济大学机械与能源工程学院,上海 201804

作者简介:周炳海(1965-),男,教授,博士生导师.研究方向:离散系统建模,调度与仿真.E-mail:bhzhou@tongji.edu.cn

基金:国家自然科学基金项目(61273035, 71471135)

摘要

为有效解决300 mm晶圆制造中整体式自动物料搬运系统OHT路径的潜在死锁问题,提出了基于图论的死锁检测/解除策略.首先对路径的潜在死锁问题进行描述,通过定义链和共享点等概念,建立图论模型,在论证其发生的充要条件后,指出解除潜在死锁的可行方法.然后以任务完成时间最小为优化目标建立数学模型,通过对OHT运行路径上的节点依次进行死锁检测和解除来确定无死锁调度方案.仿真实验表明:该方法能够有效检测和解除OHT运行路径上的潜在死锁,提高晶圆制造系统运行的稳定性和安全性.

关键词: 潜在死锁; 整体式物料搬运系统; 无死锁调度; 路径规划

中图分类号:TP29 文献标志码:A 文章编号:1671-5497(2016)02-0595-07

Impending deadlock-free scheduling method for unified AMHS in semiconductor FABs

ZHOU Bing-hai, ZHOU Qi

School of Mechanical Engineering, Tongji University, Shanghai 201804, China

Abstract

To resolve the impending deadlock problems in the path planning of Overhead Hoist Transporters (OHTs) in unified Automatic Material Handling Systems (AMHSs) of 300 mm wafer fabrication, an impending deadlock-free path planning strategy was proposed on the basis of the graphic theory. First, the impending deadlock problems were formally described. After introducing novel concepts of chains and share points, necessary and sufficient conditions were identified and an available approach was put forward using the graphic model. Then, a mathematic model was set up with an optimal objective function of minimizing the transporting time. Finally, by executing deadlock detection and resolution steps successively, an impending deadlock-free scheduling solution was assigned. Simulation experiments indicate that the proposed strategy can effectively detect and resolve the impending deadlocks occurring in OHTs' path planning during material handling processes. Thus, it can improve the security and stability of wafer fabrication systems.

Keyword: impending deadlock; unified AMHSs; deadlock-free scheduling; path planning

Show Figures

0 引言

晶圆制造的复杂流程和整体式轨道布局的耦合特性使得高空穿梭车(Overhead hoist transporter, OHT)在物料搬运作业中极易引起路径死锁的现象.学界普遍将路径死锁分为直接死锁和潜在死锁(Impending deadlock)两大类, 潜在死锁一旦形成必然会在有限步后导致直接死锁, 且更加隐蔽, 不易探测, 因此是防死锁调度问题研究的难点.

随着整体式布局的广泛应用, 运筹学理论, 规则调度和人工智能等理论被广泛应用于其调度研究.在路径规划方面, Sha等^[1]将tool和OHT相结合, 使用决策树和调度规则的方法来提升晶圆的产量.Yang等^[2]提出将第 $\begin{matrix} K \end{matrix}$ 短路径法和路径中运行的OHT数量相结合来构建调度算法, 以实现集成动态调度.在死锁研究的技术手段方面, 目前文献采用的建模方法以Petri网和图论居多.He等^[3]采用着色Petri网对半导体制造系统中的光刻机进行建模, 仿真和分析, 最后采用死锁避免机制来实现无死锁调度.Han等^[4]采用基于遗传算法和Petri网模型对柔性制造系统进行无死锁调度.在预防轨道死锁方面, Wu等^{[5, 6]}采用着色赋时Petri网作为建模手段, 以死锁避免机制实现下层控制, 用智能指标对系统进行实时无死锁调度.Kuo等^[7]利用多智能体技术建立Intrabay的控制结构, 该结构能够完整描述OHT堵塞, 死锁和冲突解决过程.Im等^[8]使用等待关系矩阵来进行死锁检测, 而后对陷入死锁的OHT进行审查, 对能够改变运输路径的OHT进行重调度.然而上述方法所侦测和避免的多为直接死锁, 并不能有效防止潜在死锁的发生.Fanti等^[9]提出了潜在死锁的概念, 在文献^[10]中其使用有向图概念, 推导了死锁发生的充要条件, 通过引入控制规则来避免或者激发某些状态变迁.

在以往研究路径规划的文献中, 一般只考虑直接死锁的检测和解除, 然而在实际生产中, 潜在死锁更为多见和隐蔽, 对系统的稳定运行构成极大威胁.整体式轨道布局中OHT运输路径高度重叠迂回, 更增加了潜在死锁的发生概率, 因此, 对其进行检测和预防具有实际意义和理论研究价值.传统方法预防死锁一般采取的是前瞻一步的策略, 然而这并不能满足潜在死锁检测的要求.为此, 本文通过定义链和共享点等概念, 提出了基于图论的死锁检测模型, 并在此基础上构造了解除潜在死锁的有效方法.其系统开销较小, 能够高效应用于OHT物料搬运系统的实际运行, 保证晶圆生产环境的安全和稳定.

1 问题描述

300 mm半导体制造中整体式自动物料搬运系统是指将Interbay和Intrabay的轨道直接相连, 使得作为物料搬运设备的OHT无需经过存储柜暂存即可实现tool与tool之间直接搬运的布局结构, 如图1所示.

	Figure Option View Download New Window
	图1 整体式自动物料搬运系统布局示意图Fig.1 Unified layout of AMHS in FAB

为有效刻画研究问题域, 做如下基本假设:① 自动物料搬运系统采用脊柱型布置; ② 晶圆搬运路径及停驻时间需要在调度过程中决定; ③ OHT在轨道上同向, 同速运行; ④ 在轨道上的机器的装卸载处及轨道的交叉点处设置节点, OHT只能在节点处驻停; ⑤ 每个节点同一时刻只允许一辆OHT运行或驻停, 节点间允许多辆OHT依次通过, 但不允许并行或超越.

为深入分析问题, 对路径上相关变量描述如下:假设系统中OHTi所装载的任务规划路径为 $\begin{matrix} P_{i} = (p_{i, 1}, p_{i, 2}, \dots, p_{i, n_{i}}) \end{matrix}$ , 其中p_{i, j} 表示其路径上经过的第j个节点; 设x_{i, j}表示OHTi的第j个节点当前时刻占用情况, 若该节点已被OHTk占用, 则x_{i, j}=k, 称为实点, 否则x_{i, j}=0, 称为空点.由以上定义, 若当前时刻OHTi运行到第j^* 个节点, 显然有 $x_{i, j^{*}} = i$ .下面引出相关死锁的引理, 推论与定理.

引理1 (一级死锁) 若在一组OHTA=(A₁, A₂, , et al., A_n)中, 设OHTk当前所在节点在其路径中序号为m, ∀ k有 $\begin{matrix} x_{k, m + 1} \in A, 且 x_{k, m + 1} \neq x_{k', m' + 1}; k, m, k', m' = 1, 2, \dots, n, \end{matrix}$ 则发生一级死锁, 如图2(a)所示.

	Figure Option View Download New Window
	图2 一级, 二级和n级死锁示意图Fig.2 Deadlock of level 1, 2 and n

证明由于对∀ k, 其下一节点x_{k, m+1}≠ 0, 因此必须等待, 设当前占据OHTk路径序号 $\begin{matrix} m \end{matrix}$ 节点的为OHTk'处于其路径序号m', 由于x_{k', m'+1}≠ 0, 因此系统陷入循环等待, 即进程死锁.

定理1 (二级死锁) 若在两组OHTA_i=( $\begin{matrix} A_{i_{1}} \end{matrix}$ , $\begin{matrix} A_{i_{2}} \end{matrix}$ , , et al., $\begin{matrix} A_{i_{n}} \end{matrix}$ ), i=1, 2中, 设OHTk当前所在节点在其路径中序号为m, 若x_{k, m+1}≠ 0, k∈ A_p 有x_{k, m+1}∈ A_p, 若x_{k, m+1}=0, k∈ A_p, 且有x_{k, m+2}∈ A_p', p≠ p', 则发生二级死锁.

证明由于对∀ k, 若其下一节点x_{k, m+1}≠ 0, 其必须等待, 若x_{k, m+1}=0, 如果无潜在死锁机制控制, 则OHTk会进入其第m+1个节点, 但是x_{k, m+2}≠ 0, 由引理1可知, 系统必然会发生一级死锁.

推论1 (N级死锁)在N组OHTA_i=( $\begin{matrix} A_{i_{1}} \end{matrix}$ , $\begin{matrix} A_{i_{2}} \end{matrix}$ , , et al., $\begin{matrix} A_{i_{n}} \end{matrix}$ )中, 若对x_{k, m+1}≠ 0, k∈ A_p 有x_{k, m+1}∈ A_p, 若x_{k, m+1}=0, k∈ A_p 且有x_{k, m+2}∈ A_p', p≠ p'; p, p'=1, 2, , et al., N, 则发生N级死锁.

为有效侦测到整体式布局下自动物料搬运系统中OHT运行路径所存在的潜在死锁问题, 以下结合图论思想, 构造潜在死锁的有向图表示方法, 在此基础上证明死锁的形成和解除的充要条件, 最后提出死锁避免的策略.

定义1 (链) 构造链 $R_{l} = (v_{l_{1}}, v_{l_{2}}, \dots, v_{l_{n}})$ ; 其中 $v_{l_{i}} \neq v_{l_{j}}; i, j = 1, 2, \dots, n$ , 设点l_i 为小车k_i 的第m_i 个节点, 对∀ i, 若有 $x_{k_{i}, m_{i} + 1} = k_{i + 1}$ , 则继续将点l_i 加入链中, 否则R_l的构造终止.

定义2 (顺向链与逆向链) 以y_i 计数点i成为空点的次数, 根据链的构造方法, 对链尾点n, 显然 $x_{k_{n}, m_{n} + 1} = 0$ , 设 $p_{k_{n}, m_{n} + 1} = i$ , 若y_i=0, 则标记 $p_{k_{n}, m_{n}}$ 所在的链为顺向链, 若y_i=1, 则标记为逆向链.

定义3 (共享点) 由以上定义, 顺向链中, 设空点序号为i点的前链序号为f_i, 后链序号为f_i+1; 逆向链中, 其前链序号为b_i, 后链序号为b_i+1 .若有 $x_{k_{(f_{i})_{n}}, m_{(f_{i})_{n}} + 2} = (f_{i + 1})_{1}$ 且 $x_{k_{(b_{i} {+ 1)}_{n}}, m_{(f_{i})_{n}} + 2} = (b_{i})_{1}$ 则称该点为共享点.

定理2 若图中共有两条链, 一个共享点, 则二级死锁成立.

证明由共享点定义, $x_{k_{{(1)}_{n}}, m_{{(1)}_{n}} + 2} = {(2)}_{1}$ , 即第一条链的链尾点的下下节点为第二条链的首节点, $x_{k_{{(2)}_{n}}, m_{{(2)}_{n}} + 2} = {(1)}_{1},$ 即第二条链的链尾点的下下节点为第一条链的首节点.如图2(b)可知, 无论是哪条链的链尾点OHT进入共享点, 都将导致死锁.

推论2 若图中共有2(n-2)+2条链, n-1个共享点, 则n级死锁成立.设空点序号为i, 有f_i=i; b_i=2n-i-1.

由图2(c)可以看到, 潜在死锁的链结构一旦形成, 则必然会在有限步之后陷入死锁, 但由于其较为隐蔽, 因此并不能被一般的死锁探测机制所侦测到, 因此导致的不合理调度会严重损害系统产能, 导致死锁发生.根据所构造的潜在死锁图论模型, 本文提出了相应的解除方法.

定理3 如果在潜在死锁链形成的前一时刻, $\begin{matrix} \exists v_{i} \in R_{l}, i \neq l_{n}, \end{matrix}$ 设其为OHTk_i的第m_i个节点, 有OHT $\begin{matrix} x_{k_{i}, m_{i} + 1} \end{matrix}$ , 则可以避免死锁发生.

证明如图3所示的二级死锁为例, 始终保证某一链的链尾点可变为空点, 此时采用顺向链和逆向链依次进入共享点的方法, 就可以有效避免死锁发生.

	Figure Option View Download New Window
	图3 二级死锁解除示意图Fig.3 Deadlock resolution of level 2

下面结合上述图论模型建立防潜在死锁的调度问题数学模型.设共有任务N个, 对某一任务i来说, 假设其搬运路径为 $P_{i} = (p_{i, 1}, p_{i, 2}, \dots, p_{i, n_{i}})$ , 定义 $t_{i, j}^{in}$ 为OHTi进入节点 $\begin{matrix} p_{i, j} 的时间, t_{i, j}^{out} \end{matrix}$ 为OHTi离开节点 $\begin{matrix} p_{i, j} \end{matrix}$ 的时间, 由于只能在节点处驻停, 其进出路径首尾节点有如下约束:

$t_{i, j + 1}^{in} = t_{i, j}^{out} + d (p_{i, j}, p_{i, j + 1}) / v$ (1)

$t_{i, j}^{out} \geq t_{i, j}^{in}$ (2)

对多辆OHT来说, 要避免潜在死锁, 则需要有:

$\begin{matrix} \exists x_{i, j + 1} = 0, v_{i} \in R_{l}, i \neq l_{n} \end{matrix}$ (3)

又由于节点间允许多辆OHT依次通过, 但不允许并行或超越, 假设 $\begin{matrix} p_{i, j} = p_{i', j'}, p_{i, j + 1} = p_{i', j' + 1}, \end{matrix}$ 需有:

$\begin{matrix} (t_{i, j}^{in} - t_{i', j'}^{in}) (t_{i, j + 1}^{out} - t_{i', j' + 1}^{out}) > 0 \end{matrix}$ (4)

以上各式均有 $\begin{matrix} i, i' = 1, 2, \dots, N; j, j' = 1, 2, \dots, n 。 \end{matrix}$

令T(P_i)为路径P_i 所需要时间, 调度目标为从所有满足约束的路径中找到最短路径P_i, 使得搬运时间最少, 即:

$\begin{matrix} \min \overset{N}{\sum_{i = 0}} (T (P_{i})) \end{matrix}$ (5)

则该问题可以表述为目标函数为式(5), 式(1)~(4)为约束的非线性规划问题.

2 算法构建

为防止整体式布局下自动物料搬运系统中的潜在死锁, 结合上述图论模型进行死锁的侦测和解除.通过采用"look forward"的死锁避免策略, 当检测到下一时刻会构成潜在死锁链结构时, 延迟当前OHT进入其下一节点, 同时对已形成的死锁链进行死锁解除.其具体方法为, 通过始终保持链中至少有一个节点在当前时刻为空点, 使得链尾节点的OHT依次有序地占用共享点, 防止OHT出现循环等待.

2.1 死锁检测模块

假设有 $\begin{matrix} N \end{matrix}$ 辆OHT, 每辆OHT路径需经过n_i个节点.令i=0链序号cx=0链内节点序号cy=0, 共享点序号cz=0

步骤1 令i=i+1对任务 $\begin{matrix} i \end{matrix}$ 规划最短路径, 令 $\begin{matrix} j \end{matrix}$ 为节点在其路径上的序号, j=0

步骤2 j=j+1开始死锁检测.设置指针, $\begin{matrix} cp 、 cr \end{matrix}$ 分别为占据当前节点的OHT序号和该节点在其路径中序号; $\begin{matrix} pr 、 pp \end{matrix}$ 分别为占据当前节点前一节点的OHT序号和该节点在其路径中序号, $\begin{matrix} ar 、 ap \end{matrix}$ 分别为占据当前节点后一节点的OHT序号和该节点在其路径中序号.首先令 $\begin{matrix} pr = i; pp = j; cr = i; cp = j + 1 。 \end{matrix}$ 设OHT $\begin{matrix} k \end{matrix}$ 目前占据节点 $\begin{matrix} (cr, cp), \end{matrix}$ 其处于路径上的第 $\begin{matrix} m \end{matrix}$ 个节点, 则有 $\begin{matrix} ar = k; ap = m 。 \end{matrix}$

步骤3 若 $\begin{matrix} x_{cr, cp} = 0, \end{matrix}$ 转步骤4, 否则转至步骤5.

步骤4 若 $\begin{matrix} x_{pr, pp} = 0, \end{matrix}$ 则无潜在死锁, 退出死锁检测模块, 否则转至步骤6.

步骤5 若 $\begin{matrix} x_{pr, pp} = 0, \end{matrix}$ 以 $\begin{matrix} z_{c_{r}, c_{p}} \end{matrix}$ 计数该点成为实点的次数, 若 $\begin{matrix} z_{c_{r}, c_{p}} = 0, \end{matrix}$ 则将该实点加入当前链, 链内节点计数 $\begin{matrix} cy = cy + 1, \end{matrix}$ 实点计数 $\begin{matrix} z_{c_{r}, c_{p}} = z_{c_{r}, c_{p}} + 1, \end{matrix}$ 移动指针 $\begin{matrix} cr = ar; cp = ap, \end{matrix}$ 转入步骤3, 否则转入步骤8.若 $\begin{matrix} x_{pr, pp} \neq 0, \end{matrix}$ 转入步骤9.

步骤6 以 $\begin{matrix} y_{c_{r}, c_{p}} \end{matrix}$ 计数该点成为空点的次数, 若 $\begin{matrix} y_{c_{r}, c_{p}} = 0, \end{matrix}$ 则将该空点作为新的共享点, 共享点计数 $\begin{matrix} cz = cz + 1; y_{c_{r}, c_{p}} = y_{c_{r}, c_{p}} + 1 。 \end{matrix}$ 链序号计数 $\begin{matrix} cx + +, \end{matrix}$ 链内节点计数归零 $\begin{matrix} cy = 0, \end{matrix}$ 下一个检测到的实点将加入新的顺向链中.移动指针 $\begin{matrix} cr = ar; cp = ap, \end{matrix}$ 转至步骤3.否则转至步骤7.

步骤7 共享点重复, 则 $\begin{matrix} cz \end{matrix}$ 不变.下一个检测到的实点将加入新的逆向链, 链序号计数 $\begin{matrix} cx + +, \end{matrix}$ 链内节点计数归零 $\begin{matrix} cy = 0 。 \end{matrix}$ 移动指针 $\begin{matrix} cr = ar; cp = ap 。 \end{matrix}$ 转至步骤3.

步骤8 将当前点所在的链 $\begin{matrix} R_{cr} \end{matrix}$ 插入 $\begin{matrix} R_{1} \end{matrix}$ 链首, $\begin{matrix} v_{{(1)}_{p} + {(cr)}_{n}} = v_{{(1)}_{p}}; p = 1, 2, \dots, {(1)}_{n}; v_{{(1)}_{q}} = v_{{(cr)}_{q}}; q = 1, 2, \dots, {(cr)}_{n}, \end{matrix}$ 潜在死锁链构造完毕进入下一阶段.

步骤9 如果 $\begin{matrix} z_{c_{r}, c_{p}} = 0 \end{matrix}$ , 将当前点所在的链 $\begin{matrix} R_{cr} \end{matrix}$ 插入 $\begin{matrix} R_{1} \end{matrix}$ 链首, $\begin{matrix} v_{{(1)}_{p} + {(cr)}_{n}} = v_{{(1)}_{p}}; p = 1, 2, \dots, {(1)}_{n}; v_{{(1)}_{q}} = v_{{(cr)}_{q}}; q = 1, 2, \dots, {(cr)}_{n}, \end{matrix}$ 潜在死锁链构造完毕进入下一阶段; 否则将当前节点加入当前链, 链内节点计数 $\begin{matrix} cy = cy + 1, \end{matrix}$ 实点计数 $\begin{matrix} z_{c_{r}, c_{p}} = z_{c_{r}, c_{p}} + 1, \end{matrix}$ 移动指针 $\begin{matrix} cr = ar; cp = ap, \end{matrix}$ 转入步骤3.

步骤10 若 $\begin{matrix} j < n_{i}, \end{matrix}$ 则转至步骤2, 否则转至步骤11.

步骤11 若 $\begin{matrix} i < N, \end{matrix}$ 则转至步骤1, 否则死锁检测结束.

2.2 死锁解除模块

首先将死锁检测模块得到的链, 链内节点和共享点按照构造顺序进行标号.

步骤1 得到最晚进入该链结构的OHT, 假设其所在位置为R_i的第j个节点.

步骤2 设mr为当前链尾节点OHT可以进入共享点的链序号.如果 $\begin{matrix} j \neq 0, \end{matrix}$ 令 $\begin{matrix} v_{p + 1} = v_{p}; p = 1, 2, \dots, j - 1, \end{matrix}$ 此时可得 $\begin{matrix} x_{{(i)}_{1}} = 0, \end{matrix}$ 即 $\begin{matrix} R_{i} \end{matrix}$ 的链头节点已成为空点, $\begin{matrix} mr = i - 1, \end{matrix}$ 并更新之前允许移动的相关节点上OHT的运行时间; 否则直接令 $\begin{matrix} mr = i \end{matrix}$ , 转至步骤3.

步骤3 若 $\begin{matrix} R_{mr} \end{matrix}$ 为顺向链, 则允许在 $\begin{matrix} R_{mr - 1} \end{matrix}$ 链尾节点的OHT进入第 $\begin{matrix} mr - 1 \end{matrix}$ 个共享点; 若 $\begin{matrix} R_{mr} \end{matrix}$ 为逆向链, 则允许在 $\begin{matrix} R_{mr - 1} \end{matrix}$ 链尾节点的OHT进入第 $\begin{matrix} 2 n - mr \end{matrix}$ 个共享点, 其中 $\begin{matrix} n \end{matrix}$ 为潜在死锁的级数, 准许进入共享点次数 $\begin{matrix} pt = pt + 1 。 \end{matrix}$ 更新允许移动的相关节点上OHT的运行时间.

步骤4 对链 $\begin{matrix} mr \end{matrix}$ 中各点, 令 $\begin{matrix} v_{p} = v_{p + 1}; p = 1, 2, \dots, n_{mr - 1}, \end{matrix}$ 更新允许移动的相关节点上OHT的运行时间.

步骤5 若 $\begin{matrix} pt < 2 n - 2; mr > 1, \end{matrix}$ 令 $\begin{matrix} mr = mr - 1, \end{matrix}$ 否则令 $\begin{matrix} mr = 2 n - 2, \end{matrix}$ 回到步骤3.

步骤6 死锁解除阶段结束.

3 仿真实验与分析

为评价本文所提出的防潜在死锁的整体式半导体自动物料搬运系统调度方法, 引入以下变量来衡量该调度结果的优劣.ACT表示晶圆搬运任务平均耗时, 该值越小, 则物料搬运系统运行效率越高; AWT表示搬运任务平均等待时间, 该值越小, OHT利用率越高; ATT表示任务平均搬运时间, 该值越小, 物料搬运系统运行效率越高.将本文提出的滚动时域调度方法用C++编程实现, 并在主频为2.00 GHz, 内存2 GB的便捷式计算机上运行, 实验结果和分析如下.

3.1 运算时间分析

分别设系统内的intrabay数目为6, 8, 10, 12, 14, 16, 18, 每个intrabay内设置6台tool, OHT数量M=20任务数量N=40取整个仿真程序运行时间的平均值, 如图4所示.

	Figure Option View Download New Window
	图4 算法运行时间Fig.4 Running time of the algorithm

从图4可知:整个程序运行时间随intrabay数量增加而缓慢递增, 即运行时间与轨道上节点数量成正相关.但总体而言, 相较于OHT搬运任务的运输时间和晶圆的加工周期, 计算调度方案所需时间可以忽略不计, 因此本文提出的调度方法能够快速便捷地得到预防潜在死锁的路径规划方案, 适用于实际生产调度.

3.2 搬运工具数目对搬运效率影响

设intrabay数目为8, 每个intrabay内设置6台tool, 任务数量 $\begin{matrix} N = 40, \end{matrix}$ 分别令OHT数量 $\begin{matrix} M = 10, 15, 20, 25, 30, \end{matrix}$ 任务的搬运效率相关指标如图5所示.

	Figure Option View Download New Window
	图5 OHT数目对调度结果影响Fig.5 Relationship between ACT, AWT and the number of OHTs

从图5可知:在相同任务数量的情况下, 由于OHT数量增加, 物料搬运系统运力提高, 算法得到的任务平均等待时间下降较为明显, 但任务平均运输时间下降稍平缓, 在小规模布局中, 这可能是由于OHT阻塞或者频繁死锁解除造成的延迟等待而对系统性能造成影响, 因此需要经过权衡合理减少OHT数量, 以减少轨道上的阻塞和等待.

3.3 布局规模对搬运效率影响

分别设系统内的intrabay数目为8, 12, 16, 20, 24, 每个intrabay内设置6台tool, OHT数量 $\begin{matrix} M = 40, \end{matrix}$ 任务数量 $\begin{matrix} N = 60, \end{matrix}$ 任务的搬运效率表现如图6所示.

	Figure Option View Download New Window
	图6 intrabay数量对调度结果影响Fig.6 Relationship between ACT, AWT, ATT and the number of intrabays

由图6可知:任务平均完成时间和等待时间均显著增加, 但其平均运输时间趋向平稳, 这表明系统布局规模增大时, 任务平均完成时间的增加主要是由于空驶路径的增长, 说明此时系统运力配置并不能够满足要求, 因此该算法可以用来在固定的小车数目下寻找合理的intrabay布局规模, 以缩短整体完工时间.

3.4 负载率对搬运效率影响

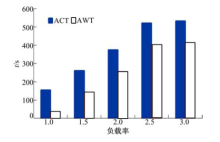
将任务数量与OHT数量的比值设置为1, 1.5, 2, 2.5, 3, 设系统内intrabay数目为10, 每个intrabay内设置6台tool, 任务的搬运效率表现如图7所示.

	Figure Option View Download New Window
	图7 负载率对调度结果影响Fig.7 Relationship between ACT, AWT and system load rate

由图7可知:在低负载的情况下, 算法性能受负载率影响较大, 完工时间和等待时间负载率增大均呈增加趋势, 其中平均等待时间增加更为显著, 但在负载率到达2.5之后两者变化明显放缓, 这表明在系统负载不平衡时, 算法表现具有一定稳定性.

3.5 与其他算法比较

由于目前文献中专门针对防止潜在死锁调度方法的研究较少, 因此引用文献[8]中只预防直接死锁的调度方法作为比较的下界, 观察搬运效率的表现情况.分别令系统内的intrabay数目为8, 12, 16, 20, 24, 每个intrabay内设置6台tool, OHT数量 $\begin{matrix} M = 30, \end{matrix}$ 任务数量 $\begin{matrix} N = 40, \end{matrix}$ 任务的搬运效率(ACT)表现如图8所示.

	Figure Option View Download New Window
	图8 调度结果与文献算法比较Fig.8 System performance compared with the benchmark

从图8可知:在小规模布局中, 两者的差距随布局规模的增加而增加, 这说明了小规模系统中, 由于路径高度重叠, 潜在死锁发生的概率较大.在中等规模布局中, 两者差距较小, 由于此时系统规模和设备配置趋于合理, 死锁概率减小.而在较大规模系统布局中, 两者差距又逐渐增大, 一旦发生潜在死锁, 其牵涉的OHT数量较多, 逐步解除需要一定耗时, 因此也属于合理范围之内.

4 结束语

针对整体式自动物料搬运系统的特点, 提出了OHT路径规划中防止潜在死锁的调度方法.通过构造链和共享点的概念, 建立了能够有效侦测潜在死锁发生的图论模型, 在论证潜在死锁发生的充要条件后, 提出通过始终保证链中有至少一个空点来逐步解除死锁的策略.仿真结果表明, 本文所提出的防潜在死锁方法运行快速, 效果良好, 能够适用于大规模生产调度.本文对OHT同速, 同向运行的脊柱式布局下路径规划的防潜在死锁方法进行了探讨, 今后将针对异速, 双向以及更加复杂多变的轨道布局下潜在死锁的探测和防止策略进行深入探究.

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Sha D Y, Yang C J. The transport strategies for fully automated manufacturing in 300 mm wafer fab[J]. International Journal of Computer Integrated Manufacturing, 2009, 22(10): 962-975. [本文引用:1]
[2]	Yang J W, Cheng H C, Chiang T C, et al. Multi-objective lot scheduling and dynamic OHT routing in a 300 mm wafer fab[C]//Proceedings of IEEE International Conference on System, Man and Cybernetics, Singapore, 2008: 1608-1613. [本文引用:1]
[3]	He X Y, Wu Z M. Deadlock-free assignment of wafer processing in photolithography equipment-by using a CPN model[J]. Transactions of the Institute of Measurement and Control, 2011, 33(3/4): 422-434. [本文引用:1]
[4]	Han L B, Xing K Y, Chen X, et al. Deadlock-free genetic scheduling for flexible manufacturing systems using Petri nets and deadlock controllers[J]. International Journal of Production Research, 2014, 52(5): 1557-1572. [本文引用:1]
[5]	Wu N Q, Zhou M C. Real-time deadlock-free scheduling for semiconductor track systems based on colored timed Petri nets[J]. OR Spectrum, 2007, 29(3): 421-443. [本文引用:1]
[6]	Wu N Q, Zhou M C. Deadlock modeling and control of semiconductor track systems using resource-oriented Petri nets[J]. International Journal of Production Research, 2007, 45(15): 3439-3456. [本文引用:1]
[7]	Kuo C H, Wang C H, Huang K W. Behavior modeling and control of 300 mm fab intrabays using distributed agent oriented Petri net[J]. IEEE Transactions on Systems, Man and Cybernetics-Part A: Systems and Humans, 2003, 33(5): 641-648. [本文引用:1]
[8]	Im K Y, Kim K, Moon Y, et al. The deadlock detection and resolution method for a unified transport system[J]. International Journal of Production Research, 2010, 48(15): 4423-4435. [本文引用:1]
[9]	Fanti M P, Maione G, Turchiano B. Digraph-theoretic approach for deadlock detection and recovery in flexible production systems[J]. Studies in Informatics and Control, 1996, 5(4): 373-383. [本文引用:1]
[10]	Fanti M P, Maione B, Mascolo S, et al. Event-based feedback control for deadlock avoidance in flexible production systems[J]. IEEE Transactions on Robotics and Automation, 1997, 13(3): 347-363. [本文引用:1]

2009

0.0

... 在路径规划方面,Sha等^[1]将tool和OHT相结合,使用决策树和调度规则的方法来提升晶圆的产量 ...

2008

0.0

... Yang等^[2]提出将第 K短路径法和路径中运行的OHT数量相结合来构建调度算法,以实现集成动态调度 ...

2011

0.0

... He等^[3]采用着色Petri网对半导体制造系统中的光刻机进行建模,仿真和分析,最后采用死锁避免机制来实现无死锁调度 ...

2014

0.0

... Han等^[4]采用基于遗传算法和Petri网模型对柔性制造系统进行无死锁调度 ...

2007

0.0

... 在预防轨道死锁方面,Wu等^[5,6]采用着色赋时Petri网作为建模手段,以死锁避免机制实现下层控制,用智能指标对系统进行实时无死锁调度 ...

2007

0.0

... 在预防轨道死锁方面,Wu等^[5,6]采用着色赋时Petri网作为建模手段,以死锁避免机制实现下层控制,用智能指标对系统进行实时无死锁调度 ...

2003

0.0

... Kuo等^[7]利用多智能体技术建立Intrabay的控制结构,该结构能够完整描述OHT堵塞,死锁和冲突解决过程 ...

2010

0.0

... Im等^[8]使用等待关系矩阵来进行死锁检测,而后对陷入死锁的OHT进行审查,对能够改变运输路径的OHT进行重调度 ...

1996

0.0

... Fanti等^[9]提出了潜在死锁的概念,在文献^[10]中其使用有向图概念,推导了死锁发生的充要条件,通过引入控制规则来避免或者激发某些状态变迁 ...

1997

0.0

... Fanti等^[9]提出了潜在死锁的概念,在文献^[10]中其使用有向图概念,推导了死锁发生的充要条件,通过引入控制规则来避免或者激发某些状态变迁 ...