基于Hammer积分的三维地面磁共振高精度正演方法

引用本文

林君, 赵越, 蒋川东, 李同, 刘孝男. 基于Hammer积分的三维地面磁共振高精度正演方法.吉林大学学报:工学版, 2016, 46(2): 609-615
LIN Jun, ZHAO Yue, JIANG Chuan-dong, LI Tong, LIU Xiao-nan. Three-dimensional forward modeling with high precision for underground MRS based on Hammer integration. Journal of Jilin University Engineering and Technology Edition, 2016, 46(2): 609-615 复制到剪切板

Permissions

基于Hammer积分的三维地面磁共振高精度正演方法

林君¹, 赵越^1,², 蒋川东¹, 李同¹, 刘孝男³

1.吉林大学仪器科学与电气工程学院, 长春 130026

2.吉林建筑大学计算机科学与工程学院, 长春 130118

3.中国信息安全测评中心, 北京 100085

通讯作者:蒋川东(1984-),男,讲师,博士.研究方向:核磁共振地下水探测方法和仪器.E-mail:chuandongjiang@gmail.com

作者简介:林君(1954-),男,教授,博士生导师.研究方向:地球物理探测技术及仪器.E-mail:lin_jun@jlu.edu.cn

基金:国家重大科学仪器设备开发和应用专项项目(2011YQ030133); 中国博士后科学基金面上项目(2014M551187); 吉林省青年科研基金项目(20140520130JH)

摘要

为满足三维地面磁共振正演计算的精度要求,本文提出了基于非结构不均匀四面体网格的Hammer积分算法.首先利用有限元方法实现了对地下空间的三维磁场计算,完成了地面磁共振灵敏度核函数表达式的推导.针对现有地面磁共振正演方法中常规网格尺寸大,计算精度差,细化网格尺寸小,但是数量大的问题,应用Hammer积分在常规网格中完成核函数的高精度计算.三维核函数和3个含水模型的正演仿真实验表明:基于Hammer积分的地面磁共振正演方法具有网格少,计算节点少,积分精度高的特点,能够高效解决核函数的正演计算问题.

关键词: 仪器仪表技术; Hammer积分; 地面磁共振; 高精度; 正演; 核函数

中图分类号:TH762 文献标志码:A 文章编号:1671-5497(2016)02-0609-07

Three-dimensional forward modeling with high precision for underground MRS based on Hammer integration

LIN Jun¹, ZHAO Yue^1,², JIANG Chuan-dong¹, LI Tong¹, LIU Xiao-nan³

1.College of Instrumentation and Electrical Engineering, Jilin University, Changchun 130026, China

2.Institute of Computer Science and Engineering, Jilin Jianzhu University, Changchun 130118, China

3.China Information Technology Security Evaluation Center, Beijing 100085, China

Abstract

To meet the accuracy requirement of surface three-dimensional (3D) Magnetic Resonance Spectroscopy (MRS) forward modeling. Hammer integration algorithm was proposed based on unstructured non-uniform tetrahedral mesh. First, finite element method was used to calculate the 3D magnetic field in the subsurface, and the sensitivity kernel expression was deduced. Then, to overcome the shortcoming of conventional mesh grid, that the precision becomes poor as grid size is large, while smaller grid size leads to enormous calculation task, Hammer integration was applied to calculate the kernel function with conventional grid. Synthetic results including 3D kernel function and aquifer models show that, using Hammer integration, higher precision can be achieved with fewer grids and nodes. The forward model can be calculated efficiently.

Keyword: technology of instrument and meter; Hammer integration; surface MRS; high precision; forward modeling; kernel function

Show Figures

0 引言

应用地面磁共振技术(Magnetic resonance sounding, MRS)探测地下水是近年来发展起来的一项尖端技术, 其优势在于针对目标无损探测, 效率高, 解唯一等^[1].就目前而言, 地下水探测中多使用一维探测模型, 探测对象为层状水.而现实中常存在裂隙水, 岩溶水等复杂探测目标体, 其特征多表现为规模小, 水量分布不均匀, 因而需要更高的分辨率和探测精度^[2].三维磁共振技术为上述问题的解决提供了很好的方法与途径, 但受其计算量大, 存储空间需求多, 程序运行效率要求高等问题的制约, 现阶段国内外成果不多^{[3, 4]}.2008年, Legchenko等^[5]使用同一线圈一维探测装置对三维溶洞进行了探测研究, 但该方法得到的体积估计误差约在± 75%, 并于2011年在法国阿尔卑斯山脉鲁塞冰川进行了三维溶洞探测实验.这些结果仅是对溶洞位置和规模进行粗略估计, 得到的参数精度较低^[6].在国内, 蒋川东^[7]针对同一线圈三维地面磁共振探测分辨率低, 工作效率低的问题, 提出了阵列线圈对角线移动测量工作方式, 并对地下水探测过程中三维分辨率进行深入研究.尽管如此, 为完成三维地下水探测任务, 有效提升地面磁共振三维正演精度和计算效率仍是亟待解决的问题^[8].

地面磁共振灵敏度核函数的正演计算直接关系到反演结果的准确性和可靠性, 因此必须对地面磁共振三维正演方法进行深入研究.本文首先使用四面体网格完成对地下空间三维剖分, 并利用有限元方法完成三维磁场强度计算.在此基础上推导了地面磁共振灵敏度核函数表达式, 并运用Hammer积分对磁共振核函数进行高精度正演计算.最后, 仿真计算了3个三维含水体模型, 并与传统的常规网格和细化网格正演计算结果进行了对比分析.

1 三维MRS正演方法

1.1 回线源磁场有限元计算

要完成对三维含水体的地面磁共振正演, 首先要计算发射和接收线圈在地下任意位置产生的磁场大小.目前的研究主要针对圆形大回线源作为等效计算模型, 地下空间为均匀导电半空间或层状导电介质^[9].而对于方形线圈或地下空间复杂导电结构下的磁场计算, 则无法直接通过现有解析式完成.针对上述情况, 本文选择商业有限元计算软件COMSOL完成地下空间磁场仿真计算.

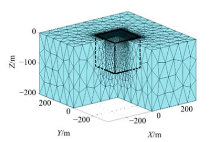
本文计算了在边长为100 m的发射线圈内通入频率为2330 Hz, 幅度为1 A的交变电流时, 地下任意位置产生的磁场B, 如图1所示, 其中黑色方框为MRS线圈.

	Figure Option View Download New Window
	图1 地下三维空间磁场计算Fig.1 3D magnetic field calculation in the subsurface generated from a square loop(black line)on the surface

1.2 任意方向角度垂直场计算

在地面铺设三维探测线圈时, 有两个方向角度需要考虑:一是地磁场B₀方向, 二是探测线圈法线方向 $\begin{matrix} \vec{n} 。 \end{matrix}$ 地磁场的方向由地磁倾角I和地磁偏角D来描述, 探测线圈法线方向由线圈的法向偏度a和法向倾度β 来标识.假设标准模型下地磁场方向指向正北, 而线圈法线方向垂直水平面向下, 故计算任意方向感应场B的垂直分量 $\begin{matrix} B^{⊥} \end{matrix}$ 时, 需将地磁场和线圈法向方向调整至标准模型完成等效计算.该过程可借助坐标系旋转实现, 将新坐标系下感应磁场记作 $\begin{matrix} B', \end{matrix}$ 具体如下^[7]:

$\begin{matrix} B' = R_{I} R_{D} {R^{T}}_{α} {R^{T}}_{β} B \end{matrix}$ (1)

式中: $\begin{matrix} R_{I} 、 R_{D} \end{matrix}$ 分别为地磁倾角和地磁偏角的旋转矩阵; $\begin{matrix} R_{α} 、 R_{β} \end{matrix}$ 分别为线圈法向偏度和法向倾度的旋转矩阵.

$\begin{matrix} \begin{matrix} R_{I} = [\begin{matrix} cosI & 0 & sinI \\ 0 & 1 & 0 \\ - sinI & 0 & cosI \end{matrix}], \\ R_{D} = [\begin{matrix} cosD & sinD & 0 \\ - sinD & cosD & 0 \\ 0 & 0 & 1 \end{matrix}], \\ R_{α} = [\begin{matrix} cosα & sinα & 0 \\ - sinα & cosα & 0 \\ 0 & 0 & 1 \end{matrix}], \\ R_{β} = [\begin{matrix} cosβ & 0 & sinβ \\ 0 & 1 & 0 \\ - sinβ & 0 & cosβ \end{matrix}] \end{matrix} \end{matrix}$

在求得新坐标系下感应磁场 $\begin{matrix} B' = B'_{x} {\hat{e}}_{x} + B'_{y} {\hat{e}}_{y} + B'_{z} {\hat{e}}_{z} \end{matrix}$ 的基础上, 由式(2)可求得感应磁场的垂直分量 $\begin{matrix} B^{⊥} : \end{matrix}$

$\begin{matrix} B^{⊥} = \sqrt[]{(B'_{y})^{2} + (B'_{z})^{2}} \end{matrix}$ (2)

1.3 椭圆极化场计算

在导电介质中, 激发磁场的垂直分量 $\begin{matrix} B^{⊥} \end{matrix}$ 会发生椭圆极化, 可分解为两个旋转方向相反, 幅值不同的圆极化场 $\begin{matrix} B^{+} \end{matrix}$ 和 $\begin{matrix} B^{-} 。 \end{matrix}$ 其中, 同向旋转部分 $\begin{matrix} B^{+} \end{matrix}$ 与氢质子自旋方向相同(顺时针方向), 反向旋转部分 $\begin{matrix} B^{-} \end{matrix}$ 沿逆时针方向旋转, 两者的旋转轴均为地磁场方向 $\begin{matrix} {\hat{b}}_{0} 。 \end{matrix}$ 频率域上的感应磁场垂直分量 $\begin{matrix} B^{⊥} \end{matrix}$ 的复数表达式如下:

$\begin{matrix} \begin{matrix} B^{⊥} (r, ω_{L}) = e^{iζ (r, ω_{L})} \cdot \\ [α (r, ω_{L}) \cdot \hat{b} + iβ (r, ω_{L}) \cdot {\hat{b}}_{0} \times \hat{b}] \end{matrix} \end{matrix}$ (2)

式中: $\begin{matrix} r \end{matrix}$ 为三维空间中某一位置; $\begin{matrix} ω_{L} \end{matrix}$ 为Larmor频率; α , β 和 $\begin{matrix} ζ \end{matrix}$ 分别为椭圆的长轴, 短轴和相位; $\begin{matrix} \hat{b} \end{matrix}$ 和 $\begin{matrix} {\hat{b}}_{0} \end{matrix}$ 分别为激发磁场和地磁场方向.

通过推导可得两个方向相反的圆极化场 $\begin{matrix} B^{+} \end{matrix}$ 和 $\begin{matrix} B^{-} \end{matrix}$ 的时域表达式^[10]:

$\begin{matrix} \begin{matrix} B^{\pm} (r, t) = \frac{1}{2} I_{0} (α \mp β) \times \\ [\cos (ω_{L} t - ζ) \hat{b} \mp \sin (ω_{L} t - ζ) {\hat{b}}_{0} \times \hat{b}] \end{matrix} \end{matrix}$ (4)

据此得到两个方向相反圆极化场的幅度值和单位方向矢量如下:

$\begin{matrix} \{\begin{matrix} |B^{\pm} (r, t)| = \frac{1}{2} I_{0} (α \mp β) \\ {\hat{b}}^{\pm} (r, t) = \frac{B^{\pm} (r, t)}{|B^{\pm} (r, t)|} \end{matrix} \end{matrix}$ (5)

1.4 灵敏度核函数计算

由以上推导可知, 地面磁共振探测核函数的三维形式为:

$\begin{matrix} \begin{matrix} K_{3 D} (q; r) = - ω_{L} M_{0} \sin (- γ_{p} \frac{q}{I_{0}} |B_{T}^{+} (r, ω_{L})|) \times \\ \frac{2}{I_{0}} |B_{R}^{-} (r, ω_{L})| \cdot e^{i [ζ_{T} (r, ω_{L}) + ζ_{R} (r, ω_{L})]} \times \\ [{\hat{b}}_{R} (r, ω_{L}) \cdot {\hat{b}}_{T} (r, ω_{L}) + \\ i b_{0} \cdot ({\hat{b}}_{R} (r, ω_{L}) \cdot {\hat{b}}_{T} (r, ω_{L}))] \end{matrix} \end{matrix}$ (6)

式中: $\begin{matrix} M_{0} \end{matrix}$ 为水的净磁化强度; 下标T和R分别为发射和接收; 单位向量 $\begin{matrix} b_{T}^{⊥} (r) 、 b_{R}^{⊥} (r) \end{matrix}$ 和 $\begin{matrix} {\hat{b}}_{0} \end{matrix}$ 分别为发射, 接收场垂直分量和地磁场的方向向量; $\begin{matrix} ζ_{T} + ζ_{R} \end{matrix}$ 为MRS信号的初始相位.

2 高精度磁共振数值计算方法

2.1 地下探测空间三维剖分

高精度数值计算磁共振灵敏度核函数是实现模型正演和反演计算的关键.要完成地面磁共振正演计算, 首先需要对探测区域进行三维网格剖分.考虑到距离线圈较近的探测区域分辨率高, 而较远的探测空间分辨率低, 故选取非均匀四面体网格剖分方式, 即根据分辨率设置四面体的大小.这样既保证了磁共振正演计算效率, 又保证了模型数据的精度, 用最少的网格数量实现高质量数据处理.

假定选取磁共振线圈为边长100 m的正方形线圈, 在铺设探测线圈下方100 m范围内, 以700 m× 700 m× 200 m为正演计算区域.其中线圈下方的200 m× 200 m× 100 m为主正演空间, 其他区域为次正演空间.全部区域均采用非均匀剖分方式, 主空间中线圈附近网格尺小较小, 最小为4.86 m.网格尺寸由主区域向次区域逐渐增大, 最大尺寸为16.6 m.次正演空间网格均较大, 最大尺寸为70 m,

	Figure Option View Download New Window
	图2 地下探测空间三维网格剖分Fig.2 3D mesh in the subsurface

这是为了尽量减小磁场计算时的边界影响.如图2所示, 最终建立地面磁共振三维探测网格, 共计106 007个剖分单元.

2.2 常规网格剖分完成磁共振正演计算

根据地下探测空间的三维剖分结果, 在所有剖分节点处计算三维磁共振核函数, 然后对每个剖分单元进行积分计算, 即可获得三维灵敏度核函数 $\begin{matrix} K (q, r_{e}) : \end{matrix}$

$\begin{matrix} K (q, r_{e}) = \int_{V_{e}} K_{3 D} (q, r) d^{3} r = V_{e} \overset{N}{\sum_{i = 1}} \frac{1}{N} K_{3 D} (q, r_{i}) \end{matrix}$ (7)

式中: $\begin{matrix} r_{e} \end{matrix}$ 和 $\begin{matrix} V_{e} \end{matrix}$ 分别为剖分单元 $\begin{matrix} e \end{matrix}$ 的空间位置和体积; N为剖分节点数(对于四面体, N=4), 如图3(a)所示.

	Figure Option View Download New Window
	图3 Hammer积分点选取Fig.3 Selection of Hammer integral point

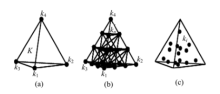
由于式(6)中存在正弦表达式, 灵敏度核函数在地表线圈附近具有快速振荡的特性, 因此需要大量密集的网格来计算三维核函数^[11].尽管图2中已经存在十万余个剖分单元, 但是在线圈附近的网格仍然较大, 正演结果的精度偏低, 为此需要对正演网格进行细化.图3(b)显示了阶数为3的网格细化结果, 即将每个剖分单位细化为27个小网格.细化后的三维核函数 $\begin{matrix} K (q, r_{e}) \end{matrix}$ 为:

$\begin{matrix} \begin{matrix} K (q, r_{e}) = \int_{V_{e}} K_{3 D} (q, r) d^{3} r = \overset{M}{\sum_{i = 1}} (V_{e_{i}} \overset{N}{\sum_{j = 1}} \frac{1}{N} K_{3 D} (q, r_{ij})) \end{matrix} \end{matrix}$ (8)

式中: $\begin{matrix} M = 27, r_{ij} \end{matrix}$ 和 $\begin{matrix} V_{e_{i}} \end{matrix}$ 分别为细化后的剖分节点和剖分单元的体积.

剖分单元细化后, 剖分单元变小, 线圈附近的网格变密, 因此正演将结果的精度提高.但是由于网格较多, 计算空间和时间将大大增加.

2.3 应用Hammer积分完成高精度磁共振正演计算

任取一个四面体单元, Hammer积分公式可表示如下:

$\begin{matrix} \begin{matrix} K (q, r_{e}) = \int_{V_{e}} K_{3 D} (q, r) d^{3} r = V_{e} \cdot \overset{H}{\sum_{i = 1}} W_{i} K_{3 D} (q, r_{ζ_{1}^{i}, ζ_{2}^{i}, ζ_{3}^{i}, ζ_{4}^{i}}) \end{matrix} \end{matrix}$ (9)

式中:H为积分节点数量; $\begin{matrix} ζ_{1}^{i}, ζ_{2}^{i}, ζ_{3}^{i}, ζ_{4}^{i} \end{matrix}$ 为Hammer求积点的坐标系数; $\begin{matrix} W_{i} \end{matrix}$ 为对应的权值.当 $\begin{matrix} H = 1 \end{matrix}$ 时, 只需通过计算四面体中心位置(1/4, 1/4, 1/4, 1/4)的核函数来代替整个单元的 $\begin{matrix} K (q, r_{e}) \end{matrix}$ 值, 此时仅能获得较低的计算精度.

增加Hammer积分的计算节点数可以提高计算精度.本文选用5阶积分格式, 此时计算精度为O(h₆), 其中, h代表网格的最小尺寸.计算节点数为H=15个, 分别按照积分节点M=(1, 4, 4, 6)原则选取.当M=1时, 计算节点位于四面体的中心位置; 当M=4时, 计算节点位于四面体的一个面的中点和其相对顶点的连接线上; 当M=6时, 计算节点位于四面体两个相对边的中点的连接线上.具体计算节点的位置坐标和积分系数由文献^[12]计算给出.

3 仿真实验与分析

3.1 三维核函数计算结果

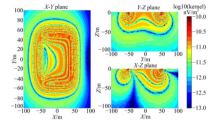
由表达式(6)可知, 磁共振核函数代表接收线圈对地下各位置处的含水量灵敏度.运用细化网格及式(8)完成了三维核函数数值计算, 结果如图4所示.仿真模型设定磁共振线圈边长100 m, Larmor频率为2330 Hz, 地磁倾角为60° , 激发脉冲矩q=10 A· s.图4中, $\begin{matrix} X - Y \end{matrix}$ 剖面为水平方向, 位于地下5 m处.由于距离线圈较近, 三维核函数振荡剧烈, 若用较粗的网格将会引起较大的误差. $\begin{matrix} Y - Z \end{matrix}$ 剖面为垂直方向, 即东西剖面.三维核函数基本呈现对称分布, 线圈附近的灵敏度最大, 随着距离和深度的增加, 灵敏度呈振荡方式逐渐降低. $\begin{matrix} X - Z \end{matrix}$ 剖面为垂直方向, 即南北剖面.由于地磁倾角的影响, 三维核函数呈现不对称分布, 但是线圈附近的灵敏度仍然最大, 并随距离和深度的增加逐渐降低.同时, 从线圈出发, 沿着近地磁倾角的方向存在探测盲区, 随着距离增加, 盲区逐渐扩大.这个区域的灵敏度最小, 因此在实际探测中应避免目标出现在盲区内, 或通过多个线圈减小探测盲区的影响.

	Figure Option View Download New Window
	图4 地下空间磁共振核函数仿真计算结果Fig.4 Simulation of kernel function in the subsurface

3.2 积分方案改进前后正演计算结果对比

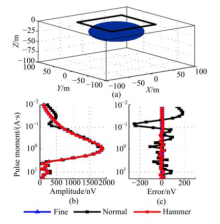
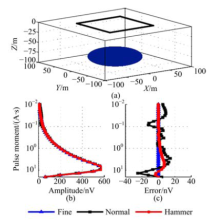
为了验证应用Hammer积分精度提升效果, 本文选取3个三维含水体进行磁共振正演研究, 模型网格剖分如图2所示.磁共振线圈放置在地面上, 边长为100 m, Larmor频率为2330 Hz, 地磁倾角为60° .现选取20个激发脉冲矩q, 范围为0.1~10 A· s, 按照指数间隔分布.3个三维含水体模型分别描述如下:① 浅层含水体.椭球体, 中心位置(0, 0, -20) m, X, Y和Z三个方向的半主轴大小分别为50 m, 50 m和20 m, 如图5(a)所示.② 深层含水体.椭球体, 中心位置(0, 0, -80) m, X, Y和Z三个方向的半主轴大小分别为50 m, 50 m和20 m, 如图6(a)所示.③ 多个含水体.两个椭球体, 中心位置分别为(± 50, 0, -20) m, X, Y和Z三个方向的半主轴大小均为20 m, 50 m和20 m, 如图7(a)所示.

	Figure Option View Download New Window
	图5 浅层单一含水体模型与正演计算结果Fig.5 Forward calculation results with one shallow water-bearing object

对于浅层含水体, 图5(b)分别计算了细化网格, 常规网格和应用Hammer积分的三维磁共振正演结果.根据前文所述, 细化网格的单元数最多, 计算精度最高, 因此可以作为理论结果.图5(c)计算了常规网格和应用Hammer积分后的正演结果与细化网格结果的绝对误差.如图5(b)(c)所示, 浅层含水体距离发射线圈较近, 而常规网格的单元数较少, 网格尺寸较大, 正演结果与细化网格的结果相差较大.尤其是在脉冲矩q较小时, 绝对误差达到250.8 nV, 平均误差为76.1 nV, 如表1所示.保持同样的网格尺寸及单元数, 应用Hammer积分后的正演结果与细化网格结果相差较小, 平均绝对误差为7.8 nV.一般磁共振探测仪器的最小信号探测能力约为10 nV, 因此, 应用Hammer积分后的正演结果满足计算要求.

	Figure Option View Download New Window
	图6 深层单一含水体模型与正演计算结果Fig.6 Forward calculation results with one deep water-bearing object

对于深层含水体, 图6(b)(c)分别计算了细化网格, 常规网格和应用Hammer积分的三维磁共振正演结果, 以及与细化网格的绝对误差.由于深层含水体距离线圈较远, 此处的三维磁共振核函数变化缓慢, 常规网格的计算精度有所提高.相对于细化网格, 最大绝对误差为25 nV.对于Hammer积分后的正演结果, 最大绝对误差仍然保持在10 nV以下.因此, 对于深层含水体, Hammer积分后的正演结果也满足计算要求.

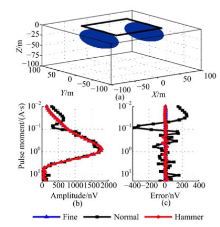
	Figure Option View Download New Window
	图7 多含水体模型与正演计算结果Fig.7 Forward calculation results with several water-bearing object

对于多个含水层, 图7(b)(c)分别计算了细化网格, 常规网格和应用Hammer积分的三维磁共振正演结果, 以及与细化网格的绝对误差.模型包含两个浅层的小型含水体, 正好位于发射和接收线圈的两个边框下方, 距离线圈很近, 而这个区域的三维磁共振核函数变化最剧烈.常规网格正演结果显示了较低的计算精度, 与细化网格相比, 绝对误差最大达到375.2 nV, 平均误差为115.2 nV, 因此正演结果不满足计算要求.但是, 应用Hammer积分后的正演结果与细化网格相近, 平均绝对误差为7.7 nV, 因此该方法保证了较高的计算精度.

3.3 计算空间和时间比较分析

为分析细化网格, 常规网格及应用Hammer积分网格磁共振正演方法的计算时间和空间需求, 表1总结了本文所用3种网格的网格数量, 积分节点数, 计算时间和3个模型的绝对误差对比.由表1可知, 常规网格和Hammer积分网格所用的网格数量相同, 而细化网格的数量是其27倍.Hammer网格积分节点数和计算时间是常规网格的3.75倍和2.13倍, 而细化网格积分节点数和计算时间是常规网格的27倍和20倍左右.同时, 通过对比三个模型的绝对误差可以得知, 应用Hammer积分方法的三维磁共振正演计算比常规网格正演计算增加了3倍左右的时间和空间, 但是降低了平均9倍的绝对误差, 而细化网格需要增加20多倍的时间和空间.因此, 通过以上分析可知, 应用Hammer积分方法进行三维磁共振正演计算的精度高于常规网格, 计算效率高于细化网格.

表1 计算时间与空间对比分析表 Table 1 Analysis on computation time and space

4 结束语

采用有限元方法计算了地下空间三维磁场, 在此基础上推导了灵敏度核函数和磁共振响应信号表达式, 并用Hammer积分方法完成了高精度和高效率的三维地面磁共振正演数值计算.3个三维含水体模型的仿真正演计算结果表明:基于Hammer积分的网格比常规网格计算精度高, 虽然计算节点数和时间增加了3倍, 但是绝对误差降低了9倍; 而相比于细化网格, 计算效率高约7倍.因此, 基于Hammer积分的网格能够高精度和高效率地完成三维地面磁共振正演计算.

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	林君, 段清明, 王应吉. 核磁共振找水仪原理与应用[M]. 北京: 科学出版社, 2011: 1-12. [本文引用:1]
[2]	蒋川东, 林君, 秦胜武, 等. 磁共振方法在堤坝渗漏探测中的实验[J]. 吉林大学学报: 地球科学版, 2012, 42(3): 858-863. Jiang Chuan-dong, Lin Jun, Qin Sheng-wu, et al. Experiment on dam leakage detection with magnetic resonance sounding[J]. Journal of Jilin University(Earth Science Edition), 2012, 42(3): 858-863. [本文引用:1]
[3]	林婷婷, 史文龙, 齐鑫, 等. 核磁共振地下水探测全波收录系统[J]. 吉林大学学报: 工学版, 2014, 44(4): 1024-1030. Lin ting-ting, Shi wen-long, Qi Xin, et al. Full-wave recording of MRS groundwater exploration system[J]. Journal of Jilin University(Engineering and Technology Editon), 2014, 44(4): 1024-1030. [本文引用:1]
[4]	田宝凤, 王悦, 张健, 等. 核磁共振测深环境电磁噪声测试系统的设计及实现[J]. 吉林大学学报: 工学版, 2015, 45(6): 2034-2042. Tian Bao-feng, Wang Yue, Zhang Jian, et al. Design and implementation of an electromagnetic noise test system in nuclear magnetic resonance sounding environment[J]. Journal of Jilin University(Engineering and Technology Editon), 2015, 45(6): 2034-2042. [本文引用:1]
[5]	Legchenko A, Ezersky M, Camerlynck C, et al. Locating water-filled karst caverns and estimating their volume using magnetic resonance soundings[J]. Geophysics, 2008, 73(5): 51-61. [本文引用:1]
[6]	Legchenko A, Descloitres M, Vincent C, et al. Three-dimensional magnetic resonance imaging for groundwater[J]. New Journal of Physics, 2011, 13(4): 1-17. [本文引用:1]
[7]	蒋川东. 核磁共振2D/3D地下水成像方法及其阵列式地面探测系统研究[D]. 长春: 吉林大学仪器科学与电气工程学院, 2013. Jiang Chuan-dong. Development of 2D/3D magnetic resonance tomography and array surface NMR system for groundwater exploration[D]. Changchun: College of Instrumentation and Electrical Engineering, Jilin University, 2013. [本文引用:2]
[8]	林君, 蒋川东, 段清明, 等. 复杂条件下地下水磁共振探测与灾害水源探查研究进展[J]. 吉林大学学报: 地球科学版, 2012, 42(5): 1560-1570. Lin Jun, Jiang Chuan-dong, Duan Qing-ming, et al. The simulation and progress of magnetic resonance sounding for groundwater investigations and underground applications[J]. Journal of Jilin University(Earth Science Edition), 2012, 42(5): 1560-1570. [本文引用:1]
[9]	翁爱华, 李舟波, 王雪秋. 层状导电介质中地面核磁共振响应特征理论研究[J]. 地球物理学报, 2004, 47(1): 156-163. Weng Ai-hua, Li Zhou-bo, Wang Xue-qiu. A study on surface nuclear magnetic resonance over layered conductive earth[J]. Chinese Journal of Geophysics, 2004, 47(1): 156-163. [本文引用:1]
[10]	蒋川东, 林君, 段清明, 等. 二维阵列线圈核磁共振地下水探测理论研究[J]. 地球物理学报, 2011, 54(11): 2973-2983. Jiang Chuan-dong, Lin Jun, Duan Qing-ming, et al. A study on 2D magnetic resonance sounding with an array loop for groundwater exploration[J]. Chinese Journal of Geophysics, 2011, 54(11): 2973-2983. [本文引用:1]
[11]	Lehmann-Horn J A, Hertrich M, Greenhalgh S A, et al. Three dimensional magnetic field and NMR sensitivity computations incorporating conductivity anomalies and variable-surface topography[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(10): 3878-3891. [本文引用:1]
[12]	Yu Jin-yun. Symmetric Gaussian quadrature formulae for tetrahedronal regions[J]. Applied Mathematics and Optimization, 1984, 43(3): 349-353. [本文引用:1]

2011

0.0

... 0 引言应用地面磁共振技术(Magnetic resonance sounding,MRS)探测地下水是近年来发展起来的一项尖端技术,其优势在于针对目标无损探测,效率高,解唯一等^[1] ...

2012

0.0

. 2012, 42(3):858-863 DOI:doi:10.3969/j.issn.1671-5888.2012.03.033

Experiment on dam leakage detection with magnetic resonance sounding

磁共振方法在堤坝渗漏探测中的实验

Jiang Chuan-dong , Lin Jun , Qin Sheng-wu

蒋川东, 林君, 秦胜武

To detect the hidden leakage problem of a dam body accurately, a new geophysical method, magnetic resonance sounding (MRS), is introduced, which can directly detect water molecules and quantitatively measure them. The basic principle and inversion method of MRS is research to determine the coil type and measurement mode for dam leakage problem. Field experiment of dam leakage detection was performed on Cuijiajie dam in Huanren, Liaoning Province, using JLMRS system developed by Jilin University. 15 points on the dam crest were measured with a 4-rurn square coil of 12.5 m side length for maximum depth 35 m. By data processing and inversing, the water content profile of the dam body in 2D is achieved. Furthermore, for eliminating the effect of upstream water, a correction method is used and the relative water content in 2D is updated. The interpretation results show that there are three leakage points (140 m, 180 m and 240 m away from the spillway, respectively) and two infiltration areas (rang of 100 m to 150 m and 170 m to 250 m) at depth of -20 m to -10 m inside Cuijiajie dam, which are gravel layer leakage. The measurement result is confirmed consistent with the engineering geology and downstream water percolation.

为精确定位堤坝渗漏点位置，介绍了一种能直接定量探测水的地球物理方法——磁共振法。通过阐述磁共振方法的基本原理和反演算法，确定适用于堤坝渗漏探测的线圈类型和测量方式。采用吉林大学自主研制的JLMRS型磁共振探水仪，在辽宁桓仁崔家街堤坝坝顶铺设4匝边长为12.5 m的正方形线圈，连续测量15个点，测量深度达35 m。经过数据处理和反演解释，得到坝体二维含水量剖面图，为消除上游水体对实验结果的影响提出了修正方法，进而得到坝体二维相对含水量剖面。实验结果表明:崔家街大坝存在3个渗漏点（距溢洪道140、180和240 m处）和2个渗透区（距溢洪道100～150 m和170～250 m处）;深度为-20~-10 m，为砾卵石层渗漏，与工程地质资料和下游渗水情况相符。

... 而现实中常存在裂隙水,岩溶水等复杂探测目标体,其特征多表现为规模小,水量分布不均匀,因而需要更高的分辨率和探测精度^[2] ...

2014

0.0

. 2014, 44(4):1024-1030 DOI:doi:10.13229/j.cnki.jdxbgxb201404019

Full-wave recording of MRS groundwater exploration system

核磁共振地下水探测全波收录系统

Lin ting-ting , Shi wen-long , Qi Xin

林婷婷, 史文龙, 齐鑫

应用分离线圈技术和双向二极管技术,使核磁共振地下水探测系统死区时间由38ms缩短至18ms,并提高了采集到的信号的幅度。通过结合全波收录系统所需高精度同步、大数据量采集、快速数据回传的特点,以状态机和多线程操作为基础,开发了基于CompactRIO平台的全波收录系统,为地面磁共振参考消噪等多种数据预处理方法的研究提供了强大的实践平台。实验结果表明,该系统工作稳定可靠,可以为核磁共振含水层精确解释提供有效的全波数据。

... 三维磁共振技术为上述问题的解决提供了很好的方法与途径,但受其计算量大,存储空间需求多,程序运行效率要求高等问题的制约,现阶段国内外成果不多^[3,4] ...

2015

0.0

. 2015, 45(6):2034-2042

Design and implementation of an electromagnetic noise test system in nuclear magnetic resonance sounding environment

核磁共振测深环境电磁噪声测试系统的设计及实现

Tian Bao-feng , Wang Yue , Zhang Jian

田宝凤, 王悦, 张健

摘　要：设计并实现了基于混合信号处理器（Mixed signal processor 430,MSP 430）和现场可编程门阵列（Field programmable gate array,FPGA）双控制器的拉莫尔频率范围内（1~3kHz）的电磁噪声测试系统。该系统采用并联低噪声运放减小等效输入噪声,通过程控窄带滤波控制通带带宽和128级增益可调,实现了对复杂空间环境下电磁噪声信息的获取;FPGA内建NIOSⅡ软核搭建数据采集系统,基于SPI总线实现数据在SD卡中的高效、快速存储。通过对室内、外实测数据的分析,验证了该系统设计的有效性。

2008

0.0

... 2008年,Legchenko等^[5]使用同一线圈一维探测装置对三维溶洞进行了探测研究,但该方法得到的体积估计误差约在#cod#x000b1 ...

2011

0.0

... 这些结果仅是对溶洞位置和规模进行粗略估计,得到的参数精度较低^[6] ...

2013

0.0

. 2013, :-

Development of 2D/3D magnetic resonance tomography and array surface NMR system for groundwater exploration

核磁共振2D/3D地下水成像方法及其阵列式地面探测系统研究[D]

Jiang Chuan-dong.

蒋川东

地面核磁共振技术（MRS）在我国北方干旱和半干旱地区寻找地下水以及高效评价层状地下水资源等领域获得了广泛应用，然而，针对西南丘陵和喀斯特地区的裂隙水和岩溶水等复杂地下水探测，该方法仍存在成像精度低、探测分辨率低和工作效率低等问题。因此，发展新型的高精度核磁共振2D/3D地下水成像方法及高效高分辨率的地面MRS探测系统一直是该领域的迫切需求。本文针对国内外现有的同一线圈移动测量模式和分离线圈轮换测量模式的缺陷，首次提出了阵列线圈测量模式，仅用一次测量的结果就可代替分离线圈多次测量的结果，具有高效率，高分辨率和高覆盖率等优势。同时，针对裂隙水和岩溶水等非层状不均匀的复杂地下水，提出了高精度的2D和3D MRS含水量成像方法以及单弛豫和多弛豫时间T_2~*的2D成像方法。基于此，研制了具有多通道采集单元的阵列式地面MRS系统，最后给出了野外实验结果和应用实例。论文主要的研究工作及取得的成果如下： 1、针对1D MRS忽略的线圈方向角度，引入旋转角度矩阵，解决了任意线圈方向角度和地磁场角度变化下的MRS正演计算问题，并仿真分析了线圈方向角度对2D测量信号的影响。 2.针对现有2D MRS测量分辨率低和效率低的问题，提出快速高分辨率和高覆盖率的阵列线圈测量模式，借助奇异值分解（SVD）进行分辨率半径研究，发现阵列线圈一次测量就可实现2D高分辨率探测，长方形发射线圈和半覆盖型接收线圈组合是最优的测量模式。 3.针对目前3D测量效率低和覆盖面积有限的缺点，提出了阵列线圈对角线移动测量模式，探测分辨率显著优于同一线圈，用较少的测量次数可实现较大覆盖面积的高分辨率3D探测。 4.针对目前2D地下水成像方法中均匀网格数量大，成像精度低，以及算法不稳定等问题，提出了以分辨率半径为尺度函数的2D空间非均匀剖分方法，结合差异准则和L曲线的正则化参数双重选择方法，目标函数线性化及非约束空间转换的Jacobain变换方法，实现了基于MRS信号初始振幅的高精度2D含水量成像。 5.通过对2D复杂地下水模型的仿真和初始振幅反演，对比了阵列线圈、分离线圈和同一线圈3种测量模式的成像结果，在较低信噪比情况下，长方形阵列线圈半覆盖型测量模式同样具有较高的分辨率，与2D MRS分辨率理论分析结论一致。 6.针对基于MRS信号包络的QT反演中无法存储多弛豫灵敏度核函数的问题，提出了两种解决方法：一种是简化为单弛豫信号的2D QT反演，实现了含水量和弛豫时间T*2的双参数成像，成像结果更稳定；另一种是基于含水单元的2D Cell反演，实现含水量和多弛豫时间分布的同时成像。 7.针对目前基于均匀网格的3D含水量成像方法精度低和含水量误差大的问题，采用目标体和围岩区域不同密度的非均匀网格剖分，实现了基于MRS信号初始振幅的3D含水量成像方法，通过对仿真的复杂地下水模型和德国Einersberger湖的实测数据，验证了3D成像方法的高精度定位和定量效果。 8.根据现有单通道地面MRS系统的组成结构和问题，研发了适用于阵列线圈测量模式的接收单元和控制软件，通过改进快速消耗电路使死区时间由原来的38ms减小到15ms，改进信号调理电路和采集电路提高数据分辨率，采用一主多从的结构和手拉手的连接方式实现了高精度的同步控制和高速数据传输等关键技术，使阵列式地面MRS系统的技术指标与国际最先进的MRS仪器基本持平。通过对以上内容的研究，完成了对核磁共振2D/3D地下水成像方法及其阵列式地面探测系统的研究，主要的创新工作在于：首次提出的阵列线圈测量模式，一次测量可实现2D剖面高分辨率探测，对角线移动测量可以实现3D大覆盖面积的高分辨率探测，解决了传统MRS的测量效率低和分辨率低的问题。提出了基于分辨率半径的地面MRS探测性能分析方法，对比得到长方形阵列线圈半覆盖型测量模式具有最优的探测分辨率，并根据分辨率半径实现了2D/3D空间的非均匀剖分，为实现地下水高精度成像提供了基础。提出了差异准则和L曲线双重选择正则化参数，Jacobain变换实现目标函数线性化和非约束空间转换等算法，解决了目前反演算法不稳定、非线性和变量约束等问题，实现了2D/3D地下水高精度的含水量成像，不仅可以判断非层状不均匀含水构造的位置和规模，而且可以精确计算含水总量。针对MRS信号包络的单弛豫和多弛豫特性，提出了含水量和单弛豫时间双参数成像的2D QT反演，反演结果更稳定；以及基于含水单元概念的Cell反演，实现多孔隙结构的含水构造含水量和多弛豫时间同时成像。本文研究的地下水成像方法和地面MRS系统已在蒙古国Halatura铁矿地下水源探测、中国辽宁桓仁崔家村堤坝渗漏探测和安徽黄山阳台村滑坡稳定性探测等工程实践中得到应用，取得了理想的探测效果和地下水成像结果，验证了方法和系统的有效性和实用性。本文提出的地下水成像方法和阵列式地面MRS系统，将为我国西南地区及复杂地质环境下的2D/3D地下水探测，提供有力的技术支撑。

... 在国内,蒋川东^[7]针对同一线圈三维地面磁共振探测分辨率低,工作效率低的问题,提出了阵列线圈对角线移动测量工作方式,并对地下水探测过程中三维分辨率进行深入研究 ...

... 该过程可借助坐标系旋转实现,将新坐标系下感应磁场记作 B',具体如下^[7]: ...

2012

0.0

. 2012, 42(5):1560-1570

The simulation and progress of magnetic resonance sounding for groundwater investigations and underground applications

复杂条件下地下水磁共振探测与灾害水源探查研究进展

Lin Jun , Jiang Chuan-dong , Duan Qing-ming

林君, 蒋川东, 段清明

Nuclear magnetic resonance (NMR) has emerged as a new geophysical technique allowing direct, noninvasive groundwater investigations from the surface. Comparing to the traditional geophysical methods, the current state-of-the-art NMR method is higher resolution, more efficiency, more information and unique interpretation for hydrogeological investigations. In the last two decades, MRS has been widely used, not only in groundwater exploration, but also in water-disaster forewarning, including dam leakage, tunnel gushing, waterimpacted landslide, and seawater intrusion. The purpose of this paper is to give an overview of various aspects of MRS for groundwater exploration in complex geophysical settings. We report the recent researches, includes adaptive signal processing for mitigating electromagnetic noise, 2D/3D MRS methods for low-volume detection, forward modeling and field-data inversion under complex conditions, as well as joint uses of MRS and TEM methods in karst aquifers. By introducing several case studies, we prospect the developing trends of MRS for groundwater assessment.

磁共振地下水探测是一种直接非侵害性探测地下水的地球物理新方法,与传统地球物理探测地下水方法相比，具有高分辨力、高效率、信息量丰富和解唯一等优点。近年来地下水磁共振探测技术发展迅速，不仅用于缺水地区的地下水勘查，还在地下灾害水源（由于地下水引起的灾害如堤坝渗漏、隧道/矿井水害、滑坡、海水入侵等）的探测预警中进行了探索性研究。综述了复杂条件下地下水磁共振探测技术的研究现状，包括强电磁干扰环境的自适应噪声压制、地下小水体的2D/3D磁共振探测、复杂条件的数据处理与反演、针对喀斯特地貌等地质环境的地下水磁共振与瞬变电磁联合探测研究成果，简要介绍了磁共振技术用于滑坡、海水入侵和隧道涌水等灾害水源探查的探索性研究示例，展望了地下水磁共振探测技术的未来发展趋势。

... 尽管如此,为完成三维地下水探测任务,有效提升地面磁共振三维正演精度和计算效率仍是亟待解决的问题^[8] ...

2004

0.0

. 2004, 47(1):156-163 DOI:doi:10.3321/j.issn:0001-5733.2004.01.024

A study on surface nuclear magnetic resonance over layered conductive earth

层状导电介质中地面核磁共振响应特征理论研究

Weng Ai-hua , Li Zhou-bo , Wang Xue-qiu.

翁爱华, 李舟波, 王雪秋

水平层状导电大地中层状含水层地面核磁共振响应的数值计算技术涉及到导电介质中回线源磁场的计算以及地下含水层中质子磁矩在线圈中产生感应信号的体积积分.文中采用直接数值积分技术,对具有振荡核函数的Hankel变换进行积分,以求取回线源磁场的径向与垂向分量,计算并研究了回线产生的径向与垂向磁场分量随空间位置的变化规律.基于磁场空间分布特点,利用不等间距空间剖分技术计算地面核磁共振的体积积分,模拟了不同模型的地面核磁共振响应并讨论了其影响因素.结果表明,结合能对任意层状导电介质中磁场进行稳定快速计算的直接数值积分技术与不等距空间模型剖分技术,可正确模拟地面核磁共振响应.导电性是产生地面核磁共振信号相位的先决条件,但影响响应振幅强度与相位的因素还有含水层的埋深、厚度以及装置大小等.

... 目前的研究主要针对圆形大回线源作为等效计算模型,地下空间为均匀导电半空间或层状导电介质^[9] ...

2011

0.0

. 2011, 54(11):2973-2983 DOI:doi:10.3969/j.issn.0001-5733.2011.11.028

A study on 2D magnetic resonance sounding with an array loop for groundwater exploration

二维阵列线圈核磁共振地下水探测理论研究

Jiang Chuan-dong , Lin Jun , Duan Qing-ming

蒋川东, 林君, 段清明

Magnetic Resonance Sounding (MRS) is a geophysical method designed for direct groundwater exploration. Initially, MRS was developed for characterizing horizontally stratified aquifers. However, for the 2D/3D target whose size may be much smaller than the loop, the accuracy and the lateral resolution may not be sufficient. In this paper, possibility of 2D MRS with an array loop for groundwater exploration is studied firstly. Then, the expressions of the elliptically polarized excitation field induced by the transmitting loop and MRS response signal received by the array loop are derived. The 2D imaging of MRS initial amplitude and detection sensitivity measured with the array loop are numerically simulated, and are compared with the result from using the coincident loop. Conclusions are as follows: (1) 2D MRS measurement with the array loop can directly detect the horizontal position of water conduit in the subsurface, but requires higher excitation current and receiver sensitivity. (2) When the horizontal position, depth and section area of the water conduit vary, the detection sensitivity of 2D MRS measurement with the array loop is higher than that using the coincident loop, and the improvement of sensitivity is most obvious when horizontal position varying. (3) The sensitivity of 2D MRS measurement with the array loop detecting horizontal position varying decreases with increasing of the water conduit depth. (4) For shallow groundwater, the horizontal, vertical and section resolution determined by the instrumental noise level is 5 m, 4.5 m, 8 m 2 , respectively. By increasing the number and turns of the receiver loop, improving excitation pulse moment and decreasing noise level, the existing instrument can be utilized to 2D MRS measurement. The theory and method presented in this paper will contribute to the application of 2D MRS with the array loop to fast detection of 2D/3D targets such as underground rivers, karstic conduits and dam seepages.

核磁共振法(Magnetic Resonance Sounding, MRS)是一种直接探测地下水的地球物理方法,目前只能对水平层状的含水层进行一维测深,对于尺寸小于线圈直径的二维或三维含水构造成像时,其灵敏度和横向分辨率很低.本文从研究二维阵列线圈核磁共振地下水探测方式的可行性出发,推导了地面发射线圈产生的椭圆极化激发场和阵列接收线圈的核磁共振响应核函数的表达式,数值计算了二维阵列线圈测量方式的MRS信号初始振幅图像和探测灵敏度,通过与二维发射/接收同一线圈测量方式对比,得到结论如下:二维阵列线圈测量方式可直接确定地下含水构造的水平位置,但需更大的激发电流强度和接收灵敏度;当中浅层( 2 ,以上三种分辨率均由仪器噪声水平所决定.通过实施增加接收线圈的数量和匝数、提高激发脉冲矩和接收灵敏度等改进措施,现有的仪器系统可用二维阵列线圈测量方式.本文提出的理论和方法,将促使二维阵列线圈核磁共振方法在地下暗河、喀斯特溶洞和堤坝渗漏等二维或三维含水构造快速探测方面得到应用.

... 通过推导可得两个方向相反的圆极化场 B+和 B-的时域表达式^[10]: ...

2011

0.0

... 由于式(6)中存在正弦表达式,灵敏度核函数在地表线圈附近具有快速振荡的特性,因此需要大量密集的网格来计算三维核函数^[11] ...

1984

0.0

... 具体计算节点的位置坐标和积分系数由文献^[12]计算给出 ...