基于信息维数的欺骗干扰存在性检测

引用本文

祝宏, 张海, 唐高弟, 李中云, 刘以农. 基于信息维数的欺骗干扰存在性检测.吉林大学学报:工学版, 2016, 46(2): 616-620
ZHU Hong, ZHANG Hai, TANG Gao-di, LI Zhong-yun, LIU Yi-nong. Detection of presence of deception jamming based on information dimension. Journal of Jilin University Engineering and Technology Edition, 2016, 46(2): 616-620 复制到剪切板

Permissions

基于信息维数的欺骗干扰存在性检测

祝宏^1,^2,³, 张海^1,³, 唐高弟¹, 李中云¹, 刘以农²

1.中国工程物理研究院电子工程研究所,四川绵阳 621999

2.清华大学工程物理系,北京 100084

3.中国工程物理研究院中物院复杂电磁环境科学与技术重点实验室,四川绵阳 621999

通讯作者:张海(1968-),男,研究员.研究方向:雷达系统及信号处理.E-mail:e2zhanghai@aliyun.com

作者简介:祝宏(1987-),男,博士研究生.研究方向:雷达信号处理,雷达抗干扰技术.E-mail:zhu-h06@163.com

基金:中物院复杂电磁环境科学与技术重点实验室项目 (2014E-05-1)

摘要

利用欺骗干扰信号与目标回波包络上的不同,基于分形理论中的信息维数提出了一种欺骗干扰的存在性检测方法.当信号本身的信息维数与信号包络的信息维数之差超过一定门限时,可判断存在欺骗干扰,同时可获知欺骗干扰的起始时刻.仿真结果表明:本文算法在干噪比不低于6 dB时,检测概率在90%以上.

关键词: 雷达工程; 抗干扰; 欺骗干扰; 分形维数; 信息维数

中图分类号:TN974 文献标志码:A 文章编号:1671-5497(2016)02-0616-05

Detection of presence of deception jamming based on information dimension

ZHU Hong^1,^2,³, ZHANG Hai^1,³, TANG Gao-di¹, LI Zhong-yun¹, LIU Yi-nong²

1.Institute of Electronic Engineering,CAEP,Mianyang 621999,China

2.Department of Engineering Physics,Tsinghua University,Beijing 100084,China

3.Key Lab of Science and Technology in Complex Electromagnetic Environment,CAEP,Mianyang 621999,China

Abstract

A detection algorithm of the presence of deception jamming is proposed based on information dimension with the fact that the signal envelopes of deception jamming and target return are different. The algorithm can detect the existence or not of a deception jamming and find its initial time after calculating the difference between the signal's information dimension and the signal envelope's dimension. Simulation results show that this approach can detect deception jamming effectively when JNR is no less than 6 dB, and the detection probability is higher than 90%.

Keyword: radar engineering; anti-jamming; deception jamming; fractal dimension; information dimension

Show Figures

0 引言

抗欺骗式干扰技术一直是雷达研究者的关注重点.目前, 关于欺骗式干扰的研究主要集中在原理分析, 性能仿真和效果评估方面, 关于抗干扰的研究则相对较少^{[1, 2]}.文献^[3]分析了数字射频存储器(DRFM)产生的距离波门拖引(RGPO)干扰信号由于DRFM相位量化误差在频域上产生的细微变化, 但这个细微变化在DRFM阶数较高时不明显, 且不适用于目标回波和干扰同时存在的情况.文献^[4]分析了目标回波与欺骗干扰信号脉内幅度起伏的差异; 文献^[5]研究了两者在幅度起伏, 高阶统计量, 双谱特性上的差异, 但均分析简单, 没有研究目标回波与欺骗干扰部分重叠的情况.

自分形理论被提出以来, 分形理论已成功地应用于图像处理, 语音识别, 雷达信号处理等领域.文献^{[6, 7, 8]}分别从不同角度研究了分形理论在雷达目标检测中的应用, 但均不适用于存在欺骗干扰的情况.对此, 本文利用欺骗式干扰与目标回波在信息维数上的差异, 提出了一种新的欺骗干扰存在性检测方法.本文采用实测的大地回波数据进行仿真, 通过分析大地回波和欺骗干扰的信息维数特征, 得出判定欺骗干扰存在与否的依据, 为后续的抗欺骗干扰算法设计打下了良好基础.

1 信息维数

分形维数是分形理论的中心概念, 它有多种定义和计算方法, 常用的是Hausdorff维数, 盒维数, 信息维数, 相似维数等^{[9, 10]}.雷达信号作为一种时间序列, 可以用分形维数对其进行刻画, 比如盒维数用以描述信号的复杂度, 信息维数用以描述信号在二维平面上的分布信息.本文采用后者对雷达信号进行研究.

设 $\begin{matrix} (X, d) \end{matrix}$ 为一个度量空间, $\begin{matrix} H 为 X \end{matrix}$ 的非空紧集族, $\begin{matrix} ε \end{matrix}$ 为一个非负实数, 令 $\begin{matrix} B (x, ε) \end{matrix}$ 表示一个中心在 $\begin{matrix} x \end{matrix}$ , 半径为 $\begin{matrix} ε \end{matrix}$ 的闭球.设A是X中的一个非空紧集, {A_j}(j=1, 2, , et al., K)是集合A的一个有限 $\begin{matrix} ε \end{matrix}$ -格形覆盖, $\begin{matrix} p_{j} \end{matrix}$ 表示 $\begin{matrix} A \end{matrix}$ 的元素在集合 $\begin{matrix} A_{j} \end{matrix}$ 中的概率.令信息熵为I(ε )=- $\begin{matrix} \overset{K}{\sum_{j = 1}} \end{matrix} \begin{matrix} p_{j} \lg p_{j}, \end{matrix}$ 如果 $\begin{matrix} I (ε) \end{matrix}$ 满足: $\begin{matrix} I (ε) ~ - \lg ε^{D_{I} (f)}, \end{matrix}$ 则称 $\begin{matrix} D_{I} \end{matrix}$ 为集合 $\begin{matrix} A \end{matrix}$ 的信息维数, 定义为^[11]:

$\begin{matrix} D_{I} = - \lim_{ε \to 0} \frac{I (ε)}{lgε} \end{matrix}$ (1)

实际计算中通常通过粗视化变换得到信息维数:

$\begin{matrix} D_{I} = [I (λ) - I (2 λ)] / \lg 2 \end{matrix}$

基于信息维数的定义, 本文设计了以下算法步骤进行计算:

Step1 数据预处理.首先, 对信号数据线性插值, 使得数据长度为2的整数次幂, 设插值后的数据长度为Length; 然后, 将每个数据点都减去这段信号的最小值, 使得这段信号数据的最小值为0, 设处理后的数据最大值为Data_max; 最后, 将每个数据同乘以Length/Data_max, 使得这段信号数据的最大值等于数据长度.以盒子覆盖信号时, 计算落入每个盒子的信号曲线长度比较麻烦, 所以本文采用计算落入每个盒子的数据点数来替代, 故而需要对信号数据进行插值, 以提高计算精度.使数据长度为2的整数次幂的目的是为了便于设定盒子尺寸, 以及便于运算.对信号的最小值和最大值预处理的目的是为了便于摆放盒子, 且能够满足分形维数与信号幅度无关的特点.

Step2 计算信息熵.依照信息维数的定义, 计算不同盒子尺度下的信息熵.盒子尺度依次选取2的整数次幂, 且不大于数据长度.

Step3 选取无标度区间.作 $\begin{matrix} I (ε) ~ - lgε \end{matrix}$ 曲线, 选取线性度较好的部分作为无标度区间.

Step4 计算信息维数.对无标度区间内的曲线进行线性拟合, 得到的斜率即为信息维数.

2 检测算法设计

2.1 检测原理

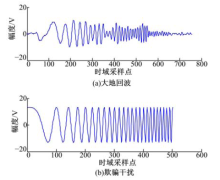
欺骗式干扰主要是通过DRFM对接收到的雷达发射脉冲进行采集, 存储, 调制放大, 转发来产生的, 从而逼真地模拟目标的相关特性, 使得二者在时域, 频域上的差异很小.随着现代数字处理软硬件技术的发展, 一些新型的干扰机在转发信号的同时能够结合脉内调制, RCS调制等复合手段, 实现欺骗信号与目标回波的高度相似.然而这些新型干扰机目前大多还处于研制和实验阶段, 并未大量装备^[2].因此, 本文从实际需要出发, 只针对传统的转发式欺骗干扰, 对于新型欺骗干扰则没有过多考虑.由于雷达的发射脉冲往往是恒包络的, 所以转发式欺骗干扰的包络也是恒定的, 而目标回波的幅度受到目标散射面的调制, 其包络是不规则的, 如图1所示.

	Figure Option View Download New Window
	图1 大地回波和欺骗干扰的时域波形Fig.1 Time-domain signal of terrain return and deception jamming

由图1可知:大地回波的包络与欺骗干扰的包络具有明显差异, 所以它们的包络的分形特征也会有明显差异, 而一般的目标分形检测并没有对信号包络的分形维数进行分析.对于存在欺骗干扰的数据段, 由于干扰信号的包络是个直流电平, 由分形理论的基本性质和信息维数的计算流程均不难看出该数据段的信息维数与噪声比较接近.在信噪比较大时, 存在目标回波的数据段信息维数将小于噪声的信息维数.经过研究发现, 如果仅仅利用对信号包络求信息维数并取最小值来检测目标回波, 其性能很差, 一是因为对信噪比的要求很高; 二是因为当欺骗干扰较强时, 在目标回波和欺骗干扰之间会存在极小值, 影响检测的准确性.为此, 本文先逐段分别计算信号包络和信号本身的信息维数, 然后求两个信息维数的差.前面的分析已经指出, 欺骗干扰的两个信息维数差值比较大, 而噪声, 目标回波的则相对比较小, 故可以据此判断是否存在欺骗干扰, 并且检测出干扰的存在位置.

2.2 算法设计

依次以每个信号数据点为起点, 划分长度为发射脉冲宽度的数据段, 计算每个数据段 $\begin{matrix} Dat a_{j} \end{matrix}$ 的信息维数 $\begin{matrix} A_{j}, \end{matrix}$ 信号包络的信息维数 $\begin{matrix} B_{j}, \end{matrix}$ 两者之差为 $\begin{matrix} L_{j} 。 \end{matrix}$ 根据前文的分析, 干扰检测算法如下:

$\begin{matrix} L_{j} = B_{j} - A_{j} \{\begin{matrix} > ε, 受到干扰 \\ \leq ε, 未受干扰 \end{matrix} \end{matrix}$ (2)

式中: $\begin{matrix} ε \end{matrix}$ 为干扰检测门限. $\begin{matrix} ε \end{matrix}$ 应大于目标回波单独存在时 $\begin{matrix} L_{j} \end{matrix}$ 能取到的最大值, 避免目标回波被误判为欺骗干扰.

(1)当 $\begin{matrix} L_{j} \leq ε \end{matrix}$ 时, 说明不存在欺骗干扰, 或者欺骗干扰不够强.此时, 可按常规的匹配滤波法进行检测, 也可以按文献^{[6, 7, 8]}研究的分形检测法进行后续检测.

(2)当 $\begin{matrix} L_{j} > ε \end{matrix}$ 时, 说明雷达受到干扰. $\begin{matrix} L_{j} \end{matrix}$ 取到最大值的时刻即为欺骗式干扰的起始时刻.知道了欺骗干扰的存在位置, 可以后续采用很多抗干扰算法来抑制干扰, 比如简单的置零处理.

3 仿真及分析

本文采用雷达高度表实测的大地回波数据作为目标回波.选取信噪比很好的某个大地回波, 将其下变频到零中频(消除载波影响), 作为干净的目标回波, 其发射脉冲是线性调频信号, 带宽为10 MHz, 脉宽为5 μ s.由于测量时挂飞的直升机垂直速度很小, 且多普勒频率对分形维数影响很小, 故本文不考虑目标回波的多普勒频率.欺骗式干扰的参数与发射脉冲参数相同, 多普勒频率也假设为零.构造一个长度为20 μ s的雷达接收数据, 其中目标回波起始时刻是1 μ s, 欺骗干扰的起始时刻是4 μ s(与目标回波部分重叠)或者8 μ s(与目标回波分离), 噪声为高斯白噪声.

分形理论所研究的系统是建立在自相似基础之上的, 对于实际的系统, 这只可能在一定的区间内成立, 即无标度区间, 超出这个区间的自相似性就不存在了, 分形也就失去了意义.图2给出了大地回波的信息熵与尺度的单对数坐标曲线, 由图可知, 应当选取曲线的中间部分进行拟合来求出信息维数.欺骗干扰和噪声的曲线与图2类似, 只是斜率不同.

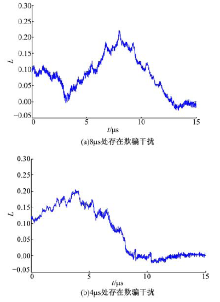
	Figure Option View Download New Window
	图2 信息熵与尺度的单对数坐标曲线Fig.2 Semi-logarithmic curve of scale and comentropy

分别对欺骗干扰信号与目标信号分离和部分重叠两种情况进行仿真, 如图3所示, 信噪比(SNR)为5 dB, 干噪比(JNR)为8 dB.两种情况下的曲线峰值都在欺骗干扰的起始位置, 图3(a)的峰值在8.01 μ s, 图3(b)的峰值在4.06 μ s, 可见本文算法对欺骗干扰的检测精度很高, 且对欺骗干扰的存在位置不敏感.

	Figure Option View Download New Window
	图3 L值的时域分布图Fig.3 Temporal distribution of L

	Figure Option View Download New Window
	图4 L值随信噪比/干噪比的变化曲线Fig.4 Curve of L changing with SNR or JNR

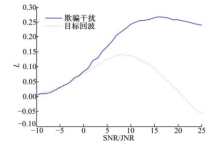
图4仿真的是目标回波和欺骗干扰的L值与信噪比, 干噪比的关系, 其光滑曲线是由50次仿真平均得到的.由图4可知:目标回波的L值在SNR为8 dB时达到最大值0.141.考虑到这是50次仿真的平均结果, 单次计算会存在波动性, 通过仿真发现目标回波的L值在SNR为8 dB时的100次仿真中最大可达0.1674, 故将干扰检测门限 $\begin{matrix} ε \end{matrix}$ 设为0.1675.在该检测门限下, 欺骗式干扰的检测概率曲线如图5所示.

	Figure Option View Download New Window
	图5 欺骗干扰的检测概率曲线Fig.5 Curve of detection probability of repeat jamming

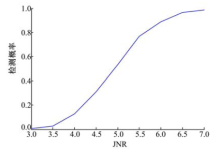
由图5可以看出:在JNR为6 dB时, 欺骗干扰的检测概率即可达到0.9.故当干噪比强于6 dB时, 本文方法可以有效地检测出欺骗干扰, 并易于进一步抑制干扰.还可以看出, 当干噪比弱于6 dB时, 只要目标回波的信噪比满足不低于6 dB, 则欺骗干扰不能构成威胁.故在信噪比不低于6 dB时, 本文算法可有效抗欺骗干扰, 而这个条件在实际应用环境中可以利用相参积累得到满足.

4 结束语

基于DRFM技术的欺骗式干扰信号在时, 频域均可与目标信号高度相似, 对雷达系统具有较强欺骗性.针对这种情况, 本文基于欺骗干扰与目标信号在信息维数上的不同, 提出了一种新的欺骗干扰存在性检测方法.通过仿真验证了本文算法的有效性, 仿真结果表明, 在干噪比不弱于6 dB时, 本文方法能有效检测欺骗干扰.本文并未研究后续的抗干扰算法, 而简单地置零处理有时也会造成目标信号的能量损失, 故下一步将研究在抑制欺骗干扰的同时不损失目标信号能量的抗干扰算法.

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	卢刚. 雷达有源假目标抑制方法研究[D]. 成都: 电子科技大学电子工程学院, 2012. Lu Gang. Study of algorithms on suppression of radar active false targets[D]. Chengdu: School of Electronic Engineering, University of Electronic Science and Technology of China, 2012. [本文引用:1]
[2]	宋志勇, 肖怀铁. 基于回波幅度特征的拖曳式诱饵存在性检测[J]. 电子与信息学报, 2011, 33(6): 1515-1519. Song Zhi-yong, Xiao Huai-tie. Detection of presence of towed radar active decoy based on amplitude characteristic[J]. Journal of Electronics & Information Technology, 2011, 33(6): 1515-1519. [本文引用:2]
[3]	Greco M, Gini F, Farina A, et al. Effect of phase and range gate pull-off delay quantization on jammer signal[J]. IEE Proceeding on Radar Sonar Navigation, 2006, 153(5): 454-459. [本文引用:1]
[4]	韩伟, 汤子跃, 朱振波, 等. 基于脉内特征的雷达抗欺骗干扰方法[J]. 雷达科学与技术, 2012, 10(5): 481-485. Han Wei, Tang Zi-yue, Zhu Zhen-bo, et al. A method against radar's deception-jamming based on intra-pulse feature[J]. Radar Science and Technology, 2012, 10(5): 481-485. [本文引用:1]
[5]	Li Jian-xun, Shen Qi, Yan Hai. Signal feature analysis and experimental verification of radar deception jamming[C]//Proceedings of 2011 IEEE CIE International Conference on Radar, Chengdu, 2011: 230-233. [本文引用:1]
[6]	Cherouat S, Soltani F. Radar signal detection using fractal analysis in K-distributed clutter[C]//2008 International Conference on Signals, Monastir, 2008: 1-4. [本文引用:2]
[7]	Guan J, Liu N B, Huang Y, et al. Fractal characteristic in frequency domain for target detection within sea clutter[J]. IET Radar, Sonar and Navigation, 2012, 6(5): 293-306. [本文引用:2]
[8]	Zhang Kun-hua, Yang Xuan, Zhang Li. Target detection in complex background based on fuzzy enhanced fractal feature[C]//2009 IEEE International Conference on Information and Automation, Zhuhai, 2009: 408-411. [本文引用:2]
[9]	庞新良, 李鹏, 范江兵, 等. 小波计盒分形维数核爆电磁脉冲信号模糊识别[J]. 强激光与粒子束, 2012, 24(9): 2259-2263. Pang Xin-liang, Li Peng, Fan Jiang-bing, et al. Fuzzy identification of NEMP signal based on wavelet and box-counting dimension eigenvalue[J]. High Power Laser and Particle Beams, 2012, 24(9): 2259-2263. [本文引用:1]
[10]	黄晚晴, 张颖, 王文义, 等. 利用分形法表征光学元件中高频相位畸变[J]. 强激光与粒子束, 2013, 25(5): 1171-1175. Huang Wan-qing, Zhang Ying, Wang Wen-yi, et al. Evaluating middle-high frequency phase distortion of optics by fractal method[J]. High Power Laser and Particle Beams, 2013, 25(5): 1171-1175. [本文引用:1]
[11]	Ye Fei, Yu Zhi-fu, Luo Jing-qing. Analysis of radar emitter signal feature based on mutifractal theory[C]//The Eighth International Conference on Electronic Measurement and Instruments, Xi'an, 2007: 114-117. [本文引用:1]

2012

0.0

. 2012, :-

Study of algorithms on suppression of radar active false targets

雷达有源假目标抑制方法研究[D]

Lu Gang.

卢刚

借助于数字射频存储器 (DRFM)对雷达信号的精确复制与再现，现代欺骗式干扰已进入相干假目标干扰时代。从雷达的角度看，这类假目标在雷达接收机中易获得相干处理增益，通过检测判决能影响甚至掩盖对真实目标的检测与录取，且不易被雷达发现；其次，通过后续处理所提取的干扰信号预置参数可能会进一步地消耗雷达资源并掩护真实目标，从而导致雷达方对当前目标或空情做出误判，是一种对抗各类雷达特别是先进体制雷达的强有力技术手段。本文针对有源假目标干扰条件下的雷达抗干扰问题，在跟踪该领域前沿和发展态势的基础上，围绕干扰与雷达处理模型，根据不同假目标样式的特点，深入研究了雷达有源距离、速度与多假目标干扰抑制算法。主要内容包括以下几个方面。其一，明确了雷达有源假目标干扰的定义与本文研究对象，回顾了国内外雷达有源欺骗干扰反对抗技术研究现状与发展趋势。在此基础上，系统地分析了基于 DRFM的雷达有源假目标干扰信号产生、在雷达端的接收与处理、以及距离假目标和多假目标干扰模型。对雷达距离跟踪原理和运行方式进行了详细分析和研究，同时在多普勒处理模型下导出了速度干扰模型，为雷达抗假目标干扰提供了依据和思路。其二，由于新型干扰机不仅可以产生高逼真距离假目标，而且还能通过对DRFM复制信号的脉内加工调制处理产生更复杂的多假目标，针对这一现状，提出了慢时域脉冲分集假目标干扰抑制算法。该算法在慢时域上采用特殊的发射信号集，利用干扰机对雷达信号的复制转发特性，在雷达接收端形成接收信号集后对干扰进行处理，能够对消掉干扰在匹配滤波器输出端所产生的假目标尖峰。这一方法还具有无需对干扰信号参数进行估计，易于工程化实现的优点。随后，着眼于慢时域算法在快变环境中的性能下降问题，提出了快-慢时域联合脉冲分集干扰抑制算法。该算法在快-慢时联合域上生成新的雷达发射信号分集，其优点是无需在不同脉冲重复周期之间进行干扰对消，因而可以应用于实际反对抗中常见的快变环境和部分新型复杂多假目标。针对实际干扰环境中常采用的部分脉冲转发技术，提出一种时-频域联合脉冲分集方法，在单个脉冲重复周期内完成一个完整正交信号集发射。即使在干扰机具备瞬时转发能力的情况下，采用该算法也能有效地对消假目标信号，且同样不受慢时域分集算法中平稳性假设与应用条件的约束。其三，针对脉冲多普勒雷达，在对速度假目标模型研究的基础上，提出一种基于慢时域匹配滤波的脉冲多普勒速度假目标抑制算法。该方法通过滑窗多普勒处理，利用干扰进行速度波门拖引时与目标信号的多普勒失配，从而在慢时域对干扰信号功率进行衰减。同时分析了该算法的干扰抑制性能，结果表明其对多普勒速度假目标具有较为理想的干扰抑制效果。其四，针对距离波门拖引干扰，利用当雷达受到距离前拖/后拖干扰时，其距离跟踪环将失去功率(能量)平衡这一特性，提出了基于自适应偏置权的雷达抗距离波门拖引方法。该方法采用偏置权对早/迟门权重进行调整，并且在每一个跟踪周期对偏置权进行自适应更新。这一方法能够在停拖期与拖引期保持雷达距离跟踪系统对感兴趣目标回波脉冲的正常跟踪。最后，针对采用大时宽-带宽的线性调频雷达在遭遇假目标干扰时，干扰信号与目标回波在时域和频域都有可能高度重叠的情况，提出一种自适应假目标干扰信号对消方法。该方法通过对受干扰污染的回波信号进行时-频解耦运算将干扰与回波信号分离，在干扰与目标回波信号分量间存在微小时延差的情况下，即能在频率轴上自适应地得到分离的目标信号分量并对干扰信号分量进行对消。同时，结合该算法给出一种对距离波门拖引干扰的抑制方案，并利用某雷达实测数据进行了分析，结果证明该方案是切实可行的。

... 目前,关于欺骗式干扰的研究主要集中在原理分析,性能仿真和效果评估方面,关于抗干扰的研究则相对较少^[1,2] ...

2011

0.0

. 2011, 33(6):1515-1519 DOI:doi:10.3724/SP.J.1146.2010.01180

Detection of presence of towed radar active decoy based on amplitude characteristic

基于回波幅度特征的拖曳式诱饵存在性检测

Song Zhi-yong , Xiao Huai-tie.

宋志勇, 肖怀铁

The detection of presence of decoy is the foundation of countering the Towed Radar Active Decoy (TRAD) and deciding the effect of ECCM. Based on the distinction of the amplitude characteristic on the condition of the decoy is present or not, the conditioned probability density functions (pdfs) of the measured amplitude are given. Generalized Maximum Likelihood (GML) detection of the presence of TRAD is developed with the amplitude characteristic. Simulation results with different condition illustrate the performance of the method.

诱饵的存在性检测是对抗拖曳式有源雷达诱饵干扰的前提，也是决定抗干扰效果的重要因素。该文基于雷达波束内诱饵存在导致的回波幅度特征变化，通过提取诱饵存在/不存在两种情况下雷达接收信号的幅度特征差异，推导了两种条件下雷达观测幅度的条件概率密度函数，在此基础上提出了基于回波幅度特征的广义最大似然存在性检测方法。结合不同干扰场景仿真验证了该方法的有效性。

... 目前,关于欺骗式干扰的研究主要集中在原理分析,性能仿真和效果评估方面,关于抗干扰的研究则相对较少^[1,2] ...

... 然而这些新型干扰机目前大多还处于研制和实验阶段,并未大量装备^[2] ...

2006

0.0

... 文献^[3]分析了数字射频存储器(DRFM)产生的距离波门拖引(RGPO)干扰信号由于DRFM相位量化误差在频域上产生的细微变化,但这个细微变化在DRFM阶数较高时不明显,且不适用于目标回波和干扰同时存在的情况 ...

2012

0.0

. 2012, 10(5):481-485

A method against radar's deception-jamming based on intra-pulse feature

基于脉内特征的雷达抗欺骗干扰方法

Han Wei , Tang Zi-yue , Zhu Zhen-bo

韩伟, 汤子跃, 朱振波

抗欺骗干扰是电子对抗环境中雷达面临的一个重要问题.针对应答式欺骗干扰问题提出了一种基于信号脉内特征的目标与干扰的识别方法.首先对目标回波信号与干扰信号进行建模,分析了两类信号的脉内幅度特征,然后将目标与干扰看作是空间不同的模式类,利用目标回波信号和干扰信号的脉内幅度起伏差异,定义出分类的特征因子,最后采用径向基(RBF)神经网络进行分类.仿真结果表明,该方法在一定的信干比范围内具有较高的目标识别概率且受信干比影响较小,能够较好地抗应答式欺骗干扰.

... 文献^[4]分析了目标回波与欺骗干扰信号脉内幅度起伏的差异 ...

2011

0.0

... 文献^[5]研究了两者在幅度起伏,高阶统计量,双谱特性上的差异,但均分析简单,没有研究目标回波与欺骗干扰部分重叠的情况 ...

2008

0.0

... 文献^[6,7,8]分别从不同角度研究了分形理论在雷达目标检测中的应用,但均不适用于存在欺骗干扰的情况 ...

... 此时,可按常规的匹配滤波法进行检测,也可以按文献^[6,7,8]研究的分形检测法进行后续检测 ...

2012

0.0

... 文献^[6,7,8]分别从不同角度研究了分形理论在雷达目标检测中的应用,但均不适用于存在欺骗干扰的情况 ...

... 此时,可按常规的匹配滤波法进行检测,也可以按文献^[6,7,8]研究的分形检测法进行后续检测 ...

2009

0.0

... 文献^[6,7,8]分别从不同角度研究了分形理论在雷达目标检测中的应用,但均不适用于存在欺骗干扰的情况 ...

... 此时,可按常规的匹配滤波法进行检测,也可以按文献^[6,7,8]研究的分形检测法进行后续检测 ...

2012

0.0

. 2012, 24(9):2259-2263 DOI:doi:10.3788/HPLPB20122409.2259

Fuzzy identification of NEMP signal based on wavelet and box-counting dimension eigenvalue

小波计盒分形维数核爆电磁脉冲信号模糊识别

Pang Xin-liang , Li Peng , Fan Jiang-bing

庞新良, 李鹏, 范江兵

The paper investigates an NEMP(nuclear electromagnetic pulse) detection technique in the absence of nuclear testing. After threshold demodulation, DC elimination, filtering, interpolation and normalization, the method uses wavelet analysis to extract the forth segment of wavelet pack energy spectrum, the first and forth segments of wavelet coefficient box-counting dimension as eigenvalues, establishes their respective membership functions according to statistical analysis, and then uses the fuzzy identification theory to identify NEMP signals. The method has been used to process measured NEMP signals and LEMP(lightning electromagnetic pulse) signals, which are the main source of interference. The identification rate is 99.41%.

为了在现有禁核试验条件下开展核爆电磁脉冲探测技术研究，对实测的非均匀采样核爆电磁脉冲数据进行阈值检波、直流剔除、滤波、插值和归一化处理后，采用小波分析提取信号第四尺度小波系数能谱熵、第一尺度和第四尺度小波系数计盒分形维数特征值，在统计分析的基础上分别建立其专用隶属度函数；利用模糊识别理论，对核爆电磁脉冲信号和作为主要探测干扰信号源的闪电电磁脉冲信号进行了模糊识别，获得了总识别率为99.41%的识别效果。

... 1 信息维数分形维数是分形理论的中心概念,它有多种定义和计算方法,常用的是Hausdorff维数,盒维数,信息维数,相似维数等^[9,10] ...

2013

0.0

. 2013, 25(5):1171-1175 DOI:doi:10.3788/HPLPB20132505.1171

Evaluating middle-high frequency phase distortion of optics by fractal method

利用分形法表征光学元件中高频相位畸变

Huang Wan-qing , Zhang Ying , Wang Wen-yi

黄晚晴, 张颖, 王文义

Based on the fractal theory, this paper analyzed statistical distribution features of middle-high frequency phase distortion of the optics for Shenguang-Ⅲ laser facility. The middle-high frequency phase distribution is found to be consistent with the model of fractional Brownian random field. The fractal dimension was calculated by structure function. The fractal dimension of large-aperture neodymium-doped phosphate amplifier glass is distributed between 2.34 and 2.43. A method of phase simulation by random midpoint-displacement was presented. In this method, the fractal dimension can be viewed as a parameter for estimating phase distortion, which helps to evaluate the high laser optics.

针对神光Ⅲ主机装置使用的光学元件，基于分形理论，分析中高频相位畸变的统计分布特征，指出其满足分数布朗随机场，并利用结构函数法对分形维数进行计算，统计结果显示，大口径钕玻璃片的分形维数在2.34~2.43之间。利用局部稳态的随机中点位移法，提出一种新的表征光学元件相位的方法，将分形维数作为参数，可衡量中高频相位畸变，对高功率激光光学元件的评价有参考意义。

... 1 信息维数分形维数是分形理论的中心概念,它有多种定义和计算方法,常用的是Hausdorff维数,盒维数,信息维数,相似维数等^[9,10] ...

2007

0.0

... )=-∑j=1Kpjlgpj,如果 I(ε)满足: I(ε)~-lgεDI(f),则称 DI为集合 A的信息维数,定义为^[11]: ...