基于多维矢量矩阵理论的KL变换

引用本文

陈绵书, 王园园, 桑爱军, 陈贺新. 基于多维矢量矩阵理论的KL变换.吉林大学学报:工学版, 2016, 46(2): 627-631
CHEN Mian-shu, WANG Yuan-yuan, SANG Ai-jun, CHEN He-xin. KL transformation based the theory of multidimensional vector matrix. Journal of Jilin University Engineering and Technology Edition, 2016, 46(2): 627-631 复制到剪切板

Permissions

基于多维矢量矩阵理论的KL变换

陈绵书, 王园园, 桑爱军, 陈贺新

吉林大学通信工程学院, 长春 130022

通讯作者:桑爱军(1973-),女,教授,博士.研究方向:多维视频流编解码.E-mail:sangaj@jlu.edu.cn

作者简介:陈绵书(1973-),男,副教授,博士.研究方向:图像处理,人工智能.E-mail:chenms@jlu.edu.cn

基金:国家自然科学基金项目(61171078); 吉林省自然科学基金项目(20130101045JC); 吉林省科技发展计划国际科技合作项目(20130413053GH,20140414013GH); 吉林省科技发展计划青年科研基金项目(20130522164JH)

摘要

为了使Karhunen-Loeve ( KL)变换适应高维数据,同时为了找出多维矢量矩阵的最优变换,本文提出了基于多维矢量矩阵理论的 M维KL变换(即MKL变换).首先结合多维矢量矩阵理论定义多维协方差矩阵,并求解多维特征向量矩阵;然后定义MKL变换,将多维数据映射到投影空间.实验结果表明:MKL变换在一维时与KL变换具有相同的最优性;对于三维视频数据,MKL变换实现了完全解相关,平均能量集中率(EPE)高达99%.

关键词: 信息处理技术; 视频图像压缩编码技术; 多维矢量矩阵; KL变换

中图分类号:TN919 文献标志码:A 文章编号:1671-5497(2016)02-0627-05

KL transformation based the theory of multidimensional vector matrix

CHEN Mian-shu, WANG Yuan-yuan, SANG Ai-jun, CHEN He-xin

College of Communication Engineering, Jilin University, Changchun 130022,China

Abstract

In order to adapt Karhunen-Loeve (KL) transform to multidimensional data, meanwhile to find out the optimal transformation of multidimensional vector matrix, a Multidimensional KL (MKL) transform based the theory of multidimensional vector matrix is proposed. First, the multidimensional covariance matrix is defined using the theory of multidimensional vector matrix, and the multidimensional characteristic matrix vector is solved. The, MKL transform is defined and the multidimensional data are mapped to the projective space. Simulation results show that the MKL transform in one-dimension has the same optimality as the KL transform. For 3D video data block, the average EPE can be as high as 99% by integral transformation, and MKL realizes decorrelation completely.

Keyword: information processing; video image compression coding technology; multidimensional vector matrix; KL transform

Show Figures

0 引言

多维理论(高维理论)很早就被提出, 并在一些领域里得到了广泛的应用, 如在力学领域^[1], 优化方面^[2], 数据存储方面^[3]等.目前, 高维理论无论是在表现形式, 还是在存储上都得到了不断发展, 但是较少应用于变换领域.Liu等^{[4, 5, 6]}提出了基于多维矢量矩阵的多维矢量变换, 并应用到彩色视频流压缩编码和多视角视频编码中, 在去除冗余, 提高能量集中性方面都取得了不错的效果.对于有限的多维矢量信号给出它的最优变换, 也就成为了进一步过程中不可避免的一部分.Karhunen-Loeve(KL)变换^{[7, 8, 9]}是均方误差准则下的最优变换, 由于它在完全解相关, 有效减少特征图像数目以及抽取更好特征图像等方面的优点, 所以即使它存在计算量大, 复杂度高, 无快速算法的缺点, 也还是在实际中应用.

离散图像的KL变换采用行, 列堆叠的方法进行近似计算, 表达形式上还存在一定的缺陷, 并且随着人们对于视频图像要求的提高, 传统的二维(2 dimensional, 2D)图像记录及重现场景的视频技术已经不能满足观看者的视觉要求, 然而现有的KL变换并不具备向着多维方向发展的延展性.为明确离散图像KL变换的表达式, 并使KL变换从一维扩展到多维, 本文从KL变换理论出发, 结合多维矢量矩阵理论, 重新定义离散图像KL变换, 并把其推广到M维, 即MKL变换.最后通过实验证明其在能量集中性和解相关性方面的优越性.

1 多维矢量矩阵理论

1.1 多维矢量矩阵的定义

定义1 F域上的m₁× m₂个元素( $\begin{matrix} a_{i_{1} i_{2}} \end{matrix}$ )排列而成的矩阵称为二维矩阵, 记为 $\begin{matrix} A_{m_{1} \times m_{2}} \end{matrix}$ ; F域上的m₁× m₂× , et al.× m_K个元素( $\begin{matrix} a_{i_{1} i_{2} \dots i_{K}} \end{matrix}$ )排列而成的矩阵称为多维矩阵, 记 $\begin{matrix} A_{m_{1} \times m_{2} \times \dots \times m_{K}} \end{matrix}$ .

定义2 将多维矩阵 $\begin{matrix} A_{m_{1} \times m_{2} \times \dots \times m_{K}} \end{matrix}$ 的维数K分成两部分, 分别表示为矢量m=(m₁, m₂, , et al., m_M), n=(n₁, n₂, , et al., n_N), 其中M+N=K, 从而多维矩阵 $\begin{matrix} A_{m_{1} \times m_{2} \times \dots \times m_{K}} \end{matrix}$ 又可以变化为 $\begin{matrix} A_{(m_{1} \times m_{2} \times \dots \times m_{M}) \times (n_{1} \times n_{2} \times \dots \times n_{N})} \end{matrix}$ , 称其为多维矢量矩阵, 简记为A_{m× n}.

定义3 若定义2中划分的矢量m和n的维数相同(M=N), 则称 $\begin{matrix} A_{(m_{1} \times m_{2} \times \dots \times m_{M}) \times (n_{1} \times n_{2} \times \dots \times n_{M})} \end{matrix}$ 为2M维矢量矩阵.

1.2 多维矢量矩阵的特征值和特征向量

由于此处的特征值和特征向量的计算都是针对于2M维的协方差矩阵, 且2M维协方差矩阵 $\begin{matrix} A_{(m_{1} \times m_{2} \times \dots \times m_{M}) \times (n_{1} \times n_{2} \times \dots \times n_{M})} \end{matrix}$ 的矢量m和n的对应阶数均相同, 所以2M维协方差矩阵可以表示为 $\begin{matrix} A_{(m_{1} \times m_{2} \times \dots \times m_{M}) \times (m_{1} \times m_{2} \times \dots \times m_{M})} \end{matrix}$ .

定义4 如果2M维矢量矩阵为 $\begin{matrix} A_{(m_{1} \times m_{2} \times \dots \times m_{M}) \times (m_{1} \times m_{2} \times \dots \times m_{M})} \end{matrix}$ , 则它的特征矩阵为λ $\begin{matrix} E_{(m_{1} \times m_{2} \times \dots \times m_{M}) \times (m_{1} \times m_{2} \times \dots \times m_{M})} \end{matrix} - \begin{matrix} A_{(m_{1} \times m_{2} \times \dots \times m_{M}) \times (m_{1} \times m_{2} \times \dots \times m_{M})} \end{matrix}$ , 其中λ ∈ F.

定义5 若2M维矢量矩阵的特征矩阵如定义4所示, 则它的行列式为|λ $\begin{matrix} E_{(m_{1} \times m_{2} \times \dots \times m_{M}) \times (m_{1} \times m_{2} \times \dots \times m_{M})} \end{matrix} - \begin{matrix} A_{(m_{1} \times m_{2} \times \dots \times m_{M}) \times (m_{1} \times m_{2} \times \dots \times m_{M})} \end{matrix}$ |, 其中行列式的表达式是一个关于λ 的多项式, 记做φ (λ ), 称此表达式为 $\begin{matrix} A_{(m_{1} \times m_{2} \times \dots \times m_{M}) \times (m_{1} \times m_{2} \times \dots \times m_{M})} \end{matrix}$ 的特征多项式.其中特征多项式的根记作 $\begin{matrix} A_{(m_{1} \times m_{2} \times \dots \times m_{M}) \times (m_{1} \times m_{2} \times \dots \times m_{M})} \end{matrix}$ 的特征值, 或是特征根.

1.3 2M维矢量矩阵的特征向量

定理1 设λ 是2M维矢量矩阵 $\begin{matrix} A_{(m_{1} \times m_{2} \times \dots \times m_{M}) \times (m_{1} \times m_{2} \times \dots \times m_{M})} \end{matrix}$ 的某个特征值.若有非零2M维向量 $\begin{matrix} α_{(m_{1} \times m_{2} \times \dots \times m_{M}) \times (1 \times 1 \times \dots \times 1)} \end{matrix}$ 使 $\begin{matrix} A_{(m_{1} \times m_{2} \times \dots \times m_{M}) \times (m_{1} \times m_{2} \times \dots \times m_{M})} \end{matrix} \begin{matrix} α_{(m_{1} \times m_{2} \times \dots \times m_{M}) \times (1 \times 1 \times \dots \times 1)} \end{matrix} = λ \begin{matrix} α_{(m_{1} \times m_{2} \times \dots \times m_{M}) \times (1 \times 1 \times \dots \times 1)} \end{matrix}$ 成立, 则称 $\begin{matrix} α_{(m_{1} \times m_{2} \times \dots \times m_{M}) \times (1 \times 1 \times \dots \times 1)} \end{matrix}$ 是对应于特征值λ 的2M维矢量矩阵 $\begin{matrix} A_{(m_{1} \times m_{2} \times \dots \times m_{M}) \times (m_{1} \times m_{2} \times \dots \times m_{M})} \end{matrix}$ 的特征向量.

2 MKL变换

KL变换最大优点是消除相关性, 它是最小均方误差准则(Minimum mean square error, MMSE)下的最优变换^{[10, 11]}, 可以获得最佳匹配图像效果, 并消除变换域里的全部相关性.本文在推导出MKL变换之前, 首先给出多维协方差的定义.

2.1 多维协方差矩阵

对于一维向量, KL变换的协方差矩阵具有明确的定义和表达形式.而对于离散图像信号, 并没有相应的定义.所以在此结合多维矢量矩阵理论, 给出了离散图像信号多维协方差矩阵的定义.

定义6 设屡被传送的N× N图像信号为X,

$\begin{matrix} X = {[\begin{matrix} x_{11} & x_{12} & \dots & x_{1 N} \\ x_{21} & x_{22} & \dots & x_{2 N} \\ ︙ & ︙ & ︙ \\ x_{N 1} & x_{N 2} & \dots & x_{NN} \end{matrix}]}_{N \times N} \end{matrix}$

则离散图像信号多维协方差矩阵为:

$\begin{matrix} \begin{matrix} Σ_{x} = E \{{(X - μ_{x})}_{(N \times N) \times (1 \times 1)} \times {(X - μ_{x})}^{T}_{(N \times N) \times (1 \times 1)}\} = {[σ_{(i_{1} i_{2}) \times (j_{1} j_{2})}^{2}]}_{(N \times N) \times (N \times N)} = {[σ_{IJ}^{2}]}_{(N \times N) \times (N \times N)} \end{matrix} \end{matrix}$ (1)

其中, I=(i₁i₂), J=(j₁j₂);

$\begin{matrix} σ_{IJ}^{2} \end{matrix} = \begin{matrix} σ_{(i_{1} i_{2}) \times (j_{1} j_{2})}^{2} \end{matrix} = E \begin{matrix} \{(x_{i_{1} i_{2}} - {\bar{x}}_{i_{1} i_{2}}) (x_{j_{1} j_{2}} - {\bar{x}}_{j_{1} j_{2}})\} \end{matrix};$

1< i₁, i₂, j₁, j₂< N;

E $\begin{matrix} \{X\} \end{matrix}$ = $\begin{matrix} {[\begin{matrix} {\bar{x}}_{11} & {\bar{x}}_{12} & \dots & {\bar{x}}_{1 N} \\ {\bar{x}}_{21} & {\bar{x}}_{22} & \dots & {\bar{x}}_{2 N} \\ ︙ & ︙ & ︙ \\ {\bar{x}}_{N 1} & x_{N 2} & \dots & {\bar{x}}_{NN} \end{matrix}]}_{N \times N} \end{matrix}$

定义6给出了离散图像信号多维协方差矩阵的定义.此外, 为了处理高维数据, 本文又通过推导给出Μ 维矢量信号的多维协方差矩阵定义, 如定义7所示.

定义7 设屡被传送的M维矢量信号为X, X=

; 1≤ i₁≤ N₁, , et al., 1≤ i_Μ≤ N_M, 则M维矢量信号的2M维协方差矩阵为:

$\begin{matrix} \begin{matrix} Σ_{x} = E \{{(X - μ_{x})}_{(N_{1} \times N_{2} \times \dots \times N_{Μ}) \times (1 \times 1 \times \dots \times 1)} \times \\ {(X - μ_{x})}^{T}_{(N_{1} \times N_{2} \times \dots \times N_{M}) \times (1 \times 1 \times \dots \times 1)} = \\ {[σ_{(i_{1} i_{2} \dots i_{M}) \times (j_{1} j_{2} \dots j_{M})}^{2}]}_{(N_{1} \times N_{2} \times \dots \times N_{M}) \times (N_{1} \times N_{2} \times \dots \times N_{M})} = \\ {[σ_{IJ}^{2}]}_{(N_{1} \times N_{2} \times \dots \times N_{M}) \times (N_{1} \times N_{2} \times \dots \times N_{M})} \end{matrix} \end{matrix}$ (2)

其中, I=(i₁i₂, et al.i_M), J=(j₁j₂, et al.j_M),

$\begin{matrix} σ_{IJ}^{2} \end{matrix}$ = $\begin{matrix} σ_{(i_{1} i_{2} \dots i_{M}) \times (j_{1} j_{2} \dots j_{M})}^{2} \end{matrix}$ =

E $\begin{matrix} \{(x_{i_{1} i_{2} \dots i_{M}} - {\bar{x}}_{i_{1} i_{2} \dots i_{M}}) (x_{j_{1} j_{2} \dots j_{M}} - {\bar{x}}_{j_{1} j_{2} \dots j_{M}})\} \end{matrix}$ , E $\begin{matrix} \{X\} \end{matrix}$ = $\begin{matrix} {[{\bar{x}}_{i_{1} i_{2} \dots i_{M}}]}_{N_{1} \times N_{2} \times \dots \times N_{M}} \end{matrix}$

定义6和定义7摒弃了传统离散图像应用堆叠思想求解协方差矩阵的思路, 直接应用多维矢量矩阵, 定义M维矢量信号的2M维协方差矩阵.

2.2 多维信号的KL变换

在多维矢量矩阵运算法则, 多维协方差矩阵定义和多维特征向量求解方法的基础上, 对多维信号的KL变换进行研究, 推导出了MKL变换.

设M维离散矢量信号为X, 其中X=[ $\begin{matrix} x_{i_{1} i_{2} \dots i_{M}} \end{matrix} \begin{matrix} ]_{N_{1} \times N_{2} \times \dots \times N_{M}} \end{matrix}$ ; 1≤ i₁≤ N₁, , et al., 1≤ i_M≤ N_M, 则MKL变换:① 首先根据定义7求解2M维协方差矩阵Σ _A.② 根据多维矢量矩阵特征向量的求解方法, 求解多维协方差矩阵Σ _A的多维特征向量矩阵.③ 把多维协方差矩阵Σ _A的特征值λ _I(其中I=(i₁i₂, et al.i_M))从大到小排列, 对应的特征向量为 $\begin{matrix} α_{(i_{1} \times i_{2} \times \dots \times i_{M}) \times (1 \times 1 \times \dots \times 1)} \end{matrix}$ , 构成2M维变换核矩阵T.

对M维离散矢量信号X进行变换:

MKL正变换为:Y_J= $\begin{matrix} {T^{T}}_{IJ} \end{matrix}$ X_I(3)

MKL反变换为:X_I=T_IJY_J(4)

其中, Y是X经过变换后得到的M维矩阵, Y=[ $\begin{matrix} y_{j_{1} j_{2} \dots j_{M}} \end{matrix} \begin{matrix} ]_{N_{1} \times N_{2} \times \dots \times N_{M}} \end{matrix}$ , 1≤ j₁≤ N₁, , et al., 1≤ j_M≤ N, T则是MKL变换的2M维变换核矩阵, 即:

$\begin{matrix} T = {[T_{IJ}]}_{(N_{1} \times N_{2} \times \dots \times N_{M}) \times (N_{1} \times N_{2} \times \dots \times N_{M})} \end{matrix}$

其中, I= $\begin{matrix} (i_{1} i_{2} \dots i_{M}) \end{matrix}$ , J=(j₁j₂, et al.j_M).

3 实验结果分析

实验采用352× 288的4:2:0的yuv视频作为实验对象, 主要包括foreman.yuv等视频, 并以解相关程度和能量集中性作为评价标准对实验数据进行分析.

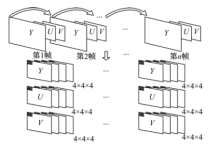
分块是把* .yuv格式的视频分为Y块, U块, V块, 并在Y, U, V块上进行扫描得4× 4× 4, 8× 8× 8或者16× 16× 16数据块.图1为分成4× 4× 4数据块的示意图.

	Figure Option View Download New Window
	图1 整体分块示意图Fig.1 Overall block diagram

3.1 解相关性比较

数据一般通过比较变换前, 后的协方差矩阵来衡量解相关的程度.本文利用VC++6.0进行实验, 分别获取变换前, 后的多维协方差矩阵, 发现变换后的多维协方差矩阵均为对角阵, 因此MKL变换具有完全解相关性.

3.2 能量集中性

能量集中率(EPE)评价标准是变换系数矩阵中某一矢量较大系数的能量与所有系数能量的百分比, 即:

$\begin{matrix} EPE (M_{0}) = \frac{\overset{M_{0} - 1}{\sum_{p = 0}} E \{{X_{P}}^{2}\}}{\overset{M - 1}{\sum_{p = 0}} E \{{X_{p}}^{2}\}} \end{matrix}$ (5)

对foreman.yuv进行MKL变换, 比较不同分块情况下变换前, 后左上角的能量集中率, 如表1所示, 其中EPE如公式(6)所示:

$\begin{matrix} EPE (M_{0}) = \frac{E^{2} [0] [0] [0]}{\overset{N - 1}{\sum_{i = 0}} \overset{N - 1}{\sum_{J = 0}} \overset{N - 1}{\sum_{k = 0}} E^{2} [i] [j] [k]} \end{matrix}$ (6)

分别对foreman, tempete, silent视频进行分块, 变换, 并以4阶三维分块为例, 比较变换前, 后左上角的平均能量集中率, 如表2所示.

由表1, 表2可以发现, 视频块经过MKL变换, 平均能量基本已经完全集中在左上角, 具有很好的能量集中性.

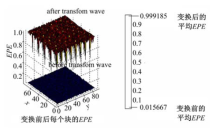
图2是以foreman的4阶三维块为例, 显示出变换前, 后所有变换块的EPE.通过对比可以发现, 变换后所有块的能量集中率都得到了很大改善.

表1 不同分块下foreman变换前, 后的平均EPE Table 1 Foreman average EPE under different block before and after the transformation

表2 不同视频源变换前, 后的平均EPE Table 2 Average EPE under different video source before and after the transformation

	Figure Option View Download New Window
	图2 所有块变换前, 后的EPEFig.2 EPE of all the blocks before and after the transformation

4 结束语

根据现有的多维矢量矩阵和Karhunen-Loeve(KL)变换理论, 创新性地定义了基于多维矢量矩阵的协方差矩阵, MKL变换.对yuv格式视频进行了三维4阶, 8阶, 16阶的MKL变换, 以验证MKL变换的解相关性和能量集中性.实验结果表明:变换后的数据可以完全解相关; 且对于数据块仅取左上角1个数据(即1/64, 1/512, 1/4096)所得Y分量的EPE均值均高达99%以上.这充分说明了MKL变换具有很好的能量集中性和解相关性.本研究还有一定的局限性和不足, 在下一步工作中, 将继续针对MKL变换的应用, MKL变换与多维矢量矩阵最优变换的关系等方面展开进一步的研究.

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	张伟, 姚明辉, 张君华, 等. 高维非线性系统的全局分岔和混沌动力学研究[J]. 力学进展, 2013 43(1): 63-91. Zhang Wei, Yao Ming-hui, Zhang Jun-hua, et al. High dimensional nonlinear systems global bifurcation and chaos dynamics research[J]. Advances in Mechanics, 2013, 43(1): 63-91. [本文引用:1]
[2]	刘凯, 李文东, 张闻钊, 等. 高维辅助的普适量子线路优化[J]. 物理学报, 2012, 61(12): 1-7. Liu Kai, Li Wen-dong, Zhang Wen-zhao, et al. High-dimensional auxiliary's moderate line optimization[J]. Acta Phys, 2012, 61(12): 1-7. [本文引用:1]
[3]	丁东生, 周志远, 史宝森, 等. 高维量子态存储[J]. 量子电子学报, 2014, 31(4): 442-449. Ding Dong-sheng, Zhou Zhi-yuan, Shi Bao-sen, et al. A quantum memory for high-dimensional states[J]. Chinese Journal of Quantum Elecronics, 2014, 31(4): 442-449. [本文引用:1]
[4]	Liu L L, Chen H X, Sang A J, et al. 4D order-4 vector matrix DCT integer transform and its application in video codec[J]. Imaging Science Journal, 2010, 58(10) : 321-330. [本文引用:1]
[5]	桑爱军, 穆森, 王墨林, 等. 基于多维矢量矩阵的多视角视频编码[J]. 吉林大学学报: 工学版, 2013, 43(4): 1110-1115. Sang Ai-jun, Mu Sen, Wang Mo-lin, et al. Multi-view video coding based on multidimensional vector matrix[J]. Journal of Jilin University (Engineering and Technology Edition), 2013, 43(4): 1110-1115. [本文引用:1]
[6]	桑爱军, 崔海廷, 王墨林, 等. 高维变换域中的系数集中分析及研究[J]. 吉林大学学报: 工学版, 2013, 43(增刊): 96-100. Sang Ai-jun, Cui Hai-ting, Wang Mo-lin, et al. Coefficients concentration analysis and research in high-dimensional transformation domain[J]. Journal of Jilin University(Engineering and Technology), 2013, 43(Sup. ): 96-100. [本文引用:1]
[7]	Puchala D. Approximating the KLT by maximizing the sum of fourth-order moments[J]. IEEE Signal Processing Letters, 2013, 20(3): 193-196. [本文引用:1]
[8]	Jana S, Moulin P. Optimality of KLT for high-rate transform coding of Gaussian vector-scale mixtures: application to reconstruction, estimation, and classification[J]. IEEE Transaction on Information Theory, 2006, 52(9) : 4049-4068. [本文引用:1]
[9]	卢山. 基于可逆整型KL变换和FS-KFDA的复杂图像压缩与分类[D]. 西安: 西安电子科技大学电子工程学院, 2013. Lu Shan. Based on the reversible integer KL transform and complex image compression and classification of FS - KFDA said[D]. Xi'an: School of Electrical Engineering, Xi'an University of Electronic Science and Technology, 2013. [本文引用:1]
[10]	王文峰. K-L变换的研究及其在图像压缩编码中的应用[D]. 沈阳: 沈阳理工大学信息科学与工程学院, 2008. Wang Wen-feng. K-L transformation research and its application in image compression coding[D]. Shenyang: School of Information Science and Engineering, Shenyang Ligong University, 2008. [本文引用:1]
[11]	Hanzlik P, Páta P. Derivate statistics for Karhunen-Loève transform[J]. Proc of SPIE, 2006, 6180: 1-7. [本文引用:1]

2013

0.0

. 2013, 43(1):63-91 DOI:10.6052/1000-0992-12-053

High dimensional nonlinear systems global bifurcation and chaos dynamics research

高维非线性系统的全局分岔和混沌动力学研究

Zhang Wei , Yao Ming-hui , Zhang Jun-hua

张伟, 姚明辉, 张君华

College of Mechanical Engineering, Beijing University of Technology, Beijing 100124, China

In this paper, the history of the Melnikov theory is summarized. In 1963, the classical Melnikov method was presented by Melnikov, a Russian scientist. Until now, the Melnikov theory has been extended and developed. The development of the Melnikov method is divided into three historical periods. The extension and application of Melnikov theory are respectively summed up in each historical period, in which the situation of study and main domestic and abroad results in this research field are enumerated. The relationships, problems and deficiencies are pointed out for a variety of Melnikov theories. In addition, another global perturbation method, i.e., energy phase theory, is set forth in order to compare with two theories which are normally used to investigate multi-pulse chaotic motion in the high-dimensional nonlinear systems. The brief history, the theory and the research achievements and engineering applications of the energy phase theory are elucidated. The origin of the energy phase theory and its inherent relations with the Melnikov theory are illustrated. The subject investigated in the energy phase method is contrast with that in the extended Melnikov method to find the difference between them. Disadvantages and open problems are indicated for both the energy phase method and the extended Melnikov method. Furthermore, theoretical frames of these two methods are stated briefly. The multi-pulse chaotic dynamics for a rectangular thin plate, simply supported at the fore-edge, is analyzed by using both of them. Numerical simulation further verifies the analytical prediction. Finally, deficiencies of these two theories are described in detail. The future development direction of the global perturbation theory is demonstrated too.

综述了Melnikov方法的发展历史, 从1963年苏联学者Melnikov提出该方法开始, 一直到目前广义Melnikov方法的提出和发展. Melnikov方法的发展历程可以概括为3 个阶段, 分别综述了每一个阶段Melnikov方法的扩展和应用, 论述了国内外在该方向的研究现状和所获得的主要结果, 指出了各种Melnikov方法之间的联系、存在的问题和不足. 为了对比两种研究高维非线性系统多脉冲混沌动力学的理论, 本文综述了另外一种全局摄动理论, 即能量相位法, 总结了该方法十几年来的发展历史以及国内外的理论研究成果和工程应用实例, 阐述了能量相位法发展的根源以及与Melnikov方法的内在联系, 比较了能量相位法和广义Melnikov方法两种理论研究对象的差别, 以及各自所存在的不足和问题. 简要论述了能量相位法和广义Melnikov方法的理论体系, 并利用广义Melnikov方法分析了四边简支矩形薄板的多脉冲混沌动力学, 数值模拟进一步验证了理论研究的结果. 最后, 详细综述了两种理论的缺点和不足, 说明今后全局摄动理论的发展方向.

... 0 引言多维理论(高维理论)很早就被提出,并在一些领域里得到了广泛的应用,如在力学领域^[1],优化方面^[2],数据存储方面^[3]等 ...

2012

0.0

... 0 引言多维理论(高维理论)很早就被提出,并在一些领域里得到了广泛的应用,如在力学领域^[1],优化方面^[2],数据存储方面^[3]等 ...

2014

0.0

... 0 引言多维理论(高维理论)很早就被提出,并在一些领域里得到了广泛的应用,如在力学领域^[1],优化方面^[2],数据存储方面^[3]等 ...

2010

0.0

... Liu等^[4,5,6]提出了基于多维矢量矩阵的多维矢量变换,并应用到彩色视频流压缩编码和多视角视频编码中,在去除冗余,提高能量集中性方面都取得了不错的效果 ...

2013

0.0

. 2013, 43(4):1110-1115 DOI:10.7964/jdxbgxb201304042

Multi-view video coding based on multidimensional vector matrix

基于多维矢量矩阵的多视角视频编码

Sang Ai-jun , Mu Sen , Wang Mo-lin

桑爱军, 穆森, 王墨林

College of Communication Engineering, Jilin University, Changchun 130022,China

The existing video compression standard possesses certain limitations on the support and expansion of the Multi-View video Coding (MVC). To solve this problem, combined with the multi-dimensional vector matrix theory, a whole set of compression encoding schemes on single-view colorful video stream proposed in previous studies was expanded and applied in eight-view video coding. This multi-view video coding includes multi-dimensional sub-blocking, multi-dimensional reorganization, multi-dimensional vector DCT orthogonal transform, multi-dimensional quantization, differential encoding, multi-dimensional scanning and run length encoding. Analysis of the experiment data verifies the feasibility of the whole scheme on multi-view coding. This research lays a foundation for further study of both multi-dimensional vector matrix and multi-view coding.

针对现行视频压缩编码标准对多视角视频编码(MVC)的支持与扩展存在一定的局限性这一问题,结合多维矢量矩阵理论,对先前研究中提出的针对单一视角彩色视频流的一整套压缩编码方案加以扩展,将其应用于八个视角的视频编码中,包括多维分块、多维重组、多维矢量DCT正交变换、多维量化、差分编码、多维扫描及行程编码。通过对实验数据的分析,验证了这一整套方案在多视角视频编码中的可行性,为多维矢量矩阵以及多视角视频编码的进一步研究奠定了基础。

2013

0.0

2013

0.0

... Karhunen-Loeve(KL)变换^[7,8,9]是均方误差准则下的最优变换,由于它在完全解相关,有效减少特征图像数目以及抽取更好特征图像等方面的优点,所以即使它存在计算量大,复杂度高,无快速算法的缺点,也还是在实际中应用 ...

2006

0.0

2013

0.0

2008

0.0

... 2 MKL变换KL变换最大优点是消除相关性,它是最小均方误差准则(Minimum mean square error,MMSE)下的最优变换^[10,11],可以获得最佳匹配图像效果,并消除变换域里的全部相关性 ...

2006

0.0