时变遗忘因子动态DOA跟踪算法

引用本文

单泽彪, 石要武, 刘小松, 李新波. 时变遗忘因子动态DOA跟踪算法.吉林大学学报:工学版, 2016, 46(2): 632-638
SHAN Ze-biao, SHI Yao-wu, LIU Xiao-song, LI Xin-bo. DOA tracking algorithm of moving target with variable forgetting factor. Journal of Jilin University Engineering and Technology Edition, 2016, 46(2): 632-638 复制到剪切板

Permissions

时变遗忘因子动态DOA跟踪算法

单泽彪^1,², 石要武^1,², 刘小松¹, 李新波¹

1.吉林大学通信工程学院,长春 130022

2.吉林大学工程仿生教育部重点实验室,长春 130022

通讯作者:李新波(1980-),男,讲师,博士.研究方向:阵列信号处理.E-mail:cinple@126.com

作者简介:单泽彪(1986-),男,博士研究生.研究方向:阵列信号处理,DOA跟踪.E-mail:zbshan@126.com

基金:国家自然科学基金项目(51075175,61571462); 吉林省青年科研基金项目(20140520064JH)

摘要

针对目标信号源波达方向(DOA)实时变化的情况,提出了一种时变遗忘因子的自适应样本协方差矩阵更新方法.时变遗忘因子根据DOA变化的快慢自适应调节自身的大小,从而合理地调整历史数据及当前采样数据在协方差矩阵更新过程中所占的权重.在更新协方差矩阵后,对其直接应用最大似然估计方法,并将序列二次规划(SQP)应用于似然函数的优化求解上,最终实现了DOA的动态跟踪.仿真结果表明:该算法具有解相干的能力和良好的跟踪精度,并且在小样本,低信噪比下仍能达到比较满意的跟踪效果.

关键词: 信息处理技术; DOA跟踪; 时变遗忘因子; 序列二次规划; 最大似然估计

中图分类号:TN911 文献标志码:A 文章编号:1671-5497(2016)02-0632-07

DOA tracking algorithm of moving target with variable forgetting factor

SHAN Ze-biao^1,², SHI Yao-wu^1,², LIU Xiao-song¹, LI Xin-bo¹

1.College of Communication Engineering, Jilin University, Changchun 130022, China

2.Key Laboratory of Bionic Engineering, Ministry of Education, Jilin University, Changchun 130022, China

Abstract

To track the Direction of Arrival (DOA) of the moving targets quickly and accurately, an adaptive subspace updating algorithm with a variable forgetting factor is proposed. First, this tracking algorithm adaptively adjusts the weights of current and historical data in a covariance matrix according to the DOA change speed. Then the maximum likelihood estimation algorithm is used and the Sequence Quadratic Program (SQP) is applied to optimize the likelihood function in order to reduce the computation cost of the algorithm. Experimental results show that the proposed DOA tracking algorithm has the ability to track coherent sources and obtain acceptable tracking results even under the condition of low SNR and small snapshot number in comparison with other methods.

Keyword: information processing; DOA tracking; variable forgetting factor; sequence quadratic program(SQP); maximun likelihood estimation

Show Figures

0 引言

静态目标波达方向(DOA)估计问题近年来得到了广泛关注和重点研究^{[1, 2, 3]}, 然而在雷达, 声纳等领域的工程实际应用中, 由于目标信号源通常是移动的, 这就需要对运动目标的DOA进行有效的跟踪估计.如果直接利用静态DOA估计的算法, 则需要不断重复地对信号协方差矩阵进行特征值分解或奇异值分解, 运算量过大.为了解决这一问题, 子空间跟踪技术^{[4, 5, 6]}得到了广泛研究, 并且已有多种算法相继被提出.其中, 比较著名的有近似投影子空间跟踪(PAST)算法^[7]和紧缩近似投影子空间跟踪(PASTd)算法^[8], PAST与PASTd算法由于收敛速度快而得到广泛应用, 然而它们得到的子空间的正交性不强; 随后Abed-Meraim等^[9]提出了改进算法, 即正交近似投影子空间跟踪(OPAST)算法.但是以上算法均未考虑到遗忘因子的可变性和目标源信号的相干性等问题, 致使算法的应用范围受到了限制.

遗忘因子的大小决定着历史数据和当前采样数据在信号协方差矩阵中所占的权重, 进而影响跟踪速度和稳态误差这一对矛盾问题.胡茂兵等^[10]在前人研究的基础上分析了遗忘因子的可变性等问题, 但只是定性地把目标源信号分为快变和慢变两种, 进而确定了遗忘因子的两种可能性选择, 显然这无法满足情况复杂多变的实际应用需求.针对该问题, 本文提出了一种时变遗忘因子的自适应样本协方差矩阵更新方法, 该方法根据目标信号源DOA变化的快慢自适应调节遗忘因子的大小, 继而调整当前数据和历史数据在协方差矩阵中所占的权重, 在保证了获得较小稳态误差的同时又可获得较快的跟踪速度.

针对目标源信号相干时的场合, Rao等^{[11, 12]}直接利用性能优越的最大似然估计方法对其进行跟踪, 避免了不断重复地进行特征值或奇异值分解等运算, 在低信噪比或小快拍情况下获得了较高的跟踪估计精度.但是最大似然函数的求解是一个非线性多维求解过程, 计算量过大, 所以在目标信号源DOA变化较快时其无法保证动态跟踪的实时要求.刁鸣等^[13]把粒子群算法应用于似然函数的求解上, 在一定程度上加快了寻优的过程, 提高了跟踪的速度, 但是粒子群算法易陷入"早熟"往往不易搜索到全局最优.并且, 如粒子群算法的随机性优化算法^{[14, 15]}等属于"盲搜索"方法, 它们在搜索过程中没有利用似然函数的梯度等相关方向性信息, 因此造成了有效资源的浪费, 这也是一般随机性优化算法的共有缺陷.针对以上问题, 本文将SQP应用于似然函数的求解中.SQP是一种非常优秀的非线性全局优化方法^[16], 可以充分运用DOA估计中已知的模型梯度这一有效信息, 再加上它本身具有的局部超线性收敛特性, 可以快速且准确地搜索到全局最优, 最终实现DOA的动态跟踪估计.文中最后进行了应用SQP方法与采用粒子群算法, 遗传算法等随机性优化算法的仿真对比实验, 结果表明本文方法不仅具有更快的寻优速度, 而且还具有更高的跟踪估计精度.

1 阵列信号数学模型

1.1 接收数据模型

假设有一个由M个阵元构成的线列阵, 其阵元位置为(0, d₁, , et al., d_M-1).同时假设具有相同载频的, 各信源波达方向角分别为(θ ₁, θ ₂, , et al., θ _P)的远场窄带运动目标信号源的数量为 $\begin{matrix} P \end{matrix}$ 个, 并且 $\begin{matrix} M > P, 则在 t \end{matrix}$ 时刻阵列所接收到的信号可表示为:

$\begin{matrix} X (t) = \overset{P}{\sum_{p = 1}} a (θ_{p}) s_{p} (t) + N (t) \end{matrix}$ (1)

式中: $\begin{matrix} s_{p} (t) \end{matrix}$ 为投射到阵列的第 $\begin{matrix} p \end{matrix}$ 个源信号; $\begin{matrix} N (t) \end{matrix}$ 为复噪声向量; $\begin{matrix} θ_{p} \end{matrix}$ 为第 $\begin{matrix} p \end{matrix}$ 个信号源的波达方向角; $\begin{matrix} a (θ_{p}) \end{matrix}$ 为 $\begin{matrix} θ_{p} \end{matrix}$ 的方向向量, 可表示为:

$\begin{matrix} a (θ_{p}) = {[1, e^{- j \frac{2 π}{λ} d_{1} \sin θ_{p}}, \dots, e^{- j \frac{2 π}{λ} d_{M - 1} \sin θ_{p}}]}^{T} \end{matrix}$ (2)

式中: $\begin{matrix} λ \end{matrix}$ 为信号中心频率处的载频波长.

式(1)可以写成如下矩阵形式:

$X (t) = AS (t) + N (t)$ (3)

式中:

$A = [a (θ_{1}), a (θ_{2}), \dots, a (θ_{P})]$

$S (t) = {[s_{1} (t), s_{2} (t), \dots, s_{P} (t)]}^{T}$

1.2 协方差矩阵的动态更新

阵列接收向量 $\begin{matrix} X (t) \end{matrix}$ 的二阶统计量用其外积的统计平均值表示, 称之为阵列协方差矩阵, 其定义为:

$\begin{matrix} R = E [X (t) X^{H} (t)] \end{matrix}$ (4)

在静态目标条件下, 因为实际接收到的数据矩阵是有限长的, 所以阵列协方差矩阵用采样协方差矩阵 $\begin{matrix} \hat{R} \end{matrix}$ 来代替, 即:

$\begin{matrix} \hat{R} = \frac{1}{L} \overset{L}{\sum_{l = 1}} X (l) X^{H} (l) \end{matrix}$ (5)

式中: $\begin{matrix} L \end{matrix}$ 为采样快拍数.

在实际应用中, 目标信号源的DOA通常是随着目标本身的运动而变化的, 所以对其进行采样后所得到的包含目标角度信息的数据矩阵 $\begin{matrix} X (t) \end{matrix}$ 也是变化的, 因此在实际应用中需要不断通过阵列采样数据来更新数据矩阵, 进而得到新的协方差矩阵.

在进行动态DOA跟踪估计时, 常用的子空间跟踪类算法PAST算法及其改进算法中的阵列信号协方差矩阵用下式进行更新估计:

$\begin{matrix} \hat{R} (k) = α \hat{R} (k - 1) + (1 - α) X (k) X^{H} (k) \end{matrix}$ (6)

式中:α 为遗传因子, 满足0≤ α ≤ 1, 其反映的是历史数据及当前采样数据在 $\hat{R} (k)$ 更新过程中所占的权重.当α 取值较小时, 历史数据保留较少, 当前数据所占权重增加, 这样协方差矩阵更新速度加快, 但是数据量不足, 致使协方差矩阵的估计容易遭受噪声干扰, 估计误差较大, 跟踪不稳; 当α 取值较大时, 当前采样数据所占权重便会下降, 协方差矩阵更新速度变慢, 进而会产生明显的跟踪延迟现象.

针对具有恒定遗忘因子的类PAST算法无法解决同时获得较小的跟踪误差和较快的收敛速度这一对矛盾问题, 本文提出了一种时变遗忘因子的自适应协方差矩阵更新方法, 即:

$\begin{matrix} \hat{R} (k) = \frac{α (k) \hat{R} (k - 1) + \frac{1}{L} \overset{L}{\sum_{l = 1}} X (k) X^{H} (k)}{1 + α (k)} \end{matrix}$ (7)

式中:

$\begin{matrix} α (k) = \cos \sqrt[]{\frac{1}{P} \overset{P}{\sum_{p = 1}} [θ_{p} (k - 1) - θ_{p} {(k - 2)]}^{2}} \end{matrix}$ 为时变遗忘因子, 且 $\begin{matrix} - π / 2 \leq θ_{p} (k - 1) - θ_{p} (k - 2) \leq π / 2, θ_{p} (k - 1) 、 θ_{p} (k - 2) \end{matrix}$ 为前两时刻所估计的波达方向角.这样在对移动的信号源进行实时跟踪时, 遗忘因子便会根据信号波达方向变化的快慢自适应调整自身的大小, 进而较合理地确定历史数据及当前采样数据在 $\begin{matrix} \hat{R} (k) \end{matrix}$ 更新过程中所占的权重.

1.3 最大似然估计

最大似然估计是基于统计理论估计方法中的一种最优估计, 在阵列信号处理中, 因其优越的估计性能和具有良好的解相干能力, 一直被广泛地应用于波达方向等参数的估计问题中.因此本文用它来实现动态目标的DOA跟踪估计.

如式(3)所示, 噪声分量是均值为零, 协方差为 $\begin{matrix} σ^{2} I \end{matrix}$ 的各态遍历复高斯过程, 其观测矢量 $\begin{matrix} L \end{matrix}$ 次快拍联合概率密度函数可表示为:

$\begin{matrix} f (X_{1}, X_{2}, \dots, X_{L}) = \overset{L}{\prod_{l = 1}} \frac{\exp (- \frac{1}{σ^{2}} {|X_{l} - A S_{l}|}^{2})}{\det (π σ^{2} I)} \end{matrix}$ (8)

对式(8)两边同时取负对数, 得到对数似然函数:

$\begin{matrix} - lnf = Llnπ + MLln σ^{2} + \frac{1}{σ^{2}} \overset{L}{\sum_{l = 1}} {|X_{l} - A S_{l}|}^{2} \end{matrix}$ (9)

式(9)是一个关于未知参量 $\begin{matrix} θ 、 σ^{2} \end{matrix}$ 和 $\begin{matrix} S_{l} \end{matrix}$ 的函数, 其中 $\begin{matrix} σ^{2} \end{matrix}$ 和 $\begin{matrix} S_{l} \end{matrix}$ 的最大似然估计为:

${\hat{σ}}^{2} = \frac{1}{M} tr [P_{A}^{⊥} \hat{R} (k)]$ (10)

${\hat{S}}_{l} = A^{+} X_{l}$ (11)

式中: $\begin{matrix} P_{A}^{⊥} \end{matrix}$ 为 $\begin{matrix} A^{H} \end{matrix}$ 零空间上的正交投影矩阵; $\begin{matrix} A^{+} \end{matrix}$ 为 $\begin{matrix} A \end{matrix}$ 的伪逆矩阵; $\begin{matrix} \hat{R} (k) \end{matrix}$ 为第k次采样更新后的样本协方差矩阵.

把式(10)(11)代入式(9), 同时忽略常数项, 则得到线阵列波达方向 $\begin{matrix} θ \end{matrix}$ 的最大似然估计:

$\begin{matrix} \{\begin{matrix} \hat{θ} = \arg \min_{θ} V (θ) \\ s . t . - 90 ° \leq θ \leq 90 ° \end{matrix} \end{matrix}$ (12)

式中: $\begin{matrix} V (θ) = tr [P_{A}^{⊥} \hat{R} (k)] 。 \end{matrix}$

由上可知, 波达方向估计就转化为求一个带不等式约束的优化问题, 式(12)的求解需要非线性多维搜索实现, 本文采用SQP方法对其进行优化求解.

2 似然函数的优化

2.1 基于SQP方法的似然函数优化

SQP方法是求解带约束优化问题的最优秀算法之一, 与其他优化算法相比较, 它具有收敛速度快(超线性收敛), 计算效率高, 数值稳定等优点.似然函数的SQP优化求解的实现分为三步:拉格朗日函数的Hesse矩阵的BFGS近似更新, 二次规划(QP)子问题的求解和一维搜索与似然函数的计算.

(1)Hesse矩阵的BFGS近似更新

在SQP每次迭代的过程中, 利用拟牛顿法的思想可以避免直接计算Hesse矩阵, 从而提高计算效率, 即用Broyden Flether Goldfarb Shanno(BFGS)的变尺度法计算一个正定拟牛顿矩阵 $\begin{matrix} H \end{matrix}$ 来逼近拉格朗日函数的Hesse矩阵.其中, Hesse矩阵的BFGS更新公式如下:

$\begin{matrix} \begin{matrix} H^{(n + 1)} = H^{(n)} + \frac{η^{(n)} {[η^{(n)}]}^{T}}{{[δ^{(n)}]}^{T} η^{(n)}} - \\ \frac{H^{(n)} δ^{(n)} {[δ^{(n)}]}^{T} H^{(n)}}{{[δ^{(n)}]}^{T} H^{(n)} δ^{(n)}} \end{matrix} \end{matrix}$ (13)

式中:

$\begin{matrix} \begin{matrix} δ^{(n)} = θ^{(n + 1)} - θ^{(n)}; \\ η^{(n)} = ϑ γ^{(n)} + (1 - ϑ) H^{(n)} δ^{(n)}; \\ γ^{(n)} = [V' (θ^{(n + 1)}) - V' (θ^{(n)})] - [J_{I} (θ^{(n)})^{T} - \\ J_{I} (θ^{(n)})^{T}] μ^{(n)} 。 \end{matrix} \end{matrix}$

当 $\begin{matrix} [δ^{(n)}]^{T} γ^{(n)} \geq 0.2 [θ^{(n)}]^{T} H^{(n)} δ^{(n)} \end{matrix}$ 时, ϑ =1;

当 $\begin{matrix} [δ^{(n)}]^{T} γ^{(n)} < 0.2 [θ^{(n)}]^{T} H^{(n)} δ^{(n)} \end{matrix}$ 时,

$\begin{matrix} ϑ = \frac{0.8 [δ^{(n)}]^{T} H^{(n)} δ^{(n)}}{[δ^{(n)}]^{T} H^{(n)} δ^{(n)} - [δ^{(n)}]^{T} γ^{(n)}} \end{matrix}$

式中: $\begin{matrix} θ^{(n)} = [θ_{1}, θ_{2}, \dots, θ_{P}]^{T} \end{matrix}$ 为第 $\begin{matrix} n \end{matrix}$ 次迭代时 $\begin{matrix} P \end{matrix}$ 个目标的DOA估计向量; $\begin{matrix} V' (θ^{(n)}) \end{matrix}$ 为似然函数 $\begin{matrix} V (θ^{(n)}) \end{matrix}$ 的梯度值; $\begin{matrix} J_{I} (θ^{(n)}) \end{matrix}$ 为不等式约束函数的Jacobi矩阵值; $\begin{matrix} μ^{(n + 1)} \end{matrix}$ 为拉格朗日乘子向量; 初始化时, 常设置 $\begin{matrix} H^{(n)} \end{matrix}$ 为单位阵.

(2)QP子问题的求解

SQP方法的基本思想就是利用一系列QP子问题来近似逼近原问题, 因此SQP方法的每次迭代都需要求解一个QP问题, 本文中其形式为:

$\begin{matrix} \{\begin{matrix} \min \frac{1}{2} δ^{T} H^{(n)} δ + δ^{T} V' (θ^{(n)}) \\ s . t . J_{I} (θ^{(n)}) δ \geq - c_{I} (θ^{(n)}) \end{matrix} \end{matrix}$ (14)

式中: $\begin{matrix} c_{I} (θ^{(n)}) \end{matrix}$ 为似然函数的不等式约束; $\begin{matrix} H^{(n)} \end{matrix}$ 即为Hesse矩阵的BFGS近似, 因为 $\begin{matrix} H^{(n)} \end{matrix}$ 总是正定矩阵, 所以式(14)是一个凸二次规划问题.

(3)一维搜索与似然函数的计算

利用Armijo非精确一维搜索方法获得效益函数的迭代步长 $\begin{matrix} β^{(n)}, \end{matrix}$ 并根据求解QP子问题得到的下降方向 $\begin{matrix} d^{(n)} \end{matrix}$ 组成如下式所示的一个迭代公式:

$\begin{matrix} θ^{(n + 1)} = θ^{(n)} + β^{(n)} d^{(n)} \end{matrix}$ (15)

把 $\begin{matrix} θ^{(n + 1)} \end{matrix}$ 代入式(12)中便可得到似然函数值.

2.2 最大似然函数的梯度

在应用SQP方法求解上述似然函数时, 需要已知似然函数 $\begin{matrix} V (θ) \end{matrix}$ 的梯度 $\begin{matrix} V' (θ) 。 \end{matrix}$

首先, 在此引入一个中间向量 $\begin{matrix} r \end{matrix}$ , 即:

$\begin{matrix} r = {[r_{1}, r_{2}, \dots, r_{M}]}^{T} \end{matrix}$ (16)

其中向量 $\begin{matrix} r \end{matrix}$ 的第 $\begin{matrix} i \end{matrix}$ 个元素为:

$\begin{matrix} r_{i} = \sqrt[]{\overset{M}{\sum_{j = 1}} ‖ P_{A}^{⊥} W ‖_{ij}^{2}}, i = 1, 2, \dots, M \end{matrix}$ (17)

式中:W为协方差矩阵R的Hermite平方根, 即 $\begin{matrix} W W^{H} = R; ‖ P_{A}^{⊥} W ‖_{ij}^{2} \end{matrix}$ 表示矩阵 $\begin{matrix} P_{A}^{⊥} W \end{matrix}$ 的第(i, j)个元素的模值的平方.所以, 似然函数V(θ )可表示为:

$\begin{matrix} V (θ) = ‖ r ‖^{2} = r^{H} r \end{matrix}$ (18)

其中 $\begin{matrix} r \end{matrix}$ 对 $\begin{matrix} θ_{p} \end{matrix}$ 的导数为:

$\begin{matrix} \frac{\partial r}{\partial θ_{p}} = [\begin{matrix} \frac{1}{r_{1}} Re {\{P_{A}^{⊥} R \frac{\partial P_{A}^{⊥}}{\partial θ_{p}}\}}_{11} \\ \frac{1}{r_{2}} Re {\{P_{A}^{⊥} R \frac{\partial P_{A}^{⊥}}{\partial θ_{p}}\}}_{22} \\ ︙ \\ \frac{1}{r_{M}} Re {\{P_{A}^{⊥} R \frac{\partial P_{A}^{⊥}}{\partial θ_{p}}\}}_{MM} \end{matrix}] \end{matrix}$ (19)

则结合式(19)可得 $\begin{matrix} V (θ) \end{matrix}$ 对 $\begin{matrix} θ_{p} \end{matrix}$ 的偏导数为:

$\begin{matrix} \begin{matrix} \frac{\partial V (θ)}{\partial θ_{p}} = 2 Re \{{r^{H}}_{θ_{p}} r\} = 2 Re \{\overset{m}{\sum_{i = 1}} Re {\{P_{A}^{⊥} R \frac{\partial P_{A}^{⊥}}{\partial θ_{p}}\}}_{ii}\} \end{matrix} \end{matrix}$ (20)

式中: $\begin{matrix} \frac{\partial P_{A}^{⊥}}{\partial θ_{p}} \end{matrix}$ 为投影矩阵 $\begin{matrix} P_{A}^{⊥} \end{matrix}$ 对 $\begin{matrix} θ_{p} \end{matrix}$ 的一阶偏导数, 即:

$\begin{matrix} \frac{\partial P_{A}^{⊥}}{\partial θ_{p}} = - \frac{\partial P_{A}}{\partial θ_{p}} = - P_{A}^{⊥} \frac{\partial A}{\partial θ_{p}} A^{+} - (P_{A}^{⊥} \frac{\partial A}{\partial θ_{p}} A^{+})^{H} \end{matrix}$ (21)

再把式(21)代回式(20), 经整理可得 $\begin{matrix} V (θ) \end{matrix}$ 对 $\begin{matrix} θ_{p} \end{matrix}$ 的偏导数为:

$\begin{matrix} \frac{\partial V (θ)}{\partial θ_{p}} = - 2 Re {\{A^{+} R P_{A}^{⊥} D\}}_{pp} \end{matrix}$ (22)

进而可得似然函数的梯度为:

$\begin{matrix} V' (θ) = - 2 Re {diag (A^{+} R P_{A}^{⊥} D)} \end{matrix}$ (23)

式中: $\begin{matrix} D \end{matrix}$ 为阵列流型 $\begin{matrix} A \end{matrix}$ 的一阶导数.

2.3 初始化角度的估计

为了加快初始跟踪时寻优的速度, 利用下述方法进行初值的确定.在开始跟踪后, 则应用上一时刻的DOA估计值作为当前时刻寻优的初始值.

首先, 求出第一个信源的DOA初始值:

$\begin{matrix} {\hat{θ}}_{1}^{(0)} = \arg \min_{θ_{1}} \{tr [P_{a ({\hat{θ}}_{1})}^{⊥} \hat{R} (0)]\} \end{matrix}$ (24)

然后假定第一个信源即位于 $\begin{matrix} {\hat{θ}}_{1}^{(0)}, \end{matrix}$ 再利用式(25)求出第二个信源的DOA初始值:

$\begin{matrix} {\hat{θ}}_{2}^{(0)} = \arg \min_{θ_{2}} \{tr [P_{[a ({\hat{θ}}_{1}), a ({\hat{θ}}_{2})]}^{⊥} \hat{R} (0)]\} \end{matrix}$ (25)

按照上述方法依次进行下去, 直至求出 $\begin{matrix} P \end{matrix}$ 个信源的初始跟踪估计值.

3 仿真实验

3.1 非相关信号源DOA跟踪实验

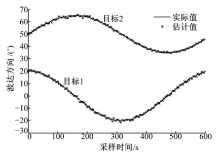
为了验证上述所提方法的可行性与有效性, 对算法进行了100次独立蒙特卡罗跟踪实验, 其中每次跟踪时长均为600个采样时刻.设有两个非相干运动信号源目标, 初始波达方向角分别为20° 和50° , 并且各自按照 $\begin{matrix} 20 \cos (0.01 t) \end{matrix}$ 和 $\begin{matrix} 15 \sin (0.01 t) \end{matrix}$ 进行变化.实验中噪声为高斯白噪声, 阵列天线采用阵元数为M=10, 阵元间隔为半波长的均匀线阵列.以式(26)所示均方根误差(RMSE)作为算法性能指标测试的标准.

$\begin{matrix} RMS E_{θ} = \sqrt[]{\frac{1}{P N_{t} N_{run}} \overset{P}{\sum_{p = 1}} \overset{N_{run}}{\sum_{q = 1}} \overset{N_{t}}{\sum_{k = 1}} {[{\hat{θ}}_{pq} (k) - θ_{pq} (k)]}^{2}} \end{matrix}$ (26)

式中: $\begin{matrix} P \end{matrix}$ 为目标信号源数目; $\begin{matrix} N_{t} \end{matrix}$ 为总的采样时刻; $\begin{matrix} N_{run} \end{matrix}$ 为独立实验次数; $\begin{matrix} θ_{pq} (k) \end{matrix}$ 为第 $\begin{matrix} p \end{matrix}$ 个信源在第 $\begin{matrix} q \end{matrix}$ 次实验的第 $\begin{matrix} k \end{matrix}$ 时刻时的DOA实际值; $\begin{matrix} {\hat{θ}}_{pq} (k) \end{matrix}$ 为第 $\begin{matrix} k \end{matrix}$ 时刻所得到的DOA估计值.

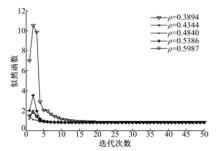
由于DOA估计问题中似然函数的约束条件比较宽松, 导致SQP算法中惩罚因子的取值对整个算法的收敛性并无多大的影响, 然而在利用Armijo方法进行一维搜索的过程中, 斜率系数 $\begin{matrix} ρ \end{matrix}$ 对整个算法的收敛速度却有着较大的影响, 所以选择合适的 $\begin{matrix} ρ \end{matrix}$ 取值对应用SQP的最大似然DOA跟踪具有重要的意义.图1给出了系数 $\begin{matrix} ρ \end{matrix}$ 取不同值时, 针对似然函数的SQP方法的收敛情况.实验条件为信噪比SNR=10 dB, 目标信号源数为2.

	Figure Option View Download New Window
	图1 不同系数ρ 时算法的收敛性比较Fig.1 Comparison of convergence for the algorithm with different coefficient ρ

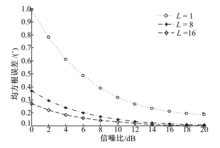
从图1中可以看出:针对本文中似然函数的优化求解, 在参数 $\begin{matrix} ρ = 0 . 93^{10} = 0.4840 \end{matrix}$ 左右时整个算法的收敛速度最大, 而且能够收敛到全局最优.

实验1 不同采样快拍数跟踪精度对比实验.每一时刻采样快拍数取值分别为 $\begin{matrix} L = 1, L = 8 \end{matrix}$ 和 $\begin{matrix} L = 16, \end{matrix}$ 则有其不同信噪比时的均方根误差, 如图2所示.从图2中可知, 在低信噪比且小快拍情况下本文方法具有较高的跟踪精度.

	Figure Option View Download New Window
	图2 不同采样快拍数均方根误差比较Fig.2 RMSE of DOA tracking with different number of snapshots

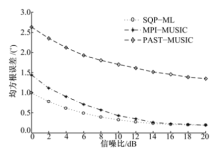
实验2 与其他跟踪算法之间的性能对比实验.选取了两个比较典型的子空间类跟踪算法:PAST算法^[7]和基于幂迭代的子空间跟踪(MPI)算法.由于PAST算法与MPI算法本身无法对相干信号源目标进行跟踪, 故仍采用非相干信号源目标进行算法对比实验.图3给出了3种不同跟踪算法对DOA跟踪的均方根误差变化曲线.从图3中可知:与PAST-MUSIC及MPI-MUSIC两种算法相比, 本文所提算法具有更高的跟踪估计精度, 主要原因有两个:一是本文所提算法中采用的最大似然估计是一种渐进无偏估计; 二是本文算法中应用的是时变遗忘因子的自适应协方差矩阵更新方法.

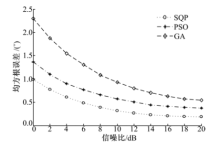
	Figure Option View Download New Window
	图3 不同跟踪算法均方根误差比较Fig.3 RMSE of DOA tracking compared with other tracking methods

实验3 与随机性优化算法的性能对比实验.采用遗传算法(GA), 粒子群(PSO)算法^{[13, 17]}与本文SQP方法对似然函数进行优化求解, 其中以上两种随机性优化算法的迭代次数均为120, 种群数量均为70.图4给出了上述3种优化算法对DOA跟踪的均方根误差变化曲线.从图4中可以看出:遗传算法或粒子群算法由于迭代次数及种群数量的限制, 不能保证每次都能搜索到全局最优, 整体收敛性较差.与之相比, SQP方法能够很好地对似然函数进行优化, 基本每次均可找到全局最优解, 数值求解稳定, 精度较高.

	Figure Option View Download New Window
	图4 不同优化算法均方根误差比较Fig.4 RMSE of DOA tracking compared with other optimization methods

表1给出了以上3种优化方法在DOA跟踪中每次寻优的平均计算时间.实验所用电脑处理器为AMD Athlon(tm)X2 240, 主频为2.80 GHz, 内存为2 GB, 仿真软件为MATLAB 2010a.从表1中可以得知, 相同信噪比下, 应用SQP对似然函数求解平均寻优用时均小于另外两种寻优方法, 原因为:① SQP方法在每步迭代过程中都运用了梯度这一方向性信息; ② SQP方法在每一时刻开始寻优时都利用了上一时刻的DOA估计值作为本时刻的初值, 而另外两种随机性算法没有运用到上述两个有效的信息.随着信噪比的不断下降, 过大的噪声对梯度的正确指向性影响加剧, 导致寻优迭代步数增加, 致使寻优所用时间有所增加.综上分析可知, SQP方法可以用较少的计算时间实现对似然函数的优化求解, 保证了算法目标跟踪时的快速性和实时性.

表1 平均计算时间比较 Table 1 Average computing time of DOA tracking s

3.2 相干信号源DOA跟踪实验

设有两个相干信号源目标, 其归一化频率均为0.7, 初始波达方向分别为20° 和50° , 并分别按照每秒0.017° 和0.013° 正弦式变化, 在信噪比为10 dB时一次典型的跟踪估计曲线如图5所示.从图5中可以看出, 本文算法在对相干信号源进行DOA跟踪时同样具有较好的跟踪性能.

	Figure Option View Download New Window
	图5 相干信号源实时跟踪曲线Fig.5 Tracking curve of the coherent signals

4 结束语

针对动态DOA跟踪估计问题, 本文提出了一种时变遗忘因子的自适应样本协方差矩阵更新方法.在更新协方差矩阵后, 直接对其进行最大似然估计, 避免了不断重复地进行特征值或奇异值分解等运算.为了减少最大似然方法的运算量, 将SQP方法应用于似然函数的优化求解上, 较大程度地加快了寻优的过程, 保证了DOA跟踪的快速性和实时性.与其他方法相比, 本文方法具有寻优时间短, 估计精度高和可以解相干等特点, 并且在小快拍, 低信噪比条件下仍能达到比较满意的跟踪效果.

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Dmochowski J, Benesty J, Affes S. Direction of arrival estimation using the parameterized spatial correlation matrix[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2007, 15(4): 1327-1339. [本文引用:1]
[2]	Wan F, Zhu W, Swamy M N S. Spacial extrapolation-based blind DOA estimation approach for closely spaced sources[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(2): 569-582. [本文引用:1]
[3]	Reddy V V, Ng B P, Khong A W H. Derivative-constrained frequency-domain wideband DOA estimation[J]. Multidimensional Systems and Signal Processing, 2014, 25(1): 211-233. [本文引用:1]
[4]	Badeau R. Fast approximated power iteration subspace tracking[J]. IEEE Transactions on Signal Processing, 2005, 53(8): 2931-2941. [本文引用:1]
[5]	Perry P O, Wolfe P J. Minimax rank estimation for subspace tracking[J]. IEEE Transactions on Signal Processing, 2010, 4(3): 504-513. [本文引用:1]
[6]	Kajimura Y, Kikuma N, Hirayama H, et al. DOA estimation using subspacing tracking method for coherent waves[C]//Proceeding of 2012 International Symposium on Antennas and Propagation, Nagoya, Japan: ISAP, 2012: 1148-1151. [本文引用:1]
[7]	Yang B. Asymptotic convergence analysis of the projection approximation subspace tracking algorithms[J]. Signal Processing, 1996, 50(1): 123-136. [本文引用:2]
[8]	Yang B. Projection approximation subspace tracking[J]. IEEE Transactions on Signal Processing, 1995, 43(1): 95-107. [本文引用:1]
[9]	Abed-Meraim K, Chkeif A, Hua Y. Fast orthonormal PAST algorithm[J]. IEEE Transactions on Signal Processing, 2000, 7(3): 60-62. [本文引用:1]
[10]	胡茂兵, 汤炜, 蔡灿辉. 一种新的子空间更新算法在DOA估计中的应用[J]. 华侨大学学报: 自然科学版, 2012, 33(4): 375-379. Hu Mao-bing, Tang Wei, Cai Can-hui. Application of a new subspace updating algorithm in DOA estimation[J]. Journal of Huaqiao University(Natural Science), 2012, 33(4): 375-379. [本文引用:1]
[11]	Rao C R. Tracking the direction of arrival of multiple moving targets[J]. IEEE Transactions on Signal Processing, 1994, 42(5): 1133-1144. [本文引用:1]
[12]	Zhou Y F. Tracking the direction-of-arrival of multiple moving targets by passive arrays algorithm[J]. IEEE Transactions on Signal Processing, 1999, 47(10): 2655-2666. [本文引用:1]
[13]	刁鸣, 袁熹, 高洪元, 等. 一种新的基于粒子群算法的DOA跟踪方法[J]. 系统工程与电子技术, 2009, 31(9): 2046-2049. Diao Ming, Yuan Xi, Gao Hong-yuan, et al. New method of estimating direction-of-arrival of moving sources based on particle swarm algorithm[J]. Systems Engineering and Electronics, 2009, 31(9): 2046-2049. [本文引用:2]
[14]	张志成, 林君, 石要武, 等. 基于人工蜂群算法的波达方向和多普勒频率联合估计[J]. 吉林大学学报: 工学版, 2013, 43(4): 1104-1109. Zhang Zhi-cheng, Lin Jun, Shi Yao-wu, et al. Joint direction-of-arrival and Doppler frequency estimation based on artificial bee colony algorithm[J]. Journal of Jilin University(Engineering and Technology Edition), 2013, 43(4): 1104-1109. [本文引用:1]
[15]	单泽彪, 石要武, 刘小松, 等. 应用人工蜂群算法的动态波达方向跟踪[J]. 光学精密工程, 2015, 23(3): 838-845. Shan Ze-biao, Shi Yao-wu, Liu Xiao-song, et al. DOA tracking of moving targets by artificial bee colony algorithm[J]. Optics and Prccision Engineering, 2015, 23(3): 838-845. [本文引用:1]
[16]	Gill P E, Walter M, Michael A. SNOPT: an SQP algorithm for large-Scale constrained optimization[J]. Siam Review, 2005, 47(1): 99-131. [本文引用:1]
[17]	张志成, 林君, 石要武, 等. 用加权子空间拟合和量子粒子群算法联合估计多普勒频率和波达方向[J]. 光学精密工程, 2013, 21(9): 2445-2451. Zhang Zhi-cheng, Lin Jun, Shi Yao-wu, et al. Joint estimation of doppler and DOAs by WSF-QPSO method[J]. Optics and Precision Engineering, 2013, 21(9): 2445-2451. [本文引用:1]

2007

0.0

... 0 引言静态目标波达方向(DOA)估计问题近年来得到了广泛关注和重点研究^[1,2,3],然而在雷达,声纳等领域的工程实际应用中,由于目标信号源通常是移动的,这就需要对运动目标的DOA进行有效的跟踪估计 ...

2010

0.0

2014

0.0

2005

0.0

... 为了解决这一问题,子空间跟踪技术^[4,5,6]得到了广泛研究,并且已有多种算法相继被提出 ...

2010

0.0

... 为了解决这一问题,子空间跟踪技术^[4,5,6]得到了广泛研究,并且已有多种算法相继被提出 ...

2012

0.0

... 为了解决这一问题,子空间跟踪技术^[4,5,6]得到了广泛研究,并且已有多种算法相继被提出 ...

1996

0.0

... 其中,比较著名的有近似投影子空间跟踪(PAST)算法^[7]和紧缩近似投影子空间跟踪(PASTd)算法^[8],PAST与PASTd算法由于收敛速度快而得到广泛应用,然而它们得到的子空间的正交性不强 ...

... 选取了两个比较典型的子空间类跟踪算法:PAST算法^[7]和基于幂迭代的子空间跟踪(MPI)算法 ...

1995

0.0

2000

0.0

... 随后Abed-Meraim等^[9]提出了改进算法,即正交近似投影子空间跟踪(OPAST)算法 ...

2012

0.0

. 2012, 33(4):375-379

Application of a new subspace updating algorithm in DOA estimation

一种新的子空间更新算法在DOA估计中的应用

Hu Mao-bing , Tang Wei , Cai Can-hui.

胡茂兵, 汤炜, 蔡灿辉

为改进传统算法对突变信号跟踪慢的缺点,提出一种有效的可变遗忘因子的子空间更新算法———逼近特征分解方法.该算法采用可变遗忘因子对阵列输出信号协方差矩阵进行秩-1更新,在该协方差矩阵特征分解的基础上,结合先验信息构造新的代价函数,并利用该代价函数的最小二乘解实现对信号子空间的实时更新.仿真结果表明:新算法的波达方向估计误差仅为原算法的1/5,而对突变信号的跟踪速度达到原算法的5倍,证实该算法的准确性和有效性.

... 胡茂兵等^[10]在前人研究的基础上分析了遗忘因子的可变性等问题,但只是定性地把目标源信号分为快变和慢变两种,进而确定了遗忘因子的两种可能性选择,显然这无法满足情况复杂多变的实际应用需求 ...

1994

0.0

... 针对目标源信号相干时的场合,Rao等^[11,12]直接利用性能优越的最大似然估计方法对其进行跟踪,避免了不断重复地进行特征值或奇异值分解等运算,在低信噪比或小快拍情况下获得了较高的跟踪估计精度 ...

1999

0.0

2009

0.0

. 2009, 31(9):2046-2049 DOI:doi:10.3321/j.issn:1001-506X.2009.09.004

New method of estimating direction-of-arrival of moving sources based on particle swarm algorithm

一种新的基于粒子群算法的DOA跟踪方法

Diao Ming , Yuan Xi , Gao Hong-yuan

刁鸣, 袁熹, 高洪元

The update of covariance matrix of samples is studied,and a new method to estimate direction-of-arrival(DOA) for moving sources is proposed.Making use of the maximum likelihood algorithm,this method avoids the decomposition of the covariance matrix which arises repetitiously in subspace tracking types methods.And this method effectively reduces the computational load by locking the targets,reducing the range of search for targets and appling swarm intelligence technologies.Simulation results show that the DOA estimation based on the improved particle swarm algorithm has the ability to track coherent sources and is better for precision and real-time characteristics.

针对信号源方向时变情况,分析了样本协方差矩阵的更新,在此基础上提出了一种基于粒子群算法的跟踪方法。该方法直接利用性能优越的最大似然估计器,避免了子空间跟踪类方法需要不断重复的协方差矩阵分解;同时通过锁定目标、大幅度缩小搜索范围和运用群智能搜索,有效降低了算法的计算量。仿真结果表明,与子空间跟踪类算法相比,该方法具备解相干的能力和较好的跟踪精度,并且能够保证算法的实时性。

... 刁鸣等^[13]把粒子群算法应用于似然函数的求解上,在一定程度上加快了寻优的过程,提高了跟踪的速度,但是粒子群算法易陷入"早熟"往往不易搜索到全局最优 ...

... 采用遗传算法(GA),粒子群(PSO)算法^[13,17]与本文SQP方法对似然函数进行优化求解,其中以上两种随机性优化算法的迭代次数均为120,种群数量均为70 ...

2013

0.0

. 2013, 43(4):1104-1109 DOI:doi:10.7964/jdxbgxb201304041

Joint direction-of-arrival and Doppler frequency estimation based on artificial bee colony algorithm

基于人工蜂群算法的波达方向和多普勒频率联合估计

Zhang Zhi-cheng , Lin Jun , Shi Yao-wu

张志成, 林君, 石要武

To achieve the joint estimation of Direction-of-Arrival (DOA) and Doppler frequency in array signal processing, the artificial bee colony theory and algorithm are applied to optimize the likelihood function. First, the extended observability matrix containing the angle-frequency parameters is established using state-space model. Then, the likelihood function containing the extended observability matrix is used to convert the problem from parameter estimation to nonlinear multidimensional function optimization. Finally, artificial bee colony algorithm is applied to optimize the process of finding the solutions of the maximum likelihood estimator in order to estimate the DOA and Doppler frequency. The proposed method reserves the asymptotic unbiased estimation of the maximum likelihood estimator and reduces the computational burden to calculate the solution of the likelihood function. Besides, the estimated parameters can be paired automatically.

将人工蜂群算法应用于似然函数的优化,实现了阵列信号波达方向(DOA)和多普勒频率的联合估计。利用状态空间模型构造包含DOA和多普勒频率信息的广义可观测矩阵,并构造包含该广义可观测矩阵的似然函数,将参数估计问题转化为多维非线性函数优化问题。进而利用人工蜂群算法对似然函数的求解过程进行优化,得到DOA和多普勒频率的估计值。算法保留了最大似然估计的渐近无偏估计性能,降低了似然函数求解的计算量,且参数能够自动配对。

... 并且,如粒子群算法的随机性优化算法^[14,15]等属于"盲搜索"方法,它们在搜索过程中没有利用似然函数的梯度等相关方向性信息,因此造成了有效资源的浪费,这也是一般随机性优化算法的共有缺陷 ...

2015

0.0

. 2015, 23(3):838-845 DOI:doi:10.3788/OPE.20152303.0838

DOA tracking of moving targets by artificial bee colony algorithm

应用人工蜂群算法的动态波达方向跟踪

Shan Ze-biao , Shi Yao-wu , Liu Xiao-song

单泽彪, 石要武, 刘小松

针对目标信号源波达方向 (DOA)的实时变化,将人工蜂群算法应用于最大似然函数的优化,实现了动态目标DOA的实时跟踪。首先,提出了一种可变遗忘因子的自适应样本协方差矩阵更新方法,该方法可根据目标信号源DOA变化的快慢自适应调整历史数据和当前采样数据在协方差矩阵中所占的权重,从而保证在获得较小稳态误差的同时又可获得较快的跟踪速度。然后,直接应用了性能优越的最大似然估计方法,避免了子空间跟踪类算法需要不断重复特征值或奇异值分解等问题。最后,采用人工蜂群仿生智能算法对似然函数的求解进行优化,从而极大地减少了算法的计算量,保证了算法的快速性和实时性。实验结果表明:在单快拍采样的情况下,信噪比为0dB 时,跟踪两个目标信号源的均方根误差为0.995 2°,基本达到了阵列信号处理中目标跟踪方法的设计要求。

2005

0.0

... SQP是一种非常优秀的非线性全局优化方法^[16],可以充分运用DOA估计中已知的模型梯度这一有效信息,再加上它本身具有的局部超线性收敛特性,可以快速且准确地搜索到全局最优,最终实现DOA的动态跟踪估计 ...

2013

0.0

. 2013, 21(9):2445-2451 DOI:doi:10.3788/OPE.20132109.2445

Joint estimation of doppler and DOAs by WSF-QPSO method

用加权子空间拟合和量子粒子群算法联合估计多普勒频率和波达方向

Zhang Zhi-cheng , Lin Jun , Shi Yao-wu

张志成, 林君, 石要武

To estimate Doppler frequency and Direction-of-Arrival (DOA) accurately and efficiently, a joint spectrum estimation method based on Weighted Subspace Fitting (WSF) algorithm and Quantum-behaved Particle Swarm Optimization (QPSO) algorithm, namely WSF-QPSO, was presented. First, an extended observability matrix containing the information of Dopplers and DOAs was constructed by using a state-space model, and the joint spectrum function was fitted by using WSF algorithm. Then, the joint parameter estimation was converted to multidimensional nonlinear function optimization. Finally, the Dopplers and DOAs were estimated by optimizing the joint spectrum function using QPSO algorithm. Experimental results indicate that the Root Medium Square Errors (RMSEs) of Dopplers and DOAs estimated from the WSF-QPSO method are 0.007 5 rad and 0.25°, respectively when SNR is 0 dB. The proposed method can get high resolution and robust parameter estimation with less control terms, and the parameters are paired automatically. In addition, the WSF-QPSO method can obtain acceptable estimation results even under the condition of low SNR or small snapshot number in comparison with the joint spectrum estimation methods based on subspace decomposition.

为了高效、准确地估计多普勒频率和波达方向（DOA），提出了基于加权子空间拟合（WSF）算法和量子粒子群优化（QPSO）算法的WSF-QPSO联合谱估计方法。首先，利用状态空间模型构造包含多普勒频率和DOA信息的广义可观测矩阵；用WSF算法拟合联合谱函数，将参数估计问题转化为多维非线性函数优化问题。然后，利用QPSO算法优化联合谱函数，得到多普勒频率和DOA的估计值。实验结果表明：在信源参数比较接近的情况下，WSF-QPSO方法在信噪比为0 dB时对多普勒频率和DOA估计的均方根误差仅为0.007 5 rad和0.25°。与其他方法相比，该方法具有估计精度高、控制参数少、鲁棒性好、参数自动配对等特点，在低信噪比和小样本条件下依然能够得到较满意的参数估计结果。

... 采用遗传算法(GA),粒子群(PSO)算法^[13,17]与本文SQP方法对似然函数进行优化求解,其中以上两种随机性优化算法的迭代次数均为120,种群数量均为70 ...