引用本文
焦淑红, 齐欢, 林维斯, 唐琳, 申维和. 基于Contourlet统计特性的无参考图像质量评价.吉林大学学报:工学版, 2016, 46(2): 639-645
JIAO Shu-hong, QI Huan, LIN Wei-si, TANG Lin, SHEN Wei-he. No-reference quality assessment based on the statistics in Cntourlet domain. Journal of Jilin University Engineering and Technology Edition, 2016, 46(2): 639-645  
Permissions
Copyright©2016, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
基于Contourlet统计特性的无参考图像质量评价
焦淑红1, 齐欢1, 林维斯2, 唐琳1, 申维和3
1.哈尔滨工程大学 信息与通信工程学院, 哈尔滨 150001
2.南洋理工大学 计算机工程学院, 新加坡 639798
3.中国运载火箭技术研究院 空间物理重点实验室, 北京100076
通讯作者:齐欢(1989-),女,博士研究生.研究方向:图像处理与机器视觉.E-mail:heuqihuan@163.com

作者简介:焦淑红(1966-),女,教授,博士.研究方向:图像处理与机器视觉.E-mail:jiaoshuhong@hrbeu.edu.com

基金:国家自然科学基金项目(61201238)
摘要

利用Contourlet统计特征建立自然统计模型与待评价图像模型,提出了Contourlet域无参考图像质量评价方法(SCIQA).通过在主观数据库上的实验表明,无论同种干扰类型的图像还是多种干扰图像集合,SCIQA均明显优于经典全参考算法和通用型无参考算法,并且具有较强的通用性.

关键词: 信息处理技术; 图像质量评价; Contourlet统计特征
中图分类号:TN911 文献标志码:A 文章编号:1671-5497(2016)02-0639-07
No-reference quality assessment based on the statistics in Cntourlet domain
JIAO Shu-hong1, QI Huan1, LIN Wei-si2, TANG Lin1, SHEN Wei-he3
1.College of Information and Communication Engineering,Harbin Engineering University,Harbin 150001,China
2.School of Computer Engineering,Nanyang Technological University,Singapore 639798,Singapore
3.Science and Technology on Space Physics Laboratory,China Academy of Launch Vehicle Technology,Beijing 100076,China
Abstract

The statistic features in Cntourlet domain are employed to build the natural statistic model and the tested image model first. Then a no-reference assessment algorithm in Contourlet domain (SCIQR) is proposed. Experiment results on subjective databases show that SCIQR outperforms the classical full-reference image quality assessment algorithm and the universal no-reference algorithm no-matter on single distortion type images and on the set of different types of distortion images. This demonstrates that SCIQR has good universality.

Keyword: information processing technology; image quality assessment; statistics in Contourlet domain

图像在处理过程中不可避免地受到各种类型的干扰.能够准确地评价图像的质量是图像处理其他各个阶段的基础[1, 2].根据原始图像的利用程度, 图像质量评价方法大致可以分为全参考(Full-reference, FR), 半参考(Reduced-reference, RR)和无参考(No-reference, NR).顾名思义, 在评估图像质量时, FR方法需要待评价图像对应的整幅原始图像[3], 而RR方法只要求原始图像的部分信息或者某些特征.但是, 无论整幅原始图像还是其部分信息或某种特征在很多实际应用中都是无法得到的.因此, NR图像质量评价拥有更高的实际应用价值.目前大部分的NR方法只针对某种特定的干扰类型, 如高斯模糊图像, JPEG压缩图像等.这类算法是根据图像干扰的特点设计的, 因此只能用来评估特定的干扰图像, 也就是说要事先知道待评价图像受到干扰的类型, 但是实际情况下, 各种干扰都可能出现, 图像受到的干扰类型事先很难判断.因此, 通用型NR方法最具实际意义, 是图像质量评价未来研究的重点.现有的通用型NR方法大多依赖机器学习, 需要借助一定量的干扰图像和每幅图像的主观评价分数训练模型.由于建立模型利用了特定干扰类型的图像, 因此评价结果必然对这些干扰类型存在依赖性.自然图像质量评估器(NIQE)[4]仅利用一定数目的原始图像建立模型, 避免了上述各类方法的缺陷.但其表征图像质量的特征与人眼感知一致性不高, 限制了其评价效果.Contourlet变换[5]可以提取出人眼敏感的图像信息, 本文利用Contourlet域的统计特征表征图像的质量, 提出一种无需利用干扰图像训练的通用型NR图像质量评价方法SCIQA.在主观数据库上测试显示, SCIQA优于经典的FR算法和通用型NR算法NIQE.

1 Contourlet变换及其统计特征
1.1 Contourlet变换

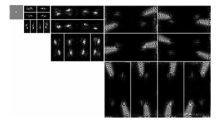
人类视觉系统(Human visual system, HVS)对不同图像内容的敏感程度不同, 对于图像中边缘轮廓信息的变化更加敏感[6].Contourlet变换可以将图像进行多尺度, 多方向的变换, 用较少的系数描述图像中的轮廓信息.Contourlet变换首先利用拉普拉斯塔形滤波器将图像分解为低通近似子带和带通子带, 然后通过方向滤波器组将带通子带分解为多个带通方向子带[5].图像"zoneplate"的3尺度, 每尺度8方向的Contourlet变换如图1所示.

图1 图像"zoneplate"的Contourlet分解Fig.1 Contourlet transform on the image "zoneplate"

1.2 统计特征

HVS具有聚焦的特性.对于某一特定的观测距离, 人类只能以较高的分辨率感知图像中某个局部区域的图像内容.因此, 本文将图像分成若干个128× 128大小的图像块, 逐块处理.对每个图像块做3尺度, 每尺度8方向的Contourlet变换, 然后提取Contourlet统计特征, 所有图像块的Contourlet统计特征组成一个用以表征图像质量的特征矩阵.图像在Contourlet域的统计特征会受到图像质量的影响.自然原始图像的统计特征在一定的范围内保持一致, 而干扰图像的统计特征会随着干扰类型和干扰程度的不同存在明显的区别.因此, 可以利用这些统计特征表征图像质量的好坏.本文从以下3个方面提取图像在Contourlet域的统计特征.

(1)精细尺度上Contourlet系数受到的干扰

越精细尺度上的Contourlet系数携带的图像质量信息越多, 最精细尺度上系数的统计特性更能反映出图像质量受到干扰的程度[7].因此, 在计算单独一个子带本身具备的统计特征时, 本文只考虑最精细尺度上的8个方向子带.对于最精细尺度上的每个方向子带, 本文从3个方面计算其统计特征.

首先, 自然图像在受到干扰时, 子带内Contourlet系数幅度的均值会发生变化, 干扰类型不同, 变化的方式不尽相同.如通常情况下, 高斯白噪声会使幅度均值变大, 而高斯模糊干扰会使幅值均值变小等.为了更加有效地计算图像在受到干扰时系数幅度均值的变化, 对于每个方向子带, 本文分别求取对数域内子带系数绝对值的均值:

lm=1MN∑j=1N∑i=1MlgCij(1)

式中:M, N分别为子带的行数和列数; Cij 为子带中第i行第j列的Contourlet系数值.

其次, 同一子带内, 子带系数与其周围系数的相关性会受到干扰的影响[8].由于相距较远的系数相关性较小, 因此仅考虑水平方向上相邻的系数(相距0个像素)和相距一个像素的邻域系数(这里为了简便只取水平方向上的邻域系数).相距 d个像素的系数相关性可以用关系系数 dhd表示:

dhd=lg1+1M(N-1)∑i=1M∑j=1N-d(Ci, j+d-Ci, j)2(2)

式中: d=1, 2。

最后, 图像在受到不同干扰时, Contourlet子带活跃性会发生相应的变化.不同质量图像的活跃性存在差异.对于最精细尺度上的某一方向子带, 沿水平方向的差分信号及其均值分别为:

dhi, j=xi, j+1-xi, j, j∈1, N-1(3)

μh=1MN-1∑i=1M∑j=1N-1dhi, j(4)

式中: x为最精细尺度上的一个方向子带; (i, j)为子带系数的索引.

将差分信号在水平方向上做基于2的抽样, 得到相同间隔下的部分差分信号, 抽样信号的均值为:

(5)

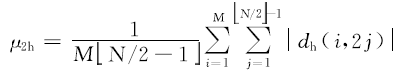
子带活跃性可以表示为:

ACh=μ2hμh(6)

综上, 分别利用子带内系数幅度的均值, 子带系数之间的关系和子带的活跃性三类统计特征衡量图像质量的变化.事实上, 除单独一个方向子带内的系数的统计特征与图像质量相关外, 不同尺度的子带之间的相关性也可以用来表征图像的质量.

(2)尺度间的相关性

图像细节的可感知性依赖于观测的条件, 如图像的分辨率, 观测者与图像之间的距离等.多尺度的变换可以体现这些因素的变化.而图像的尺度之间存在一定的关系, 当图像受到干扰时, 这种关系会发生相应的变化[7, 9].为了定量地计算尺度之间的关系随图像质量变化的情况, 本文计算低通子带和所有尺度上的每个方向子带的 dh1(见式(2)), 对于每个方向, 利用相邻两尺度子带 dh1的比值衡量尺度间关系:

Rd=dhji+1dhji(7)

式中:i=1, 2, 3; dhji为第i尺度第j方向子带的相邻系数的关系系数, i=1表示低通子带.

(3)方向相近系数的总体统计特性受到的干扰

方向相近的子带携带类似的信息, 如图1所示, 在每个尺度的8个方向子带中, 上方的4个子带更加接近水平方向(近水平方向子带), 下方的4个子带更加接近垂直方向(近垂直方向子带).将同一尺度的近水平方向子带放在一起组成新的子带, 称为水平总体子带; 类似地, 将近垂直方向子带组成的新子带称为垂直总体子带.这样在3个尺度上得到6个新子带.利用式(1)计算各新子带系数的幅值的均值得到6个特征.同时, 用同一尺度的水平总体子带幅值的均值与垂直总体子带幅值的均值的比值来衡量两类子带总体的关系, 共3个特征.另外, 用相邻尺度的同类方向总体子带幅值比描述尺度间子带总体的关系, 共4个特征.

2 自然原始图像统计模型

正如前面提到的, 自然原始图像的Contourlet统计特征能够在一定误差范围内保持一致.因此, 可以利用大量不同图像内容的自然原始图像建立统计模型.本文希望在评估某幅图像的质量时, 这一模型可以代替待评价图像对应的原始无失真图像, 从而使得评价算法不需要参考图像就可以准确评估图像质量.细节内容丰富的图像块包含更多的图像质量信息.因此, 选取包含更多图像细节的图像块建立自然统计模型, 使得所建立的模型更加准确地表征高质量图像具有的特征.这里按照如下方式[4]选取建立模型的图像块:

首先, 利用7× 7二维循环对称高斯窗通过滑窗的方式计算图像局部均值和局部方差:

μ(i, j)=∑k=-KK∑l=-LLωk, lIk, l(i+k, j+l)(8)

σ(i, j)=∑k=-KK∑l=-LLωk, l(Ik, l(i+k, j+l)-μ(i, j))2(9)

式中: ωk, l为7× 7二维循环对称高斯函数, 即K=L=3; (i, j)为图像I的空间索引.

本文选取局部方差的均值大于整幅图像各图像块局部方差均值最大值的50%的块建立自然统计模型.建立自然统计模型的图像为选自图像库[10]的125幅自然原始图像.计算每个原始图像中满足要求的图像块的上述统计特征, 将这些特征与多元高斯模型拟合, 得到自然图像的统计模型:

fx(x1, …, xk)=1(2π)12Σ12exp-12x-υTΣ-1x-υ(10)

式中: (x1, …, xk)为自然图像的统计特征; υ和 Σ分别为多元高斯模型的均值和协方差.

值得注意的是, 建立模型的自然图像数量达到120幅即可以得到稳定的模型[4], 因此本文的模型是一个可以相对稳定地表征自然原始图像质量特征的模型.另外, 本文只利用了一定量的涵盖不同图像内容的自然原始图像建立自然统计模型, 并没有像其他大部分通用型NR图像质量指标需要不同类型不同干扰程度的干扰图像和每幅图像的主观分数进行训练.这样, 模型对训练数据依赖性很小, 因此通用性更强.

3 通用型无参考图像质量指标

自然统计模型建立完成后, 在每次评估图像的质量时, 直接利用自然统计模型代替原始图像的统计特征.因此, 评价过程只需计算待评价图像的统计特征, 同样也将这些统计特征与多元高斯模型拟合, 待评价图像的质量即自然统计模型与待评价图像模型的马氏距离为:

Dυ1, υ2, Σ1, Σ2=υ1-υ2TΣ1+Σ22-1υ1-υ2(11)

上述用距离评估JPEG压缩图像的效果并不是十分理想.为了进一步改善对JPEG压缩图像质量评价的性能, 利用文献[11]的方法在空间域进行补偿, 首先计算水平方向的块效应和块内能量:

(12)

(13)

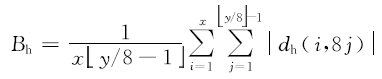
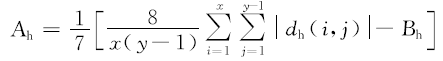
式中:(x, y)为图像的尺寸.

利用同样的方法计算垂直方向的块效应 Bv和块内能量 Av并计算整体的块效应和块内能量:

B=Bh+Bv2, A=Ah+Av2(14)

最后, 利用块效应与块内能量的比值[12]补偿JPEG压缩图像的评价效果:

C=B/A(15)

通过实验证明, 对于JPEG压缩干扰图像, 特征 C与主观评价分数有很高的一致性, 而对于其他类型干扰图像, 不论干扰程度如何, 特征 C的值均接近于1.因此, 利用特征 C对JPEG压缩干扰图像补偿, 可以保证在不影响对其他干扰类型图像评价效果的同时提升JPEG压缩干扰图像的评价性能.

将自然统计模型与待评价图像模型的马氏距离与JPEG补偿部分结合得到最终的评价指标:

Q=log2(1+DaC1-a0.01)(16)

式中: a为权重参数, 用以调整两部分的重要性, 根据经验, 这里取0.65.

4 实验结果与分析

本文首先利用由图像和视频工程实验室(LIVE)建立的质量评估数据库[13]验证算法的有效性.LIVE数据库共有5种类型干扰图像, 分别为高斯白噪声(White noise, WN), 高斯模糊(Gaussian blur, GBLUR), JPEG压缩(JPEG), JPEG2000压缩(JP2K)和快速衰落(Fastfading, FF).

为了直观地比较各个算法的性能, 选取了一幅原始无失真图像及其5种类型的干扰图像, 如图2所示, 图中列出了每幅图像的主观评价分数(Difference mean opinion score, DMOS)以及NIQE算法和本文算法SCIQA评估图像得到的分数.

由于LIVE库内各干扰图像的DMOS值以及NIQE算法和本文算法SCIQA的最终评价分数描述的都是干扰图像与无失真原始图像之间的差距, 因此3种数值越大表示图像的质量越差, 受到的干扰越严重.对于图2(b)(c)(d)三幅图像, 无论利用人眼直接观察还是LIVE库提供的DMOS值都可以发现这三幅图像的质量是依次变差的, 而利用NIQE算法评估的分数却依次减小, 说明评价的结论是错误的.SCIQA则给出了完全正确的评价结果.类似地, 对于图2(e)(f), NIQE同样做出错误的判断, 而SCIQA的评价结果与人眼感知的结果完全一致.

为了更加系统准确地评价算法的性能, 计算了评价算法结果与DMOS之间的Spearman等级相关系数(Spearman rank order correlation coefficient, SROCC)和Pearson线性相关系数(Pearson linear correlation coefficient, PLCC)用以验证算法的单调性和准确性.SROCC和PLCC越大, 证明算法的性能越好.两种经典FR算法峰值信噪比(PSNR)和结构相似度算法(SSIM)以及通用型NR算法NIQE用作对比算法.表1和表2分别列出了各算法结果与DMOS间的SROCC和PLCC.

图2 NIQE与SCIQA评价结果比较Fig.2 Performance comparison of NIQE and SCIQA

表1 LIVE IQA数据库上各算法结果与DMOS间的SROCC Table 1 SROCC between algorithms and DMOS on the LIVE database
表2 LIVE IQA数据库上各算法结果与DMOS间的PLCC Table 2 PLCC between algorithms and DMOS on the LIVE database

从表1, 表2可以看出, 大多数情况下, SCIQA的性能优于NIQE和PSNR.对于GBLUR, WN和JPEG三种干扰类型的图像, SCIQA的评价效果明显好于SSIM, 其主要原因分析如下:首先, SSIM仅在单一尺度上描述图像的质量信息, 使得其对图像分辨率影响较大的高斯模糊图像的评价效果较差.其次, SSIM采用直接取均值的方式合并各局部区域的图像质量分数, 而人眼对于纹理密集区域的高斯白噪声感知不敏感, 这使得SSIM评估高斯白噪声图像时产生过估计.最后, SSIM利用图像的方差衡量图像对比度的变化, 而方差与图像像素的位置无关, 也就是说, 当图像块内的像素大小不变但相对位置发生变化时, 图像块的方差是不变的.JPEG压缩图像会产生块效应, 图像块内出现模糊现象, 块的边界产生假边缘, 即某些像素的灰度值变大而某些变小.因此, SSIM在评估JPEG压缩图像的质量时会出现估计不足的情况.而SCIQA利用了多尺度分解并能提取人眼敏感特征的Contourlet变换, 同时提取了Contourlet的多种有效特征, 因此具有更好的评价结果.但是, SCIQA在JP2K和FF两种干扰图像情况下评价效果不及SSIM.这是因为JP2K和FF图像均存在振铃干扰, 振铃干扰使图像边缘出现波动, 在图像强度变化不尖锐的区域, 振铃干扰容易被判为图像的特征, 因此, NR方法对振铃干扰的定位容易出现偏差.综上所述, SCIQA既可用作单独干扰类型图像的质量评价, 也可用作事先无法预知干扰类型时图像的质量评价, 是一种高效的通用型NR算法.

实际情况下, 图像受到的干扰类型很难预先判断, 因此NR图像质量评价算法的通用性十分重要.专门针对某种特定干扰类型的NR方法通常是根据该种干扰类型的特点设计的, 这种算法只对特定干扰类型有效, 显然其通用性较差.而大多数通用型NR质量评价方法要求利用某些类型的干扰图像及其主观分数进行训练, 因此, 算法通常只能有效评价与训练数据集内图像具有相同干扰类型的图像质量, 因此通用性也受到限制.为了验证SCIQA具有更强的通用性, 本文将SCIQA与需要机器学习训练的通用型NR算法BRISQUE[14]进行比较.BRISQUE利用LIVE数据库内的5种干扰类型的图像进行训练, 因此, 对比实验在CSIQ数据库[15]上进行, 除了计算与LIVE库中相同的WN, GBLUR, JPEG和JP2K四种干扰类型图像外, 还计算了对比度失真图像.表3分别列出了BRISQUE和SCIQA对于CSIQ中上述5种干扰类型图像的SROCC.

表3 CSIQ IQA数据库上各算法结果与DMOS间的SROCC Table 3 SROCC between algorithms and DMOS on the CSIQ database

从实验结果可以看出, SCIQA对5种干扰类型图像的评价结果均好于BRISQUE.更值得注意的是, BRISQUE仅对训练过的4种干扰类型有效, 对于没有训练过的对比度失真图像完全失去评价作用.而所有评定算法性能的测试图像与SCIQA建立自然统计模型的图像在内容上是完全独立的.由此可以看出, SCIQA具有较强的通用性.

5 结束语

利用Contourlet域的统计特征表征图像的质量, 提出了基于Contourlet统计特征的无参考图像质量评价方法SCIQA.由于无需通过对干扰图像和主观分数的训练建立自然统计模型, SCIQA具有更强的实际应用价值.实验结果表明, SCIQA的性能优于经典全参考算法PSNR和SSIM以及无参考算法NIQE, 与人眼感知结论高度一致, 同时具有较强的通用性.

The authors have declared that no competing interests exist.

参考文献
[1] Wang Z, Bovik A C, Sheikh H R, et al. Image quality assessment: from error visibility to struc-tural similarity[J]. IEEE Transactions on Image Processing, 2004, 13(4): 600-612. [本文引用:1]
[2] 王宇庆. 基于局部方差和互信息的融合图像质量评价[J]. 光学精密工程, 2015, 23(10z): 515-521.
Wang Yu-qing. Fusion image assessment based on local variance and singular value decomposition[J]. Optics and Precision Engineering, 2015, 23(10z): 515-521. [本文引用:1]
[3] 卢彦飞, 张涛, 章程. 应用log-Gabor韦伯特征的图像质量评价[J]. 光学精密工程, 2015, 23(11): 3259-3269.
Lu Yan-fei, Zhang Tao, Zhang Cheng. Image quality assessment using log-Gabor Weber feature[J]. Optics and Precision Engineering, 2015, 23(11): 3259-3269. [本文引用:1]
[4] Mittal A, Soundararajan R, Bovik A C. Making a "completely blind" image quality analyzer[J]. IEEE Signal Processing Letters, 2013, 20(4): 209-212. [本文引用:3]
[5] Do M N, Vetterli M. The contourlet transform: an efficient directional multiresolution image representation[J]. IEEE Tansaction on Image Processing, 2005, 14(12): 2091-2106. [本文引用:2]
[6] 吕丹, 毕笃彦. 基于结构相似的DCT域图像质量评价[J]. 吉林大学学报: 工学版, 2011, 41(6): 1771-1776.
Lyu Dan, Bi Du-yan. Image quality assessment in DCT domain based on structural similarity[J]. Journal of Jilin University (Engineering and Technology Edition), 2011, 41(6): 1771-1776. [本文引用:1]
[7] Liu Li-xiong, Dong Hong-ping, Huang Hua. No-reference image quality assessment in curvelet domain[J]. Signal Processing: Image Communi-cation, 2014, 29(4), 494-505. [本文引用:2]
[8] Lu Wen, Zeng Kai, Tao Da-cheng. No-refernece image quality assessment in contourlet domain[J]. Neurocomputing, 2010, 73(6): 784-794. [本文引用:1]
[9] Moorthy A K, Bovik A C. Blind image quality assessment: from natural scene statistics to perceptual quality[J]. IEEE Transaction on Image Processing, 2011, 20(12): 3350-3364. [本文引用:1]
[10] Martin D, Fowlkes C, Tal D, et al. A database of human segmented natural images and its applica-tion to evaluating segmentation algorithms and measuring ecological statistics[C]//IEEE Inter-national Conference on Computer Vision, Van-couver, BC, USA, 2001: 416-423. [本文引用:1]
[11] Wang Z, Sheikh H R, Bovik A C. No-reference perceptual quality assessment of JPEG com-pressed images[C]//International Conference on Image Processing, New York, USA, 2002: 477-480. [本文引用:1]
[12] 金波. 基于自然图像信息统计的无参考图像质量评估研究[D]. 无锡: 江南大学物联网工程学院, 2012.
Jin Bo. The research of no-reference image quality assessment based on statistic of natural image information[D]. Wuxi: School of Internet of Things Engineering, Jiangnan University, 2012. [本文引用:1]
[13] Sheikh H R, Wang Z, Cormack L, et al. Live im-age quality assessment database release2[DB/OL]. [2009-12-14]. http://live.ece.utexas.edu/re-search/quality [本文引用:1]
[14] Mittal A, Moorthy A K, Bovik A C. No-reference image quality assessment in the spatial domain[J]. IEEE Tansaction on Image Processing, 2012, 21(12): 4695-4708. [本文引用:1]
[15] Larson E C, Chand ler D M. Categorical image quality (CSIQ) database 2009[DB/OL]. [2009-12-14]. http://vision.okstate.edu/csiq [本文引用:1]