作者简介:刘伟(1988-),女,博士研究生.研究方向:阵列信号处理.E-mail:liuwei0804@hrbeu.edu.cn
针对远场目标的时间反转聚焦问题,提出了一种传输矩阵估计下的时间反转聚焦方法.该方法利用目标探测波和目标反射回波获得传输矩阵的最小二乘估计值,进而通过计算得到时间反转算子(TRO),通过对该算子进行特征值分解可获得主特征值和主特征向量,其中主特征值的个数对应目标个数.利用除主特征向量以外的噪声向量进行搜索域内各虚拟观测点的目标函数计算,可以实现在远场目标处的聚焦.仿真结果表明:本文所提方法可以准确有效地实现在远场目标处的时间反转聚焦,而且该算法可以获得比基于TRO分解的选择性聚焦算法更好的聚焦性能.
A time reversal focusing method based on transfer matrix estimation is proposed for far field targets. In this method, first, the least square estimation of the transfer matrix is obtained using detection and reflection signals of the targets, based on which the time reversal operator (TRO) is calculated. Second, the eigenvalues and corresponding eigenvectors are obtained by performing eigenvalue decomposition of TRO, where the number of targets can be confirmed by the number of the principal eigenvalues. Finally, the far target focusing can be realized through calculating the objective function of virtual observed points in the search area using noise vectors. Experimental simulations are performed and results show that the proposed method could realize time reversal focusing for far field targets effectively and accurately. The focusing performance of this method is better than that of the selective focusing method based on decomposition of TRO.
时间反转理论的原理是利用波动方程解的时间反转不变性和空间互易性, 将阵列接收到的信号进行时间反转处理, 频域内相当于相位共轭, 然后将时间反转处理后的信号经过反向物理传输, 使信号在目标处实现聚焦[1].Fink等[2]首次提出并验证了时间反转技术在超声聚焦中的有效性, 随后Song等[3]对该技术在海洋实验中的应用进行了研究, 直到2004年, 时间反转理论开始被引入到电磁领域[4], 其目标聚焦能力也越来越受到人们的广泛关注.到目前为止, 时间反转技术已经在超声碎石[5], 无损探伤[6, 7], 目标探测[8, 9], 无线通信[10, 11]和成像[12, 13]等方面得到了广泛探讨与研究.为解决多目标时间反转聚焦问题, 一种通过有限次数的时间反转迭代逐渐削弱反射系数较小的目标处的相对聚焦信号能量, 最终实现在强反射目标上的选择性聚焦方法被提出[14], 但通过迭代时间反转使信号聚焦于弱反射目标处是不可能实现的.1996年, 一种基于时间反转算子分解的选择性聚焦技术被提出[15], 该技术利用时间反转算子特征分解后的主特征向量可以实现在各个目标处的选择性聚焦, 但该方法只利用了单一特征向量实现聚焦, 因此其聚焦性能并不理想.
为改善时间反转多目标聚焦算法的性能, 本文以时间反转算子分解聚焦原理为基础, 提出了一种利用除主特征向量以外的所有噪声向量来实现多个远场目标聚焦的方法.该方法首先利用最小二乘估计得到传输矩阵的估计值, 并利用该估计值得到时间反转算子, 通过对该算子的特征值分解可得到信号子空间和噪声子空间, 利用噪声子空间中的所有噪声向量计算搜索域内各虚拟目标观测点处的目标函数即可实现在各目标处的聚焦.最后, 通过仿真实验验证了该方法的正确性和有效性.
考虑由
式中:klm (t)为阵元m到阵元l的交叉脉冲响应.
式(1)写成频域形式为:
用矩阵表示为:
式中: E(ω )和R(ω )分别表示M个天线阵元的发射和接收信号向量;
根据互易定理, 从阵元m到阵元l之间的交叉脉冲响应与从阵元l到阵元m之间的交叉脉冲响应相同, 因此传输矩阵K(ω )具有对称性.
接收信号
对式(4)两边同时取相位共轭, 有:
记
为实现聚焦, 需要获得时间反转阵列与目标之间的传输矩阵
式中:
为估计传输矩阵
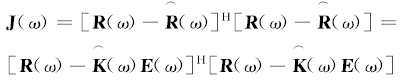
式中: 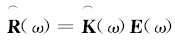
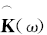
为使式(7)最小, 可由式(8)获得:
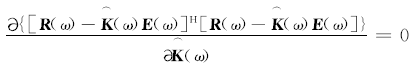
因此, 传输矩阵的估计值可表示为:
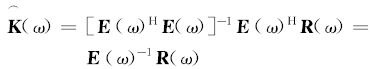
计算时要求 
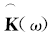

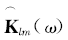

由传输矩阵的估计值可将TRO写成如下形式:
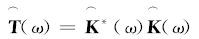
对 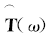
 |
式中: Λ 为非负实特征值对角矩阵; V为M个特征值对应的特征向量矩阵.
假设已知搜索域中共有p个目标, 将 
假设第i个目标与时间反转阵列之间的传输向量为:
式中:Him (ω )(1≤ i≤ p, 1≤ m≤ M)表示时间反转阵列中第m个阵元到第i个目标处的传输函数.可得信号子空间包含传输函数向量空间
根据电磁空间波动理论可知, 远场情况下的电磁波可看作平面波, 其在空间中传播时的脉冲响应函数可以写成如下形式:
式中:
其傅里叶变换为:
为实现在目标方位处的聚焦, 将整个目标搜索域均匀划分成N个虚拟目标观测点, 则时间反转阵列到第n个虚拟目标观测点处的传输向量为:
式中:Hnm (ω )=exp(-jω τ nm ), 1≤ n≤ N, 表示时间反转阵列中第m个阵元到第n个虚拟目标观测点的传输函数; τ nm 为第m个阵元到第n个虚拟目标观测点的传播时延.
由 

式中:
基于时间反转的远场目标聚焦算法的目标函数可以写成如下形式:
式中:vi0(m)为 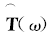
综上所述, 基于时间反转的远场目标聚焦算法的实现可分为以下几个步骤:
(1)时间反转阵列发射目标探测信号.
(2)时间反转阵列接收并记录目标回波信号.
(3)根据式(9)对传输矩阵进行最小二乘估计, 并对传输矩阵估计值进行对称性修正.
(4)根据式(10)计算 
(5)确定目标搜索域中各虚拟观测点, 并根据电磁波传播特性获得虚拟目标观测点的传输向量.
(6)根据式(17)计算各虚拟观测点处的目标函数, 实现在目标处的聚焦.
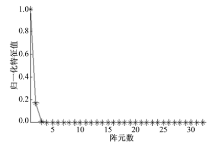
为验证基于时间反转处理的远场目标聚焦方法的有效性, 建立如图1所示的均匀圆形时间反转阵列, M个阵元均匀分布在以r为半径的圆周上.时间反转阵列发射目标探测波e(t), 通过接收到的目标回波进行传输矩阵的最小二乘估计得到 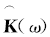
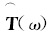
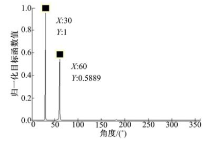
为实现在目标方位处的聚焦, 选定如图2所示的目标搜索域, 其中N个虚拟目标观测点均匀分布在以r'为半径的圆周上, 然后利用式(17)所示的目标函数计算各虚拟观测点的函数值即可实现在目标方位处的聚焦.
仿真实验中, 取M=32, r=20 m, 阵列的每个阵元发射中心频率为30 MHz, 持续时间为2 μ s的正弦电磁波信号, 系统采样率为200 MHz.设定两个目标都位于目标搜索域内, 且方位角
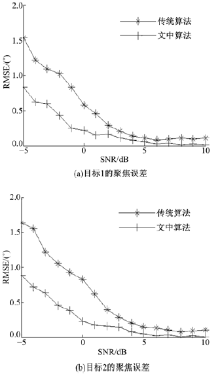
为观察噪声对该算法聚焦性能的影响, 在仿真中加入不同信噪比的高斯白噪声, 并进行100次蒙特卡洛实验, 可得图5所示两目标的聚焦均方根误差曲线图.从图5中可以看出, 在加性高斯白噪声情况下, 文中所给出的聚焦算法可以获得更小的聚焦误差, 验证了该算法的准确性.图中所示传统算法是指基于时间反转算子分解的选择性聚焦算法, 该方法利用主特征值所对应的主特征向量实现在目标处的聚焦, 其目标函数为:
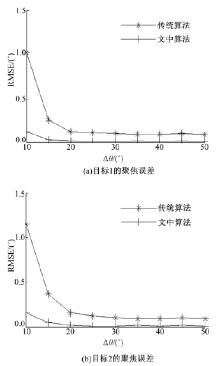
为研究两目标之间的角度差对该算法聚焦性能的影响, 在信噪比为10 dB的情况下, 改变两目标之间的角度差
基于时间反转算子分解聚焦原理, 利用时间反转阵列发射的目标探测波和接收的目标反射波, 提出了一种最小二乘传输矩阵估计下基于噪声向量的时间反转远场目标聚焦方法并给出了算法步骤.通过仿真实验发现该方法可有效实现在两目标处的方位聚焦, 验证了该聚焦方法的正确性.通过与传统基于时间反转算子分解的选择性聚焦算法进行实验对比发现, 文中所给出的算法可以获得更小的聚焦均方根误差, 而且在两目标之间的角度差较小时, 该方法可以获得比传统算法更好的聚焦性能.因此, 该方法具有多目标分辨与检测的优异性能, 实际应用前景较好.
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|