基于改进的差动差分电流传送器的模拟浮地电感

引用本文

王春悦, 王立雪, 张俊茹, 石文孝. 基于改进的差动差分电流传送器的模拟浮地电感.吉林大学学报:工学版, 2016, 46(2): 652-657
WANG Chun-yue, WANG Li-xue, ZHANG Jun-ru, SHI Wen-xiao. Simulating floating inductance based on MDDCC. Journal of Jilin University Engineering and Technology Edition, 2016, 46(2): 652-657 复制到剪切板

Permissions

基于改进的差动差分电流传送器的模拟浮地电感

王春悦, 王立雪, 张俊茹, 石文孝

吉林大学通信工程学院,长春 130012

作者简介:王春悦(1971-),女,副教授,博士.研究方向:信号与信息处理.E-mail:chunyue@jlu.edu.cn

基金:国家自然科学基金项目(61373124)

摘要

由于无源电感不易集成,本文提出了一种新的基于改进的差动差分电流传送器 (MDDCC)的理想浮地电感,分析了电流传输器在理想情况和非理想情况下的电感值,该电路仅由2个MDDCC,2个电阻和1个电容构成,结构简单,电感值可由阻容元件独立调节.将此电路用于电压模式二阶低通和二阶带通以及电流模式高阶的连续时间滤波器中,用参数为0.18 μm CMOS工艺进行PSPICE计算机仿真.仿真结果表明,设计方案是可行有效的.

关键词: 信息处理技术; 浮地电感; 改进的差动差分电流传输器; PSPICE仿真

中图分类号:TN713.8 文献标志码:A 文章编号:1671-5497(2016)02-0652-06

Simulating floating inductance based on MDDCC

WANG Chun-yue, WANG Li-xue, ZHANG Jun-ru, SHI Wen-xiao

College of Communication Engineering,Jilin University,Changchun 130012,China

Abstract

Because that the passive inductance is not easy to be integrated, a new ideal floating inductance based on Modify Differential Difference Current Conveyor (MDDCC) is proposed. The inductance values of the current conveyor in ideal and nonideal conditions are analyzed. This circuit consists of only two MDDCCs, two resistors and one grounded capacitor. So the structure of the floating inductance is simple, the inductance value can be adjusted independently by the two resistors and the capacitor. The circuit is used in continuous time voltage mode filter of two order low pass, and two order band pass and current mode high order filters. Computer simulation of PSPICE is carried out using parameters of the 0.18 μm CMOS process. Simulation results show that the proposed floating inductance has good circuit's work ability.

Keyword: information processing technology; floating inductance; modify differential difference current conveyor (MDDCC); the PSPICE simulation

Show Figures

滤波器实现技术按处理信号的类型分为采样数据技术(采样滤波器)和连续时间技术(模拟滤波器), 开关电容(SC)是典型的采样数据滤波器.采样数据滤波器的共同缺点是系统工作频率受奈奎斯特采样定理的限制; 因采样带来的时钟馈入问题导致滤波器精度下降, 噪声和失真增加.另外, 采样数据滤波器对连续时间信号进行滤波时, 需在前端加防混叠滤波器对输入信号作带限处理, 在后端加平滑滤波器以满足采样定理并得到平滑的输出.所以, 能够克服上述缺点的最佳方案就是对连续时间信号直接滤波, 即全集成连续时间滤波器.近年来, 全集成连续时间滤波器的发展特别迅速, 在通信集成电路如无线传感器网络^[1], 模数转换^{[2, 3]}, 无线接收机^{[4, 5]}等技术中得到了成功的应用.电流传输器是一种功能很强的混合模式通用滤波器件^{[6, 7, 8, 9, 10, 11]}, 它广泛应用于模拟信号处理和有源网络元件的模拟电路中^{[12, 13, 14, 15, 16, 17]}.改进的差动差分电流传输器(Modify differential difference current conveyor, MDDCC)集合了电流传输器和差动差分放大器的优点^[6], 易于集成.在模拟滤波器设计中由于无源器件体积大, 耗电量大, 不利于集成, 所以提出了用改进的电流传输器来实现模拟电感, 模拟电感滤波器具有结构设计简单, 无源元件的灵敏度低的特点, 是一种有效的全集成连续时间高级滤波器设计方法.

本文分析了模拟电感在理想特性情况下和非理想特性情况下的电感值, 并将其应用到电压模式二阶低通和二阶带通滤波器和电流模式三阶巴特沃斯和五阶切比雪夫低通滤波器中.仿真结果表明, 提出的滤波器电路是可行的, 所构成的滤波器性能符合设计指标的要求.

1 电路描述

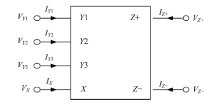
MDDCC是一个具有四端输入双端输出的六端口有源器件, 端口伏安特性如式(1)所示:

$\begin{matrix} [\begin{matrix} I_{Y 1} \\ I_{Y 2} \\ I_{Y 3} \\ V_{X} \\ I_{Z +} \\ I_{Z -} \end{matrix}] = [\begin{matrix} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & - 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & - 1 & 0 & 0 \end{matrix}] [\begin{matrix} V_{Y 1} \\ V_{Y 2} \\ V_{Y 3} \\ I_{X} \\ V_{Z +} \\ V_{Z -} \end{matrix}] \end{matrix}$ (1)

由MDDCC的端口伏安特性可以看出, $\begin{matrix} I_{Y 1} = I_{Y 2} = I_{Y 3} = 0, V_{X} = V_{Y 1} - V_{Y 2} + V_{Y 3}, I_{Z +} = I_{X}, I_{Z -} = - I_{X}, X \end{matrix}$ 端为低阻抗电流输入端, $\begin{matrix} Y \end{matrix}$ 端为高阻抗电压输入端, $\begin{matrix} Z \end{matrix}$ 端为高阻抗电流输出端, MDDCC的电路符号如图1所示.

	Figure Option View Download New Window
	图1 MDDCC电路符号Fig.1 Circuit symbol of MDDCC

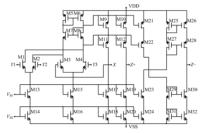图2给出了MDDCC的CMOS电路, 输入级由M1~M8, M13~M16组成, 差动电压传送由差分对M1, M2及M3, M4完成.M5, M6和M7, M8构成电流镜, 静态时M1和M4的漏电流之和等于M2和M3的漏电流之和, 即I_d1+I_d4=I_d2+I_d3, 因此I_d1-I_d2=I_d3-I_d4, V_G1-V_G2=V_G3-V_G4, 其中V_G1=V_Y1, V_G2=V_Y2, V_G3=V_X, V_G4=V_Y3, 从而得到 $\begin{matrix} V_{X} = V_{Y 1} - V_{Y 2} + V_{Y 3}, \end{matrix}$ M9, M11, M17, M18提供必要的负反馈, 使 $\begin{matrix} V_{X} \end{matrix}$ 独立于 $\begin{matrix} X \end{matrix}$ 端的输出电流, 起降低电压的作用.输出级由M10, M12, M19~M32组成, M10, M12, M19, M20构成电流复制单元, 根据电流复制技术, 得到 $\begin{matrix} X \end{matrix}$ 端与 $\begin{matrix} Z \end{matrix}$ 端的输出电流相等; M21~M32组成交叉耦合电流镜, 实现了 $\begin{matrix} X \end{matrix}$ 端与 $\begin{matrix} Z \end{matrix}$ 端的输出电流相等, 得到反向的电流, MDDCC的管道的宽长比W/L(μ m)如下:M1, M2, M3, M4, M7, M8为8.75:0.7; All PMOS为17.5:0.7; 其他NMOS为8.75:0.35.

	Figure Option View Download New Window
	图2 MDDCC的CMOS电路^[11]Fig.2 CMOS Circuit of MDDCC

2 浮地电感的模拟电路

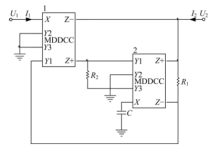
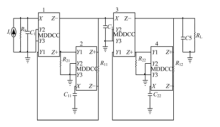
图3为本文提出的新的浮地电感模拟电路, 该电路由2个MDDCC, 2个电阻和1个电容组成, 电路结构简单.

	Figure Option View Download New Window
	图3 浮地电感实现电路Fig.3 Realization of floating inductance

对图3的端口特性进行分析, 有:

$I_{1} = I_{X 1} = I_{Z 1 +} = - I_{Z 1 -} = - I_{2}$ (2)

$V_{Y 11} = V_{X 1} = U_{1}$ (3)

$I_{Z 1 +} = - \frac{V_{Y 12}}{R_{2}} = - \frac{V_{X 2}}{R_{2}}$ (4)

$V_{X 2} = - \frac{I_{X 2}}{SC} = \frac{I_{Z 2 -}}{SC} = \frac{U_{2} - U_{1}}{SC R_{1}}$ (5)

$I_{1} = - I_{2} = \frac{U_{1} - U_{2}}{SC R_{1} R_{2}}$ (6)

式(6)写成矩阵形式为:

$\begin{matrix} [\begin{matrix} I_{1} \\ I_{2} \end{matrix}] = [\begin{matrix} 1 & - 1 \\ - 1 & 1 \end{matrix}] \cdot [\begin{matrix} U_{1} \\ U_{2} \end{matrix}] \cdot \frac{1}{SC R_{1} R_{2}} \end{matrix}$ (7)

对图3电路分析其端口的短路导纳矩阵为:

$\begin{matrix} [Y] = [\begin{matrix} 1 & - 1 \\ - 1 & 1 \end{matrix}] \cdot \frac{1}{SC R_{1} R_{2}} \end{matrix}$ (8)

由式(8)可知电路的等效电感为:

$\begin{matrix} L = C R_{1} R_{2} \end{matrix}$ (9)

此电路有以下两个特点:所需要的元器件很少, 只用2个MDDCC和1个电容, 2个电阻; 元件间无约束, 电感值可以任意调节.如若考虑非理想特性的影响, 只考虑电压对特性的影响, 则MDDCC的输入输出特性可表示为:

$\begin{matrix} I_{Y} = 0 \end{matrix}$

$\begin{matrix} V_{X} = (1 - ε) V_{Y} \end{matrix}$

$\begin{matrix} I_{X} = I_{Z +} = - I_{Z -} \end{matrix}$

$\begin{matrix} \begin{matrix} I_{1} = I_{Z 1 +} = - \frac{V_{Y 12}}{R_{2}} = - \frac{V_{X 2}}{(1 - ε_{2}) R_{2}} = \\ \frac{(V_{Y 11} - U_{2})}{(1 - ε_{2}) SC R_{2} R_{1}} = \frac{U_{1} - (1 - ε_{1}) U_{2}}{(1 - ε_{1}) (1 - ε_{2}) SC R_{2} R_{1}} \\ I_{1} = - I_{2} = \frac{1}{(1 - ε_{1}) (1 - ε_{2}) SC R_{2} R_{1}} \times \\ [U_{1} - (1 - ε_{1}) U_{2}] (11) \end{matrix} \end{matrix}$ (10)

则电路的导纳为:

$\begin{matrix} \begin{matrix} [Y] = \\ [\begin{matrix} 1 & - (1 - ε_{1}) \\ - 1 & (1 - ε_{1}) \end{matrix}] \frac{1}{(1 - ε_{1}) (1 - ε_{2}) SC R_{1} R_{2}} \end{matrix} \end{matrix}$ (12)

其理想浮地等效电感为:

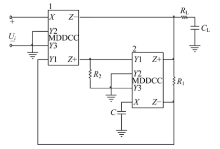
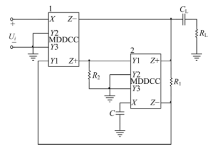
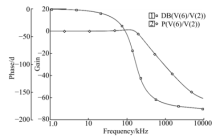
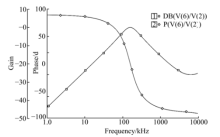
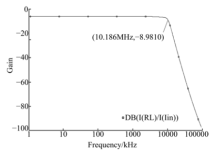
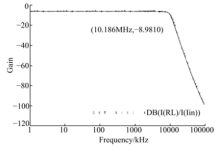
$\begin{matrix} L = (1 - ε_{1}) (1 - ε_{2}) C R_{2} R_{1} \end{matrix}$ (13)

3 滤波器电路设计与仿真

把本文提出的理想浮地电感实现电路应用于电压模式二阶低通滤波器(见图4)和二阶带通滤波器(见图5)的设计当中, 并用PSPICE仿真.设计频率 $\begin{matrix} f = 159 kHz, Q = 1, \end{matrix}$ 图2中MDDCC的CMOS电路, 电路的直流电压V_DD=-V_SS=1.65 V, 偏置电压 $\begin{matrix} V_{B 1} = 0.35 V, V_{B 2} = - 1 V, \end{matrix}$ CMOS管的参数如第1节中所示^[11].二阶滤波器的角频率如下:

$\begin{matrix} ω = \sqrt[]{1 / L C_{L}}; ω = 2 πf; Q = \sqrt[]{L / C_{L}} / R_{L} \end{matrix}$ (14)

	Figure Option View Download New Window
	图4 二阶低通滤波器Fig.4 Low pass biquad

	Figure Option View Download New Window
	图5 二阶带通滤波器Fig.5 Band pass biquad

仿真时, 令L=10mH, R₁=R₂=10kΩ , C=0.1nF, 计算出R_L=10kΩ , C_L=0.1nF, 从而得出图4, 图5的仿真图, 见图6, 图7.从仿真结果可以看出, 低通滤波器的实际截止频率为 $\begin{matrix} f = 159.22 kHz, \end{matrix}$ 带通滤波器的中心频率为 $\begin{matrix} f = 159.211 kHz, \end{matrix}$ 衰减-3 dB带宽处的频率分别为 $\begin{matrix} f_{+} = 258.821 kHz, f_{-} = 98.401 kHz, \end{matrix}$ 可计算出 $\begin{matrix} Q \end{matrix}$ 值, $\begin{matrix} Q = f / (f_{+} - f_{-}) = 0.9925, \end{matrix}$ 可见得到的频率和品质因数与设计指标接近, 本文提出的电路是可行的.

	Figure Option View Download New Window
	图6 二阶低通滤波器仿真结果Fig.6 Simulating result of low pass biquad

	Figure Option View Download New Window
	图7 二阶带通滤波器仿真结果Fig.7 Simulating result of band pass biquad

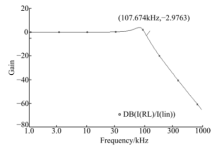
本文提出的浮地电感不仅可以应用于传统的电压模式连续时间滤波器中, 还可以应用于新型的电流模式连续时间滤波器中, 用提出的模拟浮地电感应用于三阶巴特沃斯LC无源梯形滤波器电路当中^[13], 设计截止频率 $\begin{matrix} f_{P} = 100 kHz, \end{matrix}$ 电路如图8所示, 通过查手册可知巴特沃斯三阶低通原型的元件值β ₁=β ₃=1.000, α ₂=2.000, 令R_S=R_L=R_r=2kΩ , W_r=W_3dB=6.28× 10⁵ rad/s, 得到 $\begin{matrix} L_{0} = 3.2 mH, C_{0} = 0.8 nF, \end{matrix}$ 则 $\begin{matrix} C_{1} = C_{3} = 0.8 nF, L_{2} = 6.4 mH, \end{matrix}$ 其中模拟浮地电感中 $\begin{matrix} R_{1} = R_{2} = 20 kΩ, C = 16 pF, \end{matrix}$ 图9为它的频率特性仿真曲线, 滤波器的截止频率为 $\begin{matrix} 107.674 kHz \end{matrix}$ .将浮地电感应用到5阶切比雪夫低通滤波器中, 设计截止频率 $\begin{matrix} f_{P} = 10 MHz, \end{matrix}$ 标定时最大反射系数ρ =5%, 即通带内最大衰减为 $\begin{matrix} 0.011 dB, \end{matrix}$ 经过查手册, 可知切比雪夫五阶低通原型的元件值分别为β ₁=β ₅=0.7664, β ₃=1.588, α ₂=α ₄=1.310, 标定W_r=W₃dB=6.28× 10⁷ rad/s, R_S=R_L=R_r=1kΩ , L₀=15.9155μ H, C₀=15.9155pF, 则C₃=25.274pF, C₁=C₅=12.198pF, L₂=L₄=20.85μ H, 其中2个浮地电感中电阻阻值和电容阻值分别为: $\begin{matrix} R_{11} = R_{21} = R_{12} = R_{22} = 10 kΩ, C_{11} = C_{22} = 0.2085 pF, \end{matrix}$ 滤波器的截止频率为 $\begin{matrix} 10.186 MHz, \end{matrix}$ 电路图和仿真图分别为图10和图11, 实际仿真结果与理论设计值略有偏差, 主要是MDDCC电路中MOS管的非线性引起的.为了分析滤波器的灵敏度, 使用蒙特卡罗分析方法, 共运行10次, 每个电阻在± 5%之间按器件阻值差(DEV)变化, 每个电容在± 10%之间按器件容差(DEV)变化, 分析结果如图12所示.仿真结果表明, 此滤波器电路具有低的灵敏度特性, 其滤波特性不随电阻和电容的变化而变化.

	Figure Option View Download New Window
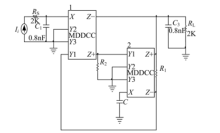	图8 三阶巴特沃斯低通滤波器^[13]Fig.8 Third-order Butterworth low pass filter

	Figure Option View Download New Window
	图9 三阶巴特沃斯频率响应Fig.9 Frequency response of third-order Butterworth filter

	Figure Option View Download New Window
	图10 五阶切比雪夫低通滤波器Fig.10 Low pass fifth-order Chebyshev filter

	Figure Option View Download New Window
	图11 五阶切比雪夫频率响应Fig.11 Frequency of fifth-order Chebyshev filter

	Figure Option View Download New Window
	图12 五阶切比雪夫蒙特卡罗分析Fig.12 Mote Carlo analysis of fifth-order Chebyshev filter

4 结束语

提出了一种新的基于MDDCC的模拟浮地电感, 该电路仅用2个MDDCC, 2个电阻和1个电容, 电路结构简单, 易于集成, 等效电感可由电阻和电容独立调节, 将其用于二阶电压模式低通和带通滤波器以及电流模式三阶巴特沃斯和五阶切比雪夫滤波器的设计, 仿真结果证实了设计电路的正确性, 且具有易于集成, 结构简单, 无源元件少, 灵敏度低等优点.

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Laifi A, Al Abaji M A, Thewes R. High resolution current-Mode CCO-based continuous time delta-sigma modulators for sensor-array applications[C]//2014 10th Conference on Ph. D, Microelectronics and Electronics (PRIME), Grenoble, 2014: 1-4. [本文引用:1]
[2]	Balasubramaniam H, Hofmann K. Calibrated switched capacitor integrators based on current conveyors and its application to delta sigma ADC[C]//2014 10th Conference on Ph. D, Microelectronics and Electronics (PRIME), Grenoble, 2014: 1-4. [本文引用:1]
[3]	Bhatia V, Madan M, Kaur B, et al. A novel CC-II based current comparator and its application as current mode flash ADC[C]//2013 International Conference on Multimedia, Signal Processing and Communication Technologies (IMPACT), Aligarh, 2013: 217-222. [本文引用:1]
[4]	Pand ey N, Paul S K, Bhattacharyya A. A novel channel select filter for multi stand ard wireless receiver[C]//2010 International Conference on Computer and Communication Technology (ICCCT), Allahabad, Uttar Pradesh, 2010: 282-284. [本文引用:1]
[5]	Soliman E A, Mahmoud S A. Multi-stand ard receiver baseband chain using digitally programmable OTA based on CCII and current division networks[C]//2012 International Conference on Engineering and Technology (ICET), Cairo, 2012: 1-5. [本文引用:1]
[6]	石文孝, 王长青, 韩庆全. 基于多输出端差动差分电流传送器的模拟电感[J]. 吉林大学学报: 信息科学版, 2003, 21(1): 42-46. Shi Wen-xiao, Wang Chang-qing, Han Qing-quan. Simulated inductance based on MDDCC[J]. Journal of Jilin University(Information Science Edition), 2003, 21(1): 42-46. [本文引用:2]
[7]	梁荣新, 丘水生. 改进型电流传输器实现接地变浮地回转器[J]. 中山大学学报: 自然科学版, 2003, 42(5): 32-34. Liang Rong-xin, Qiu Shui-sheng. The realization of grounded to floating gyrators using modified current conveyors[J]. Journal of Zhongshan University(National Science Edition), 2003, 42(5): 32-34. [本文引用:1]
[8]	邓晓, 湛春晖. 基于双输出电流传送器的模拟浮地电感[J]. 湖南大学学报: 自然科学版, 2003, 30(6): 71-73. Deng Xiao, Zhan Chun-hui. Active simulation of floating inductors based on DOCCII[J]. Journal of Hunan University(Natural Sciences), 2003, 30(6): 71-73. [本文引用:1]
[9]	梁荣新. 用改进电流传输器实现的新型理想浮地电感[J]. 电子学报, 1994, 22(8): 111-112. Liang Rong-xin. The novel ideal floating inductor realized by using modified current conveyors[J]. Chinese Journal of Electronics, 1994, 22(8): 111-112. [本文引用:1]
[10]	Ibrahim M A, Minaei S, Yuce E, et al. Lossless grounded inductance simulation using only one modified dual output DDCC[C]//2011 34th International Conference on Telecommunications and Signal Processing (TSP), Budapest, 2011: 261-264. [本文引用:1]
[11]	Wang S F, Chen H P, Lin Y H, et al. Tunable voltage-mode multifunction biqaudratic filter with grounded capacitors and resistors using two DDCCs[C]//3rd International Conference on Communication Software and Networks (ICCSN), Xi'an, 2011: 552-556. [本文引用:2]
[12]	Ferri G, Guerrini N C, Romanato R, et al. CCII-based high-valued inductance simulators with minumum number of active elements[C]//18th European Conference on Circuit Theory and Design(ECCTD), Seville, 2007: 440-443. [本文引用:1]
[13]	Metin B, Cicekoglu O. A novel floating lossy inductance realization topology with NICs using current conveyors[J]. IEEE Transactions on Circuits and Systems, 2006, 53(6): 483-486. [本文引用:2]
[14]	Ashenafi E, Chowdhury M H. Implementation of active floating inductor based on second generation current conveyor for on chip voltage regulator[C]//2013 IEEE 56th International Midwest Symposium on Circuits and Systems (MWSCAS), Columbus, OH, 2013: 768-771. [本文引用:1]
[15]	Said L A, Madian A H, Isamil M H, et al. CMOS digitally programmable lossless floating inductor[C]//2010 IEEE International Conference of Electron Devices and Solid-State Circuits (EDSSC), Hong Kong, 2010: 1-4. [本文引用:1]
[16]	Fakhfakh M, Loulou M, Tlelo-Cuautle E. Synthesis of CCIIs and design of simulated CCII based floating inductances[C]//14th IEEE International Conference on Electronics, Circuits and Systems(ICECS), Marrakech, 2007: 379-382. [本文引用:1]
[17]	Lawanwisut S, Siripruchyanun M. An electronically controllable active-only current-mode floating inductance simulator[C]//2012 35th International Conference on Telecommunications and Signal Processing (TSP), Prague, 2012: 386-389. [本文引用:1]

2014

0.0

... 近年来,全集成连续时间滤波器的发展特别迅速,在通信集成电路如无线传感器网络^[1],模数转换^[2,3],无线接收机^[4,5]等技术中得到了成功的应用 ...

2014

0.0

... 近年来,全集成连续时间滤波器的发展特别迅速,在通信集成电路如无线传感器网络^[1],模数转换^[2,3],无线接收机^[4,5]等技术中得到了成功的应用 ...

2013

0.0

... 近年来,全集成连续时间滤波器的发展特别迅速,在通信集成电路如无线传感器网络^[1],模数转换^[2,3],无线接收机^[4,5]等技术中得到了成功的应用 ...

2010

0.0

... 近年来,全集成连续时间滤波器的发展特别迅速,在通信集成电路如无线传感器网络^[1],模数转换^[2,3],无线接收机^[4,5]等技术中得到了成功的应用 ...

2012

0.0

... 近年来,全集成连续时间滤波器的发展特别迅速,在通信集成电路如无线传感器网络^[1],模数转换^[2,3],无线接收机^[4,5]等技术中得到了成功的应用 ...

2003

0.0