基于邻居节点分组的认知无线电Ad Hoc网络公共控制信道分配算法

引用本文

杨立标, 赵洪林, 贾敏. 基于邻居节点分组的认知无线电Ad Hoc网络公共控制信道分配算法.吉林大学学报:工学版, 2016, 46(2): 663-670
YANG Li-biao, ZHAO Hong-lin, JIA Min. Neighboring group control channel allocation or cognitive radio Ad Hoc network. Journal of Jilin University Engineering and Technology Edition, 2016, 46(2): 663-670 复制到剪切板

Permissions

基于邻居节点分组的认知无线电Ad Hoc网络公共控制信道分配算法

杨立标, 赵洪林, 贾敏

哈尔滨工业大学通信技术研究所,哈尔滨 150001

通讯作者:赵洪林(1969-),教授,博士生导师.研究方向:无线通信,扩频通信.E-mail:hlzhao@hit.edu.cn

作者简介:杨立标(1980-),男,博士研究生.研究方向:认知无线电Ad Hoc网络.E-mail:libiao_yang@126.com

基金:国家自然科学基金项目(61201143); 中国空间技术研究院ITS基金项目(F-W-YY-2013-016); 中央高校基本科研业务费专项项目(201309)

摘要

针对目前认知无线电Ad Hoc网络中公共控制信道分配在网络拓扑变化下性能差以及对主要用户活动鲁棒性差等问题,提出了一种基于邻居节点分组的公共控制信道分配算法.该方法根据认知无线电Ad Hoc网络频谱异构性对认知节点及其1跳邻居节点进行分组操作,然后利用最大边二分团建立起分组认知节点与可用信道集的映射关系,最后将控制信息时延和控制信道吞吐量联合起来构成可用控制信道效用函数,进而选择具有最大效用函数值的可用控制信道作为邻居节点组的最优控制信道.仿真结果表明:该算法性能优越,在认知节点密度和主用户数量增加时,能优化公共控制信道选择并有效降低业务传输时延,较好地适应了认知网络信道可用性空-时变换特性.

关键词: 通信技术; 公共控制信道; 认知Ad Hoc网络; 频谱异构性; 最大边二分团

中图分类号:TN915 文献标志码:A 文章编号:1671-5497(2016)02-0663-08

Neighboring group control channel allocation or cognitive radio Ad Hoc network

YANG Li-biao, ZHAO Hong-lin, JIA Min

Communication Research Center, Harbin Institute of Technology, Harbin 150001,China

Abstract

Current Common Control Channel (CCC) allocation in Cognitive Radio (CR) Ad Hoc network possesses several shortcomings, such as poor allocation performance in high fluctuating topology structure and poor robustness to the primary activities. To overcome these shortcomings, a novel neighboring group based CCC allocation algorithm is proposed. First, the CR node and its 1-hop neighbors are grouped based the spectrum heterogeneity. Then, the mapping from the grouped CR nodes and the idle CCC set is formulated as a maximum edge biclique problem. Finally, a novel utility function for each available CCC selection is established according to the control massage delay and its throughput; and the CCC in the set with the largest utility function value is selected as the optimal CCC. The algorithm has the advantages of robustness to primary activities and facility in dedicating control channel allocation by the agile grouping of local nodes. Simulation results show that the proposed algorithm is effective in reducing the normalized end-to-end delay when CR node density and primary user number increase; and it adapts to spatial-temporal variation in spectrum availability.

Keyword: communication technology; common control channel (CCC); cognitive radio Ad Hoc networks; spectrum heterogeneity; maximum edge biclique

Show Figures

0 引言

随着无线通信技术的快速发展, 认知无线电(Cognitive radio, CR)作为一种有效缓解频谱资源短缺的技术手段在信息通信领域得到了广泛应用^{[1, 2]}.特别地, 在认知Ad Hoc网络中, 次要用户(SU, 又被称为"认知节点")需要在缺少中心设施的情况下承担起频谱相关的认知功能^{[3, 4]}.因此, SU必须与邻居节点进行控制信息交换以改进系统输出并提高频谱利用效率.其中, 控制信息包含主用户活动, 信道可用性, 网络拓扑变化以及路由等参数.所以, 建立可靠且"按需"的公共控制信道以方便控制信息传输显得尤为重要.

目前, 认知网络中公共控制信道分配算法一般分为专用公共控制信道分配和基于分组的公共控制信道分配两种^[5].鉴于认知Ad Hoc网络动态特性较为复杂, 对所有SU可用的全局性公共控制信道分配算法实现复杂度高.因此, 本文重点讨论基于分组的公共控制信道分配算法.Kim等^[6]依据网络连接状态, 提出了基于分簇的公共控制信道分配算法.文献^[7]给出了基于频谱机会的公共控制信道分配算法, 其原理也是对网络内节点进行分簇.但是上述分簇算法并未考虑到节点移动性及控制信道覆盖范围.文献^[8]将公共控制信道选择过程归纳为群智能优化问题, 算法依靠节点间的相互协作选择出性能最好的公共控制信道.而Hsiu等^[9]提出的空间变化控制信道分配算法(SVC)则为移动节点提供了一个可用控制信道集, 网络中节点可根据"Fellow"信息的握手协议进行邻居的发现过程.尽管如此, 认知Ad Hoc网络公共控制信道分配仍然面临以下两方面挑战:一是公共控制信道频繁重分配所带来的控制开销.由于SU的移动性和主用户的活动, 当原控制信道失效后, SU需要重新选择公共控制信道交换控制信息.鉴于控制信道的频繁重建将产生巨大的网络控制开销, 因此, 需要有效的网络拓扑管理策略来减少开销.二是频谱异构性.由于认知Ad Hoc网络存在频谱异构性, SU通常会感知到不同的本地可用信道并形成列表.因此, 在控制信道覆盖范围内具有相似特性的邻居节点需要有共享可用控制信道集.

本文提出一种基于邻居节点分组的公共控制信道分配算法.该算法根据频谱可用性空-时变化的特性, 将次要用户与其1跳邻居节点进行分组.特别地, 将邻居节点分组与其对应的可用控制信道集的映射关系构造成最大边二分团问题.最后, 算法将控制信息的时延和输出联合起来作为最优控制信道选择标准, 提高了分配算法的有效性.

1 系统模型

认知Ad Hoc网络系统模型如图1所示.

	Figure Option View Download New Window
	图1 认知Ad Hoc网络中6节点连接图Fig.1 Connectivity graph of a 6-node in CR Ad Hoc networks

假设认知Ad Hoc网络中有 $\begin{matrix} N \end{matrix}$ 个认知节点, $\begin{matrix} M \end{matrix}$ 个可用信道.本文将网络拓扑连接定义为连接图 $\begin{matrix} G (V, ε), \end{matrix}$ 其中 $\begin{matrix} V \end{matrix}$ 为顶点集合, 在本文中代表所有认知节点; 而 $\begin{matrix} ε \end{matrix}$ 代表边集合, 在本文中代表当主用户活动不存在时可用通信链路集合.对于每个认知节点, 其所有1跳邻居节点就是该用户通过连接图 $\begin{matrix} G (V, ε) \end{matrix}$ 能够进行通信的用户.假设 $\begin{matrix} C_{i} \end{matrix}$ 为节点 $\begin{matrix} S U_{i} \end{matrix}$ 的可用信道集.在频谱接入过程中, 连接图 $\begin{matrix} G (V, ε) \end{matrix}$ 减少至通信图 $\begin{matrix} G (V, ε') \end{matrix}$ .其中, 两个节点的边表示在对方的通信范围内并至少有一条可用公共控制信道.通信图 $\begin{matrix} G (V, ε') \end{matrix}$ 表明了邻居间发现可用控制信道集的机制.当网络拓扑管理策略给出后, 认知节点则需要分配公共控制信道来进行用户间感知结果, 节点自身移动性及路由等控制信息的交换.

2 邻居节点发现

在认知Ad Hoc网络中, 认知节点与其1跳邻居通过可用控制信道集来交换控制信息.因此, 邻居节点发现过程就是SU在相同控制信道覆盖范围内发现其1跳邻居的频谱管理策略.在缺少专用公共控制信道的情况下, 每个认知用户通过本地信道感知来获取可用信道列表并发现其通信范围内的其他邻居用户.然后, 邻居节点间通过建立链接在相同的控制信道上进行控制信息交换, 且只有在邻居节点间在当前控制信道上的链路建立完毕后才能进行分组初始化操作.

考虑到认知Ad Hoc网络的频谱异构性, 主要用户对每个信道有优先使用权.对于控制信道来说, 其特点可以描述为:信道可用性和信道增益, 分别可定义为如下矩阵^[10]:

信道可用性: $\begin{matrix} L = {l_{n, m} \in {0, 1}}_{N \times M} \end{matrix}$ 是一个 $\begin{matrix} N \times M \end{matrix}$ 的矩阵, 其中 $\begin{matrix} l_{n, m} = 1 \end{matrix}$ 表示节点 $\begin{matrix} S U_{n} \end{matrix}$ 可用接入信道 $\begin{matrix} m, \end{matrix}$ 而 $\begin{matrix} l_{n, m} = 0 \end{matrix}$ 表示 $\begin{matrix} S U_{n} \end{matrix}$ 不能利用信道 $\begin{matrix} m 。 \end{matrix}$

信道效益: $\begin{matrix} B = {b_{n, m}}_{N \times M} \end{matrix}$ 是一个 $\begin{matrix} N \times M \end{matrix}$ 的矩阵, 其中 $\begin{matrix} b_{n, m} \end{matrix}$ 表示无竞争节点干扰的情况下, 节点 $\begin{matrix} S U_{n} \end{matrix}$ 在可用信道 $\begin{matrix} m \end{matrix}$ 上可获得的最大带宽或吞吐量.信道效益也被定义为用户在使用信道时的有效传输距离, 可表示为:

$\begin{matrix} b_{n, m} = d_{S} {(n, m)}^{2}, d_{\min} \leq d_{S} (n, m) \leq d_{\max} \end{matrix}$ (1)

每个节点可以通过改变传输功率来调整其传输范围, 从而避免对主用户活动造成干扰, 且有 $\begin{matrix} d_{S} \in [d_{\min}, d_{\max}] 。 \end{matrix}$ 因此, 可用如下邻居节点发现准则:

$\begin{matrix} \{\begin{matrix} l_{i, m} = l_{j, m} = 1 \\ d_{S} (iorj, m) > Dist (i, j) \\ Dist (i, j) < R_{SU} \end{matrix} \end{matrix}$ (2)

式中: $\begin{matrix} Dist (i, j) \end{matrix}$ 为节点i和节点j间的距离; $\begin{matrix} R_{SU} \end{matrix}$ 为认知节点发射范围.

邻居节点发现过程可以描述如下:

步骤1 节点 $\begin{matrix} S U_{i} \end{matrix}$ 通过本地信道感知获得可用信道集信息 $\begin{matrix} C_{i} = {m_{1}, m_{2}, \dots, m_{K_{i}}}, \end{matrix}$ 其中 $\begin{matrix} C_{i} \subset M 。 \end{matrix}$

步骤2 对于可用信道 $\begin{matrix} m_{i} \in C_{i} \end{matrix}$ 及任一节点 $\begin{matrix} S U_{j}, \end{matrix}$ 当满足准则式(2)后, $\begin{matrix} S U_{j} \end{matrix}$ 将其归入自身邻居节点集 $\begin{matrix} N_{j} 。 \end{matrix}$

步骤3 $\begin{matrix} S U_{i} \end{matrix}$ 选择 $\begin{matrix} C_{i} \end{matrix}$ 中的信道作为公共控制信道, 并与 $\begin{matrix} N_{j} \end{matrix}$ 中其他用户交换控制信息.

上述过程可通过图1来解释.首先, 每个认知节点通过感知获得可用控制信道集, 如 $\begin{matrix} C_{A} = {1, 2, 3, 4, 5, 6}, C_{B} = {1, 2, 3, 4, 5, 7}, C_{C} = {1, 2, 3, 4}, C_{D} = {1, 2, 3, 5, 7}, C_{E} = {2, 3, 5, 7}, C_{F} = {2, 4, 5, 6, 7} 。 \end{matrix}$ 在步骤2中, 认知节点间有共同的可用控制信道且在其覆盖范围内, 可被认为是邻居节点.在图1中, 用户A与用户B, C和D有共同的可用控制信道{2}.同时, 节点B, C和D到节点A的距离也在信道{2}覆盖范围内, 因此, 用户A认为B, C和D为邻居用户且有 $\begin{matrix} {B, C, D} \in N_{A} 。 \end{matrix}$ 本文假设邻居节点发现是一个松散时间同步过程, 以便所有邻居节点能够切换到相同的可用控制信道上.当发现所有1跳邻居节点后, SU同其邻居节点相互协作构成邻居节点组并开始公共控制信道分配过程.

3 公共控制信道分配算法

3.1 最大边二分团构造

当 $\begin{matrix} S U_{i} \end{matrix}$ 发现其1跳邻居节点及其可用控制信道集后, $\begin{matrix} S U_{i} \end{matrix}$ 根据其邻居节点集 $\begin{matrix} N_{i} \end{matrix}$ 和空闲信道集构成一个非定向二分图 $\begin{matrix} G_{i} (V_{i}, ε_{i}) 。 \end{matrix}$ 根据图论, 当顶点集 $\begin{matrix} V \end{matrix}$ 可表示为 $\begin{matrix} V = V_{1} ⋃ V_{2} \end{matrix}$ (其中 $\begin{matrix} V_{1} \end{matrix}$ 和 $\begin{matrix} V_{2} \end{matrix}$ 为两个不相交集)时, 连接图 $\begin{matrix} G (V, ε) \end{matrix}$ 被称为二部图, 且所有连接 $\begin{matrix} V_{1} \end{matrix}$ 和 $\begin{matrix} V_{2} \end{matrix}$ 的边都在集合 $\begin{matrix} ε \end{matrix}$ 中.在本文认知Ad Hoc网络中, $\begin{matrix} V_{1} \end{matrix}$ 表示 $\begin{matrix} S U_{i} \end{matrix}$ 本身及其邻居节点集 $\begin{matrix} N_{i}, \end{matrix}$ 即 $\begin{matrix} V_{1} = S U_{i} ⋃ N_{i}, \end{matrix}$ 而 $\begin{matrix} V_{2} \end{matrix}$ 表示 $\begin{matrix} V_{1} \end{matrix}$ 对应的可用信道集.当 $\begin{matrix} u \in V_{1} \end{matrix}$ 和 $\begin{matrix} v \in V_{2} \end{matrix}$ 时, 存在一条边 $\begin{matrix} (u, v) \in ε, 且 v \end{matrix}$ 在 $\begin{matrix} S U_{v} \end{matrix}$ 的可用信道列表中.根据图1所示网络模型, $\begin{matrix} S U_{A} \end{matrix}$ 所构成的二部图可表示为 $\begin{matrix} G_{A} (V_{A, 1} ⋃ V_{A, 2}, ε_{A}) 。 \end{matrix}$ 其中, $\begin{matrix} V_{A, 1} = {B, C, D, E, F} \end{matrix}$ 表示 $\begin{matrix} S U_{A} \end{matrix}$ 的1跳邻居节点集, $\begin{matrix} V_{A, 2} \end{matrix}$ 则对应于 $\begin{matrix} S U_{A} \end{matrix}$ 可用信道集合 $\begin{matrix} C_{A} = {1, 2, 3} 。 \end{matrix}$ 通过构造二部图 $\begin{matrix} G_{A} (V_{A, 1} ⋃ V_{A, 2}, ε_{A}), S U_{A} \end{matrix}$ 能够连接到 $\begin{matrix} V_{A, 2} \end{matrix}$ 中的所有顶点.

为了避免可用信道集列表与邻居节点集有较大的差异, 本文对文献[11]提出的最大边二分团的基本概念进行扩展, 以保证每个分组中节点数目最大化的同时满足可用控制信道数量最小化.当 $\begin{matrix} u' \in U_{1} 且 v' \in U_{2} 时, 如果在 u' \end{matrix}$ 和 $\begin{matrix} v' \end{matrix}$ 间存在着边, 即ε ={(u', v')|∀ u'∈ U₁ 且v'∈ U₂}, 则称二部图B(U₁⋃U₂, ε )为一个二分团.由于 $\begin{matrix} U_{1} \end{matrix}$ 和 $\begin{matrix} U_{2} \end{matrix}$ 完全决定了边集 $\begin{matrix} ε, \end{matrix}$ 因此在本文后续讨论中将其略去.对于节点 $\begin{matrix} S U_{i}, \end{matrix}$ 其二分团 $\begin{matrix} B_{i} (U_{i, 1}, U_{i, 2}) \end{matrix}$ 可通过原有的二部图 $\begin{matrix} G_{i} \end{matrix}$ 提取得到. $\begin{matrix} B_{i} (U_{i, 1}, U_{i, 2}) \end{matrix}$ 表示邻居用户集 $\begin{matrix} U_{i, 1} \end{matrix}$ 有共同的可用信道集 $\begin{matrix} U_{i, 2} \subseteq C_{i} 。 \end{matrix}$ 本文通过最大化二分团 $\begin{matrix} B_{i} \end{matrix}$ 边数量, 即最大化邻居节点集中用户数量|U_{i, 1} |与可用信道集中信道数量|U_{i, 2} |的乘积来取得二者的平衡.假设可用信道集数量的增加( $\begin{matrix} Δ |U_{i, 2}| > 0 \end{matrix}$ )将导致邻居用户集中用户数量减少( $\begin{matrix} Δ |U_{i, 1}| < 0 \end{matrix}$ ).根据最大化准则, 当满足下式时, 可从原二分团 $\begin{matrix} B_{i} \end{matrix}$ 中选出新的二分团 $\begin{matrix} B_{i}^{*} \end{matrix}$ :

$\begin{matrix} \begin{matrix} (|U_{i, 1}| + Δ |U_{i, 1}|) (|U_{i, 2}| + Δ |U_{i, 2}|) > |U_{i, 1}| |U_{i, 2}| \end{matrix} \end{matrix}$ (3)

约束条件为:

$\begin{matrix} |U_{i, 1}| + Δ |U_{i, 1}| \leq |C_{i}|, |U_{i, 2}| + Δ |U_{i, 2}| \leq |N_{i}| \end{matrix}$ (4)

不等式(3)可进一步写为:

$\begin{matrix} \frac{Δ |U_{i, 1}|}{|U_{i, 1}|} + \frac{Δ |U_{i, 2}|}{|U_{i, 2}|} > - \frac{Δ |U_{i, 1}| Δ |U_{i, 2}|}{|U_{i, 1}| |U_{i, 2}|} \end{matrix}$ (5)

式(5)表明二分团中顶点数量的分数变化要大于边数量的分数变化.最大边二分团在邻居节点分组过程中的作用可解释为:当邻居节点组中的节点都有相同的可用信道列表时, 最大边准则可保证组内节点数目最大化, 从而简化认知Ad Hoc网络拓扑结构.另一方面, 如果组内节点可用信道列表差异较大时, 最大边准则根据信道列表减少组内节点数量.通常情况下, 最大边二分团 $\begin{matrix} B_{i} \end{matrix}$ 包含原二部图 $\begin{matrix} G_{i} \end{matrix}$ 任何顶点的子集.本文最大边准则保证了节点 $\begin{matrix} S U_{i} \end{matrix}$ 及其邻居节点组对应的可用信道集都包含在二分团 $\begin{matrix} B_{i}^{*} \end{matrix}$ 中.

3.2 基于邻居节点分组的控制信道分配策略

最大二分图案计算流程如下:

1. Input: G_i=(V_{i, 1}∪ V_{i, 2}, ε _i) // SU_i的二分图

2.U_{i, 2}← V_{i, 2}

3. for j=1 to |V_{i, 1} | do

4. 寻找 SU_k∈ V_{i, 1}在V_{i, 1}中所有节点中最大化|U_{i, 2}⋂C_k|

5. if U_{i, 2}∩ C_k=Ø then

6. break

7. else

8. S_i[j]=k, 将k归入到已验证集合S_i中

9. V_{i, 1}← V_{i, 1}-SU_k, U_{i, 1}← U_{i, 1}∪ SU_k, U_{i, 2}← U_{i, 2}∩ C_k

10. P_i[j]=|U_{i, 1}|× |U_{i, 2}|计算二分团边

11. end if

12. end for

13. 寻找j^*=argmax_jP_i[j]

14. return $\begin{matrix} B_{i}^{*} \end{matrix}$ =( $\begin{matrix} U_{i, 1}^{*} \end{matrix}$ , $\begin{matrix} U_{i, 2}^{*} \end{matrix}$ ); $\begin{matrix} U_{i, 1}^{*} \end{matrix}$ ={S $\begin{matrix} U_{S_{i} [1]} \end{matrix}$ , , et al., S $\begin{matrix} U_{S_{i} [j^{*}]} \end{matrix}$ }; $\begin{matrix} U_{i, 2}^{*} \end{matrix}$ = $\begin{matrix} \cap_{k}^{=} \end{matrix} \begin{matrix} C_{S_{i} [k]} \end{matrix}$

步骤1 计算最大边二分团.对于本文较小的二部图, 通过利用贪婪算法(最大二分图案计算流程)来解决二部图中寻找最大边二分团这样一个NP完全问题.每次迭代都检验 $\begin{matrix} N_{i} \end{matrix}$ 中一个认知节点.向量 $\begin{matrix} S_{i} \end{matrix}$ 用来保存已检验过认知节点的索引值.首先, 节点 $\begin{matrix} S U_{i} \end{matrix}$ 通过本地感知获取可用信道集, 并通过式(2)确定确认其一跳邻居节点 $\begin{matrix} S U_{j} \in N_{i} 。 \end{matrix}$ 根据上述信息, $\begin{matrix} S U_{i} \end{matrix}$ 开始构造并计算"最佳"二分团. $\begin{matrix} U_{i, 1} \end{matrix}$ 为 $\begin{matrix} S U_{i} \end{matrix}$ 的一跳邻居节点集合, $\begin{matrix} U_{i, 2} \end{matrix}$ 为向量 $\begin{matrix} S_{i} \end{matrix}$ 中索引值对应的可用控制信道集.在每次迭代过程中要寻找节点 $\begin{matrix} S U_{k}, \end{matrix}$ 其可用控制信道列表 $\begin{matrix} C_{k} \end{matrix}$ 与 $\begin{matrix} U_{i, 2} \end{matrix}$ 有最高的重合度.然后将 $\begin{matrix} S U_{k} \end{matrix}$ 从 $\begin{matrix} U_{i, 1} \end{matrix}$ 中移除, 并将k移入 $\begin{matrix} S_{i} 。 \end{matrix}$ 重复此过程, 直到 $\begin{matrix} U_{i, 1} \end{matrix}$ 成为空集或者可用控制信道列表与剩余节点无交集.需要指出的是, 在每次迭代中 $\begin{matrix} B_{i} (U_{i, 1}, U_{i, 2}) \end{matrix}$ 均为二分团.每次构建完二分团后, 需要将计算出的边记录到向量 $\begin{matrix} P_{i} \end{matrix}$ 中并寻找具有最大边的二分团.一旦根据式(3)~(5)得到最优二分团 $\begin{matrix} B_{i}^{*} (U_{i, 1}^{*}, U_{i, 2}^{*}), S U_{i} \end{matrix}$ 将向其邻居节点集 $\begin{matrix} N_{i} \end{matrix}$ 广播这一信息.

步骤2 更新邻居节点组内节点信息.由于控制信道可用性变化以及节点的移动性, $\begin{matrix} S U_{i} \end{matrix}$ 将检查是否有新的二分团 $\begin{matrix} B_{j}^{k} (S U_{j} \in U_{j, 1}^{k} \end{matrix}$ )能够提供更好的分组算法, 即 $\begin{matrix} B_{j}^{k} > B_{i}^{k} 。 \end{matrix}$ 本文定义满足下列条件时, 有 $\begin{matrix} B_{j}^{k} > B_{i}^{k} : \end{matrix}$

$|U_{j, 1}| \times |U_{j, 2}| > |U_{i, 1}| \times |U_{i, 2}|$ (6)

或 $|U_{j, 1}| \times |U_{j, 2}| = |U_{i, 1}| \times |U_{i, 2}|,$

且 $|U_{j, 1}| > |U_{i, 1}|$ (7)

或 $|U_{j, 1}| = |U_{i, 1}|, |U_{j, 2}| = |U_{i, 2}|, 且 j > i$ (8)

首先, 本文比较两个二分团的边数目.如果两个二分团具有相同的边数, 则比较两个二分团邻居节点集中节点的数量.如果节点集中用户的数目也相同, 则选择具有最大索引值的认知节点构成的二分团.当节点SU_i 更新其二分团(即 $B_{i}^{k + 1} = B_{j}^{k}$ )后, SU_i 向其邻居节点广播对应的分组节点数目信息 $U_{j, 1}^{k + 1}$ 和 $U_{j, 2}^{k + 1}$ 可用控制信道信息 .

下面通过图1来说明步骤2.在图1中, 节点 $\begin{matrix} S U_{B}, S U_{C}, S U_{D}, S U_{E} \end{matrix}$ 和 $\begin{matrix} S U_{F} \end{matrix}$ 是用户 $\begin{matrix} S U_{A} \end{matrix}$ 满足准则(2)的1跳邻居节点.节点 $\begin{matrix} S U_{A} \end{matrix}$ 根据以下邻居用户信息执行二分团更新过程:① 节点 $\begin{matrix} S U_{B} \end{matrix}$ 的二分团 $\begin{matrix} B_{B}^{k} \end{matrix}$ 为 $\begin{matrix} U_{B, 1}^{k} = {S U_{A}, S U_{C}, S U_{D}}, U_{B, 2}^{k} = {1, 2, 3}; \end{matrix}$ ② 节点 $\begin{matrix} S U_{C} \end{matrix}$ 的二分团 $\begin{matrix} B_{C}^{k} \end{matrix}$ 为 $\begin{matrix} U_{C, 1}^{k} = {S U_{A}, S U_{B}, S U_{F}}, U_{C, 2}^{k} = {2, 4}; \end{matrix}$ ③ 节点 $\begin{matrix} S U_{D} \end{matrix}$ 的二分团 $\begin{matrix} B_{D}^{k} \end{matrix}$ 为 $\begin{matrix} U_{D, 1}^{k} = {S U_{A}, S U_{B}, S U_{E}}, U_{D, 2}^{k} = {2, 3, 5}; \end{matrix}$ ④ 节点 $\begin{matrix} S U_{E} \end{matrix}$ 的二分团 $\begin{matrix} B_{E}^{k} \end{matrix}$ 为 $\begin{matrix} U_{E, 1}^{k} = {S U_{A}, S U_{D}, S U_{F}}, U_{E, 2}^{k} = {2, 5}; \end{matrix}$ ⑤ 节点 $\begin{matrix} S U_{F} \end{matrix}$ 的二分团 $\begin{matrix} B_{F}^{k} \end{matrix}$ 为 $\begin{matrix} U_{F, 1}^{k} = {S U_{A}, S U_{C}, S U_{E}}, U_{F, 2}^{k} = {2, 3} 。 \end{matrix}$ 根据不等式(6)~(8), 将上述二分团进行排序, 有 $\begin{matrix} B_{A}^{k} > B_{B}^{k} > B_{D}^{k} > B_{C}^{k} > B_{E}^{k} > B_{F}^{k} 。 \end{matrix}$ 因此, 节点 $\begin{matrix} S U_{A} \end{matrix}$ 将二分团 $\begin{matrix} B_{A}^{k} \end{matrix}$ 更新为 $\begin{matrix} B_{A}^{k + 1} = B_{A}^{k}, \end{matrix}$ 因为 $\begin{matrix} B_{A}^{k} \end{matrix}$ 具有最大边数.类似的, 其他用户二分团更新为: $\begin{matrix} B_{B}^{k + 1} = B_{A}^{k}, B_{C}^{k + 1} = B_{A}^{k}, B_{D}^{k + 1} = B_{A}^{k}, B_{E}^{k + 1} = B_{A}^{k}, B_{F}^{k + 1} = B_{A}^{k} 。 \end{matrix}$

步骤3 邻居用户组内节点检验.在步骤3中, $\begin{matrix} S U_{i} \end{matrix}$ 检测其自身邻居节点集 $\begin{matrix} U_{i, 1}^{k + 1} 。 \end{matrix}$ 如果有 $\begin{matrix} S U_{i} \notin U_{j, 1}^{k + 1} \end{matrix}$ , 则 $\begin{matrix} S U_{i} \end{matrix}$ 在 $\begin{matrix} U_{i, 1}^{k + 1} \end{matrix}$ 中的将邻居节点 $\begin{matrix} S U_{j} \end{matrix}$ 从其二分团 $\begin{matrix} B_{i}^{k + 1} \end{matrix}$ 中移除.当没有其他节点被移除时, $\begin{matrix} S U_{i} \end{matrix}$ 经步骤2得到新的二分团 $\begin{matrix} B_{i}^{k + 2} 。 \end{matrix}$ 如果 $\begin{matrix} S U_{j} \end{matrix}$ 的邻居节点集中包含 $\begin{matrix} S U_{i}, \end{matrix}$ 则 $\begin{matrix} S U_{j} \end{matrix}$ 需要作为中继节点, 向 $\begin{matrix} S U_{i} \end{matrix}$ 传播其传输范围外组内其他节点的二分团信息.在图1中, 节点 $\begin{matrix} S U_{A} \end{matrix}$ 对其邻居节点集 $\begin{matrix} U_{A, 1}^{k + 1} \end{matrix}$ 进行检查.如果所有邻居节点都在二分团 $\begin{matrix} B_{A}^{k + 1} \end{matrix}$ 内, 则有 $\begin{matrix} U_{A, 1}^{k + 2} = U_{A, 1}^{k + 1} \end{matrix}$ 和 $\begin{matrix} U_{A, 2}^{k + 2} = U_{A, 2}^{k + 1} 。 \end{matrix}$ 同样, 节点 $\begin{matrix} S U_{B} \end{matrix}$ 对其邻居用户集 $\begin{matrix} U_{B, 1}^{k + 1} = {S U_{A}, S U_{B}, S U_{C}, S U_{D}, S U_{E}, S U_{F}} \end{matrix}$ 进行检查.因为 $\begin{matrix} S U_{E} \end{matrix}$ 和 $\begin{matrix} S U_{F} \end{matrix}$ 不是 $\begin{matrix} S U_{B} \end{matrix}$ 的邻居节点, 则 $\begin{matrix} S U_{B} \end{matrix}$ 需要 $\begin{matrix} S U_{A} \end{matrix}$ 作为中继节点获取二分团更新信息 $\begin{matrix} B_{E}^{k + 1} \end{matrix}$ 和 $\begin{matrix} B_{F}^{k + 1}, \end{matrix}$ 因为 $\begin{matrix} S U_{E} \end{matrix}$ 和 $\begin{matrix} S U_{F} \end{matrix}$ 均在 $\begin{matrix} S U_{A} \end{matrix}$ 的更新二分团 $\begin{matrix} B_{A}^{k} \end{matrix}$ 中.鉴于 $\begin{matrix} S U_{B} \end{matrix}$ 获知其也在 $\begin{matrix} S U_{E} \end{matrix}$ 和 $\begin{matrix} S U_{F} \end{matrix}$ 的二分团中, 因此有 $\begin{matrix} U_{B, 1}^{k + 2} = {S U_{A}, S U_{B}, S U_{C}, S U_{D}, S U_{E}, S U_{F}} 。 \end{matrix}$

步骤4 未分组节点.当有节点由于其移动性或主用户活动出现, 导致其同所有邻居节点连接失败时, 则该节点处于未分组状态, 根据步骤3该节点将被从当前二分团中移除.此时, 该用户开始重新执行邻居节点发现过程.在图1中, 假设 $\begin{matrix} S U_{E} \end{matrix}$ 被二分团 $\begin{matrix} B_{A}^{k + 1} \end{matrix}$ 移除, $\begin{matrix} S U_{E} \end{matrix}$ 需要加入到新的邻居节点分组中.然后, $\begin{matrix} S U_{E} \end{matrix}$ 将 $\begin{matrix} S U_{F}, S U_{A} \end{matrix}$ 和 $\begin{matrix} S U_{D} \end{matrix}$ 从其1跳邻居节点集中移除并同其他1跳邻居节点通过选定的公共控制信道交换控制信息, 以形成新的邻居节点分组.如果 $\begin{matrix} S U_{E} \end{matrix}$ 发射范围内没有其他节点, 则 $\begin{matrix} S U_{E} \end{matrix}$ 形成一个单节点分组.

3.3 最优控制信道选择

本文定义可用控制信道的效用函数为 $\begin{matrix} Q (\cdot), \end{matrix}$ 以表示其信道质量.当可用控制信道对邻居节点组中大多数节点来说信道质量最高时, 该信道即被选为该邻居节点组最优控制信道.本文给出两个参数反映可用控制信道质量, 分别为控制信息平均传输时延 $\begin{matrix} D \end{matrix}$ 和控制信息吞吐量 $\begin{matrix} T \end{matrix}$ .其中, 控制信息在可用控制信道 $\begin{matrix} m \end{matrix}$ 上的平均传输时延为:

$\begin{matrix} \begin{matrix} D_{m} = \overset{N - 1}{\sum_{i = 0}} \overset{N - 1}{\sum_{j = i + 1}} \min (h_{ij} \times d_{h op} + s_{ij} \times d_{switc h}) \end{matrix} \end{matrix}$ (9)

式中: $\begin{matrix} h_{ij} \end{matrix}$ 和 $\begin{matrix} s_{ij} \end{matrix}$ 分别为节点 $\begin{matrix} S U_{i} \end{matrix}$ 和 $\begin{matrix} S U_{j} \end{matrix}$ 间控制信息的多跳次数和信道切换次数; $\begin{matrix} d_{h op} \end{matrix}$ 为 $\begin{matrix} S U_{i} \end{matrix}$ 和 $\begin{matrix} S U_{j} \end{matrix}$ 间多跳时延; $\begin{matrix} d_{switc h} \end{matrix}$ 为信道切换时延.

从式(9)可以看出, 控制信息平均传输时延近似为控制信息在指定信道上传输的控制开销.

用户 $\begin{matrix} S U_{i} \end{matrix}$ 在可用控制信道 $\begin{matrix} m \end{matrix}$ 上的吞吐量定义为:

$\begin{matrix} T_{i, m} = \overset{|U_{i, 1}| - 1}{\sum_{i = 0}} \frac{\overset{|U_{i, 2}| - 1}{\sum_{m = 0}} a_{im} \cdot b_{im}}{\overset{|U_{i, 2}| - 1}{\sum_{m = 0}} a_{im}} \end{matrix}$ (10)

式中: $\begin{matrix} a_{im} = 1 \end{matrix}$ 表示 $\begin{matrix} S U_{i} \end{matrix}$ 选择可用信道m作为控制信道; $\begin{matrix} b_{im} \end{matrix}$ 为相应的信道增益.

控制信息平均传输时延和控制信道吞吐量是决定控制信道质量的两个重要参数.因此, 本文将这两个参数结合起来构成控制信道效用函数, 其表达式如下:

$\begin{matrix} \begin{matrix} Q (m) = \\ θ (1 - \frac{D}{(| U_{i, 1} | - 1) d_{h op} + (| U_{i, 2} | - 1) d_{switc h}}) + \\ (1 - θ) T / {| U_{i, 1} | \max {b_{ij}, \\ i \in {0, 1, \dots, | U_{i, 1} | - 1}; \\ j \in {0, 1, \dots, | U_{i, 2} | - 1}}} \end{matrix} \end{matrix}$ (11)

式中: $\begin{matrix} θ \in (0, 1) \end{matrix}$ 为相关因子.

从式(11)可以看出, 本文定义的信道效用函数 $\begin{matrix} Q (m) \end{matrix}$ 决定于归一化端到端时延的减少或者归一化输出增加.当每个邻居节点组对应的可用控制信道集给定时, 邻居用户将会选择具有最大效用函数值的信道作为当前用户组的公共控制信道以交换控制信息.

为了能在动态认知Ad Hoc网络环境中找到最优的信道效用函数 $\begin{matrix} Q (m), \end{matrix}$ 本文利用离散粒子群优化算法(DPSO)来解决这个问题^[12], 其表达式如下:

$\begin{matrix} \{\begin{matrix} v_{m, d} (k + 1) = \\ v_{m, d} (k) + c_{1} r_{1, d} [p_{m, d} (k) - x_{m, d} (k)] + \\ c_{2} r_{2, d} [p_{g, d} (k) - x_{m, d} (k)] \\ if (S (v_{m, d} (k + 1)) > γ) \\ t h en x_{m, d} (k + 1) \neq x_{m, d} (k) \\ else x_{m, d} (k + 1) \neq x_{m, d} (k) \end{matrix} \end{matrix}$ (12)

式中: $\begin{matrix} x_{m, d} \end{matrix}$ 为可用控制信道 $\begin{matrix} m \end{matrix}$ 的更新概率. $\begin{matrix} m \in 1, 2, \dots, |U_{i, 2}| \end{matrix}$ 和 $\begin{matrix} d \in 1, 2, \dots, D \end{matrix}$ 分别为可用控制信道集内粒子的索引值和搜索空间的维数; $\begin{matrix} p_{m, d} \end{matrix}$ 和 $\begin{matrix} p_{g, d} \end{matrix}$ 分别为可用控制信道集中的局部最优和全局最优效用值; 两个伪随机序列 $\begin{matrix} r_{1, d}, r_{2, d} ~ U (0, 1) \end{matrix}$ 为随机步长; $\begin{matrix} S (v) = 1 / (1 + e^{- v}) \end{matrix}$ 为控制信道粒子进化的概率; $\begin{matrix} γ \in (0, 1) \end{matrix}$ 为例子进化的门限集合.

基于DPSO的最优控制信道选择过程如下:

(1)初始化: $\begin{matrix} k = 0; x_{m, d} (0) \in (0, 1); v_{m, d} (0) \in [- V_{\max}, V_{\max}] \end{matrix}$ 且 $\begin{matrix} 1 \leq d \leq D 。 \end{matrix}$ 在本文中取 $\begin{matrix} D = 2 。 \end{matrix}$

(2)通过效用函数式(11)计算所有粒子值并得到初始优化效用值 $\begin{matrix} P_{m} (0) \end{matrix}$ 和 $\begin{matrix} P_{g} (0) 。 \end{matrix}$

(3)根据式(12)升级 $\begin{matrix} v_{m, d} (k) \end{matrix}$ 和 $\begin{matrix} x_{m, d} (k) 。 \end{matrix}$

(4)在第k次迭代中, 通过效用函数式(11)计算所有可用控制信道效用值, 对比当前可用控制信道效用值并更新 $\begin{matrix} P_{m} (k) \end{matrix}$ 和 $\begin{matrix} P_{g} (k) 。 \end{matrix}$

(5)如迭代收敛到某个最优值没有变化或迭代次数到达指定次数时, 算法停止, 输出最优信道索引值 $\begin{matrix} m^{*}, \end{matrix}$ 否则返回步骤(3)

3.4 控制信道的恢复

鉴于认知Ad Hoc网络的动态特性, 主用户活动很可能占用当前公共控制信道.因此, 有必要讨论当主用户活动出现时, 公共控制信道的恢复策略.一旦当前公共控制信道被主用户占用, 次要节点 $\begin{matrix} S U_{i} \end{matrix}$ 应感知到当前控制信道状态并立刻中断控制信息发送.然后, $\begin{matrix} S U_{i} \end{matrix}$ 在当前可用信道集合 $\begin{matrix} U_{i, 2}^{*} \end{matrix}$ 中移除被占用信道并根据式(11)重新选择最优控制信道作为当前用户集的公共控制信道.同时, 节点组内其他节点也应感知到控制信道的变化并切换到新选出的公共控制信道, 且邻居节点组内所有节点都应在新的公共控制信道覆盖范围内.此外, 根据图论, 邻居节点组内用户数量的 $\begin{matrix} U_{i, 1}^{*} \end{matrix}$ 与可用控制信道数量 $\begin{matrix} U_{i, 2}^{*} \end{matrix}$ 的变化也反映了上述恢复过程.当 $\begin{matrix} U_{i, 1}^{*} \end{matrix}$ 中有节点由于处于主用户活动区而不能够与任何可用控制信道建立链接时, 该用户将被从集合 $\begin{matrix} U_{i, 1}^{*} \end{matrix}$ 中去除, 同时其对应的可用信道列表也将被从可用控制信道集 $\begin{matrix} U_{i, 2}^{*} \end{matrix}$ 中去除.

4 系统仿真及性能分析

采用WINDOWS环境下的Matlab的8.1版本对所提出的基于邻居节点分组的公共控制信道分配算法的性能进行验证和分析.100个节点随机分布在 $\begin{matrix} 1000 m \times 1000 m \end{matrix}$ 的网络区域中, 可用信道数量为10, 认知节点功率覆盖半径为250 m.本节采用Random Way-point^[13]运动模型对认知无线电Ad Hoc网络的动态性进行描述, 停留时间为1 s.同时, 多跳时延和切换时延分别为200 ms和20 ms^[14].仿真时间持续600 s.对于不同场景取100次仿真结果的统计平均作为绘制仿真曲线的依据.

为了能够验证本文所提出的基于邻居节点分组的公共控制信道分配算法有效性, 与采用群智能的公共控制信道分配算法^[8]和采用空间变化策略的公共控制信道分配算法^[9]所得的结果进行比较.仿真中将主要关注采用不同的认知节点组数量, 可用控制信道数量和主用户数量对控制信道的归一化端对端时延, 吞吐量以及效用值等公共控制信道性能方面的影响情况.

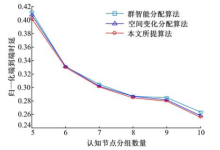
	Figure Option View Download New Window
	图2 不同认知节点分组下归一化端到端时延比较Fig.2 Normalized end-to-end delay versus the number of groups in CRAHNs

图2给出了节点分组数量对算法的性能的影响.从图2可以看出:当分组数量增加时, 相比于群智能控制信道分配算法和空间变化控制信道分配算法, 本文算法具有最小的归一化端到端时延.当分组数目较小时, 其所对应的可用控制信道集也较小, 容易受到主用户的影响, 因此3种算法平均端到端时延均相对较大.随着分组数量增多时, 可用控制信道也随之增多, 因此减少了主要用户活动对控制信道分配算法的影响, 因此取得了较小的归一化端到端时延.

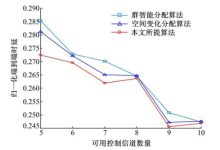
图3给出了不同算法间归一化端到端时延同可用控制信道数目的比较曲线.从图3可以看出:当可用控制信道数量增加时, 3种算法归一化端到端时延均减少.本文算法的性能要明显优于其他两种算法, 特别地, 本文算法的归一化端到端时延低于群智能分配算法达4%.这是因为本文所采取的最大边二分团策略使每个邻居用户分组都有对应的可用控制信道集, 保证了分组中认知用户能够选择出最优控制信道, 从而减少了归一化端到端时延; 而粒子群控制信道分配算法缺乏灵活的可用控制信道分集策略, 导致了较高的端到端时延.

	Figure Option View Download New Window
	图3 不同可用信道数量下归一化端到端时延比较Fig.3 Normalized end-to-end delay versus the number of available channels

	Figure Option View Download New Window
	图4 不同算法在主用户数量变化下性能比较Fig.4 Expected metric values versus the number of PUs in CRAHNs

图4给出了网络中主用户数量对算法性能的影响.从图4可以看出, 即使主用户增多导致认知节点通信受到限制, 信道质量下降的情况下, 本文算法也能保持一个相对较低的端到端时延和较高的控制信道效用函数值.相比之下, 空间变化分配算法由于依靠信道质量来进行控制信道分配, 当信道质量下降时对算法影响较为显著, 因此相比于本文算法有较大端到端时延和较低的效用函数值.而群智能分配算法由于对主用户数量变化较为敏感, 因此当前公共控制信道没有达到最大覆盖范围, 也未能使分组内认知用户数目最大化时, 无论在图4(a)还是在图4(b)中, 其端到端时延最大且效用函数值最低.

5 结束语

提出了一种基于邻居用户分组的公共控制信道分配算法.算法的主要思想是对认知Ad Hoc网络中的用户进行分组, 以简化网络拓扑复杂度.同时, 将邻居用户集合与其可用控制信道集的对应关系构造为最大边二分团问题, 从而保证了邻居用户内用户数目及对应的可用信道集之间较好的权衡.在所设定的仿真参数条件下, 对提出的算法进行了仿真分析和性能比较.仿真结果表明:提出的基于邻居用户分组的控制信道分配算法优于群智能控制信道分配算法和空间变化控制信道分配算法.同时, 该算法由于引入了DPSO优化算法寻找最优公共控制信道, 保证了认知Ad Hoc网络QoS, 具有一定的工程实用价值.

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Mitola III Joseph, Maguire Jr Gerald Q. Cognitive radio: making software radios more personal[J]. IEEE Personal Communications, 1999, 6(4): 13-18. [本文引用:1]
[2]	Akyildiz I F, Lee W Y, Vuran M C, et al. Next generation/dynamic spectrum access/cognitive radio wireless networks: a survey[J]. Computer Networks, 2006, 50(13): 2127-2159. [本文引用:1]
[3]	Akyildiz I F, Lee W Y, Chowdhury K R. CRAHNs: cognitive radio ad hoc networks[J]. Ad Hoc Networks , 2009, 7(5): 810-836. [本文引用:1]
[4]	阔永红, 杨江洪, 陈健. 认知AdHoc网络多小区资源分配方案[J]. 西安电子科技大学学报, 2013, 3(1): 79-87. Kuo Yong-hong, Yang Jiang-hong, Chen Jian. Resource allocation scheme for multi-cell cognitive radio Ad-Hoc networks[J]. Journal of Xidian University, 2013, 3(1): 79-87. [本文引用:1]
[5]	Brand on F L. A survey of common control channel design in cognitive radio networks[J]. Physical Communication, 2011, 4(1): 26-39. [本文引用:1]
[6]	Kim Mi-Ryeong, Yoo Sang-Jo. Distributed coordination protocol for common control channel Selection in multichannel Ad-Hoc cognitive radio networks[C]//IEEE International Conference on Wireless and Mobile Computing, Networking and Communications, Marrakech, 2009: 227-232. [本文引用:1]
[7]	Chowdhury K R, Akyldiz I F. OFDM-based common control channel design for cognitive radio ad hoc networks[J]. Mobile Computing, IEEE Transactions on, 2011, 10(2): 228-238. [本文引用:1]
[8]	Chen Tao, Zhang Hong-gang, Katz M D, et al. Swarm intelligence based dynamic control channel assignment in CogMesh[C]//IEEE International Conference on, Communications Workshops, Beijing, 2008: 123-128. [本文引用:2]
[9]	Hsiu Y, Su K F. Spatially varied control channel assignment in cognitive radio ad hoc networks[C]//Cognitive Radio Oriented Wireless Networks and Communications (CROWNCOM), 2011 Sixth International ICST Conference on, Osaka, 2011: 311-315. [本文引用:2]
[10]	Peng C Y, Zheng H T, ZHao B Y. Utilization and fairness in spectrum assignment for opportunistic spectrum access[J]. Mobile Networks and Applications, 2006, 11(4): 555-576. [本文引用:1]
[11]	Nussbaum D, Pu S Y, Sack J R, et al. Finding maximum edge bicliques in convex bipartite graphs[C]//16th Annual International Conference, COCOON 2010Nha Trang, Vietnam, 2010: 140-149. [本文引用:1]
[12]	Zheng S, Lou C, Yang X. Cooperative spectrum sensing using particle swarm optimization[J]. Electronics Letters, 2010, 46(22): 1525-1526. [本文引用:1]
[13]	Kumar S, Sharma S C, Suman B. Simulation based performance analysis of routing protocols using rand om waypoint mobility model immobile Ad hoc network[J]. Global Journal of Computer Science and Technology, 2011, 11(1): 17-22. [本文引用:1]
[14]	Cheng G, Liu W, Li Y, et al. Spectrum aware on-demand routing in cognitive radio networks[C]//2nd IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks, Dublin, 2007: 571-574. [本文引用:1]

1999

0.0

... 0 引言随着无线通信技术的快速发展,认知无线电(Cognitive radio,CR)作为一种有效缓解频谱资源短缺的技术手段在信息通信领域得到了广泛应用^[1,2] ...

2006

0.0

... 0 引言随着无线通信技术的快速发展,认知无线电(Cognitive radio,CR)作为一种有效缓解频谱资源短缺的技术手段在信息通信领域得到了广泛应用^[1,2] ...

2009

0.0

... 特别地,在认知Ad Hoc网络中,次要用户(SU,又被称为"认知节点")需要在缺少中心设施的情况下承担起频谱相关的认知功能^[3,4] ...

2013

0.0

. 2013, 3(1):79-87 DOI:doi:10.3969/j.issn.1001-2400.2014.03.012

Resource allocation scheme for multi-cell cognitive radio Ad-Hoc networks

认知AdHoc网络多小区资源分配方案

Kuo Yong-hong , Yang Jiang-hong , Chen Jian.

阔永红, 杨江洪, 陈健

在授权多小区频谱资源复用场景下,基于分级信道接入模型提出了一种认知Ad Hoc网络资源分配方案.授权小区将频谱资源进行区间复用,认知系统根据区域复用的不同划分可用频段,并在不同频段采取不同的接入方式;联合考虑链路传输需求及授权用户干扰保障设计传输效益因子,根据传输效益因子分配可用信道,运用拉格朗日对偶理论实现功率分配,并基于令牌环结构实现Ad Hoc链路局部信息交互.仿真表明,所提算法相对非复用认知场景系统容量可在相同指标下提升2%.

... 特别地,在认知Ad Hoc网络中,次要用户(SU,又被称为"认知节点")需要在缺少中心设施的情况下承担起频谱相关的认知功能^[3,4] ...

2011

0.0

... 目前,认知网络中公共控制信道分配算法一般分为专用公共控制信道分配和基于分组的公共控制信道分配两种^[5] ...

2009

0.0

... Kim等^[6]依据网络连接状态,提出了基于分簇的公共控制信道分配算法 ...

2011

0.0

... 文献^[7]给出了基于频谱机会的公共控制信道分配算法,其原理也是对网络内节点进行分簇 ...

2008

0.0

... 文献^[8]将公共控制信道选择过程归纳为群智能优化问题,算法依靠节点间的相互协作选择出性能最好的公共控制信道 ...

... 为了能够验证本文所提出的基于邻居节点分组的公共控制信道分配算法有效性,与采用群智能的公共控制信道分配算法^[8]和采用空间变化策略的公共控制信道分配算法^[9]所得的结果进行比较 ...

2011

0.0

... 而Hsiu等^[9]提出的空间变化控制信道分配算法(SVC)则为移动节点提供了一个可用控制信道集,网络中节点可根据"Fellow"信息的握手协议进行邻居的发现过程 ...

2006

0.0

... 对于控制信道来说,其特点可以描述为:信道可用性和信道增益,分别可定义为如下矩阵^[10]: ...

2010

0.0

2010

0.0

... 为了能在动态认知Ad Hoc网络环境中找到最优的信道效用函数 Q(m),本文利用离散粒子群优化算法(DPSO)来解决这个问题^[12],其表达式如下: ...

2011

0.0

... 本节采用Random Way-point^[13]运动模型对认知无线电Ad Hoc网络的动态性进行描述,停留时间为1 s ...

2007

0.0

... 同时,多跳时延和切换时延分别为200 ms和20 ms^[14] ...