自适应解码转发系统的增强型比例选择合并器

引用本文

赵大伟, 赵洪林, 马永奎, 贾敏. 自适应解码转发系统的增强型比例选择合并器.吉林大学学报:工学版, 2016, 46(2): 671-677
ZHAO Da-wei, ZHAO Hong-lin, MA Yong-kui, JIA Min. Enhanced scaled selection combiner for decode-and-forward systems with adaptive modulation. Journal of Jilin University Engineering and Technology Edition, 2016, 46(2): 671-677 复制到剪切板

Permissions

自适应解码转发系统的增强型比例选择合并器

赵大伟, 赵洪林, 马永奎, 贾敏

哈尔滨工业大学通信技术研究所,哈尔滨 150080

通讯作者:赵洪林(1969-),男,教授,博士生导师.研究方向:宽带抗干扰传输技术,认知无线电技术,协作通信技术.E-mail:hlzhao@hit.edu.cn

作者简介:赵大伟(1984-),男,博士研究生.研究方向:协作通信技术.E-mail:zhao_dawei@163.com

基金:国家自然科学基金项目(61201143); 中国空间技术研究院ITS基金项目(F-W-YY-2013-016); 中央高校基本科研业务费专项项目(HIT;IBRSEM.201309)

摘要

针对源和中继采用不同调制阶数以提高频谱效率的解码转发协作通信系统,提出了一种增强型的比例选择合并器(ESSC).在合并信号时,ESSC通过为源-中继-目的支路设定比例系数,降低了错误传播对协作性能的影响.推导了瑞利信道下采用ESSC的解码转发系统的误比特率公式,给出了最优比例系数的计算方法.理论分析和仿真表明,ESSC能够获得接近二阶的分集增益.在此基础上,提出了一种解码转发协作系统的功率分配方案,进一步提高了协作传输的可靠性.

关键词: 通信技术; 选择合并器; 解码转发; 协作分集; 自适应调制

中图分类号:TN925 文献标志码:A 文章编号:1671-5497(2016)02-0671-07

Enhanced scaled selection combiner for decode-and-forward systems with adaptive modulation

ZHAO Da-wei, ZHAO Hong-lin, MA Yong-kui, JIA Min

Communication Research Center, Harbin Institute of Technology, Harbin 150080, China

Abstract

An Enhanced Scaled Selection Combiner (ESSC) is proposed for Decode-and-Forward (DF) cooperative networks, where different modulation levels are adopted by the source and relay nodes to improve spectral efficiency. When the ESSC is used to combine signals from different diversity branches, the source-relay-destination branch is weighted by varying scale factors. As a result, the performance degradation caused by erroneous relaying in DF networks can be effectively mitigated by ESSC. Towards this end, the Bit-Error-Rate (BER) expression is derived for DF networks using ESSC under Rayleigh fading channels, and the scale factors of the ESSC are optimized to minimize the system BER. Theoretical analysis and simulation results demonstrate that a diversity order close to two can be achieved by ESSC. Furthermore, a power allocation scheme is proposed for DF networks based on ESSC, which can further improve the performance of cooperation.

Keyword: communication technology; selection combiner; decode-and-forward; cooperative diversity; adaptive modulation

Show Figures

0 引言

在协作通信中采用自适应调制技术, 能够有效地改善由半双工导致的协作通信频谱效率较低的问题.针对解码转发中继网络, 文献^[1-3]研究了自适应M-QAM的应用, 均设定中继采用和源相同的调制方式.而实际上由于解码转发中的中继能对信号进行数字处理, 并根据信道状态信息自主地选择与源不同的调制方式, 从而最大限度地提高频谱效率, 文献^[4-5]对其进行了研究, 但针对的是选择解码转发的情况.由于缺少固定解码转发情况下有效的不同调制阶数信号的合并器, 目前还无法对固定解码转发情况下源和中继分别自适应的方案进行研究.

由源-中继信道的影响而导致中继可能存在的错误传播, 是设计解码转发协作系统的合并器要考虑的关键问题.若采用选择解码转发, 即中继仅在解码正确时才转发, 能够消除错误传播, 此时直接采用经典合并方法^[6]即可保证满分集增益, 但选择转发相比固定转发减少了协作的机会.为了实现固定解码转发的满分集增益, 文献^[7]提出了协作最大比合并器, 考虑了源-中继信道对传输的影响, 但是需要大量的开销传输瞬时信道信息.文献^[8]提出了适用于M-PSK信号的比例选择合并器(Scaled selection combiner, SSC), 利用各支路的平均信噪比信息产生比例系数修正中继-目的的信噪比, 复杂度更低, 但未能充分利用中继-目的的瞬时信噪比信息.另一方面, 若中继采用和源不同阶数的调制方式, 则信噪比不能直接反映不同调制阶数信号传输的可靠性.为此, 文献^[9]提出了基于误比特率的选择合并器(BER-based selection combiner, BER-SC), 然而它仅针对选择解码转发的情况, 没有考虑源-中继信道对传输的影响.

本文提出一种适用于固定解码转发的增强型比例选择合并器(Enhanced scaled selection combiner, ESSC), 通过比例系数改变源-中继-目的支路信号合并时的权重, 能够有效地降低错误传播对协作性能的影响.与传统的SSC相比, ESSC不仅允许源和中继采用不同阶数的调制方式, 并且充分利用了中继-目的的瞬时信噪比信息来计算比例系数, 保证了解码转发协作的分集增益.在此基础上, 本文提出了一种功率分配方案, 以进一步提高解码转发协作系统的性能.

1 系统模型

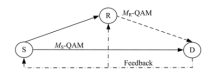
图1为采用自适应调制的解码转发协作系统模型, 包括源节点S, 目的节点D和中继节点R.所有节点仅装配单根天线并且工作于半双工模式.所有支路为符合独立非同分布的瑞利块衰落信道, 即信道衰落系数在块内保持不变.h_SD, h_SR和h_RD分别表示S-D, S-R和R-D支路的信道衰落系数, 满足h_SD~CN(0, σ _SD), h_SR~CN(0, σ _SR), h_RD~CN(0, σ _RD).其中, CN(0, σ )表示均值为零, 方差为σ 的循环对称复高斯随机变量, σ _SD=E{|h_SD|²}, σ _SR=E{|h_SR|²}, σ _RD=E{|h_RD|²}.n_D和n_R分别表示目的和中继的归一化复高斯白噪声, 满足n_D~CN(0, 1), n_R~CN(0, 1).由于信道符合瑞利衰落, 各瞬时信噪比符合如下指数分布:

$\begin{matrix} f (γ_{ij}) = \frac{1}{Γ_{ij}} e^{- \frac{γ_{ij}}{Γ_{ij}}}, γ_{ij} \geq 0 \end{matrix}$ (1)

式中:γ _ij , Γ _ij 分别为节点i到节点j支路的瞬时和平均信噪比, ij∈ {SD, SR, RD}.

	Figure Option View Download New Window
	图1 采用自适应调制的解码转发协作系统Fig.1 Decode and forward cooperative system with adaptive modulation

由于信号调制方式M-QAM具有较高的频谱效率, 因此本文采用基于格雷码的方形M-QAM.目前的研究大多采用的是快速自适应调制^[10], 即根据信道的"瞬时信噪比"来选择调制方式, 但当信道处于快衰落时, 就需要频繁地反馈信道状态信息, 在一定程度上损失了频谱效率.文献^[11]提出了慢速自适应调制, 即根据信道的"平均信噪比"来选择调制方式, 在许多情况下获得了接近快速自适应调制的性能.因此, 本文中源和中继节点根据目的节点反馈的平均信噪比信息选择不同阶数的M-QAM, 包含的比特数分别为k_S=log₂M_S, k_R=log₂M_R.

设共需发送 $\begin{matrix} K \end{matrix}$ 比特的信息, 源和中继在时间正交的信道上传输信号.第一阶段, 源节点以每比特平均E_S的功率广播L_S=K/k_S个符号x_S, 目的节点和中继收到的信号y_SD和y_SR可分别表示为:

$\begin{matrix} \begin{matrix} \{\begin{matrix} y_{SD} (l) = \sqrt[]{k_{S} E_{S}} h_{SD} x_{S} (l) + n_{D} (l) \\ y_{SR} (l) = \sqrt[]{k_{S} E_{S}} h_{SR} x_{S} (l) + n_{R} (l) \end{matrix} \\ l = 1, 2, \dots, L_{S} \end{matrix} \end{matrix}$ (2)

则每比特瞬时信噪比可表示为γ _SD=|h_SD|²E_S, γ _SR=|h_SR|²E_S, 每比特平均信噪比表示为Γ _SD=σ _SDE_S, Γ _SR=σ _SRE_S.第二阶段, 中继对收到的信号进行解码再以每比特平均E_R的功率转发L_R=K/k_R个符号x_R, 目的节点收到的信号y_RD可表示为:

$\begin{matrix} \begin{matrix} y_{RD} (l) = \sqrt[]{k_{R} E_{R}} h_{RD} x_{R} (l) + n_{D} (l) \\ l = 1, 2, \dots, L_{R} \end{matrix} \end{matrix}$ (3)

则每比特瞬时信噪比为γ _RD=|h_RD|²E_R, 平均信噪比为Γ _RD=σ _RDE_R.本文假设目的节点已知瞬时信噪比γ _SD, γ _RD以及各支路的平均信噪比Γ _SD, Γ _SR和Γ _RD.为方便讨论, 用Cn(n=1, 2, 3)表示目的节点所知的不同信道状态信息的组合, 其中C1={γ _SD, Γ _SR, γ _RD}, C2={Γ _SD, Γ _SR, γ _RD}, C3={Γ _SD, Γ _SR, Γ _RD}.

2 增强型比例选择合并器

目的节点在收到各支路信号后, 采用选择合并器对其进行合并, 设R-D支路的比例系数为β , 从而目的节点将根据如下规则选择某一路信号作为合并器的输出:

$\begin{matrix} y = \{\begin{matrix} y_{SD}, if γ_{SD} \geq β γ_{RD} \\ y_{RD}, if γ_{SD} < β γ_{RD} \end{matrix} \end{matrix}$ (4)

根据上述判决规则, 当γ _SD≥ β γ _RD时, 目的节点选中S-D支路作为输出; 当γ _SD< β γ _RD时, 目的节点选中S-R-D支路作为输出.从而比例选择合并器的瞬时误比特率可表示为:

$\begin{matrix} BE R_{ESSC} = \{\begin{matrix} BE R_{SD}, if γ_{SD} \geq β γ_{RD} \\ BE R_{SRD}, if γ_{SD} < β γ_{RD} \end{matrix} \end{matrix}$ (5)

传统的比例选择合并器(SSC)是根据信道状态信息C3={Γ _SD, Γ _SR, Γ _RD}求解R-D支路最优的比例系数β _opt, 即β _opt满足:

$\begin{matrix} β_{opt} = \underset{β}{argmin} BE R_{ESSC, C 3} \end{matrix}$ (6)

式中:BER_ESSC,_C₃=E[BER_ESSC]|γ _SD, γ _SR, γ _RD, 即BER_ESSC在γ _SD, γ _SR和γ _RD上的统计平均值.本文所提出的增强型比例选择合并器(ESSC)是根据信道状态信息C2={Γ _SD, Γ _SR, γ _RD}求解R-D支路最优的比例系数β _opt, 即β _opt满足:

$\begin{matrix} β_{opt} = \underset{β}{argmin} BE R_{ESSC, C 2} \end{matrix}$ (7)

式中:BER_ESSC,_C₂=E[BER_ESSC]|γ _SD, γ _SR, 即BER_ESSC在γ _SD和γ _SR上的统计平均值.ESSC能够充分利用中继-目的的瞬时信噪比信息γ _RD.

3 ESSC误比特率性能分析

若每比特瞬时和平均信噪比分别表示为γ 和Γ , 则基于格雷码的方形M-QAM信号的瞬时误比特率和瑞利信道下平均误比特率可分别近似为^[12]:

$\begin{matrix} P_{M} (γ) = c_{M} Q (\sqrt[]{2 d_{M}^{2} γ}), M \geq 4 \end{matrix}$ (8)

$\begin{matrix} {\bar{P}}_{M} (Γ) = \frac{1}{2} c_{M} (1 - \sqrt[]{\frac{d_{M}^{2} Γ}{1 + d_{M}^{2} Γ}}), M \geq 4 \end{matrix}$ (9)

式中:

$(x) = \frac{1}{\sqrt[]{2 π}} \int_{x}^{\infty} e^{- \frac{t^{2}}{2}} dt$ (10)

$c_{M} = 2 \frac{\sqrt[]{M} - 1}{\sqrt[]{M} lo g_{2} \sqrt[]{M}}$ (11)

$d_{M} = \sqrt[]{\frac{3 lo g_{2} M}{2 (M - 1)}}$ (12)

从而式(5)中S-D支路的瞬时误比特率可表示为:

$\begin{matrix} BE R_{SD} = P_{M_{S}} (γ_{SD}) \end{matrix}$ (13)

而S-R-D支路的瞬时误比特率可表示为^[7]:

$\begin{matrix} BE R_{SRD} = P_{M_{S}} (γ_{SR}) + (1 - 2 P_{M_{S}} (γ_{SR})) P_{M_{R}} (γ_{RD}) \end{matrix}$ (14)

对式(5)在γ _SR上求统计平均, 即可得到已知信道状态信息C1={γ _SD, Γ _SR, γ _RD}时误比特率, 即:

$\begin{matrix} BE R_{ESSC, C 1} = \{\begin{matrix} BE R_{SD, C 1}, if γ_{SD} \geq β γ_{RD} \\ BE R_{SRD, C 1}, if γ_{SD} < β γ_{RD} \end{matrix} \end{matrix}$ (15)

式中:

$BE R_{SD, C 1} = P_{M_{S}} (γ_{SD})$ (16)

$BE R_{SRD, C 1} = {\bar{P}}_{M_{S}} (Γ_{SR}) + (1 - 2 {\bar{P}}_{M_{S}} (Γ_{SR})) P_{M_{R}} (γ_{RD})$ (17)

对BER_ESSC,_C₁在γ _SD上求统计平均, 即可得到已知信道状态信息C2={Γ _SD, Γ _SR, γ _RD}时误比特率:

$\begin{matrix} \begin{matrix} BE R_{ESSC, C 2} = \int_{γ_{SD}}^{=} BE R_{SD, C 1} f (γ_{SD}) d γ_{SD} + \int_{γ_{SD}}^{=} BE R_{SRD, C 1} f (γ_{SD}) d γ_{SD} \end{matrix} \end{matrix}$ (18)

计算上述积分可得:

$\begin{matrix} \begin{matrix} BE R_{ESSC, C 2} = \\ c_{M_{S}} Q (\sqrt[]{2 d_{M_{S}}^{2} β γ_{RD}}) e^{- \frac{β γ_{RD}}{Γ_{SD}}} + BE R_{SRD, C 1} (1 - e^{- \frac{β γ_{RD}}{Γ_{SD}}}) - \\ c_{M_{S}} Q (\sqrt[]{2 (1 + d_{M_{S}}^{2} Γ_{SD}) \frac{β γ_{RD}}{Γ_{SD}}}) \sqrt[]{\frac{d_{M_{S}}^{2} Γ_{SD}}{1 + d_{M_{S}}^{2} Γ_{SD}}} \end{matrix} \end{matrix}$ (19)

对式(19)中系数 $\begin{matrix} β \end{matrix}$ 进行求导并设导数为零, 可解得最优比例系数β _opt满足:

$\begin{matrix} c_{M_{S}} Q (\sqrt[]{2 d_{M_{S}}^{2} β_{opt} γ_{RD}}) = BE R_{SRD, C 1} \end{matrix}$ (20)

由式(20)可以看出, β _optγ _RD也相当于S-R-D支路的等效信噪比.解式(20)可得:

$\begin{matrix} β_{opt} = \frac{1}{2 d_{M_{S}}^{2} γ_{RD}} {[Q^{- 1} (\frac{1}{c_{M_{S}}} BE R_{SRD, C 1})]}^{2} \end{matrix}$ (21)

式中: $\begin{matrix} Q^{- 1} (\cdot) \end{matrix}$ 为式(10)表示的Q函数的反函数.

将BER_SRD,_C₁代入式(21)可得最优比例系数为:

$\begin{matrix} \begin{matrix} β_{opt} = \frac{1}{2 d_{M_{S}}^{2} γ_{RD}} \times \\ {\{Q^{- 1} [\frac{{\bar{P}}_{M_{S}} (Γ_{SR}) + (1 - 2 {\bar{P}}_{M_{S}} (Γ_{SR})) P_{M_{R}} (γ_{RD})}{c_{M_{S}}}]\}}^{2} \end{matrix} \end{matrix}$ (22)

由式(22)可知, 随着Γ _SR的提高, 源-中继支路的可靠性增大, β _opt增大.当调制方式{M_S, M_R}和γ _RD已知时, 随着Γ _SR→ ∞ , 最优比例系数β _opt趋近于最大值:

$\begin{matrix} β_{opt, \max} = \frac{1}{2 d_{M_{S}}^{2} γ_{RD}} {[Q^{- 1} (\frac{P_{M_{R}} (γ_{RD})}{c_{M_{S}}})]}^{2} \end{matrix}$ (23)

当M_S=M_R时, β _{opt, max}=1.将β _opt代入式(19)可得:

$\begin{matrix} \begin{matrix} BE R_{ESSC, C 2} = BE R_{SRD, C 1} - \\ c_{M_{S}} Q (\sqrt[]{2 (1 + d_{M_{S}}^{2} Γ_{SD}) \frac{β_{opt} γ_{RD}}{Γ_{SD}}}) \sqrt[]{\frac{d_{M_{S}}^{2} Γ_{SD}}{1 + d_{M_{S}}^{2} Γ_{SD}}} \end{matrix} \end{matrix}$ (24)

对BER_ESSC,_C₂在γ _RD上求统计平均, 即可得到已知信道状态信息C3={Γ _SD, Γ _SR, Γ _RD}时误比特率:

$\begin{matrix} BE R_{ESSC, C 3} = \int_{γ_{RD}}^{=} BE R_{ESSC, C 2} f (γ_{RD}) d γ_{RD} \end{matrix}$ (25)

式(25)积分太复杂, 不存在显式解, 可采用数值积分求解.

4 ESSC分集阶数分析

通过推导误比特率BER_ESSC,_C₃的上界, 可以分析增强型比例选择合并器的分集阶数, 下面首先求BER_ESSC,_C₂的近似值.根据 $\begin{matrix} Q \end{matrix}$ 函数的常用近似式:

$\begin{matrix} Q (x) \approx \frac{\exp (- \frac{x^{2}}{2})}{x \sqrt[]{2 π}} \end{matrix}$ (26)

可得式(24)中第二项系数(记为 $\begin{matrix} δ \end{matrix}$ )为:

$\begin{matrix} \begin{matrix} δ = c_{M_{S}} Q (\sqrt[]{2 (1 + d_{M_{S}}^{2} Γ_{SD}) \frac{β_{opt} γ_{RD}}{Γ_{SD}}}) \approx \\ c_{M_{S}} \frac{\exp (- \frac{2 d_{M_{S}}^{2} β_{opt} γ_{RD}}{2})}{\sqrt[]{2 d_{M_{S}}^{2} β_{opt} γ_{RD}} \sqrt[]{2 π}} \sqrt[]{\frac{d_{M_{S}}^{2} Γ_{SD}}{1 + d_{M_{S}}^{2} Γ_{SD}}} \exp (- \frac{β_{opt} γ_{RD}}{Γ_{SD}}) \end{matrix} \end{matrix}$ (27)

再次利用式(20)(26)可得:

$\begin{matrix} \begin{matrix} δ \approx P_{M_{S}} (β_{opt} γ_{RD}) \sqrt[]{\frac{d_{M_{S}}^{2} Γ_{SD}}{1 + d_{M_{S}}^{2} Γ_{SD}}} \exp (- \frac{β_{opt} γ_{RD}}{Γ_{SD}}) = \\ BE R_{SRD, C 1} \sqrt[]{\frac{d_{M_{S}}^{2} Γ_{SD}}{1 + d_{M_{S}}^{2} Γ_{SD}}} \exp (- \frac{β_{opt} γ_{RD}}{Γ_{SD}}) \end{matrix} \end{matrix}$ (28)

将式(28)代入式(24)可得:

$\begin{matrix} \begin{matrix} BE R_{ESSC, C 2} \approx \\ BE R_{SRD, C 1} (1 - \frac{d_{M_{S}}^{2} Γ_{SD}}{1 + d_{M_{S}}^{2} Γ_{SD}} \exp (- \frac{β_{opt} γ_{RD}}{Γ_{SD}})) \end{matrix} \end{matrix}$ (29)

由于 $\begin{matrix} Q^{- 1} (\cdot) \end{matrix}$ 是单调递减函数, 根据式(22)取系数 $\begin{matrix} β : \end{matrix}$

$\begin{matrix} β = \frac{1}{2 d_{M_{S}}^{2} γ_{RD}} {[Q^{- 1} (\frac{1}{c_{M_{S}}} {\bar{P}}_{M_{S}} (Γ_{SR}))]}^{2} > β_{opt} \end{matrix}$ (30)

将以上比例系数代入式(29), 并在γ _RD上求统计平均可得BER_ESSC,_C₃的上界为:

$BE R_{ESSC, C 3}^{Bound} = BE R_{SRD, C 3} (1 - η \sqrt[]{\frac{d_{M_{S}}^{2} Γ_{SD}}{1 + d_{M_{S}}^{2} Γ_{SD}}})$ (31)

式中:

$BE R_{SRD, C 3} = {\bar{P}}_{M_{S}} (Γ_{SR}) + (1 - 2 {\bar{P}}_{M_{S}} (Γ_{SR})) {\bar{P}}_{M_{R}} (Γ_{RD})$

$η = \sqrt[]{\frac{d_{M_{S}}^{2} Γ_{SD}}{1 + d_{M_{S}}^{2} Γ_{SD}}} \times \exp {(- \frac{1}{2 d_{M_{S}}^{2} Γ_{SD}} [Q^{- 1} (\frac{1}{c_{M_{S}}} {\bar{P}}_{M_{S}} (Γ_{SR}))])}^{2}$

通过数值计算可以证明当信噪比Γ _SD, Γ _SR→ ∞ 时, η 接近1.例如, 对于M_S=4, 当Γ _SD=Γ _SR=25 dB时, η ≈ 0.983; 当Γ _SD=Γ _SR=30 dB时, η ≈ 0.993.而当Γ → ∞ 时, 利用泰勒展开式, 式(9)可近似为^[9]:

$\begin{matrix} {\bar{P}}_{M} (Γ) = \frac{1}{2} c_{M} (1 - \sqrt[]{\frac{d_{M}^{2} Γ}{1 + d_{M}^{2} Γ}}) \approx \frac{c_{M}}{4 d_{M}^{2} Γ} \end{matrix}$ (32)

当η =1时, 利用式(33)可得BER_ESSC,_C₃的上界:

$\begin{matrix} \begin{matrix} BE R_{ESSC, C 3}^{Bound} \approx \\ (\frac{c_{M_{S}}}{4 d_{M_{S}}^{2} Γ_{SR}} + (1 - \frac{c_{M_{S}}}{2 d_{M_{S}}^{2} Γ_{SR}}) \frac{c_{M_{R}}}{4 d_{M_{R}}^{2} Γ_{RD}}) \frac{1}{4 d_{M_{S}}^{2} Γ_{SD}} \end{matrix} \end{matrix}$ (33)

可见, 当信噪比Γ _SD, Γ _SR和Γ _RD→ ∞ 而η → 1时, 增强型比例选择合并器获得了接近二阶的分集增益.

5 功率分配方案

基于所提出的增强型比例选择合并器, 目的节点可以根据各支路的平均信噪比信息对源和中继节点的总功率进行分配, 以进一步提高系统的性能.设当未考虑功率分配时, 源和中继的每比特平均功率均为E_b, 即E_S=E_R=E_b.设α Î (0, 2]为源节点的功率分配系数, 则E_S=α E_b, E_R=(2-α )E_b.从而将式(22)(24)(25)中的平均信噪比直接替换为α Γ _SD, α Γ _SR和(2-α )Γ _RD, 求解如下优化问题:

$\begin{matrix} α_{opt} = \underset{α_{S} \in (0, 2]}{argmin} BE R_{ESSC, C 3} \end{matrix}$ (34)

即可解得最优的功率分配系数.由于BER_ESSC,_C₃不存在显式解, 上述一维优化问题可采用黄金分割或抛物线插值法^[13]求解.

6 仿真与分析

图2比较了当中继-目的的瞬时信噪比γ _RD变化时, 增强型比例选择合并器(ESSC)与传统的比例选择合并器(SSC)的性能, 其中ESSC的最优比例系数及相应的误比特率BER_ESSC,_C₂分别由式(22)和式(24)计算.设源和中继采用的调制方式{M_S, M_R}={4, 4}, 各支路平均信噪比Γ _SD=Γ _SR=Γ _RD=15 dB.由图中可以看出, ESSC更充分地利用了中继-目的的瞬时信噪比信息, 随着γ _RD的提高, β _opt降低, 误比特率随之降低; 而SSC只能根据各支路的平均信噪比产生固定的比例系数, 性能较差.

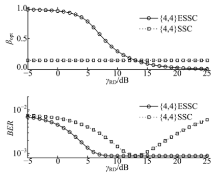	Figure Option View Download New Window
	图2 ESSC和SSC的最优比例系数及误比特率对比Fig.2 Comparison of ESSC and SSC in terms of the optimal scale factors and the corresponding BERs

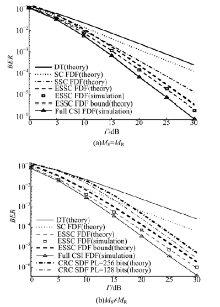
图3给出了{M_S, M_R}={4, 4}, {4, 16}时, 采用ESSC的固定解码转发与其他几种传输方案的误比特率性能比较, 其中图3(a)设Γ _SD=Γ _SR=Γ _RD=Γ , 而图3(b)设Γ _SD=Γ 且Γ _SR=Γ _RD=Γ +5 dB.ESSC误比特率的精确值BER_ESSC,_C₃可由式(25)计算, 上界由式(31)计算.采用以下几种传输方案作为比较对象:

(1)直接传输(DT), 即中继不参与协作, 仅源节点传输信息(分集阶数为一).

(2)采用传统选择合并器^[6]的固定解码转发(SC FDF)(分集阶数为一).

(3)采用基于全信道状态信息的选择合并器的固定解码转发(Full CSI FDF), 即假设目的节点已知瞬时信噪比{γ _SD, γ _SR, γ _RD}, 则可直接比较瞬时误比特率BER_SD(式(13))和BER_SRD(式(14))来选择最优支路(传输开销最大, 分集阶数为二).

(4)当源和中继的调制阶数相同时, 考虑了采用传统比例选择合并器(SSC)^[8]的固定解码转发(SSC FDF).

(5)当源和中继的调制阶数不同时, 考虑了采用BER-SC的基于循环冗余校验码的选择解码转发(CRC SDF)^[9].由于CRC SDF的性能与信息的块长度(PL)有关, 考虑了PL为128 bits和256 bits两种情况.

	Figure Option View Download New Window
	图3 几种传输方案的性能比较Fig.3 Performance comparison of several transmission schemes with

如图3所示, 受中继可能存在的错误传播的影响, 当在固定解码转发中采用传统SC时, 其分集阶数与直接传输相同, 均为1(即BER曲线的斜率可由-Δ logBER/Δ logΓ 计算), 无法获得分集增益.ESSC的仿真值与式(25)计算的理论值吻合, 而式(31)则提供了误比特率的一个紧的上界.ESSC FDF的性能远好于SSC FDF和CRC SDF, 其分集阶数与Full CSI SDF接近, 获得了接近二阶的分集增益.例如, 图3(a)中ESSC误比特率的理论值在25 dB时为1.85× 10^-5, 在30 dB时为2.11× 10^-6, 即分集阶数为:

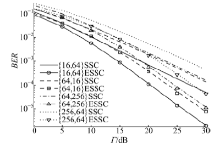
$\begin{matrix} - \frac{10 \log (2.11 \times 10^{- 6}) - 10 \log (1.82 \times 10^{- 5})}{30 - 25} \approx 1.87 。 \end{matrix}$

图4对几种高阶{M_S, M_R}下SSC和ESSC的性能进行了比较.设各支路平均信噪比满足Γ _SD=Γ 且Γ _SR=Γ _RD=Γ +10 dB.其中线条表示BER的理论值,

	Figure Option View Download New Window
	图4 高阶调制方式下SSC和ESSC的性能比较Fig.4 Performance comparison of SSC and ESSC with high modulation levels

而标号表示BER的仿真值.如图所示, 在所设定的信道条件下, ESSC的性能远好于SSC; 而对于频谱效率相同的{M_S, M_R}, M_S< M_R时系统的误比特率更低.

图5分析了源-中继支路平均信噪比Γ _SR变化时, ESSC的误比特率性能.设源和中继的调制阶数为{M_S, M_R}={4, 4}.设Γ _SD=Γ _RD=Γ , 而Γ _SR分别比Γ 高0, 10, 15 dB.如图5所示, 随着Γ _SR相比Γ _SD, Γ _RD更高, ESSC的性能以比SSC更快的速率接近最优的基于Full CSI的选择合并器.当Γ _SR=Γ +15 dB时, ESSC与基于Full CSI的选择合并器性能基本相同.另外可以算出, 当Γ =30 dB时, Γ _SR比Γ 高0, 10, 15 dB时, ESSC的分集阶数分别为1.87, 1.95和1.98.

	Figure Option View Download New Window
	图5 源-中继信噪比不同时ESSC的误比特率性能Fig.5 BER performance of ESSC with varying Γ _SR

	Figure Option View Download New Window
	图6 不同信噪比情况下功率分配方案的性能Fig.6 Performance of the proposed power allocation scheme with different SNRs

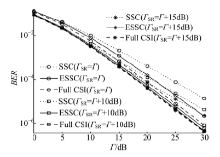
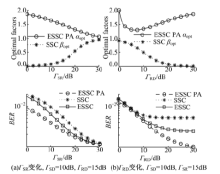
图6分析了当Γ _SR或Γ _RD变化时基于ESSC的功率分配方案(ESSC PA)的性能, 并与不采用功率分配方案时ESSC和SSC的性能进行了比较.设{M_S, M_R}={4, 4}, 图中α _opt由求解式(34)获得, 而已知C3={Γ _SD, Γ _SR, Γ _RD}时SSC的最优比例系数β _opt根据式(6)求得.如图6(a)所示, 当Γ _SR增大时, 源-中继支路可靠性增大, 功率分配系数α _opt和SSC的β _opt均趋近于1; 而由式(23)可知, 此时ESSC的β _opt也趋近于1.因此, 随着Γ _SR增大, 3种方案性能接近.由图6(b)可以看出:当Γ _RD增大时, ESSC PA的性能逐渐好于其他两种方案.而α _opt在Γ _RD=7 dB出现的驻点是由于当Γ _RD增大到一定程度, 系统性能的瓶颈不再是中继-目的支路的可靠性, 此时增大源节点的发射功率(即增大源-中继和源-目的支路的可靠性)可以获得更好的性能.

7 结束语

为了改善由错误传播导致的解码转发协作性能的下降, 提出了一种增强型的比例选择合并器, 在合并信号时通过计算比例系数调整各支路的权重, 保证了协作的分集增益.与传统的SSC相比, ESSC充分利用了中继-目的的瞬时信噪比信息, 并且允许源和中继采用不同的调制阶数以提高系统的频谱效率.理论分析和仿真表明, ESSC能够获得接近二阶的分集增益.在此基础上, 提出了一种解码转发协作系统的功率分配方案, 进一步提高了系统的性能.本文主要对单中继情况下ESSC的比例系数进行了优化, 多中继情况下各支路比例系数的优化问题仍有待进一步研究.

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Kalansuriya P, Soysa M, Tellambura C. Performance of a cooperative network using rate adaptation and cooperative combining[C]//2010 IEEE Wireless Communications and Networking Conference. Sydney, Australia: IEEE, 2010: 1-6. [本文引用:1]
[2]	Ikki S S, Amin O, Uysal M. Performance analysis of adaptive L-QAM for opportunistic decode-and -forward relaying[C]//2010 IEEE 71st Vehicular Technology Conference. Taiwan, China: IEEE, 2010: 1-5. [本文引用:1]
[3]	Altubaishi E S, Shen Xue-min. Performance analysis of decode-and -forward relaying schemes with adaptive quadrature amplitude modulation (QAM)[J]. IET Communications, 2012, 6(6): 649-658. [本文引用:1]
[4]	Ma Y, Tafazolli R, Zhang Y Y, et al. Adaptive modulation for opportunistic decode-and -forward relaying[J]. IEEE Transactions on Wireless Communications, 2011, 10(7): 2017-2022. [本文引用:1]
[5]	Song Wei, Ju Pei-jian, Zhou Di-zhi. Performance of cooperative relaying with adaptive modulation and selection combining[C]//2013 International Conference on Computing, Networking and Communications. San Diego, USA: IEEE, 2013: 1005-1009. [本文引用:1]
[6]	Brennan D G. Linear diversity combining techniques[J]. Proceedings of the IEEE, 2003, 91(2): 331-356. [本文引用:2]
[7]	Wang Tai-ran, Cano A, Giannakis G B, et al. High-performance cooperative demodulation with decode-and -forward relays[J]. IEEE Transactions on Communications, 2007, 55(7): 1427-1438. [本文引用:2]
[8]	Selvaraj M D, Mallik R K. Scaled selection combining based cooperative diversity system with decode and forward relaying[J]. IEEE Transactions on Vehicular Technology, 2010, 59(9): 4388-4399. [本文引用:2]
[9]	Sediq A B, Yanikomeroglu H. Performance analysis of selection combining of signals with different modulation levels in cooperative communications[J]. IEEE Transactions on Vehicular Technology, 2011, 60(4): 1880-1887. [本文引用:3]
[10]	Goldsmith A J, Chua S G. Variable-rate variable-power MQAM for fading channels[J]. IEEE Transactions on Communications, 1997, 45(10): 1218-1230. [本文引用:1]
[11]	Conti A, Win M Z, Chiani M. Slow adaptive M-QAM with diversity in fast fading and shadowing[J]. IEEE Transactions on Communications, 2007, 55(5): 895-905. [本文引用:1]
[12]	Cho K, Yoon D. On the general BER expression of one-and two-dimensional amplitude modulations[J]. IEEE Transactions on Communications, 2002, 50(7): 1074-1080. [本文引用:1]
[13]	Brent R P. Algorithms for Minimization without Derivatives[M]. Englewood Cliffs, New Jersey: Prentice-Hall, 1973: 61-80. [本文引用:1]

2010

0.0

2010

0.0

2012

0.0

2011

0.0

2013

0.0

2003

0.0

... 若采用选择解码转发,即中继仅在解码正确时才转发,能够消除错误传播,此时直接采用经典合并方法^[6]即可保证满分集增益,但选择转发相比固定转发减少了协作的机会 ...

... (2)采用传统选择合并器^[6]的固定解码转发(SC FDF)(分集阶数为一) ...

2007

0.0

... 为了实现固定解码转发的满分集增益,文献^[7]提出了协作最大比合并器,考虑了源-中继信道对传输的影响,但是需要大量的开销传输瞬时信道信息 ...

... 而S-R-D支路的瞬时误比特率可表示为^[7]: ...

2010

0.0

... 文献^[8]提出了适用于M-PSK信号的比例选择合并器(Scaled selection combiner,SSC),利用各支路的平均信噪比信息产生比例系数修正中继-目的的信噪比,复杂度更低,但未能充分利用中继-目的的瞬时信噪比信息 ...

... (4)当源和中继的调制阶数相同时,考虑了采用传统比例选择合并器(SSC)^[8]的固定解码转发(SSC FDF) ...

2011

0.0

... 为此,文献^[9]提出了基于误比特率的选择合并器(BER-based selection combiner,BER-SC),然而它仅针对选择解码转发的情况,没有考虑源-中继信道对传输的影响 ...

... 时,利用泰勒展开式,式(9)可近似为^[9]: ...

... (5)当源和中继的调制阶数不同时,考虑了采用BER-SC的基于循环冗余校验码的选择解码转发(CRC SDF)^[9] ...

1997

0.0

... 目前的研究大多采用的是快速自适应调制^[10],即根据信道的"瞬时信噪比"来选择调制方式,但当信道处于快衰落时,就需要频繁地反馈信道状态信息,在一定程度上损失了频谱效率 ...

2007

0.0

... 文献^[11]提出了慢速自适应调制,即根据信道的"平均信噪比"来选择调制方式,在许多情况下获得了接近快速自适应调制的性能 ...

2002

0.0

... ,则基于格雷码的方形M-QAM信号的瞬时误比特率和瑞利信道下平均误比特率可分别近似为^[12]: ...

1973

0.0

... 由于BER_ESSC,_C₃不存在显式解,上述一维优化问题可采用黄金分割或抛物线插值法^[13]求解 ...