用于高动态噪声背景的归一化谱协作感知算法

引用本文

齐佩汉, 李赞, 司江勃, 高锐, 孙浩. 用于高动态噪声背景的归一化谱协作感知算法.吉林大学学报:工学版, 2016, 46(2): 678-684
QI Pei-han, LI Zan, SI Jiang-bo, GAO Rui, SUN Hao. Normalized spectrum based cooperative spectrum sensing algorithm for high dynamic noise background. Journal of Jilin University Engineering and Technology Edition, 2016, 46(2): 678-684 复制到剪切板

Permissions

用于高动态噪声背景的归一化谱协作感知算法

齐佩汉¹, 李赞¹, 司江勃¹, 高锐¹, 孙浩²

1.西安电子科技大学综合业务网国家重点实验室,西安 710071

2.国家无线电监测中心,北京 100037

通讯作者:李赞(1975-),女,教授,博士生导师.研究方向:隐蔽通信与信号检测.E-mail:zanli@xidian.edu.cn

作者简介:齐佩汉(1986-),男,讲师,博士.研究方向:频谱感知与压缩感知.E-mail:phqi@xidian.edu.cn

基金:国家自然科学基金项目(61501356,61301179)

摘要

针对背景噪声电平在多维域上的高动态变化严重影响协作感知算法的性能这一问题,本文提出基于归一化谱的协作感知算法.该算法利用认知用户归一化谱的等增益平均作为检验统计量,依据傅里叶变换的渐进正态性和相互独立性计算功率谱的统计特性,推导出算法虚警概率和判决门限的闭式表达式.仿真表明:归一化谱协作感知算法对噪声电平的动态变化具有鲁棒性;相对于基于能量的大数判决硬协作感知算法和等增益软协作感知算法,本文算法具有更广泛的适用性.

关键词: 通信技术; 协作频谱感知; 功率谱; 背景噪声电平; 平坦慢衰落

中图分类号:TN911.23 文献标志码:A 文章编号:1671-5497(2016)02-0678-07

Normalized spectrum based cooperative spectrum sensing algorithm for high dynamic noise background

QI Pei-han¹, LI Zan¹, SI Jiang-bo¹, GAO Rui¹, SUN Hao²

1.State Key Lab of Integrated Services Networks, Xidian University, Xi'an 710071, China

2.State Radio Monitoring Center,Beijing 100037,China

Abstract

As high dynamic ranges of background noise level in time, spatial and frequency domain seriously affect the performance of cooperative spectrum sensing algorithms, a novel cooperative spectrum sensing algorithm based on Normalized Spectrum (NS) is proposed. The local NS is uploaded to the fusion center, and the equal gain average of NS is treated as detection statistics to detect signals in the fusion center. It makes use of asymptotic normality and independence of Fourier transform to get the stochastic properties of Power Spectral Density (PSD). The mathematical expression for probabilities of false alarm is derived. In accordance with the Neyman-Pearson criteria, the closed-form expression of decision threshold is calculated. The simulation results show that the NS algorithm is robust to dynamic ranges of background noise level. With respect to Majority Voting Hard Decision (MVHD) cooperative spectrum sensing algorithm and Equal Gain Soft Decision (EGSD) cooperative spectrum sensing algorithm based on energy, the NS algorithm has better performance and broader applications.

Keyword: communication technology; cooperative spectrum sensing; power spectral density; background noise level; flat slow fading

Show Figures

0 引言

认知无线电^[1](Cognitive radio)被认为是下一代蜂窝通信中解决频谱资源稀缺的重要途径之一.它包含了频谱感知, 动态频谱分配和无线频谱管理三大关键技术, 频谱感知是认知无线电动态闭环反馈系统运转的先决条件, 及时精准的频谱感知结果可为系统提供有益的反馈信息, 为有序动态的频谱分配和合理的频谱监管提供保障.协作频谱感知算法^[2]融合不同位置节点提供的感知信息, 获得分集处理的增益, 可以有效克服多径衰落, 阴影效应和隐藏终端等问题对单点频谱感知算法性能的影响.

感知节点背景噪声是由地面噪声, 大气噪声, 降雨噪声, 人为噪声, 干扰噪声以及频谱感知接收机热噪声等多种噪声形式复合而成^[3], 背景噪声电平往往在多维域上存在高动态变化的特点.固定测试频率和测试时间, 在不同测试地点得出的噪声电平最大值与最小值之间差值可达10 dBm以上^[4]; 固定测试频率和测试地点, 在不同测试时间得出的噪声电平值之间存在6 dBm以上的动态变化范围^[5]; 固定测试时间和测试地点, 在不同测试频率点上得出的噪声电平值也存在较大的动态变化范围^[6].背景噪声电平在时域, 空域和频域上存在高动态变化的特点为经典的协作频谱感知算法带来巨大的挑战.经典的协作频谱感知算法大致可分为三类, 基于合并的协作频谱感知算法^{[7, 8]}, 基于审核的协作频谱感知算法^{[9, 10]}和基于目标优化的协作频谱感知算法^{[11, 12, 13]}.这些协作频谱感知算法倾向于假设背景噪声电平稳定不变, 忽略了高动态变化背景噪声对算法性能的影响.基于合并的频谱感知算法又可分为硬合并和软合并方式.硬合并方式中, 参与协作的认知用户将本地判决结果通过报告信道发送到融合中心, 利用大数判决等准则判断有无主用户信号存在; 软合并方式中, 融合中心对来自不同认知用户的检测统计量进行加权合并后, 与相应的门限比较, 以确定主用户是否存在, 背景噪声电平不同时, 协作算法的性能取决于背景噪声电平高认知用户性能.基于审核的协作频谱感知算法依据认知用户接收信号信噪比, 置信度或者地理位置等审核指标, 对认知用户是否具备上传数据和参与协作的资格进行监管和审查, 达到减小通信开销和提升协作性能的目的, 然而这些审核指标的获取受背景噪声电平影响严重.基于目标优化的协作频谱感知算法往往以功率消耗, 感知覆盖范围, 感知性能以及通信吞吐量等指标作为最优化的目标, 进而设计合理的协作感知策略, 若考虑背景噪声电平的变化, 则为最优化问题增加了新的变元, 这使得问题的求解尤为复杂.

为应对背景噪声动态变化带来的新挑战, 本文给出一种归一化谱(Normalized spectrum, NS)协作频谱感知算法, 该算法无需主用户的先验信息, 具有适应背景噪声高动态变化的能力, 适用于高斯白噪声和平坦慢衰落信道, 可鲁棒运行于认知无线电网络中.

1 系统模型

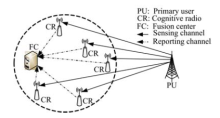
假设认知无线电网络采用中心融合架构, 参与协作的认知用户对同一频段进行感知, 并将感知信息上传至融合中心, 融合中心给出该频段是否被占用的感知结果, 认知无线电网络工作过程如图1所示, 虚线内为认知无线电网络的一个簇.

	Figure Option View Download New Window
	图1 认知无线电网络示意图Fig.1 Cognitive networks sketch map

假设L个认知用户参与协作, 每个认知用户同时监测主用户可能出现的授权频段, 认知用户接收到的信号^[14]可表示为:

$\begin{matrix} x_{l} (t) = \{\begin{matrix} H_{0} : w_{l} (t) \\ H_{1} : s_{l} (t) + w_{l} (t) \end{matrix} \end{matrix}$ (1)

式中:x_l $\begin{matrix} (t) \end{matrix}$ 为参与协作的第l个认知用户接收机感知到的信号, l=1, 2, , et al., L; s_l $\begin{matrix} (t) \end{matrix}$ 为第l个认知用户接收到的主用户发射信号, 其中包含传输损耗, 多径衰落以及时间弥散对主用户发射信号的影响; H₀和H₁分别为主用户不存在和主用户存在的情况; w_l $\begin{matrix} (t) \end{matrix}$ 为第l个认知用户周围的加性噪声, 假设w_l $\begin{matrix} (t) \end{matrix}$ 是循环对称复高斯变量, 其均值为0, 方差为 $\begin{matrix} σ_{l}^{2} \end{matrix}$ , w_l $\begin{matrix} (t) \end{matrix}$ = $\begin{matrix} w_{l}^{r} \end{matrix} \begin{matrix} (t) \end{matrix}$ +j $\begin{matrix} w_{l}^{i} \end{matrix} \begin{matrix} (t) \end{matrix}$ , $\begin{matrix} w_{l}^{r} \end{matrix} \begin{matrix} (t) \end{matrix}$ 和 $\begin{matrix} w_{l}^{i} \end{matrix} \begin{matrix} (t) \end{matrix}$ 是独立同分布的高斯随机变量, 它们的均值为0, 方差为 $\begin{matrix} σ_{l}^{2} \end{matrix}$ /2, w_l $\begin{matrix} (t) \end{matrix}$ 之间相互独立, $\begin{matrix} σ_{l}^{2} \end{matrix}$ 可以全部相同, 也可以全部不同, 或者部分相同.

2 NS协作频谱感知算法

2.1 NS协作算法步骤

(1)假设L个认知用户参与NS协作频谱感知, 每个认知接收机同步感知空间中的信号x $\begin{matrix} (t) \end{matrix}$ , 经过抗混叠滤波器和模数转换器, 模拟信号变成数字信号x_l $\begin{matrix} (n) \end{matrix}$ , x_l $\begin{matrix} (n) \end{matrix}$ 为第l个认知用户采集到的离散样本, 认知用户分别对得到的数据进行周期图功率谱估计:

$\begin{matrix} S_{l} (k) = \frac{1}{M} {|X_{l} (k)|}^{2} = \frac{1}{M} {|\overset{M - 1}{\sum_{n = 0}} x_{l} (n) e^{- j 2 πkn / M}|}^{2} \end{matrix}$ (2)

式中:k=0, 1, , et al., M-1; l=1, 2, , et al., L; M为每帧中的样本数.

(2)定义步骤(1)中认知用户得到的功率谱密度平均值为S_l $\begin{matrix} (k) \end{matrix}$ , 所有谱线强度和为S_all,_l, S_l $\begin{matrix} (k) \end{matrix}$ 中的一段谱线强度和为S_seg,_l $\begin{matrix} (u) \end{matrix}$ , u=0, 1, , et al., U-1.由于发射实信号的功率谱是对称的, 每帧数据的功率谱只需用正频率的点来表示:

$S_{all, l} = \sum_{k} S_{l} (k), k \in [1, \frac{M}{2}]$ (3)

$S_{seg, l} (u) = \sum_{k} S_{l} (k), k \in [\frac{M'u}{2} + 1, \frac{M' (u + 1)}{2}]$ (4)

式中:M'/2为分段内谱线数.

定义分段谱线强度和与所有谱线强度和的比值为归一化谱, 每个认知用户的归一化谱可表示为:

$\begin{matrix} r_{l} (u) = \frac{S_{seg, l} (u)}{S_{all, l}}, u = 0, 1, \dots, U - 1 \end{matrix}$ (5)

式中:U=M/M'为分段数.

(3)认知用户将本地得到的一组归一化谱r_l $\begin{matrix} (u) \end{matrix}$ 上传至融合中心, 融合中心计算L个认知用户归一化谱的平均值r_avg $\begin{matrix} (u) \end{matrix}$ :

$\begin{matrix} \begin{matrix} r_{avg} (u) = \frac{1}{L} \overset{L}{\sum_{l = 1}} r_{l} (u) \\ u = 0, 1, \dots, U - 1 \end{matrix} \end{matrix}$ (6)

并将归一化谱的平均值r_avg $\begin{matrix} (u) \end{matrix}$ 与预设门限γ 比较, 门限计算的闭式表达式在2.4节给出.若r_avg $\begin{matrix} (u) \end{matrix}$ ≥ γ , 则该分段被占用, 判决数组元素R $\begin{matrix} (u) \end{matrix}$ =1; 反之, 该分段空闲, 判决数组元素R $\begin{matrix} (u) \end{matrix}$ =0.如果判决数组元素的累积和大于零, 则判定H₁成立; 反之, 则判定H₀成立.

2.2 检验统计量的统计特性

在H₀假设下, 第l个认知用户采集到的离散样本x_l(n), n=0, 1, , et al., M-1; l=1, 2, , et al., L服从均值为0, 方差为 $\begin{matrix} σ_{l}^{2} \end{matrix}$ 的复高斯分布, 对M点序列进行线性傅里叶变换, 得到复变量X_l(k)= $\begin{matrix} X_{l}^{r} \end{matrix}$ (k)+j $\begin{matrix} X_{l}^{i} \end{matrix}$ (k), $\begin{matrix} X_{l}^{r} \end{matrix}$ (k)和 $\begin{matrix} X_{l}^{i} \end{matrix}$ (k)分别为X_l(k)的实部和虚部.

$\begin{matrix} \{\begin{matrix} X_{l}^{r} (k) = \overset{M - 1}{\sum_{n = 0}} \cos (\frac{2 π}{M} kn) ω_{l}^{r} (n) + \\ \overset{M - 1}{\sum_{n = 0}} \sin (\frac{2 π}{M} kn) ω_{l}^{i} (n) \\ X_{l}^{i} (k) = \overset{M - 1}{\sum_{n = 0}} \cos (\frac{2 π}{M} kn) ω_{l}^{i} (n) - \\ \overset{M - 1}{\sum_{n = 0}} \sin (\frac{2 π}{M} kn) ω_{l}^{r} (n) \end{matrix} \end{matrix}$ (7)

$\begin{matrix} X_{l}^{r} \end{matrix} \begin{matrix} (k) \end{matrix}$ 和 $\begin{matrix} X_{l}^{i} \end{matrix} \begin{matrix} (k) \end{matrix}$ 的统计特性为:

$\begin{matrix} \{\begin{matrix} X_{l}^{r} (k) ~ N (0, M σ_{l}^{2} / 2) \\ X_{l}^{i} (k) ~ N (0, M σ_{l}^{2} / 2) \end{matrix} \end{matrix}$ (8)

$\begin{matrix} X_{l}^{r} \end{matrix} \begin{matrix} (k) \end{matrix}$ 和 $\begin{matrix} X_{l}^{i} \end{matrix} \begin{matrix} (k) \end{matrix}$ 之间的协方差为:

$\begin{matrix} \begin{matrix} Cov (X_{l}^{r} (k), X_{l}^{i} (k)) = \\ E [(X_{l}^{r} (k) - E (X_{l}^{r} (k))) \cdot \\ (X_{l}^{i} (k) - E (X_{l}^{i} (k)))] = \\ \overset{M - 1}{\sum_{n = 0}} \cos (\frac{2 π}{M} kn) \sin (\frac{2 π}{M} kn) E [{(w_{l}^{r} (n))}^{2}] - \\ \overset{M - 1}{\sum_{n = 0}} \cos (\frac{2 π}{M} kn) \sin (\frac{2 π}{M} kn) E [{(w_{l}^{i} (n))}^{2}] = 0 \end{matrix} \end{matrix}$ (9)

$\begin{matrix} X_{l}^{r} \end{matrix} \begin{matrix} (k) \end{matrix}$ 和 $\begin{matrix} X_{l}^{i} \end{matrix} \begin{matrix} (k) \end{matrix}$ 是相互独立的同分布零均值高斯随机变量, 因此, S_l $\begin{matrix} (k) \end{matrix}$ 服从自由度为2的中心卡方分布, 其均值和方差分别为 $\begin{matrix} σ_{l}^{2} \end{matrix}$ 和 $\begin{matrix} σ_{l}^{4} \end{matrix}$ .

傅里叶变换X_l $\begin{matrix} (k) \end{matrix}$ 不同频点上随机变量的协方差为:

$\begin{matrix} \begin{matrix} Cov (X_{l} (p), X_{l} (q)) = \\ E [\bar{(X_{l} (p) - E (X_{l} (p)))} \cdot \\ (X_{l} (q) - E (X_{l} (q)))] = \\ \overset{M - 1}{\sum_{n = 0}} ex p (j \frac{2 π}{M} (p - q) n) E [{(w_{l} (n))}^{2}] = 0 \\ p \neq q, 0 \leq p, q < M - 1 \end{matrix} \end{matrix}$ (10)

由于协方差是以X_l $\begin{matrix} (k) \end{matrix}$ 为自变量的具有有限奇异点的连续函数, 可通过X_l $\begin{matrix} (k) \end{matrix}$ 的相互独立性得出S_l $\begin{matrix} (k) \end{matrix}$ 的相互独立性^[15].

2.3 NS协作算法门限

第l个认知用户接收信号周期图功率谱估计值S_l $\begin{matrix} (k) \end{matrix}$ , k=1, 2, , et al., M/2服从自由度为2的中心卡方分布, 均值和方差分别为μ _s_,_l= $\begin{matrix} σ_{l}^{2} \end{matrix}$ , $\begin{matrix} σ_{s, l}^{2} \end{matrix}$ = $\begin{matrix} σ_{l}^{4} \end{matrix}$ , 并且, S_l $\begin{matrix} (k) \end{matrix}$ 中不同频点上的功率谱是相互独立的, 构造随机变量X_l=S_seg,_l $\begin{matrix} (u) \end{matrix}$ 和Y_l=S_all,_l, 根据中心极限定理, 参与加和的功率谱频点足够多时(一般点数大于20), X_l, Y_l可近似为服从高斯分布的随机变量, 且都大于零, 均值和方差分别为:μ _X_,_l=M'μ _s_,_l/2, $\begin{matrix} σ_{X, l}^{2} \end{matrix}$ =M' $\begin{matrix} σ_{s, l}^{2} \end{matrix}$ /2和μ _Y_,_l=Mμ _s_,_l/2, $\begin{matrix} σ_{Y, l}^{2} \end{matrix}$ =M $\begin{matrix} σ_{s, l}^{2} \end{matrix}$ /2.

第l个认知用户一组归一化谱X_l/Y_l构成新的随机变量, 其累积分布函数可表示为:

$\begin{matrix} \begin{matrix} F_{l} (z) = P (\frac{X_{l}}{Y_{l}} < z |H_{0}) = \frac{1}{2} - \\ \frac{1}{2} Φ (\frac{μ_{X, l} / z - μ_{Y, l}}{\sqrt[]{2 {(σ_{X, l}^{2} (1 / z - 1))}^{2} + 2 {(σ_{Y, l} - σ_{X, l})}^{2}}}) = \\ \frac{1}{2} - \frac{1}{2} Φ (\frac{M' - Mz}{\sqrt[]{2 M' {(1 - z)}^{2} + 2 z^{2} {(\sqrt[]{M} - \sqrt[]{M'})}^{2}}}) \end{matrix} \end{matrix}$ (11)

假设两簇认知用户分别进行NS协作频谱感知, 第Ⅰ 簇L个认知用户周围的噪声电平可以互不相同, 也可以部分相同, 还可以全部相同, 第Ⅱ 簇L个认知用户周围的噪声电平完全相同.两簇中每个认知用户分别执行帧长度为M, 分段数为U的NS算法.

分别计算出第Ⅰ 簇中L个认知用户的分段子带功率S_seg,_l $\begin{matrix} (u) \end{matrix}$ , l=1, 2, , et al., L; u=1, 2, , et al., U, 依据NS协作算法的步骤可知, 融合中心得到的归一化谱平均值r_avg,_Ⅰ $\begin{matrix} (u) \end{matrix}$ 为:

$\begin{matrix} \begin{matrix} r_{avg, Ⅰ} (u) = \\ \frac{1}{L} (\frac{S_{seg, l} (u)}{\sum_{u} S_{seg, l} (u)} + \dots + \frac{S_{seg, L} (u)}{\sum_{u} S_{seg, L} (u)}) \end{matrix} \end{matrix}$ (12)

再计算出第Ⅱ 簇中L个认知用户的分段子带功率S'_seg,_l $\begin{matrix} (u) \end{matrix}$ , u=1, 2, , et al., U, 依据NS协作算法的步骤可知, 融合中心得到的归一化谱平均值为r_avg,_Ⅱ $\begin{matrix} (u) \end{matrix}$ :

$\begin{matrix} \begin{matrix} r_{avg, Ⅱ} (u) = \\ \frac{1}{L} (\frac{S'_{seg, l} (u)}{\sum_{u} S'_{seg, l} (u)} + \dots + \frac{S'_{seg, L} (u)}{\sum_{u} S'_{seg, L} (u)}) \end{matrix} \end{matrix}$ (13)

在式(12)(13)中, 每个归一化谱随机变量均服从由式(11)给出的分布, 该分布与参与协作节点的本地噪声方差无关, r_avg,_Ⅰ $\begin{matrix} (u) \end{matrix}$ 和r_avg,_Ⅱ $\begin{matrix} (u) \end{matrix}$ 都是L个独立同分布的随机变量相加, 因此, r_avg,_Ⅰ $\begin{matrix} (u) \end{matrix}$ 和r_avg,_Ⅱ $\begin{matrix} (u) \end{matrix}$ 表示的两个新随机变量具有相同的分布.

L个认知用户归一化谱比值的平均值r_avg $\begin{matrix} (u) \end{matrix}$ , u=1, 2, , et al., U, 可以看成L个随机变量的加和平均, 可以推导出r_avg $\begin{matrix} (u) \end{matrix}$ 的累积分布函数, 进而可以得出协作后一组归一化谱的虚警概率:

$\begin{matrix} \begin{matrix} P_{fa} = \frac{1}{2} + \\ \frac{1}{2} Φ (\frac{M' - Mz}{\sqrt[]{2 \frac{M'}{L} {(1 - z)}^{2} + 2 z^{2} {(\sqrt[]{\frac{M}{L}} - \sqrt[]{\frac{M'}{L}})}^{2}}}) \end{matrix} \end{matrix}$ (14)

NS算法的虚警概率P_{fa, NS}由U组相同的归一化谱虚警概率P_fa按"或"规则组合得到:

$\begin{matrix} P_{fa, NS} = 1 - (1 - P_{fa})^{U} \end{matrix}$ (15)

依据Neyman-Pearson准则, 由预先设定的目标虚警概率P_{fa, NS}求出每一组归一化谱的虚警概率P_fa, 将P_fa代入式(14), 并令M=LM'可以得到NS算法的门限值γ 为:

$\begin{matrix} \begin{matrix} γ = \frac{1}{U} + 2 {LM (U - 1) {[Φ^{- 1} (1 - 2 P_{fa})]}^{2} - \\ 4 (U - 1) {[Φ^{- 1} (1 - 2 P_{fa})]}^{4}}^{\frac{1}{2}} / {LMU - \\ 4 U {[Φ^{- 1} (1 - 2 P_{fa})]}^{2}} \end{matrix} \end{matrix}$ (16)

式中:Φ $\begin{matrix} (\cdot) \end{matrix}$ 为误差函数; Φ ^-¹ $\begin{matrix} (\cdot) \end{matrix}$ 为误差函数的逆函数.

由式(16)可知:NS协作感知算法的门限值与参与运算的虚警概率P_fa, 分段数U, 帧长M以及协作节点数L有关, 与各认知用户噪声方差无关, 因此, NS协作感知算法门限值的确定与各认知用户噪声电平无关, 该协作算法在噪声电平高度变化的协作环境中可以更具鲁棒性.

2.4 基于能量合并的协作频谱感知算法

为了方便后续章节采用恒虚警原则对不同协作频谱感知算法的性能进行对比和分析, 本节简要给出基于能量的大数判决硬协作(Majority voting hard decision, MVHD)频谱感知算法和基于能量的等增益软协作(Equal gain soft decision, EGSD)频谱感知算法的虚警概率和门限计算表达式.

在MVHD协作频谱感知算法中, 假设每个认知用户按照相同的虚警概率P_fa0进行单点判决, 则MVHD协作频谱感知算法的虚警概率P_{fa, MVHD}为:

(17)

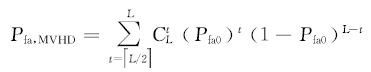
式中:L为参与协作的认知用户节点数; 为向上取整运算符.

若预先设定P_{fa, MVHD}, 则可以通过式(17)计算出单节点的虚警概率P_fa0, 然后利用下式:

$\begin{matrix} γ_{l} = σ_{l}^{2} [M + \sqrt[]{M} Q^{- 1} (P_{fa 0})] \end{matrix}$ (18)

可以计算出不同认知用户的判决门限, 其中, $\begin{matrix} σ_{l}^{2} \end{matrix}$ 为第l个认知用户周围的噪声方差, l=1, 2, , et al., L; γ _l为第l个认知用户的本地判决门限; M为每个认知用户本地运算的样本点数; Q^-¹ $\begin{matrix} (x) \end{matrix}$ 为Q $\begin{matrix} (x) \end{matrix}$ 的反函数.

$\begin{matrix} Q (x) = \int_{x}^{\infty} \exp (- y^{2} / 2) dy / \sqrt[]{2 π} \end{matrix}$

在EGSD协作频谱感知算法中, 若参与EGSD协作的认知用户节点数为L, 每个认知用户本地运算的样本点数为M, 则EGSD协作频谱感知算法的检验统计量为L个高斯变量的等增益平均, 在H₀假设下, EGSD协作算法的检验统计量服从

T_EGSD(x)~N $\begin{matrix} (\frac{1}{L} \overset{L}{\sum_{l = 1}} M σ_{l}^{2}, \frac{1}{L^{2}} \overset{L}{\sum_{l = 1}} M σ_{l}^{4}) \end{matrix}$ (19)

结合虚警概率的定义, 可以得出EGSD协作频谱感知算法的虚警表达式:

$\begin{matrix} P_{fa, EGSD} = Q (\frac{Lγ - \overset{L}{\sum_{l = 1}} M σ_{l}^{2}}{\sqrt[]{\overset{L}{\sum_{l = 1}} M σ_{l}^{4}}}) \end{matrix}$ (20)

采用恒虚警准则, 可以得出该算法在融合中心的判决门限:

$\begin{matrix} γ_{EGSD} = \frac{1}{L} [Q^{- 1} (P_{fa, EGSD}) \sqrt[]{\overset{L}{\sum_{l = 1}} M σ_{l}^{4}} + \overset{L}{\sum_{l = 1}} M σ_{l}^{2}] \end{matrix}$ (21)

3 算法仿真与结果分析

依据第2节描述的系统模型采用Monte Carlo方法对NS算法在不同噪声电平下的感知性能和衰落信道中的协作感知性能进行仿真, 并将其协作感知性能与基于能量的硬协作感知和软协作感知算法性能进行对比.假设主用户发射数字BPSK调制信号, 信号码元速率s_r为1000 kBaud, 载波频率f_c为4250 kHz.认知用户未知主用户的调制类型和特征参数等先验信息, 只能确定主用户会在0~5000 kHz内出现, 因此, 以采样频率10 000 kHz对接收信号进行采样.假定噪声电平为n₀, 则噪声功率为N= $\begin{matrix} 10^{n_{0} f_{s} / 10} \end{matrix}$ .仿真中, 信号的信噪比定义为10lg $\begin{matrix} (A^{2} / 2 N) \end{matrix}$ , 其中A为认知用户接收到的主用户信号幅度, 若已知噪声功率和信噪比, 可计算出信号幅度A.进行NS算法性能仿真和对比时, 采用恒虚警准则, 预先设定虚警概率为0.01.

3.1 不同噪声电平下单节点NS算法性能

假设在AWGN信道下, 单个认知用户节点对上文的主用户信号进行感知, 主用户的信噪比变化范围为-25~0 dB, 单个认知用户周围的噪声电平高动态变化, 在3个观测时刻背景噪声电平分别取-110, -120, 130 dBm/kHz.

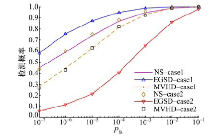
图2仿真了单个认知用户在不同背景噪声电平环境下NS算法的正确检测概率, 仿真中两种算法使用的样本长度均为4000, 且设定NS算法节点数L=1, 每帧长度M=4000, 分段数U=4.由图可见, 在融合中心, 采用固定的判决门限, 门限由式(16)计算得出, 3种不同背景噪声电平对应的3条NS算法检测性能曲线基本重合, 说明NS算法在给定信噪比的情况下, 其判决门限和感知性能可以与噪声电平无关, 这与理论分析相符合, 因此, 该算法可被用于节点背景噪声电平不同的协作信号感知中.

	Figure Option View Download New Window
	图2 背景噪声电平不同, 单节点NS感知性能Fig.2 Spectrum sensing performance of single user in different background noise level

3.2 衰落信道下NS协作算法性能

假设在Rayleigh信道下, L个认知用户节点对上文描述的主用户信号进行协作感知, 并且分别执行MVHD频谱感知算法, EGSD频谱感知算法和NS频谱感知算法, 对3种协作频谱感知算法进行性能对比.采用恒虚警准则, MVHD频谱感知算法本地判决门限由式(17)(18)计算得出, EGSD频谱感知算法的融合中心判决门限由式(21)计算得出, NS频谱感知算法在融合中心的判决门限由式(15)(16)计算得出; 仿真时, 3种协作算法使用的样本总长度均为12 000, 参与协作的认知用户数为L=3, 且设定每个认知用户使用样本数据长度M=4000, 分段数U=4.

条件① :3个参与协作的认知用户信噪比均为SNR=-10 dB, 背景噪声电平均为-110 dBm/kHz.条件② :3个参与协作的认知用户背景噪声电平分别为-110, -120, -130 dBm/kHz, 信噪比均为SNR=-10 dB.图3仿真了条件① 相同背景噪声电平下, 3个参与协作的认知用户具有相同信噪比时3种协作频谱感知算法的性能, 以及条件② 不同背景噪声电平下, 3个参与协作的认知用户具有相同信噪比时3种协作频谱感知算法的性能.由图3可知:条件① 下, NS协作频谱感知算法性能优于MVHD协作频谱感知算法, 但EGSD协作频谱感知算法的性能优于NS协作频谱感知算法; 在条件② 下, NS协作频谱感知算法性能优于EGSD协作频谱感知算法和MVHD协作频谱感知算法.这是由于参与协作的认知用户噪声方差不同, 信噪比相同时, 软协作算法的性能基本决定于噪声方差较大的认知用户单点感知性能.因此, 背景噪声的动态变化对EGSD协作频谱感知算法性能产生较大影响, 而NS协作频谱感知算法可以有效克服由不同认知用户背景噪声存在差异对感知性能带来的影响.

	Figure Option View Download New Window
	图3 协作性能对比图Fig.3 Cooperative spectrum sensing performance

3.3 NS协作算法复杂度分析

NS协作频谱感知算法的计算复杂度由各认知节点的本地归一化谱和融合中心的协作归一化谱两部分计算代价组成.每个认知用户计算一次本地归一化谱需要进行 $\begin{matrix} (Mlo g_{2} M) \end{matrix}$ /2+M次复数乘法, Mlog₂M次复数加法, M-1次实数加法运算以及U次实数除法运算, 其中, $\begin{matrix} (Mlo g_{2} M) \end{matrix}$ /2次复数乘法和Mlog₂M次复数加法用于执行一次数据长度为M的离散傅里叶变换(Discrete Fourier transform, DFT), M次复数乘法运算用于周期图估计M点的功率谱密度, M-1次实数加法运算用于计算全带和子带内的功率, U次实数除法运算用于计算本地的归一化谱.完成一次归一化谱频谱感知算法, 需要L个认知用户节点同时计算本地的归一化谱, 这需要进行 $\begin{matrix} (LMlo g_{2} M) \end{matrix}$ /2+LM次复数乘法, LMlog₂M次复数加法, L $\begin{matrix} (M - 1) \end{matrix}$ 次实数加法运算以及LU次实数除法运算, 融合中心还需要进行U $\begin{matrix} (L - 1) \end{matrix}$ 次实数加法用于计算, 进行最终判决的协作归一化谱.

4 结束语

归一化谱协作频谱感知算法可以有效应对背景噪声动态变化给协作频谱感知算法带来的新挑战.该算法的判决门限与参与运算的帧数, 分段内的谱线数以及虚警概率有关, 与噪声方差和噪声电平无关.该算法支持盲频谱感知, 无需主用户的先验信息, 具有适应背景噪声高动态变化的能力, 适用于加性高斯白噪声和平坦慢衰落信道模型, 因此, 归一化谱协作频谱感知算法可广泛应用于复杂电磁环境下的认知无线电网络.

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Haykin S. Cognitive radio: brain-empowered wireless communications[J]. IEEE Journal on Selected Areas in Communications, 2005, 23(2): 201-220. [本文引用:1]
[2]	Wang B, Liu R, Clancy C. Evolutionary cooperative spectrum sensing game: how to collaborate?[J]. IEEE Transactions on Communications, 2010, 58(3): 890-900. [本文引用:1]
[3]	王秉钧, 王少勇. 卫星通信系统[M]. 1版. 北京: 机械工业出版社, 2004: 159-172. [本文引用:1]
[4]	Sharma P S, Raju S G, Murali M, et al. Assessment of noise level due to vehicular traffic at Warangal city[J]. International Journal of Environment and Pollution, 2007, 30(1): 137-153. [本文引用:1]
[5]	Tang S K, Chu S H K. Noise level distribution functions for outdoor applications[J]. Journal of Sound and Vibration, 2001, 248(5): 887-911. [本文引用:1]
[6]	Dennis R. Satellite Communications[M]. 3rd ed. New York: McGraw Hill, 2001: 317-319. [本文引用:1]
[7]	Chaudhari S, Lunden J, Koivunen V. Cooperative sensing with imperfect reporting channels: hard decisions or soft decisions?[J]. IEEE Transactions on Signal Processing, 2012, 60(1): 18-28. [本文引用:1]
[8]	Ma J, Zhao G, Li Y. Soft combination and detection for cooperative spectrum sensing in cognitive radio networks[J]. IEEE Transactions on Wireless Communications, 2008, 7(11): 4502-4507. [本文引用:1]
[9]	Pavlovska V, Gavrilovska L. Collaborative spectrum sensing scheme: quantized weighting with censoring[C]//3rd International ICST Conference on Ad Hoc Networks, Paris, France, 2012: 93-105. [本文引用:1]
[10]	Chen Y. Analytical performance of collaborative spectrum sensing using censored energy detection[J]. IEEE Transactions on Wireless Communications, 2010, 9(12): 3856-3865. [本文引用:1]
[11]	Zhang T, Tsang K. Optimal cooperative sensing scheduling for energy-efficient cognitive radio networks[C]//IEEE Conference on Computer Communications, Shanghai, China, 2011: 2723-2731. [本文引用:1]
[12]	Nguyen N, Koo I. Application of maximum distance generalized quantiser for cooperative spectrum sensing in cognitive radio[J]. IET Communications, 2012, 6(1): 39-45. [本文引用:1]
[13]	丁汉清, 杨家玮, 赵志远. 基于分群的自适应双门限合作频谱感知[J]. 吉林大学学报: 工学版, 2011, 41(2): 537-542. Ding Han-qing, Yang Jia-wei, Zhao Zhi-yuan. Adaptive dual threshold cooperative spectrum sensing based on grouping[J]. Jounal of Jilin University (Engineering and Technology Edition), 2011, 41(2): 537-542. [本文引用:1]
[14]	Zeng Y, Liang Y. Eigenvalue-based spectrum sensing algorithms for cognitive radio[J]. IEEE Transactions on Communications, 2009, 57(6): 1784-1793. [本文引用:1]
[15]	Oppenheim A V. Discrete-Time Signal Processing[M]. 3rd ed. Upper Saddle River: Prentice Hall, 2010: 426-427. [本文引用:1]

2005

0.0

... 0 引言认知无线电^[1](Cognitive radio)被认为是下一代蜂窝通信中解决频谱资源稀缺的重要途径之一 ...

2010

0.0

... 协作频谱感知算法^[2]融合不同位置节点提供的感知信息,获得分集处理的增益,可以有效克服多径衰落,阴影效应和隐藏终端等问题对单点频谱感知算法性能的影响 ...

2004

0.0

... 感知节点背景噪声是由地面噪声,大气噪声,降雨噪声,人为噪声,干扰噪声以及频谱感知接收机热噪声等多种噪声形式复合而成^[3],背景噪声电平往往在多维域上存在高动态变化的特点 ...

2007

0.0

... 固定测试频率和测试时间,在不同测试地点得出的噪声电平最大值与最小值之间差值可达10 dBm以上^[4] ...

2001

0.0

... 固定测试频率和测试地点,在不同测试时间得出的噪声电平值之间存在6 dBm以上的动态变化范围^[5] ...

2001

0.0

... 固定测试时间和测试地点,在不同测试频率点上得出的噪声电平值也存在较大的动态变化范围^[6] ...

2012

0.0

... 经典的协作频谱感知算法大致可分为三类,基于合并的协作频谱感知算法^[7,8],基于审核的协作频谱感知算法^[9,10]和基于目标优化的协作频谱感知算法^[11,12,13] ...

2008

0.0

2012

0.0

2010

0.0

2011

0.0

2012

0.0

2011

0.0

. 2011, 41(2):537-542

Adaptive dual threshold cooperative spectrum sensing based on grouping

基于分群的自适应双门限合作频谱感知

Ding Han-qing , Yang Jia-wei , Zhao Zhi-yuan.

丁汉清, 杨家玮, 赵志远

1.State Key Lab of Integrated Service Networks, Xidian University, Xi'an 710071, China|2.School of Computer and Communication Engineering, Zhengzhou University of Light Industry, Zhengzhou 450002,China

An improved cooperative spectrum sensing mechanism is proposed to mitigate the adverse effects of the conventional cooperative spectrum sensing mechanism over unfavorable reporting channels in Cognitive Ratio (CR) system. All CR users are divided into several groups. In each group, the CR user with the largest reporting channel gain is selected as the central node. After performing cooperative spectrum sensing with adaptive dual threshold, the central node forwards its sensing result to the Cognitive Ratio Base Station (SRBS). Then the CRBS fuses the results from all groups to decide the presence or absence of the authorized users. Simulation results indicate that this method can lower the bit error rate of reporting channel. It also decreases the average data overhead with almost the same detection performance as the conventional cooperative spectrum sensing.

针对认知无线电系统中,通知信道不理想对传统合作频谱感知的不利影响，提出了一种改进的合作频谱感知机制：认知用户被分成若干群，选择群内通知信道增益最大的认知用户为中心节点，采用自适应双门限机制负责群内合作频谱检测，并将检测结果报告给认知基站进行合并以确定授权用户是否存在。仿真结果表明：相对传统的合作频谱感知，该机制能降低通知信道误码率，并且在保证检测性能的前提下，减少了认知系统频谱感知过程中的平均数据开销。

2009

0.0

... 假设L个认知用户参与协作,每个认知用户同时监测主用户可能出现的授权频段,认知用户接收到的信号^[14]可表示为: ...

2010

0.0

... 由于协方差是以X_lk为自变量的具有有限奇异点的连续函数,可通过X_lk的相互独立性得出S_lk的相互独立性^[15] ...