作者简介:李静(1974-),男,教授,博士生导师.研究方向:汽车地面力分析与控制.E-mail:liye1129@163.com
采用二自由度车辆模型作为被控对象简化模型,提出了一种基于状态反馈的 H∞鲁棒控制方法的车辆底盘集成控制策略,协调控制主动前轮转向系统和直接横摆力矩控制系统。直接横摆力矩控制系统基于HSRI轮胎模型的逆运算和PI控制实现。通过J-turn工况和正弦延迟工况对 H∞鲁棒控制器进行仿真验证,结果表明,所设计的车辆底盘集成 H∞鲁棒控制器具有良好的控制效果,能够明显地改善车辆的操纵稳定性。
Based on the strength of state feedback, a H∞ robust control approach for integrated chassis system is proposed. The two degrees of freedom vehicle model is employed as a simplified model of the controlled object. This control approach is used to coordinate the active front wheel steering system and the direct yaw moment control system. The direct yaw moment control system is based on the inverse operation of HSRI tire model and PI control. Two typical cases, J-turn and sine with dwell, are simulated. Results show that the proposed H∞ robust control approach for integrated chassis system has good control effect, and can significantly improve the handling and stability of the vehicle.
随着车辆主动安全性能要求的不断提高, 车辆主动安全控制系统受到了更多的关注, 例如:主动转向系统、电子稳定性控制系统和主动悬架系统等。这些系统可扩展车辆的线性响应区域, 使其更易操作, 并且车辆在强非线性区依然具有可控性[1]。然而这些系统的引入不但增加了车辆传感器的数量、线束长度, 而且系统之间的相互影响和耦合作用会使整车的综合性能降低。为解决这一矛盾, 车辆底盘集成技术的研究成为车辆控制领域的热点问题[2, 3]。例如:Nagai等[4]采用LQR方法实现主动后轮转向系统和直接横摆力矩系统的集成控制; Harada等[5]基于侧向动力学的半车模型并运用最优控制策略实现转向和主动悬架系统的集成控制; Karbalaei等[6]采用模糊逻辑控制策略实现主动前轮转向系统和直接横摆力矩系统的集成控制; Shen等[7]基于动态非线性滑膜控制策略实现主动悬架系统和主动四轮转向系统的集成控制。LQR方法和最优控制对控制模型的精度要求很高, 车辆实际行驶中的参数和环境的不确定性对控制算法的精度和系统的稳定性有很大影响。模糊逻辑控制的模糊化和反模糊化过程主要靠经验及试凑, 无法定义系统的控制目标, 并且该方法无积分环节, 系统的稳态精度不高。动态非线性滑膜控制方法由于非线性函数的引入使得其在实际工程中实现非常困难, 且参数选取不当, 会产生奇异问题。
基于状态反馈的H∞ 鲁棒控制采用被控对象的简化模型可有效进行控制性能的分析与综合[8]。本文采用车辆线性二自由度动力学模型作为控制参考模型, 设计状态反馈的H∞ 鲁棒控制器, 对装配主动前轮转向和主动横摆力矩控制的目标车辆实现集成控制。同时, 基于HSRI轮胎模型逆运算和PI控制实现主动横摆力矩增量的轮间分配。最后, 本文采用Matlab/Simlink构建的十五自由度车辆动力学模型对系统进行仿真分析, 以验证H∞ 鲁棒控制器的控制效果。
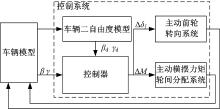
车辆底盘集成H∞ 鲁棒控制系统总体结构如图1所示。该系统根据车辆的质心侧偏角
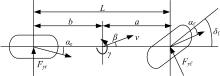
仅考虑车辆侧向和横摆运动, 忽略侧倾、悬架动态特性, 建立车辆动力学模型[9], 如图2所示。图中,
车辆侧向力平衡方程式和绕垂直轴的力矩平衡方程式为:
式中:
忽略轮胎侧向力的非线性, 车辆前、后轴的侧向力与其对应的侧偏角呈线性关系, 即:
式中:
将式(2)代入式(1)得到车辆动力学模型的状态方程:
式中:
对式(3)进行拉普拉斯变换得到质心侧偏角和横摆角速度对前轮转角的稳态增益矩阵, 记为:
式中:
式中:
结合式(4), 为更好地实现车辆侧滑控制及考虑车辆路面附着系数
式中:
具有状态可观测的系统, 其状态空间描述如下:
式中:
设计一个状态反馈控制器
通过求解如下的线性矩阵不等式得到状态反馈最优鲁棒控制律
若式(8)的线性矩阵不等式存在使扰动抑制度
本文采用式(3)的车辆动力学模型作为状态反馈鲁棒控制器设计的参考模型, 式(5)的名义质心侧偏角和名义横摆角速度作为控制目标。选取车辆实际状态的质心侧偏角和横摆角速度与控制目标的偏差
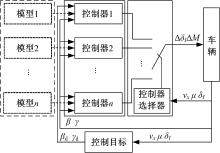
因系统的控制目标为分段函数, 且参考模型是车速的函数, 因此需要对每个单一的模型分别设计状态反馈H∞ 鲁棒控制器, 根据纵向车速
当
式中:
其中矩阵的选择包含了被调输出参量的权重系数。
当
将式(5)的第二段函数重新定义为:
将扩展之后的式(3)减去式(11)乘以矩阵
式中:
式(9)(12)可基于对式(8)线性矩阵不等式的求解得到最优控制律
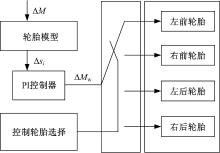
主动横摆力矩控制增量
参考文献[10]的研究结果, 按照表1的方式选择施加制动的车轮。
| 表1 横摆力矩分配原则 Table 1 Principle of yaw moment distribution |
对于选择的制动车轮, 主动横摆力矩控制增量
式中:
本文采用HSRI轮胎模型[11]计算轮胎侧向力增量
式中:
对式(14)(15)进行简化, 用
将式(16)(17)描述的轮胎侧向力增量
根据平面运动学理论可知, 车轮侧偏角与车辆纵向速度
式中:
将式(18)~(21)计算得到的轮胎侧偏角、轮胎当前时刻的垂向力、纵向滑移率和路面附着系数代入式(15), 并结合式(16)(17)即可得到轮胎的滑移率增量
基于Matlab/Simulink建立十五自由度车辆动力学模型, 包括车身的纵向运动、侧向运动、垂向运动、横摆运动、俯仰运动和侧倾运动自由度, 4个车轮转动、垂向运动自由度和前轮转向自由度。本文利用该模型对上述车辆底盘集成H∞ 鲁棒控制系统的性能、鲁棒性等进行仿真验证。选取J-turn转向和正弦延迟两种典型工况, 对比有、无底盘集成控制以及横摆力矩控制的车辆在两种工况下的操纵稳定性。车辆的部分参数如下:M=1274 kg, Iz=1523 kg· m2, L=2.578 m, Kf=Kr=40 kN/rad, a=1.016 m, b=1.562 m, c=1.739 m, Cα =20 kN/rad, Cs=80 kN/rad。仿真结果如图5和图6所示。
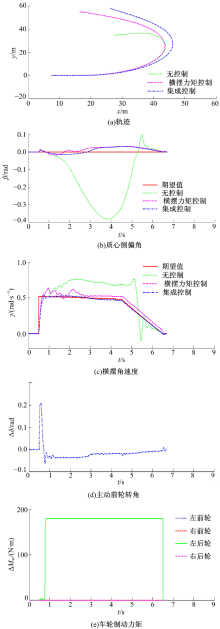
车辆直线行驶, 初始车速为60 km/h, 路面附着系数为0.8, 驾驶员松开加速踏板, 前轮转角以1000 (° )/s匀速增大至8° , 保持4 s, 之后用2 s的时间匀速回到0° 位置[12], 仿真结果如图5所示。
由图5可见:无控制时, 车辆呈现过多转向特性, 质心侧偏角和横摆角速度都明显偏离其期望值, 车辆逐渐丧失方向稳定性。采用横摆力矩控制方式后, 车辆的质心侧偏角可以控制在较小的范围内, 但横摆角速度与其期望值有较小的偏差, 导致车辆有过多转向的趋势。与横摆力矩控制方式相比, 采用底盘集成控制可以使车辆的横摆角速度更好地跟踪其期望值, 并且车辆质心侧偏角可以控制在较小的范围内, 车辆可以更好地保持方向稳定性。
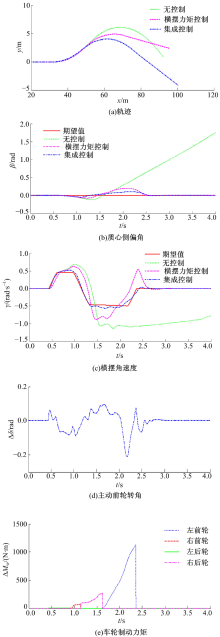
车辆直线行驶, 初始车速为80 km/h, 路面附着系统为0.8, 驾驶员松开加速踏板, 前轮转角输入幅值为10° , 频率为0.7 Hz, 延迟时间为500 ms的正弦信号[13], 仿真结果如图6所示。
由图6可见:无控制时, 车辆质心侧偏角逐渐增大, 导致车辆横摆力矩对方向盘转角的敏感性迅速下降, 在2.2 s后横摆角速度明显偏离其期望值, 车辆失去方向稳定性。采用横摆力矩控制方式后, 车辆的质心侧偏角可以控制在较小的范围内, 但横摆角速度在1 s后与其期望值有一定的偏差。与横摆力矩控制方式相比, 底盘集成控制方式可使车辆的质心侧偏角控制在更小的范围内, 并且车辆的横摆角速度可以更好地跟踪其期望值, 使车辆保持稳定性。
提出了一种基于状态反馈的车辆底盘集成H∞ 鲁棒控制, 并基于HSRI轮胎模型逆运算和PI控制实现主动横摆力矩增量的轮间分配。同时, 采用Matlab/Simulink构建的十五自由度车辆动力学模型对其进行J-turn工况和正弦延迟工况的仿真验证。结果表明, 所设计的控制系统具有良好的控制效果, 能明显地改善车辆的操纵稳定性。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|