动力总成悬置系统的稳健设计

引用本文

宋康, 陈潇凯, 林逸. 动力总成悬置系统的稳健设计.吉林大学学报:工学版, 2016, 46(3): 692-699
SONG Kang, CHEN Xiao-kai, LIN Yi. Robust design of powertrain mounting system. Journal of Jilin University Engineering and Technology Edition, 2016, 46(3): 692-699 复制到剪切板

Permissions

动力总成悬置系统的稳健设计

宋康¹, 陈潇凯¹, 林逸²

1.北京理工大学机械与车辆学院,北京 100081

2.北京汽车股份有限公司汽车工程研究院,北京 101300

通讯作者:陈潇凯(1977-),男,副教授,博士.研究方向:多学科设计优化.E-mail:chenxiaokai@263.net

作者简介:宋康(1987-),男,博士研究生.研究方向:汽车系统动力学.E-mail:bitsk@163.com

基金:国家自然科学基金项目(51275040)

摘要

针对悬置刚度的不确定性对系统性能的影响,采用稳健设计理论对动力总成悬置系统进行优化设计,并在设计过程中引入全局优化算法和并行计算技术以提高计算效率。建立系统在曲轴坐标系、扭矩轴坐标系及车辆坐标系下的运动方程,并针对系统受到的各项激励分别提出模态规划方案。制定了首先应用全局优化算法搜索可行域,然后拆分可行域并应用并行计算技术执行稳健评价的设计流程。以某动力总成悬置系统为例,建立了稳健优化模型并按照设计流程计算求解。优化结果显示:稳健设计方案模态解耦率的平均值相对确定设计方案变化不大,但是标准差却有明显减小,尤其是当设计变量的不确定水平较大时,系统的稳健性有显著改善。

关键词: 车辆工程; 动力总成悬置系统; 稳健设计; 模态规划; 全局优化; 并行计算

中图分类号:U461.1 文献标志码:A 文章编号:1671-5497(2016)03-0692-08

Robust design of powertrain mounting system

SONG Kang¹, CHEN Xiao-kai¹, LIN Yi²

1.School of Mechanical Engineering, Beijing Institute of Technology, Beijing 100081, China

2.Beijing Automotive Technology Center, BAIC Motor Corporation Ltd., Beijing 101300, China

Abstract

Robust design of powertrain mounting system is researched to improve the robustness of the system under uncertain stiffness property of the mount. Global optimization algorithm and parallel computation technique are employed to improve the computational efficiency. The motion equations of the system are built in crankshaft axis system, torque roll axis system and vehicle axis system. Modal formulation is presented for each excitation in a specific axis system. A design procedure is proposed. In this procedure global optimization algorithm is employed to search feasible region first; then the feasible region is divided and distributed into each computation core; finally, parallel computation technique is used to carry out robust evaluation. A robust optimization model is formulated based on a powertrain mounting system and optimization is carried out according to the proposed design procedure. Results indicate that the robust mean value of decoupling ratio has a little variation from the deterministic one, but the robust standard deviation is obviously smaller than the deterministic one. Especially for higher uncertain level, the robustness of the system is significantly improved.

Keyword: vehicle engineering; powertrain mounting system; robust design; modal formulation; global optimization; parallel computation

Show Figures

0 引言

作为影响汽车NVH性能的关键子系统, 动力总成悬置系统在隔离动力总成的振动向车身传递以及控制外部激励引起的系统振动和冲击等方面发挥着重要作用。

受悬置制造误差等不确定因素的影响, 动力总成悬置系统性能的实际水平与设计水平之间通常存在一定偏差。性能偏差的减小可以通过改善生产工艺等途径来实现, 但这样做通常会增加产品成本。同时, 很多不确定因素在本质上也无法消除, 因此, 稳健设计是基于已有条件来提高性能稳健性的合理选择。

在稳健设计方法中, 最成熟的方法包括Taguchi设计方法和6sigma设计方法, 二者均在悬置系统的设计中得到广泛应用。张代胜等应用Taguchi方法对初步优化后的悬置系统做进一步的稳健设计^[1]。吴杰等应用6sigma方法对悬置系统的解耦率进行稳健设计, 同时考虑频率分布和频率间隔对系统可靠性的影响^{[2, 3]}。Taguchi方法借助正交试验技术, 通过考察内、外表面的不同组合从而确定满足设计要求的稳健方案。由于该方法只对设计变量的有限个水平进行评价, 因此应用中可通过迭代计算提高设计精度。6sigma方法是一种集稳健设计和可靠设计于一体的综合设计方法。原则上, 6sigma准则是针对正态分布而制定的, 因此设计中有必要对相关函数执行正态检验。如果不满足正态分布, 可根据可靠度相等的原则计算等效sigma水平。

除了上述两种方法, 文献^{[4, 5]}将区间分析技术, 文献^{[6, 7]}将灵敏度分析技术引入稳健优化模型的构建。谢展等采用拉丁超立方抽样技术对多目标优化得到的悬置系统Pareto解集进行稳健评价, 从而实现既优化又稳健的系统设计^[8]。现有文献提出了多种新的稳健设计指标, 并可将新型算法用于稳健模型的优化求解^[9]。但是, 稳健设计的实际应用在很大程度上受限于稳健水平的评价环节, 这是由于稳健评价的计算量通常较大, 虽有近似算法提出, 但评价精度较低, 因此, 计算效率和精度通常不可兼得, 而现有文献对设计中如何处理稳健评价环节, 如何提高设计效率等内容却鲜有涉及。

本文首先建立悬置系统在多参考坐标系下的运动方程, 针对各激励分别提出相应的模态规划方案。然后应用全局优化算法与并行计算技术制定稳健设计流程以提高设计效率。最后以某悬置系统为例, 根据制定的设计流程完成系统的稳健设计。

1 动力总成悬置系统的建模

由于动力总成的弹性体固有频率远高于悬置系统的固有频率, 因此建模时动力总成简化为刚体。弹性悬置简化为3个相互正交的弹簧, 刚度分别取悬置的主压缩刚度和主剪切刚度, 同时忽略悬置阻尼的影响。动力总成悬置系统的模型如图1所示。

	Figure Option View Download New Window
	图1 动力总成悬置系统模型Fig.1 Model of powertrain mounting system

动力总成悬置系统固有属性的设计一般在3套坐标系中进行, 分别为:曲轴坐标系{X_C, Y_C, Z_C}、扭矩轴坐标系{X_T, Y_T, Z_T}和车辆坐标系{X_V, Y_V, Z_V}^[10]。

曲轴坐标系的原点位于动力总成质心处, X_C轴沿曲轴轴线指向动力总成自由端; Z_C轴沿直列气缸轴线或V型气缸角平分线指向上方; Y_C轴根据右手定则确定。该坐标系用于存在不平衡惯性力作用时的系统设计和动力总成转动惯量的测试。

扭矩轴坐标系的原点位于动力总成质心处, X_T轴沿扭矩轴指向动力总成自由端; Y_T轴位于X_C-Y_C平面内; Z_T轴根据右手定则确定。该坐标系主要用于怠速工况下的系统设计, 为横置动力总成的俯仰模态提供设计参考。

车辆坐标系的原点位于静平衡状态下的动力总成质心处, X_V轴平行于车辆纵向对称面水平指向后方; Y_V轴垂直于车辆纵向对称面指向驾驶员右侧; Z_V轴根据右手定则确定。该坐标系主要用于车身激励下的系统设计, 包括不平路面激起的垂向振动, 加、减速时的纵向激励和转向时的侧向激励。

在每个悬置处建立局部坐标系, 第i个悬置处的局部坐标系为{X_L_i, Y_L_i, Z_L_i}。悬置的刚度特性在局部坐标系中表示。

2 动力总成悬置系统解耦设计要求

由扭矩轴解耦法的数学基础可知, 如果系统在激励作用下产生了恒定方向的响应, 那么该响应一定属于系统的振动模态^[11]。根据该结论提出动力总成悬置系统的解耦设计方案如下:

(1)在曲轴坐标系中, 针对不平衡惯性力, 将系统某阶模态的形状规划为沿Z_C轴的平动, 数学表达式如下:

$\begin{matrix} (K_{C} - ω_{p}^{2} M_{C}) q_{ZC} = 0 \end{matrix}$ (1)

式中:ω _p为系统的第p阶固有频率; q_Z_C为单位向量:

$\begin{matrix} q_{ZC} = {[\begin{matrix} 0 & 0 & 1 & 0 & 0 & 0 \end{matrix}]}^{T} \end{matrix}$

(2)在扭矩轴坐标系中, 针对发动机扭矩, 将系统某阶模态的形状规划为沿X_T轴的转动, 数学表达式如下:

$\begin{matrix} (K_{T} - ω_{q}^{2} M_{T}) q_{XT} = 0 \end{matrix}$ (2)

式中:ω _q为系统的第q阶固有频率; q_X_T为单位向量:

$\begin{matrix} q_{XT} = {[\begin{matrix} 0 & 0 & 0 & 1 & 0 & 0 \end{matrix}]}^{T} \end{matrix}$

(3)在车辆坐标系中, 针对车身激励, 将系统3阶模态的形状分别规划为沿X_V轴、Y_V轴、Z_V轴的平动, 数学表达式如下:

$\begin{matrix} \{\begin{matrix} (K_{V} - ω_{x}^{2} M_{V}) q_{XV} = 0 \\ (K_{V} - ω_{y}^{2} M_{V}) q_{YV} = 0 \\ (K_{V} - ω_{z}^{2} M_{V}) q_{ZV} = 0 \end{matrix} \end{matrix}$ (3)

式中:ω _x、ω _y、ω _z分别为系统的第x阶、第y阶、第z阶固有频率; q_X_V、q_Y_V、q_Z_V均为单位向量:

q_X_V= $\begin{matrix} {[\begin{matrix} 1 & 0 & 0 & 0 & 0 & 0 \end{matrix}]}^{T} \end{matrix}$

q_Y_V= $\begin{matrix} {[\begin{matrix} 0 & 1 & 0 & 0 & 0 & 0 \end{matrix}]}^{T} \end{matrix}$

q_Z_V= $\begin{matrix} {[\begin{matrix} 0 & 0 & 1 & 0 & 0 & 0 \end{matrix}]}^{T} \end{matrix}$

上述各式中出现的质量矩阵M和刚度矩阵K分别在对应的参考坐标系中进行表示。

3 稳健设计流程

动力总成悬置系统设计中的不确定因素有很多, 其中影响最大的是悬置刚度的不确定性。以广泛采用的弹性悬置为例, 其刚度误差普遍约为15%^[3]。由于悬置刚度基本服从正态分布, 因此设计中采用计算精度最优的蒙特卡洛模拟方法对设计点的稳健性进行评价。

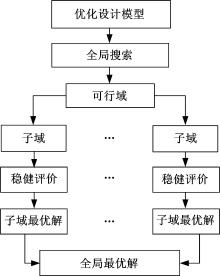
设计中需要对频率分布、解耦水平等进行约束, 因此, 不论是确定设计还是稳健设计都必须满足约束条件。约束条件在设计空间中确定出一个可行域, 该区域的每个设计点都满足约束条件, 而系统最终的设计方案也必定位于该区域。系统的可行域可采用全局优化算法进行确定, 但搜索过程有别于优化过程。在稳健设计中, 需要对可行域内的每个设计点进行稳健评价, 通过比较评价结果从而确定系统的最优方案。

在应用蒙特卡洛模拟方法时, 一个无法回避的关键问题是计算量过大。针对该问题, 在制定稳健设计流程时, 将可行域拆分为多个子域, 然后将每个子域分配至计算机的指定计算核心, 每个核心负责一个子域内所有设计点的稳健评价并确定该子域内的最优解, 最后综合各子域的计算结果得到全局最优解。通过在多核计算机上应用并行计算技术可以有效提高设计效率。

综上所述, 动力总成悬置系统的稳健设计流程如图2所示。

	Figure Option View Download New Window
	图2 稳健设计流程Fig.2 Flow of robust design

采用可行设计点的集合代表可行域相当于对可行域进行离散化, 而每个可行点就是一块可行域的代表。因此, 计算得到的最优设计点表征了理想最优点所在的区域。如果设计精度不满足要求, 可以借助蒙特卡洛抽样技术或优化算法在结果附近做进一步搜索。

4 稳健设计实例

4.1 系统结构及参数

以某动力总成悬置系统为例, 参考上述设计流程对系统进行稳健设计。已知该动力总成横向安装于车辆前部, 发动机为直列四缸四冲程形式, 怠速转速为650 r/min, 系统采用4点悬置形式。假定动力总成的安装倾角很小, 因此可近似认为X_C轴与Y_V轴, Y_C轴与X_V轴, Z_C轴与Z_V轴平行。

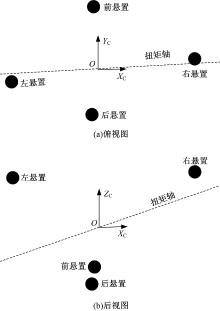
动力总成的质量为215 kg, 惯量参数在曲轴坐标系中测量, 具体数值如表1所示。系统各悬置布局及扭矩轴方向如图3所示^[3]。

表1 动力总成惯量参数 Table 1 Inertia parameters of powertrain kg· m²

	Figure Option View Download New Window
	图3 悬置布局与扭矩轴方向Fig.3 Configuration of mounts and orientation of TRA

系统中各悬置的安装位置、安装方向及初始刚度分别如表2~表4所示。悬置的安装位置在曲轴坐标系中描述; 安装方向通过局部坐标系与曲轴坐标系的各坐标轴夹角进行表示; 悬置刚度在局部坐标系中描述。

表2 悬置安装位置 Table 2 Locations of mounts mm

表3 悬置安装方向 Table 3 Orientations of mounts (° )

表4 悬置初始刚度 Table 4 Initial stiffness of mounts N/mm

4.2 稳健优化模型的建立

稳健优化与确定优化的不同之处在于设计过程中即考虑到了不确定因素对系统性能的影响, 通过构造稳健目标函数来改善系统性能的稳健性。动力总成悬置系统的稳健优化模型建立如下:

(1)设计变量:优化设计中保持悬置的安装方位不变, 只选择悬置刚度作为设计变量, 刚度的变化范围设定为[40, 200]N/mm。设计中考虑悬置刚度的3个不确定水平, 分别取为刚度设计值的5%、15%和30%。

(2)目标函数:根据固有频率由低到高的分布, 系统各阶模态的形状设置如下:纵向平动、垂向跳动、侧向平动、俯仰转动、侧倾转动、横摆转动。需要注意的是, 该设置与系统在初始状态下的各阶模态形状不同。

根据第2节提出的解耦设计要求, 需要对系统5阶模态的形状进行规划。但是, 由于Z_C轴和Z_V轴平行, 因此模态规划的数目减为4个, 对应系统的前4阶模态。设计中采用解耦率(模态能量百分比)作为模态规划的评价指标, 解耦率越高, 说明模态形状越接近目标形状。

稳健目标函数参考Taguchi稳健设计方法进行制定。对于具有望大特性的目标函数y, 其信噪比S/N的计算公式如下:

$\begin{matrix} S / N = - 10 \lg (\frac{1}{n} \overset{n}{\sum_{i = 1}} \frac{1}{y_{i}^{2}}) \end{matrix}$ (4)

式中:y_i为对应第i项噪声因子组合的目标函数值。

参考式(4)建立动力总成悬置系统第i阶模态解耦率的稳健指数RI_i如下所示:

$\begin{matrix} R I_{i} = \frac{1}{N} \overset{N}{\sum_{j = 1}} \frac{1}{R_{i, j}^{2}} \end{matrix}$ (5)

式中:R_i_,_j为第i阶模态在第j次蒙特卡洛模拟评价时的解耦率, %; N为每个设计点处执行蒙特卡洛模拟评价的次数。

动力总成悬置系统的稳健目标函数F_R取各稳健指数的加权和:

$\begin{matrix} F_{R} (k) = \overset{4}{\sum_{i = 1}} (c_{i} R I_{i}) = \overset{4}{\sum_{i = 1}} (\frac{c_{i}}{N} \overset{N}{\sum_{j = 1}} \frac{1}{R_{i, j}^{2}}) \end{matrix}$ (6)

式中:k为悬置刚度(设计变量)向量, N/mm; c_i为第i阶模态解耦率稳健指数的加权系数。

根据式(6)建立系统确定设计的目标函数F_D, 以便与稳健设计进行对比:

$\begin{matrix} F_{D} (k) = \overset{4}{\sum_{i = 1}} \frac{c_{i}}{R_{i}^{2}} \end{matrix}$ (7)

式中:R_i为第i阶模态的解耦率。

(3)约束条件:根据动力总成的怠速转速及隔振性能要求, 固有频率的设计上限取为14 Hz; 根据车辆其他子系统的频率分布等因素, 固有频率的设计下限取为6 Hz。为了保证系统的隔振性能及各阶频率的合理分布, 设定垂向跳动频率不大于8 Hz, 俯仰转动频率不大于10 Hz; 同时, 相邻两阶频率的间隔不小于1 Hz。为了保证系统的解耦水平, 设定系统的第1阶与第3阶模态解耦率不小于90%; 第2阶与第4阶模态解耦率不小于95%; 第5阶与第6阶模态解耦率不小于85%。

动力总成悬置系统的稳健优化设计模型表示如下:

min.F_R(k)= $\begin{matrix} \overset{4}{\sum_{i = 1}} \end{matrix} \begin{matrix} (\frac{c_{i}}{N} \overset{N}{\sum_{j = 1}} \frac{1}{R_{i, j}^{2}}) \end{matrix}$

s.t. $\begin{matrix} \{\begin{matrix} 40 \leq k \leq 200; \\ R_{1} \geq 90 %; R_{2} \geq 95 %; R_{3} \geq 90 %; \\ R_{4} \geq 95 %; R_{5} \geq 85 %; R_{6} \geq 85 %; \\ f_{1} \geq 6; f_{2} \leq 8; f_{4} \leq 10; f_{6} \leq 14; \\ Δ f_{i} \geq 1, i = 1, 2, \dots, 5 \end{matrix} \end{matrix}$

式中:f_i为第i阶固有频率, Hz; Δ f_i为第i阶与第i+1阶固有频率的间隔, Hz。

系统对应的确定优化设计模型表示如下:

min. F_D(k)= $\begin{matrix} \overset{4}{\sum_{i = 1}} \end{matrix} \begin{matrix} \frac{c_{i}}{R_{i}^{2}} \end{matrix}$

4.3 优化计算及结果分析

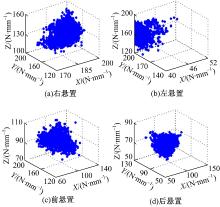
根据第3节制定的稳健设计流程, 首先根据约束条件确定该设计的可行域。采用非支配排序遗传算法(Non-dominated sorting genetic algorithm-II, NSGA-II)在整个设计空间内搜索可行设计点, 搜索得到的全部设计点组成该设计的可行域。

设置遗传算法的群体数目为20个, 进化次数为500次。计算结束后总共得到7052个可行设计点, 如图4所示。

	Figure Option View Download New Window
	图4 动力总成悬置系统设计的可行域Fig.4 Feasible region in design of powertrain mounting system

根据稳健目标函数F_R对可行域中的所有设计点进行稳健评价。在某4核计算机上应用Matlab软件提供的SPMD并行结构执行评价计算, 将可行域平均分配至各计算核心, 每颗核心对1763个可行点执行稳健评价。采用蒙特卡洛模拟技术制定稳健评价试验, 每个设计点评价次数为1000次。计算完成后, 根据评价结果选择目标函数值最小的设计点作为稳健设计的最优方案。

优化后的悬置刚度值如表5所示; 各设计方

表5 优化设计后的悬置刚度 Table 5 Stiffness of mounts in optimal design

案下的系统固有频率分布如表6所示; 解耦率理论值如表7所示; 优化模态的解耦率稳健指数如表8所示; 解耦率的平均值和标准差分别如表9和表10所示。各表中同时给出了系统的确定优化结果作为对比。

表6 优化设计后的固有频率值 Table 6 Natural frequencies of system in optimal design

表7 优化设计后的模态解耦率理论值 Table 7 Theoretical decoupling ratio in optimal design

表8 优化设计后的解耦率稳健指数 Table 8 Robust index of decoupling ratio in optimal deisgn

表9 优化模态的解耦率平均值 Table 9 Mean value of decoupling ratio in optimal design

表10 优化模态的解耦率标准差 Table 10 Standard deviation of decoupling ratio in optimal design

优化得到的确定解只有一个, 而稳健解则与设计变量的不确定水平有关。在3个不确定水平下能够得到3组不同的稳健解, 对应系统3种不同的设计方案。

根据表5中的结果可知, 优化计算得到的5%不确定水平下的稳健解与确定解相同。确定设计以系统解耦率的最大化作为设计目标, 确定解对应系统性能最佳的设计; 而各阶模态的稳健指数则是通过对蒙特卡洛模拟结果进行统计而得到的, 稳健解对应系统稳健性最佳的设计。通过比较表7和表9中的结果可知, 在5%不确定水平下, 直接计算得到的解耦率理论值与统计计算得到的解耦率平均值相差不大, 因此, 稳健目标函数与确定目标函数近似相等, 这就是稳健解与确定解相同的原因。但是, 随着不确定水平的升高, 解耦率理论值与平均值的偏差也逐渐增大, 当稳健目标函数与确定目标函数相差较大时, 优化得到的稳健解与确定解便不再相同。

根据表6中的结果可知:当不确定水平由5%升至15%时, 系统固有频率呈整体下降趋势; 当不确定水平进一步升至30%时, 前3阶频率变化不大, 第4阶频率进一步减小, 而后两阶频率呈增大趋势。根据设计的约束条件可知, 系统第2阶、第4阶和第6阶频率的减小有助于降低违背约束的概率, 提高系统的可靠性。随着不确定水平的升高, 系统的第2阶和第4阶频率呈下降趋势, 由此可知, 稳健设计在提高系统稳健性的同时, 也有助于改善系统的隔振性能。

根据表8中的结果可知, 不确定水平为15%和30%时, 各阶模态在稳健设计后的稳健水平相比确定设计有普遍提高。当悬置刚度的不确定水平很高时, 模态解耦率的分布范围也变得很大。当针对某可行点进行蒙特卡洛模拟试验时, 可能会出现与解耦设计要求偏差很大的点, 这类点会极大地降低该可行点的稳健水平, 这就是确定解在30%水平下稳健指数非常大的原因。如果悬置刚度的波动使系统恰好位于此类点附近, 那么系统性能将会受到极大影响, 因此设计中应该极力避免这种情况的发生。与确定解相比, 稳健解在该水平下的稳健指数显著减小, 这表示系统的稳健水平得到了明显改善。

由于稳健目标函数是基于信噪比而制定的, 因此它是一个综合评价指标。但是, 根据表9和表10中的结果可知, 稳健解与确定解在各水平下的解耦率平均值都相差不大, 而稳健解的标准差相对确定解则明显减小, 这说明两种优化方案在系统性能方面差别不大; 但是, 稳健设计方案的系统性能受悬置刚度波动的影响更小, 因而系统稳健性更好。

5 结论

(1)针对悬置系统受到的发动机扭矩、不平衡惯性力以及车身激励, 通过在指定坐标系中对相应模态的形状进行规划能够实现系统在特定激励下响应方向的恒定。

(2)结合全局优化算法与并行计算技术对悬置系统进行稳健设计。首先应用全局优化算法在设计空间中搜索可行域, 然后将可行域拆分并分配至计算机各核心用于执行稳健评价。借助并行计算技术能够有效提高稳健设计的效率。

(3)当不确定水平较低时, 稳健目标函数与确定目标函数的值近似相等, 因而优化得到的稳健解与确定解相同。稳健设计方案模态解耦率的平均值相对确定设计方案变化不大, 但是标准差却有明显减小, 尤其是当设计变量的不确定水平较高时, 稳健性设计方案对系统的稳健性有显著改善。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	张代胜, 张旭, 王浩, 等. 基于Taguchi方法的动力总成悬置系统稳健优化[J]. 汽车工程, 2014, 36(4): 475-480. Zhang Dai-sheng, Zhang Xu, Wang Hao, et al. Robust optimization of powertrain mounting system based on Taguchi method[J]. Automotive Engineering, 2014, 36(4): 475-480. [本文引用:1]
[2]	吴杰, 上官文斌. 基于6σ的动力总成悬置系统鲁棒优化设计[J]. 振动与冲击, 2008, 27(8): 64-67. Wu Jie, Shangguan Wen-bin. Robust optimization design of powertrain mounting systems based on six sigma[J]. Journal of Vibration and Shock, 2008, 27(8): 64-67. [本文引用:1]
[3]	Wu Jie, Shangguan Wen-bin. Robust optimization design method for powertrain mounting systems based on six sigma quality control criteria[J]. International Journal of Automotive Technology, 2010, 11(5): 651-658. [本文引用:3]
[4]	Wu J. Optimization method for powertrain mounting systems with uncertain parameters[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2012, 226(2): 147-157. [本文引用:1]
[5]	吴杰, 董志新. 动力总成悬置系统稳健设计的区间和随机模型对比研究[J]. 振动与冲击, 2013, 32(20): 76-80. Wu Jie, Dong Zhi-xin. Two optimization models for robust design of a powertrain mounting system[J]. Journal of Vibration and Shock, 2013, 32(20): 76-80. [本文引用:1]
[6]	张武, 陈剑, 夏海. 基于灵敏度分析的发动机悬置系统稳健优化设计[J]. 汽车工程, 2009, 31(8): 728-732. Zhang Wu, Chen Jian, Xia Hai. Robust optimal design of an engine mounting system based on sensitivity analysis[J]. Automotive Engineering, 2009, 31(8): 728-732. [本文引用:1]
[7]	时培成, 高立新. 基于灵敏度分析的动力总成悬置系统优化[J]. 汽车工程, 2011, 33(12): 1057-1061. Shi Pei-cheng, Gao Li-xin. Optimization of powertrain mounting system based on sensitivity analysis[J]. Automotive Engineering, 2011, 33(12): 1057-1061. [本文引用:1]
[8]	谢展, 于德介, 李蓉. 汽车发动机悬置系统的多目标稳健优化设计[J]. 汽车工程, 2013, 35(10): 893-897. Xie Zhan, Yu De-jie, Li Rong. Multi-objective robust optimization design of vehicle engine mount systems[J]. Automotive Engineering, 2013, 35(10): 893-897. [本文引用:1]
[9]	刘仁云, 张义民, 于繁华. 基于灰色粒子群算法的可靠性稳健优化设计[J]. 吉林大学学报: 工学版, 2006, 36(6): 893-897. Liu Ren-yun, Zhang Yi-min, Yu Fan-hua. Robust optimization design for reliability based on grey particle swarm algorithm[J]. Journal of Jilin University(Engineering and Technology Edition), 2006, 36(6): 893-897. [本文引用:1]
[10]	陈达亮, 吕静, 李洪亮. 动力总成悬置系统怠速隔振优化策略研究[J]. 噪声与振动控制, 2011, 31(5): 53-57. Chen Da-liang, Lü Jing, Li Hong-liang. Research on optimization strategy of power-plant mounting system for idle shake control[J]. Noise and Vibration Control, 2011, 31(5): 53-57. [本文引用:1]
[11]	Jeong T, Singh R. Analytical methods of decoupling the automotive engine torque roll axis[J]. Journal of Sound and Vibration, 2000, 234(1): 85-114. [本文引用:1]

2014

0.0

. 2014, 36(4):475-480 DOI:doi:10.3969/j.issn.1000-680X.2014.04.017

Robust optimization of powertrain mounting system based on Taguchi method

基于Taguchi方法的动力总成悬置系统稳健优化

Zhang Dai-sheng , Zhang Xu , Wang Hao

张代胜, 张旭, 王浩

为提高动力总成悬置系统的隔振性能及其优化设计的稳健性,首先建立悬置系统6自由度模型,并以各自由度方向的解耦率最大为目标,以各悬置点三向刚度为设计变量,选用遗传算法对悬置刚度参数进行初步优化;接着选择解耦率高且刚度分布合理的个体作为对象,以信噪比作为评价指标,应用Taguchi方法进行一次或者多次稳健优化,获得较为理想的优化解;最后应用蒙特卡罗方法进行稳健分析.结果表明,该方法在保证刚度合理分布的基础上,能有效提高各自由度方向上的解耦率,增强悬置系统的稳健性.

... 张代胜等应用Taguchi方法对初步优化后的悬置系统做进一步的稳健设计^[1] ...

2008

0.0

. 2008, 27(8):64-67 DOI:doi:10.3969/j.issn.1000-3835.2008.08.015

Robust optimization design of powertrain mounting systems based on six sigma

基于6#cod#x003c3;的动力总成悬置系统鲁棒优化设计

Wu Jie , Shangguan Wen-bin.

吴杰, 上官文斌

为提高动力总成悬置系统优化设计的鲁棒性,给出一种6σ鲁棒优化设计方法.将动力总成视为六自由度刚体,由四个橡胶悬置支撑在副车架上,每个悬置被简化成沿其三个垂直的弹性主轴方向具有刚度和阻尼的元件.将四个悬置的安装位置、三向静刚度和两个防扭悬置的安装方位角选为不确定性设计变量,设计变量的不确定性由其名义值加、减一个摄动量(或名义值的一个百分比)来表征.通过优化设计变量的名义值得到动力总成悬置系统的6σ鲁棒最优设计.优化结果表明,6σ鲁棒最优设计能够保证动力总成悬置系统以较好地鲁棒性满足固有频率、解耦率以及频率间隔的要求.

... 吴杰等应用6sigma方法对悬置系统的解耦率进行稳健设计,同时考虑频率分布和频率间隔对系统可靠性的影响^[2,3] ...

2010

0.0

... 吴杰等应用6sigma方法对悬置系统的解耦率进行稳健设计,同时考虑频率分布和频率间隔对系统可靠性的影响^[2,3] ...

... 以广泛采用的弹性悬置为例,其刚度误差普遍约为15%^[3] ...

... 系统各悬置布局及扭矩轴方向如图3所示^[3] ...

2012

0.0

... 除了上述两种方法,文献^[4,5]将区间分析技术,文献^[6,7]将灵敏度分析技术引入稳健优化模型的构建 ...

2013

0.0

. 2013, 32(20):76-80 DOI:doi:10.3969/j.issn.1000-3835.2013.20.015

Two optimization models for robust design of a powertrain mounting system

动力总成悬置系统稳健设计的区间和随机模型对比研究

Wu Jie , Dong Zhi-xin.

吴杰, 董志新

The mount stiffness of a powertrain mounting system (PMS) generally fluctuates around its nominal design value due to measurement inaccuracy, processing and installation errors, and material aging. To improve the robustness of the frequency allocation and decoupling layout of a PMS, an interval optimization model is presented, in which interval number is used to describe the uncertainty of the mount stiffness, and interval reliability and interval possibility indices are used to characterize the robustness of the decoupling layout and frequency allocation, respectively. Then a six-sigma robust optimization model is constructed in which the mount stiffness is assumed to obey uniform distribution. The interval optimization and six-sigma optimization approaches are used to maximize the decoupling ratios of a general car PMS under robustness requirements of frequency allocation and decoupling layout. Optimization results show that both the interval optimization and the six-sigma optimization can obtain satisfactory robust design, and the optimization results of the two optimization methods have good consistency.

由于测量、加工、安装误差及老化等原因，悬置实际刚度通常在其名义设计值附近波动。为提高悬置系统频率配置和解耦布置的稳健性，文中采用区间数描述悬置刚度的波动范围，采用区间概率度和区间可靠度分别表征频率配置和解耦布置的稳健性，首先建立了悬置系统的区间稳健优化模型。假设悬置刚度的波动服从均匀分布，建立了悬置系统的随机稳健优化模型。将两种优化模型用于对某轿车悬置系统频率和解耦率的稳健性优化，结果表明，区间和随机稳健优化结果具有较好地一致性。

... 除了上述两种方法,文献^[4,5]将区间分析技术,文献^[6,7]将灵敏度分析技术引入稳健优化模型的构建 ...

2009

0.0

. 2009, 31(8):728-732 DOI:doi:10.3321/j.issn:1000-680X.2009.08.010

Robust optimal design of an engine mounting system based on sensitivity analysis

基于灵敏度分析的发动机悬置系统稳健优化设计

Zhang Wu , Chen Jian , Xia Hai.

张武, 陈剑, 夏海

以发动机悬置系统能量解耦为目标,悬置刚度参数为设计变量,考虑目标函数和约束函数对于悬置刚度参数的灵敏度,构造了多目标优化数学模型.采用遗传优化算法对一款发动机悬置系统的悬置刚度参数进行了稳健优化设计,并用Monte Carlo方法进行了分析.结果表明,优化方法可以有效降低系统解耦度对悬置刚度参数的灵敏度,提高了悬置系统设计的实用性.

... 除了上述两种方法,文献^[4,5]将区间分析技术,文献^[6,7]将灵敏度分析技术引入稳健优化模型的构建 ...

2011

0.0

. 2011, 33(12):1057-1061

Optimization of powertrain mounting system based on sensitivity analysis

基于灵敏度分析的动力总成悬置系统优化

Shi Pei-cheng , Gao Li-xin.

时培成, 高立新

针对某车动力总成悬置系统固有频率偏高和振动耦合严重的问题,建立了该车动力总成悬置系统6自由度模型,并对悬置元件的主刚度参数进行了灵敏度分析.以分析找出的少量敏感参数为设计变量,结合振动解耦和固有频率匹配理论,对该悬置系统参数进行了优化,并对优化前后的动力总成悬置系统进行了台架试验.结果表明,优化后的悬置系统隔振能力有了较大提高,取得了显著效果.同时说明,通过对相关参数进行灵敏度分析,减少设计变量,可提高优化效率,减少设计工作量.

... 除了上述两种方法,文献^[4,5]将区间分析技术,文献^[6,7]将灵敏度分析技术引入稳健优化模型的构建 ...

2013

0.0

. 2013, 35(10):893-897 DOI:doi:10.3969/j.issn.1000-680X.2013.10.008

Multi-objective robust optimization design of vehicle engine mount systems

汽车发动机悬置系统的多目标稳健优化设计

Xie Zhan , Yu De-jie , Li Rong.

谢展, 于德介, 李蓉

摘　要：针对悬置元件的参数不确定性问题和单目标优化的局限，将稳健设计与多目标优化相结合，提出一种发动机悬置系统多目标稳健优化方法。该方法考虑了悬置刚度的不确定性，并假设其服从正态分布；通过拉丁超立方抽样得到动反力的稳健性函数，并将其作为Pareto多目标优化目标函数向量的组成部分；应用遗传算法对优化模型进行全局寻优，找到所有Pareto最优解，并通过稳健性评价得到既优化又稳健的解。最后以某型轿车的发动机悬置系统优化为例，验证了该方法的有效性。

... 谢展等采用拉丁超立方抽样技术对多目标优化得到的悬置系统Pareto解集进行稳健评价,从而实现既优化又稳健的系统设计^[8] ...

2006

0.0

. 2006, 36(6):893-897 DOI:doi:10.3969/j.issn.1671-5497.2006.06.013

Robust optimization design for reliability based on grey particle swarm algorithm

基于灰色粒子群算法的可靠性稳健优化设计

Liu Ren-yun , Zhang Yi-min , Yu Fan-hua.

刘仁云, 张义民, 于繁华

为提高车辆零部件的安全性和稳健性,应用可靠性稳健优化设计理论和多目标决策方法,将车辆前轴的可靠性稳健优化设计转化为多目标优化问题.运用灰色理论中的关联分析法,选取粒子群算法中的全局极值和个体极值,提出了适合可靠性稳健优化设计中多目标模型求解的灰色粒子群算法.与传统方法相比,该方法更能迅速准确地得到车辆前轴的可靠性稳健优化设计信息.

... 现有文献提出了多种新的稳健设计指标,并可将新型算法用于稳健模型的优化求解^[9] ...

2011

0.0

. 2011, 31(5):53-57 DOI:doi:10.3969/j.issn.1006-1355-2011.05.013

Research on optimization strategy of power-plant mounting system for idle shake control

动力总成悬置系统怠速隔振优化策略研究

Chen Da-liang , L#cod#x000fc; Jing , Li Hong-liang.

陈达亮, 吕静, 李洪亮

在车型早期开发阶段,模态解耦设计是动力总成悬置系统怠速工况隔振设计的理想选择。如何选择解耦坐标系,以及制定出合理的模态优化策略是获得具有良好隔振性能悬置系统的关键。本文通过对比研究动力总成悬置系统刚体模态参数与动态悬置力响应之间的关联性,指出悬置系统模态解耦设计时提高有效性的一般性规则。

... 动力总成悬置系统固有属性的设计一般在3套坐标系中进行,分别为:曲轴坐标系{X_C,Y_C,Z_C}、扭矩轴坐标系{X_T,Y_T,Z_T}和车辆坐标系{X_V,Y_V,Z_V}^[10] ...

2000

0.0

... 2 动力总成悬置系统解耦设计要求由扭矩轴解耦法的数学基础可知,如果系统在激励作用下产生了恒定方向的响应,那么该响应一定属于系统的振动模态^[11] ...