某双筒液阻式减振器外特性建模

引用本文

庄晔, 陈禹行, 杨业海, 徐淑芳. 某双筒液阻式减振器外特性建模.吉林大学学报:工学版, 2016, 46(3): 732-736
ZHUANG Ye, CHEN Yu-hang, YANG Ye-hai, XU Shu-fang. Twin-tube hydraulic shock absorber F-V modeling based on structure parameters. Journal of Jilin University Engineering and Technology Edition, 2016, 46(3): 732-736 复制到剪切板

Permissions

某双筒液阻式减振器外特性建模

庄晔, 陈禹行, 杨业海, 徐淑芳

吉林大学汽车仿真与控制国家重点实验室,长春 130022

作者简介:庄晔(1975-),男,副教授,博士生导师.研究方向:轮胎与悬架建模与应用.E-mail:yzhuang_cn@163.com

基金:“973”国家重点基础研究发展计划项目(2011CB711201)

摘要

首先建立了筒式液阻减振器阀片受力变形的精确有限元模型,求出了阀片所受载荷与阀片挠度曲线的数值关系,从而得到了减振器内部阀系流量与压差的关系。然后将此阀系的特性曲线代入到基于结构的减振器模型中,并把减振器模型的输出曲线与台架示功试验曲线进行对比。仿真结果与试验结果有很好的一致性,验证了该模型的准确性。最后,通过仿真研究了复原阀结构参数对阻尼特性的影响。

关键词: 车辆工程; 阀片变形; 有限元建模; 减振器

中图分类号:U463 文献标志码:A 文章编号:1671-5497(2016)03-0732-05

Twin-tube hydraulic shock absorber F-V modeling based on structure parameters

ZHUANG Ye, CHEN Yu-hang, YANG Ye-hai, XU Shu-fang

State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130022, China

Abstract

A twin-tube hydraulic shock absorber F-V model is proposed based on structure parameters. First, a finite element model of the shock absorber rebound valve plate is established, and the load versus valve deflection curve is obtained with the model. The relationship between flow rate and pressure variation is then calculated. Then, this curve is integrated into the shock absorber model. The comparison between the model output and experiment data demonstrates the high accuracy of the proposed model. Finally the influence of the structure parameters of the rebound valve on the damping performance is analyzed through simulation.

Keyword: vehicle engineering; valve plate deflection; finite element method(FEM) modeling; shock absorber

Show Figures

0 引言

减振器阻尼特性是影响汽车平顺性最主要的因素之一, 因此, 对减振器进行研究十分重要^{[1, 2, 3]}。但由于减振器阻尼特性涉及的因素很多, 基于结构的建模十分复杂。现有的理论研究大多是基于减振器内特性的经验或半经验模型^{[4, 5, 6, 7, 8]}。在实际减振器产品设计中, 人们在减振器阀片参数与其阻尼特性的关系方面积累了大量的经验, 对减振器的设计也大多是基于这些经验数据。但是建立基于结构的减振器模型, 可在减振器的样件试制之前进行结构分析, 从而更明确地选用合适的阀片参数, 大大缩短减振器设计和开发周期。减振器结构建模的关键在于阀片载荷与阀片挠度关系(也就是压差与流量之间的关系)的精确求解。阀片变形属于大挠曲变形, 一些学者用摄动法求解压力与阀片挠度的关系^[9], 取得了较好的结果。但此方法要求阀片几何形状简单, 所受载荷只能是均布载荷或集中载荷, 适用范围较小。

本文使用有限元工具建立了减振器阀片变形的精确模型, 通过此模型求出压力与阀片挠曲线的关系, 进而求出减振器内部阀系压差与流量的关系, 最后建立了基于结构的减振器外特性计算模型并进行了试验验证, 结果证明了本文仿真模型的正确性。

1 阀片变形有限元模型

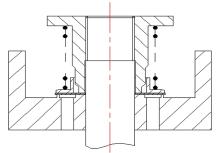
图1为减振器复原阀系结构简图, 阀片内端固定, 外端由螺旋弹簧支撑, 螺旋弹簧对阀片施加预紧力。复原阀片有两片, 靠近活塞的一片上有3个固定缺口, 当阀片所受压力小于开阀压力时, 油液通过由这些固定缺口组成的常通孔流出; 当阀片所受压力超过开阀压力后, 油液推动阀片变形, 形成一个面积可变的柱形节流孔, 油液通过常通孔和面积可变的柱形节流孔流出。

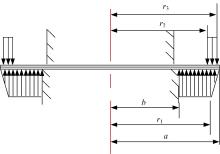
	Figure Option View Download New Window
	图1 某减振器阀片结构简图Fig.1 Structure of shim valve of shock absorber

图2为减振器阀片受力模型。其中的结构参数如下:阀片内端半径为b; 外端半径为a; 活塞上有一内径为r₁ 、外径为a的凸台, 活塞两端压差在此凸台上由Δ P降至0。阀片组受到3种载荷的共同作用:由b到r₁ 的均布载荷; 由r₁ 到a的渐降载荷, 可以认为此载荷是线性降低的; 螺旋弹簧对阀片施加的载荷, 此载荷作用范围为r₂ 至r₃的一个环形带。

	Figure Option View Download New Window
	图2 减振器复原阀片受力模型Fig.2 Diagram of the rebound valve disk under distributional pressure load

依据以上结构尺寸可在有限元软件中建立阀片的网格模型, 并依据以上3种载荷对阀片设定边界条件。由于此阀片结构具有一定的对称性特点, 为减少计算量此处可选取1/4结构进行有限元计算。经过运算, 减振器阀片在指定载荷下的变形分布有限元模型如图3所示。

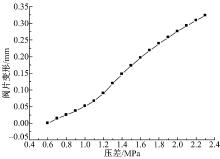
	Figure Option View Download New Window
	图3 阀片变形分布有限元模型Fig.3 Finite element modeling of the shim valve deflection distribution

进一步可计算阀片在其工作的压差变化范围内所产生的变形。其中, 在开阀前, 阀片变形一直为0; 开阀后, 求得阀片在不同压差下的端部变形曲线如图4所示。从图4可以看出:变形与压差间存在较强的非线性关系, 若将压差与变形的关系假设为线性变化, 将给减振器外特性计算带来较大误差。此非线性关系主要由于阀片的大变形导致。由图4可以看出:阀片的最大变形为0.35 mm, 但与阀片的厚度(0.15~0.3 mm)相比, 此变形已远远超出了线性变形区域。

	Figure Option View Download New Window
	图4 随压差变化的阀片变形仿真曲线Fig.4 Shim valve tip deflection under different pressure by finite element simulation

2 减振器结构模型

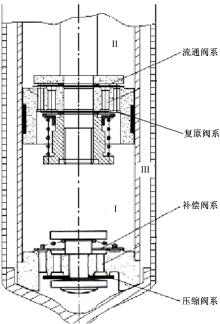
建立减振器结构模型, 就是建立各腔室之间的压力关系。普通双筒减振器有3个腔室:无杆腔I、有杆腔II、储油腔III; 4个阀系:位于活塞阀上的复原阀和流通阀, 位于底阀上的补偿阀和压缩阀, 具体如图5所示。储油腔上端有一定体积的气体, 气体体积随活塞杆推入或抽离工作缸而变化, 储油腔油压等于气体压力。由气态方程可求出气体压力和体积分别为:

$P_{g} = P_{g 0} \frac{V_{g 0}^{r}}{V_{g}^{r}}$ (1)

$V_{g} = V_{g 0} + A_{rod} x$ (2)

式中: $\begin{matrix} P_{g} 、 V_{g} \end{matrix}$ 分别为气体的压力和体积; $\begin{matrix} P_{g 0} 、 V_{g 0} \end{matrix}$ 分别为气体的初始压力和初始体积; $\begin{matrix} r \end{matrix}$ 为气体多变指数; $\begin{matrix} A_{rod} \end{matrix}$ 为活塞杆截面积。

	Figure Option View Download New Window
	图5 减振器结构图Fig.5 Structure of the shock absorber

无杆腔与储油腔之间通过底阀相连, 无杆腔I的压力为:

$\begin{matrix} P_{I} = P_{g} + Δ P_{b} \end{matrix}$ (3)

式中: $\begin{matrix} Δ P_{b} \end{matrix}$ 为油液经过底阀时的压差, 复原行程油液通过补偿阀从储油腔流入无杆腔I, 压缩行程油液通过压缩阀从无杆腔I流入储油腔, 即:

$\begin{matrix} Δ P_{b} = \{\begin{matrix} - Δ P_{comp}, v > 0 \\ Δ P_{c}, v < 0 \end{matrix} \end{matrix}$ (4)

式中: $\begin{matrix} Δ P_{comp} 、 Δ P_{c} \end{matrix}$ 分别为补偿阀、压缩阀两端压差。

有杆腔II与无杆腔I之间通过活塞阀相连, 有杆腔II的压力为:

$\begin{matrix} P_{II} = P_{I} + Δ P_{p} \end{matrix}$ (5)

式中: $\begin{matrix} Δ P_{p} \end{matrix}$ 为油液经过活塞阀时的压差, 复原行程油液通过复原阀由无杆腔I流入有杆腔II, 压缩行程油液通过流通阀由无杆腔I流入有杆腔II, 即:

$\begin{matrix} Δ P_{p} = \{\begin{matrix} Δ P_{r}, v > 0 \\ - Δ P_{cur}, v < 0 \end{matrix} \end{matrix}$ (6)

式中: $\begin{matrix} Δ P_{r} 、 Δ P_{cur} \end{matrix}$ 分别为复原阀、流通阀两端压差。

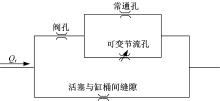
对于复原阀, 油液先通过阀孔, 继而流过阀片与活塞之间的孔隙, 速度小时油液通过复原阀片与活塞之间的常通孔, 速度大时复原阀片被推开, 油液通过常通孔和由阀片变形造成的柱形通流孔。同时, 油液可以通过活塞与缸桶之间的间隙直接在无杆腔与有杆腔之间流动。复原阀系流通路径如图6所示。

	Figure Option View Download New Window
	图6 复原阀系流通路径Fig.6 Rebound valve hydraulic diagram

对于阀孔, 流量与压差的关系为:

$\begin{matrix} Q_{1} = C_{d} A_{1} \sqrt[]{\frac{2}{ρ} Δ P_{1}} \end{matrix}$ (7)

式中: $\begin{matrix} C_{d} \end{matrix}$ 为流量系数; $\begin{matrix} Q_{1} 、 Δ P_{1} 、 A_{1} \end{matrix}$ 分别为阀孔的流量、压差和通流面积。

对于活塞与缸桶间的缝隙, 流量与压差的关系为:

$\begin{matrix} Q_{4} = \frac{πd H^{3}}{12 μl} Δ P_{4} \end{matrix}$ (8)

式中: $\begin{matrix} Q_{4} 、 Δ P_{4} \end{matrix}$ 分别为缝隙流量、压差; $\begin{matrix} H 、 l \end{matrix}$ 分别为缝隙高度、长度; $\begin{matrix} μ \end{matrix}$ 为油液动力黏度; $\begin{matrix} d \end{matrix}$ 为活塞直径。

对于常通孔, 流量与压差的关系为:

$\begin{matrix} Q_{2} = C_{d} A_{2} \sqrt[]{\frac{2}{ρ} Δ P_{2}} \end{matrix}$ (9)

式中: $\begin{matrix} Q_{2} 、 Δ P_{2} 、 A_{2} \end{matrix}$ 分别为常通孔的流量、压差和通流面积。

对于由阀片变形行成的柱形面积可变节流孔, 流量与压差的关系为:

$\begin{matrix} Q_{3} = C_{d} \cdot 2 π a_{3} ω \cdot \sqrt[]{\frac{2}{ρ} Δ P_{3}} \end{matrix}$ (10)

式中: $\begin{matrix} Q_{3} 、 Δ P_{3} \end{matrix}$ 分别为柱形通流孔的流量、压差; $\begin{matrix} a_{3} \end{matrix}$ 为复原阀片的半径; $\begin{matrix} ω \end{matrix}$ 为阀片的开口挠度, 由 $\begin{matrix} Δ P_{3} \end{matrix}$ 求出。

对于复原阀系, 流量与压差的关系为:

$\begin{matrix} \{\begin{matrix} Q_{r} = Q_{1} + Q_{4} \\ Q_{1} = Q_{2} + Q_{4} \\ Δ P_{r} = Δ P_{4} \\ Δ P_{4} = Δ P_{1} + Δ P_{2} \\ Δ P_{2} = Δ P_{3} \end{matrix} \end{matrix}$ (11)

压缩阀为一固定面积为 $\begin{matrix} A_{c 0} \end{matrix}$ 的常通孔, 其流量与压差的关系为:

$\begin{matrix} Q_{c} = C_{d} A_{c 0} \sqrt[]{\frac{2}{ρ} Δ P_{c}} \end{matrix}$ (12)

补偿阀和流通阀的通流面积较大, 产生的压降很小, 对减振器阻尼贡献较小, 可以认为其流量与两端压差成线性关系:

$Q_{comp} = K_{comp} Δ P_{comp}$ (13)

$Q_{curr} = K_{curr} Δ P_{curr}$ (14)

式中: $\begin{matrix} K_{comp} 、 K_{curr} \end{matrix}$ 分别为由补偿阀、流通阀结构参数决定的通流系数。

减振器输出力为:

$\begin{matrix} F = P_{II} (A_{piston} - A_{rod}) + P_{air} A_{rod} - P_{I} A_{piston} \end{matrix}$ (15)

式中: $\begin{matrix} A_{piston} \end{matrix}$ 为活塞截面积; $\begin{matrix} P_{air} \end{matrix}$ 为大气压力。

3 模型验证及分析

按照第2节中的方法, 在Matlab/Simulink下搭建某减振器结构模型, 并进行仿真计算。

3.1 模型验证

结合某减振器具体结构, 将其阀片的变形-压差的有限元计算结果代入减振器结构液压模型, 由第2节建立的Simulink仿真模型开展了减振器外特性的仿真计算。减振器主要结构参数如下:A_g=314.2 mm²; ρ =885 kg/m³; A₁=1963.5 mm²; C_d=0.62; P₀=1.18× 10⁵ Pa; P_air=1.01325× 10⁵ Pa; V₀=277.88 ml; a₃=13.5 mm; |F_f|=150 N; K_b=0.5× 10⁸ m³/Pa; H=0.8 mm; K_l=1.5× 10⁸ m³/Pa。

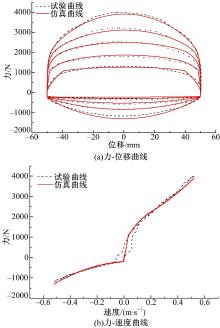
使用正弦激励模拟示功试验, 输入为减振器的拉伸变化量; 输出为减振器两端的反力。在示功机上同样进行振幅为50 mm的减振器示功试验, 并把试验结果与仿真结果进行对比。试验工况如表1所示, 对比结果如图7所示。由图7中可以看出:无论力-位移曲线还是力-速度曲线, 仿真结果与实验结果都有较好的一致性, 表明本文所建模型具有较高的精度。

表1 减振器试验工况 Table 1 Shock absorber experimental maneuvers

	Figure Option View Download New Window
	图7 减振器外特性仿真结果与试验结果对比Fig.7 Comparison of F-v between simulation and experimental result

3.2 复原阀结构参数对阻尼特性的影响

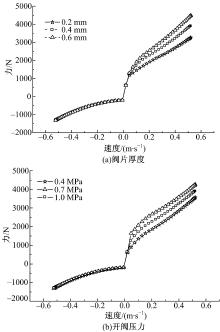
影响减振器阻尼特性的复原阀结构参数包括:螺旋弹簧预紧力(决定开阀压力)、常通孔面积、阀片厚度、内外径、材料和活塞与缸桶间缝隙等。本文以阀片厚度和开阀压力为例说明这两个结构相关参数对减振器阻尼特性的影响。三种不同阀片厚度下的减振器力-速度曲线, 如图8(a)所示。由图8(a)可见:阀片厚度的改变主要影响高速段(即开阀后)的阻尼变化, 阀片越厚其阻尼值越大。同理分析计算了不同开阀压力下的减振器力-速度曲线, 如图8(b)所示。由图8(b)可见, 三种不同的开阀压力下其阻尼力显著不同, 但与阀片厚度的影响略有不同, 开阀压力不同导致了开阀点速度不同, 开阀后不同开阀压力下的曲线中阻尼力显著不同, 但阻尼(斜率)差异很小。应用以上规律可在汽车底盘性能优化和调校中根据整车性能的需求优化调整减振器内部相应结构参数, 实现整车平顺性、操纵稳定性的改善。

	Figure Option View Download New Window
	图8 阀片厚度和开阀压力对减振器阻尼特性影响仿真曲线Fig.8 Simulation of the influence of shim valve thickness and shim valve opening pressure to shock absorber F-v curve

4 结论

(1)介绍了一种减振器结构建模方法。首先, 用有限元方法仿真阀系特性:通过求解出阀片所受载荷进一步求解出减振器各腔压差与阀系流量间的关系; 其次, 建立减振器内部液压动力学模型:通过求解减振器内部流量关系、压力关系, 得出减振器外力特性。

(2)从对比结果来看, 仿真结果与试验数据吻合得较好, 既验证了这种建模方法的有效性和准确性, 又验证了用有限元工具来求解减振器内部阀系特性的可行性。同时, 减振器结构建模为减振器的设计制造提供了依据。

(3)减振器作为一种非线性的部件, 内部仍有一些其他的非线性因素, 由于本文忽略了一些次要因素, 如试验数据中, 由于内部摩擦力的存在导致试验曲线有滞回圈的存在, 其他因素如油液内部泄漏等, 使得试验数据和仿真结果的对比上仍有差异。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	van Kasteel R. A new shock absorber model for use in vehicle dynamics studies[J]. Vehicle System Dynamics, 2005, 43(9): 613-631. [本文引用:1]
[2]	Li Shao-hua, Lu Yong-jie, Li Li-yang. Dynamical test and modeling for hydraulic shock absorber on heavy vehicle under harmonic and rand om loadings[J]. Research Journal of Applied Sciences, Engineering and Technology, 2012, 4(13): 1903-1910. [本文引用:1]
[3]	Dixon J C. The Shock Absorber Hand book[M]. 2nd ed. England : John Wiley & Sons Ltd, 2007. [本文引用:1]
[4]	Boggs C, Ahmadian M, Southward S. Efficient empirical modeling of a high-performance shock absorber for vehicle dynamics studies[J]. Vehicle System Dynamics, 2010, 48(4): 481-505. [本文引用:1]
[5]	Ferdek U, Luczko J. Modeling and analysis of a twin-tube hydraulic shock absorber[J]. Journal of Theoretical and Applied Mechanics, 2012, 50(2): 627-638. [本文引用:1]
[6]	Zacha C, Mack W, Fruhmann G, et al. On the performance of rheological shock absorber models in full vehicle simulation[J]. Vehicle System Dynamics, 2007, 45(11): 981-999. [本文引用:1]
[7]	Kate N B, Jadhav T A. Mathematical modeling of an automobile damper[J]. International Journal of Engineering Research, 2013, 2(7): 467-471. [本文引用:1]
[8]	Alonso M, Comas A. Modeling a twin tube cavitating shock absorber[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2006, 220(8): 1031-1040. [本文引用:1]
[9]	Czop P, Sławik D, Śliwa P, et al. Simplified and advanced models of a valve system used in shock absorbers[J]. Journal of Achievements in Materials and Manufacturing Engineering, 2009, 33(2): 173-180. [本文引用:1]

2005

0.0

... 0 引言减振器阻尼特性是影响汽车平顺性最主要的因素之一,因此,对减振器进行研究十分重要^[1,2,3] ...

2012

0.0

... 0 引言减振器阻尼特性是影响汽车平顺性最主要的因素之一,因此,对减振器进行研究十分重要^[1,2,3] ...

2007

0.0

... 0 引言减振器阻尼特性是影响汽车平顺性最主要的因素之一,因此,对减振器进行研究十分重要^[1,2,3] ...

2010

0.0