换道过程中越线时刻预测模型

引用本文

王畅, 杜康, 郑楚清. 换道过程中越线时刻预测模型.吉林大学学报:工学版, 2016, 46(3): 737-744
WANG Chang, DU Kang, ZHENG Chu-qing. Prediction model time-to-line-crossing during lane change process. Journal of Jilin University Engineering and Technology Edition, 2016, 46(3): 737-744 复制到剪切板

Permissions

换道过程中越线时刻预测模型

王畅, 杜康, 郑楚清

长安大学汽车学院, 西安 710064

作者简介:王畅(1984-),男,副教授,博士.研究方向:车辆主动安全技术.E-mail:wangchang@chd.edu.cn

基金:长江学者和创新团队发展计划项目(IRT1286); 国家自然科学基金项目(61374196,61473046); 中央高校基本科研业务费专项项目(310822151028)

摘要

分析了车辆换道过程中的运动几何特征,提出了车辆相对于车道线的偏航角度估算方法。在此基础上,分别建立了直道路段和弯道路段的越线时刻预测模型。利用视觉传感器、车载陀螺仪、车载CAN总线数据采集卡设计开发了测试平台,对多名被测试人员进行了驾驶测试,获取了大量的换道状态表征数据。利用实测换道数据对越线时刻预测模型进行验证,结果表明,直道路段预测结果中87.0%的误差绝对值小于等于0.1 s,弯道路段相应的比例达到了93.7%,且两类模型的预测误差值均符合正态分布规律。

关键词: 车辆工程; 越线时刻; 几何分析; 偏航角度估计; 车辆主动安全

中图分类号:U461.91 文献标志码:A 文章编号:1671-5497(2016)03-0737-08

Prediction model time-to-line-crossing during lane change process

WANG Chang, DU Kang, ZHENG Chu-qing

School of Automobile,Chang'an University,Xi'an 710064,China

Abstract

To solve the time-to-line-crossing (TLC) prediction problem during lane change process, the geometrical motion feature of vehicle during lane change was analyzed and a yaw angle estimation algorithm between vehicle and lane mark was proposed. Based on this, TLC prediction models for straight and curve roads were established. A test platform was developed which consists of vision sensor, vehicle gyro and onboard CAN bus data capture card. Real-road driving test of several drivers was carried out, and representative data of lane change state were collected. The TLC prediction models were tested using the real lane change data. Results show that 87.0% prediction errors on straight road were less than or equal 0.1 s, and the corresponding rate on curve road was 93.7%. The prediction errors of two models meet the normal distribution.

Keyword: vehicle engineering; time to line crossing; geometry analysis; yaw angle estimate; vehicle active safety

Show Figures

0 引言

换道预警系统能够自动分析车辆换道过程中与后方其他车辆发生冲突的可能性, 并根据冲突严重等级对驾驶员进行提示。从本质而言, 车辆间发生交通冲突的原因在于不同的车辆在相同的时间内达到了同一地点, 因此, 分析交通冲突时需要考虑两个因素:①从什么时间开始可能会存在冲突; ②在可能冲突的时间段内车辆是否会到达相同位置。分析车辆换道过程中的运动状态可知, 对时间序列而言, 换道过程中车辆越过车道线的时刻是引发交通冲突的开始点。因此, 如果能够准确地预测越线时刻(Time to line crossing, TLC), 则可以根据传感器所返回的车辆间相对距离、相对角度等参数来实时分析换道过程的风险性^[1]。对车辆运动过程而言, TLC的实际意义是从当前时刻开始, 车辆经过一定时间后将压到车道线, 这个时间值即为TLC。

车辆实际换道过程表明, 越线时刻与换道过程中的方向盘转角、车速、道路曲率、车辆与车道线间的距离等参数密切相关^{[2, 3]}。van Winsum等^{[4, 5]}基于换道过程中的横向位移来近似地计算TLC值, 其假设换道过程中车辆的横向速度值保持不变, 这种方法会使得TLC值较小时容易被高估。Tideman^[6]基于两种假设:①假设车辆保持当前航向; ②假设驾驶员保持当前方向盘转角不变, 然后通过几何公式对TLC值进行预测。Eidehall^[7]根据横向位移和横向速度对车辆的越线时间进行预测。一些研究人员提出利用换道轨迹对越线时刻进行预测, 但换道轨迹受到较多因素的影响。部分研究将换道过程中的横向加速度设定为满足正弦状分布, 由此通过积分原理来描述车辆在横向上的运动规律^{[8, 9]}。但从实际换道过程中采集得到的横向加速度分布表明, 正常换道过程中, 横向加速度的变化范围较小, 而这个范围通常与横向加速度的漂移区间相重合, 因而从加速度信号中分离出由换道行为引发的横向加速度是一个较为复杂的问题。

总体而言, 目前与TLC相关的预测算法并不多见, 研究人员所提出的一些模型尽管具有较好的理论深度, 但这些模型中涉及参数较多, 而车辆在实际道路行驶过程中这些参数的获取本身就较为复杂, 从而使得这类模型无法得到较好的应用。TLC产生的机理在于车辆相对于车道线的距离变化, 因此, 如果对该参数的变化规律进行分析, 从几何角度而言可以实现对TLC值的预测。针对这种情况, 本文通过进行实际道路真实换道试验, 基于视觉传感器测量得到车辆与车道线的距离数据, 获取换道过程中车辆的运动状态表征数据, 并基于这些数据建立TLC预测模型, 实现对换道过程中TLC值的在线实时预测。

1 换道过程中TLC预测模型

驾驶员转动方向盘之后, 车辆将相对于车道线发生横向位移, 将车辆开始发生横向运动的时刻定义为换道开始时刻。从当前时刻起经过一定时间车辆将越过车道线而进入到目标车道, 这个时间被定义为TLC。车辆换道过程中, 大多数研究人员将其轨迹理解为圆弧, 这与车辆在道路上的实际行驶情况比较贴切。从这个角度出发, 本文提出一种基于几何参数分析建模的TLC预测方法, 分别实现车辆在直道路段和弯道路段换道过程中的TLC预测, 具体建模过程如下所示。

1.1 直道路段TLC预测模型

以换道方向为依据, 可以将换道过程分为向左换道和向右换道。以向左换道为例对直道路段TLC的预测方法描述如下。

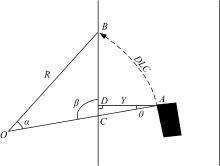
图1为直道路段向左换道示意图。图1中, DLC为沿着车辆轨迹到达车道边线的曲线弧段; R为在换道过程中车辆以点O为圆心作圆周运动的半径; α 为在换道的某一时刻动态位置A点和车道线定点B点这两点到圆心O的夹角; β 为动态点A到圆心O点的连线与所要越过的车道线的夹角; θ 为动态点A至所要越过车道线的垂线(即横向位移Y)与动态点A至圆心O连线的夹角。

	Figure Option View Download New Window
	图1 直道路段向左换道Fig.1 Lane change to left in straight road

由图1可知, 对TLC的预测实际上是预测车辆在曲线弧段DLC沿着换道轨迹到达越过车道线的时间。假定车辆在换道过程中的车速为u, 则TLC的计算方法如下:

$\begin{matrix} TLC = | DLC |/ u \end{matrix}$ (1)

在以半径为R的圆弧轨迹中, 曲线弧段DLC长度的计算公式为:

$\begin{matrix} | DLC |= α \times R \end{matrix}$ (2)

车辆以半径R作圆周运动, 则半径R的计算公式为:

$\begin{matrix} R = u / ω \end{matrix}$ (3)

式中: $\begin{matrix} ω \end{matrix}$ 为车辆横摆角速度。

图1中, 由几何关系可得:

$\begin{matrix} \{\begin{matrix} |AC| = Y / cosθ \\ |OC| = R - |AC| \end{matrix} \end{matrix}$ (4)

由此可得:

$\begin{matrix} \{\begin{matrix} β - θ = 90 ° \\ R^{2} = {|OC|}^{2} + {|BC|}^{2} - 2 |OC| |BC| cosβ \end{matrix} \end{matrix}$ (5)

同理可得:

$\begin{matrix} \{\begin{matrix} {|BC|}^{2} = {|OC|}^{2} + R^{2} - 2 |OC| Rcosα \\ α = \arccos (\frac{{|OC|}^{2} + R^{2} - {|BC|}^{2}}{2 \times |OC| \times R}) \end{matrix} \end{matrix}$ (6)

联立求解式(1)(2)(3)(6)可得:

$\begin{matrix} TLC = \frac{\arccos (\frac{{|OC|}^{2} + R^{2} - {|BC|}^{2}}{2 \times |OC| \times R})}{ω} \end{matrix}$ (7)

式(7)即为车辆在换道过程中TLC预测模型。对于每一个采样时刻, 车辆所在位置点A与车道线之间的距离Y值可由传感器测量得到。同时, 车辆的速度与横摆角速度值也可由车载陀螺仪测量得到。参考图1, 分析TLC的计算模型可知, 如果已知角度θ , 则能够实现TLC的预测计算。角度θ 反映车辆相对于车道线的偏航行为, 本文中, 考虑车辆的行驶特性和数据采集特性, 提出一种角度θ 的近似估计算法, 过程如图2所示。

	Figure Option View Download New Window
	图2 角度θ 的估计Fig.2 Estimation of angle θ

图2中, 在当前时刻, 车辆处于A点, 此时从A点引出车辆行驶轨迹的切线AF, 则角度γ 为车辆行驶轨迹与车道线之间的夹角, 由此可以将角度θ 的估计问题转换为角度γ 的估计。分析车辆换道过程, 车辆在某一时刻的运动状态是由车辆在这个时刻之前的运动状态所决定的。参考此道理, 如果已知某个时刻之前车辆的运动特征, 例如, 对于图2中车辆到达A点的时刻, 在此之前车辆与车道线之间的距离数据是被持续监测的, 因此, 通过分析在时刻A点之前的横向运动规律, 可以近似地对角度θ 进行估计, 步骤如下:

(1)分析A点时刻之前t₀时间段内车辆在横向方向上所发生的位移。换道行为隶属于一个时间段的行为, 因此, 换道预警系统首先需要对车辆是否发生换道行为进行识别。Mandalia的研究结论表明, 通过使用方向盘转角或车道线距离参数, 在0.8~1.2 s的识别时窗情况下可以达到90%以上的识别率^[10]。只有在识别出车辆已经发生换道的情况下, 对TLC进行计算才有意义。由此可知, 对于换道过程中的任意时刻点A, 此时刻之前t₀时间段内车辆的运动特征是已知的, 由此, 取t₀=0.8 s, 计算车辆在t₀ 时间段内所发生的相对横向位移L₀ 。由车辆与车道线之间的距离数据, 可以计算得到L₀ 。

(2)估算角度γ 。对于时刻点A, 计算车辆在t₀ 时间段内行驶轨迹的长度D₀ 。

$\begin{matrix} D_{0} = u \times t_{0} \end{matrix}$ (8)

则角度 $\begin{matrix} γ \end{matrix}$ 的估算公式为:

$\begin{matrix} γ = \arcsin (L_{0} / D_{0}) \end{matrix}$ (9)

上述模型推导过程中, 车速 $\begin{matrix} u \end{matrix}$ 被当成匀速处理, 但实际换道过程中车辆也存在加速或者减速的可能。由于本文所提出的模型的计算时窗通常较短, 在速度较高的情况下车速变化不会太大, 因而不会引起较大的误差, 具体误差分析见后续模型检验部分。总体而言, 对TLC的预测首先需要依据当前时刻之前的车辆运动状态来对车辆偏航情况进行估计, 然后根据车辆运动几何关系实现对TLC的预测。

1.2 弯道路段TLC预测模型

弯道路段分为向左转弯和向右转弯, 同时在向左转弯的道路上也存在向左换道和向右换道两种情况, 因此, 弯道路段车辆发生换道时共存在4种情况。以向左转弯道路上发生向左换道为例, 弯道路段TLC的预测模型建立过程如图3所示。

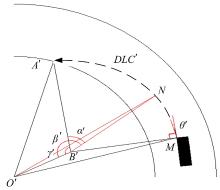
	Figure Option View Download New Window
	图3 弯道路段向左换道Fig.3 Lane change to left in curve road

图3中, DLC'为沿着车辆轨迹到达车道边线的曲线弧段; |A'B'|为在换道过程中车辆以B'点为圆心作圆周运动的半径; |A'O'|为弯道道路的曲率半径; α '为在换道的某一时刻动态M点和车道线定点A点这两点到圆心B'的夹角; β '为动态点N到B'点的连线与连线|B'O'|的夹角; θ '为车辆在换道过程中的偏航角。

假定车辆在换道过程中的车速为 $\begin{matrix} u', \end{matrix}$ 则TLC的计算公式为:

$\begin{matrix} TLC = | DLC' | / u' \end{matrix}$ (10)

在以半径为R_v 的圆弧轨迹中, 曲线弧段DLC'长度的计算公式为:

$\begin{matrix} | DLC' | = α' \times R_{v} \end{matrix}$ (11)

图3中, 有:

$\begin{matrix} α' = β' - γ' \end{matrix}$ (12)

车辆以半径R_v (R_v=|MB'|)作圆周运动, 则半径R_v的计算公式为:

$\begin{matrix} R_{v} = u' / ω_{1} \end{matrix}$ (13)

式中: $\begin{matrix} ω_{1} \end{matrix}$ 为换道开始之后的车身横摆角速度。

同理, 弯道的曲率半径 $\begin{matrix} R_{r} (R_{r} = | MO' |) \end{matrix}$ 为:

$\begin{matrix} \{\begin{matrix} R_{r} = u' / ω_{2} \\ |A' O'| = |MO'| - Y' \end{matrix} \end{matrix}$ (14)

式中:ω ₂ 为换道开始前的横摆角速度; Y'为车辆在换道过程中的横向位移。

图3中, 由几何关系可得:

$\{\begin{matrix} {|B'O'|}^{2} = {|MB'|}^{2} + {|MO'|}^{2} - \\ 2 | MB' | | MO' | cos∠B'MO' \\ cosβ' = \frac{{|B'N|}^{2} + {|B'O'|}^{2} - {|NO'|}^{2}}{2 \times | B'N |\times| B'O'|} \\ cosγ' = \frac{{|A'B'|}^{2} + {|B'O'|}^{2} - {|A'O'|}^{2}}{2 \times | A'B' | \times | B'O'|} \end{matrix}$ (15)

由此可得：

$\{\begin{matrix} γ = \arccos (\frac{{|A'B'|}^{2} + {|B'O'|}^{2} - {|A'O'|}^{2}}{2 \times | A'B' | \times | B'O'|}) \\ β = \arccos (\frac{{|B'N|}^{2} + {|B'O'|}^{2} - {|NO'|}^{2}}{2 \times |B'N| \times | B'O'|}) \\ α' = β' - γ' \end{matrix}$ (16)

联立式(10)(11)(12)(13)可得:

$\begin{matrix} \{\begin{matrix} R_{v} = u' / ω_{1} \\ TLC = \frac{R_{v} \times (β' - γ')}{u'} \end{matrix} \end{matrix}$ (17)

弯道路段TLC计算模型中, 偏航角度 $\begin{matrix} θ' \end{matrix}$ 的计算方法与直道路段相同, 而车身横摆角速度与直道路段存在区别。弯道路段上, 如果车辆按照车道线正常行驶, 则车身横摆角速度由道路曲率而决定, 即上述模型中的ω ₂ 主要由道路曲率决定。当车辆在弯道路段发生换道时, 则车身横摆角速度ω ₁由道路曲率和车辆的换道行为共同决定, 因此在弯道路段TLC预测模型中使用了两个横摆角速度参数。

1.3 TLC预测模型中的横摆角速度滤波

车辆运行过程中, 车身横摆角速度存在较大的波动。基于惯性原理所测量得到的横摆角速度数据包含较大的噪声。为了降低横摆角速度数据的误差, 本文采用卡尔曼滤波器对横摆角速度数据进行滤波。由于采集得到的原始数据是离散型, 所以选用Kalman离散型滤波器。离散过程的状态变量为 $\begin{matrix} X \in R^{n}, \end{matrix}$ 离散线性定常系统的状态方程和观测方程如下^{[11, 12, 13]}:

$X (k) = EX (k - 1) + FU (k) + W (k)$ (18)

$Z (k) = HX (k) + V (k)$ (19)

式中: $\begin{matrix} W (k) 、 V (k) \end{matrix}$ 分别为过程激励噪声和观测噪声, 在实际系统中近似认为它们是相互独立且服从正态分布的白色噪声:

$p (W) ~N (0, Q)$ (20)

$p (V) ~N (0, R)$ (21)

为了简化计算, 假定协方差矩阵Q, R均为常数。 ${\hat{X}}^{^{-}} (k) \in R^{n}$ (“ -” 代表先验, “ ^” 代表估计)为在已知第k步以前状态情况下第k步的先验状态估计。 $\hat{X} (k) \in R^{n}$ 为已知测量变量Z(k)第k步的后验状态估计。由此定义先验估计误差和后验估计误差为:

$\begin{matrix} \{\begin{matrix} e_{k}^{-} = X (k) - {\hat{X}}^{^{-}} (k) \\ e_{k} = X (k) - \hat{X} (k) \end{matrix} \end{matrix}$ (22)

利用观测变量和预测变量对先验估计 $\begin{matrix} {\hat{X}}^{^{-}} (k) \end{matrix}$ 进行修正:

$\begin{matrix} \hat{X} (k) = {\hat{X}}^{^{-}} (k) + K (Z (k) - H {\hat{X}}^{^{-}} (k)) \end{matrix}$ (23)

式中: $\begin{matrix} K \end{matrix}$ 为残余增益。

2 模型验证

2.1 数据来源

与TLC预测模型相关的参数包括车辆与车道线的距离(车轮外侧与车道标线之间的距离)、车身横摆角速度、车辆行驶速度。其中, 车辆与车道线的距离来源于AWS视觉传感器, 该传感器基于机器视觉原理对车辆与车道线的距离进行实时测量, 输出参数包括车辆与左侧车道线距离d_L; 车辆与右侧车道线距离d_R; 测量精度为5 cm; 测量范围为± 635 cm; 输出频率为10 Hz。

车身横摆角速度数据来源安装于车辆中央的IMU02陀螺仪, 该传感器实时测量车身的横摆角速度数据, 横摆角速度测量范围为± 150 ° /s; 分辨率为0.1 ° /s; 输出频率最大为100 Hz。

此外, 所采集的自车行驶速度 $\begin{matrix} u \end{matrix}$ 来源于车身CAN总线数据, 车速采样精度为0.01 km/h。试验过程中, 利用自行开发的数据采集程序同步采集上述参数, 采样频率设置为10 Hz。

数据采集设备安装于小型试验车上, 通过公开招募方式选择了11名被测试人员进行真实道路驾驶试验, 提取车辆换道过程中的相关数据。其中8名为男性, 3名为女性, 所有被试人员均能熟练地操作试验车辆。试验过程中天气良好, 所有被试人员生理心理情况正常。试验路段为G40沪陕高速蓝田段, 道路为双向6车道, 试验过程中道路通行正常。

2.2 直道路段模型验证

对于实际道路正常驾驶过程中的试验数据, 选择某次换道过程中的原始测量参数, 利用本文提出的TLC预测模型对换道过程中的TLC值进行预测。其中, 原始测量数据如图4所示。

	Figure Option View Download New Window
	图4 直道路段原始测量数据Fig.4 Original data of straight road

	Figure Option View Download New Window
	图5 直道路段TLC值预测结果Fig.5 Predict result of TLC in straight road

图4为完整的换道过程数据, 越线时刻预测部分处于该换道过程的初期阶段。图4中, 横轴为采样时间序列, 由于系统采样频率固定为10 Hz, 因此每两次采样之间的时间差为0.1 s。直接采用时间序列作为自变量可以减少求解过程中的计算量, 最后计算得到的TLC也可以由时间序列值直接表征。对于上述过程, 利用本文提出的TLC预测模型, 计算从换道开始0.8 s后到车辆越线时间段内的TLC数据, 结果如图5所示。

图5中, 实线为实际记录的越线时刻数据, 虚线为本文TLC预测模型所预测得到的TLC值。总体而言, 本文模型预测得到的TLC数据与真实值较接近, 但呈现一定的差异性。TLC模型预测结果为越线时刻TLC_f, 而实际数据中的越线时刻TLC_t是已知的, 通过对比分析TLC_f与TLC_t即可对越线预测模型的准确性进行检验。由于AWS视觉传感器工作频率为10 Hz, 即每两次数据采集之间的时间差为0.1 s, 因此对于计算得到的越线时刻TLC_f保留1位小数, 方便与实际越线时刻TLC_t进行对比^{[13, 14, 15]}。以绝对时间误差值e为评价参数判断预测模型的准确性, 其中e的定义如下:

$\begin{matrix} e = TL C_{t} - TL C_{f} \end{matrix}$ (24)

式中:e> 0表示预测越线时刻要早于实际越线时刻; e< 0则表示预测越线时刻要晚于实际越线时刻。

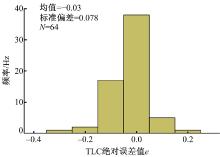
对检验样本的误差值 $\begin{matrix} e \end{matrix}$ 进行检验, 结果如图6所示, 图中 $\begin{matrix} N \end{matrix}$ 为检验样本数量。

	Figure Option View Download New Window
	图6 直道路段TLC预测误差的直方图Fig.6 Histogram of TLC predict error in straight road

	Figure Option View Download New Window
	图7 直道路段越线时刻预测误差数据检验Fig.7 Error test of TLC predict in straight road

图6表明, 本文所建立的TLC预测模型所预测的越线时间预测误差整体较小, 所有数据的误差都被限制在± 0.2 s内。检验数据中, 43.5%的预测值与真实越线时间保持一致, 87.0%的预测值与真实越线时间之间的误差绝对值小于等于0.1 s, 其他数据预测误差为± 0.2 s, 比例为13.0%。对所有误差数据进行正态分布Q-Q图检验, 结果如图7所示。

图7表明, Q-Q图法所得到的数据散点均集中于 $\begin{matrix} y = x \end{matrix}$ 直线附近, 这表明本文模型所计算得到的越线时刻预测误差值符合正态分布规律。结合图6和图7结果可知, 本文提出的直道路段换道过程中的TLC预测模型具有较好的精度和稳定性。

2.3 弯道路段模型验证

选择实际驾驶过程中在弯道路段发生换道的时间段, 截取相应时间段内的原始数据, 利用本文提出的TLC预测模型对换道过程中的TLC值进行预测。对于某一次越线行为, 原始测量数据如图8所示。

	Figure Option View Download New Window
	图8 弯道路段原始测量数据Fig.8 Original data of curve road

对于上述过程, 利用本文提出的TLC预测模型计算从换道开始0.8 s后到车辆越线时间段内的TLC数据, 结果如图9所示。

	Figure Option View Download New Window
	图9 弯道路段TLC值预测结果Fig.9 Predict result of TLC in curve road

图9中, 实线为通过分析车道线距离数据所得到的真实越线时刻, 虚线为本文TLC预测模型所预测得到的TLC值。总体而言, 本文模型预测得到的弯道路段TLC数据与真实值较接近。对时间序列而言, 在越线的前期和后期越线结果与真实值接近, 在越线过程的中间呈现出一定的差异。

图10为利用绝对时间误差值 $\begin{matrix} e \end{matrix}$ 进行误差统计分布的结果, 从图10中可知, 本文所建立的TLC预测模型所预测的越线时间预测误差整体较小, 所有数据的误差都被限制在± 0.2 s内, 且误差为0或者± 0.1 s占据的比例较大。检验结果中, 59.4%的预测值与真实越线时间保持一致, 93.7%的预测值与真实越线时间之间误差绝对值小于等于0.1 s。对所有误差数据进行正态分布Q-Q图检验, 结果如图11所示。

	Figure Option View Download New Window
	图10 弯道路段TLC预测误差的直方图Fig.10 Histogram of TLC predict error in curve road

	Figure Option View Download New Window
	图11 弯道路段越线时刻预测误差数据检验Fig.11 Error test of TLC predict

图11表明, Q-Q图法所得到的数据散点均集中于 $\begin{matrix} y = x \end{matrix}$ 直线附近, 这表明本文模型所计算得到的越线时刻预测误差值符合正态分布规律。结合图10和图11可知, 本文提出的弯道路段换道过程中的TLC预测模型具有较好的精度和稳定性。

3 结束语

(1)基于车辆运动过程中与车道线距离参数, 在对车辆偏航角度进行估计的情况下, 采用几何分析方法分别建立换道过程中的越线时刻预测模型, 实现了对直道路段和弯道路段换道过程中的越线时刻的实时预测。

(2)采用实测越线过程数据对模型有效性进行检验, 结果表明:直道路段预测误差绝对值小于等于0.1 s的比例达到了87.0%, 弯道路段相应的比例达到了93.7%, 且两种模型的预测误差均符合正态分布规律。

(3)弯道情况下, 根据弯道方向和换道方向共存在4种不同的类型, 本文只对其中一种类型进行了分析, 但建模思路同样适合于其他3种情况。当弯道路段设置有缓和曲线时, 本文模型的有效性没有进行单独验证, 原因在于缓和曲线的几何参数无法准确获取。本文进行的弯道验证试验中也存在部分缓和曲线, 实际检验结果表明模型准确度较好, 原因在于缓和曲线的曲率变化通常较为平缓, 模型对曲率误差的包容性能够解决缓和曲线的曲率变化问题。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Eidehall A, Pohl J, Gustafsson F. Joint road geometry estimation and vehicle tracking[J]. Control Engineering Practice, 2007, 15(12): 1484-1494. [本文引用:1]
[2]	Naohiro Y, Jun T. Multi-driver agent-based traffic simulation systems for evaluating the effects of advanced driver assistance systems on road traffic accidents[J]. Cognition, Technology & Work, 2006, 8(4): 283-300. [本文引用:1]
[3]	Möbus R, Baotic M, Morari M. Multi-object adaptive cruise control[J]. Lecture Notes in Computer Science, 2003, 2623: 359-374. [本文引用:1]
[4]	van Winsum W, Brookhuis K A, de Waard D. A comparison of different ways to approximate timeto-line crossing (TLC) during car driving[J]. Accident Analysis and Prevention, 2000, 32(1): 47-56. [本文引用:1]
[5]	van Winsum W, de Waard D, Brookhuis K A. Lane change maneuvers and safety margins[J]. Transportation Research Part F: Traffic Psychology and Behaviour, 1999, 2(3): 139-149. [本文引用:1]
[6]	Tideman M, van der Voort M C, van Arem B, et al. A review of lateral driver support systems[C]//Proceedings of the 2007 IEEE Intelligent Transportation Systems Conference Seattle, WA, USA, 2007: 992-999. [本文引用:1]
[7]	Eidehall A. An automotive lane guidance system[D]. Linköping: Department of Electrical Engineering, Automatic Control, Linköping University, 2004. [本文引用:1]
[8]	徐慧智, 裴玉龙, 程国柱. 基于期望运行轨迹的车道变换行为安全性分析[J]. 中国安全科学学报, 2010, 20(1): 90-95. Xu Hui-zhi, Pei Yu-long, Cheng Guo-zhu. Study on the safety of lane-changing based on virtual desire trajectory[J]. China Safety Science Journal(CSSJ), 2010, 20(1): 90-95. [本文引用:1]
[9]	任殿波, 张继业, 张京明, 等. 智能车辆弯路换道轨迹规划与横摆率跟踪控制[J]. 中国科学: 技术科学, 2011, 41(3): 306-317. Ren Dian-bo, Zhang Ji-ye, Zhang Jing-ming, et al. Trajectory planning and yaw rate tracking control for lane changing of intelligent vehicle on curved road[J]. Sci China Tech Sci, 2011, 41(3): 306-317. [本文引用:1]
[10]	Mand alia H M, Salvucci D D. Using support vector machines for lane-change detection[J]. Proceedings of the Human Factors and Ergonomics Society Annual Meeting September, 2005, 49(22): 1965-1969. [本文引用:1]
[11]	娄路, 赵玲, 耿涛. 运动车辆检测与跟踪方法[J]. 交通运输工程学报, 2012, 12(4): 107-113. Lou Lu, Zhao Ling, Geng Tao. Detecting and tracking method of moving vehicle[J]. Journal of Traffic and Transportation Engineering, 2012, 12(4): 107-113. [本文引用:1]
[12]	高振海, 王竣, 佟静, 等. 车载毫米波雷达对前方目标的运动状态估计[J]. 吉林大学学报: 工学版, 2014, 44(6): 1537-1544. Gao Zhen-hai, Wang Jun, Tong Jing, et al. Target motion state estimation for vehicle-borne millimeter-wave radar[J]. Journal of Jilin University(Engineering and Technology Edition), 2014, 44(6): 1537-1544. [本文引用:1]
[13]	Li Liang, Song Jian, Wang Hui-yi, et al. Fast estimation and compensation of the tire force in real time control for vehicle dynamic stability control system[J]. International Journal of Vehicle Design, 2008, 46(3-4): 208-229. [本文引用:2]
[14]	罗莉华, 龚李龙, 李平, 等. 考虑驾驶员行驶特性的双模式自适应巡航控制设计[J]. 浙江大学学报: 工学版, 2011, 45(12): 2073-2077. Luo Li-hua, Gong Li-long, Li Ping, et al. Two-mode adaptive cruise control design with humans driving habits consideration[J]. Journal of Zhejiang University(Engineering Science), 2011, 45(12): 2073-2077. [本文引用:1]
[15]	赵又群. 汽车动力学中若干关键状态和参数估计研究的现状与发展[J]. 中国机械工程, 2010, 21(10): 1250-1253. Zhao You-qun. Present state and perspectives of estimation research for several key states and parameters in vehicle dynamics[J]. China Mechanic Engineering, 2010, 21(10): 1250-1253. [本文引用:1]

2007

0.0

... 因此,如果能够准确地预测越线时刻(Time to line crossing,TLC),则可以根据传感器所返回的车辆间相对距离、相对角度等参数来实时分析换道过程的风险性^[1] ...

2006

0.0

... 车辆实际换道过程表明,越线时刻与换道过程中的方向盘转角、车速、道路曲率、车辆与车道线间的距离等参数密切相关^[2,3] ...

2003

0.0

... 车辆实际换道过程表明,越线时刻与换道过程中的方向盘转角、车速、道路曲率、车辆与车道线间的距离等参数密切相关^[2,3] ...

2000

0.0

... van Winsum等^[4,5]基于换道过程中的横向位移来近似地计算TLC值,其假设换道过程中车辆的横向速度值保持不变,这种方法会使得TLC值较小时容易被高估 ...

1999

0.0

... van Winsum等^[4,5]基于换道过程中的横向位移来近似地计算TLC值,其假设换道过程中车辆的横向速度值保持不变,这种方法会使得TLC值较小时容易被高估 ...

2007

0.0

... Tideman^[6]基于两种假设:①假设车辆保持当前航向 ...

2004

0.0

... Eidehall^[7]根据横向位移和横向速度对车辆的越线时间进行预测 ...

2010

0.0

. 2010, 20(1):90-95 DOI:doi:10.3969/j.issn.1003-3033.2010.01.015

Study on the safety of lane-changing based on virtual desire trajectory

基于期望运行轨迹的车道变换行为安全性分析

Xu Hui-zhi , Pei Yu-long , Cheng Guo-zhu.

徐慧智, 裴玉龙, 程国柱

In order to solve the quantitative analysis problems of lane-changing influence on traffic safety, a Virtual Desire Trajectory of lane-changing is constructed based on the vehicle and driver's behavior characteristics. By combining 4 types of collisions caused by lane-changing, a safe operation judgment equation and restriction equation are respectively built in the vertical and horizontal direction. And the sensitivity of vehicle speed and lateral acceleration gradients to lane-changing safety is analyzed. Finally, an application example is given. This study shows that the changes of the lateral acceleration gradient have a direct impact on the safety of lane-changing.

为解决车道变换行为对交通运行安全影响的定量分析难题,基于车辆和驾驶员行为特性,构建车道变换行为期望运行轨迹,提出基于缓和曲线的轨迹形式,并结合车道变换行为引发的4种碰撞形式,在车辆运行纵向和横向分别构建安全运行判断方程和安全运行限制方程,分析安全距离对运行速度和车辆侧向加速度梯度的敏感度,给出车道变换行为安全运行判断方程的应用案例.研究结果表明,侧向加速度的变化梯度直接影响车道变换的安全性.

... 部分研究将换道过程中的横向加速度设定为满足正弦状分布,由此通过积分原理来描述车辆在横向上的运动规律^[8,9] ...

2011

0.0

. 2011, 41(3):306-317 DOI:doi:10.4028/www.scientific.net/AMR.211-212.106

Trajectory planning and yaw rate tracking control for lane changing of intelligent vehicle on curved road

智能车辆弯路换道轨迹规划与横摆率跟踪控制

Ren Dian-bo , Zhang Ji-ye , Zhang Jing-ming

任殿波, 张继业, 张京明

对自动化公路系统弯路上智能车辆换道控制进行了研究.假设期望的侧向加速度满足正反梯形的约束条件,考虑起始车道和目的车道曲率的差别,提出了一种弯路上车辆换道轨迹规划方法,推导了换道时车辆在惯性坐标系的期望运动状态计算公式;根据车辆期望运动状态计算了车辆换道时的期望横摆角、横摆角速度和横摆角加速度;假定依靠角速度传感器获得横摆角速度信息,基于车辆侧向动力学模型,采用非奇异终端滑模控制方法,设计了横摆角速度跟踪车辆换道滑模控制规律.基于李雅普诺夫稳定性理论,采用相平面法,对控制系统的有限时间收敛性进行了分析.仿真结果显示,若不考虑内外侧车道曲率差别,规划的期望换道轨迹,在换道结束时与目的车道位置之间总是存在偏离,偏离程度随曲率半径减小而增大;本文考虑内外侧车道曲率的差别,能得到无偏差的期望换道轨迹;设计的横摆率跟踪控制规律能实现对换道轨迹的理想跟踪.

... 部分研究将换道过程中的横向加速度设定为满足正弦状分布,由此通过积分原理来描述车辆在横向上的运动规律^[8,9] ...

2005

0.0

... 2 s的识别时窗情况下可以达到90%以上的识别率^[10] ...

2012

0.0

... 离散过程的状态变量为 X∈Rn,离散线性定常系统的状态方程和观测方程如下^[11,12,13]: ...

2014

0.0

. 2014, 44(6):1537-1544 DOI:doi:10.13229/j.cnki.jdxbgxb201406001

Target motion state estimation for vehicle-borne millimeter-wave radar

车载毫米波雷达对前方目标的运动状态估计

Gao Zhen-hai , Wang Jun , Tong Jing

高振海, 王竣, 佟静

With the analysis of preceding object motion feature and vehicle-borne radar measuring principle, a novel target motion model is established in the vehicle-borne radar coordinate system. This target motion model considers the relative motion of the intertial coordinate, the vehicle coordinate and the radar coordinate system. Also other specialness of ground vehicle were taken into account in the model, such as that the motion of ground vehicle is a 2D motion because of the limitation of ground surface, the vehicle mobility is small and the tracking coordinate system is moving. The whole motion states of the preceding target, including the longitudinal and lateral velocities, the longitudinal and lateral positions were estimated by the algorithm of adaptive Kalman filter, because it was difficult to determine the statistics of the system process noise and measure noise. Finally, road experiments, in which the host car was equipped with millimeter-wave radar and the preceding car was equipped with high precision automotive testing equipments, were carried out to verify the feasibility and performance of the estimation method. The results prove that the method can provide fine estimation accuracy, better filter convergence and stability.

基于对汽车前方目标运动特点和车载雷达信息检测机理的分析,在大地坐标系、本车的车辆运动坐标系和车载雷达运动坐标系的相对运动关系基础上,考虑了地面车辆运动以地表平面上二维运动为主、机动性小、跟踪坐标系运动的特点,建立了基于车载雷达运动坐标系的前方目标的运动状态模型。并考虑到系统过程噪声及雷达等车载传感器观测噪声的统计特性难以事先确定的问题,采用自适应卡尔曼滤波算法实现了前方目标的侧纵向速度和侧纵向位置等运动状态的完备准确实时估计。最终通过真实道路交通环境下装备毫米波雷达和高精度汽车状态测试系统的实车对比试验,对算法的可行性和估计精度进行了试验验证,试验结果显示:估计结果具有良好的精度,且长时间跟踪过程中滤波收敛稳定。

... 离散过程的状态变量为 X∈Rn,离散线性定常系统的状态方程和观测方程如下^[11,12,13]: ...

2008

0.0

... 离散过程的状态变量为 X∈Rn,离散线性定常系统的状态方程和观测方程如下^[11,12,13]: ...

... 1 s,因此对于计算得到的越线时刻TLC_f保留1位小数,方便与实际越线时刻TLC_t进行对比^[13,14,15] ...

2011

0.0

. 2011, 45(12):2073-2077 DOI:doi:10.3785/j.issn.1008-973X.2011.12.001

Two-mode adaptive cruise control design with humans driving habits consideration

考虑驾驶员行驶特性的双模式自适应巡航控制设计

Luo Li-hua , Gong Li-long , Li Ping

罗莉华, 龚李龙, 李平

作为一种先进的汽车驾驶辅助系统，自适应巡航控制(ACC)系统的行驶行为应尽可能的模拟人的日常行驶习惯，从而提高驾驶员对ACC系统的满意程度和接受度。本文通过分析驾驶员的行驶特性，在模型预测控制(MPC)的框架基础上提出了一个双模式的自适应巡航控制策略：当远离前车时，ACC系统采取快速接近模式，在满足安全舒适的前提下以尽量短的时间减小两车间距；一旦车间距调整至期望值附近时，ACC系统切换到平稳跟车模式，使车辆安全、平稳、舒适地对前车进行跟车。为使两种模式切换时能平滑过渡，本文根据驾驶员的行驶习惯制定了一套模糊规则作为切换机制。最后通过仿真试验证实了该双模式ACC控制策略在保证安全性和舒适性的同时，提高了行驶效率，表现出来的行驶行为更加符合人的日常行驶习惯，因而更易于被驾驶员接受。

... 1 s,因此对于计算得到的越线时刻TLC_f保留1位小数,方便与实际越线时刻TLC_t进行对比^[13,14,15] ...

2010

0.0

. 2010, 21(10):1250-1253

Present state and perspectives of estimation research for several key states and parameters in vehicle dynamics

汽车动力学中若干关键状态和参数估计研究的现状与发展

Zhao You-qun.

赵又群

摘　要：阐述了汽车动力学中若干关键状态和参数估计研究的重要性。描述了汽车动力学中若干关键状态和参数估计的内涵,给出了主要的研究方法和一些应用实例。最后指出了汽车动力学中若干关键状态和参数估计研究中的关键问题,并指出该项研究能够为汽车动力学建模、汽车底盘控制系统开发奠定必要的理论基础。

... 1 s,因此对于计算得到的越线时刻TLC_f保留1位小数,方便与实际越线时刻TLC_t进行对比^[13,14,15] ...