泡沫铝填充矩形截面薄壁梁压溃力理论表达式

引用本文

张君媛, 张秋实, 刘卫国, 张乐, 武栎楠, 周浩. 泡沫铝填充矩形截面薄壁梁压溃力理论表达式.吉林大学学报:工学版, 2016, 46(3): 745-750
ZHANG Jun-yuan, ZHANG Qiu-shi, LIU Wei-guo, ZHANG Le, WU Li-nan, ZHOU Hao. Crushing model of rectangular section thin-walled beam filled with aluminum foam. Journal of Jilin University Engineering and Technology Edition, 2016, 46(3): 745-750 复制到剪切板

Permissions

泡沫铝填充矩形截面薄壁梁压溃力理论表达式

张君媛^1,², 张秋实¹, 刘卫国³, 张乐¹, 武栎楠¹, 周浩¹

1.吉林大学汽车仿真与控制国家重点实验室,长春 130022

2.清华大学汽车安全与节能国家重点实验室,北京 100084

3.浙江吉利汽车研究院有限公司,杭州 311228

作者简介:张君媛(1965-),女,教授,博士生导师.研究方向:车身现代设计和汽车被动安全性.E-mail:junyuan@jlu.edu.cn

基金:国家自然科学基金项目(51375203); 汽车安全与节能国家重点实验室开放基金项目(KF16152); 吉林省科技发展计划项目(20160101269JC); 浙江省汽车安全技术重点实验室项目(YSD0C11-02)

摘要

在矩形截面空管薄壁梁压溃理论基础上,考虑压溃过程中泡沫铝填充对压溃距离的影响以及薄壁梁管壁与泡沫铝之间相互作用对压溃力的影响,推导出了泡沫铝填充的矩形截面薄壁梁压溃力表达式。该压溃力理论表达式由修正的薄壁梁空管压溃力、泡沫铝压溃力以及薄壁梁与泡沫铝的相互作用力三部分构成。应用已有的泡沫铝填充低碳钢和铝合金正方形截面薄壁梁实验数据对压溃力理论表达式进行验证,结果表明:理论表达式具有较高的精度。

关键词: 车辆工程; 泡沫铝填充; 矩形薄壁梁; 压溃理论

中图分类号:U461.91 文献标志码:A 文章编号:1671-5497(2016)03-0745-06

Crushing model of rectangular section thin-walled beam filled with aluminum foam

ZHANG Jun-yuan^1,², ZHANG Qiu-shi¹, LIU Wei-guo³, ZHANG Le¹, WU Li-nan¹, ZHOU Hao¹

1.State Key Laboratory of Automotive Simulation and Control, Jilin University,Changchun 130022,China

2.State Key Laboratory of Automotive Safety and Energy,Tsinghua University,Beijing 100084,China

3.Zhejiang Geely Automobile Institute Co.,Ltd.,Hangzhou 311228,China

Abstract

A crushing model of rectangular section thin-walled beam filled with aluminum foam is proposed based on the theory of hollow rectangular section beams. The influence of the aluminum foam on the effective crushing length and the interaction between the foam and the thin-walled beam in crushing are considered in this crushing model. The average crushing force is composed of three parts, the modified hollow beam crushing force, the aluminum foam crushing force and the interaction force between the foam and the beam. Experiment data of mild steel and aluminum thin-walled beams filled with aluminum foam are adopted to validate the proposed crushing model. It is shown that the theoretical results are in good agreement with the experiment results.

Keyword: vehicle engineering; aluminum foam-filled; rectangular section thin-walled beam; rushing theory

Show Figures

0 引言

矩形截面薄壁梁结构常用于汽车、船舶、飞机等运输工具的吸能部件, 其轴向压溃变形稳定、吸能显著, 是抗撞性研究的重要课题。泡沫铝作为一种新型的多功能材料, 具有密度小、缓冲吸能特性好等优点^[1], 将其填充到薄壁梁中可在满足碰撞吸能功效的同时实现轻量化。利用理论研究所得的压溃力表达式, 可在详细设计结构断面之前快速选择满足抗撞性和轻量化要求的薄壁梁材料、尺寸等参数, 相比于有限元计算及实验, 压溃力表达式从本质上揭示出了薄壁梁的抗撞性能与其材料、尺寸参数之间的力学关系, 可实现对薄壁梁结构的正向设计, 大大减少有限元试错及实验的次数, 缩短了设计开发周期。

国内外许多学者对泡沫铝填充的矩形薄壁梁压溃理论进行了研究, Reid等^[2]考虑泡沫铝在压溃时的密实应变, 通过对空正方形薄壁梁的压溃进行修正, 获得泡沫铝填充的正方形薄壁梁压溃表达式。Hanssen等^{[3, 4]}进行大量的静态和动态泡沫铝填充铝合金薄壁梁的实验, 并采用经验公式表达了平均压溃力。王青春等^[5]进行了泡沫铝填充帽形薄壁梁的动态冲击试验。Zarei和Krö ger^{[6, 7]}通过多目标优化的方法, 对蜂窝铝和泡沫铝填充的铝管进行了压溃性能优化和轻量化设计。然而目前的研究也存在一些不足, Reid提出的压溃力理论表达式未考虑薄壁梁管壁和泡沫铝之间的相互作用力; Hanssen等虽然通过大量实验拟合出了含有相互作用力的压溃力经验表达式, 但是该表达式未揭示压溃力与材料、尺寸参数之间的力学关系, 且当薄壁梁截面或填充材料参数发生变化时, 该表达式就不再适用。

针对以上问题, 本文在考虑泡沫铝填充对压溃距离影响的基础上, 探讨了压溃过程中由于薄壁梁褶皱变形而导致的薄壁梁管壁与泡沫铝之间相互作用对压溃力的影响, 进而推导出泡沫铝填充的薄壁梁压溃力的理论表达式, 并用实验数据对理论公式进行验证。

1 矩形截面薄壁梁压溃理论

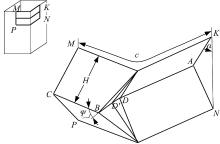
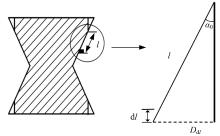
Abramowicz 和Jones^[8]将压溃时的矩形截面薄壁梁划分为4个超折叠单元, 如图1所示。每个超折叠单元的塑形变形可简化为5种能量耗散机制:①环形面变形; ②沿固定塑性绞线的弯曲变形; ③倾斜绞线的变形; ④锥形面的扩展; ⑤锥形面的弯曲。各部分的能量耗散分别用 $\begin{matrix} E_{i} (i = 1, 2, \dots, 5) \end{matrix}$ 表示。

	Figure Option View Download New Window
	图1 超折叠单元Fig.1 Superfolding element

矩形截面薄壁梁压溃2H距离时, 考虑超折叠单元的有效压溃距离δ _ef, 可得平均压溃反力F_m所做的功为:

$F_{m} δ_{ef} = 4 \overset{5}{\sum_{i = 1}} E_{i} = 4 M_{0} (16 I_{1} \frac{Hb}{h} + 4 α_{0} c + 4 I_{3} \frac{H^{2}}{b} + 8 I_{4} \frac{H^{2}}{h} + 2 H I_{5})$ (1)

式中:c为折叠单元两翼边长之和, 即矩形截面周长的四分之一; H为折叠半波长; M₀ 为单位塑性极限弯矩, $\begin{matrix} M_{0} = σ_{0} h^{2} / 4, σ_{0} \end{matrix}$ 为等效流动应力, h为薄壁梁壁厚; b为环形面弯曲半径。

当最终折叠角度 $\begin{matrix} α_{0} \end{matrix}$ 为π /2, 中心角度 $\begin{matrix} ψ \end{matrix}$ 为π /2时, $\begin{matrix} I_{1} 为 0.53, I_{3} 为 1.15, I_{4} = I_{5} = 0 。 \end{matrix}$

进一步可得:

$\frac{F_{m}}{M_{0}} = 4 (8 I_{1} \frac{b}{h} + 2 α_{f} \frac{c}{H} + 2 I_{3} \frac{H^{2}}{b} + 4 I_{4} \frac{H}{h} + I_{5}) \frac{2 H}{δ_{ef}}$ (2)

实际上单元的有效压溃距离δ _ef 小于2H^[9], 如式(3)所示:

$\begin{matrix} \frac{δ_{ef}}{2 H} = 0.73 \end{matrix}$ (3)

根据能量最小原理, 即:

$\begin{matrix} \frac{\partial F_{m}}{\partial H} = 0; \frac{\partial F_{m}}{\partial b} = 0 \end{matrix}$

最终, 得到矩形截面薄壁梁的平均压溃反力为:

$\begin{matrix} \frac{F_{m}}{M_{0}} = 52.22 {(\frac{c}{h})}^{\frac{1}{3}} \end{matrix}$ (4)

2 泡沫铝填充矩形薄壁梁平均压溃力表达式推导

Reid^[2]认为泡沫铝填充矩形薄壁梁发生压溃时, 由于泡沫铝的密实应变, 最终的折叠角度不再是π /2, 可以通过泡沫的密实应变ε _d确定折叠角度α ₀, 如式(5)所示:

$\begin{matrix} ε_{d} = δ / (2 H) = 1 - \cos α_{0} \end{matrix}$ (5)

式中: $\begin{matrix} δ \end{matrix}$ 为泡沫铝缩短的长度。

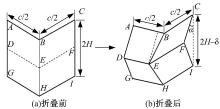
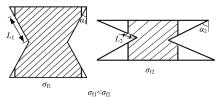
折叠机制如图2所示。因此, 在矩形空管压溃反力公式的基础上进行修正, 得到当泡沫铝的平台应力为σ _f, 最终折叠角度为α ₀时, 泡沫铝填充的矩形薄壁梁的平均压溃力为:

$\begin{matrix} F_{filled} = F_{m} (α_{0}) + σ_{f} c^{2} \end{matrix}$ (6)

但式(6)未考虑到薄壁梁与泡沫铝相互作用力所做的功及其消耗的能量。

	Figure Option View Download New Window
	图2 折叠机制Fig.2 Folding mechanism

本文将泡沫铝填充的矩形薄壁梁压溃时的能量耗散分成薄壁梁吸能量E_beam 、泡沫铝吸能量E_foam 和薄壁梁与泡沫铝的相互作用吸能量E_int三部分。

$\begin{matrix} E_{filled} = E_{beam} + E_{foam} + E_{int} \end{matrix}$ (7)

式中: $\begin{matrix} E_{foam} = σ_{f} S, S \end{matrix}$ 为泡沫铝的截面积。

泡沫铝的密实应变可由泡沫铝密度ρ _f 和泡沫铝基础材料密度ρ _s通过式(8)进行估计^[10]:

$\begin{matrix} ε_{d} = 1 - 1.4 (ρ_{f} / ρ_{s}) \end{matrix}$ (8)

当泡沫铝被压实时, 缩短的长度δ 和超折叠单元的折叠角度α ₀可由式(9)(10)求出:

$δ = 2 H ε_{d}$ (9)

$α_{0} = \arccos (1 - ε_{d})$ (10)

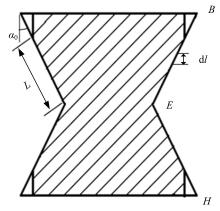
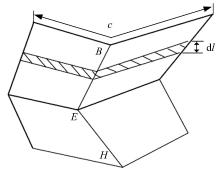
压溃时, 薄壁梁向内压缩泡沫铝, 产生相互作用力, 当压实时, 设泡沫铝的接触压缩长度为L, 如图3所示, 选取其中一段长度为dl的相互接触面积作为研究对象, 如图4所示。

	Figure Option View Download New Window
	图3 泡沫铝压实时的变形示意图Fig.3 Deformation behavior of aluminum foam when compacted

	Figure Option View Download New Window
	图4 长度为dl的相互接触面积Fig.4 Contact area when length is dl

作用在该段接触面积上的相互作用力为:

$\begin{matrix} F_{dl} = σ_{f} \cdot S_{dl} = σ_{f} cdl = σ_{f} cdl \end{matrix}$ (11)

作用力在该段面积上产生的位移为(见图5):

$\begin{matrix} D_{dl} = lsin α_{0} \end{matrix}$ (12)

	Figure Option View Download New Window
	图5 位移示意图Fig.5 Displacement schematic diagram

则可得相互作用力在长度为dl的接触面积上所做的功为:

$\begin{matrix} E_{dl} = F_{dl} D_{dl} = σ_{f} lcsin α_{0} dl \end{matrix}$ (13)

再积分得到在一个超折叠单元中, 压缩长度为 $\begin{matrix} L \end{matrix}$ 的接触面积上, 相互作用力所做的功为:

$\begin{matrix} E_{L} = \int_{0}^{L} σ_{f} lcsin α_{0} dl \end{matrix}$ (14)

由于相互作用力对薄壁梁和泡沫二者均做功且相等, 泡沫铝挤压呈上下对称形式, 对上下截面做功也相等, 则对于含有4个超折叠单元的矩形截面来说, 相互作用力所做的功为:

$E_{int} = 2 \times 2 \times 4 E_{L} = 16 σ_{f} \int_{0}^{L} l csin α_{0} dl = 8 σ_{f} L^{2} csin α_{0}$ (15)

对于式(15)中的接触压缩长度L, 填充不同平台应力的泡沫铝材料, 薄壁梁与泡沫铝接触所形成的L不同, 如图6所示。

	Figure Option View Download New Window
	图6 不同的压缩长度Fig.6 Different compressed lengths

本文研究平台应力为1.0~12.5 MPa时的泡沫铝填充薄壁梁压溃性能, 根据经验数据, 填充泡沫铝的平台应力为1.0 MPa时, $\begin{matrix} L \end{matrix}$ 可取为0.9H; 当填充泡沫铝的平台应力为12.5 MPa时, 接触压缩长度L几乎为0。设L随泡沫铝平台应力线性变化, 则可近似拟合得到L与σ _f的关系为:

$\begin{matrix} L = - 0.078 H σ_{f} + 0.978 H \end{matrix}$ (16)

则由相互作用产生的平均压溃力为:

$\begin{matrix} F_{int} = \frac{E_{int}}{2 H ε_{d}} \end{matrix}$ (17)

由于泡沫铝填充的作用, $\begin{matrix} α \end{matrix}$ 的上限由空薄壁梁时的π /2变为 $\begin{matrix} α_{0}, \end{matrix}$ 因此对薄壁梁的压溃力进行修正, 得到泡沫铝填充薄壁梁平均压溃反力为:

$\begin{matrix} F_{filled} = F_{m} (α_{0}) + F_{foam} + F_{int} \end{matrix}$ (18)

3 实验验证

3.1 泡沫铝填充低碳钢薄壁梁压溃理论验证

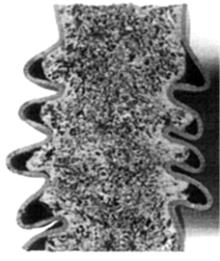
Seitzberger等^[11]进行了泡沫铝填充的低碳钢薄壁梁轴向压溃实验。实验试件为低碳钢方管填充泡沫铝, 薄壁梁材料为RSt37, 材料参数如表1所示, 正方形截面外侧边长为40 mm; 壁厚为1.4 mm; 长度为150 mm; 填充MEPURA泡沫铝; 基础材料为AlMg0.6Si0.3Tl; 密度为0.52 g/cm³, 泡沫铝材料应力应变曲线如图7所示。实验采用压溃加载工况, 样件两端都没有约束, 在两个平板之间轴向压缩, 加载速度为1 mm/s。实验中薄壁梁变形如图8所示。

表1 RSt37应力-应变数据 Table 1 Stress-strain data of RSt37

	Figure Option View Download New Window
	图7 MEPURA泡沫铝材料单向压缩应力-应变曲线Fig.7 Stress-strain curve of MEPURA in uniaxial compression

	Figure Option View Download New Window
	图8 实验中薄壁梁的变形图Fig.8 Deformation behavior of thin-walled beam filled with aluminum foam in experiment

将实验试件的相关参数带入本文泡沫铝填充薄壁梁平均压溃反力理论公式(18), 其中h=1.4 mm, ρ _f=0.52 g/cm³, ρ _s=2.7 g/cm³, 等效流动应力 $\begin{matrix} σ_{0} \end{matrix}$ 为^[3]:

$\begin{matrix} σ_{0} = 2 . 23^{n} \frac{σ_{u}}{n + 1} {(\frac{2}{n + 2})}^{\frac{2}{3}} {(\frac{h}{c})}^{4 n / 9} \end{matrix}$ (19)

式中: $\begin{matrix} σ_{u} \end{matrix}$ 为材料的极限应力, 本文中σ _u=339 MPa; $\begin{matrix} n \end{matrix}$ 为材料的硬化因子, 硬化因子与应力应变的关系为^[3]:

$\begin{matrix} σ = σ_{u} {[\frac{ε}{ε_{u}}]}^{n} \end{matrix}$ (20)

式中:ε _u 为极限应力对应的应变, 本文中ε _u=0.174。

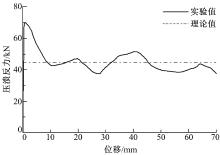
应用理论表达式求得的泡沫铝填充低碳钢矩形薄壁梁的平均压溃反力为44.8 kN。将理论与实验结果进行对比, 如图9所示, 实验平均压溃反力为45.5 kN, 理论结果比实验约低1.5%。

	Figure Option View Download New Window
	图9 理论与实验压溃反力对比Fig.9 Comparison of the average crushing reaction force between experimental and theoretical results

3.2 泡沫铝填充铝合金薄壁梁压溃理论验证

Hanssen等^[3]进行了薄壁梁空管及各种密度泡沫铝填充的铝合金薄壁梁轴向压溃实验, 薄壁梁材料为AA6060T4以及AA6082T4, 材料参数如表2所示; 填充材料为Hydro泡沫铝。由于式(19)推导中采用的泡沫铝平台应力范围为1.0~12.5 MPa, 因此, 本文选取泡沫铝材料位于该平台应力范围内的压溃实验作为验证实验。其中, 未考虑发生破裂的实验数据, 且同一截面尺寸、壁厚和泡沫密度进行重复实验得到的压溃力取平均值。

表2 AA6060T4和AA6082T4应力-应变数据 Table 2 Stress-strain data of AA6060T4 and AA6082T4

实验试件相关参数c、h、σ _u 、σ _f 和ρ _f 的取值如表3所示, n和σ ₀的取值由式(19)(20)求出。将这些参数代入理论公式(18)中可求出泡沫铝填充铝合金矩形薄壁梁的平均压溃反力。

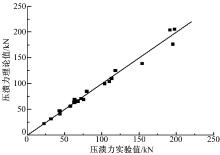
图10为实验与理论计算所得压溃力的对比, 图中数据点越接近中间斜率为1的直线, 说明理论计算得到的压溃力越接近实验所得压溃力。

	Figure Option View Download New Window
	图10 压溃力实验与理论值对比Fig.10 Comparison of crushing force between experimental and theoretical results

由图10和表3可以看出:本文推导的泡沫铝填充薄壁梁压溃力表达式在应用于泡沫铝填充铝合金正方形截面时得到的平均压溃力与实验所得的数据十分接近, 其中大部分(有15组)的误差在7%以内, 只有少数几组(第8、10、11、15、19和20组)的误差在10%左右, 对比可得实验与理论的误差基本在10%以内。

表3 实验与理论计算结果对比 Table 3 Comparison between experimental and theoretical results

由于泡沫铝不同的发泡工艺和基础材料, 在相同密度下, 会有不同的力学特性, 在利用理论公式进行估算时, 难免会出现一些偏差。因此, 采用理论预测泡沫铝填充的薄壁梁压溃力学特性前, 应对可能采用的泡沫铝材料特性进行充分的分析, 以保证理论在设计中的准确性。

4 结束语

考虑泡沫铝填充薄壁梁压溃过程中泡沫铝对压溃距离的影响以及薄壁梁管壁与泡沫铝之间的相互作用, 推导出泡沫铝填充薄壁梁的压溃力表达式, 应用已有的泡沫铝填充低碳钢和铝合金正方形截面薄壁梁实验数据对压溃力理论表达式进行验证, 结果表明该理论公式具有较高的精度。利用该理论公式可以在详细设计结构断面之前对泡沫铝填充薄壁梁的材料及尺寸进行快速设计, 对其压溃性能及轻量化效果进行快速估算。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	桂良进, 范子杰, 王青春. 泡沫填充圆管的轴向压缩能量吸收特性[J]. 清华大学学报: 自然科学版, 2003, 43(11): 1526-1529. Gui Liang-jin, Fan Zi-jie, Wang Qing-chun. Energy absorption properties of foam-filled circular tube subjected to axial crushing[J]. Journal of Tsinghua University(Science and Technology), 2003, 43(11): 1526-1529. [本文引用:1]
[2]	Reid S R, Reddy T Y, Gray M D. Static and dynamic axial crushing of foam-filled sheet metal tubes[J]. International Journal of Mechanical Sciences, 1986, 28(5): 295-322. [本文引用:2]
[3]	Hanssen A G, Langseth M, Hopperstad O S. Static crushing of square aluminium extrusions with aluminium foam filler[J]. International Journal of Mechanical Sciences, 1999, 41(8): 967-993. [本文引用:4]
[4]	Hanssen A G, Langseth M, Hopperstad O S. Static and dynamic crushing of square aluminium extrusions with aluminium foam filler[J]. International Journal of Impact Engineering, 2000, 24(4): 347-383. [本文引用:1]
[5]	王青春, 范子杰, 桂良进, 等. 泡沫铝填充帽型结构轴向冲击吸能特性的试验研究[J]. 机械工程学报, 2006, 42(4): 101-106. Wang Qing-chun, Fan Zi-jie, Gui Liang-jin, et al. Experimental studies on the axial crash behaviour of aluminium foam-filled hat sections[J]. Chinese Journal of Mechanical Engineering, 2006, 42(4): 101-106. [本文引用:1]
[6]	Zarei H R, Kröger M. Optimum honeycomb filled crash absorber design[J]. Materials & Design, 2008, 29(1): 193-204. [本文引用:1]
[7]	Zarei H R, Kröger M. Optimization of the foam-filled aluminum tubes for crush box application[J]. Thin-Walled Structures, 2008, 46(2): 214-221. [本文引用:1]
[8]	Abramowicz W, Jones N. Dynamic axial crushing of square tubes[J]. International Journal of Impact Engineering, 1984, 2(2): 179-208. [本文引用:1]
[9]	Kecman D. Bending collapse of rectangular and square section tubes[J]. International Journal of Mechanical Sciences, 1983, 25(9): 623-636. [本文引用:1]
[10]	Santosa S P. Crashworthiness analysis of ultralight metal structures[D]. Cambridge: Massachusetts Institute of Technology, 1999. [本文引用:1]
[11]	Seitzberger M, Rammerstorfer F G, Degischer H P, et al. Crushing of axially compressed steel tubes filled with aluminium foam[J]. Acta Mechanica, 1997, 125(1-4): 93-105. [本文引用:1]

2003

0.0

. 2003, 43(11):1526-1529 DOI:doi:10.3321/j.issn:1000-0054.2003.11.023

Energy absorption properties of foam-filled circular tube subjected to axial crushing

泡沫填充圆管的轴向压缩能量吸收特性

Gui Liang-jin , Fan Zi-jie , Wang Qing-chun.

桂良进, 范子杰, 王青春

摘　要：建立了泡沫填充圆管在准静态轴向压缩载荷作用下的吸能特性分析模型,分析了材料参数、几何参数对其比吸能(单位质量吸收的能量)的影响,并对其结构参数进行了优化.研究结果表明: 泡沫填充圆管具有很好的吸能能力; 泡沫材料的相对密度对比吸能有显著的影响,相对密度取适当值可使比吸能最大.另外,提高构成泡沫的实体材料的强度可有效地提高比吸能.

... 泡沫铝作为一种新型的多功能材料,具有密度小、缓冲吸能特性好等优点^[1],将其填充到薄壁梁中可在满足碰撞吸能功效的同时实现轻量化 ...

1986

0.0

... 国内外许多学者对泡沫铝填充的矩形薄壁梁压溃理论进行了研究,Reid等^[2]考虑泡沫铝在压溃时的密实应变,通过对空正方形薄壁梁的压溃进行修正,获得泡沫铝填充的正方形薄壁梁压溃表达式 ...

... 2 泡沫铝填充矩形薄壁梁平均压溃力表达式推导Reid^[2]认为泡沫铝填充矩形薄壁梁发生压溃时,由于泡沫铝的密实应变,最终的折叠角度不再是#cod#x003c0 ...

1999

0.0

... Hanssen等^[3,4]进行大量的静态和动态泡沫铝填充铝合金薄壁梁的实验,并采用经验公式表达了平均压溃力 ...

... 7 g/cm³,等效流动应力 σ0为^[3]: ...

... n为材料的硬化因子,硬化因子与应力应变的关系为^[3]: ...

... 2 泡沫铝填充铝合金薄壁梁压溃理论验证Hanssen等^[3]进行了薄壁梁空管及各种密度泡沫铝填充的铝合金薄壁梁轴向压溃实验,薄壁梁材料为AA6060T4以及AA6082T4,材料参数如表2所示 ...

2000

0.0

... Hanssen等^[3,4]进行大量的静态和动态泡沫铝填充铝合金薄壁梁的实验,并采用经验公式表达了平均压溃力 ...

2006

0.0

. 2006, 42(4):101-106 DOI:doi:10.3321/j.issn:0577-6686.2006.04.018

Experimental studies on the axial crash behaviour of aluminium foam-filled hat sections

泡沫铝填充帽型结构轴向冲击吸能特性的试验研究

Wang Qing-chun , Fan Zi-jie , Gui Liang-jin

王青春, 范子杰, 桂良进

利用冲击试验系统,通过试验方法研究了泡沫铝填充帽型结构在轴向冲击工况下的吸能特性.首先进行了泡沫铝、空心帽型结构以及泡沫铝填充帽型结构的轴向冲击试验;然后根据试验结果,对泡沫铝填充帽型结构轴向冲击工况下的吸能特性进行了分析,评估了填充泡沫铝以及应变率对帽型结构吸能特性的影响.试验结果表明,与空心结构相比,填充泡沫铝之后帽型结构的轴向压缩稳定性和吸能特性有明显的改善;由于材料对应变率敏感,与准静态压缩相比,结构的吸能特性有一定的提高.

... 王青春等^[5]进行了泡沫铝填充帽形薄壁梁的动态冲击试验 ...

2008

0.0

... ger^[6,7]通过多目标优化的方法,对蜂窝铝和泡沫铝填充的铝管进行了压溃性能优化和轻量化设计 ...

2008

0.0

... ger^[6,7]通过多目标优化的方法,对蜂窝铝和泡沫铝填充的铝管进行了压溃性能优化和轻量化设计 ...

1984

0.0

... 1 矩形截面薄壁梁压溃理论Abramowicz 和Jones^[8]将压溃时的矩形截面薄壁梁划分为4个超折叠单元,如图1所示 ...

1983

0.0

... _ef 小于2H^[9],如式(3)所示: ...

1999

0.0

... _s通过式(8)进行估计^[10]: ...

1997

0.0

... 1 泡沫铝填充低碳钢薄壁梁压溃理论验证Seitzberger等^[11]进行了泡沫铝填充的低碳钢薄壁梁轴向压溃实验 ...