基于单个地磁传感器的交叉口排队长度估计

引用本文

贾利民, 陈娜, 李海舰, 董宏辉. 基于单个地磁传感器的交叉口排队长度估计.吉林大学学报:工学版, 2016, 46(3): 756-763
JIA Li-min, CHEN Na, LI Hai-jian, DONG Hong-hui. Intersection queue length estimation with single magnetic sensor. Journal of Jilin University Engineering and Technology Edition, 2016, 46(3): 756-763 复制到剪切板

Permissions

基于单个地磁传感器的交叉口排队长度估计

贾利民¹, 陈娜¹, 李海舰^1,², 董宏辉^1,³

1.北京交通大学轨道交通控制与安全国家重点实验室, 北京 100044

2.北京工业大学北京市交通工程重点实验室, 北京 100124

3.北京交通大学北京市城市交通信息智能感知与服务工程技术研究中心, 北京 100044

作者简介:贾利民(1963-),男,教授,博士生导师.研究方向:智能交通,交通安全.E-mail:jialm@vip.sina.com

基金:国家科技支撑计划项目(2014BAG01B02)

摘要

通过对车辆排队机理进行建模,利用车辆通过传感器时间及车尾时距描述车辆排队演化过程,从而估计邻近信号灯周期内的车辆排队长度。分析了车辆通过传感器时间及车辆车尾时距的动态变化规律,并提出车尾时距模型、通过时间模型和综合模型等对排队长度进行估计。最后,利用现场试验对本方法进行验证,试验结果表明本文提出的模型和方法能够准确估计交叉口车辆排队长度,且系统成本低廉、部署方便,便于大规模推广应用,能够为信号灯周期优化、交通服务水平评价等应用提供基础数据。

关键词: 交通运输系统工程; 地磁传感器; 信号交叉口; 排队长度估计; 排队车辆数

中图分类号:U491 文献标志码:A 文章编号:1671-5497(2016)03-0756-08

Intersection queue length estimation with single magnetic sensor

JIA Li-min¹, CHEN Na¹, LI Hai-jian^1,², DONG Hong-hui^1,³

1.State Key Laboratory of Rail Traffic Control and Safety, Beijing Jiaotong University, Beijing 100044, China

2.Beijing Key Laboratory of Traffic Engineering, Beijing University of Technology, Beijing 100124, China

3.Beijing Engineering Research Center of Urban Traffic Information Intelligent Sensing and Service Technologies, Beijing Jiaotong University, Beijing 100044, China

Abstract

To estimate the intersection queue length, a magnetic sensor is deployed near the stop line at the intersection. Through the vehicle queue mechanism modeling, the evolution of vehicle occupancy sensor time and the departure interval can be obtained. Eventually, the queue length of the last signal cycle can be estimated. This paper analyzes the variance of vehicle occupancy sensor time and the departure interval with the increase in queued vehicle number, thereby proposes departure interval model, vehicle occupancy sensor time model and comprehensive model to estimate the queue length. The accuracies of the proposed models are compared using field experiments. Results show that the proposed queue length estimation method can accurately get the queue length of the last signal cycle. The method costs low and can be deployed easily, and thus, it can facilitate large-scale popularization and application. It can provide intersection queue length information for signal cycle optimization and traffic service level evaluation in road signal intersections.

Keyword: engineering of transportation and communication system; magnetic sensor; signal intersection; queue length estimation; queued vehicle numbers

Show Figures

0 引言

道路交叉口作为城市路网的关键结点, 其通行能力和控制机制直接影响着路网的畅通程度和服务水平, 车辆排队长度是衡量道路畅通程度和服务水平的一个重要指标。排队长度指某一红灯时刻, 进道口的停车线与最后一辆停止车辆间的距离, 实际计算中多以排队队列中的车辆数代替, 它也是评价信号交叉口运行效率的一个重要指标, 能及时反映交叉口处的运行状况, 对信号配时优化、道路服务水平评价等有至关重要的作用^[1]。

现有车辆检测设备分为固定式检测器和移动式检测器。固定式检测器主要包括视频检测器^{[2, 3]}、线圈检测器、地磁传感器^[4]、红外线检测器、超声波检测器等, 它们利用某种物理原理对车辆进行检测, 并通过一定的算法获取车辆运行参数。移动式检测器主要为浮动车, 包括传统的浮动车和载有GPS或移动手机的行驶车辆。现有交叉口排队长度估计采用的车辆检测设备主要有视频检测器、线圈检测器、地磁传感器和浮动车等。视频检测器安装过程中需要对摄像机进行标定, 并且其获取的交通视频图像需进行一定的预处理及抖动消除, 之后利用车辆检测算法进行排队长度检测, 如基于移动虚拟线圈的排队长度检测算法^{[2, 5]}、模式识别方法^[6]等。基于线圈检测器的排队长度检测模型主要有交通波理论和累计到达-离去法^{[1, 7]}。随着移动手机和车载GPS车辆的增多, 基于浮动车的排队长度检测模型日益增加, 其主要方法为在确定浮动车的分布规律后, 建立排队长度检测模型, 如基于车辆到达特性的排队长度估计模型^[8]、利用队尾浮动车位置估算最大排队长度的方法^{[1, 9, 10]}、随机建模方法^[11]等。除此之外, 部分学者将浮动车与线圈检测数据相结合进行排队长度估计研究^{[12, 13]}。地磁传感器同样可以准确获取交通流参数^{[14, 15, 16, 17]}, 并且可以用于车辆排队长度估计^[18]。

利用视频、线圈检测器进行交叉口车辆排队检测具有检测成本高、布设及调试复杂等缺点; 传统浮动车检测具有成本高、操作复杂等特点, 且基于车载GPS或移动手机的检测方法容易受车辆条件限制, 导致这些技术都不便于大规模应用, 无法适应现今交叉口车辆排队长度信息的网络化需求。而地磁传感器便于组成功能丰富的无线传感器网络, 具有成本低廉、布设简单等优点, 可以有效地克服其他检测方法的不足, 并且其检测不受车辆条件限制。

目前, 基于地磁传感器的排队长度估计方法研究多利用多个传感器, 各传感器之间的时钟同步算法复杂, 其成本相对于单个地磁传感器较高, 调试和布设施工相对复杂。本文重点研究基于单个地磁传感器的交叉口车辆排队长度估计方法, 利用车辆通过单个地磁传感器时的关键信息, 对上一信号周期内车辆排队长度进行估计, 为信号灯周期优化、交通服务水平评价等应用提供基础数据。

1 单地磁传感器排队长度后估计

1.1 问题描述

交叉口车辆的排队行为符合车辆跟驰行为特征, 本文参照车辆跟驰模型对交叉口车辆排队情形进行类比描述。假设所有排队车辆满足匀速-加速-匀速模式, 即排队车辆均由匀速(某初始速度)开始起步(由于车辆从静止到某初始速度的时间和运行距离都较短, 为了简化问题, 忽略不计), 当与前车距离大于d_need时, 开始加速运动, 若起步瞬间已经满足加速条件, 则直接加速运动; 当车辆运行速度达到速度上限v_max时, 开始匀速运动, 典型交叉口排队场景如图1所示。图1中, l_car为平均车辆长度; l_inter为相邻车辆的跟车距离; d₁为车辆停止线到第一辆排队车辆车尾的距离。本文将通过分析排队车辆通过单地磁传感器的时间特性估计上一信号周期内的排队车辆数。

	Figure Option View Download New Window
	图1 典型道路交叉口排队场景Fig.1 Typical road intersection queuing scene

1.2 问题分析

通过单地磁传感器可以获取多种交通流参数^{[15, 16, 17]}, 包括各车辆邻近和离开传感器的时间点、车流量、车速和车型等。利用车辆检测算法^{[16, 17]}, 获取车辆邻近时间点和离开时间点, 由此可得到连续时间车流中各车辆依次通过该地磁传感器的时间点对示意图, 如图2所示, 其中前后两车辆离开传感器时间之差定义为车尾时距, 记为Δ t_s; 车辆邻近和离开传感器的时间差定义为车辆通过时间, 记为Δ t。

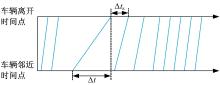	Figure Option View Download New Window
	图2 各车辆依次通过地磁传感器的时间点对示意图Fig.2 Time pairs of vehicles passing through magnetic sensor in turn in schematic

为了更好地描述车辆在交叉口的跟驰和排队机理, 本文做出如下假设和参数设定:①第一辆排队车辆车头紧贴停止线; ②排队车流的平均车辆长度为l_car, 则d₁=l_car; ③相邻车辆的跟车距离为l_inter; ④驾驶员的反应时间与动作时间之和为t_r;⑤车辆加速度为a;⑥地磁传感器紧贴停止线布置; ⑦车辆初始速度为v_start; ⑧排队车辆数为N; ⑨第i辆车开始加速之前匀速运行的时间为t_c (i), 经过停止线的时间为t_s (i), 车尾离开停止线的速度为v(i), 通过地磁传感器的时间为Δ t(i), 与第i-1辆车经过停止线的时间差为Δ t_s (i); ⑩第i辆排队车辆车尾距离停止线的距离为d_i, 则 $\begin{matrix} d_{i} = i \times l_{car} + (i - 1) \times l_{inter} \end{matrix}$ 。

设排队车辆中第一辆车开始启动时为0时刻, 易得 $Δt (1) = \sqrt[]{2 l_{car} / a}$ ; 则第一辆车车尾通过停止线的时刻 $t_{s} (1) = \sqrt[]{2 l_{car} / a}$ , 也即 $Δ t_{s} (1) = \sqrt[]{2 l_{car} / a}$ 。

本文通过揭示车辆跟驰和排队机理, 分析车辆通过地磁传感器的时间Δ t(i)及相邻排队车辆车尾时距Δ t_s(i)的动态变化情况, 并在此基础上研究基于单个地磁传感器的排队长度后估计方法。

1.3 时间模型

(1)车尾时距模型(即Δ t_s(i)模型)

研究Δ t_s (i)的变化规律需先获得t_s (i), t_s (i)的取值与第i-1辆车的运行状态相关, 由此可分为以下两种情形。

情形一(满足直接加速条件):当第二辆排队车辆起步时, 它与前车距离已经达到d_need, 即 $\begin{matrix} a t_{r}^{2} / 2 + l_{inter} \geq d_{need}, \end{matrix}$ 此时第二辆及之后的排队车辆直接加速行驶。

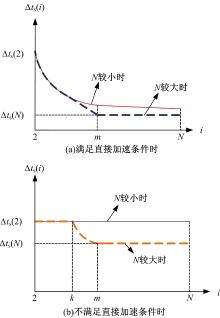
分析排队车辆消散过程可知, $\begin{matrix} N \end{matrix}$ 较小, 排队车辆消散完毕, 所有车辆的车尾到达停车线前速度都小于v_max; 当排队车辆数 $\begin{matrix} N \end{matrix}$ 足够大时, 必存在从某排队车辆 $\begin{matrix} m \end{matrix}$ 起, 其加速行驶速度增至v_max时车尾尚未或刚好达到停车线, 而此后该车辆以v_max匀速行驶。排队车辆 $\begin{matrix} m \end{matrix}$ 可根据情形一中的条件计算或仿真获得。如果使用计算的方法获得m, 计算过程中可暂不考虑v_max。若计算得车辆 $\begin{matrix} M \end{matrix}$ 车尾到达停车线前速度小于等于v_max, 车辆M+1车尾到达停车线前速度大于v_max, 则 $\begin{matrix} m = M 。 \end{matrix}$

若N较小,第N个排队车辆的车尾到达停车线前速度未增至v_max, 即v(N)< v_max, 则按照式(1)计算Δ t_s (i):

$\begin{matrix} \begin{matrix} Δ t_{s} (i) = \sqrt[]{2 d_{i} / a} - \sqrt[]{2 d_{i - 1} / a} + t_{r} \\ i = 2, 3, \dots, N \end{matrix} \end{matrix}$ (1)

若N较大, 则按照式(2)计算Δ t_s (i):

$\begin{matrix} Δ t_{s} (i) = \{\begin{matrix} \sqrt[]{2 d_{i} / a} - \sqrt[]{2 d_{i - 1} / a} + t_{r}, 2 \leq i < m \\ (l_{inter} + l_{car}) / v_{\max} + t_{r}, m \leq i \leq N \end{matrix} \end{matrix}$ (2)

情形二(不满足直接加速条件):当第二辆排队车辆起步时, 它与前车距离未达到d_need, 即 $\begin{matrix} a t_{r}^{2} / 2 + l_{inter} < d_{need}, \end{matrix}$ 此时第二辆及之后的排队车辆先以初始速度v_start行驶一段时间, 之后再加速行驶。

此情形下需要判断第二辆车何时加速。同样, N较小时, 在车尾到达停止线之前第二辆车及之后车辆都无法满足加速条件, 即各车辆以初始速度匀速通过停止线, 则Δ t_s (i)如式(3)所示。相邻车辆的加速时间差满足式(4)。

$Δ t_{s} (i) = \frac{(l_{inter} + l_{car})}{v_{start}} + t_{r} i = 2, 3, \dots, N$ (3)

$t_{c} (i + 1) - t_{c} (i) = \sqrt[]{2 (d_{need} - l_{inter} - v_{start} t_{r}) / a}$ (4)

若N较大, 必存在某排队车辆k开始加速时, 车尾未通过停止线, 并且其车尾到达停止线时的速度未达到v_max 。排队车辆k为情形二中所有排队车辆中首个满足加速时车辆运行距离与相应的d_i 之差为负的车辆。排队车辆m可根据情形二中的条件计算或仿真获得, 与情形一中相类似。随着排队车辆数的继续增加, 必存在某排队车辆m, 其车尾到达停止线之前速度增至v_max, 并以速度v_max行驶至停止线, 则按照式(5)计算 $\begin{matrix} Δ t_{s} (i) : \end{matrix}$

$\begin{matrix} \begin{matrix} Δ t_{s} (i) = \\ \{\begin{matrix} (l_{inter} + l_{car}) / v_{s t art} + t_{r}, 2 \leq i < k \\ t_{c} (i) - t_{c} (i - 1) + (v (i) + v (i - 1)) / 2, k \leq i < m \\ (l_{inter} + l_{car}) / v_{\max} + t_{c} (i + 1) - t_{c} (i), m \leq i \leq N \end{matrix} \end{matrix} \end{matrix}$ (5)

式中:

$\begin{matrix} v (i) = \sqrt[]{v_{start}^{2} + 2 a (d_{i} - v_{start} (t_{c} (i) - (i - 1) t_{r}))} 。 \end{matrix}$

图3给出了在一次排队车辆消散过程中不同情形下的Δ t_s(i)的变化趋势, 在排队车辆数较少时, Δ t_s(i)的变化曲线单调不增, 但无分段点; 排队车辆数较多时, 由于车辆性能和道路条件的物理约束, Δ t_s(i)的变化曲线单调不增时出现若干分段点。通过Δ t_s(i)的变化情况能够清晰地描述一次排队的车辆消散过程。

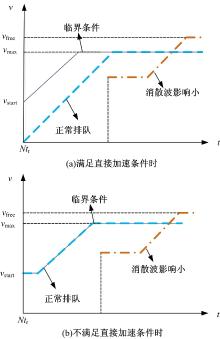
	Figure Option View Download New Window
	图3 Δ t_s(i)的变化趋势图Fig.3 Trend of Δ t_s(i)

在排队消散过程中, 上游到达受到排队消散影响的车辆 $\overset{+}{N}$ , 其临界条件为, 当虚拟排队车辆N+1开始启动时, 车辆 $\overset{+}{N}$ 在d_N+1 处运行速度为v_start, 在停止线到d_N+1处的距离之间, 其v-t曲线如图4所示。由v-t曲线的性质可知, 在临界条件下, 情形一中, $Δ t_{s} (\overset{+}{N}) < Δ t_{s} (N + 1)$ ; 在情形二中, $Δ t_{s} (\overset{+}{N}) = Δ t_{s} (N + 1)$ 。而随着排队消散波影响强度的减弱, 最终, $Δ t_{s} (\overset{+}{N}) ≫ Δ t_{s} (N + 1)$ 。所以, 上游到达受到排队消散影响的车辆Δ t_s(i)具有递增性。

	Figure Option View Download New Window
	图4 上游到达受排队消散影响车辆的v-t曲线图Fig.4 v-t diagram of upstream vehicle arrival affected by queue dissipation

(2)通过时间模型(即 $\begin{matrix} Δt (i) \end{matrix}$ 模型)

同Δ t_s(i)模型, 根据是否满足车辆加速条件, Δ t(i)模型同样需要分为两种情形讨论。

情形一(满足直接加速条件):同Δ t_s(i)模型所述。若N较小, 第N个排队车辆的车尾到达停车线前速度未增至v_max, 即v(N)< v_max, 则根据式(6)计算Δ t(i):

$\begin{matrix} Δt (i) = (\sqrt[]{2 d_{i} / a} - \sqrt[]{2 (d_{i} - l_{car}) / a}) \end{matrix}$ (6)

若N较大, 必存在某排队车辆m的车尾行驶至停止线时, 其速度已经或刚好达到v_max, 即 $\sqrt[]{2 a (d_{m} - l_{car})} \geq v_{\max}$ , 则按照式(7)计算Δ t(i):

$\begin{matrix} \begin{matrix} Δt (i) = \\ \{\begin{matrix} (\sqrt[]{2 d_{i} / a} - \sqrt[]{2 (d_{i} - l_{car}) / a}), 2 \leq i < m \\ l_{car} / v_{\max}, m \leq i \leq N \end{matrix} \end{matrix} \end{matrix}$ (7)

排队车辆m的标定方法同Δ t_s(i)模型的情形一。

情形二(不满足直接加速条件):同 $\begin{matrix} Δ t_{s} (i) \end{matrix}$ 模型所述。同样, N较小时, 在车尾到达停止线之前第二辆车及之后的车辆都无法满足加速条件, 即各车辆以初始速度匀速通过地磁传感器, 则Δ t(i)如式(8)所示:

$\begin{matrix} Δt (i) = l_{car} / v_{start} \end{matrix}$ (8)

若N较大, 后续排队车辆会在某时刻加速运动, 随着排队车辆数N的增大, 必存在某排队车辆k开始加速时, 车尾未通过停止线, 并且其车尾到达停止线时的速度未达到v_max; 随着排队车辆数的继续增加, 必存在某排队车辆m, 其车尾到达停止线之前速度增至v_max, 并以速度v_max行驶至停止线, 则 $\begin{matrix} Δt (i) \end{matrix}$ 如式(9)所示:

$\begin{matrix} Δt (i) = \{\begin{matrix} l_{car} / v_{start}, 2 \leq i < k \\ l_{car} / ((v (i) + v_{h} (i)) / 2), k \leq i < m \\ l_{car} / v_{\max}, m \leq i \leq N \end{matrix} \end{matrix}$ (9)

v_h(i)为车辆i的车头到达停止线时的车速:

$v_{h} (i) = \sqrt[]{v_{start}^{2} + 2 a (d_{i - 1} + l_{inter} - v_{start} (t_{c} (i) - (i - 1) t_{r}))};$

v(i)与式(5)中相同; 排队车辆k与m标定方法同Δ t_s(i))模型的情形二。

在一次排队车辆消散过程中不同情形下的Δ t(i)的变化趋势和变化规律与Δ t_s(i)类似, 文中不再赘述。可以看出, 在每一次排队车辆消散过程中Δ t_s(i)和Δ t(i)具有不增性和有限性, 这也是基于单个地磁传感器进行排队长度后估计的理论基础。同样, 根据图4可以分析得出, 上游到达受到排队消散影响的车辆v(i)具有递增性, 即Δ t(i)具有递减性。

由文献^[15]和^[17]可知, 地磁传感器获取的车辆波形数据反映了传感器周围的磁场强度在不同时间点的变化情况, 利用车辆检测算法^{[15, 17]}获取车辆邻近和离开传感器时间点时会存在一个附加长度l_e, 这样需要对通过时间模型进行修正, 设r为修正系数, 则可利用式(10)对Δ t(i)进行修正:

$\begin{matrix} Δ t_{new} (i) = r \times Δt (i) \end{matrix}$ (10)

式中:Δ t_new为修正后的车辆通过时间; r为修正系数, $\begin{matrix} r = (l_{car} + l_{e}) / l_{car}, l_{e} \end{matrix}$ 为附加车长。

1.4 排队长度后估计方法

在连续时间交通流中, 有些车辆在绿灯期间没有排队便行驶通过传感器, 称为通过车辆; 有些车辆则在红灯期间排队之后通过传感器, 称为排队车辆。在进行排队长度后估计之前, 需要确定连续时间交通流中的排队车辆。本文给出通过信号灯交叉口的连续时间交通流中每个排队周期的排队车辆判别依据:① $Δ t_{s} (i) + Δt (i - 1) \geq t_{red}$ , 其中, t_red 表示交叉口的红灯时长, 等号表示当信号灯恰巧为红灯时, 前车离去而后车紧接着开始排队, 并且, 当信号灯转为绿灯时, 车辆直接离去; ②Δ t(i)≥ Δ t(1), 等号表示恰巧车辆刚由于红灯停车后, 行驶方向信号灯由红灯变成了绿灯。当连续时间交通流的车辆i同时满足上述两个条件时, 则车辆i为某信号周期内的第一个排队车辆, 即给出了该信号周期内的起始排队车辆, 根据本文提出模型确定该信号周期内的终止排队车辆, 从而确定该信号周期内的排队车辆数。

(1)车尾时距模型

车尾时距模型为仅根据计算Δ t_s(i)来估计排队长度。理论上, 在判定出信号周期内第一辆排队车辆后, 在绿灯和黄灯时间内, 依次对比通过车辆的Δ t_s(i)与理论排队车辆的Δ t_s(i), 结合上游到达受到排队消散影响的车辆Δ t_s(i)具有递增性这一特性, 计算两者差值, 若相对误差在可控范围δ 内, 即可判断其是排队车辆, 反之不是。假设从第一个排队车辆起, 第k+1个车首先被判断为不是排队车辆, 则此周期内的排队长度估计值l_estimate=d_k 。其算法如下:

(1)根据停车判定条件判断出第一辆停车车辆, k=1, i=1

(2)if绿灯与黄灯时间内无后续车辆

then执行第(4)步

else i=i+1进入第(3)步

end if

(3)if实际计算的Δ t_s(i)值不大于(1+δ )倍的理论值Δ t_s(i)

then k=k+1, 重复执行第2步

else 执行第4步

end if

(4)排队长度估计值l_estimate=d_k, 返回1继续判断下个排队周期

为了简单起见, 可单独使用一个或多个Δ t_s(i)值进行排队车辆判断, 比如前k个车辆用Δ t_s(k)判断是否排队, 第k+1到N用Δ t_s(k+1)判定等。

(2)通过时间模型

通过时间模型是仅根据计算Δ t(i)来估计排队长度的方法。其判别算法只需将车尾时距模型中第(3)步的判定条件改为“ 实际计算的Δ t(i)不小于(1+δ )倍的理论值Δ t_new(i)” 。同样, 也可单独使用一个或多个通过时间理论值进行判断。若使用一个值, 则可选用rl_car/v_max作为排队车辆中实际计算的Δ t(i)的下限, 若实际计算的Δ t(i)不小于(1+δ )倍的rl_car/v_max, 则车辆i为排队车辆, 否则不是。若使用多个离散值进行判定, 类似车尾时距模型, 比如前k个车用Δ t_new (k)判断, 第k+1到N辆车用Δ t_new (k+1)判定。

(3)综合模型

综合模型同时考虑了车尾时距模型和通过时间模型, 即两者的判别条件都需要满足。设用车尾时距模型得到的排队车辆数为n_d, 用通过时间模型得到的排队车辆数为n_v, 用综合模型得到的排队车辆数为n_c, 则满足n_c=min{n_d, n_v}。

2 实例分析

通过在某车辆排队交叉口部署单个地磁传感器对本文方法进行验证, 利用视频记录现场排队情况, 并作为实验结果的对比依据。由定数排队理论可知, 排队车辆数可近似代替排队长度^[19]。本试验将分别利用车尾时距模型、通过时间模型和综合模型估计排队车辆数, 进而分析各模型的试验结果。

2.1 地磁传感器现场部署

该试验地点位于北京市海淀区交大东路, 如图5所示, 地磁传感器布设于交大东路某信号灯停车线处。交大东路为南北双向两车道, 排队车辆为单车道分布。

	Figure Option View Download New Window
	图5 单地磁传感器交大东路布设地点Fig.5 Layout of single magnetic sensor at Jiaodadonglu in Beijing

2.2 试验数据

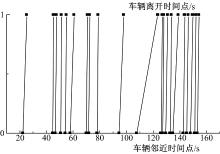
利用该地磁传感器实时采集现场交通信息数据, 得到连续地磁波形数据, 利用车辆检测算法^[15]得到连续交通流中各车辆通过该地磁传感器时的邻近时间点和离开时间点, 图6为实际某交通流各车辆依次通过地磁传感器的时间点对图, 并在图中标示出了交通流车尾时距Δt_s(i)及车辆通过时间Δt(i)。

	Figure Option View Download New Window
	图6 实际各车辆依次通过地磁传感器的时间点对图Fig.6 Real time pairs of vehicles passing through magnetic sensor in turn

2.3 参数标定

试验选取2009年6月30日17:26~18:00视频检测数据, 以小汽车为主要车型进行参数标定, 信号周期为72 s, 其中, 红灯时间t_red=24 s, 黄灯时间2 s, 绿灯时间56 s。本文参照已有研究成果及相关标准、规范进行参数标定。取l_car=4.5 m, l_e=1.8 m^[15], 则修正系数r=(l_car+l_e)/l_car=1.4; 驾驶员驶入交叉口的加速度与具体交叉口条件相关, 需单独测定^[20]。本文对试验交叉口加速度进行标定, 取平均值a=1.89 m/s²; v_start取停车邻近速度5 km/h^[1]; v_max采用直行驶进交叉口排队车辆的最大速度25 km/h^[20]; t_r取男女加速反应时间均值1.5 s^[21]; l_inter取车辆慢速行驶的安全间隔2 m^{[3, 22]}; 本文选取5个排队周期内第二辆排队车辆开始加速时与前车的距离值并取平均值, 标定d_need=10.88 m。

根据已知参数, 可得Δ t_s(1)=Δ t(1)=2.18 s, Δ t_new(1)=1.4× Δ t(1)=3.052 s。利用停车判定条件, 得2009年6月30日17:26~18:00内, 共有17次排队, 与实际情况相符合。

2.4 试验结果

通过模型参数标定可知, 该试验路段在计算Δ t_s(i)与Δ t(i)时均符合情形二, 且k=2。第2辆及之后排队车辆的Δ t_s(i)和Δ t_new(i)理论值如表1所示。

表1 Δ t_s(i)和Δ t_new(i)的理论值 Table 1 Theoretical values of Δ t_s(i) and Δ t_new(i)

取δ =20%, 根据各模型所得的排队车辆数如表2所示。

表2 排队车辆数对比 Table 2 Queuing vehicles contrast 单位:辆

由表2可得:车尾时距模型、通过时间模型、综合模型的整体相对误差分别为13.04%、22.83%、2.17%。

2.5 分析和讨论

由上述试验结果可以看出, 本文提出的3种模型中车尾时距模型和综合模型效果均较好, 通过时间模型效果相对较差。结合对试验交叉口观测结果可知, 通过时间模型客观干扰因素主要有:①试验交叉口车型不统一, 存在大型公交车, 需要结合车型识别系统提高l_car的估计精度; ②交叉口处行人闯红灯现象较多, 对正常的车辆跟驰行为产生一定的影响。由估计误差可知, 车尾时距模型和综合模型对混合交通的鲁棒性较好, 可进行实际应用。另外, 本文提出的估计方法每车道仅需要一个地磁传感器即可实现, 成本低廉, 便于大规模部署和实际推广。由各模型的判别算法可知, 该估计方法计算简洁, 通过标定各交叉口的模型参数, 可以离线求得表1中的通过时间和车尾时距参数, 结合传感器检测得到的交通流时间参数可以直接进行比较和判别, 无需复杂的机器学习和数据处理算法, 便于在线估计。

3 结束语

通过对排队车辆消散过程进行建模, 得到可有效估计车辆排队长度的时间模型, 包括车尾时距模型、通过时间模型和综合模型。通过现场试验验证了3种模型的有效性, 其中综合模型在准确率和鲁棒性方面优势明显。与传统基于视频检测器、多线圈检测器融合、多地磁传感器融合或浮动车的排队长度估计方法相比, 本文估计方法计算简单, 便于在线系统实现。另外每车道仅需一个地磁传感器, 成本低并且布设方便, 便于大规模部署和实际推广。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	庄立坚, 何兆成, 叶伟佳, 等. 基于浮动车数据的排队长度检测方法研究[J]. 交通运输系统工程与信息, 2013, 13(3): 78-84. Zhuang Li-jian, He Zhao-cheng, Ye Wei-jia, et al. Queue length estimation based on floating car data[J]. Journal of Transportation System Engineering and Information Technology, 2013, 13(3): 78-84. [本文引用:4]
[2]	时彦洞. 基于视频的车辆排队长度检测技术研究[D]. 江门: 五邑大学信息工程学院, 2009. Shi Yan-dong. Queue detection based on video technology[D]. Jiangmen: School of Information Engineering, Wuyi University, 2009. [本文引用:2]
[3]	刘喆. 基于计算机视觉的运动车辆检测与跟踪算法研究[D]. 北京: 北京工业大学电子信息与控制工程学院, 2009. Liu Zhe. Moving vehicle detection based on computer vision[D]. Beijing: College of Electronic Information and Control Engineering, Beijing University of Technology, 2009. [本文引用:2]
[4]	史元超. 基于新型传感器的交通状态获取技术的研究[D]. 北京: 北京交通大学交通运输学院, 2009. Shi Yuan-chao. Traffic condition acquirement technology based on New-type sensor[D]. Beijing: School of Traffic and Transportation, Beijing Jiaotong University, 2009. [本文引用:1]
[5]	Zheng J, Ma X, Wu Y J, et al. Measuring signalized intersection performance in real-time with traffic sensors[J]. Journal of Intelligent Transportation Systems, 2013, 17(4): 304-316. [本文引用:1]
[6]	Negri P. Estimating the queue length at street intersections by using a movement feature space approach[J]. IET Image Processing, 2014, 8(7): 406-416. [本文引用:1]
[7]	Vigos G, Papageorgiou M, Wang Y. Real-time estimation of vehicle-count within signalized links[J]. Transportation Research Part C: Emerging Technologies, 2008, 16(1): 18-35. [本文引用:1]
[8]	买艳辉. 基于出租车GPS数据的速度分布和排队长度估计研究[D]. 长沙: 长沙理工大学交通运输工程学院, 2013. Mai Yan-hui. The study on an estimation of speed distribution and queue length traffic state based on taxi GPS data[D]. Changsha: School of Traffic and Transportation Engineering, Changsha University of Science & Technology, 2013. [本文引用:1]
[9]	Comert G, Cetin M. Queue length estimation from probe vehicle location and the impacts of sample size[J]. European Journal of Operational Research, 2009, 197(1): 196-202. [本文引用:1]
[10]	Cai Q, Wang Z, Guo X, et al. New calculating method for HCM 2000 queue length estimation procedures with the application of floating car data[J]. Procedia-Social and Behavioral Sciences, 2013, 96: 2201-2210. [本文引用:1]
[11]	Comert G. Simple analytical models for estimating the queue lengths from probe vehicles at traffic signals[J]. Transportation Research Part B: Methodological, 2013, 55: 59-74. [本文引用:1]
[12]	Badillo B E, Rakha H, Rioux T W, et al. Queue length estimation using conventional vehicle detector and probe vehicle data[C]//15th International IEEE Conference on Intelligent Transportation Systems (ITSC2012). United States: Institute of Electrical and Electronics Engineers Inc, 2012: 1674-1681. [本文引用:1]
[13]	Comert G. Effect of stop line detection in queue length estimation at traffic signals from probe vehicles data[J]. European Journal of Operational Research, 2013, 226(1): 67-76. [本文引用:1]
[14]	夏发钦. 利用地感应线圈检测机动车辆的原理与实现[D]. 武汉: 武汉科技大学信息科学与工程学院, 2011. Xia Fa-qin. Vehicle detection using induction coil detector[D]. Wuhan: School of Information Science and Engineering, Wuhan University of Science and Technology, 2011. [本文引用:1]
[15]	Li H, Dong H, Jia L, et al. Some practical vehicle speed estimation methods by a single traffic magnetic sensor[C]//14th International IEEE Conference on Intelligent Transportation Systems. United States: Institute of Electrical and Electronics Engineers Inc, 2011: 1566-1573. [本文引用:6]
[16]	Li Hai-jian, Dong Hong-hui, Jia Li-min, et al. Vehicle classification with single multi-functional magnetic sensor and optimal MNS-based CART[J]. Measurement, 2014, 55: 142-152. [本文引用:3]
[17]	李海舰. 道路交通信息获取多参量感知与传感器网络优化[D]. 北京: 北京交通大学交通运输学院, 2014. Li Hai-jian. Multi-parameter sensing and sensor network optimization for road traffic information acquisition[D]. Beijing: School of Traffic and Transportation, Beijing Jiaotong University, 2014. [本文引用:5]
[18]	Sanchez R O, Horowitz R, Varaiya P. Analysis of queue estimation methods using wireless magnetic sensors[J]. Transportation Research Record: Journal of the Transportation Research Board, 2011, 2229(1): 34-45. [本文引用:1]
[19]	代磊磊, 姜桂艳, 裴玉龙, 等. 饱和信号交叉口排队长度预测[J]. 吉林大学学报: 工学版, 2008, 38(6): 1287-1290. Dai Lei-lei, Jiang Gui-yan, Pei Yu-long, et al. Prediction of queue length at saturate signalized intersection[J]. Journal of Jilin University (Engineering and Technology Edition), 2008, 38(6): 1287-1290. [本文引用:1]
[20]	施晓芬. 城市信号交叉口驾驶员速度控制和视觉搜索行为研究[D]. 西安: 长安大学公路学院, 2011. Shi Xiao-fen. Speed control and visual search of driving behavior at the intersection[D]. Xi'an: School of Highway, Chang'an University, 2011. [本文引用:2]
[21]	王晶. 基于驾驶员性别的城市快速路跟驰模型研究[D]. 北京: 北京工业大学城市交通学院, 2008. Wang Jing. A car following model in urban expressway based on driver's gender[D]. Beijing: College of Metropolitan Transportation, Beijing University of Technology, 2008. [本文引用:1]
[22]	刘影. 基于机器视觉的交叉路口车速和车辆排队长度检测[D]. 天津: 天津工业大学电子信息与工程学院, 2012. Liu Ying. Vehicle speed and vehicle queue length detection based on video at plane intersection[D]. Tianjin: School of Electronic and Information Engineering, Tianjin Polytechnic University, 2012. [本文引用:1]

2013

0.0

. 2013, 13(3):78-84 DOI:doi:10.3969/j.issn.1009-6744.2013.03.012

Queue length estimation based on floating car data

基于浮动车数据的排队长度检测方法研究

Zhuang Li-jian , He Zhao-cheng , Ye Wei-jia

庄立坚, 何兆成, 叶伟佳

摘　要：排队长度作为评价信号交叉口运行效率的一个重要指标,能有效反映交叉口处的运行状况.传统排队检测模型大多基于线圈检测器,且模型假设过于理想化,本文提出一种面向低采样率浮动车数据、具有良好数据驱动性的信控交叉口在线排队长度检测方法,方法关键在于利用队尾浮动车位置估算最大排队长度.检测过程采用固定时间间隔,主要步骤包括地图匹配、等距划分交叉口进口道并统计停车点数量、判定队尾浮动车的位置、修正得到最大排队长度估计值.实测数据表明,此方法的精度与浮动车比率有直接的关系,在浮动车比率较高的许多主干路交叉口,精度可以达到理想效果,30 m以内的平均绝对误差对高峰期的排队检测依旧具有很大价值.

... 排队长度指某一红灯时刻,进道口的停车线与最后一辆停止车辆间的距离,实际计算中多以排队队列中的车辆数代替,它也是评价信号交叉口运行效率的一个重要指标,能及时反映交叉口处的运行状况,对信号配时优化、道路服务水平评价等有至关重要的作用^[1] ...

... 基于线圈检测器的排队长度检测模型主要有交通波理论和累计到达-离去法^[1,7] ...

... 随着移动手机和车载GPS车辆的增多,基于浮动车的排队长度检测模型日益增加,其主要方法为在确定浮动车的分布规律后,建立排队长度检测模型,如基于车辆到达特性的排队长度估计模型^[8]、利用队尾浮动车位置估算最大排队长度的方法^[1,9,10]、随机建模方法^[11]等 ...

... v_start取停车邻近速度5 km/h^[1] ...

2009

0.0

... 固定式检测器主要包括视频检测器^[2,3]、线圈检测器、地磁传感器^[4]、红外线检测器、超声波检测器等,它们利用某种物理原理对车辆进行检测,并通过一定的算法获取车辆运行参数 ...

... 视频检测器安装过程中需要对摄像机进行标定,并且其获取的交通视频图像需进行一定的预处理及抖动消除,之后利用车辆检测算法进行排队长度检测,如基于移动虚拟线圈的排队长度检测算法^[2,5]、模式识别方法^[6]等 ...

2009

0.0

... l_inter取车辆慢速行驶的安全间隔2 m^[3,22] ...

2009

0.0

. 2009, :- DOI:doi:10.7666/d.y1576276

Traffic condition acquirement technology based on New-type sensor

基于新型传感器的交通状态获取技术的研究[D]

Shi Yuan-chao.

史元超

道路交通状态获取是进行交通流控制和诱导等交通管理的重要前提，是制定交通安全管理策略、交通事故检测、交通事故致因分析等交通安全保障措施的必要基础。因此交通状态获取是交通管理、交通安全保障和交通基础设施监控维护的基础性重要问题。本文依托于国家高技术研究与开发项目（863）——《交通状态获取的新型传感器、传感器网络优化与融合》，选择新型传感器的交通状态获取技术作为研究内容，着重研究基于新型传感器的交通流量检测，时间占有率检测，车辆瞬时速度检测以及车型识别技术。具体内容如下：使用数字滤波技术对传感器采集的数据进行去噪处理...

2013

0.0

2014

0.0

2008

0.0

... 基于线圈检测器的排队长度检测模型主要有交通波理论和累计到达-离去法^[1,7] ...

2013

0.0

. 2013, :-

The study on an estimation of speed distribution and queue length traffic state based on taxi GPS data

基于出租车GPS数据的速度分布和排队长度估计研究[D]

Mai Yan-hui.

买艳辉

交通拥堵是当前大中城市面临的主要“城市病”之一，表现为拥堵程度加剧、拥挤时段延长、拥堵范围扩大。能够实时掌握路网交通状态对于交通管理者有重要意义。装有GPS的出租车作为移动检测器在路网中分布较广，是探测路网交通状态的一种有效手段。基于出租车GPS数据来估计路网实时的交通状态，以此优化信号配时，提高交通管理效率，已经成为目前的研究热点。本文主要有两个成果。1）基于出租车GPS数据估计交通拥堵特征。由于信号控制的存在、驾驶行为和车辆特性的随机性等因素，城市交通状态是典型的混合分布。针对这一特点，本文首先利用核密度估计技术对出租车GPS采集的速度数据进行无参数概率密度估计。在确定速度分布服从高斯混合分布的前提下，利用高斯混合模型对拥堵特征进行定量分析，得出的数量指标能够描述交通拥堵的严重程度、波动程度、各种状态的混合权重。研究成果实现了通过出租车GPS数据直接判定交通拥堵特征，为制定交通管理预案和评价交通管控设施的性能提供了有力依据。2）研究排队长度估计模型，并通过GPS数据标定模型参数。首先通过GPS数据对交叉口的车辆驶离特性进行分析，在分析现有离散模型的基础上，考虑驶离受交叉口排队车辆影响的因素，提出了离散转换模型，并建立了基于车辆到达特性的排队长度估算模型，利用实测排队长度数据对基于GPS数据的模型结果进行误差对比。出租车作为浮动车采集数据被广泛应用，本文研究成果对于如何处理这类数据提供了理论方法，具有一定的借鉴价值。

2009

0.0

2013

0.0

2013

0.0

2012

0.0

... 除此之外,部分学者将浮动车与线圈检测数据相结合进行排队长度估计研究^[12,13] ...

2013

0.0

... 除此之外,部分学者将浮动车与线圈检测数据相结合进行排队长度估计研究^[12,13] ...

2011

0.0

. 2011, :- DOI:doi:10.7666/d.y1943980

Vehicle detection using induction coil detector

利用地感应线圈检测机动车辆的原理与实现[D]

Xia Fa-qin.

夏发钦

随着现代交通的快速发展,在道路交通管理与控制中对交通信息的需求是越来越多。现代交通信息的采集是通过车辆检测器实现的,根据检测器所采用的不同的技术它可以分为感应线圈检测、视频检测、微波检测、红外线检测、雷达检测、激光检测等,本文研究的就是其中的感应线圈检测方法,环形线圈车辆检测器相对于其它的检测器具有低成本、高检测精度、全天候工作的优点,是目前应用的比较广泛的车辆检测器。本文介绍的采用地感应线圈技术的检测器具有独立检测、数据处理、数据通信的功能,可以提供车辆流量、车速、车型分类、排队长度的综合交通信息,并且可以应用在更广的范围。对于电磁感应原理的应用十分广泛,环形线圈车辆检测器就是利用它的思想。环形线圈作为传感器被埋在地底,当路面上有车辆通过埋设线圈区域,这时候会引起线圈的回路电感量发生变化,在这种情况下检测器就能检测出该变化,从而可以知道路面上有车辆的存在。关于这个电感变化量的检测有几种方法:使用相位锁存器和相位比较器来检测出相位,再根据这个相位的变化来确定路面车辆的通过;还有就是检测由环形线圈组成的耦合电路的振荡频率,通过对振荡频率变化的分析,从而可以判断路面车辆的存在。

... 地磁传感器同样可以准确获取交通流参数^{[14,15,16,17]},并且可以用于车辆排队长度估计^[18] ...

2011

0.0

... 地磁传感器同样可以准确获取交通流参数^{[14,15,16,17]},并且可以用于车辆排队长度估计^[18] ...

... 2 问题分析通过单地磁传感器可以获取多种交通流参数^[15,16,17],包括各车辆邻近和离开传感器的时间点、车流量、车速和车型等 ...

... 由文献^[15]和^[17]可知,地磁传感器获取的车辆波形数据反映了传感器周围的磁场强度在不同时间点的变化情况,利用车辆检测算法^[15,17]获取车辆邻近和离开传感器时间点时会存在一个附加长度l_e,这样需要对通过时间模型进行修正,设r为修正系数,则可利用式(10)对#cod#x00394 ...

... 2 试验数据利用该地磁传感器实时采集现场交通信息数据,得到连续地磁波形数据,利用车辆检测算法^[15]得到连续交通流中各车辆通过该地磁传感器时的邻近时间点和离开时间点,图6为实际某交通流各车辆依次通过地磁传感器的时间点对图,并在图中标示出了交通流车尾时距 Δts(i)及车辆通过时间Δt(i) ...

... 8 m^[15],则修正系数r=(l_car+l_e)/l_car=1 ...

2014

0.0

... 地磁传感器同样可以准确获取交通流参数^{[14,15,16,17]},并且可以用于车辆排队长度估计^[18] ...

... 2 问题分析通过单地磁传感器可以获取多种交通流参数^[15,16,17],包括各车辆邻近和离开传感器的时间点、车流量、车速和车型等 ...

... 利用车辆检测算法^[16,17],获取车辆邻近时间点和离开时间点,由此可得到连续时间车流中各车辆依次通过该地磁传感器的时间点对示意图,如图2所示,其中前后两车辆离开传感器时间之差定义为车尾时距,记为#cod#x00394 ...

2014

0.0

. 2014, :-

Multi-parameter sensing and sensor network optimization for road traffic information acquisition

道路交通信息获取多参量感知与传感器网络优化[D]

Li Hai-jian.

李海舰

全时空、网络化、大规模的道路交通信息获取为智能交通系统提供重要的数据基础,尤其是利用传感器网络技术实现路网中的单点、断面、区域交通流信息获取已成为当前智能交通系统获取道路交通信息的一个重要方式,并在世界各国大、中城市中表现的越来越突出。由于交通信息的时空相关性,路段、路网交通信息能够以道路上关键点的交通信息为基础,通过时空模型、交通流模型、关系模型等推导得知。另外,由于交通信息的时空相关性,加之工程资金、建设成本等约束条件,利用传感器网络技术研究单点、断面、区域的综合交通信息获取方法已成为智能交通系统研究领域的重点方向,对道路交通信息获取传感器网络(TIASN)相关理论、技术和方法的研究具有重要的理论和现实意义。本文以全时空、网络化、大规模的道路交通信息获取的实际需求为背景,重点解决如何实现TIASN网络中单个传感器获取尽可能丰富的多参量交通信息(微观层)、如何实现TIASN网络的信息标准化及最优物理拓扑和逻辑拓扑(中观层)以及如何实现TIASN网络大规模部署时的最优传感器布局(宏观层)等问题。本文针对这些问题及其子问题进行了深入研究,主要研究成果具体表现在以下几个方面： (1)形成了一种基于多功能地磁传感器的交通信息多参量获取方法,综合实现交通流参数和交通流构成要素等交通信息感知与获取针对微观层的TIASN网络检测节点问题,本文分别提出了双窗口车辆检测算法、车辆停驶检测算法和环境自适应的改进算法实现了面向不同实际应用、适应不同道路交通环境的高准确率交通流量检测；针对不同的多功能地磁传感器硬件配置环境,分别提出基于单模块传感器和双模块传感器的车辆速度获取方法,并通过视频数据对计算结果进行了验证；通过提取车辆波形数据的时、频域特征,分别提出时域、频域车型分类模型和算法,以适应不同的传感器硬件特点,实现了交通流构成要素的实时检测。 (2)提出了一种实现信息标准化的网络节点语义编码方法及一套以低成本、低功耗为目标的传感器网络拓扑优化方法针对中观层的TIASN网络信息标准化及各子网拓扑优化问题,探讨了TIASN网络的层次架构和节点功能,并给出了网络节点语义编码方法,为交通信息共享和节点语义编码标准化提供支持；提出了物理拓扑优化的多次多重背包模型和通信拓扑优化的边权图模型,实现了TIASN网络物理拓扑及通信拓扑优化,保证了工程上TIASN网络部署的经济性和信息传输的高效性,从而构建出经济、高效、长寿命的TIASN网络。 (3)提出了基于固定传感器的交通信息可信度空间分布模型及测度,基于该测度面向不同实际应用需求建立了传感器网络布局优化模型及方法针对宏观层的TIASN网络空间大规模部署问题,基于固定传感器的交通信息可信度空间分布特性,建立了三维交通信息可信度空间分布模型,定义了不同空间粒度下的交通信息可信度空间分布测度——传感器、路段、路网信息可信度函数,并进行了实证研究；基于该测度,考虑到交通信息完备性和有效性需求,建立了单向路段最小投资模型；通过引入传感器附加价值因子,建立了单向路段最大效益模型；为了能够分析各模型参数对传感器网络布局优化问题的影响模式,对离散模型连续化,分别给出两类模型的简化形式。研究结果表明本文提出的模型和算法能够在工程上指导TIASN网络大规模布局优化问题。最后从理论上对不同交通信息可信度空间分布特性和路段端点约束条件下的传感器网络布局优化问题进行了分析和讨论,证明了本文提出的新测度在交通信息可信度空间分布度量和传感器网络布局优化应用中的有效性。本文通过对TIASN网络多参量感知、网络信息标准与拓扑优化、大规模空间布局优化等问题的研究,并以交通信息获取的实际需求为背景,利用工程实例、场景实例或数值实例对本文提出的技术、方法和理论进行了验证；并针对工程中的实际情形给出了解决方案,证明了本文提出的各方法的实用性和有效性。最后,在当前研究工作的基础上,本文还确定了需要进一步开展研究的问题和方向。

... 地磁传感器同样可以准确获取交通流参数^{[14,15,16,17]},并且可以用于车辆排队长度估计^[18] ...

... 2 问题分析通过单地磁传感器可以获取多种交通流参数^[15,16,17],包括各车辆邻近和离开传感器的时间点、车流量、车速和车型等 ...

2011

0.0

... 地磁传感器同样可以准确获取交通流参数^{[14,15,16,17]},并且可以用于车辆排队长度估计^[18] ...

2008

0.0

. 2008, 38(6):1287-1290

Prediction of queue length at saturate signalized intersection

饱和信号交叉口排队长度预测

Dai Lei-lei , Jiang Gui-yan , Pei Yu-long

代磊磊, 姜桂艳, 裴玉龙

通过采用自适应权重指数平滑法,对进口车道的实时流量进行预测,建立了以定数排队理论为基础的排队长度预测模型.该模型可以实现对饱和信号交叉口排队长度的预测,预测结果具有较强的自适应性,更符合交通流的实际运行状况.实际数据验证结果表明:在拥挤的交通状态下,该模型的预测精度可达到85%以上,可以满足信号配时和交通管理的需要.

... 由定数排队理论可知,排队车辆数可近似代替排队长度^[19] ...

2011

0.0

. 2011, :- DOI:doi:10.7666/d.y1948549

Speed control and visual search of driving behavior at the intersection

城市信号交叉口驾驶员速度控制和视觉搜索行为研究[D]

Shi Xiao-fen.

施晓芬

交叉口的机非混合特征直接导致其成为道路交通的瓶颈,成为交通事故的高发路段。在通过公路平面交叉口时,驾驶员要能筛选关键信息,合理控制车速,才能有效避开各向冲突。因此,研究平面交叉口驾驶员的速度控制方式和视觉搜索模式对于指导驾驶员安全通过交叉口、有效避免交通冲突、减少交通事故以及提高整个路网的通行能力有重要意义。本文立足于城市平面信号交叉口,通过在真实交通环境中进行实车试验,用GPS记录驾驶员驾驶车辆驶近交叉口及通过交叉口的车速,并用眼动仪全程实时测录驾驶员的视觉搜索行为,定量地分析驾驶员在交叉口的驾驶行为特征。对试验数据进行统计分析时,将一个完整的交叉口行驶过程按照停车线划分为驶近交叉口和通过交叉口两部分,并按通行方式的不同将交叉口分为直行、左转及右转3大类,再分别将每一大类按照交叉口之前的行驶状态划分为畅行通过、停线等待和排队等待3种情况。根据不同的情况,分析驾驶员驶近交叉口和通过交叉口的速度控制方式和视觉搜索模式。试验数据分析结果表明,驶近交叉口,畅行通过情况下,驾驶员在到达交叉口之前基本都有适当的降速；排队等待情况下,交叉口左转之前的行驶驾驶员行至交叉口略有降速,右转和直行交叉口之前的行驶驾驶员行至交叉口则没有明显降速。直行停线等待情况下,驾驶员在距交叉口100m处开始减速,平均减速度为0.74m/s2；右转停线等待情况下,驾驶员在距离交叉口大致60m有明显降速行为,且平均减速度为0.54m/s2。通过交叉口,直行停线等待情况下,驾驶员从停车线起步,以平均0.53m/s2的加速度加速驶出交叉口；右转停线等待情况下,驾驶员以平均0.73m/s2的加速度从停车线加速驶入交叉口,经过短暂的稳速行驶之后,以平均0.57m/s2的加速度加速驶出交叉口；右转排队等待情况下,驾驶员以平均0.43m/s2的减速度从停车线减速驶入交叉口,之后以平均0.54m/s2的加速度加速驶出交叉口。通过对交叉口划分视觉区域发现,在整个交叉口行驶过程中,不论驾驶员以何种通行方式驶近及通过交叉口,驾驶员对前方区域的关注最多,且视觉搜索大多数从前方区域发出经过某一区域之后又回到前方区域。直行时,驾驶员还通过对左右侧视觉区域的关注进行信息补偿,而很少关注车辆后方。左转时,在驶近交叉口时驾驶员对左侧关注较多,主要进行C-L-C(前方区域到左侧区域再回到前方区域)模式的视觉搜索,通过交叉口时则对右侧关注较多,主要进行C-R-C(前方区域到右侧区域再回到前方区域)模式的视觉搜索。右转时,在驶近交叉口时驾驶员对右侧关注较多,主要进行C-R-C模式的视觉搜索,通过交叉口时也对右侧关注较多,但主要进行C-L-C模式的视觉搜索。交叉口之前行驶时,畅行通过和停线等待情况下,大多数驾驶员存在超速行为；且驾驶员存在视觉搜索不够广泛,或者未对信号灯给予关注等视觉搜索缺陷；通过交叉口,驾驶员则主要表现为视觉搜索不够广泛。本研究得到了国家自然科学基金项目(50908019)的资助。

... 驾驶员驶入交叉口的加速度与具体交叉口条件相关,需单独测定^[20] ...

... v_max采用直行驶进交叉口排队车辆的最大速度25 km/h^[20] ...

2008

0.0

. 2008, :-

A car following model in urban expressway based on driver's gender

基于驾驶员性别的城市快速路跟驰模型研究[D]

Wang Jing.

王晶

驾驶员是交通系统中的主体因素,在交通系统整体性能及各ITS子系统功能的实现中起着主导作用。车辆跟驰模型是从交通流的基本元素--人车单元运动与相互作用的层次上分析交通流微观特性,对交通安全、交通管理、通行能力、服务水平等方面的分析都有着重要的意义。车辆跟驰行为的研究与交通环境、交通流构成、驾驶员心理特性等方面都有关系。本文主要是以驾驶员的性别为基础,对车辆跟驰行为进行了细致分析。本文首先回顾了国内外跟驰模型的研究历史,分析了各种不同角度研究的跟驰模型的特点。在总结前人研究经验和分析存在问题的基础上,明确了将建立基...

... 5 s^[21] ...

2012

0.0

. 2012, :-

Vehicle speed and vehicle queue length detection based on video at plane intersection

基于机器视觉的交叉路口车速和车辆排队长度检测[D]

Liu Ying.

刘影

本文为了实现城市交通中交叉路口车速和排队长度的测量，提出了基于机器视觉的交叉路口车速和车辆排队长度的检测算法。　　摄像机架设在交叉路口，逆着行车方向进行视频采集，在停车线和人行横道之间设置检测带。在检测带内进行背景差分运算、阴影去除和形态学区域填充，然后对得到的二值图像进行垂直投影，利用垂直投影曲线图判断车辆是否存在并计算车辆驶入和驶出检测带所用的帧数，根据摄像机的帧率和检测带的宽度计算瞬时速度，进而求出交叉路口的平均车速。　　车辆出现排队现象一般出现在红灯期间或者路口出现车辆通行缓慢即绿灯期间车速...

... l_inter取车辆慢速行驶的安全间隔2 m^[3,22] ...