考虑诱导影响的公交优先信号配时模型

引用本文

魏丽英, 李鸣君. 考虑诱导影响的公交优先信号配时模型.吉林大学学报:工学版, 2016, 46(3): 777-784
WEI Li-ying, LI Ming-jun. Bus priority signal timing model considering the influence of traffic guidance. Journal of Jilin University Engineering and Technology Edition, 2016, 46(3): 777-784 复制到剪切板

Permissions

考虑诱导影响的公交优先信号配时模型

魏丽英, 李鸣君

北京交通大学交通运输学院,北京 100044

作者简介:魏丽英(1974-),女,副教授,博士.研究方向:交通组织优化及仿真建模.E-mail:lywei@bjtu.edu.cn

基金:“973”国家重点基础研究发展计划项目(2012CB725403); 国家自然科学基金青年基金项目(71101008;61473028); 国家留学基金项目

摘要

考虑了诱导信息对交叉口小汽车驾驶员路径选择的影响,建立了替换路径概率选择模型和交通状态实时更新模型,共同约束信号配时模型的求解,进而得到交通诱导与公交优先协同作用的交叉口信号配时模型。应用改进遗传算法对优化模型进行求解,求解结果显示模型中考虑诱导信息影响后,乘客总延误、车辆总延误、人均车辆尾气排放降低幅度分别为4.4%、2.8%和1.4%,说明通过合理诱导交通流,可以一定程度上降低路网整体负荷、减少尾气排放。

关键词: 交通运输系统工程; 交通诱导信息; 公交优先; 尾气排放; 信号配时; 改进遗传算法

中图分类号:U491.2 文献标志码:A 文章编号:1671-5497(2016)03-0777-08

Bus priority signal timing model considering the influence of traffic guidance

WEI Li-ying, LI Ming-jun

School of Traffic and Transportation,Beijing Jiaotong University,Beijing 100044,China

Abstract

In this paper, a probability detour path choice model and a traffic state updating model were established, considering the influence of traffic guidance information on car drivers' route choice at intersection. These models were considered as two important constraints. Then, an optimal signal timing model was built under the coordination control of traffic guidance and bus priority. An improved genetic algorithm was applied to solve the optimization model. Results show that the total passenger delay, vehicle delay and the exhaust emissions per capita are reduced by 4.1%, 2.8% and 1.4% respectively after considering the influence of traffic guidance information. It is certified that the goals to reduce the overall traffic network load and vehicle exhaust can be achieved to certain extent by reasonable traffic guidance.

Keyword: engineering of communications and transportation systems; traffic guidance; bus priority; exhaust emissions; signal timing; improved genetic algorithm

Show Figures

0 引言

交通拥堵问题已经成为制约城市发展的一个重要因素。为了有效解决城市交通问题, 满足日益增大的交通需求, 必须在有限的资源下, 坚持公交优先发展战略。目前, 通过设置公交专用道的方式实现路段公交优先比较容易, 但如何在交叉口实现或考虑公交优先比较困难, 主要是因为它将造成社会车辆延误、油耗、尾气排放的大幅提升。因此, 如何科学制定交叉口信号配时方案, 面向公交优先的同时兼顾环境和其他社会车辆的利益是非常有意义的研究课题。

信号配时研究中, 最重要的是优化目标的建立。尽管目前已经有很多经典的优化模型, 但由于优化目标或出发点不同, 各模型所考虑的因素也有很大区别, 应用效果也千差万别。有的比较关注公交优先, 对公交优先信号配时进行了专门研究^{[1, 2, 3]}, 如Wu等^[1]针对英国城市交通拥堵问题提出了公交预信号设置及其信号配时方法, 选用车均延误作为交叉口是否设置公交优先的效益评价指标, 效果评价中主要考虑了3种不同公交优先设置方式对通行能力和延误的影响, 没有考虑排放和交通诱导的影响。也有学者从延误、油耗和尾气排放控制的角度建立信号配时模型^{[4, 5]}, 这些模型对环境效益关注较多, 但很少考虑公交优先。此外, 也有学者根据交通诱导与信号配时的协同作用进行建模^{[6, 7, 8, 9, 10]}, 如Allsop^[6]在1974年最先提出交通信号控制与交通分配的相互作用问题; 王亮等^[7]也对交通控制和诱导问题进行了递阶协调优化方面的建模。Ceylan和Bell^[11]则建立了基于遗传算法的信号配时模型, 考虑了驾驶员路径选择的影响, 该模型优化目标主要是延误和停车次数, 未考虑公交优先和尾气排放等因素。

实际的交通情况是多个主要影响因素综合作用的结果, 信号配时研究中不应该只强调一项而忽略其他几项。本文以北京市的交通环境为研究背景, 考虑了日益严重的交通拥堵、空气污染、规模化的可变信息交通标志(Variable messege signs, VMS)诱导信息发布等因素, 以公交优先、尾气排放控制、诱导信息的影响作为建模目标, 同时提出了快速、有效的模型求解方法。

1 运行效益评价指标

对设有公交专用道且处于未完全饱和状态的交叉口进行研究, 即交叉口还有能力接收一些由于诱导信息发布而引来的分流车辆。以绿色交通、公交优先的理念为指导, 选取乘客总延误以及人均尾气排放为效益评价指标进行模型构建, 这里尾气排放主要考虑碳排放的控制。模型构建中侧重考虑了公交优先对社会车辆的影响, 通过引入相关参数实现公交车辆和社会车辆利益的均衡。

1.1 乘客总延误

交叉口一个进口方向的乘客总延误等于该进口方向车均延误与车载乘客的乘积, 而交叉口的乘客总延误应该等于各进口方向乘客总延误之和。这里, 进口方向的车均延误采用经典的Webster延误公式计算^[12]:

$\begin{matrix} d = \frac{c {(1 - λ)}^{2}}{2 (1 - λx)} + \frac{x^{2}}{2 q (1 - x)} - 0.65 {(\frac{c}{q^{2}})}^{\frac{1}{3}} x^{(2 + 5 λ)} \end{matrix}$ (1)

式中: $\begin{matrix} d \end{matrix}$ 为每辆车的平均延误, s; c为信号周期时长, s; $\begin{matrix} λ \end{matrix}$ 为绿信比; q为进口道车流率, pcu/s; x为饱和度, 其值为观测最大流量与信号交叉口进口道通行能力之比。

据此, 一个周期内进入交叉口的乘客总延误 $\begin{matrix} D \end{matrix}$ 为:

$\begin{matrix} D = \overset{n}{\sum_{i = 1}} \overset{m_{i}}{\sum_{j = 1}} (d_{ij}^{b} q_{ij}^{b} P^{b} ρ + d_{ij}^{c} P^{c} \overset{l_{j}}{\sum_{k = 1}} δ_{k} q_{ij}^{k}) \end{matrix}$ (2)

式中: $\begin{matrix} d_{ij}^{b} \end{matrix}$ 为1个周期内第 $\begin{matrix} i \end{matrix}$ 相位、第 $\begin{matrix} j \end{matrix}$ 进口道公交车的平均延误, s; $\begin{matrix} d_{ij}^{c} \end{matrix}$ 为1个周期内第 $\begin{matrix} i \end{matrix}$ 相位、第 $\begin{matrix} j \end{matrix}$ 进口道其他社会车辆的平均延误, s; $\begin{matrix} q_{ij}^{b} \end{matrix}$ 为1个周期内第 $\begin{matrix} i \end{matrix}$ 相位、第 $\begin{matrix} j \end{matrix}$ 进口道公交车的到达率, pcu/s; $\begin{matrix} q_{ij}^{k} \end{matrix}$ 为1个周期内第 $\begin{matrix} i \end{matrix}$ 相位、第 $\begin{matrix} j \end{matrix}$ 进口道、第 $\begin{matrix} k \end{matrix}$ 种社会车辆的到达率, pcu/s; $\begin{matrix} P^{b} \end{matrix}$ 为公交车辆的平均载客人数, 人; $\begin{matrix} P^{c} \end{matrix}$ 为其他社会车辆的平均载客人数, 人; $\begin{matrix} ρ \end{matrix}$ 为考虑公交优先对社会车辆造成的影响而引入的公交车辆折减系数; $\begin{matrix} δ_{k} \end{matrix}$ 为第 $\begin{matrix} k \end{matrix}$ 种社会车辆折算成标准小汽车的折算系数; $\begin{matrix} n \end{matrix}$ 为交叉口相位数量; $\begin{matrix} m_{i} \end{matrix}$ 为第 $\begin{matrix} i \end{matrix}$ 相位的进口方向数量; $\begin{matrix} l_{j} \end{matrix}$ 为其他社会车辆的类型数。

1.2 人均尾气排放

车辆尾气排放包括路段行车时的尾气排放和交叉口怠速时的尾气排放^{[2, 7]}。其中行车尾气排放E₁为标准排放因子与里程、流量的乘积; 怠速尾气排放E₂为怠速排放因子与车总延误的乘积。这里将车辆分为公交车和社会车辆进行统计处理。若 $\begin{matrix} P \end{matrix}$ 为交叉口一个周期内各相位通过的乘客总数, 则一周期内的人均尾气排放量E可表达为:

$\begin{matrix} E = (E_{1} + E_{2}) / P \end{matrix}$ (3)

式中: $\begin{matrix} E \end{matrix}$ 为路网的尾气总排放量, g;

$E_{1} = \overset{n}{\sum_{i = 1}} \overset{m_{i}}{\sum_{j = 1}} E F^{PCU} \times L_{ij} \times (α \times q_{ij}^{b} + \overset{l_{j}}{\sum_{k = 1}} δ_{k} q_{ij}^{k});$

$E_{2} = \frac{1}{3600} \overset{n}{\sum_{i = 1}} \overset{m_{i}}{\sum_{j = 1}} EF I^{PCU} \times (β \times q_{ij}^{b} \times d_{ij}^{b} + d_{ij}^{c} \times \overset{l_{j}}{\sum_{k = 1}} δ_{k} q_{ij}^{k});$

$P = \overset{n}{\sum_{i = 1}} \overset{m_{i}}{\sum_{j = 1}} [q_{ij}^{b} \times P^{b} + \overset{l_{j}}{\sum_{k = 1}} (δ_{k} q_{ij}^{k}) \times P^{c}] 。$

式中: $\begin{matrix} E F^{PCU} \end{matrix}$ 为标准小汽车单位排放因子, g/(pcu· km); $\begin{matrix} α \end{matrix}$ 为公交车常速行驶的排放修正系数; $\begin{matrix} EF I^{PCU} \end{matrix}$ 为标准小汽车单位怠速排放因子, g/(pcu· h); $\begin{matrix} β \end{matrix}$ 为公交车怠速行驶的排放修正系数; $\begin{matrix} L_{ij} \end{matrix}$ 为第 $\begin{matrix} i \end{matrix}$ 相位、第 $\begin{matrix} j \end{matrix}$ 进口道的路段长度, km。

2 模型建立

2.1 目标函数

综合考虑延误、排放的重要度及两者单位量纲的不同, 通过引入参数 $\begin{matrix} λ_{1} \end{matrix}$ 和 $\begin{matrix} λ_{2}, \end{matrix}$ 将不同量纲的延误和排放统一化处理, 并赋予权重, 可得如下总目标:

$\begin{matrix} minW = λ_{1} D + λ_{2} E \end{matrix}$ (4)

式中: $\begin{matrix} W \end{matrix}$ 为整体目标; $\begin{matrix} λ_{1} \end{matrix}$ 为统一单位的参数; $\begin{matrix} λ_{2} \end{matrix}$ 为排放和延误的权重比, 本文中 $\begin{matrix} λ_{2} = 1, \end{matrix}$ 即假定延误和排放目标具有相同权重; 目标函数中涉及的其他参数 $\begin{matrix} λ_{1} 、 ρ 、 α 、 β \end{matrix}$ 的取值和标定过程将在后文详细介绍。

2.2 约束条件

(1)最长周期

考虑到信号周期时长超过一定值以后, 通行能力的增大便趋于停滞, 而车辆延误时间却急速增长, 借鉴相关研究成果^[13], 本文将120 s设为最佳信号周期的上限值。当然, 在信号相位较多(多达4~5个以上相位)时, 或者为了照顾某一方向的车流而需要延长信号周期时, 可不必受120 s这一上限值的约束。

(2)最短周期

最短周期由各相位最短绿灯时间确定, 通常是以行人通过交叉口的时间为依据进行计算。借鉴《美国交通信号控制手册》(MUTCD)中行人过街时间计算的经典公式, 有:

$\begin{matrix} t_{imin} = \frac{l_{c}}{v_{p}} + 7 - I \end{matrix}$ (5)

式中: $\begin{matrix} t_{imin} \end{matrix}$ 为第 $\begin{matrix} i \end{matrix}$ 相位的最短过街绿灯时间; $\begin{matrix} l_{c} \end{matrix}$ 为交叉口距离, m; $\begin{matrix} v_{p} \end{matrix}$ 为第15百分位的行人步行速度, m/s; $\begin{matrix} I \end{matrix}$ 为绿灯间隔时间, s, 为了行人过街安全起见, 本文计算时没有减去绿灯间隔时间 $\begin{matrix} I 。 \end{matrix}$

最短周期可由式(6)计算:

$\begin{matrix} C_{\min} = \overset{n}{\sum_{i = 1}} t_{imin} + L \end{matrix}$ (6)

式中: $\begin{matrix} L \end{matrix}$ 为每个周期内的总损失时间, s。

(3)Webster最佳周期

Webster最佳周期的计算公式为:

$\begin{matrix} C_{0} = \frac{1.5 L + 5}{1 - Y} \end{matrix}$ (7)

式中: $\begin{matrix} C_{0} \end{matrix}$ 为最佳周期长度, m; $\begin{matrix} Y \end{matrix}$ 为所有相位关键车流的流量比之和。

依据最佳周期时长 $\begin{matrix} C_{0} \end{matrix}$ 和定时信号配时计算方法可获得各相位最大绿灯时间t_i_max。

Webster最佳周期模型是本文计算车均延误、界定变量绿灯时长t_i和周期时长C上、下边界条件的理论依据。此外, 还需要满足饱和度 $\begin{matrix} x_{j} \end{matrix}$ 不高于0.9这一约束条件。综上, 可获得信号配时的约束条件为:

$\begin{matrix} s.t. \{\begin{matrix} \overset{4}{\sum_{i = 1}} t_{i} = C - L \\ C_{\min} \leq C \leq C_{\max} \\ t_{imin} \leq t_{i} \leq t_{imax} \\ x_{j} \leq 0.9 \end{matrix} \end{matrix}$ (8)

3 考虑诱导的公交优先控制模型

3.1 VMS诱导信息作用下的路径概率选择模型

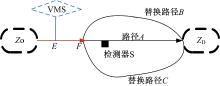
交叉口上游的VMS(Variable message sign)会根据交叉口下游检测器S处获得的流量等信息发布下游路况。驾驶员会根据VMS发布的信息并结合自己的驾驶特性, 选择合适的路径行驶。

图1中, 驾驶员在点 $\begin{matrix} E \end{matrix}$ 看到VMS发布的下游路况信息后, 将在交叉口 $\begin{matrix} F \end{matrix}$ 处决定是继续走行主线路径 $\begin{matrix} A, \end{matrix}$ 还是选择替换路径 $\begin{matrix} B 或 C, \end{matrix}$ 从而避开主线下游附近的拥堵区域。VMS信息发布的内容, 即下游区域的拥挤程度或下游道路的饱和程度, 将对交叉口 $\begin{matrix} F \end{matrix}$ 主线方向的出口O的通过率产生一定影响, 从而影响交通流的时空分布。其中, 公交车行走固定线路, 不受交通状态发布信息的影响; 而一部分小汽车驾驶员会根据当前行驶路径以及替换路径的交通状态, 结合自己对路网的熟悉程度、驾驶习惯等因素, 判断是否选择替换路径, 同时只有当替换路径的路况(效用)优于当前行驶路径且达到一定程度时, 小汽车驾驶员才会考虑选择替换路径。为此, 本文以传统Logit模型为基础, 以出口路段饱和度为度量指标建立了交叉口处路径选择的效用函数, 并为当前路径设置一个决策阈值, 确保只有在当前路径与替换路径的饱和度差值大于设定的阈值时, 才会发生路径替换行为, 即只有当选择替换路径带来的效用达到一定程度时, 驾驶员才会考虑绕行; 否则将按原路径继续行驶。

	Figure Option View Download New Window
	图1 VMS对下游道路交通状态的影响示意图Fig.1 Influence of VMS on downstream traffic

本文以交叉口各出口的饱和度为度量指标构建效用函数, 如式(9)所示:

$\begin{matrix} U (O) = \frac{- Q_{O}}{S_{O} \times λ_{O}} \end{matrix}$ (9)

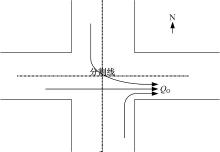
式中:U(O)为选择出口O作为下一出口的效用函数, 其取值为该出口路段饱和度, 需强调的是效用取值为负值; $\begin{matrix} S_{O} \end{matrix}$ 为出口O的饱和流率, pcu/s; $\begin{matrix} λ_{O} \end{matrix}$ 为出口O的绿信比QO为一个周期内出口O的平均流率, pcu/s。

计算下游交叉口出口O的饱和度时, 出口流量Q_O 是一个关键变量, 它是所有以出口O为通行路径的各入口流量q_ij 之和(见图2), Q_O计算公式如下:

$\begin{matrix} Q_{O} = \overset{n}{\sum_{i = 1}} ω q_{ij} \end{matrix}$ (10)

式中:q_ij为各入口输入流量; ω 为0-1变量, 1表示相位 $\begin{matrix} i \end{matrix}$ 车辆能到达出口O, 0表示不能到达。

	Figure Option View Download New Window
	图2 交叉口出口流量Q_OFig.2 Outbound approach flow Q_O at intersection

在分析效用函数的基础上, 依据Logit模型, 引入补偿系数η , 建立诱导路径选择概率模型为:

$\begin{matrix} \{\begin{matrix} p (O_{r}) = \frac{expU (O_{r}) - expU (O)}{expU (O) + expU (O_{r})}, \\ U (O_{r}) - U (O) > η, η > 0; \\ p (O) + p (O_{r}) = 1; \\ p (O_{r}) = 0, p (O) = 1, \\ U (O_{r}) - U (O) \leq η, η > 0 \end{matrix} \end{matrix}$ (11)

式中:p(O)为各进口车辆选择出口O的概率; p(O_r)为主路方向的车辆在T时段内选择行走其他替换路径的概率, 即不通过出口O的概率; η 为补偿系数, 它是一个决策阈值, 表明只有替代路径与原始路径的效用差值大于η 时才会选择替换路径。

本文通过引入路径之间的效用函数差值 $\begin{matrix} η, \end{matrix}$ 可以体现不同路径之间的相互影响。此外, 各路径选择概率均非负, 且和为1, 路径选择概率与饱和度呈负相关, 在存在多条替换路径时, 以饱和度最小的路径作为替换路径。

3.2 交通状态实时更新模型

输入流量q_ij和出口流量Q_O都是随时间实时变化的量, 如北京市VMS发布的交通状态信息为实时更新, 2 min刷新一次。这里, 出口流量Q_O 的更新主要取决于统计间隔内各进口道流量q_ij 以及各进口道在出口O方向的绿信比。而入口道流量q_ij的更新则比较复杂, 它除了与上一时段的流量有关外, 还与受新发布的VMS信息影响而选择其他替换路径的流出量、受其他邻近区域发布的诱导信息影响而选择以当前出口O为绕行点的流入量有关。

据此, 可建立输入流量 $\begin{matrix} q_{ij} \end{matrix}$ 的状态更新方程为:

$q_{ij}^{T + 1} = q_{ij}^{T} - q_{ij}^{T} \times φ \times p (O_{r}) + \overset{n}{\sum_{u = 1, u \neq i}} q_{uj}^{T} \times φ \times p (O)$ (12)

式中:T为统计间隔; $q_{ij}^{T}$ 为第i相位、第j进口道在T间隔内流率的更新值, pcu/s; $\begin{matrix} q_{uj}^{T} \end{matrix}$ 为其他相位u、第j进口道在T间隔内的流率, pcu/s; $\begin{matrix} φ \end{matrix}$ 为愿意接受路网实时诱导信息且可能会做出路径调整的驾驶员比例。

综上, 可建立起反映诱导信息影响的动态公交优先信号配时模型, 包括面向公交优先和排放的多目标模型(式(4)(8))、VMS诱导信息作用下的路径概率选择模型(式(11))和交通状态实时更新模型(式(12))三个部分。

4 模型参数标定

4.1 交叉口相关参数

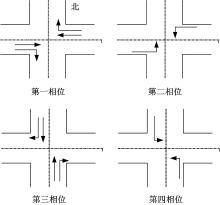
假定一个四相位交叉口各入口均设有公交专用道, 各相位车流如图3所示。各进口道对称布置, 其结构如图4所示。各出口道饱和度存在差异, 使得交通诱导存在可能。为了研究方便, 假设直行、右转共用一个相位, 即红灯时间禁止车辆右转, 这种措施有利于保证行人过街安全^[13]。

	Figure Option View Download New Window
	图3 四相位示意图Fig.3 Diagram of 4 phases

	Figure Option View Download New Window
	图4 进口道渠化示意图Fig.4 Channelization of inbound approach

借鉴北京市大柳树路-学院南路交叉口高峰和平峰时段流量的实地采集数据及文献^[13]的相关成果, 设定进口流量矩阵Q及其对应的饱和流量矩阵S。

(1)各相位的公交车流量和饱和流量分别为:

$\begin{matrix} \begin{matrix} Q_{bus} = [\begin{matrix} 25 + 2 μ & 20 + 2 μ \\ 12 + μ & 12 + μ \\ 15 + 2 μ & 18 + 2 μ \\ 10 + μ & 15 + μ \end{matrix}] \\ S_{bus} = [\begin{matrix} 700 & 700 \\ 300 & 300 \\ 600 & 600 \\ 300 & 300 \end{matrix}] \end{matrix} \end{matrix}$

(2)各相位的社会车流量和饱和流量分别为:

$\begin{matrix} \begin{matrix} Q_{car} = [\begin{matrix} 400 + 20 μ & 250 + 20 μ \\ 49 + 5 μ & 59 + 5 μ \\ 225 + 10 μ & 150 + 10 μ \\ 33 + 2 μ & 42 + 2 μ \end{matrix}] \\ S_{car} = [\begin{matrix} 2000 & 2000 \\ 750 & 750 \\ 1500 & 1500 \\ 500 & 500 \end{matrix}] \end{matrix} \end{matrix}$

式中: $\begin{matrix} μ \end{matrix}$ 为流量对应的一个调节变量(一般取整数), 用于界定流量从平峰到高峰的变化范围; $\begin{matrix} S_{bus} 、 S_{car} \end{matrix}$ 分别为公交车和社会车辆的饱和流量, pcu/h; $\begin{matrix} Q_{bus} 、 Q_{car} \end{matrix}$ 分别为各进口的公交车和社会车辆的流量pcu/h, 其中东西向为主干路, 南北向为次干路, 且假定右转流量占直行流量的四分之一; Q_bus(i, j)(i=1, 2, 3, 4; j=1, 2)为第i相位、第j进口道的公交车流量, 即当i=1, 2时, 对应图3中的第1和第2相位, 同时j=1表示西进口道, j=2表示东进口道, 当i=3, 4时, 对应图3中的第3和第4相位, 同时j=1表示北进口道, j=2表示南进口道。

4.2 模型参数标定

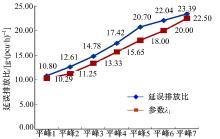
为了使延误和排放在同一量纲下进行求解, 需要对λ ₁ 进行参数标定。当μ 分别取值5, 6, 7, …, 15, 16时, 表示流量从平峰到高峰的一系列变化过程。令μ =10~16, 可得到7种交通状态, 将其对应的流量矩阵分别按延误最小和尾气排放量最小进行单目标最优化求解, 得到不同流量下公交优先配时模型的延误、尾气排放及二者比值, 结果如表1所示。

表1 不同流量下的延误及尾气排放 Table 1 Delay and emission ratio under different flow cases

	平峰1	平峰2	平峰3	平峰4	高峰1	高峰2	高峰3
$\begin{matrix} μ \end{matrix}$	10	11	12	13	14	15	16
延误/10⁴ s	35.90	43.30	52.35	63.63	77.94	85.45	93.29
尾气排放/10⁴ g	3.32	3.43	3.54	3.65	3.76	3.88	3.99
比例	10.80	12.61	14.78	17.42	20.70	22.04	23.39

表1 不同流量下的延误及尾气排放 Table 1 Delay and emission ratio under different flow cases

考虑延误的单位为s, 排放的单位为g, 为了统一单位, 且使得延误和排放在一个数量级下进行运算, $\begin{matrix} λ_{1} \end{matrix}$ 需要取一个较小的值来平衡延误和尾气排放。表1中的延误与尾气排放比值是由模型计算得到的 $\begin{matrix} λ_{1} \end{matrix}$ 参考值。

此外, 从理论分析角度, 通过多次试验, 对照表1中结果, 最终确定 $\begin{matrix} λ_{1} \end{matrix}$ 的表达式为:

$\begin{matrix} λ_{1} = \frac{1}{5} \times \frac{E F^{pcu} \times V}{3600} \end{matrix}$ (13)

式中:V为当前交通状态下的平均行驶速度, km/h。这样既统一了单位, 也使得延误、尾气排放在同一个数量级下进行运算。

$\begin{matrix} λ_{1} \end{matrix}$ 可以统一不同量纲的理论推导过程如下:

$\begin{matrix} \begin{matrix} λ_{1} D + λ_{2} E = \frac{E F^{pcu} \times V}{18 000} \cdot D + λ_{2} E = \\ \frac{[g / (pcu \cdot km)] \times (km / h) \times (s \times pcu)}{3600} + g = g \end{matrix} \end{matrix}$

图5为表1中的延误排放比值与由式(13)计算获得的λ ₁的对比图。由图5可以看出, 二者变化趋势一致, 这也充分证明本文试验推导标定的λ ₁是合适的。

	Figure Option View Download New Window
	图5 不同流量下参数λ ₁的标定结果对比Fig.5 Comparison of calibration parameter λ ₁ under different flow

此外, 考虑到如果以人均尾气排放为目标, 公交车由于载客量大使得人均尾气排放较小, 这种赋予公交车过高优先权重的方法与实际不符, 不能兼顾社会车辆的通行效益。公交车尾气排放量一般是小汽车尾气排放量的5~6倍, 且公交车占用道路资源是小汽车3~4倍, 综合考虑公交车尾气排放量和占道空间两个因素的影响, 本文将参数 $\begin{matrix} α \end{matrix}$ 取值15, $\begin{matrix} β \end{matrix}$ 取值21, 用以表征与小汽车排放因子相比, 公交人均排放指标在标准状态和怠速状态下的扩展系数。此外, 从占用道路空间角度考虑, 本文将公交车辆折减系数 $\begin{matrix} ρ \end{matrix}$ 取值为0.3。上述这些设置均是为了一定程度上降低公交优先级别, 兼顾社会车辆效益。

由于目标交叉口是双向8车道交叉口, 街道比较宽, 行人过街时间较长, 易出现行人过街所需绿灯时间超过机动车通行时间的情况, 因此可采用二次过街方式, 在中央分隔带处设置二次过街安全岛。然后以第15百分位的行人步行速度(1.5 m/s)作为依据, 由式(5)可得需要的最小绿灯时间为17 s。

5 基于改进遗传算法的优化求解

5.1 算法求解过程

传统的Webster固定信号配时方法一般是先以系统最优为目标求解最优信号周期, 再通过流量比进行绿灯时间的分配。

遗传算法(GA)是一种自适应全局优化的随机搜索方法, Ceylan和Bell^[11]的研究表明其在信号配时优化求解领域的应用是有效的。本文应用Matlab工具箱中的改进遗传算法对各相位的有效绿灯时间 $\begin{matrix} t_{i} \end{matrix}$ 直接求解。设定40 s和120 s作为周期的上、下边界条件, 同时以式(7)求得的信号周期为依据, 对产生的子代进行判别, 不满足最小绿灯时间约束和周期边界约束的个体直接剔除, 同时重新随机产生新的个体。此外, 采用适应度函数、引入饱和度作为惩罚函数以及每代严格保优三个措施, 在满足基本的约束条件下同时优化信号周期和绿信比。

运用遗传算法进行信号配时优化的流程如下:

Step1 求得各相位绿灯时间的编码取值范围。根据式(7)求得韦伯斯特最佳周期C₀, 判断是否在边界条件内。判别结果如下所示:

$\begin{matrix} \{\begin{matrix} C = \{\begin{matrix} 40, & C_{0} < 40 \\ C_{0}, & 40 \leq C_{0} \leq 120 \\ 120, & C_{0} > 120 \end{matrix} \\ t_{\min} = \max {0.9 C \times X_{j}, l_{c} / v_{p} + 7} \\ t_{\min} \leq t_{i} \leq t_{\min} + 30 \end{matrix} \end{matrix}$

式中:X_j 为进口道j关键相位的饱和度。

Step2 算法初始化:设定种群数目、染色体长度、迭代总代数、交叉概率、变异概率。本文设定种群大小为80; 二进制编码长度为4× 15, 每条染色体由4个相位的有效绿灯时间组成, 并形成一个信号配时方案, 解码后取值范围对应于各相位的约束条件(由Step1求得); 种群进化代数为1000代; 交叉概率为0.75; 变异概率为0.01。

Step3 采用实数编码, 随机产生种群数目大小的染色体。

Step4 解码计算每条染色体是否满足周期和最小绿灯时间约束条件, 如满足则进行Step5; 否则转Step3重新生成染色体。为了提高运算效率, 当 $\begin{matrix} t_{1} + t_{2} + t_{3} + t_{4} \in [C - 5, C + 5], \end{matrix}$ 则认为满足周期约束条件; 否则重新生成染色体。

Step5 将适应度函数取值为目标函数的负值。然后计算每个个体的适应度并排序, 对适应度最高的5个个体严格保优。其余个体以赌轮盘方式进行选择, 适应度越高, 被选择的概率越大; 反之则淘汰的概率越大。

Step6 按照一定的交叉概率和交叉方法, 产生新的个体。

Step7 按照一定的变异概率和变异方法, 产生新的个体。

Step8 通过交叉、变异和严格保优后的新一代种群, 判断是否达到迭代总数, 若没有, 则转Step3; 否则, 输出最佳个体; 即每个相位的有效绿灯时间和信号周期时长。

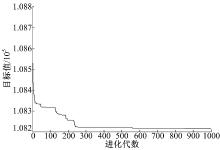
应用Matlab软件得到的遗传算法进化曲线收敛, 结果如图6所示。

	Figure Option View Download New Window
	图6 遗传算法进化曲线Fig.6 Evolution curve of genetic algorithm

5.2 结果分析

假定车流由公交车和小汽车构成, 不考虑其他车型影响。依据相关经验数据和研究成果^[5], 本文取公交载客数为30人; 小汽车载客数为1.5人; 小汽车标准排放因子为45 g/(pcu· km); 怠速排放因子为5 g/(pcu· h); 进口道长度为0.5 km。出口道信号配时方案中绿信比取0.4; 出口道饱和流量取值为2000; $\begin{matrix} φ \end{matrix}$ 取50%; $\begin{matrix} η \end{matrix}$ 取0.15; $\begin{matrix} V \end{matrix}$ 取25 km/h。

案例研究取μ =14, 其对应的交通状态是表1中的高峰1。当T=0时, 得到初始方案如表2第1行所示。由表2可知:第一相位(东西方向直行)绿灯时间最长, 为52 s, 主要是因为东西进口直行车辆最多。此外, 由于各进口方向左转车辆均不多, 因此第二、第四左转相位只需满足最小绿灯时长即可。计算得到的各出口道流量及饱和度如表3所示。

表2 运算结果统计表 Table 2 Statistics of calculation results

表3 各出口道流量及饱和度 Table 3 Volume and saturation rate of outbound approaches

东西向为主路方向, 西进口是当前进口, 预定驶出目标是东出口。但因目前东出口饱和度最大, 且与北出口饱和度差值大于0.15, 即大于文中设定的补偿系数 $\begin{matrix} η, \end{matrix}$ 故部分驾驶员会根据VMS发布的路况信息, 选择避开拥堵的东出口, 通过驶出北出口去走替换路径, 而替换路径的选择概率为:

$\begin{matrix} p (O_{r}) = \frac{\exp (- 0.57) - \exp (- 0.83)}{\exp (- 0.57) + \exp (- 0.83)} = 0.13 \end{matrix}$

当μ =14时, 查Q_car矩阵可得其对应的西进口直右相位的总车流量为680 pcu/h。因西进口直右相位的直行车比例为80%, 接受诱导的驾驶员比例 $\begin{matrix} φ \end{matrix}$ 为50%, 则选择走替换路径的车流量为:

680´ 0.8´ 0.5´ 0.13=35 pcu/h

因此T=1时, 更新后的Q_car流量矩阵为:

$\begin{matrix} Q_{car} = [\begin{matrix} 680 - 35 & 530 \\ 119 + 35 & 129 \\ 365 & 290 \\ 61 & 70 \end{matrix}] = [\begin{matrix} 645 & 530 \\ 154 & 129 \\ 365 & 290 \\ 61 & 70 \end{matrix}] \end{matrix}$

以此作为输入, 用遗传算法重新求解, 重复此过程, 当统计时段T=2时, 所有出口道饱和度之间相差均不超过0.15, 计算结束, 结果如表2所示。

从表2可以看出:该算例中T=2时, 按人统计的乘客总延误和按车统计的总延误与T=0(不考虑诱导信息的影响)时相比均有所降低, 降低幅度分别为4.4%和2.8%, 而人均尾气排放降低幅度为1.4%, 低于延误的降低幅度。这是由于本算例中μ =14时对应的交叉口饱和度不算特别高, 尾气排放部分主要是正常行驶带来的排放量, 怠速排放量比例比较小, 故而排放指标的降低幅度低于延误指标的降低幅度。

6 结束语

以乘客总延误和人均尾气排放量作为目标, 构建了公交优先信号配时优化模型。其间, 考虑到交通诱导信息对驾驶员路径选择的影响, 通过设立效用函数、替换路径补偿系数等建立路径选择概率模型, 并结合交通状态实时更新模型, 共同约束整个信号配时模型的求解。本文模型较好地体现了公交优先、尾气排放控制和诱导信息影响等多个主要因素的协同作用, 参数取值和标定中亦兼顾了公交优先策略下社会车辆的通行效益。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Wu Jian-ping, Hounsell N. Bus priority using pre-signals[J]. Transportation Research Part A: Policy and Practice, 1998, 32(8): 563-583. [本文引用:2]
[2]	张卫华, 陆化普, 石琴, 等. 公交优先的信号交叉口配时优化方法[J]. 交通运输工程学报, 2004, 4(3): 49-53. Zhang Wei-hua, Lu Hua-pu, Shi Qin, et al. Optimal signal-planning method of intersections based on bus priority[J]. Journal of Traffic and Transportation Engineering, 2004, 4(3): 49-53. [本文引用:2]
[3]	别一名, 朱慧, 王殿海, 等. 一种单点被动公交优先控制算法及其效益评价[J]. 北京工业大学学报, 2011, 37(4): 522-528. Bie Yi-ming, Zhu Hui, Wang Dian-hai, et al. Development and evaluation of a passive bus signal priority algorithm at isolated intersection[J]. Journal of Beijing Polytechnic University, 2011, 37(4): 522-528. [本文引用:1]
[4]	Li Xiu-gang, Li Guo-qiang, Pang Su-seng, et al. Signal timing of intersections using integrated optimization of traffic quality, emissions and fuel consumption: a note[J]. Transportation Research Part D: Transport and Environment, 2004, 9(5): 401-407. [本文引用:1]
[5]	周申培. 考虑排放因素的城市交叉口交通信号控制策略的研究[D]. 武汉: 武汉理工大学航运学院, 2009. Zhou Shen-pei. The traffic signal control strategy of urban intersections based on emission factors[D]. Wuhan: School of Navigation, Wuhan University of Technology, 2009. [本文引用:2]
[6]	Allsop R E. Some possibilities for using traffic control to influence trip distribution and route choice[C]//Proceedings of the 6th International Symposium on Traffic and Transportation Theory, Sydney, 1974: 345-375. [本文引用:2]
[7]	王亮, 马寿峰, 贺国光. 一种交通控制与诱导递阶协调优化模型[J]. 系统工程理论与实践, 2004, 24(6): 126-133. Wang Liang, Ma Shou-feng, He Guo-guang. A hierarchical coordination model between traffic control and route guidance[J]. Systems Engineering-Theory & Practice, 2004, 24(6): 126-133. [本文引用:3]
[8]	保利霞, 杨兆生, 胡建萌, 等. 交通流诱导与控制协同的双目标优化模型及准最优求解算法[J]. 吉林大学学报: 工学版, 2007, 37(2): 319-324. Bao Li-xia, Yang Zhao-sheng, Hu Jian-meng, et al. Quasi-optimal algorithm for double objective optimization model of traffic flow guidance coordinated with signal control[J]. Journal of Jilin University(Engineering and Technology Edition), 2007, 37(2): 319-324. [本文引用:1]
[9]	Sheffi Y, Powell W B. Optimal signal settings over transportation networks[J]. Journal of Transportation Engineering, 1983, 109(6): 824-839. [本文引用:1]
[10]	徐建闽, 首艳芳, 卢凯. 基于双层规划模型的交通信号区域协调控制[J]. 华南理工大学学报: 自然科学版, 2011, 39(3): 95-100, 106. Xu Jian-min, Shou Yan-fang, Lu Kai. Area coordinated control of traffic signals based on bi-level programming model[J]. Journal of South China University of Technology(Natural Science Edition), 2011, 39(3): 95-100, 106. [本文引用:1]
[11]	Ceylan H, Bell M G H. Traffic signal timing optimisation based on genetic algorithm approach, including drivers' routing[J]. Transportation Research Part B: Methodological, 2004, 38(4): 329-342. [本文引用:2]
[12]	陆化普. 城市交通现代化管理[M]. 北京: 人民交通出版社, 1999. [本文引用:1]
[13]	陈群, 晏克非. 考虑公交优先的城市交叉口遗传算法信号配时研究[J]. 系统工程理论与实践, 2005, 25(11): 133-138. Chen Qun, Yan Ke-fei. Research on signal timing for urban intersections with genetic algorithms optimizing with the idea of bus priority[J]. Systems Engineering-Theory & Practice, 2005, 25(11): 133-138. [本文引用:3]

1998

0.0

... 有的比较关注公交优先,对公交优先信号配时进行了专门研究^[1,2,3],如Wu等^[1]针对英国城市交通拥堵问题提出了公交预信号设置及其信号配时方法,选用车均延误作为交叉口是否设置公交优先的效益评价指标,效果评价中主要考虑了3种不同公交优先设置方式对通行能力和延误的影响,没有考虑排放和交通诱导的影响 ...

2004

0.0

. 2004, 4(3):49-53 DOI:doi:10.3321/j.issn:1671-1637.2004.03.012

Optimal signal-planning method of intersections based on bus priority

公交优先的信号交叉口配时优化方法

Zhang Wei-hua , Lu Hua-pu , Shi Qin

张卫华, 陆化普, 石琴

传统的交叉口信号配时方法将所有车辆同等对待,对于公交车辆比例较大的相位是不公平的.提出了以人总延误最小为信号周期时长的优化目标,以相位乘客流量比和相位饱和度确定绿信比的方法.应用分析表明,按照这一方法进行配时,虽然车均延误比用传统方法进行配时略大,但公交车辆和人均延误却降低了约30%,在保障交叉口交通顺畅的前提下体现了公交优先,减少了公交车辆在信号交叉口的延误.

... 2 人均尾气排放车辆尾气排放包括路段行车时的尾气排放和交叉口怠速时的尾气排放^[2,7] ...

2011

0.0

. 2011, 37(4):522-528

Development and evaluation of a passive bus signal priority algorithm at isolated intersection

一种单点被动公交优先控制算法及其效益评价

Bie Yi-ming , Zhu Hui , Wang Dian-hai

别一名, 朱慧, 王殿海

分析了周期时长与交叉口人均延误、车均延误指标的关系,确定了周期时长的计算方法;为进一步减少人均延误,提出了在不发生拥堵前提下根据各相位乘客数量分配富余绿灯时间的绿信比优化方法;最后采用算例验证的方式,分别计算了当交叉口实施单相、多相被动公交优先前后的交叉口效益,并与无公交优先控制方案进行对比分析,结果表明:被动公交优先算法的控制效益与公交优先相位数存在密切关系,当优先相位数较少时,该算法能有效减少交叉口人均延误.

2004

0.0

... 也有学者从延误、油耗和尾气排放控制的角度建立信号配时模型^[4,5],这些模型对环境效益关注较多,但很少考虑公交优先 ...

2009

0.0

. 2009, :- DOI:doi:10.7666/d.y1559709

The traffic signal control strategy of urban intersections based on emission factors

考虑排放因素的城市交叉口交通信号控制策略的研究[D]

Zhou Shen-pei.

周申培

交通是现代社会的基础,是人类社会经济的命脉,人们的社会行为与交通息息相关。在我国,由于机动车保有量迅速增加、交通设施建设滞后以及管理措施不够完善等原因,交叉路口的交通堵塞现象日趋严重,从而影响到城市路网通行能力的发挥。车辆在交叉路口处反复地分流、合流及交叉,交通状况复杂,使得交叉路口已经成为制约城市道路交通功能的瓶颈。维持城市交通正常运转,需要加强交通控制与管理,积极开展对交叉路口的研究,努力提高交叉路口的通行能力。交通信号控制是运输网络的一种基本管理手段,随着智能运输系统(Intelligent Transponation System,ITS)的发展,交通信号控制的智能化研究越来越受到重视。到目前为止,已经研究了许多交通信号控制模型。但是目前这些研究建立的模型大多数都是针对交通流的,没有将其他因素考虑在内。随着城市交通和社会经济的日益发展,汽车的保有量不断创下新高,大量机动车的出现在造成严重的交通拥挤和堵塞的同时,也引起了严重的空气污染和噪声污染。据权威统计分析,主要大城市大气污染物中机动车排放分担率呈明显上升趋势。如何在发展经济的同时,建立一个人、车、路、环境和谐发展的交通体系,这个问题已经被认为是全球最严重也是最具挑战性的课题之一。因此建立一个同时兼顾交通流情况和机动车尾气排放情况的交通信号控制模型具有重要的理论意义和实用价值。论文总结了国内外城市交通信号控制的研究进展,分析了该领域研究的发展趋势。在此基础上,针对城市交通信号优化控制问题进行了智能优化的理论分析和应用方法的研究。提出了考虑排放因素的城市交通信号优化控制系统的架构、建模方法和求解算法。通过对城市信号控制路口的交通流分析,从单点两相位、单点多相位和干线协调控制的不同层面,建立了城市交通信号优化控制的双层多目标规划模型。采用遗传算法和遗传蚁群融合算法对模型进行了仿真试验,通过与传统仿真试验结果进行比较,证明了这两种优化算法的优越性,其中,遗传蚁群融合算法优化性能更好。本论文的主要研究工作总结如下: (1)设计了考虑排放因素的交通信号优化控制系统框架。通过对城市交叉口交通信号控制发展现状和趋势的分析,将双层规划模型的研究方法与考虑排放因素的交通信号配时控制联系起来进行研究,设计了交通信号优化控制系统的架构,指出信号优化模块是交通信号优化控制系统的核心,其实质是交通信号控制模型及其求解算法。 (2)从单点控制和协调控制的角度,建立了城市交通信号控制的双层多目标规划模型。以双层规划模型为工具建立了交通信号控制模型,分别对上下层模型进行详细的问题描述和数学表达。其中,路网中的机动车尾气排放量作为一个优化目标,嵌入上层模型的目标函数中。模型以路网中的车辆延误和尾气排放总量为性能指标,通过改变信号控制策略,在保证交通基本畅通的前提下,将城市机动车尾气排放量限制在一定范围内。 (3)提出并实现了求解函数优化问题的遗传蚁群融合算法。遗传蚁群融合算法的基本思路是首先采用遗传算法产生有关问题的初始信息素分布;然后采用蚂蚁算法,在有一定初始信息素分布的情况下,充分利用蚂蚁算法的并行性、正反馈机制以及求解效率高等特性,高速高效地得到函数的优化解。本文以Camel函数作为测试函数,同时还以单点两相位信号优化控制模型的求解为例,通过与传统优化方法的仿真试验进行比较,采用遗传蚁群融合算法可获得最优性能指标,证明该算法是一种时间效率和求解效率都比较好的求解函数优化问题的有效算法。 (4)设计并实现了基于启发式遗传算法的模型求解方法。在利用惩罚策略处理双层多目标规划模型约束条件的基础上,针对具体建立的交通信号控制模型,设计了基于启发式遗传算法的模型求解方法,并运用MATLAB软件对所设计的城市单交叉口交通信号控制的双层多目标规划模型进行实时仿真,仿真表明能达到良好的控制效果。 (5)完成典型城市路网交通流情况的仿真。利用VISSIM交通仿真软件对典型城市路网的交通流情况进行仿真运行,得出了在固定信号配时方案下各项模拟输出的结果。其结果一方面可以作为参数代入典型城市路网交通信号控制的双层多目标规划模型,另一方面可以作为比较值验证以上两种优化算法的优化性能。

... 也有学者从延误、油耗和尾气排放控制的角度建立信号配时模型^[4,5],这些模型对环境效益关注较多,但很少考虑公交优先 ...

... 依据相关经验数据和研究成果^[5],本文取公交载客数为30人 ...

1974

0.0

... 此外,也有学者根据交通诱导与信号配时的协同作用进行建模^[6,7,8,9,10],如Allsop^[6]在1974年最先提出交通信号控制与交通分配的相互作用问题 ...

2004

0.0

. 2004, 24(6):126-133 DOI:doi:10.3321/j.issn:1000-6788.2004.06.022

A hierarchical coordination model between traffic control and route guidance

一种交通控制与诱导递阶协调优化模型

Wang Liang , Ma Shou-feng , He Guo-guang.

王亮, 马寿峰, 贺国光

Traffic signal control and route guidance are the two main ways of on-line management for urban traffic and the integrating signal control with route guidance is one the most important researches in ITS. After the characteristics for control and guidance are analyzed in this paper, a two-level hierarchical system architecture, in which a coordination system is contracted above control system and guidance system to find coordination solutions between control signal plan and guidance route. An optimal model f...

在对交通控制与诱导的关系进行分析的基础上,借鉴大系统递阶优化的思想,利用动态交通分配模型和交通最优控制模型,提出了一种二级结构控制与诱导递阶协调的系统结构,建立协调优化模型,给出了一种迭代的协调求解算法;并针对一个仿真的路网给出模拟的协调结果,对本文的模型和算法进行了验证.

... 此外,也有学者根据交通诱导与信号配时的协同作用进行建模^[6,7,8,9,10],如Allsop^[6]在1974年最先提出交通信号控制与交通分配的相互作用问题 ...

... 王亮等^[7]也对交通控制和诱导问题进行了递阶协调优化方面的建模 ...

... 2 人均尾气排放车辆尾气排放包括路段行车时的尾气排放和交叉口怠速时的尾气排放^[2,7] ...

2007

0.0

. 2007, 37(2):319-324 DOI:doi:10.3969/j.issn.1671-5497.2007.02.014

Quasi-optimal algorithm for double objective optimization model of traffic flow guidance coordinated with signal control

交通流诱导与控制协同的双目标优化模型及准最优求解算法

Bao Li-xia , Yang Zhao-sheng , Hu Jian-meng

保利霞, 杨兆生, 胡建萌

摘　要：提出了一种基于消散拥堵和系统总出行时间最小的双目标诱导控制协同优化模型,算法引入饱和度的概念,采用小步距微量调整信号配时、试算优化的方法,适当加载或卸载交通量,优化交叉口信号配时,使交通流在不断反馈与不断调整过程中达到最优.采用VISSIM建立模拟路网进行了协同算法试验,并对协同实施效果进行了评价,结果表明：在进行3次协同后拥堵基本消散,经过第4、5次协同能实现系统总行程时间尽可能小.

... 此外,也有学者根据交通诱导与信号配时的协同作用进行建模^[6,7,8,9,10],如Allsop^[6]在1974年最先提出交通信号控制与交通分配的相互作用问题 ...

1983

0.0

... 此外,也有学者根据交通诱导与信号配时的协同作用进行建模^[6,7,8,9,10],如Allsop^[6]在1974年最先提出交通信号控制与交通分配的相互作用问题 ...

2011

0.0

. 2011, 39(3):95-100,106 DOI:doi:10.3969/j.issn.1000-565X.2011.03.019

Area coordinated control of traffic signals based on bi-level programming model

基于双层规划模型的交通信号区域协调控制

Xu Jian-min , Shou Yan-fang , Lu Kai.

徐建闽, 首艳芳, 卢凯

针对过饱和状态下的交通信号配时,以区域整体输出总流量最大化和各交叉口进口道总延误时间最小化为目标,构建了基于动态子区划分的交通信号区域协调控制双层规划模型(BP模型).通过分析交叉口滞留排队车辆、进口道交通量以及相位相序对区域协调控制的影响,建立了交叉口相位差、有效绿灯时间和动态交通流量等协调控制变量的约束关系式.采用基于遗传-模拟退火算法的混合优化策略对模型进行求解,提高全局最优解的可靠性和计算效率.仿真结果表明,该模型与实际情况较为吻合.

... 此外,也有学者根据交通诱导与信号配时的协同作用进行建模^[6,7,8,9,10],如Allsop^[6]在1974年最先提出交通信号控制与交通分配的相互作用问题 ...

2004

0.0

... Ceylan和Bell^[11]则建立了基于遗传算法的信号配时模型,考虑了驾驶员路径选择的影响,该模型优化目标主要是延误和停车次数,未考虑公交优先和尾气排放等因素 ...

... 遗传算法(GA)是一种自适应全局优化的随机搜索方法,Ceylan和Bell^[11]的研究表明其在信号配时优化求解领域的应用是有效的 ...

1999

0.0

... 这里,进口方向的车均延误采用经典的Webster延误公式计算^[12]: ...

2005

0.0

. 2005, 25(11):133-138 DOI:doi:10.3321/j.issn:1000-6788.2005.11.021

Research on signal timing for urban intersections with genetic algorithms optimizing with the idea of bus priority

考虑公交优先的城市交叉口遗传算法信号配时研究

Chen Qun , Yan Ke-fei.

陈群, 晏克非

对设置公交专用进口道的城市交叉口信号配时作了研究.考虑公交优先,并从我国城市交叉口的交通特征出发,构造了多目标规划函数:一是使公交总延误最小,二是使一般小汽车交通各相饱和度之间的均方差最小.对于多目标规划,采用功效系数法建立目标评价函数.并利用遗传算法对函数进行优化求解得到信号配时方案.通过仿真实例说明了函数构造及求解的过程.

... 考虑到信号周期时长超过一定值以后,通行能力的增大便趋于停滞,而车辆延误时间却急速增长,借鉴相关研究成果^[13],本文将120 s设为最佳信号周期的上限值 ...

... 为了研究方便,假设直行、右转共用一个相位,即红灯时间禁止车辆右转,这种措施有利于保证行人过街安全^[13] ...

... 借鉴北京市大柳树路-学院南路交叉口高峰和平峰时段流量的实地采集数据及文献^[13]的相关成果,设定进口流量矩阵Q及其对应的饱和流量矩阵S ...