作者简介:谭国金(1981-),男,副教授,博士.研究方向:桥梁检测与加固.E-mail:tgj@jlu.edu.cn
为了揭示偏心直线配置预应力筋情况下简支梁自振频率变化的内在机理,首先把预应力简支梁振动体系分解为预应力筋和简支梁梁体两个振动子系统,从结构振动的基本原理出发,分别建立了两个子系统的动力平衡方程;然后对子系统的振动方程进行耦合分析、处理,提出了偏心直线配筋情况下预应力简支梁的自振频率计算方法;最后将该方法与有限元方法的计算结果进行对比分析,验证了该方法的有效性和可靠性。
In order to reveal the mechanisms of natural vibration frequency of simply supported beam reinforced with eccentric prestressed tendons, a calculation method of the natural frequency is proposed, and the influence of effective prestress on the natural frequency is analyzed. First, the vibration system of the simply supported and prestressed beam is decomposed into two subsystems, the prestressed tendons and the simply supported beam. The dynamic equilibrium equations of the two subsystems are established using the principle of structural vibration. Then, based on the coupling analysis and processing of the vibration equations of the subsystems, a calculation method of the natural frequency of beam is derived. Using this method, the calculated natural vibration frequencies of the simply supported and prestressed beam are in good agreement with that predicted by finite element method.
预应力简支梁是土木工程领域常用的结构形式, 如何准确计算其自振频率对该类结构的设计和运营期的状态评估都有着极其重要的意义。
20世纪90年代, Hop[1]通过室内实测数据, 首次发现预应力对混凝土梁的自振频率有一定的影响, 并且随着预应力的增大, 自振频率增大。随后Saiidi等[2]通过室内实验和金门大桥的现场试验, 得出了与Hop相同的结论。华中科技大学的张耀庭教授分别测试了有粘结和无粘结预应力作用下的简支预应力混凝土梁的自振频率[3]。长安大学的贺拴海教授在室内测试了简支预应力空心板梁的自振频率, 并归纳分析了预应力对简支预应力空心板梁自振频率的影响规律[4]。
有些学者把预应力导致简支梁自振频率变化的原因归结为预应力改变了简支梁的动刚度。Kim[5]认为预应力使预应力筋产生了一个等效刚度, 把预应力筋的等效刚度和混凝土梁的刚度叠加作为预应力简支梁的刚度。张耀庭基于实测数据给出了预应力简支梁动刚度的修正公式[6]。
为了得到该类结构自振频率的理论计算值, 有些学者把有限元方法引入其中。熊健民[7]采用ANSYS软件分析了不同配筋形式的预应力简支梁的自振频率。郑尚敏[8]采用ANSYS软件分析了预应力简支波形钢腹板箱梁的自振频率。吉林大学的刘寒冰和谭国金等[9]采用有限元方法对体外预应力简支钢梁的自振频率进行了数值计算。
尽管有限元方法能够计算出理论值, 但不能很好地对其内在机理进行详尽的剖析。于是有些学者试图从结构振动的基本原理出发, 提出预应力简支梁自振频率的计算方法。Farasat[10]基于Kirchhoff动力模型, 建立了预应力混凝土梁自振频率的计算公式。Miyamoto[11]基于初等梁理论, 建立了考虑预应力筋偏心矩的预应力钢-混凝土组合梁的自振频率计算公式。由于Parasat和Miyamoto[10, 11]在形成计算方法的过程中把预应力当成作用于梁体上的外力, 因此导致计算方法存在严重缺陷。Hamed[12]建立了预应力简支梁的非线性振动理论模型, 在此基础上求解预应力简支梁的自振频率, 但该方法只适用于振动变形比较大的情况。针对预应力简支梁自振频率计算存在的问题, 本文从结构振动的基本理论出发, 建立了预应力简支梁结构体系的振动方程, 从而实现对该类结构自振频率的求解。
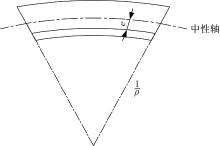
图1为偏心距为
由预应力筋振动子系统的受力模式可知, 使得预应力筋竖向合力之和等于0, 则有:
式中:
由梁体振动子系统的受力模式可知, 梁体竖向力平衡方程为:
式中:
梁体对
式中:
由于偏心预应力会使梁体产生一个初始位移, 则梁体位移可表示为:
式中:
由结构力学的知识, 可求得:
式中:
综合式(4)(5), 把y(x, t)分别对x, t求偏导可得:
根据梁体变形的几何关系(见图3), 基于平截面假定, 可以计算得到
由应变增量
式中:
由式(8)可得:
把式(6)分别代入式(1)(2)(3)中, 并忽略高阶小项, 可得:
将式(10)中的前两式相加, 并令
把式(10)中的最后一式对
用式(11)减去式(12), 可得:
注意到
式(14)即为无粘结偏心直线配筋情况下预应力简支梁体系的振动方程。
采用Galerkin方法对式(14)进行求解, 可得预应力简支梁体系的自振频率。现以求解第1阶自振频率为例, 来简述从式(14)求解自振频率的过程。
把简支梁的1阶振型表示为:
将式(15)代入到式(14)中, 并进行加权积分运算, 可得:
由式(16)可计算1阶自振频率
式中:
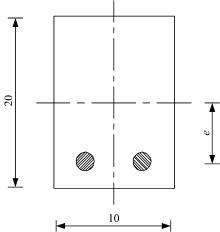
数值模拟对象为5 m长偏心直线配筋预应力简支梁, 截面如图4所示。梁体材料为C30混凝土, 弹性模量为3.45× 104 MPa。预应力筋材料为钢绞线, 弹性模量为1.95× 105 MPa, 单根面积为139 mm2。梁体采用实体单元SOLID65模拟, 预应力筋采用杆单元LINK8模拟, 有限元模型如图5所示, 其中X为梁体宽度方向, Y为梁体高度方向, Z为梁体长度方向。在有限元模型中, 采用节点耦合方法来模拟预应力筋与梁体的相互作用。在简支梁端部预应力筋与梁体在X、Y、Z三个方向都存在相互作用, 所以在梁端部把预应力筋节点与其附近的梁体节点在X、Y、Z三个方向都进行耦合。而在梁体的其他部位预应力筋与梁体不存在水平方向(梁长度方向)的相互作用, 在梁体的高度和宽度方向仍然存在相互作用, 因此该部分把预应力筋节点与其附近的梁体节点在X、Y两个方向进行耦合。
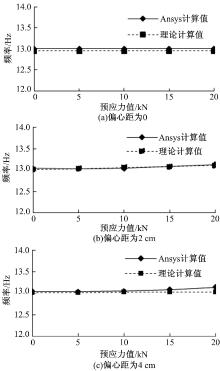
采用本文方法和有限元方法计算了偏心距为0、2、4 cm情况下多组预应力值对应的预应力简支梁1阶频率, 计算结果如图6所示。
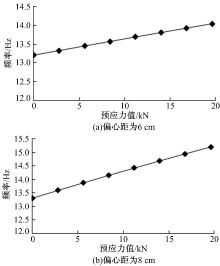 | 图7 不同偏心距情况下自振频率与预应力的关系Fig.7 Relation of natural frequency and prestressing force when different eccentricity |
由图6可知, 本文方法的计算结果与有限元方法的计算结果非常接近, 这充分说明了本文方法的可靠性和有效性。
为了探讨预应力值和偏心距对预应力简支梁自振频率的影响, 采用本文方法计算了同一偏心距情况下多组预应力值对应的预应力简支梁1阶频率, 如图7所示; 并且计算了同一预应力值情况下多组偏心距对应的预应力简支梁1阶自振频率, 如图8所示。
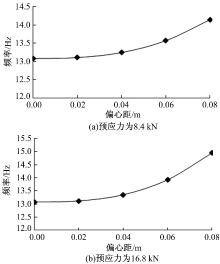 | 图8 不同预应力值时自振频率与偏心距的关系Fig.8 Relation of natural frequency and eccentricity when different prestressing force |
由计算结果可知:①当偏心距一定时, 自振频率随着预应力值的增大而增大, 预应力值与自振频率呈近似线形关系。②当预应力值一定时, 自振频率随着偏心距的增大而增大, 偏心距与自振频率的关系呈非线性关系。
(1)采用本文方法计算无粘结偏心直线预应力简支梁的频率是可靠、有效的。
(2)当偏心距一定时, 自振频率随着预应力值的增大而增大, 预应力值与自振频率呈近似线性关系。
(3)当预应力值一定时, 自振频率随着偏心距的增大而增大, 偏心距与自振频率的关系呈非线性关系。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|