考虑区间不确定性的钢结构疲劳寿命分析

引用本文

曹珊珊, 雷俊卿. 考虑区间不确定性的钢结构疲劳寿命分析.吉林大学学报:工学版, 2016, 46(3): 804-810
CAO Shan-shan, LEI Jun-qing. Fatigue life prediction of steel structure considering interval uncertainty. Journal of Jilin University Engineering and Technology Edition, 2016, 46(3): 804-810 复制到剪切板

Permissions

考虑区间不确定性的钢结构疲劳寿命分析

曹珊珊, 雷俊卿

北京交通大学土木建筑工程学院,北京 100044

通讯作者:雷俊卿(1956-),女,教授,博士生导师.研究方向:大跨度桥梁结构理论与应用.E-mail:lei_jq@126.com

作者简介:曹珊珊(1989-),女,博士研究生.研究方向:大跨度桥梁结构理论与应用,桥梁钢结构疲劳性能.E-mail:oconan@163.com

基金:北京交通大学研究生创新基金项目(2014YJS097/C14JB00340); 国家自然科学基金项目(51178042,51578047); 中国铁路总公司科技研究开发计划项目(2014G004-B); 中国交通建设股份有限公司科技特大研发项目(2014-ZJKJ-03)

摘要

针对传统的钢结构疲劳寿命预测误差较大的问题,判别线性累积损伤模型和裂纹扩展模型中变量不确定性和随机性,基于区间-概率理论推导区间模型和含有对数正态分布的概率模型的一致性关系,给出可同时考虑区间变量和随机变量的区间-概率可靠度分析模型和求解方法。实桥中典型疲劳细节验证表明,在模型中变量应力幅的变异系数为0.25~0.35时,本文方法比传统概率算法更为保守,可作为预测钢结构疲劳寿命的一种有效手段。

关键词: 桥梁工程; 统计力学; Miner准则; 裂纹扩展准则; 区间-概率可靠度模型; 疲劳寿命

中图分类号:U441 文献标志码:A 文章编号:1671-5497(2016)03-0804-07

Fatigue life prediction of steel structure considering interval uncertainty

CAO Shan-shan, LEI Jun-qing

School of Civil Engineering,Beijing Jiaotong University,Beijing 100044, China

Abstract

To reduce the fatigue life prediction error of steel structure using traditional fatigue prediction algorithm, the interval-probability reliability analysis method was presented to deal the fatigue life prediction of steel structure with the consideration of variables uncertainty. The parameters of the linear accumulative damage model and the crack propagation model were distinguished as probabilistic variables and interval variables based on previous studies. The theoretical foundation was established by the consistency relationship between the interval reliability and the probability reliability model with lognormal distributed variables in theory. The solving process was combined with definition of interval reliability index and the probabilistic algorithm. The results of typical fatigue details of actual bridge show that, when the variable coefficient of the stress amplitude is in the range from 0.25 to 0.35, the results of the interval-probability analysis are more conservative than that of traditional probability method.

Keyword: bridge engineering; statistical mechanics; Miner's rule; crack propagation criterions; hybrid reliability model; fatigue life

Show Figures

0 引言

结构疲劳失效是土木工程领域钢结构的主要破坏形式, 现有有效的样本疲劳试验数据远远无法满足统计学的需求, 缺乏样本数据的参数在结构传统概率可靠度分析中可能会产生不可估量的误差^{[1, 2]}。为此, 学者们提出了非概率可靠度分析法^[1], 并以此为基础研究了区间-概率和凸集-概率两类混合可靠度分析方法^{[2, 3]}等。区间-概率可靠度分析方法^[2]需同时考虑概率模型和区间模型, 对两个模型的一致性关系和相容性要求极高。服从均匀分布的概率模型与区间模型的一致性已得到证明^[3], 但服从常用分布形式(如对数正态分布等)变量的概率模型与区间模型的一致性关系鲜有研究, 而且其适用范围也缺乏深入的讨论和研究。这两方面的欠缺严重影响了区间-概率可靠度模型在结构寿命分析等领域中的应用。

本文针对钢结构疲劳寿命分析中的线性累积损伤模型和裂纹扩展模型, 结合已有试验研究成果, 分析了Miner准则和Paris公式中的参数特征。针对疲劳寿命分析中应力幅和初始裂纹等变量的不确定性, 提出了疲劳寿命分析的区间-概率可靠度一致性关系理论和分析求解方法。并结合已有实桥检测结果验证了区间-概率可靠度模型分析方法的合理性和适用性。

1 疲劳寿命模型

钢结构的疲劳寿命极限状态方程可采用疲劳寿命极限 $\begin{matrix} \bar{N} \end{matrix}$ 和实际应力循环次数 $\begin{matrix} N \end{matrix}$ 表达, 如式(1)所示:

$\begin{matrix} g (X) = \bar{N} - N \end{matrix}$ (1)

当 $\begin{matrix} g (X) \geq 0 \end{matrix}$ 时, 认为结构不发生疲劳失效; 当 $\begin{matrix} g (X) < 0 \end{matrix}$ 时, 认为结构疲劳失效。

1.1 累积损伤分析模型

在疲劳裂纹出现前, 对于长期承受变幅应力幅的钢结构, 基于Miner准则的累积损伤模型的表达式为^[4]:

$\begin{matrix} D = \sum n_{i} / N_{i} = N \cdot (S_{eq})^{m} / A \leq \bar{D} / e \end{matrix}$ (2)

式中:n_i为第i组应力幅值S_i循环次数; N_i为第i组应力幅值S_i循环破坏的寿命; $\begin{matrix} \bar{D} \end{matrix}$ 为钢材的Miner临界累积损伤值, 可假定为服从对数正态分布, 均值为1.0, 变异系数为0.3^[5]; $\begin{matrix} e \end{matrix}$ 为测量误差修正系数, 可以假定为对数正态分布, 均值为1.0, 变异系数为0.04^[6]; $\begin{matrix} A \end{matrix}$ 为疲劳细节参数, AASHTO中假定为服从对数正态分布^[7], 变异系数均可取为0.45^[8]; m取为常数。S_eq为等效常幅应力幅, 其表达式为:

$\begin{matrix} S_{eq} = (\overset{k}{\sum_{i = 1}} \frac{n_{i}}{N} \cdot S_{i}^{m})^{1 / m} \end{matrix}$ (3)

采用临界累积损伤值 $\begin{matrix} \bar{D} \end{matrix}$ 描述疲劳寿命极限 $\begin{matrix} \bar{N}, \end{matrix}$ 功能函数可转化为:

$\begin{matrix} g (X) = \frac{A \cdot \bar{D}}{e \cdot (S_{eq})^{m}} - N \end{matrix}$ (4)

对于等效应力幅 $\begin{matrix} S_{eq} \end{matrix}$ 的参数特征, 应根据现场数据, 由内力直方图回归获取, 常用来描述 $\begin{matrix} S_{eq} \end{matrix}$ 分布特征的有正态分布、对数正态分布、Weibull分布以及瑞利分布等, 且分布形式会使疲劳寿命预测结果产生较大差异^{[9, 10, 11]}。

1.2 裂纹扩展分析模型

基于Paris公式, 结构的裂纹扩展模型的表达式为:

$\begin{matrix} \frac{da}{dN} = C \cdot {(Δ K)}^{m} \end{matrix}$ (5)

式中: $\begin{matrix} a \end{matrix}$ 为结构裂纹尺寸; $\begin{matrix} C 、 m \end{matrix}$ 均为材料的疲劳特性参数; $\begin{matrix} ΔK \end{matrix}$ 为应力强度因子幅值, 可借助与结构试件尺寸和裂纹尺寸有关的无量纲函数 $\begin{matrix} Y (a), \end{matrix}$ 表达为等效应力幅 $\begin{matrix} S_{eq} 和裂纹尺寸 a \end{matrix}$ 的函数:

$\begin{matrix} ΔK = Y (a) \cdot S_{eq} \cdot \sqrt[]{πa} \end{matrix}$ (6)

将式(6)代入式(5), 进行积分运算, 得到结构裂纹由初始裂纹 $\begin{matrix} a_{0} \end{matrix}$ 扩展到极限裂纹 $\begin{matrix} a_{f} \end{matrix}$ 的疲劳寿命关系式:

$\begin{matrix} \frac{1}{C \cdot S_{eq}^{m}} \int_{a_{0}}^{a_{f}} \frac{da}{(Y {(a) \sqrt[]{πa})}^{m}} = \bar{N} - N_{0} \end{matrix}$ (7)

若认为工程结构中存在初始裂纹, 即 $\begin{matrix} N_{0} = 0, \end{matrix}$ 则功能函数(式(1))可表达为:

$\begin{matrix} g (X) = \frac{1}{C \cdot S_{eq}^{m}} \int_{a_{0}}^{a_{f}} \frac{da}{(Y {(a) \sqrt[]{πa})}^{m}} - N \end{matrix}$ (8)

结构裂纹尺寸参数 $\begin{matrix} a_{0} \end{matrix}$ 与结构几何尺寸、细节类型以及加工精度等因素有关, 实测数据的离散性突出, 常用分布形式有对数正态分布或Weibull分布, 表1中列举了盖板裂纹的典型实测统计数据^[12]。对于临界极限裂纹 $\begin{matrix} a_{f}, \end{matrix}$ 可根据断裂力学理论, 由断裂韧性 $\begin{matrix} K_{c} \end{matrix}$ 确定; 在实际工程中亦可根据结构的安全使用性能确定, 英国海岸结构技术文件^[13]中建议将临界极限裂纹 $\begin{matrix} a_{f} \end{matrix}$ 取为相应板件的厚度或者宽度的尺寸常数。

表1 初始裂纹a₀的参数特征表 Table 1 Parameter characteristic of a₀

基于Miner准则的累积损伤模型中的变量 $\begin{matrix} \bar{D} 、 e 、 A \end{matrix}$ 和基于Paris公式的裂纹扩展模型的 $\begin{matrix} C \end{matrix}$ 均可认为服从对数正态分布, 而变量 $\begin{matrix} S_{eq} \end{matrix}$ 和 $\begin{matrix} a_{0} \end{matrix}$ 的不确定性十分显著, 结构在设计阶段或缺乏实测数据资料的情况下, 无法准确给出 $\begin{matrix} S_{eq} \end{matrix}$ 和 $\begin{matrix} a_{0} \end{matrix}$ 的分布特征。此时, 可以在有限数据的基础上, 将 $\begin{matrix} S_{eq} \end{matrix}$ 和 $\begin{matrix} a_{0} \end{matrix}$ 定义为区间变量进行分析。

2 区间-概率可靠度模型

针对变量服从对数正态分布的概率模型, 推导其与区间模型的一致性关系, 给出基于区间-概率可靠度的疲劳寿命分析模型和数值求解方法。

2.1 一致性关系推导

概率可靠度模型中仅含有随机变量^[3], 区间可靠度模型是非概率可靠度模型的一种形式, 模型中仅含有区间变量。为了简化推导, 作如下假设:①各变量相互独立; ②概率可靠度模型求解采用一次二阶矩法; ③区间可靠度模型的求解依照定义方法^[1]; ④结构可靠度模型中含有抗力R和荷载效应S_i(i=1, 2, …, n-1)n个变量。

若概率模型中的随机变量均服从对数正态分布, 功能函数可以表达为式(9), 功能函数的均值和标准差分别如式(10)(11)所示:

$g (R, S_{1}, S_{2}, \dots, S_{n - 1}) = lnR - \overset{n - 1}{\underset{i = 1}{\sum \ln S_{i}}} i = 1, 2, \dots, n - 1$ (9)

$μ_{g} = μ_{lnR} - \overset{n - 1}{\sum_{i = 1}} μ_{\ln S_{i}} = n (\frac{μ_{R}}{\sqrt[]{1 + γ_{R}^{2}}} \overset{n - 1}{\prod_{i = 1}} \frac{\sqrt[]{1 + γ_{S_{i}}^{2}}}{μ_{S_{i}}})$ (10)

$σ_{g} = \sqrt[]{(σ_{lnR})^{2} + \overset{n - 1}{\sum_{i = 1}} (σ_{\ln S_{i}})^{2}} = \sqrt[]{\ln (1 + γ_{R}^{2}) \overset{n - 1}{\prod_{i = 1}} (1 + γ_{S_{i}}^{2})}$ (11)

可靠度指标如式(12)所示:

$\begin{matrix} β = \frac{μ_{g}}{σ_{g}} = \frac{\ln (\frac{μ_{R}}{\sqrt[]{1 + γ_{R}^{2}}} \overset{n - 1}{\prod_{i = 1}} \frac{\sqrt[]{1 + γ_{S_{i}}^{2}}}{μ_{S_{i}}})}{\sqrt[]{\ln (1 + γ_{R}^{2}) \overset{n - 1}{\prod_{i = 1}} (1 + γ_{S_{i}}^{2})}} \end{matrix}$ (12)

将随机变量 $\begin{matrix} R 、 S_{i} \end{matrix}$ 转化为区间变量, 取 $\begin{matrix} R' = lnR \in [μ_{lnR} - m_{R} σ_{lnR}, μ_{lnR} + m_{R} σ_{lnR}], S'_{i} = \ln S_{i} \in [μ_{\ln S_{i}} - m_{S_{i}} σ_{\ln S_{i}}, μ_{\ln S_{i}} + m_{S_{i}} σ_{\ln S_{i}}], \end{matrix}$ 此时, 区间可靠度模型中变量的均值仍为 $\begin{matrix} μ_{R} \end{matrix}$ 和 $\begin{matrix} μ_{S_{i}} (i = 1, 2, \dots, n - 1), \end{matrix}$ 离差 $\begin{matrix} Δ_{R} = m_{R} σ_{R} 、 Δ_{S_{i}} = m_{S_{i}} σ_{S_{i}} (i = 1, 2, \dots, n - 1), \end{matrix}$ 区间变量对应的结构安全系数可以表达为:

$\begin{matrix} K'_{m} = \frac{μ'_{R}}{\overset{n - 1}{\sum_{i = 1}} μ_{S'_{i}}} = \frac{\ln μ_{R} - \ln \sqrt[]{1 + γ_{R}^{2}}}{\overset{n - 1}{\sum_{i = 1}} (\ln μ_{S_{i}} - \ln \sqrt[]{1 + γ_{S_{i}}^{2}})} \end{matrix}$ (13)

结合区间可靠度的定义^[3], 相应的区间可靠度指标可转化为式(14):

$\begin{matrix} η = \frac{β \sqrt[]{\ln (1 + γ_{R}^{2}) \cdot \overset{n - 1}{\prod_{i = 1}} (1 + γ_{S_{i}}^{2})}}{m_{R} \sqrt[]{\ln (1 + γ_{R}^{2})} + \overset{n - 1}{\sum_{i = 1}} m_{S_{i}} \sqrt[]{\ln (1 + γ_{S_{i}}^{2})}} \end{matrix}$ (14)

由式(14)可以看出: $\begin{matrix} η \end{matrix}$ 可以直接采用 $\begin{matrix} β \end{matrix}$ 和概率可靠度模型中的相关参数( $\begin{matrix} γ_{R}, γ_{S_{i}} \end{matrix}$ )来表达, 为两阶段混合模型的建立奠定了基础。

在实际结构中, 离差系数一般均假设为是相等的, 即 $\begin{matrix} m_{R} = m_{S_{i}} = m, \end{matrix}$ 区间可靠度指标也可以表达为式(15):

$\begin{matrix} η = \frac{β}{m} \cdot \frac{\sqrt[]{\ln (1 + γ_{R}^{2}) + \overset{n - 1}{\sum_{i = 1}} \ln (1 + γ_{S_{i}}^{2})}}{\sqrt[]{\ln (1 + γ_{R}^{2})} + \overset{n - 1}{\sum_{i = 1}} \sqrt[]{\ln (1 + γ_{S_{i}}^{2})}} < \frac{β}{m} \end{matrix}$ (15)

由式(15)可以看出, 概率可靠度指标与区间可靠度指标之间的转化关系可以通过参数 $\begin{matrix} m \end{matrix}$ 和一个小于1.0的比值来表达, 即满足 $\begin{matrix} η < β / m 。 \end{matrix}$

2.2 区间-概率可靠度模型及求解方法

2.2.1 基本模型

区间-概率可靠度模型中包含随机变量(X={X₁, X₂, …, X_n})和区间变量(Z={Z₁, Z₂, …, Z_m}), 假设各变量相互独立, 根据具有两阶段功能函数的混合模型概念^[2] , 建立第一阶段的区间可靠度模型, 如式(16)所示, 由区间算法得到的区间可靠度指标为随机变量X的函数, 如式(17)所示。

${g_{H}}^{(1)} = g_{H} (X, Z)$ (16)

$η_{I} (X) = g_{H} {(X, Z)}^{c} / g_{H} {(X, Z)}^{r}$ (17)

式中: $g_{H} {(X, Z)}^{c}$ 为 $g_{H} {(X, Z)}^{c}$ 区间数的算术平均值; $\begin{matrix} g_{H} {(X, Z)}^{r} 为 g_{H} (X, Z) \end{matrix}$ 相对于均值的分散程度。

随后, 第二阶段的功能函数借助区间可靠度指标的限制值来建立(见式(18)), 当功能函数 $\begin{matrix} {g_{H}}^{(2)} \geq 0 \end{matrix}$ 时, 结构是安全的。概率可靠度指标即为最后的区间-概率可靠度指标(见式(19))。

${g_{H}}^{(2)} = | η (X) | - 1$ (18)

$β_{H} = Φ (1 - P_{rob} \{{g_{H}}^{(2)} (X) < 0\})$ (19)

式中:Φ (• )为标准正态分布函数; P_rob(• )为概率。

2.2.2 数值求解方法

基于上述理论基础, 本文针对疲劳寿命分析模型, 借助Matlab平台实现数值求解, 给出区间-概率可靠度分析方法和求解步骤如下:

(1)根据累积损伤模型和裂纹扩展模型, 建立第一阶段功能函数 $\begin{matrix} {g_{H}}^{(1)} = g_{H} (X, Z), 当 {g_{H}}^{(1)} \geq 0 \end{matrix}$ 时, 结构不会发生疲劳失效。

(2)根据功能函数具体确定变量的特性。对于随机变量, 给出足够准确的分布形式和分布参数; 对于区间变量, 给出对应的均值和离差。将 $\begin{matrix} S_{eq} \end{matrix}$ 和 $\begin{matrix} a_{0} \end{matrix}$ 作为区间变量进行分析, 并根据3σ 准则确定区间变量的离差, 若参数变异系数较大时, 离差系数取值1.0, 且需满足 $\begin{matrix} η < β / m \end{matrix}$ (见式(15))。

(3)将随机变量作为常量, 进行区间可靠度模型的求解。可以采用定义算法^[1]、一维优化算法、多维优化算法和仿射算法^[14]等。

(4)为了避免非线性功能函数在运算时的区间扩张, 对步骤(3)中的计算有效性进行验证, 满足 $\begin{matrix} η_{I} (\bar{X}) < β_{I} (\bar{X}) / m, η_{I} \end{matrix}$ 为单独将区间变量作为正态分布变量时的概率可靠度指标, $\begin{matrix} \bar{X} \end{matrix}$ 为随机变量X的某一特定值。若不满足, 重新进行步骤(3)。

(5)借助区间可靠度指标的限制值来建立第二阶段的概率可靠度模型 $\begin{matrix} {g_{H}}^{(2)} = |η (X)| - 1 。 \end{matrix}$ 对于工程结构, 当 $\begin{matrix} {g_{H}}^{(2)} \geq 0 \end{matrix}$ 时, 结构不会发生疲劳失效。

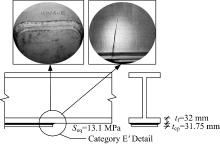
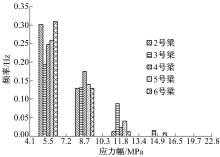
(6)进行概率可靠度模型的求解, 可借助JC法、蒙特卡罗法、响应面法等, 求得概率可靠度指标 $\begin{matrix} β_{H}, \end{matrix}$ 即为最终区间-概率可靠度指标。

3 结构疲劳寿命分析实例

针对国外某桥梁的工字梁E'类细节^[7]进行疲劳寿命分析, 结构细节和裂纹扩展情况如图1所示, 图中, t_f为底板厚度; t_cp为盖板厚度。根据实测数据, 盖板工字梁E'类细节的应力幅94%~99%为4.1~19.7 MPa, 由式(3)得等效常幅应力幅S_eq为13.1 MPa, 如图2所示。初期统计平均每日交通量为4430次, 每年交通量增长率α =2%, 实际各年份交通量作用次数 $\begin{matrix} N = 365 \cdot ADTT \cdot [{(1 + α)}^{y} - 1] / \ln (1 + α) 。 \end{matrix}$

	Figure Option View Download New Window
	图1 工字梁疲劳细节E’ Fig.1 Fatigue details

	Figure Option View Download New Window
	图2 应力幅频率分布图Fig.2 Stress range bin histogram

3.1 累积损伤分析法

概率可靠度模型中仅含有随机变量^[3], 区间可结合Miner准则和AASHTO中的S-N曲线^[4]得到, 功能函数可表达为式(4), 式中参数数据如表2所示。

表2 累积损伤模型的参数特征表 Table 2 Parameter characteristic for cumulative fatigue damage model

参数	均值	变异系数	特征	引文
$\begin{matrix} m \end{matrix}$	3.0	-	常量	文献[4]
$\begin{matrix} \bar{D} \end{matrix}$	1.0	0.3	对数正态分布	文献[5]
A/MPa³	1.28× 10¹²	0.45	对数正态分布	文献[8]
$\begin{matrix} e \end{matrix}$	1.0	0.04	对数正态分布	文献[6]
S_ep/MPa	13.1	0.25	不确定性变量	文献[7, 16]

表2 累积损伤模型的参数特征表 Table 2 Parameter characteristic for cumulative fatigue damage model

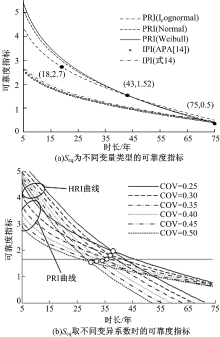
首先采用传统JC法对工字梁E'类细节进行概率可靠度分析, 依次假定S_eq服从正态分布、对数正态分布和Weibull分布^[11], 各年份下的概率可靠度指标如图3(a)中曲线PRI(Normal)、PRI(Lognormal)和PRI(Weibull)所示。其中, 曲线PRI含有点(18, 2.7)、(43, 1.52)和(75, 0.5), 与文献^[11]中的结果一致。同时可以看出, S_eq在不同分布情况下, 结构的可靠度指标存在差异, 当S_eq为对数正态分布时, 结构可靠度指标最为保守, 与文献^[15]结论一致。

	Figure Option View Download New Window
	图3 基于累积损伤模型的疲劳可靠度指标Fig.3 Fatigue reliability index based on the cumulative fatigue damage model

随后考虑变量的不确定性, 若假定将各变量作为区间变量, 建立区间可靠度模型, 由于变量的变异系数普遍较高, 离差系数 $\begin{matrix} m \end{matrix}$ 均假定为1.0, 分别采用式(14)和仿射法^[14]获得区间可靠度指标如图3(a)所示, 可以看出两曲线基本吻合, 最大误差为7.76%, 式(14)可以有效转化概率区间模型之间的可靠度指标, 即文中推导的概率模型与区间模型的一致性关系是合理有效的。

采用2.2节中的数值分析方法, 对E'细节进行区间-概率可靠度研究, 取S_eq为区间变量, 离差系数为1.0, 变异系数为0.25时的基本变化区间为[27.776, 51.584], 其他变量为概率变量(见表2)。S_eq取不同变异系数时, 分别获得区间-概率可靠度指标(HRI)曲线组和概率可靠度指标(PRI)曲线组(见图3(b))。随着循环次数的增加, 区间-概率可靠度指标下降速率明显高于概率可靠度指标; 随着变异系数的增大, 各年数对应的区间-概率可靠度指标降低程度更为明显, 这可以更合理地解释循环次数的增加和应力幅的离散性在一定条件下会加重结构疲劳损伤累积效应的现象。

在考虑结构95%的保证率, 即5%失效概率的情况下, 取1.65作为结构安全的目标可靠度指标, 由图3(b)可看出, 在等效应力幅的变异系数取为0.25、0.30、0.35时, E'类细节采用区间-概率可靠度指标预测的疲劳寿命较采用概率可靠度指标预测的疲劳寿命短, 区间-概率可靠度预测结果更为保守。

3.2 裂纹扩展分析法

结合基于Paris公式的裂纹扩展准则, 功能函数可表达为式(8)。根据实测数据^[7], 初始裂纹a₀均值取0.6 mm, 临界裂纹a_f取25.4 mm, 无量纲函数 $\begin{matrix} Y (a) \end{matrix}$ 可借助4个尺寸参数表达为:

$\begin{matrix} Y (a) = F_{e} (a) \cdot F_{s} (a) \cdot F_{w} (a) \cdot F_{g} (a) \end{matrix}$ (20)

式中:F_e(a)=0.952为裂纹尺寸参数, a为裂纹深度; F_s(a)为自由边界影响参数; $\begin{matrix} F_{w} (a) = 1.0 \end{matrix}$ 为有限宽度参数; F_g(a)为不均匀应力参数; $\begin{matrix} F_{g} (a) = - 3.539 \cdot \ln (z / t_{f}) + 1.981 \cdot \ln (t_{cp} / t_{f}) + 5.798 z \end{matrix}$ 为焊接尺寸。

参数特性如表3所示。

表3 裂纹扩展模型的参数特征表 Table 3 Parameters details for crack propagation model

采用2.2节中的区间-概率可靠度分析求解方法, 分别将不确定性参数a₀和S_eq作为区间变量对比区间-概率可靠度指标与传统概率可靠度指标的差异, 如图4(a)所示。可以看出, 将a₀单独作为区间变量时, 区间-概率可靠度指标曲线与传统概率可靠度指标曲线变化规律基本相同, 故在结构疲劳寿命分析中将a₀作为区间变量分析是合理的。

	Figure Option View Download New Window
	图4 基于裂纹扩展模型的疲劳可靠度指标Fig.4 Fatigue reliability index based on crack propagation model

将S_eq单独作为区间参数时, 区间-概率可靠度指标曲线与传统概率可靠度指标曲线存在较大差异, 在第7年之前可靠度指标高于概率可靠度指标, 在此之后, 可靠度指标低于概率可靠度指标, 随着循环次数的增加, 区间-概率可靠度指标的下降速率要明显高于概率可靠度指标。改变S_eq的取值, 分别获得区间-概率可靠度指标(HRI)曲线和概率可靠度指标(PRI)曲线如图4(b)所示。随着循环次数的增加, 区间-概率可靠度指标下降速率明显高于概率可靠度指标; 随着变异系数的增大, 各年数对应的结构区间-概率可靠度指标降低程度更为明显, 这可以更为合理地解释循环次数的增加和应力幅的离散性在一定条件下会加速疲劳破坏现象的发生。此外, 在等效应力幅的变异系数取为0.25、0.30、0.35时, 细节E'采用区间-概率可靠度指标预测的疲劳寿命比采用概率可靠度指标预测的疲劳寿命短, 区间-概率可靠度预测结果更为保守。

4 结论

针对钢结构疲劳寿命分析中的线性累积损伤模型和裂纹扩展模型, 分析Miner准则和Paris公式中的参数特征。针对疲劳寿命分析中应力幅S_eq和初始裂纹a₀等变量的不确定性参数特征, 理论推导了服从对数正态分布的概率模型和区间模型的一致性关系, 给出了区间-概率可靠度基本模型和数值求解方法, 实例分析结果表明:

(1)由本文推导的概率模型和区间模型的一致性关系式求得的区间可靠度指标与仿射算法的结果最大误差为7.76%, 一致性关系式是合理有效的。在此基础上建立的区间-概率可靠度基本模型和数值求解方法是高效收敛的。

(2)在基于累积损伤模型的疲劳寿命可靠度分析中, 当变量S_eq的变异系数为0.25~0.35时, 将变量S_eq作为区间变量, 采用区间-概率可靠度分析方法, 结果更为保守; 在基于裂纹扩展模型的疲劳寿命分析中, 将变量a₀作为区间变量, 采用区间-概率可靠度分析方法, 结果更为保守; 当变量S_eq的变异系数为0.25~0.35时, 可将变量S_eq和变量a₀同时作为区间变量, 采用区间-概率可靠度分析方法, 结果更为保守。即区间-概率可靠度分析方法可以作为概率可靠性方法的重要补充。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	郭书祥, 吕震宙, 冯元生. 基于区间分析的结构非概率可靠性模型[J]. 计算力学学报, 2001, 18(1): 56-60. Guo Shu-xiang, Lü Zhen-zhou, Feng Yuan-sheng. The structure of probabilistic reliability model based on interval analysis[J]. Chinese Journal of Computational Mechanics, 2001, 18(1): 56-60. [本文引用:4]
[2]	郭书祥, 吕震宙. 结构可靠性分析的概率和非概率混合模型[J]. 机械强度, 2002, 24(4): 524-526, 530. Guo Shu-xiang, Lü Zhen-zhou. Hybrid probabilistic and non-probabilistic model of structural reliability[J]. Journal of Mechanical Strength, 2002, 24(4): 524-526, 530. [本文引用:4]
[3]	王军, 邱志平. 结构的概率-非概率混合可靠性模型[J]. 航空学报, 2009, 30(8): 1398-1404. Wang Jun, Qiu Zhi-ping. Probabilistic and non -probabilistic hybrid reliability model of structures[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(8): 1398-1404. [本文引用:5]
[4]	AASHTO Guidelines. AASHTO stand ard specification 6th edtion for highway bridges[S]. Washington: American Association of State Highway and Transportation Officials, 2012. [本文引用:2]
[5]	Wirsching P H. Fatigue reliability for offshore structures[J]. Journal of Structural Engineering, 1984, 110(10): 2340-2356. [本文引用:1]
[6]	Frangopol D M, Strauss A, Kim S. Bridge reliability assessment based on monitoring[J]. Journal of Bridge Engineering, 2008, 13(3): 258-270. [本文引用:1]
[7]	Fisher J W. Fatigue and Fracture in Steel Bridges[M]. New York: John Willey and Sons, 1984. [本文引用:3]
[8]	Wirsching P H, Ortiz K, Chen Y N. Fracture mechanics fatigue model in a reliability format[C]//6th Int Syrup on OMAE, Houston, TX, 1987: 331-337. [本文引用:1]
[9]	刘克格, 闫楚良. 结构疲劳试验寿命数据分布类型对其使用寿命的影响[J]. 吉林大学学报: 工学版, 2011, 41(2): 419-423. Liu Ke-ge, Yan Chu-liang. Probability distribution of fatigue test data and fatigue life of aircraft structure[J]. Journal of Jilin University (Engineering and Technology Edition), 2011, 41(2): 419-423. [本文引用:1]
[10]	肖斌贝, 雷俊卿, 张坤, 等. 多级变幅度劳荷载下预应力混凝土梁刚度退化[J]. 吉林大学学报: 工学版, 2013, 43(3): 665-670. Xiao Yun, Lei Jun-qing, Zhang Kun, et al. Fatigue stiffness degradation of prestressed concrete beam under multilevel amplitude cycle loading[J]. Journal of Jilin University(Engineering and Technology Edition), 2013, 43(3): 665-670. [本文引用:1]
[11]	Kwon K, Frangopol D M. Bridge fatigue reliability assessment using probability density functions of equivalent stress range based on field monitoring data[J]. International Journal of Fatigue, 2010, 32(8): 1221-1232. [本文引用:3]
[12]	Chung H Y. Fatigue reliability and optimal inspection strategies for steel bridges[D]. Austin: Cockrell School of Engineering, The University of Texas at Austin, 2004. [本文引用:1]
[13]	Aker Offshore Partner A S. Review of probabilistic inspection analysis methods[DB/OL]. [2015-05-26]. http://www.docin.com/p-368376916.html. [本文引用:1]
[14]	江涛, 陈建军, 张弛江. 区间模型非概率可靠性指标的仿射算法[J]. 机械强度, 2007, 29(2): 251-255. Jiang Tao, Chen Jian-jun, Zhang Chi-jiang. Non-probabilistic reliability index and affine arithmetic[J]. Journal of Mechanical Strength, 2007, 29(2): 251-255. [本文引用:2]
[15]	Kwon K, Frangopol D M. Bridge fatigue assessment and management using reliability-based crack growth and probability of detection models[J]. Probabilistic Engineering Mechanics, 2011, 26(3): 471-480. [本文引用:1]
[16]	Kwon K, Frangopol D M, Soliman M. Probabilistic fatigue life estimation of steel bridges by using a bilinear approach[J]. Journal of Bridge Engineering, 2012, 17(1): 58-70. [本文引用:1]

2001

0.0

. 2001, 18(1):56-60 DOI:doi:10.3969/j.issn.1007-4708.2001.01.010

The structure of probabilistic reliability model based on interval analysis

基于区间分析的结构非概率可靠性模型

Guo Shu-xiang , L#cod#x000fc; Zhen-zhou , Feng Yuan-sheng.

郭书祥, 吕震宙, 冯元生

In this paper,the uncertain parameters of structures are expressed by non\|probabilistic interval variables. Based on interval arithmetic, a non\|probabilistic measure and analysis methodology for structural reliability computpation is presented. The measure index of the non\|probabilistic reliability developed here has a clear meaning in physics and geometry. The rationality and feasibility of the proposed theory is explained. Examples of practical application are given.

本文用非概率的凸集模型模拟结构的不确定性，将结构的不确定参数描述为区间变量，基于区间分析，提出了一种新的非概率可靠性度量体系分析方法，从物理、几何意义等方面解释了文中理论的合理性，其计算方法简便，衫，给出了算例分析。

... 0 引言结构疲劳失效是土木工程领域钢结构的主要破坏形式,现有有效的样本疲劳试验数据远远无法满足统计学的需求,缺乏样本数据的参数在结构传统概率可靠度分析中可能会产生不可估量的误差^[1,2] ...

... 为此,学者们提出了非概率可靠度分析法^[1],并以此为基础研究了区间-概率和凸集-概率两类混合可靠度分析方法^[2,3]等 ...

... ③区间可靠度模型的求解依照定义方法^[1] ...

... 可以采用定义算法^[1]、一维优化算法、多维优化算法和仿射算法^[14]等 ...

2002

0.0

. 2002, 24(4):524-526,530 DOI:doi:10.3321/j.issn:1001-9669.2002.04.012

Hybrid probabilistic and non-probabilistic model of structural reliability

结构可靠性分析的概率和非概率混合模型

Guo Shu-xiang , L#cod#x000fc; Zhen-zhou.

郭书祥, 吕震宙

在结构可靠性分析中需要合理地定量处理影响结构性能的诸多不确定性.不确定性的模拟既可以是概率的,也可以是非概率的.文中简要介绍结构可靠性分析的概率方法和基于区间模型的非概率可靠性方法.提出结构可靠性分析的概率和非概率混合模型.通过两级功能方程的逐次建立及可靠性分析,给出结构可靠的概率度量.实例分析说明在结构可靠性分析中,应根据不确定性的产生机理及所掌握的数据信息合理地选取分析模型.

... 为此,学者们提出了非概率可靠度分析法^[1],并以此为基础研究了区间-概率和凸集-概率两类混合可靠度分析方法^[2,3]等 ...

... 区间-概率可靠度分析方法^[2]需同时考虑概率模型和区间模型,对两个模型的一致性关系和相容性要求极高 ...

... 区间-概率可靠度模型中包含随机变量(X={X₁,X₂,…,X_n})和区间变量(Z={Z₁,Z₂,…,Z_m}),假设各变量相互独立,根据具有两阶段功能函数的混合模型概念^[2] ,建立第一阶段的区间可靠度模型,如式(16)所示,由区间算法得到的区间可靠度指标为随机变量X的函数,如式(17)所示 ...

2009

0.0

. 2009, 30(8):1398-1404

Probabilistic and non -probabilistic hybrid reliability model of structures

结构的概率-非概率混合可靠性模型

Wang Jun , Qiu Zhi-ping.

王军, 邱志平

Institute of Solid Mechanics, Beijing University of Aeronautics and Astronautics

This article uses a combination of probabilistic and non-probabilistic methods to describe the uncertain factors that influence structural reliability analysis. Based on the probabilistic reliability model and non-probabilistic set-based reliability model, a new hybrid probabilistic and nonprobabilistic reliability model is proposed. First， the performance function is analyzed by the non-probabilistic set-based reliability model, and then the reliability of all regions in the normalized interval variable space is summed up. In this way, the reliability of a structure can be obtained. Based on the same uncertain information, the calculated results of the hybrid reliability model and the probabilistic reliability model are equivalent. The computation of the reliability of a classical structure and a wing stiffening plate are used to illustrate that the hybrid model is as effective as the traditional probabilistic reliability model. The results indicate that this hybrid model is more reasonable for the analysis and design of structures and can ensure their security.

将影响结构可靠性分析的不确定性因素用概率和非概率两种方式模拟。并基于结构可靠性分析中的概率可靠性模型和非概率集合可靠性模型，提出一种新的结构可靠性分析的概率-非概率混合模型。该模型首先通过将功能函数进行非概率可靠性分析，然后将标准化区间变量空间所有区域的可靠度进行求和计算，从而给出结构的可靠度。并根据相同的不确定信息，由混合可靠性模型与概率可靠性模型得到的结果是相等的，证明了方法的有效性。最后，通过一个典型结构和一个机翼下壁加筋板与传统概率可靠性模型进行比较，表明该混合模型对于结构的分析和设计更为合理，能够更好地保证结构的安全性。

... 为此,学者们提出了非概率可靠度分析法^[1],并以此为基础研究了区间-概率和凸集-概率两类混合可靠度分析方法^[2,3]等 ...

... 服从均匀分布的概率模型与区间模型的一致性已得到证明^[3],但服从常用分布形式(如对数正态分布等)变量的概率模型与区间模型的一致性关系鲜有研究,而且其适用范围也缺乏深入的讨论和研究 ...

... 1 一致性关系推导概率可靠度模型中仅含有随机变量^[3],区间可靠度模型是非概率可靠度模型的一种形式,模型中仅含有区间变量 ...

... 结合区间可靠度的定义^[3],相应的区间可靠度指标可转化为式(14): ...

... 1 累积损伤分析法概率可靠度模型中仅含有随机变量^[3],区间可结合Miner准则和AASHTO中的S-N曲线^[4]得到,功能函数可表达为式(4),式中参数数据如表2所示 ...

2012

0.0

... 1 累积损伤分析模型在疲劳裂纹出现前,对于长期承受变幅应力幅的钢结构,基于Miner准则的累积损伤模型的表达式为^[4]: ...

1984

0.0

... 3^[5] ...

2008

0.0

... 04^[6] ...

1984

0.0

... A为疲劳细节参数,AASHTO中假定为服从对数正态分布^[7],变异系数均可取为0 ...

... 3 结构疲劳寿命分析实例针对国外某桥梁的工字梁E'类细节^[7]进行疲劳寿命分析,结构细节和裂纹扩展情况如图1所示,图中,t_f为底板厚度 ...

... 根据实测数据^[7],初始裂纹a₀均值取0 ...

1987

0.0

... 45^[8] ...

2011

0.0

. 2011, 41(2):419-423

Probability distribution of fatigue test data and fatigue life of aircraft structure

结构疲劳试验寿命数据分布类型对其使用寿命的影响

Liu Ke-ge , Yan Chu-liang.

刘克格, 闫楚良

摘　要：对于飞机结构疲劳试验寿命数据,工程上一般采用概率纸结合相关系数法来确定其分布类型,但用此方法,有时同一试验数据既能通过对数正态分布又能通过双参数Weibull分布的检验,而不同分布时疲劳寿命分散系数不同,用不同分散系数计算出的结构使用寿命有时会有较大的差别,给结构的定寿延寿工作带来困难。本文对此问题进行了研究,结论为：当可靠度要求低于99%时,可以采用概率纸结合相关系数法来确定其分布类型;当可靠度高于99%时,应该采用效率较高的分布检验法。

... 对于等效应力幅 Seq的参数特征,应根据现场数据,由内力直方图回归获取,常用来描述 Seq分布特征的有正态分布、对数正态分布、Weibull分布以及瑞利分布等,且分布形式会使疲劳寿命预测结果产生较大差异^[9,10,11] ...

2013

0.0

. 2013, 43(3):665-670 DOI:doi:10.7964/jdxbgxb201303018

Fatigue stiffness degradation of prestressed concrete beam under multilevel amplitude cycle loading

多级变幅度劳荷载下预应力混凝土梁刚度退化

Xiao Yun , Lei Jun-qing , Zhang Kun

肖斌贝, 雷俊卿, 张坤

摘　要：基于材料疲劳损伤和损伤累积的非线性模型,将混凝土损伤弹模和钢筋损伤剩余面积引入到截面刚度计算中,推导了预应力混凝土梁在多级变幅疲劳荷载下的刚度退化模型。结合遗传算法进行了参数拟合,提出了疲劳刚度损伤退化预测的神经网络方法,编制了相应的Matlab计算程序。通过预应力混凝土梁多级变幅疲劳试验对模型参数和结果进行了拟合、修正和验证。结果表明：多级变幅疲劳荷载下预应力混凝土梁刚度退化存在类似混凝土损伤发展的三阶段规律,混凝土材料应采用能体现损伤发展三阶段规律的损伤模型;刚度退化模型各参数物理意义明确,理论分析结果与试验结果偏差普遍在5%以下;基于遗传算法进行参数拟合方法和基于神经网络预测方法的结果具有较高精度,可以为预应力混凝土梁的疲劳耐久性评估提供一定的参考。

2010

0.0

... 首先采用传统JC法对工字梁E'类细节进行概率可靠度分析,依次假定S_eq服从正态分布、对数正态分布和Weibull分布^[11],各年份下的概率可靠度指标如图3(a)中曲线PRI(Normal)、PRI(Lognormal)和PRI(Weibull)所示 ...

... 5),与文献^[11]中的结果一致 ...

2004

0.0

... 结构裂纹尺寸参数 a0与结构几何尺寸、细节类型以及加工精度等因素有关,实测数据的离散性突出,常用分布形式有对数正态分布或Weibull分布,表1中列举了盖板裂纹的典型实测统计数据^[12] ...

2015

0.0

... 在实际工程中亦可根据结构的安全使用性能确定,英国海岸结构技术文件^[13]中建议将临界极限裂纹 af取为相应板件的厚度或者宽度的尺寸常数 ...

2007

0.0

. 2007, 29(2):251-255 DOI:doi:10.3321/j.issn:1001-9669.2007.02.016

Non-probabilistic reliability index and affine arithmetic

区间模型非概率可靠性指标的仿射算法

Jiang Tao , Chen Jian-jun , Zhang Chi-jiang.

江涛, 陈建军, 张弛江

针对标准区间运算易引发误差爆炸,导致计算结果丧失实用价值的缺陷,文中将不确定性变量的仿射型及仿射运算引入区间模型非概率可靠性指标的计算中.利用仿射型表示变量的不确定性,由仿射运算计算出结构的响应区间(功能函数的上下界),并由响应区间与其许用区间获得非概率可靠性指标.仿射运算的规则具有优化意义,不会引发误差爆炸.以仿射运算求取区间模型非概率可靠性指标,其计算精度远高于区间运算.

... 可以采用定义算法^[1]、一维优化算法、多维优化算法和仿射算法^[14]等 ...

... 0,分别采用式(14)和仿射法^[14]获得区间可靠度指标如图3(a)所示,可以看出两曲线基本吻合,最大误差为7 ...

2011

0.0

... 同时可以看出,S_eq在不同分布情况下,结构的可靠度指标存在差异,当S_eq为对数正态分布时,结构可靠度指标最为保守,与文献^[15]结论一致 ...

2012

0.0