精密螺杆转子齿廓成形磨削的误差分析

引用本文

沈志煌, 姚斌, 陆如升, 冯伟, 张祥雷, 王萌萌. 精密螺杆转子齿廓成形磨削的误差分析.吉林大学学报:工学版, 2016, 46(3): 831-838
SHEN Zhi-huang, YAO Bin, LU Ru-sheng, FENG Wei, ZHANG Xiang-lei, WANG Meng-meng. Form grinding error analysis of precision screw rotor profiles. Journal of Jilin University Engineering and Technology Edition, 2016, 46(3): 831-838 复制到剪切板

Permissions

精密螺杆转子齿廓成形磨削的误差分析

沈志煌¹, 姚斌^1,², 陆如升¹, 冯伟¹, 张祥雷¹, 王萌萌¹

1.厦门大学物理与机电工程学院,福建厦门 361005

2.陕西理工学院机械工程学院,陕西汉中 723001

通讯作者:姚斌(1963-),男,教授,博士生导师.研究方向:复杂曲面成形及其智能加工装备技术.E-mail:yaobin@xmu.edu.com

作者简介:沈志煌(1988-),男,博士研究生.研究方向:复杂曲面成形及其先进制造技术.E-mail:shenzhihuang2008@sina.com

基金:国家科技重大专项项目(2011ZX04003-021); 陕西省科技统筹创新工程计划(2014KTDZ01-04)

摘要

为了全面分析磨削工艺系统误差对转子齿廓制造精度的影响,提出了一种基于5个独立、1个合成的数学模型的误差分析方法。通过该模型计算磨削转子的实际齿廓,揭示中心距误差、偏心距误差、轴向位置误差、安装角误差以及仰角误差等五项误差因子对转子齿廓精度的影响规律。最后,基于误差分析结果提出了一种齿廓误差的补偿方法,补偿后的转子齿廓误差可控制在0.01 mm内。

关键词: 机械制造自动化; 螺杆转子; 磨削; 成形砂轮; 齿廓; 加工误差

中图分类号:TH455 文献标志码:A 文章编号:1671-5497(2016)03-0831-08

Form grinding error analysis of precision screw rotor profiles

SHEN Zhi-huang¹, YAO Bin^1,², LU Ru-sheng¹, FENG Wei¹, ZHANG Xiang-lei¹, WANG Meng-meng¹

1.School of Physics and Mechanical & Electrical Engineering, Xiamen University, Xiamen 361005, China

2.School of Mechanical Engineering, Shanxi University of Technology, Hanzhong 723001, China

Abstract

In order to comprehensively analyze the influence of the grinding process system error on the manufacturing precision of rotor profile, a new method of error analysis of rotor profile is presented. This method consists of five independent error models and one synthetic error model. The machined rotor profiles are calculated by the error models, and the effects of center distance error, offset error, axial position error, setting angle error and pitch error on rotor profile are then revealed. Finally, the error of rotor profile is compensated based on the above error analysis and the tolerance is controlled within 0.01 mm. The results show that the proposed method can be well used to improve the manufacturing precision of rotor profile.

Keyword: automation of mechanical manufacturing; screw rotor; grinding; forming tool; profile; machining error

Show Figures

0 引言

双螺杆压缩机具有工作可靠、使用寿命长、结构紧凑和能效高等优点, 被广泛应用于压缩、制冷、动力等工业领域中。双螺杆压缩机的关键核心部件是一对相互啮合的螺杆转子, 螺杆转子的加工质量是保证双螺杆压缩机性能及能效的关键, 提高转子的齿廓加工精度有利于降低其能耗, 对节能减排具有非常重要的意义。采用成形磨削工艺加工精密螺杆转子齿廓是目前最有效的方法, 其理论在吴序堂^[1]、Litvin^[2]所著书中均有详细叙述。但是在转子的磨削加工过程中, 由磨削热力耦合、初始安装的定位误差导致的工艺系统误差制约着转子齿廓的加工精度。为此, 许多学者做了相关研究, Guo等^[3]基于数学模型计算了中心距误差、安装角误差、转子分度误差、导程误差以及刀具跳动等多项误差引起的转子齿廓的变化。Stosic^{[4, 5, 6]}在两轴线交错的螺杆转子加工用成形刀具的计算方法基础上, 引入了成形刀具安装角误差、中心距误差以及轴向位置误差3个误差因子, 分析了这3个误差因子对转子齿廓的影响规律, 最后利用所得的规律对刀具变形和磨损引起的齿廓误差进行补偿。陶丽佳等^[7]在Stosic引入的3个误差因子的基础上, 以转子整体廓形误差为评价指标, 详细分析了误差因子影响下的螺杆转子廓形变化规律及程度。Wu等^[8]定义了两个旋转误差和一个中心距误差, 分析了误差因子影响下的转子齿廓变化。以上研究中引入的误差因子仅反映了初始安装时砂轮与转子空间在3个自由度上的误差, 由于3个安装误差因子对转子齿廓的影响规律未能全面表述转子与砂轮之间的6个自由度偏差对转子齿廓造成的影响, 故仅能指导低精度转子的齿廓误差补偿, 并不适用于精密转子的加工。

为此, 本文基于转子与砂轮之间的空间位姿, 引入了中心距误差、偏心距误差、轴向位置误差、安装角误差以及仰角误差5个安装误差因子, 并建立了基于这5个安装误差因子的误差模型, 通过误差模型分析了各误差因子对转子齿廓精度的影响规律。最后, 在理论分析指导下调整实际加工工艺参数, 实现了对磨削精密螺杆转子齿廓误差的补偿, 本文方法为转子齿廓误差的补偿提供了一种全新的思路。

1 螺杆转子与砂轮位置的相互换算

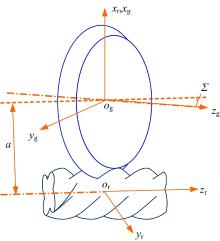
在螺杆转子数控磨床上加工转子齿面时, 砂轮回转面同转子齿面之间具有一条空间接触线, 当接触线绕转子轴线 $\begin{matrix} z_{r} \end{matrix}$ 作与转子齿面相同的螺旋运动时, 得到的是转子螺旋齿面。当接触线绕成形砂轮轴线 $\begin{matrix} z_{g} \end{matrix}$ 作回转运动时, 得到的是成形砂轮回转面。如图1所示, $\begin{matrix} S_{r} : o_{r} x_{r} y_{r} z_{r} \end{matrix}$ 为固定在转子上的坐标系, $\begin{matrix} z_{r} \end{matrix}$ 轴与转子轴线重合; $\begin{matrix} S_{g} : o_{g} x_{g} y_{g} z_{g} \end{matrix}$ 为固定在成形砂轮上的坐标系, $\begin{matrix} z_{g} \end{matrix}$ 轴与成形砂轮轴线重合, 转子轴线与成形砂轮轴线之间最短距离为 $\begin{matrix} a, \end{matrix}$ 夹角为 $\begin{matrix} Σ 。 \end{matrix}$ 则根据空间几何关系可知, 从 $\begin{matrix} S_{r} \end{matrix}$ 到 $\begin{matrix} S_{g} \end{matrix}$ 的变换矩阵为 $\begin{matrix} M_{1}, \end{matrix}$ 从 $\begin{matrix} S_{g} \end{matrix}$ 到 $\begin{matrix} S_{r} \end{matrix}$ 的变换矩阵为 $\begin{matrix} M_{2} : \end{matrix}$

$M_{1} = [\begin{matrix} 1 & 0 & 0 & - a \\ 0 & cosΣ & - sinΣ & 0 \\ 0 & sinΣ & cosΣ & 0 \\ 0 & 0 & 0 & 0 \end{matrix}]$ (1)

$M_{2} = [\begin{matrix} 1 & 0 & 0 & a \\ 0 & cosΣ & sinΣ & 0 \\ 0 & - sinΣ & cosΣ & 0 \\ 0 & 0 & 0 & 0 \end{matrix}]$ (2)

	Figure Option View Download New Window
	图1 转子与成形砂轮之间的坐标系统Fig.1 Coordinate systems between rotor and forming tool

1.1 根据转子型线计算成形砂轮廓形

设转子型线的参数方程为 $\begin{matrix} r_{0} (t) = [x_{0} (t), y_{0} (t)], \end{matrix}$ 其中 $\begin{matrix} t \end{matrix}$ 为弧长。转子螺旋面方程由转子型线绕转子轴线 $\begin{matrix} z_{r} \end{matrix}$ 作螺旋运动:

$\begin{matrix} \begin{matrix} r_{r} (t, θ) = [x_{r}, y_{r}, z_{r}] = [x_{0} (t) cosθ - \\ k y_{0} (t) sinθ, k x_{0} (t) sinθ + y_{0} (t) cosθ, pθ] \end{matrix} \end{matrix}$ (3)

式中: $\begin{matrix} k = \pm 1 \end{matrix}$ 代表旋向; $\begin{matrix} θ \end{matrix}$ 为转子旋转角; $\begin{matrix} p \end{matrix}$ 为螺旋系数。

在成形砂轮回转面与螺杆转子齿面的接触点处有公切线和公法线。接触线的接触条件是在接触点处转子与成形砂轮的相对运动速度 $\begin{matrix} v \end{matrix}$ 与公法线 $\begin{matrix} n_{r} \end{matrix}$ 垂直, 即 $\begin{matrix} v \cdot n_{r} = 0, \end{matrix}$ 则有接触线条件^[9]:

$\begin{matrix} f_{1} (t, θ) = 0 \end{matrix}$ (4)

将接触线条件式(4)代入方程(3)中, 得到转子与成形砂轮的接触线方程 $\begin{matrix} r_{cr} = [x_{cr}, y_{cr}, z_{cr}], \end{matrix}$ 接触线在坐标系 $\begin{matrix} S_{g} \end{matrix}$ 中的表示为:

$\begin{matrix} r_{cg}^{T} = [x_{cg}, y_{cg}, z_{cg}]^{T} = M_{1} r_{cr}^{T} \end{matrix}$ (5)

刀具的回转面是通过接触线绕着刀具轴线旋转形成的, 因此成形砂轮廓形方程为:

$\begin{matrix} r_{g 0} = [R_{g}, Z_{g}] = [\sqrt[]{x_{cg}^{2} + y_{cg}^{2}}, z_{cg}] \end{matrix}$ (6)

1.2 根据成形砂轮廓形计算转子型线

已知成形砂轮的廓形方程为 $\begin{matrix} r_{g 0} = [R_{g}, Z_{g}], \end{matrix}$ 则成形砂轮回转面方程为:

$\begin{matrix} r_{g} = [R_{g} cosφ, R_{g} sinφ, Z_{g}] \end{matrix}$ (7)

式中: $\begin{matrix} φ \end{matrix}$ 为成形砂轮回转角。

将成形砂轮回转面方程从坐标系 $\begin{matrix} S_{g} \end{matrix}$ 变换到坐标系 $\begin{matrix} S_{r} \end{matrix}$ 中:

$\begin{matrix} r_{gr}^{T} = [x_{gr}, y_{gr}, z_{gr}]^{T} = M_{2} r_{g}^{T} \end{matrix}$ (8)

同样地, 成形砂轮计算转子型线有接触条件式:

$\begin{matrix} f_{2} (z_{gr}, φ) = 0 \end{matrix}$ (9)

将接触线条件式(9)代入方程(8)中, 得到接触线方程 $\begin{matrix} r_{cr 1} = [x_{cr 1}, y_{cr 1}, z_{cr 1}], \end{matrix}$ 接触线绕转子轴线 $\begin{matrix} z_{r} \end{matrix}$ 作螺旋运动, 得转子螺旋面方程:

$\begin{matrix} \begin{matrix} r_{r 1} = [x_{r 1}, y_{r 1}, z_{r 1}] = [x_{cr 1} cosθ + k y_{cr 1} sinθ, \\ - k x_{cr 1} sinθ + y_{cr 1} cosθ, z_{c r 1} - pθ] \end{matrix} \end{matrix}$ (10)

当 $\begin{matrix} z_{r 1} = 0 \end{matrix}$ 时, 转子螺旋面的端截形即为转子型线, 所以可令 $\begin{matrix} z_{r 1} = 0 \end{matrix}$ 求得 $\begin{matrix} θ = z_{cr 1} / p, \end{matrix}$ 将 $\begin{matrix} θ \end{matrix}$ 值带入方程(10)中求得转子型线方程:

$\begin{matrix} r_{1} (t) = [x_{1} (t), y_{1} (t)] \end{matrix}$ (11)

2 砂轮安装误差模型建立

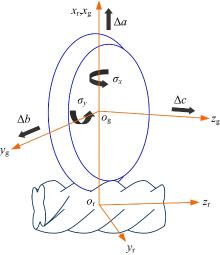
从式(7)~(11)中可以看出, 砂轮沿 $\begin{matrix} x_{g} \end{matrix}$ 轴存在中心距误差 $\begin{matrix} Δa 、 \end{matrix}$ 沿 $\begin{matrix} y_{g} \end{matrix}$ 轴存在偏心距误差 $\begin{matrix} Δb 、 \end{matrix}$ 沿 $\begin{matrix} z_{g} \end{matrix}$ 轴存在轴向位置误差 $\begin{matrix} Δc \end{matrix}$ 以及绕 $\begin{matrix} x_{g} \end{matrix}$ 轴旋转存在安装角误差 $\begin{matrix} σ_{x} 、 \end{matrix}$ 绕 $\begin{matrix} y_{g} \end{matrix}$ 轴旋转存在仰角误差 $\begin{matrix} σ_{y} 。 \end{matrix}$

根据上述理论分析以及图2可以计算得到基于成形砂轮安装误差因子的5个独立、1个合成的误差模型:

	Figure Option View Download New Window
	图2 转子与成形砂轮之间的误差坐标系统Fig.2 Coordinate systems of setting errors between rotor and forming tool

(1)中心距误差 $\begin{matrix} Δa : \end{matrix}$

$\begin{matrix} M_{a} = [\begin{matrix} 1 & 0 & 0 & Δa + a \\ 0 & cosΣ & sinΣ & 0 \\ 0 & - sinΣ & cosΣ & 0 \\ 0 & 0 & 0 & 0 \end{matrix}] \end{matrix}$ (12)

(2)偏心距误差 $\begin{matrix} Δb : \end{matrix}$

$\begin{matrix} M_{b} = [\begin{matrix} 1 & 0 & 0 & a \\ 0 & cosΣ & sinΣ & Δb cosΣ \\ 0 & - sinΣ & cosΣ & - ΔbsinΣ \\ 0 & 0 & 0 & 0 \end{matrix}] \end{matrix}$ (13)

(3)轴向位置误差 $\begin{matrix} Δc : \end{matrix}$

$\begin{matrix} M_{c} = [\begin{matrix} 1 & 0 & 0 & a \\ 0 & cosΣ & sinΣ & ΔcsinΣ \\ 0 & - sinΣ & cosΣ & ΔccosΣ \\ 0 & 0 & 0 & 0 \end{matrix}] \end{matrix}$ (14)

(4)安装角误差 $\begin{matrix} σ_{x} : \end{matrix}$

$\begin{matrix} M_{σx} = [\begin{matrix} 1 & 0 & 0 & a \\ 0 & λ_{1} & λ_{3} & 0 & λ_{2} \\ 0 & λ_{2} & λ_{4} & 0 \\ 0 & 0 & 0 & 1 \end{matrix}] \end{matrix}$ (15)

式中: $\begin{matrix} \begin{matrix} λ_{1} = \cos σ_{x} cosΣ + \sin σ_{x} sinΣ; \\ λ_{2} = - \cos σ_{x} sinΣ + \sin σ_{x} cosΣ; \\ λ_{3} = - \sin σ_{x} cosΣ + \cos σ_{x} sinΣ; \\ λ_{4} = \sin σ_{x} sinΣ + \cos σ_{x} cosΣ 。 \end{matrix} \end{matrix}$

(5)仰角误差 $\begin{matrix} σ_{y} : \end{matrix}$

$\begin{matrix} M_{σy} = [\begin{matrix} \cos σ_{y} & 0 & - \sin σ_{y} & a \\ \sin σ_{y} sinΣ & cosΣ & \cos σ_{y} sinΣ & 0 \\ \sin σ_{y} cosΣ & - sinΣ & \cos σ_{y} cosΣ & 0 \\ 0 & 0 & 0 & 1 \end{matrix}] \end{matrix}$ (16)

(6)合成误差模型为

$\begin{matrix} \begin{matrix} M_{s} = \\ [\begin{matrix} \cos σ_{y} & - \sin σ_{x} \sin σ_{y} & - \cos σ_{x} \sin σ_{y} & Δa + a \\ \sin σ_{y} sinΣ & ε_{1} & ε_{3} & ΔbcosΣ + ΔcsinΣ \\ \sin σ_{y} cosΣ & ε_{2} & ε_{4} & - ΔbsinΣ + ΔccosΣ \\ 0 & 0 & 0 & 1 \end{matrix}] \end{matrix} \end{matrix}$ (17)

式中: $\begin{matrix} \begin{matrix} ε_{1} = \cos σ_{x} cosΣ + \sin σ_{x} \cos σ_{y} sinΣ; \\ ε_{2} = - \cos σ_{x} sinΣ + \sin σ_{x} \cos σ_{y} cosΣ; \\ ε_{3} = - \sin σ_{x} cosΣ + \cos σ_{x} \cos σ_{y} sinΣ; \\ ε_{4} = \sin σ_{x} sinΣ + \cos σ_{x} \cos σ_{y} cosΣ 。 \end{matrix} \end{matrix}$

式(12)~(17)更加精确地揭示了磨削过程中转子与成形砂轮的相互位置关系, 转子实际齿廓的求解可分别通过将式(12)~(17)的矩阵替换方程(8)中的矩阵 $\begin{matrix} M_{2} \end{matrix}$ 求得。

3 砂轮安装误差对转子齿廓的影响

以某公司的转子型线为例, 研究了5个误差因子影响下阴、阳转子的齿廓变化规律。转子的相关参数如表1所示。计算过程中误差因子分别各取3组数值代入误差模型中计算相应的转子齿廓, 各个误差因子取图2中箭头方向时为正值。误差分析结果如图3~图7所示。

表1 螺杆转子结构参数 Table 1 Parameters of screw rotors

3.1 中心距误差Δ a对转子齿廓的影响

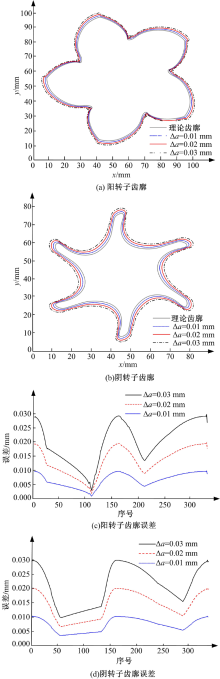
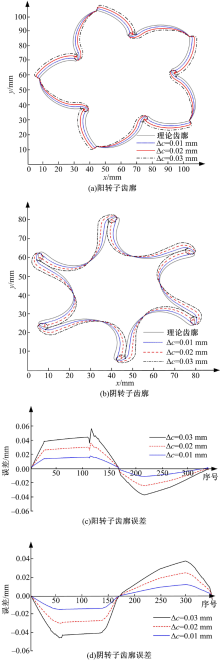
图3为中心距误差Δ a对转子齿廓的影响, 在计算过程中砂轮的实际中心距为a+Δ a, 转子的实际齿廓可通过将式(8)中矩阵 $\begin{matrix} M_{2} \end{matrix}$ 替换为矩阵 $\begin{matrix} M_{a} \end{matrix}$ 计算得到。由图3可知, 随着Δ a的增大, 成形砂轮与转子中心距的增大, 阴、阳转子齿廓沿转子中心向外平移, 转子实际齿廓大于理论齿廓; 反之, 当Δ a减小时, 转子齿廓沿转子中心向内平移, 转子加工齿廓小于理论齿廓。当Δ a=0.01 mm时, 阴、阳转子齿廓误差最大值分别为0.0101 mm、0.0102 mm。中心距过大使转子实际尺寸大于理论尺寸, 导致了阴、阳转子啮合间隙过小, 进而增大压缩机功率、噪声, 降低压缩机效率; 中心距过小则增大阴阳转子的啮合间隙, 使压缩过程中气体通过接触线的泄露增大, 降低了压缩机的效率。

	Figure Option View Download New Window
	图3 中心距误差Δ a对转子齿廓的影响Fig.3 Influence of Δ a on rotor profile

	Figure Option View Download New Window
	图4 偏心距误差Δ b对转子齿廓的影响Fig.4 Influence of Δ b on rotor profile

	Figure Option View Download New Window
	图5 轴向位置误差Δ c对转子齿廓的影响Fig.5 Influence of Δ c on rotor profile

	Figure Option View Download New Window
	图6 安装角误差σ _x对转子齿廓的影响Fig.6 Influence of σ _x on rotor profile

	Figure Option View Download New Window
	图7 仰角误差σ _y对转子齿廓的影响Fig.7 Influence of σ _y on rotor profile

3.2 偏心距误差Δ b对转子齿廓的影响

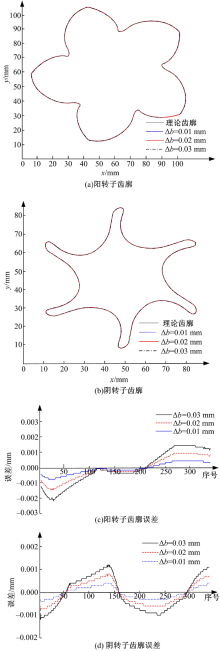
图4为偏心距误差Δ b对转子齿廓的影响, 在计算过程中成形砂轮的实际偏心距为Δ b, 转子的实际齿廓可通过将式(8)中矩阵 $\begin{matrix} M_{2} \end{matrix}$ 替换为矩阵 $\begin{matrix} M_{b} \end{matrix}$ 计算得到。由图4可知, 随着Δ b的变化, 阴、阳转子的齿廓发生变形, 由齿廓误差图可知, 当Δ b=0.01 mm时, 阴、阳转子齿廓误差最大值分别为0.0004 mm、0.0007 mm。其中阴、阳转子在齿顶处受Δ b影响较大, 而齿根处影响很小, 另外阴转子在齿形中间区域受Δ b影响也较大。

3.3 轴向位置误差Δ c对转子齿廓的影响

图5为轴向位置误差Δ c对转子齿廓的影响, 在计算过程中成形砂轮的实际轴向位置为Δ c, 转子的实际齿廓可通过将式(8)中矩阵 $\begin{matrix} M_{2} \end{matrix}$ 替换为矩阵 $\begin{matrix} M_{c} \end{matrix}$ 计算得到。由图5中可知, 当Δ c取正值时, 图5中阴、阳转子分别绕着转子轴心逆、顺时针旋转。当Δ c=0.01 mm时, 阴、阳转子齿廓误差最大值分别为0.014 mm、0.0149 mm。

3.4 安装角误差σ _x对转子齿廓的影响

图6为安装角误差 $\begin{matrix} σ_{x} \end{matrix}$ 对转子齿廓的影响, 在计算过程中成形砂轮的实际安装角为 $\begin{matrix} Σ + σ_{x}, \end{matrix}$ 转子的实际齿廓可通过将式(8)中矩阵 $\begin{matrix} M_{2} \end{matrix}$ 替换为矩阵 $\begin{matrix} M_{σx} \end{matrix}$ 计算得到。从图6可知, 阳转子的齿厚随安装角的增大而逐渐变小, 而阴转子的齿厚随安装角的增大而逐渐增大, 且阴、阳转子齿廓高压边受 $\begin{matrix} σ_{x} \end{matrix}$ 的影响大于低压边。当 $\begin{matrix} σ_{x} = 0.01 ° \end{matrix}$ 时, 阴转子齿廓误差最大值为0.0045 mm, 阳转子齿廓误差最小值为-0.0056 mm。

3.5 仰角误差σ _y对转子齿廓的影响

图7为仰角误差 $\begin{matrix} σ_{y} \end{matrix}$ 对转子齿廓的影响, 在计算过程中成形砂轮的实际仰角为 $\begin{matrix} σ_{y}, \end{matrix}$ 转子的实际齿廓可通过将式(8)中矩阵 $\begin{matrix} M_{2} \end{matrix}$ 替换为矩阵 $\begin{matrix} M_{σy} \end{matrix}$ 计算得到。由图7中可知, 当 $\begin{matrix} σ_{y} \end{matrix}$ 取正值时, 阴、阳转子分别绕着转子轴心顺、逆时针旋转, 在旋转的过程中转子的齿廓发生变形。当σ _y=0.01° 时, 阴、阳转子齿廓误差最大值分别为0.007、0.0061 mm。

4 实例验证

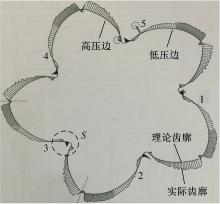
图8为某公司的阳转子实际测量报告, 取3号齿形作为试验对象, 测量所得的误差数据如图9所示, 由于测量过程中受测头半径的影响, 阳转子齿根区域有部分数据点无法进行正常的测绘, 会出现图8中虚线区域 $\begin{matrix} S \end{matrix}$ 所示的丢点和跳动现象。通过对实际齿廓与理论齿廓的对比分析可知:

	Figure Option View Download New Window
	图8 补偿前的转子齿廓Fig.8 Rotor profile before compensation

	Figure Option View Download New Window
	图9 转子实际齿廓与补偿齿廓的误差数据对比图Fig.9 Comparison of errors between actual and compensated rotor profile

(1)阳转子在低压边最靠近齿根部位有过磨削区域, 过磨了约0.012 mm。

(2)转子齿廓误差沿齿根到齿顶逐渐增大, 阳转子高压边、低压边最大误差分别为0.0537、0.0502 mm。

因此, 通过以上所得的分析数据计算得到当Δ a=-0.012 mm、Δ b=0、Δ c=0.002 mm、σ _x=-0.12° 、σ _y=-0.001° 时, 将所得的5个误差因子值带入式(17)中, 得到如图10所示的转子补偿齿廓(误差放大100倍)。

	Figure Option View Download New Window
	图10 转子补偿齿廓Fig.10 Compensation of rotor profile

通过计算转子补偿齿廓与理论齿廓间的法向误差值, 得到补偿齿廓误差与实际齿廓误差的对比图, 如图9所示。经理论验证后的误差因子值可通过机床的数控系统实现误差补偿。图11为误差补偿后的转子齿廓, 与图8对比可见, 转子齿廓误差平均减小0.04 mm, 转子齿廓加工精度被控制在(-0.01, 0.01)内。由此可见本文方法能够满足转子精密加工的要求。

	Figure Option View Download New Window
	图11 补偿后的转子齿廓Fig.11 Rotor profile after compensation

5 结论

(1)为了研究实际磨削过程中成形砂轮安装误差对螺杆转子齿廓加工精度的影响, 首先研究了螺杆转子与成形砂轮位置之间的相互换算关系, 其次引入了中心距误差、偏心距误差、轴向位置误差、安装角误差以及仰角误差5个安装误差因子, 在此基础上建立了5个独立、1个合成的误差模型, 最后通过误差模型计算成形磨削转子的实际齿廓, 得到各误差因子对转子齿廓精度的影响规律。

(2)5个误差因子的分析结果为:随着中心距误差的变化, 转子齿廓沿转子中心线内外平移, 且中心距误差对转子的齿顶、齿根精度影响较大; 偏心距误差使转子齿廓产生变形, 齿顶处变形较大, 齿根处变形较小, 另外, 阴转子在齿形中间区域受偏心距误差影响也较大; 轴向位置误差引起转子齿廓绕转子轴心的旋转, 阴、阳转子由于旋向不同使得齿廓绕轴心的旋转方向不同; 安装角误差引起转子齿厚的变化, 阴、阳转子由于旋向不同使得齿厚变化也不一致, 二者受影响效果相反, 此外, 阴、阳转子齿廓高压边受安装角误差的影响大于低压边; 仰角误差对转子齿廓的影响与轴向位置误差相似, 同样引起转子齿廓的旋转, 但不同于轴向位置误差的是:转子齿廓旋转的同时也发生了变形, 特别是在转子齿顶处尤为明显。

(3)利用分析结果调整实际砂轮安装参数, 实现了对磨削螺杆转子齿廓误差的补偿, 补偿后的转子齿廓误差可被控制在0.01 mm内, 得到比较理想的补偿结果, 本文方法为提高精密螺杆转子齿廓磨削精度提供了一种全面又可靠的思路。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	吴序堂. 齿轮啮合原理[M]. 2版. 西安: 西安交通大学出版社, 2009. [本文引用:1]
[2]	Litvin F L, Fuentes A. Gear Geometry and Applied Theory[M]. Cambridge: Cambridge University Press, 2004. [本文引用:1]
[3]	Guo C, Tang Y. Influence of process parameters on screw rotor profiles[J]. Machining Science and Technology, 2003, 7(1): 105-118. [本文引用:1]
[4]	Stosic N, Smith I K, Kovacevic A, et al. Geometry of screw compressor rotors and their tools[J]. Journal of Zhejiang University Science A (Applied Physics & Engineering), 2011, 12(4): 310-326. [本文引用:1]
[5]	Stosic N. Evaluating errors in screw rotor machining by tool to rotor transformation[J]. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 2006, 220(10): 1589-1596. [本文引用:]
[6]	Stosic N. A geometric approach to calculating tool wear in screw rotor machining[J]. International Journal of Machine Tools and Manufacture, 2006, 46(15): 1961-1965. [本文引用:1]
[7]	陶丽佳, 王禹林, 周斌, 等. 人工扰动下螺杆转子成形磨削的廓形误差分析[J]. 南京理工大学学报: 自然科学版, 2013, 37(5): 664-669. Tao Li-jia, Wang Yu-lin, Zhou Bin, et al. Profile error analysis of form grinding for screw rotor under artificial perturbatance[J]. Journal of Nanjing University of Science and Technology, 2013, 37(5): 664-669. [本文引用:1]
[8]	Wu Y R. Novel design methods of rotor and cutter profiles for the twin-screw compressor[D]. Chia-Yi: Department of Mechanical Engineering, National Chung-Cheng University, 2007. [本文引用:1]
[9]	吴宝海, 张娟, 杨建华, 等. 螺杆压缩机转子成形砂轮刃形计算[J]. 机械工程学报, 2012, 48(19): 192-198. Wu Bao-hai, Zhang Juan, Yang Jian-hua, et al. Calculation method for edge shape of forming wheel for screw rotors machining[J]. Journal of Mechanical Engineering, 2012, 48(19): 192-198. [本文引用:1]

2009

0.0

... 采用成形磨削工艺加工精密螺杆转子齿廓是目前最有效的方法,其理论在吴序堂^[1]、Litvin^[2]所著书中均有详细叙述 ...

2004

0.0

... 采用成形磨削工艺加工精密螺杆转子齿廓是目前最有效的方法,其理论在吴序堂^[1]、Litvin^[2]所著书中均有详细叙述 ...

2003

0.0

... 为此,许多学者做了相关研究,Guo等^[3]基于数学模型计算了中心距误差、安装角误差、转子分度误差、导程误差以及刀具跳动等多项误差引起的转子齿廓的变化 ...

2011

0.0

... Stosic^[4,5,6]在两轴线交错的螺杆转子加工用成形刀具的计算方法基础上,引入了成形刀具安装角误差、中心距误差以及轴向位置误差3个误差因子,分析了这3个误差因子对转子齿廓的影响规律,最后利用所得的规律对刀具变形和磨损引起的齿廓误差进行补偿 ...

2006

0.0

2013

0.0

. 2013, 37(5):664-669 DOI:doi:10.3969/j.issn.1005-9830.2013.05.003

Profile error analysis of form grinding for screw rotor under artificial perturbatance

人工扰动下螺杆转子成形磨削的廓形误差分析

Tao Li-jia , Wang Yu-lin , Zhou Bin

陶丽佳, 王禹林, 周斌

螺杆转子的形状精度直接影响螺杆压缩机的性能.为分析成形磨削加工螺杆转子的廓形误差,该文基于砂轮-转子间的坐标变换及啮合原理,以转子整体廓形误差为评价指标,提出了一种螺杆转子廓形误差分析方法.通过调整砂轮的安装参数,分析了人工扰动下成形磨削螺杆转子的实际廓形,得到砂轮各安装误差对螺杆转子廓形精度的影响规律及程度.结果表明,砂轮安装角误差和砂轮与转子中心距的误差导致转子廓形缩放,砂轮轴向位置误差导致转子廓形自转,且砂轮安装参数对阳转子廓形的影响大于对阴转子廓形的影响.

... 陶丽佳等^[7]在Stosic引入的3个误差因子的基础上,以转子整体廓形误差为评价指标,详细分析了误差因子影响下的螺杆转子廓形变化规律及程度 ...

2007

0.0

... Wu等^[8]定义了两个旋转误差和一个中心距误差,分析了误差因子影响下的转子齿廓变化 ...

2012

0.0

. 2012, 48(19):192-198 DOI:doi:10.3901/JME.2012.19.192

Calculation method for edge shape of forming wheel for screw rotors machining

螺杆压缩机转子成形砂轮刃形计算

Wu Bao-hai , Zhang Juan , Yang Jian-hua

吴宝海, 张娟, 杨建华

针对给出任意转子型线时转子齿面加工的成形砂轮刃形设计,利用螺杆转子加工过程中转子和砂轮的相对位置关系,通过对转子型线坐标系的旋转变换,建立空间转子坐标系和成形砂轮坐标系之间的几何映射关系;基于啮合原理,建立转子齿面与成形砂轮的接触线方程,并给出解析和离散两种转子型线表达方式的刃形求解方法。在此基础上,根据转子砂轮之间的设计间隙,通过对接触线沿转子齿面法向进行偏置,获得了修整后的砂轮等距齿面刃形,避免了传统修整方法导致的法向齿间间隙不均等问题。加工结果表明, 该方法能够满足螺杆转子的加工精度要求,是一种有效的螺杆转子齿面成形砂轮的刃形设计方法,并可推广应用于其他螺旋面成形砂轮或盘形铣刀的刃形设计。

... 接触线的接触条件是在接触点处转子与成形砂轮的相对运动速度 v与公法线 nr垂直,即 v·nr=0,则有接触线条件^[9]: ...