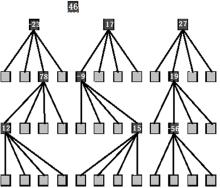
SPIHT算法采用空间方向树结构, 树中的每一个节点与一个小波系数对应。树中最低频子带的系数和最高频子带的系数没有孩子节点(树中用叶子节点表示), 其余的节点(i, j)均有4个孩子节点:(2i, 2j), (2i, 2j+1), (2i+1, 2j)和(2i+1, 2j+1)。在算法编码过程中使用了三个链表记录相关信息:不重要集合链表LIS、不重要像素链表LIP及重要像素链表LSP。具体有4个步骤:

Step 1 初始化。对阈值T=2ⁿ, LSP, LIP, LIS表初始化。

Step 2 排序扫描。扫描排序表, 对每一个表内系数(集合)进行重要性测试, 重要性测试函数如公式(1)所示, 该函数输出重要性标志, 如果系数对于当前阈值来说是重要的, 则输出其符号并移至LSP链表中。

Step 3 精细扫描。对于LSP中元素, 输出前一次排序扫描的第n重要位。

Step 4 下一次更新。n减至n-1, 返回Step 2继续进行排序和细化, 直到编码结束。

重要性测试函数定义为:设集合X是小波系数的坐标集合:X={(i, j)}。对于正整数n, 记:

Sn(X)=1, max(i, j)∈X|Ci, j|}≥2n0, 其他(1)

如果S_n(X)=1, 则称X关于阈值2ⁿ是重要的, 否则称X关于阈值2ⁿ是不重要的^[8]。

针对SPIHT算法的空间占有量大、需要进行大量重复计算等不足, 已有学者提出了不同的SPIHT算法优化方案。文献[9]提出了一种对SPIHT编码中D型集合分裂的改进算法; 文献[10-12]通过调整排序过程改变链表结构等改进了SPIHT算法; 文献[13]从小波系数的角度来构建平衡多小波从而提升SPIHT算法效率; 文献[14]用多小波基及预滤波方法改进了SPIHT算法, 文献[15]采用多阈值的四路并行处理结构, 提高了SPIHT编码效率。

表1为不同小波变换次数的情况下, 利用SPIHT算法对256* 256数据进行图片压缩编码的编码时间和解码时间(实验所记录的编码/解码时间只是运行SPIHT算法所用的压缩时间和解码时间, 并不包含对文件的读取和写入时间)。

从表1中可以看出:小波变换的次数越多, SPIHT的编码时间越长, 但是SPIHT的解码时间却基本保持稳定。所以要提高SPIHT算法的整体效率, 对其编码部分进行优化就会起到事半功倍的效果。

表1

Table 1

表1(Table 1)

表1 小波变换次数对SPIHT编码和解码时间的影响 Table 1 Result of WDT times for SPIHT encode/decode time 变换次数 编码时间/ms 解码时间/ms 1 9668 4562 2 14806 5173 3 14932 5502 4 16411 4168 5 15000 4556 6 16166 4598 7 21120 5068

表1 小波变换次数对SPIHT编码和解码时间的影响 Table 1 Result of WDT times for SPIHT encode/decode time

SPIHT算法编码时, 随着阈值的降低, 排序扫描的次数不断增加, 在扫描时要对当前的节点或者节点集合进行重要性测试以输出当前最重要的位流, 从而达到重要系数优先编码的目的。然而在多次扫描排序过程中需要进行大量的重要性测试, 这需要耗费大量的时间。为解决重要性测试函数的优化问题, 本文提出了一种基于大顶堆的优化方法。

算法的优化主要是对重要性测试函数的优化。在SPIHT算法中, 重要性测试函数主要分为两种:一种是对某个节点(i, j)系数进行重要性测试, 另一种是对某个节点所构成的系数集合进行重要性测试(如D(i, j)和L(i, j))。对某个节点系数的重要性测试只需要一次判断即可, 而对节点集合的重要性测试却需要对这个节点的空间方向树递归测试, 而本文提出的基于大顶堆的优化方法在对某个节点或其集合的重要性测试时, 只需要进行一次判断。

优化的思路是:首先对空间方向树构建成一个大顶堆树(Max heap tree, MHT), 然后在进行扫描排序的重要性测试时, 对于某个节点(i, j)的重要性测试只需比较C_{i, j}和2ⁿ; 而对于节点集合D(i, j)的重要性测试只需比较MHT_{i, j}和2ⁿ; 对于节点集合L(i, j)的重要性测试只需比较MHT_{k, l}(其中(k, l)∈ O(i, j))和2ⁿ, 这样重要性测试函数只需通过一次比较即可得到结果。

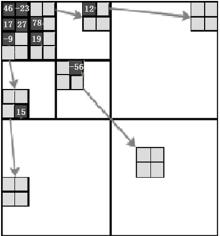
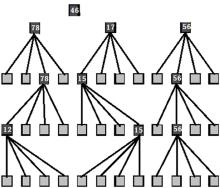
首先将二维小波系数矩阵(图1)构建成空间方向树(图2), 然后将该空间方向树构建成大顶堆。构建过程中有两个关键步骤:取系数的绝对值进行比较。若子节点的系数绝对值大于父节点时, 将子节点的系数绝对值直接赋值给父节点。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 2-D小波系数矩阵Fig.1 2-D wavelet coefficient matrix

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 空间方向树Fig.2 Space direction tree

大顶堆构建算法如算法1和算法2所示。由于SPIHT四叉树有4个最高级根节点, 其中节点(0, 0)没有子孙节点, 所以对SPIHT四叉树构建大顶堆树时, 只需对其余3个根节点((0, 1), (1, 0)和(1, 1))分别构建大顶堆树。算法1为构建整个SPIHT算法大顶堆树, 算法2为对某一个根节点(i, j)构建大顶堆树, 如此便构建了大顶堆空间方向树, 如图3所示。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 基于大顶堆的空间方向树Fig.3 Space direction tree based Max Heap

算法1

BuildMaxHeapTree(data):

Step 1 对最高级根节点(0, 1)建立大顶堆树:

GetMaxHeapTree((0, 1), data);

Step 2 对最高级根节点(1, 0)建立大顶堆树:

GetMaxHeapTree((1, 0), data);

Step 3 对最高级根节点(1, 1)建立大顶堆树:

GetMaxHeapTree((1, 1), data)。

算法2

GetMaxHeapTree((i, j), data):

Step 1 计算节点(i, j)的儿子节点O(i, j), 其中

O(i, j)={(2i, 2j), (2i, 2j+1), (2i+1, 2j), (2i+1, 2j+1)};

Step 2 对每一个儿子节点(k, l)∈ O(i, j)构建大顶堆树:GetMaxHeapTree((k, l), data);

Step 3 比较节点(i, j)的4个儿子节点的绝对值, 找出最大的绝对值:

Max(k, l)=max(|data(k, l)|), (k, l)∈ O(i, j);

Step 4 若Max(k, l)> data(i, j)则将Max(k, l)赋值给节点(i, j);

Step 5 返回节点(i, j)的值, 即data(i, j)。

针对SPIHT算法中集合X的三种情况:X为单个节点(i, j), 集合D(i, j), 集合L(i, j), 分别对其依据大顶堆进行优化。

X为一个节点(i, j)时:

Sn(i, j)=1, |Ci, j≥2n0, 其他(2)

X为集合D(i, j)时:

Sn(D(i, j))=1, |MHTi, j≥2n0, 其他(3)

X为集合L(i, j)时:

Sn(L(i, j))=1, |MHTi, j≥2n, (k, l)∈O(i, j)0, 其他(4)

式中:C_{i, j}为节点(i, j)的小波系数值, MHT_{i, j}为节点(i, j)在大顶堆树中值。

Step 1 初始化

阈值的初始化:设阈值T=2ⁿ, 其中:

n=⎣log₂(max_{(i, j)}{|C_{i, j}|})⎦;

有序表的初始化:

LSP=∅;

LIP={(i, j)|(i, j)∈ H}={(0, 0), (0, 1), (1, 0), (1, 1)};

LIS={D(i, j)|(i, j)∈ H且(i, j)具有非零子孙}={D(0, 1), D(1, 0), D(1, 1)}。

Step 2 排序扫描

对于每一个LIP中的(i, j):输出S_n(i, j), 如果S_n(i, j)=1, 即C_{i, j}是重要的, 则将(i, j)移动到LSP中并输出C_{i, j}的符号;

对于每一个LIS中的(i, j):

1)如果(i, j)是D(i, j), 即D型表项, 则输出为S_n(D(i, j)), 如果其值为1则:

a)对每一个(k, l)∈ O(i, j), 输出S_n(k, l), 如果S_n(k, l)=1, 则将(k, l)移动到LSP中, 并输出C_{i, j}符号, 如果S_n(k, l)=0, 则将(k, l)移到LIP中;

b)如果L(i, j)≠ ∅, 则将(i, j)作为L型表项移动到LIS的末尾, 否则将D(i, j)从LIS中删除;

2)如果(i, j)是L(i, j), 即L型表项, 则输出为S_n(L(i, j)), 如果其值为1, 则将每一个(k, l)∈ O(i, j)作为D表项添加到LIS中, 并从LIS中移除L(i, j)。

Step 3 精细扫描

对于LSP中的(i, j), 输出前一次排序扫描的LSP中 Ci, j的第n重要位的值。

Step 4下一次更新

将n减至n-1, 即设定新阈值T=2^n-1, 并返回

Step 5继续下一次排序扫描。

重要性测试函数未改进时, 当X为集合D(i, j)和L(i, j)时, 其时间复杂度为O(logn); 改进后只需与大顶堆中相对应的系数值进行一次性比较, 其时间复杂度为O(1)。

虽然改进后会增加大顶堆树的建立时间, 但这对于SPIHT算法的大量重要性测试而言, 将时间复杂度从O(logn)变成一个常量O(1), 其所节省的时间远远大于大顶堆树的建立时间; 况且当SPIHT压缩编码数据非常大时, 重要性测试次数远远大于大顶堆树的建立次数(只有一次)。

按照上述的SPIHT改进算法进行实验, 选取256× 256大小的数据来计算改进前后的SPIHT压缩编码的时间, 改变小波变换次数以进行多次实验来进行纵向比较, 最后得到如表2所示的实验结果。

表2

Table 2

表2(Table 2)

表2 算法改进前后SPIHT各项属性比较 Table 2 The comparison result of the algorithm improved before and after 变换次数 编码时间 改进前/ms 编码时间 改进后/ms 建大顶堆 时间/ms 编码时间 提升比/% 1 8141 6675 99 21.96 2 9271 5211 102 77.91 3 10829 4700 128 130.40 4 11883 4518 105 163.01 5 13380 4504 101 197.07 6 16023 4517 107 254.72 7 16683 4488 93 271.72

表2 算法改进前后SPIHT各项属性比较 Table 2 The comparison result of the algorithm improved before and after

从表2中可以看出改进后算法编码时间稳定在4500 ms左右, 其大顶堆的建立时间也比较稳定, 一直在100 ms左右, 相比SPIHT的编码时间(占编码时间的2.2%)可以忽略不计。从表中的编码提升比一栏, 可以观察出小波变换次数较大时, 编码时间减少的非常明显, 能比SPIHT算法节省1~3倍的编码时间, 由此表明该改进算法非常有效。