基于信道补偿的说话人识别算法

引用本文

申铉京, 翟玉杰, 卢禹彤, 王玉, 陈海鹏. 基于信道补偿的说话人识别算法.吉林大学学报:工学版, 2016, 46(3): 870-875
SHEN Xuan-jing, ZHAI Yu-jie, LU Yu-tong, WANG Yu, CHEN Hai-peng. Speaker recognition algorithm based on channel compensation. Journal of Jilin University Engineering and Technology Edition, 2016, 46(3): 870-875 复制到剪切板

Permissions

基于信道补偿的说话人识别算法

申铉京^1,², 翟玉杰^1,², 卢禹彤³, 王玉^1,^2,⁴, 陈海鹏^1,²

1.吉林大学计算机科学与技术学院,长春 130012

2.吉林大学符号计算与知识工程教育部重点实验室,长春 130012

3.香港理工大学工程学院,香港 999077

4.吉林大学应用技术学院, 长春 130012

通讯作者:陈海鹏(1978-),男,副教授,博士.研究方向:图像处理及模式识别,多媒体信息安全.E-mail:chenhp@jlu.edu.cn

作者简介:申铉京(1958-),男,教授,博士生导师.研究方向:图像处理及模式识别,多媒体信息安全,智能控制技术.E-mail:xjshen@jlu.edu.cn

基金:国家青年科学基金项目(61305046); 吉林省自然科学基金项目(20140101193JC); 吉林省青年科学基金项目(20130522117JH)

摘要

现有说话人识别算法普遍受信道因素的干扰,为了提高算法的准确率,在特征级利用特征弯折算法对语音特征参数进行处理,在模型级利用因子分析技术对说话人混合高斯模型(GMM)进行信道处理。对端点进行检测后,利用特征弯折算法对语音特征参数梅尔倒谱系数(MFCC)进行处理,去除线性信道和背景噪声的影响,并建立说话人GMM。然后利用因子分析技术拟合说话人特征空间与信道空间的差异,去除信道因子的影响。最后提取高斯超向量并通过支持向量机(SVM)得到识别结果。实验结果证明了信道补偿算法与GMM-SVM相结合能获得更好的识别率,并能保证算法的鲁棒性。

关键词: 计算机应用; 说话人识别; 支持向量机; 混合高斯模型; 特征弯折; 隐藏因子分析

中图分类号:TP391 文献标志码:A 文章编号:1671-5497(2016)03-0870-06

Speaker recognition algorithm based on channel compensation

SHEN Xuan-jing^1,², ZHAI Yu-jie^1,², LU Yu-tong³, WANG Yu^1,^2,⁴, CHEN Hai-peng^1,²

1.College of Computer Science and Technology, Jilin University, Changchun 130012, China

2.Key Laboratory of Symbolic Computation and Knowledge Engineering of Ministry of Education,Jilin University, Changchun 130012, China

3.Faculty of Engineering,The Hong Kong Polytechnic University,Hong Kong 999077,China

4.Applied Technology College of Jilin University, Changchun 130012, China

Abstract

Channel interference factor for the identification results is prevalent among the existing speaker recognition algorithm. In order to improve the accuracy of the system, in this paper, feature warping is used to compensate the channel factor of Mel-Frequency Cepstral Coefficient (MFCC) features. Then, factor analysis technique is applied to deal with the channel factors of the speaker's Gaussian Mixture Model (GMM). In the endpoint detection phase of speech of this recognition system, the GMM for speech modeling is built to accurately determine the beginning and end points of the speech segment, and then the features after feature warping are used to establish speaker GMM. Using factor analysis technique to fit the differences between the speaker characteristics space and the channel space, the algorithm removes channel factor from GMM, and then extracts GMM super-vectors as input of the Support Vector Machine (SVM) to obtain recognition results. Experimental results show that the combination of channel compensation technique and SVM can obtain better recognition rate, and ensure the robustness of the system.

Keyword: computer application; speaker recognition; support vector machine(SVM); Gaussian mixture model(GMM); feature warp; latent factor analysis(LFA)

Show Figures

0 引言

目前流行的说话人识别方法主要有概率统计方法、辨别分类器方法。概率统计方法包括隐马尔可夫(HMM)方法^[1], 高斯混合模型(GMM)^[2]; 辨别分类器方法包括人工神经网络(ANN)方法^[3], 支持向量机(SVM)方法^[4]等。2001年Kasuriya等^[5]开发出将HMM与ANN相结合的识别算法, 其识别效果及运算速度均得到提升, 但是仍依赖于文本提示, 信道因素仍然制约着算法性能的进一步提升。2006年Campbell等^[6]在高斯模型的基础上引入SVM分类器, 该方法不仅具有GMM的表征能力和SVM优秀的分类性能, 并且引入了新的核函数, 使得分类特征具备了GMM均值、方差、权值的属性。后来提出的多核SVM识别方法使得识别效果得到提高, 但是这些方法并没有考虑信道因素, 会导致语音失真, 使得训练环境与实际环境不匹配, 从而影响实际应用中的方法识别性能。2010年Munteanu等^[7]改进的HMM系统取得了不错的识别效果并且识别时间大大降低, 但却需要依赖于文本提示, 训练过程依然需要占用相当大的存储空间, 没有考虑信道因素的影响。Badran等^[8]提出的ANN方法, 具有很强的聚类能力和静态分类能力, 可将它用于特征提取和说话人的分类判决, 但由于训练时间较长及动态时间规整能力弱等缺点难以实际应用。

现有的说话人识别算法受到信道因素的影响使得其难以获得理想的识别效果^[9], 因此本文利用特征弯折算法和因子分析技术分别对识别过程中的特征级和模型级数据进行信道处理。首先对说话人识别算法进行了详细介绍, 主要包括语音信号端点检测、说话人GMM建立、GMM超向量及支持向量机等。然后利用说话人特征建立全局背景模型(UBM), 使用自适应算法得到说话人GMM。同时, 为了消除信道因素对于识别结果的影响, 引入信道补偿技术, 特征级的特征弯折算法与模型级的因子分析技术分别对说话人语音特征及GMM进行处理。最后提取GMM超向量作为SVM分类器输入得到识别结果。

1 本文算法框架

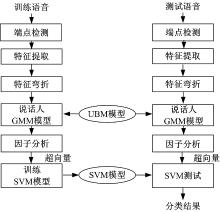
本文的说话人识别算法是在现有GMM-SVM算法基础上改进而来的, 训练过程中首先利用高斯模型法确定语音段中的有效语音, 提取梅尔倒谱系数(MFCC)特征, 在UBM上自适应得到说话人GMM, 然后提取GMM超向量作为SVM分类器的输入, 建立SVM模型。识别过程中, 通过测试语音得到高斯超向量后作为SVM分类器的输入得出识别结果。本文识别算法框架如图1所示。

	Figure Option View Download New Window
	图1 引入信道补偿算法后识别过程Fig.1 Identification process with channel compensation algorithms

1.1 说话人GMM的建立

GMM是一种多维概率密度函数的线性组合, 从说话人中提取的D维矢量特征x,可以使用包含M个分量的高斯混合分布的概率密度函数来描述^[2]:

$\begin{matrix} p (x | λ) = \overset{K}{\sum_{i}} ω_{i} p_{i} (x) \end{matrix}$ (1)

式中:p_i(x)为概率密度函数分量, i=1, 2, …, K; ω _i为各分量的权值, 且满足 $\begin{matrix} \overset{K}{\sum_{i = 1}} \end{matrix}$ ω _i=1。

使用三元组形式表示 $\begin{matrix} K \end{matrix}$ 阶高斯混合模型:

$\begin{matrix} λ = {ω_{i}, μ_{i}, Σ_{i}}, i = 1, 2, \dots, K \end{matrix}$ (2)

在UBM基础上, 通过贝叶斯自适应方法得到说话人模型。自适应过程在UBM模型和说话人模型中提供了严格的耦合, 其中自适应因子为模型更新前后权值、均值、方差联系的桥梁, 维持着模型间数据的平衡^[10]。

高斯超向量是将说话人GMM的均值组合成一个超大维度向量, 用以表示说话人。如果每个说话人GMM有M个高斯混合数, 特征选择为N维, 则此向量维度为M× N。

高斯超向量与SVM结合, 弥补了传统SVM分类器对于说话人特征表征能力弱的缺点, 并且发挥了SVM对于数据分类性能强的优势, 提高了说话人识别算法的准确率。

1.2 基于高斯模型的端点检测算法

算法利用Jeffery值作为高斯模型的距离参数, 用GMM来描述环境中的噪声, 以确定语音的起止点^[11]。定义高斯混合模型由3个独立的高斯分量组成, 根据语音特征与噪声模型匹配值判断是否属于噪声, 并实时更新模型参数。步骤如下:

(1)模型建立

假定语音段开始的时间T内为初始背景噪声, 对于时间段0~T内, 计算各帧均值及方差。使用EM算法进行高斯建模, 得到描述初始背景噪声的高斯混合模型 $\begin{matrix} λ (ω_{k}, μ_{k}, Σ_{k}) 。 \end{matrix}$

(2)匹配计算

使用Jeffery值作为距离参数进行比较, 利用当前帧的均值及方差计算Jeffrey值:

$\begin{matrix} J (f_{i}, t) = \frac{3}{2} {(\frac{Σ_{i}}{Σ_{t}} - \frac{Σ_{t}}{Σ_{i}})}^{2} + \frac{1}{2} (\frac{1}{Σ_{i}} + \frac{1}{Σ_{t}}) (μ_{t} - μ_{i}) \end{matrix}$ (3)

令 $\begin{matrix} J^{*} (f_{j}, g) \end{matrix}$ 为当前帧与背景噪声模型各分布的Jeffrey值中的最小值, 当其小于预设阈值时认为当前帧为噪声帧, 并对背景噪声模型进行更新; 否则此帧为语音帧, 继续对下一帧进行检测。

(3)模型更新

对于噪声帧, 取学习因子常量为 $\begin{matrix} α, \end{matrix}$ 其反应了背景噪声的变化率, 第 $\begin{matrix} t \end{matrix}$ 帧语音的更新公式为:

$ω_{k, t} = (1 - α) ω_{k, t - 1}$ (4)

$μ_{k, t} = (1 - α) μ_{k, t - 1}$ (5)

$Σ_{k, t} = (1 - α) Σ_{k, t - 1} + α (μ_{k, t} - μ_{k, t - 1})^{2}$ (6)

式中: $\begin{matrix} ω_{k, t}, μ_{k, t}, Σ_{k, t} \end{matrix}$ 分别为第t帧语音为噪声时更新后的权值、均值及方差。

1.3 支持向量机

GMM识别模型与SVM的结合保证了最小化期望风险, 避免了过训练问题, 还可以使用核函数解决非线性问题。在SVM方法中, 核函数至关重要, 它取代了内积, 减小了计算复杂性, 避免了维度灾难^[12]。

SVM模型可以理解为一种二分类模型, 通过学习使得特征空间间隔最大化, 从而转化为凸二次规划问题。SVM使用核函数对应于特征变换的内积, 与之对应的决策规则可以表示为:

$\begin{matrix} f (x) = \overset{l}{\sum_{i = 1}} α_{i} t_{i} K (x_{i}, x_{j}) + b \end{matrix}$ (7)

式中: $\begin{matrix} α_{i} \end{matrix}$ 为支持向量机的理想输出; $\begin{matrix} b \end{matrix}$ 为学习常量; $\begin{matrix} \sum_{i}^{=} \end{matrix}$ α _it_i=0, 并且 $\begin{matrix} α_{i} > 0; x_{i} 、 x_{j} \end{matrix}$ 分别为从训练数据集中提取的高斯超向量, 分类结果取决于 $\begin{matrix} f (x) \end{matrix}$ 与预设阈值差值的大小。

由于核函数满足Mercer条件, 核函数可以表示为:

$\begin{matrix} K (x_{i}, x_{j}) = b (x_{i})^{t} b (x_{j}) \end{matrix}$ (8)

式中: $\begin{matrix} b (x_{i}) \end{matrix}$ 为特征向量从输入空间到高维空间的隐式映射。

对于SVM分类器而言, 其依赖于边界最大化方法, 即可分数据集通过在高维空间中确定一个分类超平面使得满足边界最大化。训练集中处于分类边界上的特征点是SVM的支持向量, SVM模型的训练过程就是确定类间支持向量的过程。本文选取以下两类核函数。

线性核函数:

$\begin{matrix} K (x_{i}, x_{j}) = < x_{i}, x_{j} > \end{matrix}$ (9)

高斯核函数:

$\begin{matrix} K (x_{i}, x_{j}) = \exp (- ‖ x_{i} - x_{j} ‖^{2} / (2 σ^{2})) \end{matrix}$ (10)

2 改进的说话人识别算法

实际应用中, 语音采集环境的复杂性及设备的多样性容易导致语音信道失配。背景噪声和信道因素等是影响系统识别率的重要原因。说话人语音信号特征易受到加性噪声及线性信道干扰而引起失配, 针对这一问题本文提出采用特征弯折技术对语音特征数据进行处理。

训练说话人模型GMM的过程中利用特定信道下的大量语音集, 在UBM的基础上自适应得到特定的说话人模型。由于UBM的数据信息主要包含有背景噪声、信道噪声、与特定说话人无关的特征参数分布等, 在其基础上自适应得到的说话模型必然会保留其信道和噪声信息。因此本文又在模型级引入因子分析技术, 从说话人模型分离出说话人空间、信道空间及各自分别对应的特征向量。最终获得与信道无关的说话人模型数据作为支持向量机的训练数据。

2.1 特征弯折算法

特征弯折利用基础分布函数的原理, 把说话人提取的原始特征向量序列变为符合标准分布的规则化特征序列。语音信号在本质上是多模态的, 理想的目标分布也需要是多模态的并且可以代表说话人特征的真实分布。当选择完合适的目标分布后, 开始参数化过程。

特征弯折原理假设各个频谱特征间相互独立, 并且将语音信号进行加窗处理后再进行排列, 最终得到的居中倒谱系数在排序后位置变为 $\begin{matrix} R, \end{matrix}$ 对应的累积分布函数则变为^[13]:

$\begin{matrix} Φ = (N - R + 1 / 2) / N \end{matrix}$ (11)

原始音频信号特征序列的中心位置倒谱系数 $\begin{matrix} x \end{matrix}$ 在进行特征弯折后变为 $\begin{matrix} x', \end{matrix}$ 且其满足下式:

$\begin{matrix} Φ = \int_{-}^{\infty} f (z) dz \end{matrix}$ (12)

式中: $\begin{matrix} f (z) \end{matrix}$ 为标准正态分布的概率密度函数:

$\begin{matrix} f (z) = \frac{1}{\sqrt[]{2 π}} \exp (- z^{2} / 2) \end{matrix}$ (13)

特征弯折算法一方面补偿了线性信道内的短时均值干扰; 另一方面试图更加接近特征信号的源分布, 并且限制了噪声影响。作为特征归一化方法应用于说话人识别中, 能够进一步提高其信道鲁棒性, 加强其对于不同应用环境的适应性能, 从而提高说话人识别的准确性。

2.2 Factor analysis因子分析

为了减小信道因素的干扰, 对说话人模型进行补偿, 以达到提高识别准确率的目的, 将因子分析技术与GMM-SVM紧密结合。

通过语音信号得到GMM后使用LFA方法去除信道因素的影响, 补偿测试语音中与说话人身份相关的特征空间。因子分析模型为:

$\begin{matrix} μ_{(h, s)} = μ + D y_{s} + U x_{(h, s)} \end{matrix}$ (14)

该模型将由说话人 $\begin{matrix} s \end{matrix}$ 的语音段 $\begin{matrix} h \end{matrix}$ 确定的 $\begin{matrix} μ_{(h, s)} \end{matrix}$ 看作由背景模型的均值 $\begin{matrix} μ, \end{matrix}$ 说话人相关的模型分量 $\begin{matrix} y_{s} \end{matrix}$ 以及信道分量 $\begin{matrix} x_{(h, s)} \end{matrix}$ 组成, 其中 $\begin{matrix} y_{s} 和 x_{(h, s)} \end{matrix}$ 均符合高斯分布。使用此模型的目的是将说话人中的信道分量 $\begin{matrix} U x_{(h, s)} \end{matrix}$ 去除, 作为SVM分类器的输入向量, 提高识别率。

在信道空间估计的过程中, 令 $\begin{matrix} {N_{s}}^{[g]} \end{matrix}$ 和 $\begin{matrix} {N_{(h, s)}}^{[g]} \end{matrix}$ 分别为说话人相关统计量及信道空间相关统计量:

${N_{s}}^{[g]} = \sum_{t \in s} γ_{g} (t)$ (15)

${N_{(h, s)}}^{[g]} = \sum_{t \in (h, s)} γ_{g} (t)$ (16)

式中: $\begin{matrix} γ_{g} (t) \end{matrix}$ 为特征t对于高斯分量g的后验概率; $\begin{matrix} \sum_{t \in s} \end{matrix}$ γ _g(t)为说话人相关的特征帧的后验概率之和; $\begin{matrix} \sum_{t \in (h, s)} \end{matrix}$ γ _g(t)为所有属于说话人s的语音段h的后验概率之和。

令 $\begin{matrix} X_{s} \end{matrix}$ 和 $\begin{matrix} X_{(h, s)} \end{matrix}$ 分别为说话人相关及信道相关统计量:

${\{X_{s}\}}^{[g]} = \sum_{t \in s} γ_{g} (t) \cdot t$ (17)

${\{X_{(h, s)}\}}^{[g]} = \sum_{t \in (h, s)} γ_{g} (t) \cdot t$ (18)

最终获得说话人及信道统计量如下:

${\{{\bar{X}}_{s}\}}^{[g]} = {\{X_{s}\}}^{[g]} - \sum_{h \in s} {N_{(h, s)}}^{[g]} \cdot {U X_{(h, s)}}^{[g]}$ (19)

${\{{\bar{X}}_{(h, s)}\}}^{[g]} = {\{X_{(h, s)}\}}^{[g]} - {μ + D y_{s}}^{[g]} \cdot \sum_{h \in s} {N_{(h, s)}}^{[g]}$ (20)

$\begin{matrix} {\bar{X}}_{s}^{[g]} \end{matrix}$ 和 $\begin{matrix} {\bar{X}}_{(h, s)}^{[g]} \end{matrix}$ 分别用来估计说话人特征空间、信道因子及信道转换矩阵 $\begin{matrix} U, \end{matrix}$ 采用标准似然函数来评价估计结果的收敛性。

3 实验结果及分析

实验所使用语音库为TIMIT语音库, 共选取36个人, 其中男、女各18人, 每人10段语音用于UBM模型的训练。SVM分类器是台湾大学林智仁等^[14]开发设计的LIBSVM开发包, 并使用线性核及高斯核两种核函数作对比分析。GMM超向量作为SVM的输入向量, 采用one-versus-one的多分类模型, 每两个说话人建立一个二分类的SVM分类器, 如果有K个人, 则共需要K(K-1)/2个子分类器。

本文进行两组对比实验。训练集及测试集均选取76个人的语音。特征参数MFCC是将一维空间中的语音信号变换到频域中, 对人耳听觉特性充分模拟后得到的非线性倒谱域特征, 识别性及抗干扰能力强。第一组实验以12阶MFCC作为初始使用的特征向量, 并分别加入其一阶、二阶差分组成24维(MFCC_D)、36维(MFCC_D_A)特征向量。验证在普通MFCC参数下及加入差分系数后信道补偿算法对识别结果的影响, 以获得更好的识别算法, GMM混合数为512; 第二组实验则采用单一MFCC, 取维度逐渐递增的20~28阶MFCC, GMM混合数为512。分别统计两组实验加入信道补偿算法前、后的识别效果。

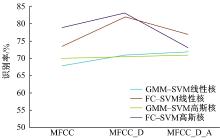
表1为使用12阶的MFCC及加入一阶差分、二阶差分后的识别结果。从实验结果可以看出:当引入特征参数的一阶差分(MFCC_D)及二阶差分(MFCC_D_A)后算法识别率均逐步提高, 当引入信道补偿后在线性核及高斯核的SVM下识别率均得到提高。未引入信道补偿前(GMM-SVM)加入特征参数一阶差分, 算法识别率提高不明显。引入信道补偿后(FC-SVM)算法识别率明显提高。二阶差分使得算法识别率下降, 特征增加使得高斯模型建模维度增加, 以及加入二阶差分系数导致身份信息的丢失, 使得区分性变差、干扰性增加, 信道补偿算法无法去除二阶差分带来的特征干扰, 识别率下降, 相对于没有引入信道补偿算法的识别率均有所提高。

表1 使用信道补偿前后算法识别率 Table 1 Recognition rate before and after using channel compensation %

通过图2对实验结果进行分析, 未引入信道补偿前特征参数维度增加, 算法识别率变化不大, 引入信道补偿之后算法的识别率得到提高。

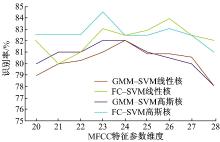
	Figure Option View Download New Window
	图2 信道补偿对比图Fig.2 Comparison chart of channel compensation

表2为使用单一MFCC作为训练模型的特征参数, 并逐渐增加特征参数维度, 信道补偿对于系统性能的影响。由表2可以看出:当特征参数维度逐渐增加时算法识别率提升, 当维度达到24维以后识别率趋于稳定, 逐渐增加特征维度后其识别率不再提高甚至有所降低。一方面由于MFCC不同维度下的系数所能代表的说话人的能力不同, 并且分类器在高纬度数据时其分类效果受到影响, 另一方面在建立模型时其所提供的不同说话人之间的区分度信息不相同, MFCC在低维系数时鲁棒性较好, 高频系数时鲁棒性降低。引入信道补偿算法后, 在线性核及高斯核下其识别率均比未引入信道补偿算法前得到提升。

表2 单一特征使用信道补偿前后算法识别率 Table 2 Recognition rate using single feature before and after using channel compensation %

使用图3对表2结果进行统计分析, 发现使用信道补偿后算法识别率优于改进前并且趋于稳定。参数维度的继续增加使得识别率逐步降低, 是由于MFCC参数在低频系数时具有较好的鲁棒性, 高频系数时不具有较高的分辨率。

从实验结果可知, 改进后的算法性能得到明显提升, 这是由于一方面利用了GMM超向量的特征表征能力, 一方面又利用SVM模型对于说话人分类效果的改善, 在此基础上加入因子分析, 增强了说话人自身特征在GMM的区分性, 减弱了信道因素的影响, 提升了识别算法对于信道影响的鲁棒性。

	Figure Option View Download New Window
	图3 识别率对比Fig.3 Comparison of recognition rate

4 结束语

在特征级利用特征弯折有效地降低了信道因素及背景噪声的干扰, 减小了信号畸变对建立说话人模型的影响。在模型级利用因子分析技术进行跨信道处理, 通过对已有高斯超向量中的信道因子进行估计和消除, 降低了信道空间对说话人识别的影响, 提升了识别性能, 相对于传统的GMM-SVM说话人识别算法具有更好的鲁棒性。实验中随着特征维度的增加, 识别率逐渐提高, 当达到一定维度后识别效果下降, MFCC高维数据影响了识别效果, 不同维度数据对说话人模型的区分性贡献不同, 高频系数的表征能力较弱。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Takiguchi T, Nakamura S, Shikano K. HMM-separation-based speech recognition for a distant moving speaker[J]. IEEE Transactions on Speech and Audio Processing, 2001, 9(2): 127-140. [本文引用:1]
[2]	吴迪, 曹洁, 王进花. 基于自适应高斯混合模型与静动态听觉特征融合的说话人识别[J]. 光学精密工程, 2013, 21(6): 1598-1604. Wu Di, Cao Jie, Wang Jin-hua. Speaker recognition based on adapted Gaussian mixture model and static and dynamic auditory feature fusion[J]. Optics and Precision Engineering, 2013, 21(6): 1598-1604. [本文引用:2]
[3]	Johnson M, Sinha P. A compact model for speaker-adaptive training[J]. Powder Technology, 2013, 237(3): 506-513. [本文引用:1]
[4]	Kinnunen T, Li H. An overview of text-independent speaker recognition: from features to supervectors[J]. Speech Communication, 2010, 52(1): 12-40. [本文引用:1]
[5]	Kasuriya S, Wutiwiwatchai C, Achariyakulporn V, et al. Comparative study of continuous hidden Markov models (CHMM) and artificial neural network (ANN) on speaker identification system[J]. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 2001, 9(6): 673-683. [本文引用:1]
[6]	Campbell W M, Sturim D E, Reynolds D A. Support vector machines using GMM supervectors for speaker verification[J]. Signal Processing Letters, 2006, 13(5): 308-311. [本文引用:1]
[7]	Munteanu D P, Toma S A. Automatic speaker verification experiments using HMM[C]//8th International Conference on Communications, Bucharest, Romanian, 2010: 107-110. [本文引用:1]
[8]	Badran E F M F, Selim H. Speaker recognition using artificial neural networks based on vowel phonemes[C]//5th International Conference on Signal Processing, Beijing, China, 2000: 796-802. [本文引用:1]
[9]	张素敏, 苏东林, 王炜. 改进的基于决策树的说话人在线聚类[J]. 光学精密工程, 2010, 18(1): 227-233. Zhang Su-min, Su Dong-lin, Wang Wei. Improved online speaker clustering based on decision tree[J]. Optics and Precision Engineering, 2010, 18(1): 227-233. [本文引用:1]
[10]	Ding I J, Yen C T. Enhancing GMM speaker identification by incorporating SVM speaker verification for intelligent web-based speech applications[J]. Multimedia Tools and Applications, 2015, 74(14): 5131-5140. [本文引用:1]
[11]	Sen N, Patil H A, Mand al S K D, et al. Importance of Utterance Partitioning in SVM Classifier with GMM Supervectors for Text-Independent Speaker Verification[M]. Heidelberg: Springer International Publishing, 2013: 780-789. [本文引用:1]
[12]	王玉, 申铉京, 陈海鹏, 等. 多角度特征融合的视频人脸纹理表示及识别[J]. 吉林大学学报: 工学版, 2015, 45(6): 1954-1960. Wang Yu, Shen Xuan-jing, Chen Hai-peng, et al. Video-based face texture representation and recognitionwith fusion features from multi-view[J]. Journal of Jilin University(Engineering and Technology Edition), 2015, 45(6): 1954-1960. [本文引用:1]
[13]	Neff M, Kipp M, Albrecht I, et al. Gesture modeling and animation based on a probabilistic re-creation of speaker style[J]. Acm Transactions on Graphics, 2008, 27(1): 329-339. [本文引用:1]
[14]	Chang C C, Lin C J. LIBSVM: a library for support vector machines[DB/OL]. [2014-07-26]. http://www.csie.ntu.edu.tw/~cjlin/papers/libsvm.pdf. [本文引用:1]

2001

0.0

... 概率统计方法包括隐马尔可夫(HMM)方法^[1],高斯混合模型(GMM)^[2] ...

2013

0.0

. 2013, 21(6):1598-1604 DOI:doi:10.3788/OPE.20132106.1598

Speaker recognition based on adapted Gaussian mixture model and static and dynamic auditory feature fusion

基于自适应高斯混合模型与静动态听觉特征融合的说话人识别

Wu Di , Cao Jie , Wang Jin-hua.

吴迪, 曹洁, 王进花

By optimizing the feature vectors and Gaussian Mixture Models(GMMs), a hybrid compensation method in model and feature domains is proposed. With the method, the speaker recognition features effected by the noise and the declined performance of GMM with reducing length of the training data under different unexpected noise environments are improved. By emulating human auditory, Gammatone Filter Cepstral Coefficients(GFCC) is given out based on Gammatone Filter bank models. As the GFCC only reflects the static properties, the Gammatone Filter Shifted Delta Cepstral Coefficients(GFSDCC) is extracted based on Shifted Delta Cepstral. Then, the adaptive process for each GMM model with sufficient training data is transformed to the shift factor based on factor analysis. Furthermore, when the training data are insufficient, the coordinate of the shift factor is learned from the GMM mixtures of insensitive to the training data and then it is adapted to compensate other GMM mixtures. The experiment result shows that the recognition rate of the method proposed is 98.46% . The conclusion is that the performance of speaker recognition system is improved under several kinds of noise environments.

对特征参数和高斯混合模型进行改进，提出了一种特征域和模型域混合补偿的方法用于解决说话人识别特征受噪声影响较大以及高斯混合模型随训练样本长度减小而性能下降的问题。通过模拟人耳听觉，给出了基于伽马通滤波器的伽马通滤波倒谱系数；考虑其只反映了语音的静态特征，提取了能够反映语音动态特征的伽马通滑动差分倒谱系数。基于因子分析技术，利用移动因子表示高斯混合模型的自适应过程，通过训练语料较充分的说话人模型中的均值向量补偿受训练语料长度影响较大的分量的均值向量。仿真实验表明：在纯净背景下，本文方法的识别率达到了98.46%；在不同噪声环境下，本文提出的混合补偿方法能有效提高说话人识别系统的性能。

... 概率统计方法包括隐马尔可夫(HMM)方法^[1],高斯混合模型(GMM)^[2] ...

... 1 说话人GMM的建立GMM是一种多维概率密度函数的线性组合,从说话人中提取的 D维矢量特征x,可以使用包含M个分量的高斯混合分布的概率密度函数来描述^[2]: ...

2013

0.0

... 辨别分类器方法包括人工神经网络(ANN)方法^[3],支持向量机(SVM)方法^[4]等 ...

2010

0.0

... 辨别分类器方法包括人工神经网络(ANN)方法^[3],支持向量机(SVM)方法^[4]等 ...

2001

0.0

... 2001年Kasuriya等^[5]开发出将HMM与ANN相结合的识别算法,其识别效果及运算速度均得到提升,但是仍依赖于文本提示,信道因素仍然制约着算法性能的进一步提升 ...

2006

0.0

... 2006年Campbell等^[6]在高斯模型的基础上引入SVM分类器,该方法不仅具有GMM的表征能力和SVM优秀的分类性能,并且引入了新的核函数,使得分类特征具备了GMM均值、方差、权值的属性 ...

2010

0.0

... 2010年Munteanu等^[7]改进的HMM系统取得了不错的识别效果并且识别时间大大降低,但却需要依赖于文本提示,训练过程依然需要占用相当大的存储空间,没有考虑信道因素的影响 ...

2000

0.0

... Badran等^[8]提出的ANN方法,具有很强的聚类能力和静态分类能力,可将它用于特征提取和说话人的分类判决,但由于训练时间较长及动态时间规整能力弱等缺点难以实际应用 ...

2010

0.0

. 2010, 18(1):227-233

Improved online speaker clustering based on decision tree

改进的基于决策树的说话人在线聚类

Zhang Su-min , Su Dong-lin , Wang Wei.

张素敏, 苏东林, 王炜

摘　要：针对采用传统的在线聚类方法时后续判决错误率较高的缺点,提出了一种改进的基于决策树的在线说话人聚类算法。通过构建一个决策树,增加判决分支,对语音段进行判决聚类,从而有效降低前期错误判决对后续聚类的影响。为了进一步提高算法效率,缩短运算时间,还给出了一种决策树剪枝方法,减少了不合理的判决分支。通过对广播新闻语料进行的说话人聚类实验表明,相比传统的层次聚类算法,新算法的平均类纯度和说话人纯度分别提高了0.9%和1.1%,计算时间减少了57%。实验结果还表明,相比手工标注说话人信息,将该算法的聚类结果应用于说话人自适应可降低系统的误识率。

... 现有的说话人识别算法受到信道因素的影响使得其难以获得理想的识别效果^[9],因此本文利用特征弯折算法和因子分析技术分别对识别过程中的特征级和模型级数据进行信道处理 ...

2015

0.0

... 自适应过程在UBM模型和说话人模型中提供了严格的耦合,其中自适应因子为模型更新前后权值、均值、方差联系的桥梁,维持着模型间数据的平衡^[10] ...

2013

0.0

... 2 基于高斯模型的端点检测算法算法利用Jeffery值作为高斯模型的距离参数,用GMM来描述环境中的噪声,以确定语音的起止点^[11] ...

2015

0.0

. 2015, 45(6):1954-1960 DOI:doi:10.13229/j.cnki.jdxbgxb201506032

Video-based face texture representation and recognitionwith fusion features from multi-view

多角度特征融合的视频人脸纹理表示及识别

Wang Yu , Shen Xuan-jing , Chen Hai-peng

王玉, 申铉京, 陈海鹏

摘　要：提出了一种在Gabor变换幅值域内提取3个正交平面上的局部二值模式的多角度特征融合的视频人脸纹理表示及其识别方法。首先对视频帧集合中归一化的每幅人脸图像进行不同尺度和方向的Gabor小波变换得到增强的Gabor幅值图谱。然后采用3个正交平面上的局部二值模式提取视频纹理特征。最后采用基于Fisher加权的Chi平方概率统计最近邻方法进行视觉人脸识别。通过在Honda/UCSD视频库进行的相关实验,验证了算法的有效性,该方法对光照变化、表情变化等具有较好的鲁棒性。

... 在SVM方法中,核函数至关重要,它取代了内积,减小了计算复杂性,避免了维度灾难^[12] ...

2008

0.0

... 特征弯折原理假设各个频谱特征间相互独立,并且将语音信号进行加窗处理后再进行排列,最终得到的居中倒谱系数在排序后位置变为 R,对应的累积分布函数则变为^[13]: ...

0.0

... SVM分类器是台湾大学林智仁等^[14]开发设计的LIBSVM开发包,并使用线性核及高斯核两种核函数作对比分析 ...