无线传感器网络簇半径自适应调整策略

引用本文

张婧, 刘衍珩, 张晋东, 孙庚. 无线传感器网络簇半径自适应调整策略.吉林大学学报:工学版, 2016, 46(3): 876-883
ZHANG Jing, LIU Yan-heng, ZHANG Jin-dong, SUN Geng. Cluster size adaptive adjustable strategy for wireless sensor networks. Journal of Jilin University Engineering and Technology Edition, 2016, 46(3): 876-883 复制到剪切板

Permissions

无线传感器网络簇半径自适应调整策略

张婧^1,², 刘衍珩^1,², 张晋东^1,², 孙庚^1,²

1.吉林大学计算机科学与技术学院,长春 130012

2.吉林大学符号计算与知识工程教育部重点实验室,长春 130012

通讯作者:张晋东(1980-),男,副教授,博士.研究方向:无线传感器网络,智能控制.E-mail:zhangjindong_100@163.com

作者简介:张婧(1986-),女,博士研究生.研究方向:无线传感器网络.E-mail:tiger-habit@163.com

基金:国家自然科学基金项目(61373123,61073164)

摘要

首先,基于节点的剩余能量对节点簇半径进行周期性调整,将网络划分为大小非均匀的若干簇。其次,设计了簇头选举策略,使得网络中簇头分布更加合理,提升簇头节点能量利用率,均衡节点的能耗。实验结果表明:与UCR算法和CUCRA算法相比,本文提出的算法将网络生命周期分别延长了55.2%和38.2%,同时具有较低的传输延时。

关键词: 计算机应用; 无线传感器网络; 非均匀分簇; 簇头选举; 生命周期

中图分类号:TP393 文献标志码:A 文章编号:1671-5497(2016)03-0876-08

Cluster size adaptive adjustable strategy for wireless sensor networks

ZHANG Jing^1,², LIU Yan-heng^1,², ZHANG Jin-dong^1,², SUN Geng^1,²

1.College of Computer Science and Technology, Jilin University, Changchun 130012, China

2.Key Laboratory of Symbolic Computation and Knowledge Engineering of Ministry of Education, Changchun 130012, China

Abstract

First, the cluster radius is adjusted periodically based on the node residual energy and the network is divided into several unequal clusters. Then, the cluster head election strategy is designed, which ensures the distribution of the cluster head more reasonable, improves the energy utilization of the cluster head, and balances the energy consumption of the nodes. Simulation results show that, compared to the Unequal Clustering Routing Algorithm (UCRA) and Cross Unequal Clustering Routing Algorithm (CUCRA), the CSAAS extends the network lifetime up to 55.2% and 38.2%, and meanwhile the transmission delay is lower.

Keyword: computer application; wireless sensor networks; unequal cluster; cluster head election; lifetime

Show Figures

0 引言

无线传感器网络技术的不断发展和完善使其被广泛应用于众多领域^{[1, 2, 3]}, 而多对一的传输模式造成节点负载分布不均的现象无法避免。在分簇策略中, 网络的簇半径通常是在算法运行之初设定, 随着网络的运行, 负载大的区域将加速成为热点区域, 从而限制了网络的生命周期。如果随着网络的运行, 簇半径能够自适应地进行调整, 将能耗大的区域的簇半径减小, 即增加簇头的数量, 减小数据传输的距离, 节省该区域的能量; 将能耗小的区域簇半径适当增大, 分担剩余能量少的区域的簇成员节点, 则能实现网络中节点能耗的均衡, 达到延长网络生命周期的目的。

低功耗自适应集簇分层型(Low energy adaptive clustering hierarchy, LEACH)协议^[4]为最早的分簇策略, 文献^{[5, 6, 7, 8, 9]}对其进行了改进, 由于各簇半径都是相等的, 因此仍然存在能耗不均衡的现象。EAUCF^[10]算法采用模糊逻辑构建节点与基站距离、节点剩余能量和竞争半径之间的不确定关系, 选用梯形关系函数和三角形关系函数对变量之间的关系进行描述, 但是算法中选择的公式未必是最优的。为了解决能耗不平衡现象产生的热点问题, 文献^[11]基于特征向量中心度提出了一种用于簇半径控制的启发式算法, 该算法不受节点部署策略的影响。文献^[12]分析了在不同场景下最优簇头节点数, 给出了网络中簇半径的最优值, 但仍然假设所有簇的簇半径大小是一致的。文献^[13]采用ACT算法调整簇半径的大小和传输范围, 在对簇头负载进行分析的基础上理论分析了节点能耗, 从而计算簇半径的大小, 然而其负载分析存在不精确性。UCR算法^[14]给出了一种非均匀分簇方法, 但在算法运行过程中, 节点的竞争半径不发生变化, 因此能耗不平衡的现象同样显现。CUCRA算法^[15]同样也是基于竞争半径的思想, 并在计算竞争半径时考虑了能量因素, 使得节点的竞争半径随着节点能量的减少而减小, 但最终导致簇头过多, 造成传输延时变长。

本文首先基于竞争半径机制设计了一种簇半径自适应调整策略(CSAAS), 通过引入能量参数周期性调整节点的竞争半径, 避免了簇头数量过多对网络传输延时的影响。然后, 为了均衡簇内通信能量消耗, 提出簇头推荐和簇的二次划分机制, 实现簇头的均匀分布, 均衡节点能量消耗, 有效地延长了网络的生命周期。

1 簇半径调整策略

节点的竞争半径、剩余能量、节点与基站之间的距离三个参数相互间接作用, 共同影响网络的性能。在CSAAS算法中, 每个节点维护自己的簇半径, 即竞争半径^[14], 节点之间通过竞争产生簇头, 如果竞争半径一直不变, 不利于保护剩余能量少的节点, 因此本文的目标是使节点在算法运行过程中根据当前剩余能量自适应地调整竞争半径, 从而提高网络中节点能耗的均衡性。竞争半径调整策略为:剩余能量多的节点适当增大自己的竞争半径, 扩大自己的竞争范围, 而剩余能量小的节点适当减小自己的竞争半径, 缩小自己的竞争范围, 以保护自己的能量。从而随着能量的变化, 节点的竞争半径得到自适应调整。为了保证簇头选举机制的有效性, 本文设计了簇头推荐机制选举簇头, 同时联合簇的二次划分, 实现各簇的数据量均衡, 均衡网络中节点的能耗。

1.1 网络模型

(1)假定被监测区域的大小为 $\begin{matrix} L \times W, N \end{matrix}$ 个同构传感器节点随机均匀分布在监测区域内, 且部署后不再发生移动; 每个节点具有唯一的ID号; 节点集合定义为 $\begin{matrix} S = {n_{1}, n_{2}, \dots, n_{N}} 。 \end{matrix}$

(2)簇成员节点获取的感知数据传输给各自簇头, 簇头节点将收集的数据进行数据融合。

(3)簇头节点借助其他簇头节点将数据多跳传输到基站。

(4)节点发射功率可调节, 节点可以根据接收信号的强度(RSSI)计算出发送者到自己的近似距离。

1.2 簇半径调整规则

簇头节点的能耗分为传输数据的能量消耗和接收数据的能量消耗两部分。传输能耗为簇间数据传输消耗的能量。接收能耗为接收簇成员的感知数据消耗的能量和接收来自于其他簇头的数据消耗的能量。因此簇头节点n_c向其他簇头节点传输数据为k bit, 其能量消耗^[16]为:

$\begin{matrix} E_{\tan} = \{\begin{matrix} k (E_{elec} + ε_{fs} d^{2}), d < d_{0} \\ k (E_{elec} + ε_{amp} d^{4}), d \geq d_{0} \end{matrix} \end{matrix}$ (1)

式中:E_elec为发射电路损耗的能量; ε _fs和ε _amp为不同传播模型下的功率放大电路能耗系数; d为两簇头节点之间的距离, 根据d值的不同传输模型可分别采用自由空间模型和多路径衰减模型, d₀通常设置为87。

簇头节点n_c接收本簇的簇成员节点 $\begin{matrix} n_{i} \end{matrix}$ 的数据量为k bit, 其能量消耗为:

$\begin{matrix} E_{rec} = k E_{elec} \end{matrix}$ (2)

因此, 簇头节点消耗的总能量为:

$\begin{matrix} \begin{matrix} E_{total} = E_{rec} + E_{\tan} = \\ (π r^{2} ρk + l) E_{elec} + k (E_{elec} + ε_{fs} d^{2}) \end{matrix} \end{matrix}$ (3)

式中:r为簇半径的大小; ρ 为网络中的节点密度; l为接收来自于其他簇的数据量。

从式(3)中可以看出, 簇半径的大小影响簇内接收能耗, 因此, 当节点剩余能量小时, 可减小其簇半径, 减少自己维护的簇成员数, 降低簇头节点的接收能耗, 从而延缓死亡速度。同时簇头节点分布影响簇头节点之间的传输距离 $\begin{matrix} d, \end{matrix}$ 当网络中簇头增加时, 簇头的传输能耗降低, 反之, 则会增加。

在无线传感器网络中, 由于采用多对一的数据流传输模式, 这使得越靠近基站的簇头节点承担的数据量越大, 其能量消耗越快。因此节点的竞争半径与节点和基站之间的距离有对应关系, 本文采用文献[14]中定义的这两个变量的关系, 其表达式为:

$\begin{matrix} R = [1 - c \frac{d_{\max} - d}{d_{\max} - d_{\min}}] R_{0} \end{matrix}$ (4)

式(4)定义的节点的竞争半径为初始竞争半径, 其中, c为调节该值变化范围的因子, 决定着距离对竞争半径的影响, c值越大, 距离对竞争半径的影响越大; R₀为最大竞争半径。当c增大时, R值的变化范围减少; 反之, 当c值减小时, R值的变化范围扩大, 而R₀则直接影响R值的大小。如当c为0.4, R₀为80时, R值的变化范围为48~80; 当c为0.6, R₀不变时, 其变化范围为32~80; 当c值不变, R₀为70时, 其变化范围为28~70。

在CUCRA算法^[15]中, 节点的竞争半径随着能量的变化而变化, 该策略导致的后果是随着网络中节点能量减少, 节点的竞争半径减小, 进而造成网络中的簇头不断增多, 网络传输延时增加。如果能让节点的竞争半径根据自身剩余能量自适应调整, 则会避免这一问题的出现。在本文中, 随着算法的运行, 节点将根据自身剩余能量与周围节点的平均剩余能量差自适应地调整竞争半径的大小。剩余能量多的节点按固定步长增大竞争半径, 剩余能量少的节点按固定步长减小竞争半径, 否则节点维持基础竞争半径。该竞争半径调整规则使得节点的竞争半径波动变化而不是逐渐减小。

若节点 $\begin{matrix} i \end{matrix}$ 的自身剩余能量为E_remain, 其邻居节点的平均剩余能量为E_average, 则有:

$\begin{matrix} E_{average} = \overset{m}{\sum_{j = 1}} E_{remain}^{j} / m \end{matrix}$ (5)

式中:m为节点i的邻居节点数, 即与节点i在同一个簇内的节点, 则节点i更新后的竞争半径R'为:

$\begin{matrix} R' = R + sgn (E_{remain} - E_{average}) Δr \end{matrix}$ (6)

式中: $\begin{matrix} Δr \end{matrix}$ 为簇半径的变化步长; sgn(x)为符号函数。

在本文中, 节点的自身剩余能量可直接获取而不消耗能量, 簇成员节点在向簇头发送数据包时, 将占用一个字节存储自身的能量信息, 簇头节点收集簇内成员数据包时即可获取其剩余能量信息, 簇内节点的平均剩余能量可通过广播包的方式告知簇内节点, 由于该过程中能量信息占用很小的字节, 因此产生的能耗非常小。每个节点在每轮开始时调整自己的竞争半径并确定最终值, 随后网络进入簇头选举阶段。

2 CSAAS算法

2.1 簇头选举机制

通常节点成为候选簇头的概率阈值为T, 为一个额定值, 当某个节点生成的随机概率值小于该阈值T时, 则成为候选簇头, 保证了当前网络中参与竞争簇头的节点数量。虽然候选簇头通过能量竞争的方式确定最终簇头, 但候选簇头选择的随机性造成某些剩余能量低的节点成为候选簇头, 从而限制了网络的生命周期。为了增大网络中簇头的有效性, 即避免网络中某些剩余能量低的节点成为最终簇头, 本文采用推荐机制选出候选簇头, 即上一轮簇头节点推荐本簇中剩余能量多的节点为候选簇头节点。

首轮时, 网络中节点的能量相等, 按照文献^{[14, 15]}方法以概率的方式选举候选簇头, 节点的竞争半径为 $\begin{matrix} R 。 \end{matrix}$ 第一轮过后, 簇头选举的伪代码如下所示:

1 For each cluster head n_c in the last round

2 choose M cluster members in its cluster with most energy

3 broadcast NOTIFY_MSG with these cluster member IDs

4 For each cluster member in the cluster

5 on receiving a NOTIFY_MSG from a cluster head

6 If my ID is in the NOTIFY_MSG

7 CandidateHead← True

8 broadcast COMPETE_HEAD_MSG(ID, R, RE)

9 else

10 sleep

11 end if

12 end For

13 For each CandidateHead n_i

14 On receiving a COMPETE_HEAD_MSG from Candidate Head n_j

15 If d(n_i, n_j)< n_i.R OR d(n_i, n_j)< n_j.R then

16 add n_j to n_i's neighbor set

17 end if

18 end For

19 For each CandidateHead n_i

20 on receiving a FINAL_HEAD_MSG from n_j

21 if n_i∈ n_j.neighber set then

22 CandidateHead← False

23 end if

24 if CandidateHead==true

25 if ∀ n_j∈ n_i.CS, n_i.RE> n_j.RE then

26 broadcast FINAL_HEAD_MSG(ID)

27 end if

28 end if

29 end For

当节点的能量出现偏差, 网络中节点根据能量差值调整自己的竞争半径, 完成簇头的更换。由于簇成员节点与簇头节点进行周期通信, 因此簇头节点根据掌握的簇成员信息推选出剩余能量多的M个节点为候选簇头, 如伪代码中第1~12行所示。M的值可按照式(7)进行计算:

$\begin{matrix} M = T \cdot N_{csize} \end{matrix}$ (7)

式中:T为推荐节点成为候选簇头的百分比; N_csize为簇头管理的簇成员数。

当节点成为候选簇头后, 将自己的信息广播给周围半径为 $\begin{matrix} R_{0} \end{matrix}$ 范围内的邻居候选簇头, 信息包括竞争半径、剩余能量和节点ID。根据收集的邻居候选簇头信息, 建立候选簇头邻居集, 如伪代码中第13~18行所示。当候选簇头邻居集确定后, 进行簇头的选择。假设节点之间的通信是对称的, 即, 若A与B能通信, 则B与A也能通信。若候选簇头节点A竞争胜出, 则A的竞争半径内的其他候选簇头节点退出竞争, 以保证同一竞争半径内只有一个簇头胜出, 如伪代码中第19~28行所示。

2.2 簇的二次划分

无论是候选簇头的概率选举机制还是推荐机制, 都存在竞争盲区, 即某些区域没有候选簇头, 造成某些簇的簇成员数超过其可以负载的数量。因此, 对于这样的簇, 本文进一步提出簇的二次划分机制, 通过对簇成员数超量的簇进行有限次划分, 保证每个簇内的节点数不超过其竞争范围覆盖的节点数量。判断簇是否需要二次划分的条件如下所示:

(1)簇成员节点的数量超过其应该负载的数量一倍;

(2)若存在簇成员节点与簇头的距离大于簇头竞争半径, 这样的簇成员节点数大于簇成员总数的一半。

条件(1)避免了簇成员数超出簇头应该负载数量情况的出现, 条件(2)避免了簇头位置过偏而导致簇内通信能耗大的情况出现。一旦某个簇满足上述两种情况之一, 则进行二次划分。簇头从簇成员节点中选择剩余能量多且使新划分的簇不再满足上述两种情况的簇成员节点成为新的簇头。

2.3 数据传输

在分簇的无线传感器网络中, 数据传输包括簇内传输和簇间传输两个部分。簇内传输则为簇头与簇成员之间的通信, 簇成员直接将感知数据传递给簇头; 簇间传输则为簇头与簇头之间的数据传输。中继簇头节点应该具有更多的剩余能量, 且与基站之间的距离更小。本文将这两个条件进行折中, 采用如下代价函数作为簇头选择下一跳的依据:

$\begin{matrix} cost (i, j) = \{\begin{matrix} α \frac{E_{avg}^{i}}{E_{cur}^{j}} + β \frac{d (i, j) + d (j, BS)}{2 d (i, BS)}, \\ ifd (i, BS) \geq d_{t h r} \\ - 1, else \end{matrix} \end{matrix}$ (8)

式中:α 和β 为能量和距离对代价函数的影响, 且α =β =0.5; E_avg为邻居簇头节点的平均剩余能量; E_cur为簇头的当前剩余能量; d(i, j)为节点i和节点j之间的距离; d(i, BS)、d(j, BS)分别为节点i、j与基站之间的距离; d_thr为簇头节点和基站之间距离的一个阈值。

从式(8)可以看出, 节点j的剩余能量越多, 代价函数值越小; 节点i经节点j到达基站的距离越小, 代价函数值越小。该代价函数的计算复杂度为O(n), 相应信息的获取可通过数据包捎带传输的形式实现, 因此将消耗非常小的能量。簇头节点n_i计算邻居簇头表中节点n_j的代价, 选择具有最小代价值的簇头节点n_j作为下一跳, 进行数据传输。当d(i, BS)小于d_thr时, 簇头节点n_i将直接将数据传输到基站。

3 模拟实验

为了对CSAAS算法的性能进行验证和评估, 本文对算法CSAAS进行了仿真, 实验参数的设置如表1所示。根据若干次实验的平均数据, 得出了本算法参数设置的最优值, 并与UCR算法和CUCRA算法在6个方面进行性能比较。

表1 参数设置 Table 1 Parameter Setting

3.1 算法参数的设置

(1) $\begin{matrix} R_{0} 和 c \end{matrix}$

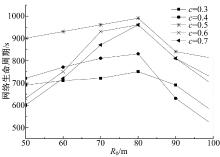
对R₀和c设置不同数值, 观察网络生命周期的变化。从图1可以看出, 当c设置为0.5时, 无论最大竞争半径设置为何值, 都比c设置为其他值的网络生命周期长。其中, 当c设置为0.5、R₀ 设置为80时, 网络的生命周期最长。因此, 在下文的实验中, R₀ 设置为80, c设置为0.5。

	Figure Option View Download New Window
	图1 R₀和c最优值Fig.1 Optimal value of R₀ and c

(2)Δ r

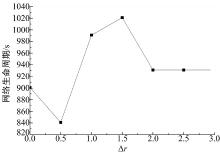
在本文设置的参数基础上, 将节点的竞争半径调整步长设置为不同值, 根据网络的生命周期确定Δ r的最优值。如图2所示, 当Δ r设置为1.5时, 网络的生命周期最长。

	Figure Option View Download New Window
	图2 调整步长最优值Fig.2 Optimal value of adjusting step

3.2 算法性能比较

(1)簇头数

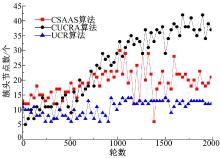
本文提出的簇半径自适应调整策略直接影响着簇头数。从图3中可以看出, 由于在UCR算法中节点的竞争半径不发生变化, 因此簇头数相对稳定。而在本文算法中, 节点的竞争半径是根据自身剩余能量和周围节点的平均剩余能量浮动变化, 在CUCRA算法中节点的竞争半径随着节点的剩余能量减少而减小。因此, 这两个算法的簇头数均呈现上升趋势, 说明簇半径的调整使得簇头数增加。同时, 随着算法的运行, CUCRA算法的簇头数增加趋势显著, 而CSAAS算法的簇头数到后来增加趋势趋于稳定。

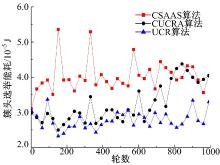
	Figure Option View Download New Window
	图3 簇头节点数量Fig.3 Number of cluster heads

(2)簇头能量消耗

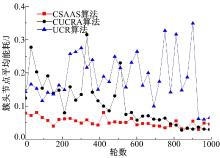
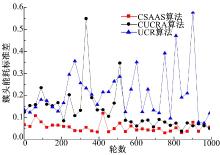
簇头能量消耗包含簇头接收簇成员节点的监测数据产生的能耗和簇头间的数据传输产生的能耗, 通过概率随机产生簇头节点会导致某些簇头不是最优簇头。本文通过上一轮簇头节点推荐本簇内能量大的簇成员节点作为候选簇头, 从而保证选出的簇头能量较大。通过簇的二次划分, 保证了簇头节点管理的节点数量不超过其竞争半径覆盖的节点数量, 使得网络中簇头的分布更加有效, 更好地完成数据传输任务。从图4中可以看出, CSAAS算法的簇头能量消耗要小于CUCRA算法和UCR算法的簇头能量消耗, 验证了本文算法的簇头分布的有效性。同时, 从图5可以看出, CSAAS算法使簇头的能耗更加均衡, 而UCR算法仅通过随机方式选取簇头, 其簇头能量消耗标准差波动最大, CUCRA算法由于进行了簇半径调节, 因此要优于UCR算法。

	Figure Option View Download New Window
	图4 簇头平均能量消耗Fig.4 Average energy consumption of cluster heads

	Figure Option View Download New Window
	图5 簇头节点能耗标准差Fig.5 Standard deviation of cluster head energy consumption

(3)节点的平均剩余能量

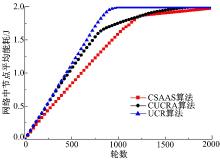
图6给出了3种算法的网络中节点平均剩余能量曲线图, 从图6中可以看出, UCR算法的平均剩余能量要低于CUCRA算法, 而两者均低于CSAAS算法, 说明CSAAS算法选出的簇头节点具有较均匀的分布, 降低了簇内传输能耗和簇间传输能耗, 从而使得节点的平均剩余能量高于其他两种算法。

	Figure Option View Download New Window
	图6 节点的平均能耗Fig.6 Average energy consumption of nodes

	Figure Option View Download New Window
	图7 死亡节点数Fig.7 Number of dead nodes

(4)死亡节点数

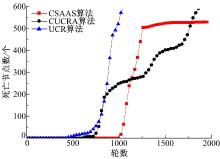
将第一个节点的死亡时间定义为网络的生命周期。如图7所示, 由于UCR算法不同于CUCRA算法和CSAAS算法, 没有节点的竞争半径调整过程, 因此UCR算法中的网络生命周期要小于CUCRA算法和CSAAS算法。同时CUCRA算法中候选簇头节点是通过概率随机选取的, 导致存在非优簇头节点成为最终簇头的可能, 进而加速了第一个节点的死亡时间, 限制了其生命周期。CUCRA算法的死亡节点数量呈现上升趋势, 在1100轮到1800轮之间, 其死亡节点数要低于CSAAS算法, 因为CUCRA算法随着节点能量的减小, 其竞争半径减小, 进而簇头节点增多, 使得网络中的数据传输距离减小, 降低了节点的能量消耗速度, 但增加了数据的传输延时。经比较得出, CSAAS算法比UCR算法和CUCRA算法分别延长网络生命周期55.2%和38.2%。

(5)传输时延

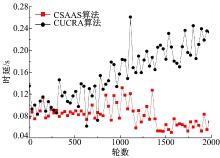
图8为CSAAS算法和CUCRA算法传输时延的比较。从图8中可以看出:随着算法的运行, CUCRA算法的传输时延随着簇头的增多而增大, 而无线传感器网络的应用相关性非常强, 对于某些对实时性要求高的应用场景, 过大的时延无疑会影响监测结果, 如温度监控等。而CSAAS算法虽然同样进行了簇半径调节, 但没有出现CUCRA算法的现象, 说明了本文提出的策略有效。

	Figure Option View Download New Window
	图8 传输时延Fig.8 Transmission delay

(6)簇头选举代价

在CSAAS算法中, 由于增加了簇的二次分割过程, 造成了簇头选举代价的增大, 如图9所示, 但是该代价远小于数据传输能耗, 在没有增加网络中节点平均能耗的同时使得网络的簇头节点分布更加有效, 因此可以认为该代价是值得的。

	Figure Option View Download New Window
	图9 簇头选举能耗Fig.9 Energy Consumption of Cluster Head Selection

4 讨论

对CSAAS算法和CUCRA算法的竞争半径调整过程进行讨论。两个算法中都将参数c设置为0.5; R₀设置为80。对于CUCRA算法, 其竞争半径为:

$\begin{matrix} R = [λ_{1} (1 - c \cdot \frac{d_{\max} - d}{d_{\max} - d_{\min}}) + λ_{2} (\frac{E_{remain}}{E_{init}})] \cdot R_{0} \end{matrix}$ (9)

式中:λ ₁ 和λ ₂ 的值均为0.5; E_init为节点的初始能量。

在算法运行之初, R的变化范围为0.5R_0~R_0, 即40~80。随着网络的运行, 节点的能耗变小, 当网络中节点剩余能量为原来的一半时, 其变化范围为0.25R₀~0.75R₀, 即20~60。当网络中节点剩余能量为原来的四分之一时, 其变化范围为0.125R₀~0.625R₀, 即10~50。而节点的竞争半径越小, 相应产生的簇头会越多, 如图3所示。对于CSAAS算法, 在算法运行之初, R的变化范围为0.5R₀~R₀, 即40~80。随后, 节点的竞争半径根据节点的自身剩余能量与周围节点的平均剩余能量差进行波动。由于网络中的节点每一轮都要进行数据传输, 因此, 不存在某个节点的竞争半径总在减小或总在增大的情况, 进而不会出现网络中簇头节点数一直增多的现象。

5 结束语

分簇算法的提出有效地延长了网络的生命周期, 但簇半径相等将导致靠近基站的簇头节点因承担大量负载而过早死亡, 而非均匀分簇且簇半径固定不变加速了剩余能量低的簇头节点的死亡。因此, 本文提出一种簇半径自适应调整策略(CSAAS), 通过将节点的剩余能量与邻居节点的剩余能量进行比较, 决策其竞争半径的增大或者减小, 同时结合簇头推荐机制和簇的二次划分, 使得网络中的簇头分布更有效, 均衡了网络中节点的能耗, 进而延长网络的生命周期。与UCR算法和CUCRA算法相比, CSAAS算法将网络生命周期分别延长了55.2%和38.2%。同时, 相较于CUCRA算法, 具有较低的数据传输时延, 保证了数据的实时性。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Yang Hui, Qin Yong, Feng Ge-fei, et al. Online monitoring of geological CO₂ storage and leakage based on wireless sensor networks[J]. IEEE Sensor Journal, 2013, 13(2): 556-562. [本文引用:1]
[2]	Chen Ming-che, Chang Wang-rong, Lin Hui-tang, et al. Design and performance evaluation of aquatic-pollution monitoring scheme over a waterborne wireless sensor networks[J]. Computer Communications, 2014, 40: 51-64. [本文引用:1]
[3]	Zhou J, Chen C L P, Chen L, et al. A user-customizable urban traffic information collection method based on wireless sensor networks[J]. IEEE Transactions on Intelligent Transportation Systems, 2013, 14(3): 1119-1128. [本文引用:1]
[4]	Heinzelman W B, Chand rakasan A P, Balakrishnan H. An application-specific protocol architecture for wireless microsensor networks[J]. IEEE Transactions on Wireless Communications, 2002, 1(4): 660-670. [本文引用:1]
[5]	Younis O, Fahmy S. HEED: a hybrid, energy-efficient, distributed clustering approach for Ad Hoc sensor networks[J]. IEEE Transactions on Mobile Computing, 2004, 3(4): 366-379. [本文引用:1]
[6]	林恺, 赵海, 尹震宇, 等. 一种基于能量预测的无线传感器网络分簇算法[J]. 电子学报, 2008, 36(4): 824-828. Lin Kai, Zhao Hai, Yin Zhen-yu, et al. A clustering hierarchy arithmetic based on energy predicition for wireless sensor networks[J]. Acta Electronical Sinica, 2008, 36(4): 824-828. [本文引用:1]
[7]	Le Jin-Shyan, Cheng Wei-Liang. Fuzzy-logic-based clustering approach for wireless sensor networks using energy predication[J]. IEEE Sensors Journal, 2012, 12(9): 2891-2897. [本文引用:1]
[8]	李斌, 林亚平, 胡玉鹏, 等. 无线传感器网络一种基于聚合收益的动态成簇算法[J]. 电子学报, 2010, 38(2A): 128-132. Li Bin, Lin Ya-ping, Hu Yu-peng, et al. A dynamic clustering algorithm based on polymerization proceeds for wireless sensor networks[J]. Acta Electronical Sinica, 2010, 38(2A): 128-132. [本文引用:1]
[9]	Kang S H, Nguyen T. Distance based thresholds for cluster head selection in wireless sensor networks[J]. IEEE Communications Letters, 2012, 16(9): 1396-1399. [本文引用:1]
[10]	Bagci H, Yazici A. An energy aware fuzzy approach to unequal clustering in wireless sensor networks[J]. Applied Soft Computing, 2013(13): 1741-1749. [本文引用:1]
[11]	Jain A, Reddy B V R. Eigenvector centrality based cluster size control in rand omly deployed wireless sensor networks[J]. Expert Systems with Applications, 2015, 42(5): 2657-2669. [本文引用:1]
[12]	Amini N, Vahdatpour A, Xu W Y, et al. Cluster size optimization in sensor networks with decentralized cluster-based protocols[J]. Computer Communications, 2012, 35(2): 207-220. [本文引用:1]
[13]	Lai W K, Fan C S, Lin L Y. Arranging cluster sizes and transmission ranges for wireless sensor networks[J]. Information Sciences, 2012, 183(1): 117-131. [本文引用:1]
[14]	Chen Gui-hai, Li Cheng-fa, Ye Mao, et al. An unequal cluster-based routing protocol in wireless sensor networks[J]. Wireless Networks, 2009, 15(2): 193-207. [本文引用:3]
[15]	Wang Tong, Wu Ji-yi, Xu He, et al. A cross unequal clustering routing algorithm for sensor network[J]. Measurement Science Review, 2013, 13(4): 200-205. [本文引用:3]
[16]	Heinzelman W B. Application-specific protocol architectures for wireless networks[D]. Cambridge: Massachusetts Institute of Technology, 2000. [本文引用:1]

2013

0.0

... 0 引言无线传感器网络技术的不断发展和完善使其被广泛应用于众多领域^[1,2,3],而多对一的传输模式造成节点负载分布不均的现象无法避免 ...

2014

0.0

... 0 引言无线传感器网络技术的不断发展和完善使其被广泛应用于众多领域^[1,2,3],而多对一的传输模式造成节点负载分布不均的现象无法避免 ...

2013

0.0

... 0 引言无线传感器网络技术的不断发展和完善使其被广泛应用于众多领域^[1,2,3],而多对一的传输模式造成节点负载分布不均的现象无法避免 ...

2002

0.0

... 低功耗自适应集簇分层型(Low energy adaptive clustering hierarchy,LEACH)协议^[4]为最早的分簇策略,文献^[5,6,7,8,9]对其进行了改进,由于各簇半径都是相等的,因此仍然存在能耗不均衡的现象 ...

2004

0.0

2008

0.0

. 2008, 36(4):824-828 DOI:doi:10.3321/j.issn:0372-2112.2008.04.039

A clustering hierarchy arithmetic based on energy predicition for wireless sensor networks

一种基于能量预测的无线传感器网络分簇算法

Lin Kai , Zhao Hai , Yin Zhen-yu

林恺, 赵海, 尹震宇

To solve the energy efficiency problem in the wireless sensor networks(WSNs),a clustering hierarchy arithmetic based on energy prediction (CHEP) was presented.Taking use of the sensor nodes state diversion module,the proposed remaining energy was added as a considered parameter in calculating the threshold in CHEP.Hence it can guarantee the node with high remaining energy be chosen as the cluster-head node in priority in each round.From the experiments,we analyzed the performance of CHEP and compared it with other cluster-based routing arithmetics where there was no prediction used in selecting the cluster-head node.It was satisfied that the arithmetic of CHEP could prove the validity of energy prediction mechanism and threshold amended.Simulation results show that the process of CHEP can balance the energy load in the network and prolong the lifetime of the network.

为了解决无线传感器网络能量有效利用的问题,提出一种利用能量预测选择簇头节点的分簇算法:CHEP利用文中建立的传感器节点工作状态转换模型,CHEP算法将所得的剩余能量预测参数作为考虑因素引入阀值的计算,从而使高剩余能量且能耗较慢的节点能够在每一轮中被优先选为簇头节点.通过仿真实验,将CHEP与其他分簇算法进行分析和比较,验证了CHEP算法中能量预测机制以及阀值改进的有效性.结果表明CHEP能够更好地平衡网络负载,延长网络寿命.

2012

0.0

2010

0.0

. 2010, 38(2A):128-132

A dynamic clustering algorithm based on polymerization proceeds for wireless sensor networks

无线传感器网络一种基于聚合收益的动态成簇算法

Li Bin , Lin Ya-ping , Hu Yu-peng

李斌, 林亚平, 胡玉鹏

With limited resources,wireless sensor networks usually use clustering aggregation to decrease traffic.This paper proposes a dynamic clustering algorithm based on aggregation gains.Firstly,we present a nonlinear integer programming model for the overall energy consumption of the network optimization problem,and then propose a low complex and near optimal heuristic cluster head election algorithm.A dynamic clustering algorithm is proposed based on aggregation gains,which can elect the cluster head in a distributed way.Theoretical analysis and experimental results show that the proposed dynamic clustering algorithm can resolve the load balance problem,improve the network energy efficiency,and prolong the network lifetime.

无线传感器网络资源有限，通常采用分簇聚合减少传输数据，本文提出了一种基于聚合收益的动态成簇算法.首先，针对网络整体能耗最优化问题，建立一个非线性整数规划模型，进而提出一种近似最优、低复杂度的启发式簇头选举算法.在此基础上，提出一种分布式的、基于聚合收益的动态成簇算法，可分布式实现该簇头选举算法并进行成簇.理论分析和实验仿真表明，基于聚合收益的动态成簇算法能较好地解决节点负载均衡问题，提高网络能耗效率，延长网络生命周期.

2012

0.0

2013

0.0

... EAUCF^[10]算法采用模糊逻辑构建节点与基站距离、节点剩余能量和竞争半径之间的不确定关系,选用梯形关系函数和三角形关系函数对变量之间的关系进行描述,但是算法中选择的公式未必是最优的 ...

2015

0.0

... 为了解决能耗不平衡现象产生的热点问题,文献^[11]基于特征向量中心度提出了一种用于簇半径控制的启发式算法,该算法不受节点部署策略的影响 ...

2012

0.0

... 文献^[12]分析了在不同场景下最优簇头节点数,给出了网络中簇半径的最优值,但仍然假设所有簇的簇半径大小是一致的 ...

2012

0.0

... 文献^[13]采用ACT算法调整簇半径的大小和传输范围,在对簇头负载进行分析的基础上理论分析了节点能耗,从而计算簇半径的大小,然而其负载分析存在不精确性 ...

2009

0.0

... UCR算法^[14]给出了一种非均匀分簇方法,但在算法运行过程中,节点的竞争半径不发生变化,因此能耗不平衡的现象同样显现 ...

... 在CSAAS算法中,每个节点维护自己的簇半径,即竞争半径^[14],节点之间通过竞争产生簇头,如果竞争半径一直不变,不利于保护剩余能量少的节点,因此本文的目标是使节点在算法运行过程中根据当前剩余能量自适应地调整竞争半径,从而提高网络中节点能耗的均衡性 ...

... 首轮时,网络中节点的能量相等,按照文献^[14,15]方法以概率的方式选举候选簇头,节点的竞争半径为 R ...

2013

0.0

... CUCRA算法^[15]同样也是基于竞争半径的思想,并在计算竞争半径时考虑了能量因素,使得节点的竞争半径随着节点能量的减少而减小,但最终导致簇头过多,造成传输延时变长 ...

... 在CUCRA算法^[15]中,节点的竞争半径随着能量的变化而变化,该策略导致的后果是随着网络中节点能量减少,节点的竞争半径减小,进而造成网络中的簇头不断增多,网络传输延时增加 ...

... 首轮时,网络中节点的能量相等,按照文献^[14,15]方法以概率的方式选举候选簇头,节点的竞争半径为 R ...

2000

0.0

... 因此簇头节点n_c向其他簇头节点传输数据为k bit,其能量消耗^[16]为: ...