基于半监督学习的朴素贝叶斯分类新算法

引用本文

董立岩, 隋鹏, 孙鹏, 李永丽. 基于半监督学习的朴素贝叶斯分类新算法.吉林大学学报:工学版, 2016, 46(3): 884-889
DONG Li-yan, SUI Peng, SUN Peng, LI Yong-li. Novel naive Bayes classification algorithm based on semi-supervised learning. Journal of Jilin University Engineering and Technology Edition, 2016, 46(3): 884-889 复制到剪切板

Permissions

基于半监督学习的朴素贝叶斯分类新算法

董立岩¹, 隋鹏¹, 孙鹏¹, 李永丽²

1.吉林大学计算机科学与技术学院, 长春 130012

2.东北师范大学计算机科学与信息技术学院,长春 130117

作者简介:董立岩(1966-),男,教授,博士生导师.研究方向:数据挖掘.E-mail:dongly@jlu.edu.cn

基金:国家自然科学基金项目(61272209)

摘要

为了在有标签的训练集中保留高质量的样本,首先利用无标签训练集得出置信度高的 k个样本,再结合有标签训练样本,不断迭代直至训练完成。实验结果表明:随着无标记样本比例的不断增加,本文算法预测准确性明显高于朴素贝叶斯分类算法,而且其性能比传统半监督学习方法有所改善。

关键词: 计算机应用; 半监督学习; 朴素贝叶斯; 无类标签分类

中图分类号:TP301.6 文献标志码:A 文章编号:1671-5497(2016)03-0884-06

Novel naive Bayes classification algorithm based on semi-supervised learning

DONG Li-yan¹, SUI Peng¹, SUN Peng¹, LI Yong-li²

1.College of Computer Science and Technology , Jilin University , Changchun 130012, China

2.School of Computer Science and Technology, Northeast Normal University, Changchun 130117,China

Abstract

A novel naive Bayes classification algorithm based on semi-supervised learning is proposed. First, to retain high quality samples in the training sect with class label, the unlabeled training set is sued to obtain k samples of high confidence. Then, these high confidence samples are combined with the labeled-training samples to iterate until the training is complete. The experimental results show that with the increasing proportion of unlabeled samples, the predictive accuracy of the proposed algorithm is significant higher than that of the Na?ve Bayesian classification. In addition, the effectiveness and performance of the algorithm are improved compared with the traditional semi-supervised learning algorithm.

Keyword: computer application; semi-supervised study; Naive Bayes; unknown label classification

Show Figures

0 引言

朴素贝叶斯算法因其具有简单、快速和高准确率等特点被广泛应用于分类任务中。但是朴素贝叶斯分类算法存在一定的弊端, 它要求条件属性间满足类条件独立假设, 这在实际应用中是很难满足的。如果实际数据属性间高度相关, 就会导致分类效果大大下降。许多学者提出了一些改进方法, Zhang等^[1]根据属性的重要性, 提出了给不同属性赋予不同权值的加权朴素贝叶斯(Weighted naive Bayes, WNB)模型, 并给出了采用爬山算法和Monte Carlo技术确定权值的加权朴素贝叶斯分类方法。Zheng等^[2]利用懒惰式学习策略提出了一种懒惰式贝叶斯规则(Lazy Bayesian rule, LBR)学习技术, 该方法在局部朴素贝叶斯规则的归纳中使用懒惰式技术, 虽然大大地提高了分类精确度, 但是效率很低。Wang等^[3]提出了一种半懒惰式(Semi-Lazy)的限制性贝叶斯网络分类器的条件概率调整方法, 在某些情况下可以减小错误分类率。Yager^[4]利用有序算子, 提出一种新的朴素贝叶斯的扩展算法。当无标记的数据集数量较大时, 有监督的学习不能准确地预测出元组的类别, 而无监督学习由于没有指导所以难以得到较高精度的学习结果^[5]。因此, 半监督学习(Semi-supervised study)显得尤为重要。半监督学习的研究从Shahshahani和Landgrebe的工作开始^[6], 它结合了监督学习和无监督学习的优点^[7], 可以根据数据固有的特性, 既不丢失完整的有标记的数据信息, 又能够利用大量不完整数据(无类标号数据)的信息进行学习, 因此具有更好的应用前景, 而且处理的问题也更具普遍性。但是在传统的半监督学习贝叶斯分类过程中, 将预测后的元组添加到训练集中可能会在迭代的过程中强化错误, 从而降低准确率。因此本文提出一种新型半监督朴素贝叶斯算法(Novel semi-supervised naive Bayes, NSNB), 它可以提取高置信度的无类标号样本, 将它们依次添加到训练集中, 进而可以对测试集中的元组所属的类别做出准确的预测。该方法比传统半监督朴素贝叶斯(Semi-supervised naive Bayes, SNB)算法以及朴素贝叶斯(Naive Bayes, NB)算法有更高的预测准确率, 比传统的半监督贝叶斯分类算法有更快的训练速度。

1 朴素贝叶斯理论和半监督学习

1.1 朴素贝叶斯分类器

朴素贝叶斯分类器(Naive Bayes classifier, NBC)是贝叶斯分类器中应用最广泛的模型之一。该模型描述如下:设训练集中包含m个类C={C₁, C₂, …, C_m}, n个条件属性X={X₁, X₂, …, X_n}。假设所有的条件属性X都作为类变量C的子节点。当且仅当:P(C_i|X)> P(C_j|X)(1≤ i, j≤ m, i≠ j)成立, 将给定的一个待分类样本X={x₁, x₂, …, x_n}分配给类C_i (1≤ i≤ m)。根据贝叶斯定理, C_i类的后验概率为:

$\begin{matrix} P (C_{i} | X) = \frac{P (C_{i}) P (X | C_{i})}{P (X)} \end{matrix}$ (1)

如果事先不清楚类在训练集上的概率, 可以假定每个类别概率相等, 即 $\begin{matrix} P (C_{i}) = P (C_{j}), \end{matrix}$ 并将 $\begin{matrix} P (X | C_{i}) \end{matrix}$ 最大化。如果各类概率已知, 则最大化 $\begin{matrix} P (C_{i}) P (X | C_{i}) 。式 (1) 中 P (X) \end{matrix}$ 对于所有类别均为常数, 可以省略, 故有:

$\begin{matrix} \begin{matrix} P (C_{i} | X) = \frac{P (C_{i}) P (X | C_{i})}{P (X)} \propto \\ P (C_{i}) P (X | C_{i}) \end{matrix} \end{matrix}$ (2)

根据朴素贝叶斯分类算法的条件属性相互独立的假设, 有P $\begin{matrix} (C_{i} | X) \end{matrix}$ ∝ P $\begin{matrix} (C_{i}) \end{matrix} \begin{matrix} \overset{n}{\prod_{i = 1}} \end{matrix}$ P $\begin{matrix} (X_{i} | C_{i}) \end{matrix}$ , 其中 $\begin{matrix} P (C_{i}) = N_{i} / N, N_{i} \end{matrix}$ 为类 $\begin{matrix} C_{i} 在训练样本中的实例数, N \end{matrix}$ 为训练样本的总数。所以NB模型为:

$\begin{matrix} P (C_{i} | X) = maxP (C_{i}) \overset{n}{\prod_{i = 1}} P (X_{i} | C_{i}) \end{matrix}$ (3)

概率 $\begin{matrix} P (X_{1} | C_{i}), P (X_{2} | C_{i}), \dots, P (X_{n} | C_{i}) \end{matrix}$ 可由训练样本估值, 为避免式(3)中 $\begin{matrix} P (X_{i} | C_{i}) \end{matrix}$ 为0, 本文使用拉普拉斯校准:

$\begin{matrix} P (X_{i} | C_{i}) = \frac{N (X_{i} | C_{i}) + 1}{| C_{i} |+ q} \end{matrix}$

式中: $\begin{matrix} N (X_{i} | C_{i}) \end{matrix}$ 为 $\begin{matrix} C_{i} \end{matrix}$ 类训练样本中出现特征 $\begin{matrix} X_{i} \end{matrix}$ 的样本数; $\begin{matrix} | C_{i} | \end{matrix}$ 为训练样本中类别为 $\begin{matrix} C_{i} \end{matrix}$ 的样本总数;q为类别为C_i的样本中 $\begin{matrix} X_{i} \end{matrix}$ 值的种类数^[8]。

朴素贝叶斯分类算法对待具有不同数据特点的数据集合, 分类性能的差别不大, 稳定性较强^[9]。对于数据缺损的情况, 该算法会通过预处理来提高数据的完整性。朴素贝叶斯分类算法从训练集中得到类先验概率和特征项的类条件概率来预测后验概率, 再根据公式得出需要被分类的实例的类情况。有限的训练数据集的分布难以完全代表总体情况的分布, 所以计算得到的先验概率的可信度有待修正。如果训练集没有良好的数据完备性, 那么预测的测试数据的类别标签的准确性就有可能下降。

1.2 半监督学习

半监督学习同时使用大量的无类标号的数据以及有类标号的数据来进行模式识别工作^[10]。

由于传统的朴素贝叶斯分类算法使用有类标号的训练集来预测测试集中数据的类别, 所以这里将式(3)记为:

$\begin{matrix} \begin{matrix} P (C_{i} | X) = \\ maxP (C_{i}) l \overset{n}{\prod_{i = 1}} P (X_{i} | C_{i}) l \end{matrix} \end{matrix}$ (4)

本文使用基于半监督学习的半监督朴素贝叶斯算法, 所以将式(4)修改为:

$\begin{matrix} \begin{matrix} P (C_{i} | X) = \\ maxP (C_{i}) (l + u) \overset{n}{\prod_{i = 1}} P (X_{i} | C_{i}) (l + u) \end{matrix} \end{matrix}$ (5)

式中: $\begin{matrix} P (C_{i}) (l + u) 和 P (X_{i} | C_{i}) (l + u) \end{matrix}$ 的计算是从修改后的训练集中得到的, 该训练集新增了无标号的测试集中预测得到的高置信度数据^{[11, 12]}。

当使用半监督学习时, 将会要求尽量少的人员来参与工作, 同时, 又能够带来比较高的准确性, 因此, 半监督学习越来越受到人们的重视。目前, 人们正在理论和实践上对半监督学习进行分析^{[13, 14]}。本文改进了半监督自我训练模型, 并结合朴素贝叶斯分类算法, 给出一种新型的分类方法。

2 本文算法

2.1 算法框架

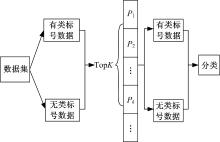
使用半监督学习和朴素贝叶斯结合的方法对大量未知类标号的数据进行分类, 半监督学习基本原理是基于少量的带类标注的训练样本建立初始分类器, 每次学习过程中分类器可以主动在未带类标注的候选样本集中选择最能体现分类器性能的样本, 并将这些样本以一定的方式加入到有类标号训练集中进一步训练分类器。传统的方法是将从无类标号候选集样本中预测所得的类标签连同样本数据一起添加到有类标号训练样本集当中, 从而提供更多的训练样本, 提高对测试集预测的准确率, 但是如果预测结果错误, 则会导致在循环的迭代中把大量带有错误类标注的元组添加到有类标号训练样本集中, 从而降低训练样本的正确率, 进而降低预测的正确率。本文使用NSNB算法通过选择无类标号样本集中预测准确程度比较高的样本, 将此类样本添加到有类标号训练集中, 使得有类标号训练样本集中保存的是高质量的样本, 进而能够高准确率地预测候选样本中的数据的类标号。利用NSNB算法生成数据的类标号的过程如图1所示, 其中TopK表示从无类标号数据集中选取的置信度高的 $\begin{matrix} K \end{matrix}$ 个样本。

	Figure Option View Download New Window
	图1 数据类标号生成过程Fig.1 Process of generating class of data

2.2 NSNB算法描述

输入:有类标号的训练集L; 无类标号的数据集U以及其中任一个样本 $x_{i}^{u}$ ; 数据置信度列表Tlist(初始为空); 选取的高置信度样本数为K。

输出:U中数据的预测类别C; 分类准确率R。

方法:

Step1 统计训练集L的类标号集合, 记为C{C₁, C₂, …, C_n}。

Step2 从U中任取一个样本 $\begin{matrix} X_{i}^{u} \end{matrix}$ ,

Step3 计算 $\begin{matrix} X_{i}^{u} \end{matrix}$ 其属于C中某个类别C_i的后验概率P(C_i| $\begin{matrix} X_{i}^{u} \end{matrix}$ ), 以及属于非C_i类的平均概率 $\begin{matrix} \frac{1}{N - 1} \end{matrix} \begin{matrix} \sum_{C'_{i} \neq C_{i}} \end{matrix}$ P(C'_i| $\begin{matrix} X_{i}^{u} \end{matrix}$ )。

Step4 令confidence_i为P(C_i| $\begin{matrix} X_{i}^{u} \end{matrix}$ )与 $\begin{matrix} \frac{1}{N - 1} \end{matrix} \begin{matrix} \sum_{C'_{i} \neq C_{i}} \end{matrix}$ P(C'_i| $\begin{matrix} X_{i}^{u} \end{matrix}$ )的差。

Step5 |C|=|C|-1, 如果|C|不为零, 返回到Step3。

Step6 返回所有confidence_i中数值最大的作为 $\begin{matrix} X_{i}^{u} \end{matrix}$ 的置信度, 将confidence_i添加到Tlist中。

Step7 |U|=|U|-1, 如果|U|不为零, 返回到Step2。

Step8 对Tlist中的 $\begin{matrix} X_{i}^{u} \end{matrix}$ 按confidence_i降序排序。

Step9 从Tlist中取出前K个样本 $\begin{matrix} X_{i}^{u} \end{matrix}$ , 将其添加到L中。

Step10 利用新得到的L来预测测试集中的样本的所属类别C, 并计算预测准确率R。

从算法中可以看出, 当K值越小, 也就是被加入到训练集L中的数据越少, 训练性能越高, 此时NSNB算法接近于NB算法; 当K值越大, 也就是被加入到训练集L中的数据越多, 训练性能越低, 此时NSNB算法接近于SNB算法。为了兼顾训练准确率和训练性能, 本文根据不同数据集手动选取适合各个数据集的K值。

2.3 NSNB算法总结

(1)如果对测试集中数据预测得比较准确, 则应该取较大的K值, 也就是将尽可能多的、准确的从训练集U中得到的预测结果及数据添加到训练集L中。

(2)如果对测试集中数据预测得不是很准确, 则应该取较小的 $\begin{matrix} K \end{matrix}$ 值, 此时认为数据置信度列表Tlist中值较大的为预测比较准确的, 也就是将尽可能少的、高准确率的从训练集U中得到的预测结果及数据添加到训练集L中, 这样可以避免将大量不正确的分类添加到训练集当中, 进而影响预测结果的准确性。

(3)通过计算 $\begin{matrix} P (C_{i}) (l + u) \end{matrix}$ 和 $\begin{matrix} P (X_{i} | C_{i}) (l + u) \end{matrix}$ 使得训练集L中不断地加入高准确率的数据, 从而使算法的准确性越来越高。

3 实验及结果分析

3.1 实验数据集

为了证明NSNB算法的有效性, 在UCI^[15]机器学习资源库中选取了比较有代表性的5个数据集进行了实验。5个数据集的基本信息如表1所示, 对于每个数据集, 比较新型半监督朴素贝叶斯(NSNB)算法, 传统半监督朴素贝叶斯(SNB)算法以及朴素贝叶斯(NB)算法3种算法的分类的准确率和所用时间。

表1 实验中所用数据集的描述 Table 1 Description of dataset used in experiment

由于ID一类的属性对于分类是无用的, 而且还会降低预测的准确率, 因而对部分实验数据集进行预处理, 例如实验前删除Adult数据集第3个属性fnlwgt。

3.2 准确率比较

本文选用的Micro-precision标准^[16]的计算公式如下:

$\begin{matrix} MP = \frac{1}{N} \overset{C}{\sum_{t = 1}} a_{t} \end{matrix}$

式中: $\begin{matrix} a_{t} \end{matrix}$ 为对数据某一类分类正确的数量; $\begin{matrix} N \end{matrix}$ 为数据集中数据对象的数量。

重复进行多次实验, 采用平均正确率来衡量分类的正确率:

$\begin{matrix} Average - MP = \frac{1}{N \times T} \overset{T}{\sum_{i = 1}} \overset{C}{\sum_{t = 1}} a_{t} \end{matrix}$

式中: T为重复实验的次数, 本文中T=10。

测试数据集中有类标号和无类标号数据比例不同对聚类效果的影响。有类标号数据量与无类标号数据量的比例 $\begin{matrix} γ \end{matrix}$ 分别为1:5、1:10、1:50、1:100。设Tlist.size()为数据置信度列表Tlist的大小, 并手动设置K值, 根据经验将各个数据集所用的K值分别设定:Adult为Tlist.size()* 20%; CarEvaluation为Tlist.size()* 90%; Nursery为Tlist.size()* 20%; Mushroom为Tlist.size()* 55%; Liver Disorders为Tlist.size()* 20%。NSNB、SNB、NB三种算法的准确率如表2~表5所示。

表2 三种算法的准确率对比(γ =1:5) Table 2 Contrast of accuracy rate of three algorithms

表3 三种算法的准确率对比(γ =1:10) Table 3 Contrast of accuracy rate of three algorithms

表4 三种算法的准确率对比(γ =1:50) Table 4 Contrast of accuracy rate of three algorithms

表5 三种算法的准确率对比(γ =1:100) Table 5 Contrast of accuracy rate of three algorithms

实验所得准确率是通过多次计算取平均值得出的, 对于大部分数据集该值的浮动都比较小, 但有个别数据集通过多次计算所得的准确率浮动较大。从表2~表5中数据可以看出, 当数据集中有类标号的数据量较多时, NSNB算法与NB算法的准确率比较接近, 随着无类标号的数据量的增加, NSNB算法的准确率就明显高于SNB算法和NB算法, 当数据集中γ =1:50时, NSNB算法的准确率比NB算法的准确率提高20%以上, 所以对于有大量未知类标号的数据来说NSNB算法是比较有优势的。三种算法在5个数据集上的平均预测准确率如图2所示。

	Figure Option View Download New Window
	图2 三种算法在数据集上预测平均准确率对比曲线Fig.2 Average prediction accuracy rate contrast curve of three kinds of algorithms in dataset

从4种比例的分割中还可以看出:对于大部分数据集来说, NSNB算法的准确率要优于SNB算法, 但也有部分数据集中SNB算法要优于NSNB算法, 这是由于从此类数据集中得出的分类大多数都是准确率较高的预测, 而本文选择的 $\begin{matrix} K \end{matrix}$ 值使得大量高预测精度的数据无法添加到训练样本中, 从而使SNB算法有更多可靠的数据用来预测, 因此预测准确率比NSNB算法高。

	Figure Option View Download New Window
	图3 五个数据集上算法NSNB和SNB的时间对比Fig.3 Contrast of NSNB and SNB consuming time in 5 kinds of datasets

3.3 算法执行时间比较

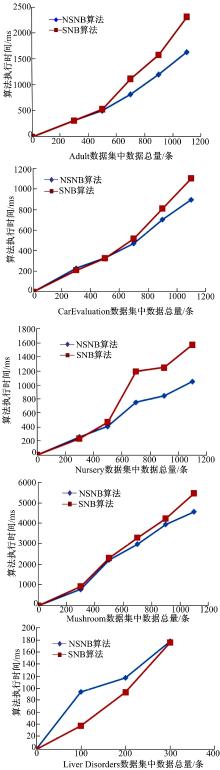
对比NSNB算法和SNB算法的运行时间, 本文以有类标号和无类标号数据比例为1:10为例分别计算两种算法在5个数据集上针对不同数据量的算法执行时间, 结果如图3所示。

实验结果证明:对于大部分数据集, 随着数据量的逐渐增加NSNB算法耗时小于SNB算法, 而且数据量越大NSNB算法的优势越明显。这是由于在NSNB算法第9步中筛选掉了大量不太可能正确的记录, 使得训练集不会迅速地增加, 从而节省了训练时间。但是从图3中可以看出, Liver Disorders数据集本身数据量比较少, 在300条数据记录内, NSNB算法优势无法凸显, 从其他四个数据集也可看出300条数据记录内, NSNB算法与SNB算法所用时间基本持平。其原因为:当数据量较少时, NSNB算法仍然需要生成数据置信度列表, 而SNB算法无需从无类标号数据集填入大量数据到有类标号训练数据集中, 所以会出现在个别数据集上SNB算法略显优势的情况。

4 结束语

在数据特征独立性假设的基础上, 讨论了朴素贝叶斯分类器的原理, 朴素贝叶斯算法需要对已知类别的大量数据进行训练, 但实际中又很难得到较为完备的训练数据, 所以本文在小型的有类标的训练集中, 利用NSNB算法自动增加高质量的训练量, 以强化朴素贝叶斯分类器的预测准确率。研究发现, NSNB算法分类精度较高, 而且还能提高分类器的性能。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Zhang H, Sheng S. Learning weighted naive Bayes with accurate ranking[C]//Proceedings of the Fourth IEEE International Conference on Data Mining, Brighton, 2004: 567-570. [本文引用:1]
[2]	Zheng Z, Webb G I. Lazy learning of bayesian rules[J]. Machine Learning, 2000, 41(1): 53-84. [本文引用:1]
[3]	Wang Z H, Webb G I, Zheng F. Adjusting Dependence Relations for Semi-lazy TAN Classfier[M]. Berlin: Springer, 2003: 453-456. [本文引用:1]
[4]	Yager R R. An extension of the naive Bayesian classifier[J]. Information Sciences, 2006, 176(5): 577-588. [本文引用:1]
[5]	江凯, 高阳. 并行化的半监督朴素贝叶斯分类算法[J]. 计算机科学与探索, 2012, 6(10): 912-918. Jiang Kai, Gao Yang. A parallelized semi-supervised na?ve bayes classifier[J]. Journal of Frontiers of Computer Science and Technology, 2012, 6(10): 912-918. [本文引用:1]
[6]	Shahshahani B M, Land grebe D A. The effect of unlabeled samples in reducing the small sample size problem and mitigating the Hughes phenomenon[J]. IEEE Transactions on Geoscience and Remote Sensing, 1994, 32(5): 1087-1095. [本文引用:1]
[7]	Kulis B, Basu S, Dhillon I, et al. Semi-supervised graph clustering: a kernel approach[J]. Machine learning, 2009, 74(1): 1-22. [本文引用:1]
[8]	彭兴媛. 朴素贝叶斯分类改进算法的研究[D]. 重庆: 重庆大学数学与统计学院, 2012. Peng Xin-yuan. Research on naive Bayesian classifier algorithm[D]. Chongqing: School of Mathematics and Statistics, Chongqing University, 2012. [本文引用:1]
[9]	Su J, Shirab J S, Matwin S. Large scale text classification using semi-supervised multinomial naive bayes[C]//Proceedings of the 28th International Conference on Machine Learning, Bellevue, WA, USA, 2011: 97-104. [本文引用:1]
[10]	孔怡青. 半监督学习及其应用研究[D]. 无锡: 江南大学信息工程学院, 2009. Kong Yi-qing. Studies on semi-supervised learning and its applications[D]. Wuxi: School of Information Engineering, Jiangnan University, 2009. [本文引用:1]
[11]	Mann G S, McCallum A. Generalized expectation criteria for semi-supervised learning with weakly labeled data[J]. The Journal of Machine Learning Research, 2010, 11: 955-984. [本文引用:1]
[12]	Hall M, Frank E, Holmes G, et al. The WEKA data mining software: an update[J]. ACM SIGKDD Explorations Newsletter, 2009, 11(1): 10-18. [本文引用:1]
[13]	Zhu X J, Goldberg A B. Introduction to semi-supervised learning[J]. Synthesis Lectures on Artificial Intelligence and Machine Learning, 2009, 3(1): 1-130. [本文引用:1]
[14]	Kveton B, Valko M, Rahimi A, et al. Semi-supervised learning with max-margin graph cuts[C]//Thirteenth International Conference on Artificial Intelligence and Statistics, Sardinia, Italy, 2010: 421-428. [本文引用:1]
[15]	UCI machine learning repository[DB/OL]. [2013-05-20]. http://archive.ics.uci.edu/ml/index.html [本文引用:1]
[16]	Modha D S, Spangler W S. Feature weighting in k-means clustering[J]. Machine Learning, 2003, 52(3): 217-237. [本文引用:1]

2004

0.0

... 许多学者提出了一些改进方法,Zhang等^[1]根据属性的重要性,提出了给不同属性赋予不同权值的加权朴素贝叶斯(Weighted naive Bayes,WNB)模型,并给出了采用爬山算法和Monte Carlo技术确定权值的加权朴素贝叶斯分类方法 ...

2000

0.0

... Zheng等^[2]利用懒惰式学习策略提出了一种懒惰式贝叶斯规则(Lazy Bayesian rule,LBR)学习技术,该方法在局部朴素贝叶斯规则的归纳中使用懒惰式技术,虽然大大地提高了分类精确度,但是效率很低 ...

2003

0.0

... Wang等^[3]提出了一种半懒惰式(Semi-Lazy)的限制性贝叶斯网络分类器的条件概率调整方法,在某些情况下可以减小错误分类率 ...

2006

0.0

... Yager^[4]利用有序算子,提出一种新的朴素贝叶斯的扩展算法 ...

2012

0.0

. 2012, 6(10):912-918 DOI:doi:10.3778/j.issn.1673-9418.2012.10.006

A parallelized semi-supervised na?ve bayes classifier

并行化的半监督朴素贝叶斯分类算法

Jiang Kai , Gao Yang.

江凯, 高阳

Nowadays TBs or even PBs data burst out every day, but there are so few labeled instances for training. For these two problems, this paper combines a semi-supervised Naïve Bayes algorithm and the Map-Reduce programming model, and proposes a new algorithm called parallelized semi-supervised Naïve Bayes (PSNB) algorithm. Experimental results show that the proposed algorithm can tackle with massive data efficiently, and use the unlabeled instances to improve the performance of the classifier.

针对当前需要对海量的文本数据进行分类和用于训练的带标记的文本数据非常匮乏这两个问题，结合半监督的朴素贝叶斯分类算法和Map-Reduce编程模型，提出了一种新型的并行化的半监督朴素贝叶斯分类（parallelized semi-supervised Naïve Bayes，PSNB）算法。通过实验可以看出，PSNB算法不仅可以高效地处理海量的文本数据，还可以有效地利用无标记的文本数据来提高分类器准确率。

... 当无标记的数据集数量较大时,有监督的学习不能准确地预测出元组的类别,而无监督学习由于没有指导所以难以得到较高精度的学习结果^[5] ...

1994

0.0

... 半监督学习的研究从Shahshahani和Landgrebe的工作开始^[6],它结合了监督学习和无监督学习的优点^[7],可以根据数据固有的特性,既不丢失完整的有标记的数据信息,又能够利用大量不完整数据(无类标号数据)的信息进行学习,因此具有更好的应用前景,而且处理的问题也更具普遍性 ...

2009

0.0

2012

0.0

... q为类别为Ci的样本中 Xi值的种类数^[8] ...

2011

0.0

... 朴素贝叶斯分类算法对待具有不同数据特点的数据集合,分类性能的差别不大,稳定性较强^[9] ...

2009

0.0

. 2009, :- DOI:doi:10.7666/d.y1661988

Studies on semi-supervised learning and its applications

半监督学习及其应用研究[D]

Kong Yi-qing.

孔怡青

本文研究了半监督学习算法及其在数据挖掘技术中的应用。首先,本文对机器学习、数据挖掘的相关知识进行了简单介绍,主要对它们的定义、发展历史和相关流程等进行了讨论。其次,介绍了本文所使用的半监督学习算法。最后,以信用卡数据和望远镜数据为例,进行了数据挖掘技术算法实现。在数据挖掘技术中,涉及到机器学习问题。半监督学习是在机器学习领域中同时利用训练样本的类别标记信息和未标记信息的学习方法。监督学习作为机器学习中的一种很主要的方法,基于类别标记已知的前提。在实际问题中,往往需要大的样本集,而提供大量已知类别的样本却存在一定的困难。非监督学习是机器学习中的另一种主要的方法,它不要求类别标记是已知的。但是,与监督学习相比,非监督学习存在着更大的不确定性。由于半监督学习同时利用训练样本的类别标记信息和未标记信息,所以它可以作为传统的监督学习和非监督学习的有益补充。我们所研究的半监督学习算法,就是基于这些基本原理。本文的主要创新点以及研究工作如下: (1)对半监督学习所涉及的理论基础及相关工作进行了研究,以便后文对算法进行相应的改进研究。目前在机器学习界,主要还是传统的监督学习和非监督学习两大类别,半监督学习还属于一个比较新颖的领域。对数据挖掘所涉及的相关工作领域进行了研究,以便后文对数据挖掘应用进行相应的分析研究。 (2)给出了一个基于贝叶斯分类的半监督学习算法。该算法基于贝叶斯决策理论,通过概率密度函数进行分布估计,对两类别半监督学习问题进行判定。 (3)给出了一个基于FCM的半监督学习算法。该算法来源于非监督学习的聚类方法,采用类别分离的间接方法来度量,并且加入了模糊模式识别方法,可以同时进行特征选择,对多类别半监督学习问题进行判定。 (4)给出了在信用卡数据挖掘模型中,加入半监督学习算法作为技术解决方案的方法。该方案使用的算法就是基于FCM的半监督学习算法,同时可以进行特征选择。并且,因考虑到信用卡审批模型的特点,引入了损失函数,从而得到了一种新的半监督学习算法,来进行不同类别用户的判定。对天文数据分析进行了应用,给出了MAGIC望远镜数据的信息分析,这些数据将高能射线信号与背景区分开来。

... 2 半监督学习半监督学习同时使用大量的无类标号的数据以及有类标号的数据来进行模式识别工作^[10] ...

2010

0.0

... 式中: P(Ci)(l+u)和P(Xi|Ci)(l+u)的计算是从修改后的训练集中得到的,该训练集新增了无标号的测试集中预测得到的高置信度数据^[11,12] ...

2009

0.0

... 式中: P(Ci)(l+u)和P(Xi|Ci)(l+u)的计算是从修改后的训练集中得到的,该训练集新增了无标号的测试集中预测得到的高置信度数据^[11,12] ...

2009

0.0

... 目前,人们正在理论和实践上对半监督学习进行分析^[13,14] ...

2010

0.0

... 目前,人们正在理论和实践上对半监督学习进行分析^[13,14] ...

2013

0.0

... 1 实验数据集为了证明NSNB算法的有效性,在UCI^[15]机器学习资源库中选取了比较有代表性的5个数据集进行了实验 ...

2003

0.0

... 2 准确率比较本文选用的Micro-precision标准^[16]的计算公式如下: ...