基于语音存在概率的噪声功率谱估计

引用本文

赵彦平, 赵晓晖, 王波. 基于语音存在概率的噪声功率谱估计.吉林大学学报:工学版, 2016, 46(3): 917-922
ZHAO Yan-ping, ZHAO Xiao-hui, WANG Bo. Noise power spectrum estimation based on speech presence probability. Journal of Jilin University Engineering and Technology Edition, 2016, 46(3): 917-922 复制到剪切板

Permissions

基于语音存在概率的噪声功率谱估计

赵彦平, 赵晓晖, 王波

吉林大学通信工程学院,长春 130012

通讯作者:赵晓晖(1957-),男,教授,博士生导师.研究方向:信号处理在通信中的应用.E-mail:xhzhao@jlu.edu.cn

作者简介:赵彦平(1978-),女,讲师,博士研究生.研究方向:语音信号处理.E-mail:zhaoyp@jlu.edu.cn

基金:国家自然科学基金项目(61171079)

摘要

在幅度平方谱模型下,利用语音和噪声信号的幅度平方谱服从指数分布,结合由后验信噪比不确定性决定的后验语音存在概率来更新噪声功率谱估计,很好地抑制了噪声且避免了语音信号失真。仿真实验结果表明:本文方法能够准确跟踪噪声功率谱、快速跟踪噪声功率谱变化,可以在一定程度上提高增强后语音信号的质量。

关键词: 信息处理技术; 语音增强; 噪声功率谱估计; 语音存在概率

中图分类号:TN912 文献标志码:A 文章编号:1671-5497(2016)03-0917-06

Noise power spectrum estimation based on speech presence probability

ZHAO Yan-ping, ZHAO Xiao-hui, WANG Bo

College of Communication Engineering, Jilin University, Changchun 130012, China

Abstract

Using the magnitude-square spectrum model and the exponential probability densities of the magnitude-square spectrum of the clean speech and noise. The new method updates the noise power spectrum estimation using the posteriori speech presence probability by incorporating a posteriori signal to noise ratio uncertainty. It can suppress effectively the background noise without introducing speech distortion. The simulation results reveal that the new method is characterized by tracking noise power spectrum accurately and following quickly abrupt changes in the noise spectrum. The quality of enhanced speech signal is improved in a certain extent.following quickly abrupt changes in the noise spectrum. The quality of the enhanced speech signal is improved in a certain extent.

Keyword: information processing; speech enhancement; noise power spectrum estimation; speech presence probability

Show Figures

0 引言

大多数语音增强方法都要对噪声进行估计^{[1, 2]}, 这意味着噪声估计的准确程度决定着语音增强系统的性能。噪声估计过高会导致信号失真; 噪声估计过低会产生音乐噪声。传统方法常利用带噪语音信号起始段没有语音的部分或根据语音活动性检测(Voice activity detectors, VAD)结果确定的噪声部分进行噪声功率谱估计, 但这种方法只适用于平稳噪声。对于非平稳噪声, 该方法不能跟踪噪声功率谱的快速变化, 导致语音增强系统性能降低。

文献^[3]提出了一种基于最优滤波和最小统计的噪声功率谱估计(Minimum statistics, MS)。文献^[4]提出了最小控制递归平均(Minima controlled recursive averaging, MCRA)方法。文献^[5]提出了改进的最小控制递归平均(Improved minima controlled recursive averaging, IMCRA)方法。上述三种方法^{[3, 4, 5]}虽然都能对非平稳噪声进行估计, 但它们对噪声功率谱的突然变化不能做出迅速的反应, 跟踪噪声变化都有一定的延迟时间。文献^[6]提出了一种低复杂度、低时延的无偏噪声功率谱估计方法。该方法用语音存在概率代替VAD, 无需偏差补偿。与传统的基于最小均方误差的噪声功率谱估计方法相比, 该方法减少了噪声功率谱的过估计。但是该方法假设语音信号不存在和存在的先验概率都为固定值0.5, 使得这两个概率的比值对计算后验概率没有贡献。

针对这一问题, 本文利用结合后验信噪比不确定的后验语音存在概率来更新噪声功率谱的估计。利用该方法得到的噪声功率谱估计的最大值与利用文献^[6]方法得到的最大值接近, 但提高了低估计值, 所以既很好地估计了噪声又避免了过高估计导致的信号失真。同时该方法能快速跟踪噪声功率谱的变化, 对平稳噪声和非平稳噪声都具有良好的估计效果。

1 固定先验概率的噪声估计方法

用大写字母表示随机变量, 对应的小写字母表示时域观测值, 带尖号(“ ^” )的字母表示估计值, 如: $\begin{matrix} \hat{γ} \end{matrix}$ 是 $\begin{matrix} γ \end{matrix}$ 的估计值。时域加窗分帧信号经过离散傅里叶变换(DFT)转换到频域。 $\begin{matrix} X_{k} (l) \end{matrix}$ 和 $\begin{matrix} D_{k} (l) \end{matrix}$ 分别表示第 $\begin{matrix} l \end{matrix}$ 帧第 $\begin{matrix} k \end{matrix}$ 个频率点语音和噪声信号的谱系数。假设语音信号和噪声信号在短时傅里叶变换域是加性的, 带噪信号的谱系数为 $\begin{matrix} Y_{k} (l) = X_{k} (l) + D_{k} (l) 。 \end{matrix}$ 为了方便表达, 省略帧序号 $\begin{matrix} l \end{matrix}$ 和频率点序号 $\begin{matrix} k, \end{matrix}$ 有:

$\begin{matrix} Y = X + D \end{matrix}$ (1)

假设语音信号和噪声信号是零均值且相互独立的, 有:

$\begin{matrix} E (| Y |^{2}) = E (| X |^{2}) + E (| D |^{2}) \end{matrix}$ (2)

式中: $\begin{matrix} E (\cdot) \end{matrix}$ 表示数学期望。

语音和噪声的功率谱分别定义为 $\begin{matrix} E (| X |^{2}) = σ_{X}^{2} \end{matrix}$ 和 $\begin{matrix} E (| D |^{2}) = σ_{D}^{2}, \end{matrix}$ 相应地定义先验信噪比为 $\begin{matrix} ξ = σ_{X}^{2} / σ_{D}^{2}; \end{matrix}$ 后验信噪比为 $\begin{matrix} γ = | y |^{2} / σ_{D}^{2} 。 \end{matrix}$

1.1 基于最小均方误差的噪声功率谱估计

基于最小均方误差(Minimum mean-square error, MMSE)的噪声功率谱估计方法假设语音和噪声的谱系数均服从复高斯分布:

$p_{X} (x) = \frac{1}{σ_{X}^{2} π} \exp (- \frac{| x |^{2}}{σ_{X}^{2}})$ (3)

$p_{D} (d) = \frac{1}{σ_{D}^{2} π} \exp (- \frac{| d |^{2}}{σ_{D}^{2}})$ (4)

在语音存在概率不确定条件下, 噪声功率谱的MMSE估计为^[6]:

$\begin{matrix} \begin{matrix} E (| D |^{2} | y) = P (Η_{0} | y) E (| D |^{2} | y, Η_{0}) + \\ P (Η_{1} | y) E (| D |^{2} | y, Η_{1}) \end{matrix} \end{matrix}$ (5)

式中: $\begin{matrix} Η_{0} \end{matrix}$ 表示语音不存在; $\begin{matrix} Η_{1} \end{matrix}$ 表示语音存在。

1.2 后验语音存在概率的计算

基于语音、噪声谱系数服从复高斯分布的假设和贝叶斯理论, 得到后验语音存在概率为:

$\begin{matrix} P (Η_{1} | y) = \frac{P (Η_{1}) p_{Y | Η_{1}} (y)}{P (Η_{0}) p_{Y | Η_{0}} (y) + P (Η_{1}) p_{Y | Η_{1}} (y)} \end{matrix}$ (6)

式中:似然函数 $\begin{matrix} p_{Y | Η_{1}} (y) \end{matrix}$ 和 $\begin{matrix} p_{Y | Η_{0}} (y) \end{matrix}$ 分别表示在语音存在和不存在的条件下, 观测值 $\begin{matrix} y \end{matrix}$ 符合模型参数的程度:

$p_{Y | Η_{0}} (y) = \frac{1}{{\hat{σ}}_{D}^{2} π} \exp (- \frac{| y |^{2}}{{\hat{σ}}_{D}^{2}})$ (7)

$p_{Y | Η_{1}} (y) = \frac{1}{{\hat{σ}}_{D}^{2} (1 + ξ_{Η_{1}}) π} \exp (- \frac{| y |^{2}}{{\hat{σ}}_{D}^{2} (1 + ξ_{Η_{1}})})$ (8)

式中: $\begin{matrix} {\hat{σ}}_{D}^{2} \end{matrix}$ 为 $\begin{matrix} σ_{D}^{2} \end{matrix}$ 的估计值, 计算中噪声功率谱的估计值用前一帧的代替, 即 $\begin{matrix} {\hat{σ}}_{D}^{2} = {\hat{σ}}_{D}^{2} (l - 1); ξ_{Η_{1}} \end{matrix}$ 为语音存在的先验信噪比, 可以解释成长时信噪比而不是短时局部信噪比。

将式(7)(8)代入式(6)得到后验语音存在概率为:

$\begin{matrix} P (Η_{1} | y) = {(1 + \frac{P (Η_{0})}{P (Η_{1})} (1 + ξ_{Η_{1}}) e^{- \frac{| y |^{2}}{{\hat{σ}}_{D}^{2}} (\frac{ξ_{Η_{1}}}{1 + ξ_{Η_{1}}})})}^{- 1} \end{matrix}$ (9)

1.3 E(|D|²|y, Η ₀)和E(|D|²|y, Η ₁)的推导

由式(9)得到后验信噪比估计 $\begin{matrix} \hat{γ} = | y |^{2} / D^{2} \end{matrix}$ 是 $\begin{matrix} ξ_{Η_{1}} \end{matrix}$ 的函数:

$\begin{matrix} \hat{γ} = \log (\frac{1 + ξ_{Η_{1}}}{P (Η_{1} {| y)}^{- 1} - 1}) \frac{1 + ξ_{Η_{1}}}{ξ_{Η_{1}}} \end{matrix}$ (10)

而且很容易满足 $\begin{matrix} \hat{γ} > 1 。 \end{matrix}$ 当语音存在时, $\begin{matrix} P (Η_{1} | y) \end{matrix}$ 值很大, 先验信噪比可用最大似然估计得到, 所以在语音存在的条件下噪声的功率谱估计为:

$\begin{matrix} \begin{matrix} E (| D |^{2} | y, \hat{ξ}, Η_{1}) = \\ E (| D |^{2} | y, {\hat{ξ}}^{ML} = \hat{γ} - 1) = {\hat{σ}}_{D}^{2} \end{matrix} \end{matrix}$ (11)

在语音不存在的条件下有:

$\begin{matrix} \begin{matrix} E (| D |^{2} | y, Η_{0}) = E (| D |^{2} | d) = \\ | d |^{2} = | y |^{2} \end{matrix} \end{matrix}$ (12)

将式(11)(12)代人式(5), 得:

$\begin{matrix} \begin{matrix} E (| D |^{2} | y) = P (Η_{0} | y) | y |^{2} + \\ P (Η_{1} | y) {\hat{σ}}_{D}^{2} \end{matrix} \end{matrix}$ (13)

式中: $\begin{matrix} P (Η_{0} | y) = 1 - P (Η_{1} | y) 。 \end{matrix}$

最终噪声功率谱估计为:

$\begin{matrix} {\hat{σ}}_{D}^{2} (l) = α {\hat{σ}}_{D}^{2} (l - 1) + (1 - α) E (| D |^{2} | y (l)) \end{matrix}$ (14)

式中: $\begin{matrix} α 为平滑因子; {\hat{σ}}_{D}^{2} (l) 和 {\hat{σ}}_{D}^{2} (l - 1) \end{matrix}$ 分别为当前帧和前一帧的噪声功率谱估计。

2 本文方法

2.1 统计模型

带噪语音信号的功率谱可表示为^[1]:

$\begin{matrix} P_{Y} = P_{X} + P_{D} \end{matrix}$ (15)

式中: $\begin{matrix} P_{Y} 、 P_{X} \end{matrix}$ 和 $\begin{matrix} P_{D} \end{matrix}$ 分别表示带噪语音信号、纯净语音和噪声的功率谱。

虽然式(15)具有统计意义, 但为简化噪声抑制方法, 可以用幅度平方谱近似表示功率谱, 有:

$\begin{matrix} | Y |^{2} \approx | X |^{2} + | D |^{2} \end{matrix}$ (16)

与基于MMSE的噪声功率谱估计方法假设一致, 本文仍然假设纯净语音和噪声的谱系数服从复高斯分布, 所以纯净语音幅度平方谱 $\begin{matrix} | X |^{2} \end{matrix}$ 和噪声幅度平方谱 $\begin{matrix} | D |^{2} \end{matrix}$ 分别服从指数分布:

$p_{| X |^{2}} (| x |^{2}) = \frac{1}{σ_{X}^{2}} \exp (- \frac{| x |^{2}}{σ_{X}^{2}})$ (17)

$p_{| D |^{2}} (| d |^{2}) = \frac{1}{σ_{D}^{2}} \exp (- \frac{| d |^{2}}{σ_{D}^{2}})$ (18)

利用贝叶斯理论得到纯净语音幅度平方谱的后验概率密度为:

$\begin{matrix} \begin{matrix} p_{| X |^{2} || y |^{2}} (| x |^{2}) = \\ \frac{p_{| Y |^{2} || x |^{2}} (| y |^{2}) p_{| X |^{2}} (| x |^{2})}{p_{| Y |^{2}} (| y |^{2})} = \\ \{\begin{matrix} Ψ e^{- \frac{| x |^{2}}{Φ}}, σ_{X}^{2} \neq σ_{D}^{2} \\ \frac{1}{| y |^{2}}, σ_{X}^{2} = σ_{D}^{2} \end{matrix} \end{matrix} \end{matrix}$ (19)

式中: x²∈[0,|y|²];Φ的定义为:

$\frac{1}{Φ} \equiv \frac{1}{σ_{X}^{2}} - \frac{1}{σ_{D}^{2}}, σ_{X}^{2} \neq σ_{D}^{2}$ (20)

而且：

$Ψ \equiv Φ {\{1 - \exp [- \frac{| y |^{2}}{Φ}]\}}^{- 1}$ (21)

2.2 后验语音存在概率

利用文献[11]的方法求后验语音存在概率 $\begin{matrix} P (Η_{1} || y |^{2}) 。 \end{matrix}$ 瞬时信噪比定义为:

$\begin{matrix} ξ_{I} = | x |^{2} / | d |^{2} \end{matrix}$ (22)

与基于MMSE的噪声功率谱估计方法一样, 用 $\begin{matrix} Η_{1} \end{matrix}$ 和 $\begin{matrix} Η_{0} \end{matrix}$ 表示语音存在和不存在两个假设。

$\begin{matrix} \{\begin{matrix} Η_{0} : ξ_{I} < ε, 语音不存在 \\ Η_{1} : ξ_{I} \geq ε, 语音存在 \end{matrix} \end{matrix}$ (23)

式中: $\begin{matrix} ε \end{matrix}$ 为门限值。

假设的概率计算公式为:

$\begin{matrix} \begin{matrix} P (Η_{1} || y |^{2}) = P (ξ_{I} \geq ε || y |^{2}) = \\ P (| x |^{2} \geq \frac{ε}{ε + 1} | y |^{2} || y |^{2}) = \\ \int_{\frac{ε}{ε + 1}}^{|} p_{| X |^{2} || y |^{2}} (z) dz \end{matrix} \end{matrix}$ (24)

将式(19)代入式(24)得:

$\begin{matrix} P (Η_{1} || y |^{2}) = \{\begin{matrix} \frac{e^{\frac{ν}{ε + 1}} - 1}{e^{ν - 1}}, & σ_{X}^{2} \neq σ_{D}^{2} \\ \frac{1}{ε + 1}, & σ_{X}^{2} = σ_{D}^{2} \end{matrix} \end{matrix}$ (25)

式中: $\begin{matrix} ν = (1 - ξ) γ / ξ 。 \end{matrix}$

在幅度平方谱的模型下, 式(13)可表示为:

$\begin{matrix} \begin{matrix} E (| D |^{2} || y |^{2}) = \\ P (Η_{0} || y |^{2}) | y |^{2} + P (Η_{1} || y |^{2}) {\hat{σ}}_{D}^{2} \end{matrix} \end{matrix}$ (26)

式中: $\begin{matrix} P (Η_{0} || y |^{2}) = 1 - P (Η_{1} || y |^{2}) 。 \end{matrix}$

最终得到新的噪声功率谱估计为:

${\hat{σ}}_{D}^{2} (l) = β {\hat{σ}}_{D}^{2} (l - 1) + (1 - β) E (| D |^{2} || y (l) |^{2})$ (27)

式中: $\begin{matrix} β \end{matrix}$ 为平滑因子。

2.3 两种语音存在概率比较

文献^[6]方法与本文方法的不同主要在于计算后验语音存在概率方法的不同。式(9)中, 先验概率 $\begin{matrix} P (Η_{1}) = 1 - P (Η_{0}) = 0.5, ξ_{Η_{1}} = 10^{\frac{15}{10}}, \end{matrix}$ 这样式(9)就表示成后验信噪比的关系式, 而且有:

$\begin{matrix} \lim_{γ \to \infty} P (Η_{1} | y) = {[1 + (1 + ξ_{Η_{1}}) e^{- γ \frac{ξ_{Η_{1}}}{1 + ξ_{Η_{1}}}}]}^{- 1} = 1 \end{matrix}$ (28)

实际上, 当 $\begin{matrix} γ \end{matrix}$ 为10 dB左右时, $\begin{matrix} P (Η_{1} | y) \end{matrix}$ 接近于1, 如图1中实线所示。

	Figure Option View Download New Window
	图1 语音存在概率对比Fig.1 Comparison of speech presence probability

同样当语音存在时, 先验信噪比可用最大似然估计得到。式(25)中, 有 $\begin{matrix} \hat{ξ} = \max (0, \hat{γ} - 1), \end{matrix}$ 这样 $\begin{matrix} P (Η_{1} || y |^{2}) \end{matrix}$ 也只与后验信噪比 $\begin{matrix} γ \end{matrix}$ 有关。当 $\begin{matrix} ε \end{matrix}$ 取不同值时, 语音存在的后验概率曲线如图1中虚线所示。当 $\begin{matrix} ε = - 5 dB \end{matrix}$ 时, 曲线上升最快; 当 $\begin{matrix} ε = 5 dB \end{matrix}$ 时, 曲线比较平缓; 当 $\begin{matrix} ε = 0 dB \end{matrix}$ 时, 曲线居中。从图1中可以看出:当 $\begin{matrix} γ \end{matrix}$ 为15 dB左右时, 无论 $\begin{matrix} ε \end{matrix}$ 取何值, $\begin{matrix} P (Η_{1} || y |^{2}) \end{matrix}$ 都接近于1。也就是说低信噪比时, 这两种求后验语音存在概率的方法得到的概率值有差别, 而高信噪比时这两种方法近似, 概率值都接近于1。

3 仿真实验

为了验证本文方法的性能, 对本文方法和文献^[4]提出的MCRA方法、文献^[6]提出的固定先验概率噪声功率谱估计方法进行了对比。文献^[6]方法中为避免由于噪声功率谱估计过低引起的后验语音存在概率估计更新的停滞, 采用下面的方法进行处理。首先对 $\begin{matrix} P (Η_{1} | y (l)) \end{matrix}$ 进行迭代平滑:

$\begin{matrix} P (l) = 0.9 P (l - 1) + 0.1 P (Η_{1} | y (l)) \end{matrix}$ (29)

然后通过 $\begin{matrix} P (l) \end{matrix}$ 值控制 $\begin{matrix} P (Η_{1} | y (l)) : \end{matrix}$

$\begin{matrix} \begin{matrix} P (Η_{1} | y (l)) = \\ \{\begin{matrix} \min (0.99, P (Η_{1} | y (l)), P (l) > 0.99 \\ P (Η_{1} | y (l)), 其他 \end{matrix} \end{matrix} \end{matrix}$ (30)

本文方法也应用了此方法对后验语音存在概率进行了处理。实验中取 $\begin{matrix} 10 \lg (ξ_{Η_{1}}) = 15 dB, \end{matrix}$ 平滑因子 $\begin{matrix} α = β = 0.8 。 \end{matrix}$

仿真实验中纯净语音来自TIMIT语音库^[7], 噪声来自Noisex92噪声库^[8], 噪声采样频率转换为16 kHz, 实验中帧长为512点, 50%帧重叠, 加汉宁窗。

3.1 噪声功率谱估计

为了对比不同方法对噪声功率谱的估计能力, 随机在语音库中选取一段语音, 分别加入白噪声和Babble噪声, 信噪比均为5 dB, $\begin{matrix} ε = 0 dB 。 \end{matrix}$ 噪声功率谱的真实值为^[9]:

$\begin{matrix} {\hat{σ}}_{D}^{2} (l) = 0.9 {\hat{σ}}_{D}^{2} (l - 1) + 0.1 | D (l) |^{2} \end{matrix}$ (31)

仿真结果如图2~图4所示。

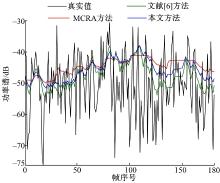
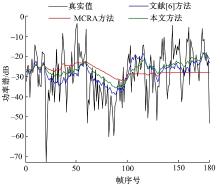
图2为白噪声背景下, 信噪比为5 dB, 频率为312 Hz时三种方法的估计结果对比图。从图2可以看出, 三种方法对白噪声都有很好的跟踪能力。噪声功率谱较大时, 三种方法估计效果近似; 噪声功率谱较小时, 本文方法估计效果介于MCRA方法和文献[6]方法之间。图3是Babble噪声背景下, 信噪比为5 dB, 频率为312 Hz时三种方法的估计结果对比图。从图3可以看出, 对于非平稳噪声, 功率谱波动较大, 本文方法和文献[6]方法都能很好地跟踪噪声变化, 而MCRA方法估计能力较差, 曲线较平坦。

	Figure Option View Download New Window
	图2 白噪声功率谱估计对比Fig.2 Comparison of the estimation of the noise power spectrum for white noise

	Figure Option View Download New Window
	图3 Babble噪声功率谱估计对比Fig.3 Comparison of the estimation of the noise power spectrum for babble noise

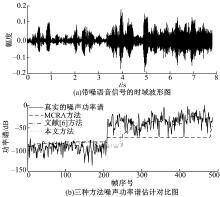
图4为不同噪声组合背景下, 三种噪声功率谱估计方法性能对比。图4(a)中前3.3 s加入Volvo汽车噪声, 信噪比为5 dB; 后4.4 s加入Babble噪声, 信噪比为0 dB, 频率都为1 kHz。图4(b)为三种方法噪声功率谱估计对比图。从图4(b)中可以看出, 对于Volvo汽车噪声, 三种方法都能较准确地估计噪声的功率谱, 而对于Babble噪声, MCRA方法随噪声功率谱变化能力较差, 本文方法和文献[6]方法能较快地跟踪噪声的变化, 而且本文方法跟踪能力较好一些。

	Figure Option View Download New Window
	图4 不同噪声功率谱估计对比Fig.4 Comparison of estimation of the different noise power spectrum

3.2 语音增强

噪声功率谱估计方法可以与大多数语音增强方法相结合来提高语音增强系统的性能。本文从TIMIT语音库中随机选取200个句子, 分别加白噪声、Babble噪声、Volvo汽车噪声和F16机舱噪声, 在0、5、10和15 dB信噪比条件下进行测试。语音增强方法采用的是文献^[1]中的MMSE-SPZC方法。利用语音质量客观评价方法中对数似然比(Log likelihood ratio, LLR)、分段信噪比(Segmental SNR, SegSNR)、加权谱包络(Weighted spectral slope, WSS)和语音质量感知评价(Perceptual evaluation of speech quality, PESQ)4个参数对方法的估计效果进行评价^[10]。这4个参数从不同角度衡量增强后语音的质量, LLR和WSS值越小表示系统性能越好; 而SegSNR和PESQ值越大表示系统性能越好, 实验结果如表1~表4所示。

表1 LLR对比 Table 1 Comparison of the LLR

表2 SegSNR对比 Table 2 Comparison of the SegSNR

从表1可以看出, 对于LLR, 在白噪声和Volvo汽车噪声背景下, 无论何种信噪比, 本文方法都能取得较好的估计效果。对于Babble噪声和F16机舱噪声, 文献^[6]方法优于本文方法。表2对比了SegSNR, 在白噪声和F16机舱噪声背景下, 本文方法优势明显; 在Babble噪声背景下, 本文方法在低信噪比时性能较好。从表3可以看出, 对于WSS, 本文方法在白噪声、Volvo汽车噪声和F16机舱噪声背景下估计性能较优; 在Babble噪声背景下, 低信噪比时估计效果较好。表4对比了PESQ, 可以看出在白噪声、Babble噪声和F16机舱噪声背景下, 本文方法估计性能较好; 在Volvo汽车噪声条件下, 文献^[6]方法略好于本文方法。综合来看, 与其他算法相比, 本文方法在大多数噪声条件下都能取得较好的估计性能, 提高了增强后语音信号的质量。

表3 WSS对比 Table 3 Comparison of the WSS

表4 PESQ对比 Table 4 Comparison of the PESQ

4 结束语

基于幅度平方谱语音模型, 提出了一种基于后验信噪比不确定的后验语音存在概率的噪声功率谱估计方法。该方法对平稳的白噪声具有较好的估计性能, 对非平稳的Babble噪声也有较好的跟踪能力, 并且能对噪声的突然变化做出快速反应。语音增强实验验证了低信噪比时, 本文方法可以在一定程度上提高增强后语音信号的质量; 高信噪比时本文方法性能与文献[6]方法近似。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Lu Y, Loizou P C. Estimators of the magnitude-squared spectrum and methods for incorporating SNR uncertainty[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2011, 19(5): 1123-1137. [本文引用:3]
[2]	欧世峰, 赵晓晖. 改进型先验信噪比估计语音增强算法[J]. 吉林大学学报: 工学版, 2009, 39(3): 787-791. Ou Shi-feng, Zhao Xiao-hui. Modified priori SNR estimation for noisy speech enhancement[J]. Journal of Jilin University (Engineering and Technology Edition), 2009, 39(3): 787-791. [本文引用:1]
[3]	Martin R. Noise power spectral density estimation based on optimal smoothing and minimum statistics[J]. IEEE Transactions on Speech and Audio Processing, 2001, 9(5): 504-512. [本文引用:2]
[4]	Cohen I, Berdugo B. Noise estimation by minima controlled recursive averaging for robust speech enhancement[J]. IEEE Signal Processing Letters, 2002, 9(1): 12-15. [本文引用:3]
[5]	Cohen I. Noise spectrum estimation in adverse environments: improved minima controlled recursive averaging[J]. IEEE Transactions on Speech and Audio Processing, 2003, 11(5): 466-475. [本文引用:2]
[6]	Gerkmann T, Hendriks R C. Unbiased MMSE-based noise power estimation with low complexity and low tracking delay[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2012, 20(4): 1383-1392. [本文引用:8]
[7]	Garofolo J S. DARPA TIMIT acoustic phonetic continuous speech database[J]. National Inst Stand ards Technol, 1988, 15: 29-50. [本文引用:1]
[8]	Varga A, Steeneken H J M. Assessment for automatic speech recognition: II. NOISEX-92: a database and an experiment to study the effect of additive noise on speech recognition systems[J]. Speech Communication, 1993, 12(3): 247-251. [本文引用:1]
[9]	Faraji N, Hendriks R C. Noise power spectral density estimation for public address systems in noisy reverberant environments[C]//International Workshop on Acoustic Signal Enhancement, Aachen, 2012: 61-64. [本文引用:1]
[10]	Hu Y, Loizou P C. Evaluation of objective quality measures for speech enhancement[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2008, 16(1): 229-238. [本文引用:1]

2011

0.0

... 0 引言大多数语音增强方法都要对噪声进行估计^[1,2],这意味着噪声估计的准确程度决定着语音增强系统的性能 ...

... 1 统计模型带噪语音信号的功率谱可表示为^[1]: ...

... 语音增强方法采用的是文献^[1]中的MMSE-SPZC方法 ...

2009

0.0

. 2009, 39(3):787-791

Modified priori SNR estimation for noisy speech enhancement

改进型先验信噪比估计语音增强算法

Ou Shi-feng , Zhao Xiao-hui.

欧世峰, 赵晓晖

摘　要：在DCT域提出了一种改进STNR(M-STNR)算法,其在原算法的第二步中利用信号的高斯模型假设条件,采用MMSE估计来获取当前帧先验信噪比的估计,算法无需语音增强系统增益因子的任何先验条件,在保持简单结构的同时避免了原算法的不足。仿真结果表明,基于该改进方案的语音增强算法在多种噪声背景下具有更出色的语音增强效果。

... 0 引言大多数语音增强方法都要对噪声进行估计^[1,2],这意味着噪声估计的准确程度决定着语音增强系统的性能 ...

2001

0.0

... 文献^[3]提出了一种基于最优滤波和最小统计的噪声功率谱估计(Minimum statistics,MS) ...

... 上述三种方法^[3,4,5]虽然都能对非平稳噪声进行估计,但它们对噪声功率谱的突然变化不能做出迅速的反应,跟踪噪声变化都有一定的延迟时间 ...

2002

0.0

... 文献^[4]提出了最小控制递归平均(Minima controlled recursive averaging,MCRA)方法 ...

... 上述三种方法^[3,4,5]虽然都能对非平稳噪声进行估计,但它们对噪声功率谱的突然变化不能做出迅速的反应,跟踪噪声变化都有一定的延迟时间 ...

... 3 仿真实验为了验证本文方法的性能,对本文方法和文献^[4]提出的MCRA方法、文献^[6]提出的固定先验概率噪声功率谱估计方法进行了对比 ...

2003

0.0

... 文献^[5]提出了改进的最小控制递归平均(Improved minima controlled recursive averaging,IMCRA)方法 ...

... 上述三种方法^[3,4,5]虽然都能对非平稳噪声进行估计,但它们对噪声功率谱的突然变化不能做出迅速的反应,跟踪噪声变化都有一定的延迟时间 ...

2012

0.0

... 文献^[6]提出了一种低复杂度、低时延的无偏噪声功率谱估计方法 ...

... 利用该方法得到的噪声功率谱估计的最大值与利用文献^[6]方法得到的最大值接近,但提高了低估计值,所以既很好地估计了噪声又避免了过高估计导致的信号失真 ...

... 在语音存在概率不确定条件下,噪声功率谱的MMSE估计为^[6]: ...

... 3 两种语音存在概率比较文献^[6]方法与本文方法的不同主要在于计算后验语音存在概率方法的不同 ...

... 3 仿真实验为了验证本文方法的性能,对本文方法和文献^[4]提出的MCRA方法、文献^[6]提出的固定先验概率噪声功率谱估计方法进行了对比 ...

... 文献^[6]方法中为避免由于噪声功率谱估计过低引起的后验语音存在概率估计更新的停滞,采用下面的方法进行处理 ...

... 对于Babble噪声和F16机舱噪声,文献^[6]方法优于本文方法 ...

... 在Volvo汽车噪声条件下,文献^[6]方法略好于本文方法 ...

1988

0.0

... 仿真实验中纯净语音来自TIMIT语音库^[7],噪声来自Noisex92噪声库^[8],噪声采样频率转换为16 kHz,实验中帧长为512点,50%帧重叠,加汉宁窗 ...

1993

0.0

... 仿真实验中纯净语音来自TIMIT语音库^[7],噪声来自Noisex92噪声库^[8],噪声采样频率转换为16 kHz,实验中帧长为512点,50%帧重叠,加汉宁窗 ...

2012

0.0

... 噪声功率谱的真实值为^[9]: ...

2008

0.0

... 利用语音质量客观评价方法中对数似然比(Log likelihood ratio,LLR)、分段信噪比(Segmental SNR,SegSNR)、加权谱包络(Weighted spectral slope,WSS)和语音质量感知评价(Perceptual evaluation of speech quality,PESQ)4个参数对方法的估计效果进行评价^[10] ...