<em> α</em>噪声背景下基于标准归一化相关函数的谐波信号频率估计的MUSIC方法

引用本文

石屹然, 赵晓晖, 李新波, 石要武. α噪声背景下基于标准归一化相关函数的谐波信号频率估计的MUSIC方法 .吉林大学学报:工学版, 2016, 46(3): 923-928
SHI Yi-ran, ZHAO Xiao-hui, LI Xin-bo, SHI Yao-wu. Standard normalized correlation-based MUSIC method for harmonic signal frequency estimation in α Noise . Journal of Jilin University Engineering and Technology Edition, 2016, 46(3): 923-928 复制到剪切板

Permissions

α噪声背景下基于标准归一化相关函数的谐波信号频率估计的MUSIC方法

石屹然^1,², 赵晓晖¹, 李新波¹, 石要武³

1.吉林大学通信工程学院, 长春 130022

2.长春气象仪器研究所, 长春 130012

3.吉林大学生物与农业工程学院, 长春 130022

通讯作者:赵晓晖(1957-),男,教授,博士生导师.研究方向:自适应信号处理理论与应用.E-mail:xhzhao@jlu.edu.cn

作者简介:石屹然(1984-),男,讲师,在站博士后.研究方向:信号处理.E-mail:shiyiran@jlu.edu.cn

基金:国家自然科学基金项目(61171079)

摘要

首先,针对噪声不存在有限方差的问题,对标准归一化相关函数的定义域进行了扩展,实现了背景噪声的抑制。在此基础上,利用谐波信号频率与噪声子空间的正交性,提出了谐波信号频率估计的MUSIC方法。仿真结果表明,与分数低阶类方法相比,由于标准归一化相关函数是一个线性算子,极大地简化了稳定分布信号处理的计算和分析过程。

关键词: 信号处理; 稳定分布; 谐波恢复; 归一化相关函数

中图分类号:TN911.23 文献标志码:A 文章编号:1671-5497(2016)03-0923-06

Standard normalized correlation-based MUSIC method for harmonic signal frequency estimation in α Noise

SHI Yi-ran^1,², ZHAO Xiao-hui¹, LI Xin-bo¹, SHI Yao-wu³

1.College of Communication Engineering, Jilin University, Changchun 130022, China

2.Cahngchun Meteorological Instrument Research Institute, Changchun 130012, China

3.College of Biological and Agricultural Engineering, Jilin University, Changchun 130022, China

Abstract

A standard normalized correlation-based MUSIC method is developed for harmonic signal frequency estimation in α noise. First, as there is no finite variance in the α noise, the domain of the standard normalized correlation function is extended, and the α noise is suppressed by this function. Based on these, the MUSIC method for harmonic signal frequency estimation is proposed using the orthogonality between the harmonic signal frequency and the noise subspace. Compared with the fractional lower order classification method, the standard normalized correlation function is a linear operator, which greatly simplifies the calculation and analysis of the α stable distributed signal processing.

Keyword: signal processing; stable distribution; harmonic recovery; standard normalized correlation function

Show Figures

0 引言

噪声背景下的谐波恢复是信号处理领域的核心问题之一, 传统的谐波恢复方法一般都是假设背景噪声为高斯噪声。然而在自然界中, 能够真正符合高斯分布的随机过程毕竟是少数。在大量的信号处理实践中, 其背景噪声通常为非高斯噪声^{[1, 2, 3, 4]}, 例如由放电引起的大气噪声, 水下生物引起的水下声学噪声, 数字电路的开关噪声, 无线通信中的信号窜扰等噪声。它们比高斯噪声出现大幅度的数据突变的频率更高。反映在时域上, 它们显现出大量的显著尖峰脉冲特性; 反映在概率密度上, 它们具有比高斯分布更加厚重的拖尾现象^{[5, 6]}。

研究结果^[6]表明, 这种非高斯冲击噪声可以用 $\begin{matrix} α \end{matrix}$ 稳定分布来表征, 一般称为 $\begin{matrix} α \end{matrix}$ 稳定分布噪声(简称为 $\begin{matrix} α \end{matrix}$ 噪声)。 $\begin{matrix} α \end{matrix}$ 稳定分布是唯一一种满足广义中心极限定理的广义高斯分布, 高斯分布是 $\begin{matrix} α \end{matrix}$ 稳定分布中, 当 $\begin{matrix} α = 2 \end{matrix}$ 的一个特例, 因此 $\begin{matrix} α \end{matrix}$ 稳定分布比高斯分布具有更广泛的代表意义。 $\begin{matrix} α \end{matrix}$ 稳定分布的一个重要性质是它不存在 $\begin{matrix} p > α \end{matrix}$ (当 $\begin{matrix} α < 2 \end{matrix}$ 时)的统计量^[6], 当 $\begin{matrix} α < 1 \end{matrix}$ 时, 甚至连均值的运算也不可能。因此, 在 $\begin{matrix} α \end{matrix}$ 噪声存在的场合, 现有的各种基于二阶矩、高阶矩和高阶累积量的信号处理方法均失效^[7]。目前, 任何涉及 $\begin{matrix} α \end{matrix}$ 稳定分布的信号基本上都是采用 $\begin{matrix} p < α < 2 \end{matrix}$ 的分数低阶矩^[7]或由其派生的统计工具进行处理。但采用分数低阶矩类方法解决 $\begin{matrix} α \end{matrix}$ 噪声背景下的谐波恢复问题时, 由于 $\begin{matrix} α \end{matrix}$ 稳定分布过程不存在有限的方差, 因此, 传统信号处理常用的方法, 如极大似然法、最小二乘法等, 均无法使用^[6]; 分数低阶矩类方法由于其本身固有的非线性, 无法得到该问题的闭式解^[8]。针对上述问题, 文献^[8]将 $\begin{matrix} α \end{matrix}$ 噪声背景下的谐波信号用一个 $\begin{matrix} α \end{matrix}$ 白噪声驱动的高阶AR模型表示, 然后利用分数低阶矩中, 当且仅当其阶次 $\begin{matrix} p = 1 \end{matrix}$ 时具有线性的性质, 采用GCC(Generalized covariation coefficient)方法巧妙地解决了这一问题。但该方法仅适于阶次 $\begin{matrix} p = 1 \end{matrix}$ 的情况, 当 $\begin{matrix} p \neq 1 \end{matrix}$ 时, 其谐波信号的频率估计精度显著下降, 因而该方法仅适用于 $\begin{matrix} α > 1 \end{matrix}$ 的稳定分布噪声的情况。

针对分数低阶矩类方法所存在的非线性问题, 文献^{[9, 10]}指出, 若 $\begin{matrix} α \end{matrix}$ 稳定分布过程 $\begin{matrix} y (n) \end{matrix}$ 可以用一个极点均在单位圆内的AR模型描述, 则适当定义的归一化相关函数估计(Normalized correlation estimate)存在, 因而可以用于 $\begin{matrix} α \end{matrix}$ 稳定分布信号处理。然而这种归一化相关函数虽然具有线性特性, 但其AR模型极点均在单位圆内这一约束条件却使得它无法用来解决谐波信号频率估计问题。本文对标准归一化相关函数的定义域进行了扩展, 证明了对于 $\begin{matrix} α \end{matrix}$ 稳定分布过程( $\begin{matrix} 0 < α \leq 2 \end{matrix}$ ), 其标准归一化相关函数存在。在此基础上提出了一种 $\begin{matrix} α \end{matrix}$ 噪声背景下, 基于标准归一化相关函数的谐波信号频率估计的MUSIC方法。

1 含噪谐波信号的数学模型

本文主要考虑这样一类噪声中的谐波信号频率估计问题:

$\begin{matrix} x (n) = \overset{q}{\sum_{i = 1}} α_{i} \exp (j (ω_{i} n + φ_{i})) \end{matrix}$ (1)

式中: $\begin{matrix} x (n) \end{matrix}$ 为待测无噪谐波信号; $\begin{matrix} α_{i} 、 ω_{i} (i = 1, \dots, q \end{matrix}$ )分别为谐波信号幅值和频率, 均为实常数; $\begin{matrix} φ_{i} \end{matrix}$ 为在 $\begin{matrix} [- π, π] \end{matrix}$ 内均匀分布的独立同分布随机相位; $\begin{matrix} q \end{matrix}$ 为谐波个数, 可以是未知的; j为虚部标志。

$\begin{matrix} x (n) \end{matrix}$ 的含噪观测信号 $\begin{matrix} y (n) \end{matrix}$ 为:

$\begin{matrix} y (n) = x (n) + e (n), n = 1, \dots, N \end{matrix}$ (2)

式中: e(n)为独立同分布Sα S稳定分布随机噪声, 且与 $\begin{matrix} x (n) \end{matrix}$ 相互独立; $\begin{matrix} N \end{matrix}$ 为观测序列长度。

式(2)中的 $\begin{matrix} SαS \end{matrix}$ 稳定分布过程的定义为^[6]:

若存在参数 $\begin{matrix} 0 < α \leq 2, γ \geq 0, - 1 \leq β \leq 1 \end{matrix}$ 和实数 $\begin{matrix} a \end{matrix}$ 使得随机变量 $\begin{matrix} x \end{matrix}$ 的特征函数具有式(3)的形式:

$φ (u) = \exp \{jau - γ {|u|}^{α} [1+ jβsgn (u) ω (u, α)]\}$ (3)

式中：

$ω (u, α) = \{\begin{matrix} \tan (πα / 2), α \neq 1 \\ (2 / π) \log |u|, α = 1 \end{matrix}$ (4)

$sg n (u) = \{\begin{matrix} 1, u > 0 \\ 0, u = 0 \\ - 1, u < 0 \end{matrix}$ (5)

则随机变量 $\begin{matrix} x \end{matrix}$ 服从 $\begin{matrix} α \end{matrix}$ 稳定分布, 记为: $\begin{matrix} x ~ S_{α} (γ, β, a) 。 \end{matrix}$

式(3)中, 若有 $\begin{matrix} β = a = 0, \end{matrix}$ 则称随机变量 $\begin{matrix} x \end{matrix}$ 服从Sα S稳定分布。

显然, 谐波信号 $\begin{matrix} x (n) \end{matrix}$ 的 $\begin{matrix} q \end{matrix}$ 个谐波频率可由特征方程(6)的根( $\begin{matrix} |z_{i}| = 1 \end{matrix}$ )决定^[11], 方程(6)的表达式如下:

$\begin{matrix} \overset{p}{\prod_{i = 1}} (z - z_{i}) (z - z_{i}^{*}) = \overset{2 p}{\sum_{i = 0}} b_{i} z^{2 p - i} = 0 \end{matrix}$ (6)

因而式(1)所示的谐波信号所对应的差分方程为:

$\begin{matrix} x (n) + \overset{2 q}{\sum_{i = 1}} b_{i} x (n - i) = 0 \end{matrix}$ (7)

将式(2)代入式(7)可得:

$\begin{matrix} y (n) + \overset{2 q}{\sum_{i = 1}} b_{i} y (n - i) = e (n) + \overset{2 q}{\sum_{i = 1}} b_{i} e (n - i) \end{matrix}$ (8)

由式(8)可见: $\begin{matrix} α \end{matrix}$ 白噪声背景下的谐波过程 $\begin{matrix} y (n) \end{matrix}$ 为一个特殊的ARMA( $\begin{matrix} 2 q, 2 q) \end{matrix}$ 过程, 该ARMA模型的极点均在单位圆上, 且其AR参数与MA参数相同。

2 本文方法

式(8)中, 由于 $\begin{matrix} e (n) \end{matrix}$ 为 $\begin{matrix} α \end{matrix}$ 稳定分布随机过程, 所以 $\begin{matrix} y (n) \end{matrix}$ 不存在有限的方差。若采用分数低阶矩类方法, 由于该方法本身所固有的非线性( $\begin{matrix} 0 < p < α, p \neq 1 \end{matrix}$ ), 所以无法得到含噪谐波信号的封闭表达式^[8]。

文献[9, 10]指出, 若 $\begin{matrix} α \end{matrix}$ 稳定分布过程 $\begin{matrix} y (n) \end{matrix}$ 可以用一个极点均在单位圆内的AR模型描述, 则有如下归一化相关函数估计存在:

$\begin{matrix} {\hat{r}}_{yy} (m) = \frac{\overset{N}{\sum_{n = 1}} y (n) y (n + m)}{\overset{N}{\sum_{n = 1}} y^{2} (n)} \end{matrix}$ (9)

但该归一化相关函数的定义要求 $\begin{matrix} α \end{matrix}$ 稳定分布过程 $\begin{matrix} y (n) \end{matrix}$ 所满足的AR模型的极点均在单位圆内, 这一条件过于严格。由于谐波信号模型的零极点均在单位圆上, 因而无法使用这种归一化相关函数来解决谐波信号的频率估计问题。

为了解决这一问题, 本文将文献^{[9, 10]}所提出的归一化相关函数的定义域进行扩展, 提出如下对于 $\begin{matrix} α \end{matrix}$ 稳定分布过程的标准归一化相关函数存在的定理。

定理设 $\begin{matrix} y (n) \end{matrix}$ 为服从 $\begin{matrix} S_{α} (σ, β, a) \end{matrix}$ 稳定分布的随机过程, 且 $\begin{matrix} 0 < α \leq 2, \end{matrix}$ 则有如下标准归一化相关函数存在:

$r_{yy} (m) = \frac{R_{yy} (m)}{R_{yy} (0)} = \frac{E [y (n) y (n + m)]}{E [y^{2} (n)]}$ (10)

证明由标准归一化相关函数的定义, 有:

$R_{yy} (m) = \frac{E [y (k) y (k + m)]}{E [y^{2} (k)]} = \frac{\lim_{N \to \infty} \overset{N}{\sum_{k = 1}} [y (k) y (k + m)]}{\lim_{N \to \infty} \overset{N}{\sum_{k = 1}} [y^{2} (k)]}$ (11)

因为：

$\overset{N}{\sum_{k = 1}} {[y (k) - y (k + m)]}^{2} \geq 0$ (12)

将式(12)展开, 有:

$\overset{N}{\sum_{k = 1}} {[y (k) - y (k + m)]}^{2} = \overset{N}{\sum_{k = 1}} y^{2} (k) - 2 \overset{N}{\sum_{k = 1}} y (k) y (k + m) + \overset{N}{\sum_{k = 1}} y^{2} (k + m)$ (13)

由于 $\begin{matrix} y (n) \end{matrix}$ 为服从 $\begin{matrix} S_{α} (σ, β, a) \end{matrix}$ 稳定分布, 因此y(k)具有平稳遍历性, 所以当N很大时, 有:

$\begin{matrix} \overset{N}{\sum_{k = 1}} y^{2} (k) = \overset{N}{\sum_{k = 1}} y^{2} (k + m) \end{matrix}$ (14)

则式(12)为:

$\overset{N}{\sum_{k = 1}} {[y (k) - y (k + m)]}^{2} = 2 \overset{N}{\sum_{k = 1}} y^{2} (k) - 2 \overset{N}{\sum_{k = 1}} y (k) y (k + m) \geq 0$ (15)

所以有：

$\overset{N}{\sum_{k = 1}} y^{2} (k) \geq \overset{N}{\sum_{k = 1}} y (k) y (k + m)$ (16)

将式(16)代入式(10), 有:

$\begin{matrix} \begin{matrix} r_{yy} (m) = \frac{E [y (k) y (k + m)]}{E [y^{2} (k)]} = \\ \frac{\lim_{N \to \infty} \overset{N}{\sum_{k = 1}} [y (k) y (k + m)]}{\lim_{N \to \infty} \overset{N}{\sum_{k = 1}} [y^{2} (k)]} \leq \\ \lim_{N \to \infty} \frac{\overset{N}{\sum_{k = 1}} [y^{2} (k)]}{\overset{N}{\sum_{k = 1}} [y^{2} (k)]} = 1 \end{matrix} \end{matrix}$ (17)

这说明式(10)所示的标准归一化相关函数有界, 即对于 $\begin{matrix} y (n) ~ S_{α} (γ, β, a) \end{matrix}$ 的稳定随机过程, 式(10)所示的标准归一化相关函数存在。

证毕。

定理将文献^{[9, 10]}所提出的归一化相关函数的定义域扩展至任何服从 $\begin{matrix} S_{α} (σ, β, a) \end{matrix}$ 稳定分布的随机过程。注意到在定理中, $\begin{matrix} α \end{matrix}$ 稳定分布过程的特征指数 $\begin{matrix} α \end{matrix}$ 的值域为 $\begin{matrix} 0 < α \leq 2, \end{matrix}$ 当 $\begin{matrix} α = 2 \end{matrix}$ 时, $\begin{matrix} α \end{matrix}$ 稳定分布退化为高斯分布, 因此, 标准归一化相关函数不仅对 $\begin{matrix} 0 < α < 2 \end{matrix}$ 稳定分布信号有效, 对高斯分布信号也是适用的。

特别值得指出的是, 与目前在 $\begin{matrix} α \end{matrix}$ 稳定分布信号处理中广泛使用的分数低阶矩类方法相比, 本文所提出的标准归一化相关函数的最大优点在于它是一个线性函数, 这不仅大大简化了 $\begin{matrix} α \end{matrix}$ 稳定分布信号处理的分析和计算过程, 而且使得现有的各种在高斯背景噪声下基于二阶矩的信号处理方法均可以很容易地应用于 $\begin{matrix} α \end{matrix}$ 稳定分布信号处理, 这一点对于 $\begin{matrix} α \end{matrix}$ 稳定分布噪声背景下的信号处理具有重要意义。

在实际应用中, 标准归一化相关函数可以使用式(18)估计:

$\begin{matrix} {\hat{r}}_{yy} (m) = \frac{\overset{N}{\sum_{k = 1}} [y (k) y (k + m)]}{\overset{N}{\sum_{k = 1}} [y^{2} (k)]} \end{matrix}$ (18)

根据定理, 对式(2)所示的含噪谐波信号取标准归一化相关函数, 得:

$\begin{matrix} r_{yy} (m) = \overset{q}{\sum_{i = 1}} e^{j ω_{i} m} + σ^{2} δ (m) \end{matrix}$ (19)

式中: $\begin{matrix} σ^{2} \end{matrix}$ 为Sα S稳定分布白噪声方差。

将式(19)代入如下 $\begin{matrix} k \times k (k > q) \end{matrix}$ 维相关函数矩阵, 有:

$R = [\begin{matrix} 1 & r_{yy} (1) & \dots & r_{yy} (k - 1) \\ r_{yy} (1) & 1 & \dots & r_{yy} (k - 2) \\ ︙ & ︙ & ︙ \\ r_{yy} (k - 1) & r_{yy} (k - 2) & \dots & 1 \end{matrix}]$ (20)

可得：

$R = \overset{q}{\sum_{i = 1}} F_{i} {F^{H}}_{i} + σ^{2} I = F F^{H} + σ^{2} I$ (21)

式中: $\begin{matrix} F_{i} = {[\begin{matrix} 1 & e^{j ω_{i}} & \dots & e^{j (k - 1) ω_{i}} \end{matrix}]}^{T} \end{matrix}$ 为一个 $\begin{matrix} k \times 1 \end{matrix}$ 维复列向量; $\begin{matrix} F = [\begin{matrix} F_{1} & F_{2} & \dots & F_{q} \end{matrix}] \end{matrix}$ 为 $\begin{matrix} k \times q \end{matrix}$ 维复矩阵。

由于矩阵 $\begin{matrix} F \end{matrix}$ 完全是由信号的 $\begin{matrix} q \end{matrix}$ 个谐波构成, 因此称矩阵 $\begin{matrix} F \end{matrix}$ 为谐波矢量阵。

不难证明, 式(20)中的矩阵 $\begin{matrix} R \end{matrix}$ 的秩为 $\begin{matrix} q 。 \end{matrix}$ 对矩阵 $\begin{matrix} R \end{matrix}$ 进行特征值分解, 并将特征值递减排列, 得:

$\begin{matrix} R = UΣ U^{H} \end{matrix}$ (22)

式中: $\begin{matrix} U \end{matrix}$ 为其特征矢量阵; $\begin{matrix} Σ \end{matrix}$ 为其特征值矩阵, $\begin{matrix} Σ = diag [\begin{matrix} σ_{1}^{2}, & σ_{2}^{2}, & \dots, & σ_{k}^{2} \end{matrix}] 。 \end{matrix}$

由于矩阵 $\begin{matrix} R \end{matrix}$ 的秩为 $\begin{matrix} q, \end{matrix}$ 且其按特征值递减排列, 所以有:

$\begin{matrix} σ_{1}^{2} \geq σ_{2}^{2} \geq \dots \geq σ_{q}^{2} > σ^{2} = \dots = σ^{2} \end{matrix}$ (23)

即矩阵 $\begin{matrix} R \end{matrix}$ 有 $\begin{matrix} q \end{matrix}$ 个较大特征值, 而另外 $\begin{matrix} k - q \end{matrix}$ 个特征值明显较小, 因此, 当谐波个数未知时, 可以据此作为谐波个数的估计。

将特征矢量矩阵 $\begin{matrix} U \end{matrix}$ 分块, $\begin{matrix} U = [U_{1} ︙ U_{2}]^{T} \end{matrix}$ , 其中 $\begin{matrix} U_{1} \end{matrix}$ 由 $\begin{matrix} U \end{matrix}$ 的前 $\begin{matrix} q \end{matrix}$ 个较大特征值所对应的特征矢量构成, $\begin{matrix} U_{2} \end{matrix}$ 由 $\begin{matrix} U \end{matrix}$ 的后 $\begin{matrix} k - q \end{matrix}$ 个较小特征值所对应的特征矢量构成, 并依此对应地将特征值矩阵 $\begin{matrix} Σ \end{matrix}$ 分块成 $\begin{matrix} Σ_{1} \end{matrix}$ 和 $\begin{matrix} Σ_{2}, \end{matrix}$ 则式(22)可写成:

$\begin{matrix} R = [\begin{matrix} U_{1} \\ U_{2} \end{matrix}] [\begin{matrix} Σ_{1} \\ Σ_{2} \end{matrix}] {[\begin{matrix} U_{1} \\ U_{2} \end{matrix}]}^{H} \end{matrix}$ (24)

用 $\begin{matrix} U \end{matrix}$ 右乘式(24)两端, 并进行整理, 有:

$\begin{matrix} R U_{2} = σ^{2} U_{2} \end{matrix}$ (25)

另一方面, 用 $\begin{matrix} U_{2} \end{matrix}$ 右乘式(21)两端, 得:

$\begin{matrix} R U_{2} = F F^{H} U_{2} + σ^{2} U_{2} \end{matrix}$ (26)

比较式(25)和式(26), 明显有:

$\begin{matrix} F F^{H} U_{2} = 0 \end{matrix}$ (27)

由于谐波矢量阵 $\begin{matrix} F \end{matrix}$ 为高矩阵, 因此可得:

$\begin{matrix} F^{H} U_{2} = 0 \end{matrix}$ (28)

这说明 $\begin{matrix} q \end{matrix}$ 个谐波信号分量均为由式(28)所构成的特征方程的根。因此令:

$\begin{matrix} P (jω) = \frac{1}{{|F U_{2}|}^{2}} = \frac{1}{F U_{2} {U^{H}}_{2} F^{H}} \end{matrix}$ (29)

然后通过搜索 $\begin{matrix} P (jω) \end{matrix}$ 的峰值即可得到 $\begin{matrix} q \end{matrix}$ 个谐波信号频率的估值。这就是本文所提出的基于标准归一化相关函数的谐波信号频率估计的MUSIC方法。

3 仿真实验

取含噪观测信号模型为:

$\begin{matrix} \begin{matrix} y (k) = s (k) + n (k) = \\ \cos (2 π f_{1} k) + \cos (2 π f_{2} k) + n (k) \end{matrix} \end{matrix}$ (30)

式中: $\begin{matrix} f_{1} 、 f_{2} 均为归一化数字频率, f_{1} = 0.26 rad / s, f_{2} = 0.27 rad / s; n (k) \end{matrix}$ 为附加噪声。

数据长度 $\begin{matrix} N = 512, \end{matrix}$ 归一化相关函数矩阵 $\begin{matrix} R \end{matrix}$ 的维数为50× 50。

仿真实验1 为了考察本文方法在 $\begin{matrix} α \end{matrix}$ 噪声背景下的谐波信号频率估计性能, 取 $\begin{matrix} n (k) ~ S_{α} (γ, 0, 0) \end{matrix}$ 的独立同分布的稳定分布噪声, $\begin{matrix} α = 1.1, n (k) \end{matrix}$ 按文献^[12]方法产生; 其信噪比(SNR)按文献^[13]所提出的广义信噪比(GSNR)计算, 即:

$\begin{matrix} GSNR = 10 \log (\frac{1}{γN} \overset{N}{\sum_{k = 1}} {|s (k)|}^{2}) \end{matrix}$ (31)

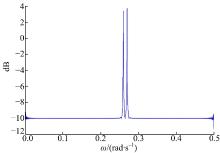
取GSNR=0 dB, 使用本文方法所得到的一个典型实验结果如图1所示。

	Figure Option View Download New Window
	图1 Sα S噪声背景下谐波频率估计结果(GSNR=0 dB)Fig.1 Harmonic frequency estimation result in Sα S noise(GSNR=0 dB)

由图1可见, 在 $\begin{matrix} α \end{matrix}$ 噪声背景下, 本文所提方法的谐波信号频率估计的精度及分辨率比较高。

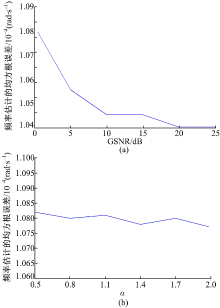
仿真实验2 为了考察本文所提方法在各种不同GSNR条件下的谐波信号频率估计性能, 采用与实验1相同的实验条件及实验方法, 但GSNR从0 dB到25 dB变化, 变化间隔为5 dB, 每个实验点均进行50次Monte Carlo实验, 所得到的谐波信号频率估计的均方根误差(Root-mean-square error, RMSE)随GSNR变化曲线如图2(a)所示。

	Figure Option View Download New Window
	图2 均方根误差曲线Fig.2 The RMSE curve

由图2(a)可以看出, 本文所提方法对 $\begin{matrix} α \end{matrix}$ 噪声具有很强的抑制能力, 并且随着GSNR的增加, 其谐波信号频率估计的RMSE逐渐降低。

仿真实验3 为了考察本文所提方法在各种不同特征指数的 $\begin{matrix} α \end{matrix}$ 背景噪声条件下的谐波信号频率估计性能, 采用与实验1相同的实验条件及实验方法, 但 $\begin{matrix} α \end{matrix}$ 噪声的特征指数从0.5到2变化, 变化间隔为0.3, 每个实验点均进行50次Monte Carlo实验, 所得到的谐波信号频率估计的均方根误差(RMSE)随特征指数 $\begin{matrix} α \end{matrix}$ 的变化曲线如图2(b)所示。

由图2(b)可见, 谐波信号频率估计的RMSE随 $\begin{matrix} α \end{matrix}$ 噪声的特征指数 $\begin{matrix} α \end{matrix}$ 的增加变化不大, 这说明标准归一化相关函数对不同特征指数的 $\begin{matrix} α \end{matrix}$ 噪声具有很强的适应能力。特别是在该实验中, 当特征指数 $\begin{matrix} α = 2 \end{matrix}$ 时, $\begin{matrix} α \end{matrix}$ 稳定分布噪声已经退化为常见的高斯噪声, 因而对高斯噪声背景下的谐波信号处理依然有效, 说明本文方法具有良好的鲁棒性。

4 结论

(1)对于特征指数 $\begin{matrix} 0 < α \leq 2 \end{matrix}$ 的任何稳定分布过程, 标准归一化相关函数存在, 从而为 $\begin{matrix} α \end{matrix}$ 稳定分布信号处理提供了一个更加有效、方便的信号处理工具。

(2)标准归一化相关函数是一个线性统计算子, 这不仅大大简化了 $\begin{matrix} α \end{matrix}$ 稳定分布过程信号处理的分析和计算过程, 而且使得目前许多在高斯噪声背景下基于二阶矩的优化算法, 如最小二乘法、极大似然法等, 都可以应用到 $\begin{matrix} α \end{matrix}$ 噪声背景下的信号处理中。

(3)本文方法不仅具有优良的谐波频率估计性能, 而且对于包括高斯噪声在内的 $\begin{matrix} α \end{matrix}$ 稳定分布噪声均具有很强的鲁棒性。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Nikias C L, Shao M. Signal Processing with Alpha-stable Distributions and Applications[M]. USA: Wiley-Interscience, 1995. [本文引用:1]
[2]	Moghimi F, Nasri A, Schober R. Lp-norm spectrum sensing for cognitive radio networks impaired by non-gaussian noise[C]//Global Telecommunications Conference, 2009: 1-6. [本文引用:1]
[3]	Kassam S A. Signal Detection in Non-Gaussian Noise[M]. USA: Springer Science & Business Media, 2012. [本文引用:1]
[4]	贺继渊, 田松, 王星, 等. 模拟信息转换处理高带宽稀疏信号的噪声分析[J]. 光学精密工程, 2015, 23(10z): 637-643. He Ji-yuan, Tian Song, Wang Xing, et al. Noise analysis of high band width sparse signals processed by AIC[J]. Optics and Precision Engineering, 2015, 23(10z): 637-643. [本文引用:1]
[5]	孙晓东, 权爱娟, 李勇. 复杂噪声背景下谐波信号频率估计新方法[J]. 吉林大学学报: 工学版, 2015, 45(2): 653-657. Sun Xiao-dong, Quan Ai-juan, Li Yong. New frequency estimation method for harmonic signal submerged in complex noise background[J]. Journal of Jilin University(Engineering and Technology Edition), 2015, 45(2): 653-657. [本文引用:1]
[6]	Shao M, Nikias C L. Signal processing with fractional lower order moments: stable processes and their applications[J]. Proceedings of the IEEE, 1993, 81(7): 986-1010. [本文引用:5]
[7]	邱天爽. 统计信号处理: 非高斯信号处理及其应用[M]. 北京: 电子工业出版社, 2004. [本文引用:2]
[8]	Altinkaya M A, Deliç H, Sankur B, et al. Subspace-based frequency estimation of sinusoidal signals in alpha-stable noise[J]. Signal Processing, 2002, 82(12): 1807-1827. [本文引用:3]
[9]	Kanter M, Steiger W. Regression and autoregression with infinite variance[J]. Advances in Applied Probability, 1974: 768-783. [本文引用:3]
[10]	Swami A, Sadler B. Parameter estimation for linear alpha-stable processes[J]. Signal Processing Letters, 1998, 5(2): 48-50. [本文引用:3]
[11]	张贤达. 现代信号处理[M]. 北京: 清华大学出版社, 2002. [本文引用:1]
[12]	Chambers J M, Mallows C L, Stuck B. A method for simulating stable rand om variables[J]. Journal of the American Statistical Association, 1976, 71(354): 340-344. [本文引用:1]
[13]	Tsakalides P, Nikias C L. The robust covariation-based MUSIC (ROC-MUSIC) algorithm for bearing estimation in impulsive noise environments[J]. IEEE Transactions on Signal Processing, 1996, 44(7): 1623-1633. [本文引用:1]

1995

0.0

... 在大量的信号处理实践中,其背景噪声通常为非高斯噪声^[1,2,3,4],例如由放电引起的大气噪声,水下生物引起的水下声学噪声,数字电路的开关噪声,无线通信中的信号窜扰等噪声 ...

2009

0.0

2012

0.0

2015

0.0

2015

0.0

. 2015, 45(2):653-657 DOI:doi:10.13229/j.cnki.jdxbgxb201502047

New frequency estimation method for harmonic signal submerged in complex noise background

复杂噪声背景下谐波信号频率估计新方法

Sun Xiao-dong , Quan Ai-juan , Li Yong.

孙晓东, 权爱娟, 李勇

摘　要：利用待测谐波信号的周期性及混沌信号能量集中在低频部分的特性,提出一种将倍频法、小波包分解与互谱分析相结合的强混沌噪声背景下谐波频率估计新方法。首先,利用谐波信号的周期性,将采样数据等距取值构造谐波信号倍频的新数据序列,且倍频谐波偏离混沌能量中心频段;其次,利用小波包分析法对新数据进行多层分解,使倍频谐波信号与混沌噪声主能量分离;最后,对谐波信号能量集中的分量进行互谱功率谱分析,估计谐波频率。该方法适用于强混沌信号与强观测噪声共存背景下的周期小信号频率估计。仿真实验结果表明：该方法十分有效,且计算量小。

... 反映在概率密度上,它们具有比高斯分布更加厚重的拖尾现象^[5,6] ...

1993

0.0

... 反映在概率密度上,它们具有比高斯分布更加厚重的拖尾现象^[5,6] ...

... 研究结果^[6]表明,这种非高斯冲击噪声可以用 α稳定分布来表征,一般称为 α稳定分布噪声(简称为 α噪声) ...

... α稳定分布的一个重要性质是它不存在 p>α(当 α2时)的统计量^[6],当 α1时,甚至连均值的运算也不可能 ...

... 但采用分数低阶矩类方法解决 α噪声背景下的谐波恢复问题时,由于 α稳定分布过程不存在有限的方差,因此,传统信号处理常用的方法,如极大似然法、最小二乘法等,均无法使用^[6] ...

... 式(2)中的 SαS稳定分布过程的定义为^[6]: ...

2004

0.0

... 因此,在 α噪声存在的场合,现有的各种基于二阶矩、高阶矩和高阶累积量的信号处理方法均失效^[7] ...

... 目前,任何涉及 α稳定分布的信号基本上都是采用 pα2的分数低阶矩^[7]或由其派生的统计工具进行处理 ...

2002

0.0

... 分数低阶矩类方法由于其本身固有的非线性,无法得到该问题的闭式解^[8] ...

... 针对上述问题,文献^[8]将 α噪声背景下的谐波信号用一个 α白噪声驱动的高阶AR模型表示,然后利用分数低阶矩中,当且仅当其阶次 p=1时具有线性的性质,采用GCC(Generalized covariation coefficient)方法巧妙地解决了这一问题 ...

... 若采用分数低阶矩类方法,由于该方法本身所固有的非线性( 0pα,p≠1),所以无法得到含噪谐波信号的封闭表达式^[8] ...

1974

0.0

... 针对分数低阶矩类方法所存在的非线性问题,文献^[9,10]指出,若 α稳定分布过程 y(n)可以用一个极点均在单位圆内的AR模型描述,则适当定义的归一化相关函数估计(Normalized correlation estimate)存在,因而可以用于 α稳定分布信号处理 ...

... 为了解决这一问题,本文将文献^[9,10]所提出的归一化相关函数的定义域进行扩展,提出如下对于 α稳定分布过程的标准归一化相关函数存在的定理 ...

... 定理将文献^[9,10]所提出的归一化相关函数的定义域扩展至任何服从 Sα(σ,β,a)稳定分布的随机过程 ...

1998

0.0

... 为了解决这一问题,本文将文献^[9,10]所提出的归一化相关函数的定义域进行扩展,提出如下对于 α稳定分布过程的标准归一化相关函数存在的定理 ...

... 定理将文献^[9,10]所提出的归一化相关函数的定义域扩展至任何服从 Sα(σ,β,a)稳定分布的随机过程 ...

2002

0.0

... 显然,谐波信号 x(n)的 q个谐波频率可由特征方程(6)的根( zi=1)决定^[11],方程(6)的表达式如下: ...

1976

0.0

... 1,n(k)按文献^[12]方法产生 ...

1996

0.0

... 其信噪比(SNR)按文献^[13]所提出的广义信噪比(GSNR)计算,即: ...