作者简介:李钊(1981-),男,副教授,博士.研究方向:宽带无线通信.E-mail:zli@xidian.edu.cn
针对单小区MU-MIMO下行广播信道传统的公平调度算法在逐次添加用户的过程中不能准确计算用户可达速率,从而无法兼顾良好的公平性及系统和速率的问题,提出一种基于加权用户空间相关度的公平调度算法(WUCFS)。采用该方法,用户的添加基于对候选用户与已选用户以及潜在的可能被选择用户之间的相关度的综合考虑,以加权相关值最大为调度准则,能够更准确地估计用户实际传输速率,并且更公平、合理地激活一组相互之间干扰小的用户。相比于已有方法,所提算法能够在获得高的系统和速率的同时更好地保证用户之间的公平性。
Traditional fair scheduling algorithms cannot accurately compute the achievable rate for each user in the process of iterative user selection, which results in non-favorable tradeoff between fairness and system sum rate. To address this problem, a fair scheduling algorithm based on weighted user-correlation (WUCFS) is proposed for MU-MIMO downlink broadcast channels. In this algorithm, users are activated based on comprehensive consideration of the correlation between candidate users and selected users as well as those to be scheduled potentially. Weighted correlation maximization is employed as scheduling criterion. The proposed algorithm could estimate the actual transmission rate of each user more precisely, and activate a set of users of small mutual interference with more fairness and appropriateness. Compared with existing schemes, the propose algorithm could achieve better fairness among users while ensuring high system sum rate.
多输入多输出(Multiple input multiple output, MIMO)作为未来移动通信系统的关键技术, 能够在不增加系统带宽需求的条件下显著改善频谱效率和传输可靠性[1]。相比于单用户MIMO(Single-user MIMO, SU-MIMO)系统, 多用户MIMO(Multi-user MIMO, MU-MIMO)更符合实际通信的需求, 并且可以获得更高的系统速率, 因此受到更多的关注[2]。在MU-MIMO系统中, 由于基站的硬件约束和处理能力的限制, 通常需要从多个用户中选择一组进行服务, 这些用户通过空间复用实现对相同频率资源的共享[3]。但由于共道干扰(Co-channel interference, CCI)的存在, 可达系统和速率与服务用户集合的选取有关, 如何获得一组相互之间干扰小的用户成为许多调度算法的设计目标。当基站能够获得完整的信道状态信息(Channel state information, CSI)时, 采用穷举搜索可以获得最优的调度结果, 但是该方法复杂度高, 实际中难以应用。为了降低复杂度, 一些次优的贪婪算法[4, 5, 6, 7, 8]相继被提出。与穷举搜索遍历所有可能的用户组合不同, 贪婪算法根据特定的调度准则, 采用迭代的方式逐步添加用户。其中, 文献[4]提出一种基于信道相关度的准正交用户组调度算法, 首先选择信道增益最大的用户, 然后在每次调度中选择与上次新添加用户的正交程度符合预设门限要求的用户组, 最后从该用户组中选出在已选用户信道构成的空间上投影最大的用户。文献[5]对文献[4]算法进行了改进, 仅根据用户空间信道的方向信息进行调度, 并对控制用户正交程度的参数进行了最优化设计。文献[6]在不损失系统和速率的前提下, 降低了文献[4]的复杂度。文献[7]基于相关度进行用户天线选择, 利用同一用户的天线之间的协作, 选择使系统和速率最大的天线集合。文献[8]采用块对角化处理方法, 依次添加与已选用户相关度小并且能产生最大系统和速率增量的用户。
上述算法都是基于用户之间的相关度, 以系统和速率最大化为目标进行用户调度的。但是对于经历不同衰落的用户传输而言, 这些调度算法[4, 5, 6, 7, 8]通常选择信道质量好的用户、信道和速率最大的天线集合。文献[8]采用块对角化处理方法, 依次添加与已选用户相关度小并且能产生最大系统和速率增量的用户。质量差的用户无法获得通信资源, 导致用户的公平性无法得到保障。比例公平(Proportional fair, PF)是一种考虑公平性的用户调度算法[9], 它以用户当前速率与其平均速率的比值来确定用户获得调度的优先级, 在提高系统吞吐量和保障公平性之间取得折中。然而, 在贪婪算法[4, 5, 6, 7, 8]中, 用户是逐步添加的, 在整个调度过程结束前, 各个已选用户的可达速率是未知的, 因此基于贪婪算法进行公平设计时, 如何准确估计迭代过程中各个用户的实际数据速率成为值得研究的问题[4, 10, 11]。文献[4]在设计中忽略了准正交用户之间的共道干扰, 采用在已选用户信道矩阵构成的空间上的投影矩阵的Frobenius范数作为信道增益, 计算用户可达速率。文献[10]基于用户信道矩阵的Frobenius范数设计比例公平准则。文献[11]采用用户信道矩阵行向量的Frobenius范数平方代替用户信道矩阵的特征值计算用户速率。但是上述研究仍然无法准确计算迭代调度过程中的用户速率, 从而无法兼顾良好的系统和速率及用户公平性。与此同时, 基于用户信道空间相关度的调度算法[4, 5, 8]可能造成第
为了解决上述问题, 本文提出一种基于加权用户信道空间相关度的比例公平调度算法, 综合考虑候选用户与已选用户、潜在的可能被调度的用户之间的相关度, 并为其赋予权值, 控制调度的公平性, 兼顾了系统和速率及用户公平性。
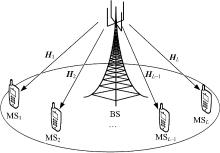
研究目标为单小区MU-MIMO下行广播信道(Broadcast channel, BC)。系统模型如图1所示, 基站(Base station, BS)和移动台(Mobile station, MS)的天线数分别为
基站与用户MSk之间的信道矩阵用
本节给出MU-MIMO BC的基本信号处理, 由于BS从
式中:
假设基站采用单波束(Beamforming)向用户
式(2)等号右端第1项表示用户
对信道矩阵
式中:
取预编码向量
式中:
假设BS采用等功率分配, 即将
式中:
对式(5)进行化简, 可得:
式中:
由于BS与不同MS之间的空间子信道非相互正交, BS向
用户
系统的和速率为:
根据第2节的分析, 为了获得高的系统和速率, 需要选择一组相互之间干扰小的用户, 但是该准则可能导致信道条件好的用户长期占据通信资源, 而信道质量差的用户得不到服务。比例公平(PF)调度算法能够保障用户间的公平性[9]。此外, 在贪婪调度算法[4, 5, 6, 7, 8]中用户是逐个添加的, 因此在最后一个用户被确定前, 已经被调度的用户的信干噪比(SINR)无法准确计算, 也就无法获得这些用户的可达数据速率, 即在调度用户集合
以加权系统和速率最大化为目标, PF算法的通式定义如下[14]:
式中:
当
式中:
根据式(4)和式(7), 给定
根据上面的讨论, 对用户可达速率的估计可以转换为对第
式中:
以任意传输周期
步骤1 初始化已选用户集合
步骤2 基站对用户
步骤3 基站根据分解后的矩阵构造中间矩阵
步骤4 基站构造相关矩阵
步骤6 根据式(12)计算
可得列向量
步骤7 按照式(14)选择第
式中:
更新
步骤8 若
调度完成后, 基站通知激活用户并进行下行数据通信。在下一个传输周期
基于CCI最小化的用户调度准则, 可能导致与其他用户相互干扰大的用户得不到调度。为了使这样的用户能够公平地获得通信资源, 算法在传输周期
对所提调度算法的复杂度进行分析, 并与以下5种方法进行比较:①穷举调度(Exhaustive scheduling, ES); ②准正交用户调度[4](Semi-orthogonal user selection, SUS); ③比例公平准正交用户调度[4](Proportional fair SUS, PF-SUS); ④后验式调度(Reactive scheduling, RS), 用户的选择仅基于候选用户与已选用户的相互干扰[15]; ⑤先验式调度(Proactive scheduling, PS), 相比于RS, 增加了对候选用户与潜在的、后续可能被选择的用户之间干扰的考虑[12]。采用flops作为算法复杂度的度量, 1个flop表示1次实数乘法或加法运算, 1个复数加法需要2个flop, 1个复数乘法需要6个flop。对维度为
对于ES、RS、PS和所提的WUCFS, 复信道矩阵的SVD是其复杂度的主要构成之一, 此外, ES的复杂度还包括对
由表1可以得到ES、SUS/PF-SUS、RS、PS和WUCFS的复杂度分别为
| 表1 复杂度分析 Table 1 Complexity analysis |
通过仿真对所提算法WUCFS的性能进行分析, 并与第4节的5种方法, 以及扩展的PF调度(Extended PF, ePF)的性能进行比较。ePF将原本用于每个传输周期调度一个用户、旨在获得用户间的公平性的PF算法扩展至调度多个用户的场景, 但为了简便, 忽略了用户间干扰, 即存在用户速率无法准确计算的问题。用户信道向量采用Dent模型[16]产生, 其中最大多普勒频移取7 Hz, 合成路径数为32。在不同的信噪比SNR、用户数
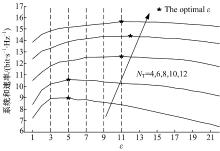
图2给出SNR=10 dB, 用户数
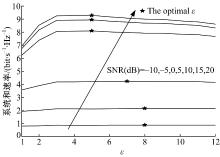
图4给出
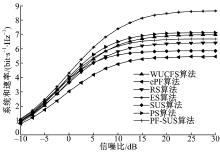
图5为NT=4, SNR=10 dB,
对于WUCFS和ePF, 所有用户在仿真过程中均得到了调度, 且各个用户的调度概率的分布比较均匀, 特别是ePF算法, 每个用户被激活的概率约为1/30。对于PF-SUS, 在进行比例公平调度前需要对待选用户做相关度筛选, 缩小了候选用户的范围, 可能导致某些待选用户的可达速率与平均速率的比值虽然较大, 但由于不满足筛选门限要求而不能被调度。所以, 虽然相比于SUS, 采用PF-SUS可以使大部分用户获得调度机会, 但是用户被调度概率的差距仍然较大。对于PS、RS和SUS, 部分用户被调度的机会远高于其他用户, 那些调度机会小的用户, 获得通信资源的概率低。
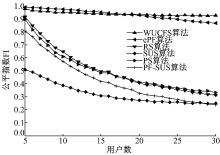
图6为NT=4, SNR=10 dB时不同算法的公平性随用户数
式中:
FI是0到1之间的连续值, FI越大, 表示公平性越好。当每个用户的调度机会相等时,
针对MU-MIMO下行广播信道提出一种基于加权用户相关的公平调度算法(WUCFS)。该方法在用户调度过程中综合考虑候选用户与已选用户以及潜在的后续可能被选择的用户之间的相互干扰, 以加权相关值最大为准则进行用户调度, 通过准确估计用户实际传输速率, 能够公平、合理地选择一组相互之间干扰小的用户。相比于已有方法, 所提算法能够在获得较高的系统和速率的同时, 更好地保证用户之间的公平性, 兼顾了系统和速率及公平性。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|