基于压缩感知的三相电能质量扰动信号压缩及分类新方法

引用本文

于华楠, 代芳琳, 苏天恺. 基于压缩感知的三相电能质量扰动信号压缩及分类新方法.吉林大学学报:工学版, 2016, 46(3): 964-971
YU Hua-nan, DAI Fang-lin, SU Tian-kai. New compression and classification method of three-phase power quality disturbance signal based on compressed sensing. Journal of Jilin University Engineering and Technology Edition, 2016, 46(3): 964-971 复制到剪切板

Permissions

基于压缩感知的三相电能质量扰动信号压缩及分类新方法

于华楠, 代芳琳, 苏天恺

东北电力大学信息工程学院,吉林省吉林市 132012

作者简介:于华楠(1981-),女,副教授,博士.研究方向:压缩传感理论,无线通信信道估计.E-mail:yhn810117@163.com

基金:国家自然科学基金项目(51307020)

摘要

首先,选取傅立叶基作为压缩感知中的过完备字典、高斯随机矩阵作为观测矩阵、正交匹配追踪(OMP)算法作为重构算法,对电能质量扰动信号进行压缩采样。然后,采用灰度共生矩阵纹理特征中的能量特征值、灰度值出现概率两种方法对压缩感知重构信号进行分类检测。试验结果表明:本文方法可以同时实现对三相电能质量信号的压缩重构,也可以实现对信号的准确分类,并减少了信号压缩采样过程中的数据量。

关键词: 信息处理技术; 电能质量; 压缩感知; 灰度图; 灰度共生矩阵

中图分类号:TM933 文献标志码:A 文章编号:1671-5497(2016)03-0964-08

New compression and classification method of three-phase power quality disturbance signal based on compressed sensing

YU Hua-nan, DAI Fang-lin, SU Tian-kai

College of Information Engineering,Northeast Dianli University,Jilin 132012,China

Abstract

First, in order to reconstruct three-phase power quality disturbance signals, the Fourier basis is chosen as the over-complete dictionary; Gaussian random matrices as the observation matrix; and orthogonal pursuit algorithm as the reconstruction algorithm. Then, the energy eigenvalue of gray level cooccurrence matrix texture features and the probability of the occurrence of grey value are used to classify the disturbance signals. The experiment results show that the proposed method can not only realize simultaneous compression and reconstruction of three-phase electric signals and accurate classification of such signals, but also reconstruct the original signal samples, reducing the data volume of signal compression and sampling.

Keyword: information processing; power quality; compressed sensing(CS); grayscale; gray level cooccurrence matrix

Show Figures

0 引言

近年来, 电能质量已成为影响用电设备安全可靠运行的重要因素之一。研究电能质量信号的压缩和分类具有重要意义。对信号压缩、检测和分类的方法主要有小波变换理论、S变换等, 它们都是以Nyquist采样定理为基础的传统处理方法, 采样数据量较大。Donoho等提出了一种新的理论— — 压缩感知(Compressed sensing, CS)理论^{[1, 2, 3]}, 它同时实现了信号采样和压缩, 突破了Nyquist采样定理的限制, 极大地减少了采样数据量, 具有广泛的应用前景^{[4, 5, 6, 7]}。文献^[8]首次将压缩感知应用于短时电能质量扰动信号压缩采样中, 研究了CS短时电能质量信号压缩采样的实现方法。文献^[9]研究了应用于电能质量信号的CS稀疏基及其性能。文献^[10]将CS应用于暂态短时电能质量扰动信号处理中, 并将一维时间信号转换为二维矩阵进行处理, 进一步减少了采样数据量。目前对于电能质量扰动信号的分类方法研究已取得一定进展。文献^[11]提出了一种基于dq0变换和专家系统的扰动信号区分方法, 但是对信号的区分过程比较复杂。文献^[12]利用小波神经网络分类器对电能质量扰动进行识别, 该方法需要进行大量的训练, 计算量非常大。文献^[13]提出了电力信号短时扰动检测及自动分类方法, 分类时利用二进制序列, 不直观、不易于观测。文献^[14]提出了一种基于广义S变换的暂态电能质量扰动定位及识别。

目前, 电能质量信号压缩检测方法几乎都是针对单相信号进行压缩检测。然而, 实际的电能质量监测系统往往是同时监测三相数据信息, 而且三相电信号之间存在很大的相关性。因此, 本文提出了一种同时处理三相电能质量扰动信号的方法。通过变换使三相电信号同时通过本文设计的压缩感知算法进行重构, 然后利用灰度共生矩阵纹理特征中的能量特征值、检测灰度值出现概率两种方法对三相电信号进行分类。从而同时实现对三相电能质量扰动信号的快速、准确压缩重构及分类。

1 信号压缩及分类整体方案

本文所提出的三相电能质量短时扰动信号压缩及分类整体方案如图1所示。

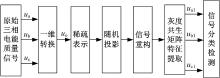	Figure Option View Download New Window
	图1 三相电能质量信号压缩及分类框图Fig.1 Diagram of the three-phase power quality signal compression and classification

首先将三相电能质量短时扰动信号(u_a、u_b、u_c)转换为连续的一维时间信号u₀, 便于在下一步同时对三相电信号进行压缩感知; 然后选择稀疏表示中的稀疏基、随机投影中的观测矩阵和重构算法, 对信号进行压缩感知; 在对信号进行压缩感知时, 为了减少信号之间的冗余, 采用了将一维时间信号转换为二维灰度图的方法, 因此, 重构的信号是以二维灰度图的形式表示的。然后, 通过以下两种方法对灰度图进行特征提取:①通过灰度共生矩阵对重构信号进行纹理特征提取:提取出各种扰动信号的纹理特征, 经过比较分析, 找到能够准确区分各种信号的特征量, 然后通过观测找到这种特征量的某种变换的值, 作为以后试验时对信号进行区分的标准; ②信号灰度图的各灰度值出现概率统计:绘制出各种扰动信号对应的灰度值出现概率图, 经过分析, 找到能够区分各种信号的规律。

当对某未知的每相至多含有一种短时扰动的三相电信号, 采用本文方法进行CS重构出二维灰度图后, 采用以上两种方法对灰度图进行特征提取, 提取时涉及到对灰度图的分块, 按照第①种分类方法将得到3个纹理特征量(u_a1、u_b1、u_c1), 这3个量代表了三相电信号扰动时刻的特征量, 通过将这3个量与已经得到的区分各类扰动信号规律的量进行比较, 可以对信号进行快速分类。采用第②种方法可以得到三幅灰度值概率图, 根据这3幅图和得到的信号分类规律来对信号进行分类。综合比较两种方法对信号分类的准确性、复杂性等特征, 选择其中一种较好的方法。

2 压缩感知原理

压缩感知(CS)的核心思想是:若长度为N的信号x本身是稀疏的, 或者在某个正交基Ψ 上具有稀疏性, 那么可将原始信号x通过一个与正交基Ψ 不相关的测量矩阵 $Ф_{M \times N} (M > K, M ≪ N)$ 进行非自适应线性投影, 得到保持原始信号结构并且远小于信号长度的测量值y(M× 1)。最后通过求解数值最优化问题来精确重构原始信号x。

CS理论直接获取数据压缩后的表达, 省略了获取 $\begin{matrix} N \end{matrix}$ 维信号这个中间步骤, 其线性测量模型如式(1)所示:

$\begin{matrix} y = Ф x = Ф ΨS = ΘS \end{matrix}$ (1)

式中:Θ =Ф Ψ 为M× N的线性测量矩阵; S中只有K个非零元素, 即S为N维K-稀疏向量; 观测量y的维数满足M=CKlogN≪N, C为与重建精度有关的过采样系数, C≥ 1。

CS的重构过程就是从测量向量y=Θ S中恢复N维信号x的过程。首先通过对式(1)的逆问题(见式(2))进行求解, 获取稀疏系数S然后将S代入 $\begin{matrix} x = ΨS \end{matrix}$ 中, 将稀疏度为K的信号x正确恢复出来。

$\begin{matrix} \{\begin{matrix} \min ‖ Ψ^{T \land} x ‖ \\ s . t . y = ΦΨS \end{matrix} \end{matrix}$ (2)

3 算法实现

3.1 CS算法实现

稀疏基在CS理论中的角色与传统采样理论中的Nyquist采样频率类似, 是实现压缩重构的必要条件之一。能否高精度地重构原始信号主要依赖于该信号的稀疏表示。对短时电能质量扰动信号进行压缩采样时, 需要选择合适的稀疏基对短时电能质量扰动信号进行稀疏表示。由于电能质量信号的基波是频率为50 Hz的正弦信号, 而傅立叶基也是正弦信号, 且为正交基。因此, 本文选择傅立叶基作为稀疏表示中的稀疏基。本文选择高斯随机矩阵作为测量矩阵, 为了提高测量矩阵的随机性, 将对测量矩阵进行近似QR分解及单位化处理。本文选择了运行效率和重构精度适中的正交匹配追踪(Orthogonal matching pursuit, OMP)算法作为重构算法, 再利用测量值 $\begin{matrix} y \end{matrix}$ 对信号进行重构。从而确定了CS方法中的稀疏基、测量矩阵及重构算法。

本文对信号进行CS处理过程中采用了文献^[10]中的将一维时间信号转换为二维灰度图的方法。一维时间信号的相邻数据为2个, 只能表示信号在水平方向上的变化, 而二维灰度图像中的相邻数据为8个, 能表示信号在水平、垂直和对角线三个方向上的变化。所以, 对信号进行分析时将一维时间信号转换为二维灰度图进行分析具有分析角度灵活、直观等特点。由于二维图像比一维信号具有更大的冗余度, 因此可以通过去除图像各像素之间的相关性, 进一步提高压缩性能和重构质量。因此, 本文将时间信号转换为灰度图进行处理。

3.2 基于灰度共生矩阵的纹理检测算法实现

3.2.1算法实现步骤

灰度共生矩阵是通过计算图像中特定方向和特定距离的两像素之间灰度差值出现的次数, 得到图像在方向、间隔、幅度变化大小和速度的综合信息, 从而将图像的灰度值转化为纹理信息^[15], 进而对图像进行分类等研究。

灰度共生矩阵是指灰度级为i的点到灰度级为j的点的概率, 其中灰度级为i的点是按照某个固定的位置关系d=(D_x, D_y)离开i点的。用P_d (i, j)(i, j=0, 1, 2, L-1)来表示灰度共生矩阵, 其中i, j为像素的灰度, L为图像共有多少个灰度级, d为两个像素的空间位置间的关系, d的不同代表了两个像素之间的距离和方向不同。灰度共生矩阵的生成方向用 $\begin{matrix} θ \end{matrix}$ 表示, 取值分别为0° , 45° , 90° 和135° 。当d确定以后, 就可以生成在关系d下的灰度共生矩阵, 如式(3)所示:

$\begin{matrix} \begin{matrix} P_{d} = \\ [\begin{matrix} P_{d} (0, 0) & \dots & P_{d} (0, j) & \dots & P_{d} (0, L - 1) \\ P_{d} (1, 0) & \dots & P_{d} (1, j) & \dots & P_{d} (1, L - 1) \\ ︙ & ︙ & ︙ \\ P_{d} (i, 0) & \dots & P_{d} (i, j) & \dots & P_{d} (i, L - 1) \\ ︙ & ︙ & ︙ \\ P_{d} (L - 1, 0) & \dots & P_{d} (L - 1, j) & \dots & P_{d} (L - 1, L - 1) \end{matrix}] \end{matrix} \end{matrix}$ (3)

式中:P_d 的每个元素代表一种灰度组合下出现的次数, 例如:P_d (0, 1)表示在图像上位置关系为d时, 两个像素的灰度为0和1的情况出现的次数, 本文中d取1, 则P_d 可记为P。

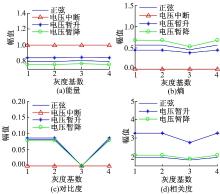
灰度共生矩阵的纹理特征有14种, 一般采用下面4个最常用的不相关的纹理特征:

$能量 : f_{1} = \overset{L - 1}{\sum_{i = 0}} \overset{L - 1}{\sum_{j = 0}} P^{2} (i, j)$ (4)

$对比度 : f_{2} = \overset{L - 1}{\sum_{n = 0}} n^{2} \{\overset{L - 1}{\sum_{i = 0}} \overset{L - 1}{\sum_{j = 0}} \hat{P} (i, j)\}$ (5)

$熵 : f_{4} = - \overset{L - 1}{\sum_{i = 0}} \overset{L - 1}{\sum_{j = 0}} \hat{P} (i, j) \log \hat{P} (i, j)$ (6)

$相关 : f_{3} = \frac{\overset{L - 1}{\sum_{i = 0}} \overset{L - 1}{\sum_{j = 0}} ij \hat{P} (i, j) - u_{1} u_{2}}{σ_{1}^{2} σ_{2}^{2}}$ (7)

式中: $\begin{matrix} u_{1} 、 u_{2} 、 σ_{1} 和 σ_{2} \end{matrix}$ 分别定义为:

$\begin{matrix} \begin{matrix} u_{1} = \overset{L - 1}{\sum_{i = 0}} i \overset{L - 1}{\sum_{j = 0}} \hat{P} (i, j); \\ u_{2} = \overset{L - 1}{\sum_{i = 0}} j \overset{L - 1}{\sum_{j = 0}} \hat{P} (i, j); \\ σ_{1}^{2} = \overset{L - 1}{\sum_{i = 0}} (i - u_{1})^{2} \overset{L - 1}{\sum_{j = 0}} \hat{P} (i, j); \\ σ_{2}^{2} = \overset{L - 1}{\sum_{i = 0}} (i - u_{2})^{2} \overset{L - 1}{\sum_{j = 0}} \hat{P} (i, j) 。 \end{matrix} \end{matrix}$

本文将对三相电能质量短时扰动信号进行压缩重构和分类研究。短时电压波动的具体分类情况如表1所示。

表1 IEEE制定的短时电压波动特征参数及分类 Table 1 Short-term voltage fluctuation characteristic parameters and classification of IEEE

由表1可以看出, IEEE制定的电压波动特征参数中, 0.5周波(10 ms)、30周波(0.6 s)、3 s、1 min是各类别的持续时间的分界点; 0.1、0.9、1.1、1.2、1.4、1.8 p.u.是各类别的幅值的分界点。由上文知当三相电为表1中的短时扰动时, 通过CS方法重构的信号以灰度图的形式存在, 本文利用灰度共生矩阵的4种纹理特征对电能质量扰动信号进行分类检测, 实现步骤为:

(1)通过CS方法对表1所示的电压中断、电压暂升、电压暂降及标准的电能质量信号进行重构, 得到重构的灰度图。

(2)对步骤(1)所得的4个灰度图进行灰度共生矩阵分析, 计算本文所提到的4个纹理特征。通过4个纹理特征, 对其进行分析, 找到能够区分信号的特征量。

(3)利用步骤(2)得到的特征量做进一步变换, 使之在对灰度图进行区分时直观明了。

3.2.2 纹理特征量的选取

利用CS方法对实现步骤(1)进行Matlab仿真试验。仿真的三相电信号基波频率 $\begin{matrix} f \end{matrix}$ 为50 Hz; 奈奎斯特采样频率为6.4 kHz; 信号时长为0.85 s; 数据长度 $\begin{matrix} N \end{matrix}$ 为16 384; 观测数 $\begin{matrix} M \end{matrix}$ 为12 160。按照本文方法得到仿真结果如图2所示(本文以扰动存在于信号全部时间中得到的灰度图为例)。重构出了电压中断、电压暂升、电压暂降及正弦信号的灰度图。由于灰度图的亮暗及纹理均不同, 因此可以利用纹理的特征来区分灰度图。假设正弦信号的灰度图为标准灰度图, 由图2可见:电压中断信号的灰度图为全黑, 且无纹理变换; 电压暂升信号的灰度图比标准灰度图亮很多, 即白色区域的面积增加, 纹理变化明显; 电压暂降信号的灰度图比标准灰度图暗, 无白色区域, 只有黑色和灰色, 纹理特征较明显。为了直观表示各灰度图的不同, 对灰度图进行算法实现步骤(2)的计算, 灰度共生矩阵取0° , 45° , 90° 和135° 四个方向, 结果如图3所示。四种信号的能量值的平均值如表2所示。

	Figure Option View Download New Window
	图2 正弦信号及扰动信号的灰度图Fig.2 Grayscale of sine signal and the disturbance signal

	Figure Option View Download New Window
	图3 灰度共生矩阵的4个特征值Fig.3 Four eigenvalues of gray level cooccurrence matrix

表2 四种信号的能量值的平均值 Table 2 Energy average value of four kinds signals

3.3 基于灰度值出现概率的检测算法实现

3.3.1 算法实现步骤

利用各种扰动的灰度图计算灰度图中每种灰度值出现的概率。利用灰度值出现概率检验扰动信号类型的步骤为:

(1)计算正弦信号、电压中断、电压暂升及电压暂降信号的灰度值的出现概率。此处, 扰动存在于整个扰动时间内。

(2)对步骤(1)所得的4个灰度值出现概率图进行分析, 找到区分4种信号的方法。

3.3.2 信号分类标准的选择

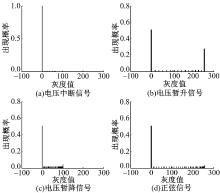
灰度图中黑色的灰度值为0, 白色的灰度值为255, 其他介于黑色和白色之间的灰度值为0~255。由图2中各图像可以通过Matlab得到对应的灰度值出现概率图, 如图4所示。

	Figure Option View Download New Window
	图4 四种信号的灰度值及出现概率图Fig.4 Grey value and probability graph of four kinds of signals

由图4可见:中断信号只在灰度值为0处出现概率不为0, 概率为1; 电压暂升信号在灰度值为0及255两处出现概率较大, 灰度值为0处出现概率与正弦信号值一样, 灰度值为255处出现概率大于正弦信号此处的出现概率; 电压暂降信号的灰度值的取值范围小于255, 在灰度值为0处出现概率与正弦信号值一样; 而正弦信号的灰度值为0~255, 且在灰度值为0处出现概率最大且只有一个最大值点。因此, 通过以上分析可知:当在灰度值为0处的出现概率大于0.5时, 存在中断扰动; 当灰度值为255处的出现概率大于0.025时, 存在电压暂升扰动; 当灰度值的取值范围小于255且在非零处有值时, 存在电压暂降扰动。所以, 通过灰度值的出现概率图可以对以上几种扰动信号进行分类。

4 仿真分析

对本文方法进行仿真试验。三相电信号的表达式为:

$\begin{matrix} \{\begin{matrix} u_{x} (t) = p (t) \times \sin (2 πft) \\ p (t) = \{\begin{matrix} 1, t \in [0, t_{1}] ⋃ [t_{2}, 0.85] \\ m, t \in [t_{1}, t_{2}] \end{matrix} \end{matrix} \end{matrix}$ (8)

式中:基波频率 $\begin{matrix} f \end{matrix}$ 为50 Hz。

仿真的三相电信号为正弦信号, 奈奎斯特采样频率为6.4 kHz, 数据长度N为16384; 观测数M为12 160; x=a, b, c; 0.01 s≤ t₂-t₁≤ 3 s, 此处的t₁=0.24 s, t₂=0.64 s。

(1)当 $x = a, m = 0 时, u_{a} 为暂时中断信号。$

(2) $当 x = b, m = 1.2 时, u_{b} 为暂时暂升信号。$

(3) $当 x = c, m = 0.8 时, u_{c}$ 为暂时暂降信号。

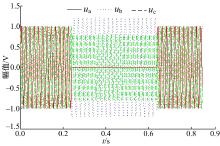
三相电信号的Matlab仿真结果如图5所示。

	Figure Option View Download New Window
	图5 三相电原始信号Fig.5 Three-phase electric original signal

构造出三相电信号后, 采用本文方法先将三相电信号转换为二维灰度图, 然后对其进行压缩重构, 原灰度图及压缩感知重构的灰度图如图6所示。

	Figure Option View Download New Window
	图6 三相电信号原灰度图及重构的灰度图Fig.6 Original and refactoring gray image grayscale of three-phase electrical signals

	Figure Option View Download New Window
	图7 采样值下压缩感知的重构质量Fig.7 Reconstruction quality of compression under different sampling value perception

本文采用峰值信噪比PSNR来评价CS算法对信号重构的效果。图7为128× 128图像原灰度图和重构灰度图的PSNR对比。试验结果为重复20次后取平均值得到的。从图7中可知, 随着采样值的增加即压缩比的增大, PSNR呈上升趋势, 重构准确度提高。图6中原灰度图数据为16 384, 重构灰度图数据为12 160。此外, 采用本文方法当使用的采样数据比Nyquist采样数据少23%时, PSNR为35 dB, 可以很好地重构出原灰度图。

由图6可见, 其中有三块位置变化明显, 此三块灰度图为扰动发生时刻的灰度图。为了提取出扰动时刻的灰度图, 对重构的灰度图进行分块。因为已知重构的灰度图由三相电信号顺次组成, 所以, 首先将灰度图分为三块(见图8), 理论上每一块灰度图中都应该只包含一种扰动; 然后, 再根据本文的两种方法对灰度图进行扰动信号检测。当采用灰度共生矩阵检测方法时, 将图8得到的每一块灰度图均分为三小块灰度图, 并将这三小块灰度图作为一组, 计算每小块灰度图的4个角度的能量平均值, 如表3所示。

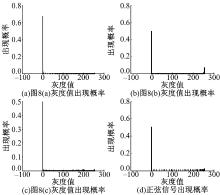
	Figure Option View Download New Window
	图8 重构的灰度图均分为三块后的灰度图Fig.8 After the grayscale reconstruction are divided into three pieces of gray

在表3中, 对每一组中的三个能量值进行分析, 找出与表2中接近的数值, 进而区分出扰动的类型及扰动存在的灰度图小块。当采用灰度值出现概率的方法对扰动信号进行分类时, 对图8得到的3幅灰度图进行Matlab仿真, 得到如图9所示的灰度值出现概率图, 然后对其进行分类。最后, 对两种方法的分类效果进行比较。

表3 图8中的每块灰度图均分为3块后每块的能量平均值 Table 3 Each block of energy after each grayscale are divided into three in figure 8

由表3可知, 图8中的(a)(b)(c)图各均分为三块后每一块在4个角度的能量的平均值。由于图8(a)的三个能量值中的第二个值是1, 且每个图只有一种扰动, 所以可以快速地判定出图8(a)为中断信号的重构结果, 即三相电信号中u_a 为中断信号。依次进行判定, 可知u_b 为电压暂升信号, u_c为电压暂降信号。

图9中的(a)(b)(c)图对应图8中的(a)(b)(c)图, 图(d)为正弦信号的灰度值概率图。

	Figure Option View Download New Window
	图9 扰动信号及正弦信号的灰度值出现概率Fig.9 Gray level value probability of disturbance signal and sine signal

由图9(a)可见, 灰度值为0处出现概率约为0.65, 远大于0.5, 所以图9(a)中存在电压中断信号; 图9(b)中的灰度值为255处的出现概率接近于0.06, 远大于0.025, 所以图9(b)中存在电压暂升扰动; 图9(c)中灰度值为255处的出现概率小于正弦信号的值, 且其他值处出现概率密集, 因此, 图9(c)为暂降信号。

综上可知, 两种方法都可以对扰动信号进行检测。灰度共生矩阵方法是对几个数据进行比较就可以得到结果, 比较简单方便; 灰度值出现概率的方法是对直方图之间进行观测, 这种方法的优点是当扰动时间较长时可以快速地分辨出各种扰动, 但是当扰动时间较短时各个灰度值出现概率的直方图就比较接近于正弦信号的直方图, 此时, 很难用肉眼观测出信号有没有扰动及为何种扰动, 而灰度共生矩阵的方法却可以对这种情况进行快速检测。所以, 由以上分析可知, 采用灰度共生矩阵的方法更加合理。

采用灰度共生矩阵的方法的Matlab仿真试验时间为2.1910 s; 采用对三相电信号的每一相分别进行仿真的时间为4.6890 s。由此可知:采用本文方法将三相电信号进行转换为一维时间信号再对信号进行处理的运行时间比对每一相信号分别处理的时间要短, 而且可以同时对三相电信号进行处理, 试验结果一次性得出, 还避免了重复进行试验的麻烦。所以, 本文方法是简便易行的。

采用本文灰度共生矩阵的方法对表1中的各类信号进行扰动分类试验100次, 结果如表4所示。

表4 扰动信号分类试验结果 Table 4 Disturbance signal classification experiment results

由表4可知, 采用灰度共生矩阵方法区分瞬时扰动信号的正确率较低, 因为当扰动时间较短时, 灰度图的能量值与正弦信号的能量值较接近, 所以容易造成区分错误; 区分暂时扰动信号时, 准确率有所提升, 因为扰动时间增加, 扰动部分在灰度图中占的面积变大, 能量值越来越接近表2中的值, 容易区分; 区分短时扰动信号时, 由于扰动时间很长, 所以扰动部分的灰度图更明显, 能量值与表2的值更为接近, 准确率更高。通过以上试验可知, 在信号扰动时长、幅度适当时, 本文方法可以快速、准确地区分出信号的扰动类型。

5 结束语

采用本文方法可以同时对三相电信号进行压缩, 且采样值比以Nyquist采样定理为基础的传统处理方法少20%时也能够很好地重构原灰度图。本文方法减少了信号压缩采样过程中的数据量, 突破了奈奎斯特采样限制。在对信号进行分类时, 利用灰度共生矩阵纹理特征量中的能量平均值作为区分扰动信号的标准, 可以简单、快速地对扰动信号进行准确区分。通过试验验证可知, 本文方法简单、容易实现, 是一种采样数据少、可以同时区分三相电扰动信号的有效方法。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Cand ès E J. Compressive sampling[C]//Proceedings of the International Congress of Mathematicians, Madrid, Spain, 2006: 1433-1452. [本文引用:1]
[2]	Cand ès E J, Tao T. Near optimal signal recovery from rand om projections: Universal encoding strategies[J]. IEEE Transactions on Information Theory, 2006, 52(12): 5406-5425. [本文引用:1]
[3]	Donoho D. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. [本文引用:1]
[4]	张颖超, 茅丹, 胡凯. 压缩传感理论在心电图信号恢复问题上的研究[J]. 计算机研究与发展, 2014, 51(5): 1018-1027. Zhang Ying-chao, Mao Dan, Hu Kai. ECG signal recovery problem based on compressed sensing theory[J]. Journal of Computer Research and Development, 2014, 51(5): 1018-1027. [本文引用:1]
[5]	于华楠, 张敬傑, 代芳琳. 压缩传感在电能质量扰动信号分析中的应用[J]. 吉林大学学报: 信息科学版, 2014, 32(6): 618-623. Yu Hua-nan, Zhang Jing-jie, Dai Fang-lin. Appliction of power quality disturbance signal based on compressed sensing[J]. Journal of Jilin University(Information Science Edition), 2014, 32(6): 618-623. [本文引用:1]
[6]	田文飚, 芮国胜, 张海波, 等. 压缩感知框架下非均匀信息采集及重构[J]. 吉林大学学报: 工学版, 2014, 44(4): 1209-1214. Tian Wen-biao, Rui Guo-sheng, Zhang Hai-bo, et al. Non-uniform information acquisition and reconstruction within copmpressed sensing framework[J]. Journal of Jilin University(Engineering and Technology Edition), 2014, 44(4): 1209-1214. [本文引用:1]
[7]	Cand ès E, Romberg J, Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509. [本文引用:1]
[8]	苗桂君, 王学伟, 杨立国, 等. 短时电能质量信号压缩采样方法的研究[J]. 电测与仪表, 2010, 47(12): 8-11, 19. Miao Gui-jun, Wang Xue-wei, Yang Li-guo, et al. Research on compression sampling algorithm of short-time power quality[J]. Electrical Measurement & Instrumentation, 2010, 47(12): 8-11, 19. [本文引用:1]
[9]	李雪梅, 苗桂君, 王学伟, 等. 电能质量信号压缩采样稀疏基性能研究[J]. 电测与仪表, 2011, 48(9): 14-17. Li Xue-mei, Miao Gui-jun, Wang Xue-wei, et al. A research on performance of compression sampling sparse matrix of power quality signal[J]. Electrical Measurement & Instrumentation, 2011, 48(9): 14-17. [本文引用:1]
[10]	王学伟, 王琳, 苗桂君, 等. 暂态和短时电能质量扰动信号压缩采样与重构方法[J]. 电网技术, 2012, 36(3): 191-196. Wang Xue-wei, Wang Lin, Miao Gui-jun, et al. An approach for compressive sampling and reconstruction of transient and short-time power quality disturbance signals[J]. Power System Technology, 2012, 36(3): 191-196. [本文引用:2]
[11]	欧阳森, 王建华, 宋政湘, 等. 一种基于dq0 变换和专家系统的电能质量信号辩识方法[J]. 电力系统及其自动化学报, 2003, 15(5): 21-24, 33. Ouyang Sen, Wang Jian-hua, Song Zheng-xiang, et al. A power quality identification method based on dq0 conversion and expert system[J]. Proceedings of the EPSA, 2003, 15(5): 21-24, 33. [本文引用:1]
[12]	Wang M, Mamishev E V. Classification of power quality events using optimaltim e-frequency representations-part 1: theory[J]. IEEE Transactions on Power Delivery, 2004, 19(3): 1488-1495. [本文引用:1]
[13]	田刚, 包志华, 堵俊, 等. 电力信号短时扰动的检测及自动分类[J]. 电力系统及其自动化学报, 2006, 18(2): 31-34, 40. Tian Gang, Bao Zhi-hua, Du Jun, et al. Detection and auto-classification of short-time disturbance of electric signal[J]. Proceedings of the CSU-EPSA, 2006, 18(2): 31-34, 40. [本文引用:1]
[14]	刘奇, 周雒维, 卢伟国. 基于广义S变换的暂态电能质量扰动定位与识别[J]. 电力系统保护与控制, 2012, 40(7): 60-65. Liu Qi, Zhou Luo-wei, Lu Wei-guo. Localization and identification of transient power quality disturbances based on generalized S-transform[J]. Power System Protection and Control, 2012, 40(7): 60-65. [本文引用:1]
[15]	李慧娜, 郭超峰, 平源. 灰度共生矩阵在指纹图像分割中的应用[J]. 数据采集与处理, 2012, 27(1): 63-67. Li Hui-nan, Guo Chao-feng, Ping Yuan. Application of gray level co-occurrence matrix for fingerprint segmentation[J]. Journal of Data Acquisition &Processing, 2012, 27(1): 63-67. [本文引用:1]

2006

0.0

... 压缩感知(Compressed sensing,CS)理论^[1,2,3],它同时实现了信号采样和压缩,突破了Nyquist采样定理的限制,极大地减少了采样数据量,具有广泛的应用前景^[4,5,6,7] ...

2006

0.0

2006

0.0

2014

0.0

. 2014, 51(5):1018-1027 DOI:doi:10.7544/issn1000-1239.2014.20121161

ECG signal recovery problem based on compressed sensing theory

压缩传感理论在心电图信号恢复问题上的研究

Zhang Ying-chao , Mao Dan , Hu Kai.

张颖超, 茅丹, 胡凯

Body sensor network (BSN) is a new network which can monitor the patient’s physiological characteristics in real time, thus the network is widely utilized to improve the level of healthcare for people through the computer techniques, such as intelligent information processing, new network services and so on. Compressed sensing (CS) is a new theory of signal acquisition and decoding, which not only breaks through the bottleneck of the law of traditional sampling, but also makes the signal sampling and compression done at the same time. So, CS is extensively used in medicine, astronomy, pattern recognition and so on. For now, CS is paid more and more attention to by many researchers. This paper faces the recovery problem of electrocardiogram (ECG) signals through compressed sensing theory. According to the various performance of all kinds of wavelet basis conducted as sparse basis, we hope to find an optimal wavelet basis that makes the ECG signal restored precisely and stably through a lot of experiments. The experimental results demonstrate that there exists a set of wavelet basis which can make a variety of ECG signals recuperated with high accuracy and strong robustness. The result can provide ideas for discussing the recovery problem of ECG signals furthermore.

身体传感器网络(body sensor network, BSN)是实时监护病人生理特征的一种新型网络，压缩传感(compressed sensing, CS)是一种全新的信号采集、编解码理论.面对CS理论用于基于BSN的心电信号的恢复问题，针对现有多种小波基作为稀疏基使用时的表现，通过大量实验，希望寻找到一个最优的小波基，使得心电信号能够精确且稳定地恢复.实验结果证明存在一组小波基，能够使得多种心电信号的恢复结果不但精度高，而且鲁棒性强，该研究结果可以为进一步研究心电信号恢复问题提供参考意见.

2014

0.0

. 2014, 32(6):618-623 DOI:doi:10.3969/j.issn.1671-5896.2014.06.010

Appliction of power quality disturbance signal based on compressed sensing

压缩传感在电能质量扰动信号分析中的应用

Yu Hua-nan , Zhang Jing-jie , Dai Fang-lin.

于华楠, 张敬傑, 代芳琳

摘　要：针对电能质量扰动信号分析中,传统信号处理方法存在采样数据量极大、采样时间长、压缩时浪费采样资源等问题,将压缩传感（CS：Compressed Sensing）应用于电能质量扰动信号分析中.实现了采样与压缩同时完成,极大地降低了采集的数据量和采样速率.通过对压缩传感的过完备字典设计,实现了压缩传感同时检测多个电能质量扰动信号,以及压缩传感对信号在一维、二维上的重构,并对重构的电能质量扰动信号进行分析.实验结果表明,与传统的电能质量扰动信号处理方法相比,该算法在采样数据量、重构效果方面都有很大提升,得到的重构信号误差更小,对信号的分析更准确.

2014

0.0

. 2014, 44(4):1209-1214 DOI:doi:10.13229/j.cnki.jdxbgxb201404047

Non-uniform information acquisition and reconstruction within copmpressed sensing framework

压缩感知框架下非均匀信息采集及重构

Tian Wen-biao , Rui Guo-sheng , Zhang Hai-bo

田文飚, 芮国胜, 张海波

摘　要：为提高现有直接信息均匀压缩采样（Analog to information conversion，AIC）的观测效率和性能，在能量准则下，提出非均匀信息采集（Non—uniform information acquisition，NUIA），充分利用信息的重要性先验，即对信号随机调制后，依据能量进行变速率的采集，能量越大的信号段采样速率越高，反之亦然。结合支撑域扩充、剪枝的思路提出变速匹配追踪（Variable rate matching pursuit，VRMP）算法，通过引入非均匀观测的先验支撑集，并在追踪过程中将其与迭代估计出的支撑集相并，提高了重构精度。理论分析和实验结果表明了NUIA—VRMP的有效性。特别地，相比于常规AIC的子空间追踪重构，NUIA—VRMP的组合能在低采样速率条件（如20％的Nyquist速率）下获得50dB的重构增益。

2006

0.0

2010

0.0

. 2010, 47(12):8-11,19 DOI:doi:10.3969/j.issn.1001-1390.2010.12.003

Research on compression sampling algorithm of short-time power quality

短时电能质量信号压缩采样方法的研究

Miao Gui-jun , Wang Xue-wei , Yang Li-guo

苗桂君, 王学伟, 杨立国

根据压缩传感(Compressed Sensing,cs)理论,首次提出了短时电能质量扰动信号的压缩采样方法,该方法突破了奈奎斯特采样频率的限制,实现了低于奈奎斯特采样频率的低速率采样.文中对比分析了CS理论与传统采样理论,研究了CS短时电能质量信号压缩采样的实现方法,包括:测量矩阵的构建、稀疏基的选取和电能质量信号快速贝叶斯匹配追踪重构算法(FBMP).文中针对6种短时电能质量信号进行了仿真实验,给出了不同压缩采样比的条件下,该压缩采样方法所能达到的性能指标,结果标明本文提出的方法正确有效.

... 文献^[8]首次将压缩感知应用于短时电能质量扰动信号压缩采样中,研究了CS短时电能质量信号压缩采样的实现方法 ...

2011

0.0

. 2011, 48(9):14-17 DOI:doi:10.3969/j.issn.1001-1390.2011.09.004

A research on performance of compression sampling sparse matrix of power quality signal

电能质量信号压缩采样稀疏基性能研究

Li Xue-mei , Miao Gui-jun , Wang Xue-wei

李雪梅, 苗桂君, 王学伟

为解决电能质量信号传统采集压缩方法所面临的采样率高、采样资源浪费及硬件实现成本高的问题,本文研究并实现了对非稳态和稳态电能质量数据的压缩采样、采样数据空间稀疏基的选取和基于TV最小化共轭梯度法的信号重构. 文中针对几类常见单一扰动和含有多重扰动的校准源实测信号进行算法的仿真分析和实验验证,并对比分析了傅立叶基和小波基对两种扰动信号的重构效果.仿真和实验表明,所提出的方法采样率比Nyquist采样率低73％,对于单一扰动信号,稀疏基采用傅里叶基时重构信噪比除暂态脉冲信号外均大于35dB；对于多重扰动信号,稀疏基采用小波基时重构信号信噪比大于22dB,满足电能质量分析的要求.

... 文献^[9]研究了应用于电能质量信号的CS稀疏基及其性能 ...

2012

0.0

. 2012, 36(3):191-196

An approach for compressive sampling and reconstruction of transient and short-time power quality disturbance signals

暂态和短时电能质量扰动信号压缩采样与重构方法

Wang Xue-wei , Wang Lin , Miao Gui-jun

王学伟, 王琳, 苗桂君

Traditional methods for acquisition and compression of power quality signals are faced with such troubles as high sampling rate, waste of sampling resources and high attainable cost for hardware. To solve these problems, based on compressive sensing theory a method for compressive sampling and reconstruction of transient and short-time power quality disturbance signals is proposed for the first time. In the proposed method one-dimensional power quality signals are mapped to two-dimensional signals, and according to the principle of image sparse representation original signals are reconstructed by sampled random projection values and the sampled data to be used in this way is reduced by more than 60% than those used in Nyquist sampling, thus the compressive sampling, the selection of sparse basis in data space and the signal reconstruction based on total variation conjugate gradient minimization method are implemented. Simulation analysis and experimental verification of the proposed method are performed by the most common single disturbances and measured signals of calibration source containing multiple disturbances, simulation and verification results show that when sampling rate of the proposed method is lower than 73% of that for Nyquist sampling, except transient impulse signals the S/N ratios of the reconstructed signals of single disturbances are greater than 35dB, the S/N ratios of the reconstructed signals of multiple disturbances are greater than 22dB, thus the requirement of power quality analysis can be met.

为解决传统的电能质量信号采集压缩方法所面临的采样率高、采样资源浪费及硬件实现成本高的问题，根据压缩传感理论首次提出了暂态和短时电能质量扰动信号的压缩采样与重构方法。该方法将电能质量信号由一维信号变换为二维信号，并根据图像可稀疏表示的原理，使用比Nyquist采样数据少60%以上的随机投影采样值重构原始信号，实现了对暂态和短时电能质量测量数据的压缩采样、采样数据空间稀疏基的选取和基于全变分最小化共轭梯度法的信号重构。针对几类常见单一扰动和含有多重扰动的校准源实测信号进行了算法的仿真分析和实验验证。结果表明，所提出的方法在采样率低于Nyquist采样率73%时，单一扰动的重构信号信噪比除暂态脉冲信号外均大于35 dB，多重扰动的重构信号信噪比大于22 dB，满足电能质量分析的要求。

... 文献^[10]将CS应用于暂态短时电能质量扰动信号处理中,并将一维时间信号转换为二维矩阵进行处理,进一步减少了采样数据量 ...

... 本文对信号进行CS处理过程中采用了文献^[10]中的将一维时间信号转换为二维灰度图的方法 ...

2003

0.0

. 2003, 15(5):21-24,33 DOI:doi:10.3969/j.issn.1003-8930.2003.05.007

A power quality identification method based on dq0 conversion and expert system

一种基于dq0 变换和专家系统的电能质量信号辩识方法

Ouyang Sen , Wang Jian-hua , Song Zheng-xiang

欧阳森, 王建华, 宋政湘

提出了一种基于dq0变换和专家系统的电能质量信号辨识新方法.利用dq0变换后的d、q和0序分量,能对单相、两相或三相电压出现电能质量问题的电力系统电压进行准确有效的信号特征提取;利用这些信号特征,结合相应的基于规则的专家系统能有效地进行电能质量信号辨识.仿真计算结果表明该方法是有效的.

... 文献^[11]提出了一种基于dq0变换和专家系统的扰动信号区分方法,但是对信号的区分过程比较复杂 ...

2004

0.0

... 文献^[12]利用小波神经网络分类器对电能质量扰动进行识别,该方法需要进行大量的训练,计算量非常大 ...

2006

0.0

. 2006, 18(2):31-34,40 DOI:doi:10.3969/j.issn.1003-8930.2006.02.007

Detection and auto-classification of short-time disturbance of electric signal

电力信号短时扰动的检测及自动分类

Tian Gang , Bao Zhi-hua , Du Jun

田刚, 包志华, 堵俊

针对电力短时扰动信号具有非平稳、突发性的特点,应用小波变换的多分辨率分析特性检测扰动信号的特征参量,依据IEEE制定的短时电能质量扰动标准,提出了一种逐次逼近型的快速分类法.利用小波变换对扰动信号的奇异点进行检测,发现通过对扰动信号奇异点的检测可以准确地定位短时扰动的起始时刻、持续时间和扰动幅度.提出的逐次逼近型分类法,用一组8位二进制数逼近扰动的持续时间和扰动幅度两个参数,不仅可以将短时扰动信号按照IEEE制定的标准进行准确分类,而且还可以大大减少分类过程中的计算量,充分满足了电力信号监测的实时性要求.

... 文献^[13]提出了电力信号短时扰动检测及自动分类方法,分类时利用二进制序列,不直观、不易于观测 ...

2012

0.0

. 2012, 40(7):60-65 DOI:doi:10.3969/j.issn.1674-3415.2012.07.011

Localization and identification of transient power quality disturbances based on generalized S-transform

基于广义S变换的暂态电能质量扰动定位与识别

Liu Qi , Zhou Luo-wei , Lu Wei-guo.

刘奇, 周雒维, 卢伟国

S变换由于时频分辨率固定,从而导致定位暂态电能质量扰动的效果差。提出一种基于广义S变换的扰动定位新方法,利用高频处时间幅值曲线的突变点峰值进行定位检测,以提高扰动的定位精度。首先通过广义S变换得到扰动信号的模时频矩阵,然后利用高频处时间幅值曲线定位扰动的起止时刻,再根据最大频谱曲线、基频幅值曲线与定位结果提取四个识别特征量,最后基于分类规则树方法实现扰动信号的自动分类。仿真结果表明,所提出的定位方法简单直观,精度较高;提取的识别特征量少而有效,分类效果良好。

... 文献^[14]提出了一种基于广义S变换的暂态电能质量扰动定位及识别 ...

2012

0.0

. 2012, 27(1):63-67 DOI:doi:10.3969/j.issn.1004-9037.2012.01.010

Application of gray level co-occurrence matrix for fingerprint segmentation

灰度共生矩阵在指纹图像分割中的应用

Li Hui-nan , Guo Chao-feng , Ping Yuan.

李慧娜, 郭超峰, 平源

指纹图像分割是自动指纹识别系统的关键步骤之一.通过分析指纹图像的灰度级数、位移量及相对方向与其灰度共生矩阵的二次统计特征之间的关系,提出了一种基于灰度共生矩阵的指纹图像分割算法.该算法先将指纹图像分割成矩形块,得到每个矩形块在不同相对方向上的灰度共生矩阵的对比度,然后将其对比度方差与预设阈值进行比较,完成前景或背景区的快速判断.分析和实验表明,该算法分割指纹效果较好,并且对不同的采集环境和图像质量都体现出较强的健壮性.

... 灰度共生矩阵是通过计算图像中特定方向和特定距离的两像素之间灰度差值出现的次数,得到图像在方向、间隔、幅度变化大小和速度的综合信息,从而将图像的灰度值转化为纹理信息^[15],进而对图像进行分类等研究 ...