最小二乘权值平滑滤波技术在核磁共振信号处理中的应用

引用本文

孙淑琴, 刘骏妍, 蒋川东, 孟庆云, 林君, 彭良玉. 最小二乘权值平滑滤波技术在核磁共振信号处理中的应用.吉林大学学报:工学版, 2016, 46(3): 985-995
SUN Shu-qin, LIU Jun-yan, JIANG Chuang-dong, MENG Qing-yun, LIN Jun, PENG Liang-yu. Least-square weighted smoothing filter technology applied in magnetic resonance sounding signal processing. Journal of Jilin University Engineering and Technology Edition, 2016, 46(3): 985-995 复制到剪切板

Permissions

最小二乘权值平滑滤波技术在核磁共振信号处理中的应用

孙淑琴^1,², 刘骏妍^1,², 蒋川东^1,², 孟庆云^1,², 林君^1,², 彭良玉^1,²

1.吉林大学仪器科学与电气工程学院,长春 130026

2.吉林大学地球信息探测仪器教育部重点实验室,长春 130026

通讯作者:林君(1954-),男,教授,博士生导师.研究方向:地球物理探测技术及仪器.E-mail:lin_jun@jlu.edu.cn

作者简介:孙淑琴(1969-),女,教授,博士.研究方向:数字信号处理.E-mail:sunsq@jlu.edu.cn

基金:国家重大科学仪器设备开发专项项目(2011YQ030133)

摘要

采用最小二乘权值平滑滤波法对核磁共振地下水探测仪接收到的信号进行滤波处理,并与滑动平均权值滤波方法进行比较。仿真试验结果表明:利用最小二乘权值平滑滤波法能够取得更准确的核磁共振(Magnetic resonance sounding,MRS)信号特征参数,信噪比也得到了提高;最小二乘权值平滑滤波法更适合于随机噪声和尖峰噪声的去除;利用最小二乘权值平滑滤波法进行去噪时要选择合适的权值。其中MRS信号特征参数的拟合误差能够控制在1%以内,且信号曲线的平滑度得到了很大的改善。同时实测数据的滤波处理进一步证明了该方法的可行性。

关键词: 电气工程; 核磁共振; 数据滤波; 滑动平均; 最小二乘

中图分类号:TN911.7 文献标志码:A 文章编号:1671-5497(2016)03-0985-11

Least-square weighted smoothing filter technology applied in magnetic resonance sounding signal processing

SUN Shu-qin^1,², LIU Jun-yan^1,², JIANG Chuang-dong^1,², MENG Qing-yun^1,², LIN Jun^1,², PENG Liang-yu^1,²

1.College of Instrumentation and Electrical Engineering, Jilin University, Changchun 130026, China

2.Laboratory of Geo-Exploration and the Instrumentation Ministry of Education of China, Jilin University, Changchun 130026, China

Abstract

Least Square Weighted Smoothing Filter (LSW-SF) method is used to filter Magnetic Resonance Sound (MRS) signals, which is compared with the moving average filter method. Results of a large number of simulation experiments show the following characteristics. First, the more accurate characteristic parameters of MRS can be obtained using the LSW-SF method, and the Signal to Noise Ratio (SNR) is also improved. Second, the LSW-SF method is more suitable for random noise and rush noise removal. Third, appropriate weights should be chosen when the LSW-SF method is used to wipe out noise. Among them fitting error of MRS signal characteristic parameters can be controlled within 1%, and the smoothness of the signal curve is greatly improved. Meanwhile, the filter processing of the measured data indicates this method is effective.

Keyword: electrical engineering; magnetic resonance sounding (MRS); data filtering; moving average; least squares

Show Figures

0 引言

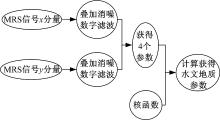
地面核磁共振(Magnetic resonance sounding, MRS)技术是目前最为直接的探测地下水的地球物理方法, 得到了广泛的应用^{[1, 2]}。野外试验采集到的数据需要进行滤波处理, 才能获得准确的特征参数, 为后续数据的反演解释提供了依据。目前JLMRS仪器数据处理软件中采用的数据滤波方法有自适应滤波法、FIR低通滤波法和滑动平均滤波法等^{[3, 4, 5, 6]}。自适应滤波和FIR低通滤波方法均存在一定局限性, 当信号与噪声干扰频率相近时会造成有用信号的失真^{[7, 8]}。滑动平均滤波其实是一个低通滤波的过程, 它的计算方法简单、易于实现。目前滑动平均滤波法中对于数据权值的选取是采用中间值最大, 向前向后递减的方式, 常规的选择是三角形分布, 但是三角形分布的权值只是根据一般规律给出, 并不精确^{[7, 8, 9]}。

本文针对现有滑动平均滤波方法(以下称为三角形滑动平均法)中权值选取的不足^{[10, 11, 12]}, 提出了一种更为精确的权值确定方法— — 最小二乘权值方法。最小二乘权值法是提出一个多项式, 求取使多项式的值无限趋近于数据 $\begin{matrix} y \end{matrix}$ 值的多项式系数, 即权值, 采用这种方法计算出的权值更为精确, 获得了较好的滑动平均滤波效果。

1 核磁共振信号数据处理

1.1 数据处理过程

核磁共振野外采集到的数据含有大量噪声, 如果不进行消噪处理, 则不能准确提取信号的特征参数^{[13, 14]}。针对仪器的野外测试信号, 首先对MRS信号进行消噪处理, 其中包括叠加消噪和数字滤波方法消噪, 之后提取MRS相应的信号特征参数: $\begin{matrix} E_{0} \end{matrix}$ 为初始振幅; $\begin{matrix} T_{2}^{*} \end{matrix}$ 为平均衰减时间; $\begin{matrix} f \end{matrix}$ 为接收频率; $\begin{matrix} φ_{0} \end{matrix}$ 为初始相位。最后根据这些参数, 结合核函数, 计算出水文地质参数。测试信号数据处理过程如图1所示。

	Figure Option View Download New Window
	图1 MRS信号数据处理流程图Fig.1 Flow chart of MRS signal data processing

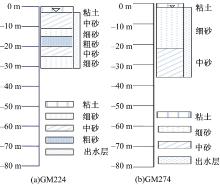
MRS信号的特征参数经过反演可得到相应的水文地质情况。核磁共振数据参数与相应的水文地质参数的对应关系如表1所示。

表1 MRS数据参数与相应的水文地质参数对应关系 Table 1 Relation of MRS data parameters and corresponding hydrogeological parameters

MRS数据特征参数	水文地质参数
初始振幅 $\begin{matrix} E_{0} \end{matrix}$ /nV	单位体积含水量(有效孔隙度)
平均衰减时间 $\begin{matrix} T_{2}^{*} \end{matrix}$ /ms	孔隙大小(渗透性)
初始相位 $\begin{matrix} φ_{0} \end{matrix}$ /(° )	含水层导电性(电阻率)

表1 MRS数据参数与相应的水文地质参数对应关系 Table 1 Relation of MRS data parameters and corresponding hydrogeological parameters

1.2 FID弱信号检测技术

基于全波形采集的MRS信号检测器数据量大, 而核磁共振地下水探测方法则需要采用叠加的方法来消除噪声, 从而导致了仪器测量效率过低。

自由感应衰减信号(Free induction decay, FID)是MRS信号包络, 它包含了地下水探测的关键参数, 所以只需要获取FID信号即可, 这样既能够评价地下水信息, 也可以提高仪器的测量速度。核磁共振地下水检测技术中采用4倍频采样的数字正交技术来获得包络信号^[15]。其MRS包络信号如式(1)所示:

$\begin{matrix} \begin{matrix} E_{c} (t) = E_{0} \cdot e^{- t / T_{2}^{*}} \cdot [\cos (2 πΔft + φ_{0}) + \\ i \cdot \sin (2 πΔft + φ_{0})] \end{matrix} \end{matrix}$ (1)

式中: $\begin{matrix} Δf \end{matrix}$ 为信号的接收频率 $\begin{matrix} f_{r} \end{matrix}$ 和信号的发射频率 $\begin{matrix} f_{0} \end{matrix}$ 之间的偏差, $\begin{matrix} Δf = f_{r} - f_{0}; E_{0} 、 T_{2}^{*} 、 φ_{0} \end{matrix}$ 为核磁共振信号特征参数, 用于后续反演解释; i为虚部标志。

1.3 核磁共振信号中的噪声分析

一般MRS信号中的噪声分为3种:①工频噪声, 由电力线路产生, 其频率为50 Hz的整数倍; ②随机噪声, 分布在整个频率范围内; ③尖峰噪声, 幅度高出信号, 但是持续时间极短。

三角形滑动平均法主要适用于非平稳数据, 其权值的选取直接影响信号的平滑效果, 该方法的权值是根据一般规律给出的, 在中间选取最大权值, 因此该方法主要适用于随机噪声, 对尖峰噪声滤波效果不明显。最小二乘权值滑动平均滤波法(以下简称为最小二乘滑动平均法)改进权值的设置方式, 使之更为精确。最小二乘滑动平均法对噪声有较强的适应能力, 适应于随机噪声和尖峰噪声, 最小二乘滑动平均法可以采用不同的数据点个数和不同次方对信号进行拟合, 拟合阶数越高, 其平滑曲线与实测数据拟合得越好, 曲线越平滑, 消噪效果更为理想, 信号信噪比提高更多^[16]。

1.4 三角形权值滤波技术

目前核磁共振地下水探测技术中的三角形滑动平均法主要是在时间序列中某点前、后各取k个数据点, 进行滑动滤波, 滑动时在2k+1个数据点中间取最大权值, 然后向前、后对称递减, 采用三角形分布, 属线性递减。权值 $\begin{matrix} a_{i} \end{matrix}$ 如式(2)所示:

$\begin{matrix} a_{i} = \frac{1}{{(k + 1)}^{2}} \end{matrix}$ (2)

式中: $\begin{matrix} k = 1, 2, \dots, k, k + 1, k, \dots, 2, 1; i = 1, 2, \dots, k 。 \end{matrix}$

1.5 最小二乘权值滤波技术

对于2N+1组数据(x_i, y_i), 假设多项式 $\begin{matrix} P_{n} (x_{i}) = a_{0} + a_{1} x_{1} + a_{2} x_{2}^{2} + \dots + a_{k} x_{k}^{k}, \end{matrix}$ 滑动平均法就是使这个多项式无限趋近原始数据中的 $\begin{matrix} y_{i}, \end{matrix}$ 也就是求使误差 $\begin{matrix} P_{n} (x_{i}) - y_{i} \end{matrix}$ 的平方和最小, 即求满足条件的多项式各项系数a_i, 其中i=1, 2, …, k。设目标函数为I(即误差的最小平方和), 可得I的表达式为:

$\begin{matrix} I = \overset{m}{\sum_{i = 0}} [P_{n} (x_{i}) - y_{i}]^{2} = \overset{m}{\sum_{i = 0}} (\overset{n}{\sum_{k = 0}} a_{k} x_{i}^{k} - y_{i})^{2} \end{matrix}$ (3)

求目标函数的最小值, 分别对a₀, a₁, a₂, …, a_k 求偏导数, 对a₀求偏导数, 可得如下结果:

$\begin{matrix} \frac{\partial I}{\partial a_{0}} = \frac{\partial [\overset{m}{\sum_{t = 0}} ((\overset{n}{\sum_{k = 0}} a_{k} x_{i}^{k})^{2} - 2 y_{i} \overset{n}{\sum_{k = 0}} a_{k} x_{i}^{k} + y_{i}^{2})]}{\partial a_{0}} \end{matrix}$ (4)

同理对其他几项求偏导数, 结果如下所示:

$\begin{matrix} \frac{\partial I}{\partial a_{j}} = 2 \overset{m}{\sum_{i = 0}} \overset{n}{\sum_{k = 0}} a_{k} x_{i}^{k + j} - 2 \overset{m}{\sum_{i = 0}} y_{i} x_{i}^{j} \end{matrix}$ (5)

式中: $\begin{matrix} j = 0, 1, \dots, n 。 \end{matrix}$

令各偏导数为零, 可得:

$\begin{matrix} \overset{m}{\sum_{i = 0}} \overset{n}{\sum_{k = 0}} a_{k} x_{i}^{k + j} = \overset{m}{\sum_{i = 0}} y_{i} x_{i}^{j} \end{matrix}$ (6)

式中: $\begin{matrix} j = 0, 1, \dots, n 。 \end{matrix}$

由式(6)得矩阵方程组为:

$\begin{matrix} \begin{matrix} (\begin{matrix} m + 1 & \overset{m}{\sum_{i = 0}} x_{i} & \overset{m}{\sum_{i = 0}} x_{i}^{2} & \dots & \overset{m}{\sum_{i = 0}} x_{i}^{n} \\ \overset{m}{\sum_{i = 0}} x_{i} & \overset{m}{\sum_{i = 0}} x_{i}^{2} & \overset{m}{\sum_{i = 0}} x_{i}^{3} & \dots & \overset{m}{\sum_{i = 0}} x_{i}^{n + 1} \\ ︙ & ︙ & ︙ & ︙ \\ \overset{m}{\sum_{i = 0}} x_{i}^{n} & \overset{m}{\sum_{i = 0}} x_{i}^{n + 1} & \overset{m}{\sum_{i = 0}} x_{i}^{n + 2} & \dots & \overset{m}{\sum_{i = 0}} x_{i}^{2 n} \end{matrix}) (\begin{matrix} a_{0} \\ a_{1} \\ ︙ \\ a_{n} \end{matrix}) = \\ (\begin{matrix} \overset{m}{\sum_{i = 0}} y_{i} \\ \overset{m}{\sum_{i = 0}} y_{i} \cdot x_{i} \\ ︙ \\ \overset{m}{\sum_{i = 0}} y_{i} \cdot x_{i}^{n} \end{matrix}) \end{matrix} \end{matrix}$ (7)

式(7)右端变形为如下形式:

$\begin{matrix} (\begin{matrix} \overset{m}{\sum_{i = 0}} y_{i} \\ \overset{m}{\sum_{i = 0}} y_{i} \cdot x_{i} \\ ︙ \\ \overset{m}{\sum_{i = 0}} y_{i} \cdot x_{i}^{n} \end{matrix}) = (\begin{matrix} 1 & 1 & \dots & 1 \\ x_{0} & x_{1} & \dots & x_{m} \\ x_{0}^{2} & x_{1}^{2} & \dots & x_{m}^{2} \\ ︙ & ︙ & ︙ \\ x_{0}^{n} & x_{1}^{n} & \dots & x_{m}^{n} \end{matrix}) (\begin{matrix} y_{0} \\ y_{2} \\ y_{3} \\ ︙ \\ y_{m} \end{matrix}) \end{matrix}$ (8)

最终简化为如下形式:

$\begin{matrix} A (\begin{matrix} a_{0} \\ a_{1} \\ ︙ \\ a_{n} \end{matrix}) = B (\begin{matrix} y_{0} \\ y_{1} \\ ︙ \\ y_{n} \end{matrix}) \end{matrix}$ (9)

由式(9)可以求解任意点数任意次方满足某种噪声滤波效果的最小二乘权值系数。需要指出的是, 2N+1对数据组, 最高次方只可取到2N次。

2 模型仿真

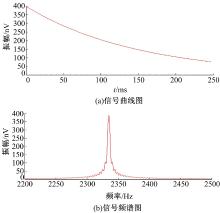
全波采集的核磁共振信号是一个衰减的正弦波, 但是数据量大、测量效率低。采用基于4倍频采样的数字正交FID弱信号检测技术, 采集到的核磁共振信号为包络曲线。模拟一个理想的核磁共振信号(见式(1)), 并加入干扰噪声来验证本文方法的有效性。MRS信号中常见的干扰噪声为工频噪声、随机噪声和尖峰噪声, 在理想信号中加入这几种噪声后进行最小二乘权值滑动平均滤波处理。通过比较任意点数、任意次方权值的最小二乘滑动平均法对上述噪声进行滤波处理的效果, 最终选择五点三次, 七点三次和九点四次这三种权值的最小二乘滑动平均法, 并与三角形权值滑动平均法的滤波结果作比较, 验证本文方法的可信性和可行性。

2.1 建立理想模型

MRS理想信号包络和频谱图如图2所示, 其初始振幅 $\begin{matrix} E_{0} \end{matrix}$ 为400 nV; 初始相位 $\begin{matrix} φ_{0} \end{matrix}$ 为150° ; 平均衰减时间 $\begin{matrix} T_{2}^{*} \end{matrix}$ 为150 ms; 频率 $\begin{matrix} f \end{matrix}$ 为2335 Hz。

	Figure Option View Download New Window
	图2 理想信号包络和频谱图Fig.2 Ideal signal envelope and spectrum diagram

2.2 信号加随机噪声

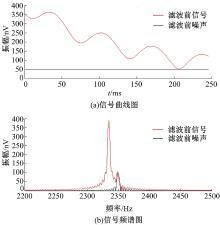
在理想信号中加入幅度为150 nV的随机噪声, 如图3所示。其信噪比为1.49, 且曲线的平滑度降低。

	Figure Option View Download New Window
	图3 理想MRS信号中加入随机噪声Fig.3 Ideal signal of MRS including random noise

	Figure Option View Download New Window
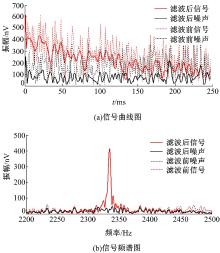	图4 三角形滑动平均法处理后的信号曲线(加入随机噪声)Fig.4 Signal curve after triangle moving average processing (including random noise)

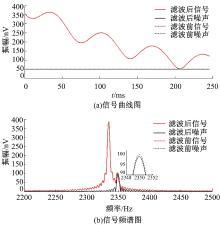
采用三角形滑动平均法处理后的信号曲线如图4所示, 其信噪比为2.72。从图4中可看出:信号与噪声明显地分离, 信号曲线变得比较平滑。采用最小二乘滑动平均法处理后的曲线如图5所示, 处理之后的信噪比可达到3.49。从图5中可以看出, 七点三次滑动滤波后曲线的平滑度最好。所以采用最小二乘滑动平均法进行滤波时要选取合适的权值。

综合图4和图5可以看出:最小二乘滑动平均法比三角形滑动平均法所得到的曲线平滑度要高, 且信号曲线与噪声曲线分离的效果好。

最后, 结合图5和表2可知:对于随机噪声, 两种滤波方法都可以很好地将噪声与信号分离开来, 但是最小二乘滑动平均法所得到的信号曲线更加平滑。表2中的数据更进一步证明了最小二乘滑动平均法的可信性。

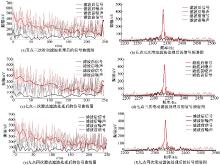	Figure Option View Download New Window
	图5 经最小二乘滑动平均法处理后的信号曲线(加入随机噪声)Fig.5 Signal curve after by the least squares moving average processing(including random noise)

表2 随机噪声情况下模型仿真数据经不同滤波方式处理后的参数提取结果对比 Table 2 Parameter extraction result contrast of random noise case model simulation data after different filtering method

	振幅E₀ /nV	衰减时间 $\begin{matrix} T_{2}^{*} \end{matrix}$ /ms	相位 $\begin{matrix} φ_{0} \end{matrix}$ /(° )	信噪比	拟合误差			频谱幅度衰减率/%
	振幅E₀ /nV	衰减时间 $\begin{matrix} T_{2}^{*} \end{matrix}$ /ms	相位 $\begin{matrix} φ_{0} \end{matrix}$ /(° )	信噪比	E₀/%	$\begin{matrix} T_{2}^{*} \end{matrix}$ /%	$\begin{matrix} φ_{0} \end{matrix}$ /%	频谱幅度衰减率/%
理想信号	400	150	150	$\begin{matrix} \infty \end{matrix}$	-	-	-	-
加入随机噪声	396.0	168.1	147.4	1.49	-	-	-	-
三角形权值滑动平均	395.3	168.4	147.8	2.71	1.17	12.2	1.7	0.28
五点三次滑动平均	385.6	178.2	151.3	2.91	3.6	18.8	1.5	0.28
七点三次滑动平均	375.9	167.9	151.6	3.49	6.02	11.9	1.1	0.23
九点四次滑动平均	395.8	168.6	147.5	3.16	1.05	12.2	1.7	0.27

2.3 信号加尖峰噪声

在理想信号中加入尖峰噪声和幅度为100 nV的随机噪声后的信号曲线如图6所示, 其信噪比为1.25。从图6中可以看出, 信号中混入了两个尖峰噪声, 其幅值都为1500 nV。

	Figure Option View Download New Window
	图6 理想MRS信号中加入尖峰噪声Fig.6 Ideal signal of MRS including peak noise

采用三角形滑动平均法处理后的信号曲线如图7所示, 其信噪比为5.47。从图7中可以看出:噪声得到了明显的抑制, 信号曲线的平滑度得到了较好的改善。采用最小二乘滑动平均法处理后的信号曲线如图8所示, 处理之后的信噪比可达7.55。从图8中可以看出, 经七点三次滑动滤波方法处理后的曲线平滑度最好且噪声抑制得最好, 故选择合适权值的最小二乘滑动平均法对信号处理非常重要。结合图7和图8可以得出:最小二乘滑动平均法比三角形滑动平均法所得到的曲线平滑度要高且噪声得到了很好的抑制, 信号曲线与噪声得到了很好的分离。

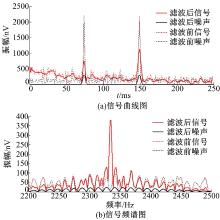	Figure Option View Download New Window
	图7 三角形滑动平均法处理后的信号曲线(加入尖峰噪声)Fig.7 Signal curve after triangle moving average processing(including peak noise)

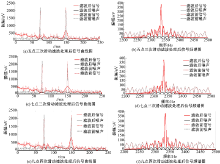	Figure Option View Download New Window
	图8 经最小二乘滑动平均法处理后的信号曲线(加入尖峰噪声)Fig.8 Signal curve after by the least squares moving average processing(including peak noise)

含有尖峰噪声的MRS信号经过不同滤波方法处理后得到特征参数的拟合误差、信噪比、频谱幅度衰减率如表3所示。经过最小二乘滑动平均法处理后特征参数 $\begin{matrix} E_{0} 、 T_{2}^{*} 、 φ_{0} \end{matrix}$ 的拟合误差分别达到2.9%、0.77%、1.2%。频谱幅度衰减率达到0.17%, 频谱幅度衰减率较小, 符合特征参数的提取精度。由表3可知, 对于平均衰减时间的拟合误差, 五点三次滑动平均法可达到最小, 但总体来看七点三次滑动平均法所获取的效果是最好的。

表3 尖峰噪声情况下模型仿真数据经不同滤波方式处理后的参数提取结果对比 Table 3 Parameter extraction result contrast of peak noise case model simulation data after different filtering method

	振幅E₀ /nV	衰减时间 $\begin{matrix} T_{2}^{*} \end{matrix}$ /ms	相位 $\begin{matrix} φ_{0} \end{matrix}$ /(° )	信噪比	拟合误差			频谱幅度衰减率/%
	振幅E₀ /nV	衰减时间 $\begin{matrix} T_{2}^{*} \end{matrix}$ /ms	相位 $\begin{matrix} φ_{0} \end{matrix}$ /(° )	信噪比	E₀/%	$\begin{matrix} T_{2}^{*} \end{matrix}$ /%	$\begin{matrix} φ_{0} \end{matrix}$ /%	频谱幅度衰减率/%
理想信号	400.0	150.00	150.0	$\begin{matrix} \infty \end{matrix}$	-	-	-	-
加入尖峰噪声	376.8	163.03	148.0	1.25	-	-	-	-
三角形权值滑动平均	378.1	161.86	147.9	5.47	5.47	7.91	1.4	0.24
五点三次滑动平均	378.9	156.93	147.2	6.51	5.27	4.62	1.7	0.23
七点三次滑动平均	388.4	148.84	147.2	7.55	2.90	0.77	1.7	0.17
九点四次滑动平均	376.2	163.33	148.1	5.86	5.47	8.88	1.2	0.24

最后, 综合图8和表3可得, 对于随机噪声来说两种滤波方法都可以很好地抑制噪声。但是最小二乘滑动平均法所得到的信号曲线更加平滑, 最终信噪比可达到13.49, 七点三次的滤波结果最好。因此, 要选择合适的权值进行数据处理, 提高特征参数的提取精度。

2.4 信号加入工频噪声

在MRS响应信号中加入频率为50 Hz, 幅值为50 nV的工频噪声, 分别采用三角形权值滑动平均法和最小二乘滑动平均法进行滤波处理。加入工频噪声后的信号包络和频谱图如图9所示, 加入噪声后的信噪比为4.39。

	Figure Option View Download New Window
	图9 理想MRS信号中加入工频噪声Fig.9 Ideal signal of MRS including frequency noise

采用三角形滑动平均法处理后的信号曲线如图10所示, 处理之后的信噪比为4.44。采用最小二乘滑动平均法处理后的信号如图11所示, 处理之后的信噪比可达到4.5。

	Figure Option View Download New Window
	图10 三角形滑动平均法处理后的信号曲线(加入工频噪声)Fig.10 Signal curve after triangle weight sliding filter processing

	Figure Option View Download New Window
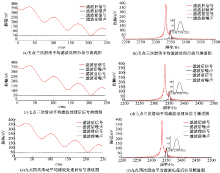	图11 经最小二乘滑动平均法处理后的信号曲线(加入工频噪声)Fig.11 Signal curve after by the least squares moving average processing(induding frequency noise)

从图10和图11可以得到:含噪信号经过两种方法进行滤波后, 信号曲线的平滑度并没有得到改善。但最小二乘滑动平均法`比三角形滑动平均法所得到的信噪比有一定提高。

核磁共振含噪信号经过不同滤波方法处理后得到特征参数的拟合误差、信噪比以及频谱幅度衰减率, 如表4所示。从表4可以看出:不同权值的最小二乘滑动平均法与三角形滑动平均法所得到的特征参数的拟合误差、信噪比和频谱幅度衰减率得到了不同程度的提高, 且七点三次滑动平均法获取的效果最好。

最后, 结合图11和表4得出:对于工频噪声两种滤波方法效果不是很明显, 但是最小二乘滑动平均法仍然比三角形滑动平均法滤波效果有一定程度的提高。对于最小二乘滑动平均法不同权值所得到的结果是不同的。由表4可知:七点三次滑劝平均法的滤波效果最好, 故进行数据处理时要选取合适的权值。

表4 工频噪声情况下模型仿真数据经不同滤波方式处理后的参数提取结果对比 Table 4 Parameter extraction result contrast of frequency noise case model simulation data after different filtering methods

	振幅E₀ /nV	衰减时间 $\begin{matrix} T_{2}^{*} \end{matrix}$ /ms	相位 $\begin{matrix} φ_{0} \end{matrix}$ /(° )	信噪比	拟合误差			频谱幅度衰减率/%
	振幅E₀ /nV	衰减时间 $\begin{matrix} T_{2}^{*} \end{matrix}$ /ms	相位 $\begin{matrix} φ_{0} \end{matrix}$ /(° )	信噪比	E₀/%		$\begin{matrix} T_{2}^{*} \end{matrix}$ /%	$\begin{matrix} φ_{0} \end{matrix}$ /%
理想信号	400	150	150	$\begin{matrix} \infty \end{matrix}$	-	-	-	-
加入工频噪声	382.8	160.33	160.9	4.39	-	-	-	-
三角形权值滑动平均	385.9	155.24	158.7	4.44	3.525	3.49	5.80	0.34
五点三次滑动平均	388.8	154.96	156.3	4.45	2.800	3.31	4.20	0.32
七点三次滑动平均	393.7	151.45	153.9	4.50	1.575	0.97	2.60	0.27
九点四次滑动平均	390.4	155.12	157.4	4.44	2.400	3.41	4.93	0.31

3 实测数据的滤波处理

为了验证最小二乘滑动平均法对于实测信号的滤波效果, 采用2005年4月作者所在核磁组在内蒙古某地野外试验的测试数据进行数据处理。

实际野外应用中, 针对某一地点的地下水测量, 一般需要仪器发射14~16个脉冲, 同时可以获得一组测试数据, 需要对每个测点的14~16个测试数据分别进行滤波处理, 提取信号的初始振幅、弛豫时间、初始相位等, 再进行水文地质参数的估算。

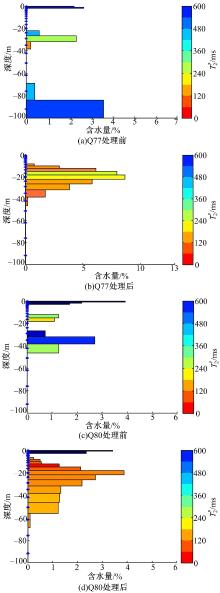
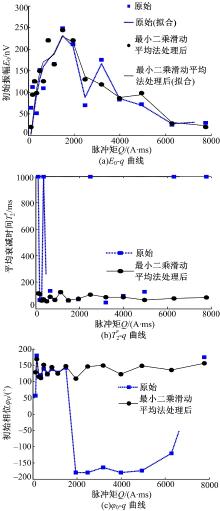(1)测点Q77, 采用100 m× 100 m线圈, 当地的拉莫尔频率为2370 Hz, 噪声范围为2413~3660 nV, 对该测点共发射16个脉冲, 对16个测试数据进行滤波处理, 分别提取MRS信号的特征参数 $\begin{matrix} E_{0}, T_{2}^{*}, φ_{0} 。 \end{matrix}$ MRS测试信号的 $\begin{matrix} E_{0} - q 、 T_{2}^{*} - q 、 φ_{0} - q \end{matrix}$ 对应关系曲线如图12所示。从图中可知, 经过最小二乘滑动平均法处理后,E₀-q、T₂^*-q、φ₀-q等曲线比滤波处理前的曲线平滑度提高。

	Figure Option View Download New Window
	图12 Q77处理前后的MRS信号特征参数曲线Fig.12 MRS signal characteristic parameter curves before and after processing

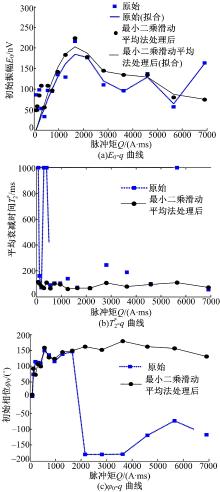(2)测点Q80, 当地的拉莫尔频率为2367 Hz, 噪声范围为1992~3575 nV, 由该测点发射16个脉冲, 对16个测试数据进行滤波处理, 分别提取MRS信号的特征参数 $\begin{matrix} E_{0}, T_{2}^{*}, φ_{0} 。 \end{matrix}$ MRS测试信号的 $\begin{matrix} E_{0} - q 、 T_{2}^{*} - q 、 φ_{0} - q \end{matrix}$ 对应关系曲线如图13所示。从图中可知, 经过最小二乘滑动平均法处理后, $\begin{matrix} E_{0} - q 、 T_{2}^{*} - q 、 φ_{0} - q \end{matrix}$ 等曲线的平滑度比滤波处理前提高了。

	Figure Option View Download New Window
	图13 Q80处理前后的MRS信号特征参数曲线Fig.13 MRS signal characteristic parameter curves before and after processing

	Figure Option View Download New Window
	图14 打井点水文地质情况Fig.14 Drilling point hydrological geology

打井点的水文地质情况如图14所示, 测点Q77距离打井点GM224为1.12 km, 测点Q80距离打井点GM274为2.82 km, 距离较近, 可近似认为测点与钻孔的水文地质情况相似。

	Figure Option View Download New Window
	图15 Q77、Q80处理前后的含水量柱状图Fig.15 Point Q77 and Q80 inversion results before and after processing

利用 $\begin{matrix} E_{0} - q 、 T_{2}^{*} - q \end{matrix}$ 等可以计算测点的地层含水量数据, 经最小二乘滑动平均法处理前后的含水量柱状图和打井点地质岩性如图15所示。由图可知, 两个测点测试数据经过滤波处理之后的计算的含水层位置与钻孔结果都基本一致, 弛豫时间范围与地层中砂、细砂层的地质情况也基本相符。

4 结论

提出了最小二乘滑动平均滤波方法, 利用优化方法确定了最小二乘权值系数, 并将该方法应用于含有电磁噪声的理想信号及实测信号的处理过程中, 得出以下结论:

(1)通过比较MRS信号中三种主要噪声的滤波效果后可知, 最小二乘滑动平均法更适合随机噪声、尖峰噪声的消除; 滤波处理后, 信号曲线的平滑度得到了改善; 信号的信噪比、特征参数的拟合误差、频谱幅度衰减率等都满足实际要求。

(2)最小二乘权值法优于三角形权值法, 仿真试验表明, 应选择适当的滑动点数进行消噪, 实测数据的处理结果也证明了该方法的可行性。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Lubczynski M, Roy J. Hydrogeological interpretation and potential of the new magnetic resonance sounding (MRS) method[J]. Journal of Hydrology, 2003, 283(1-4): 19-40. [本文引用:1]
[2]	Roy J, Lubczynski M. The magnetic resonance sounding technique and its use for groundwater investigations[J]. Hydrogeology Journal, 2003, 11(4): 455-465. [本文引用:1]
[3]	郝荟萃. 基于自适应参考对消的磁共振全波信号处理方法研究[D]. 长春: 吉林大学仪器科学与电气工程学院, 2013. Hao Hui-cui. Processing method of full-wave magnetic resonance sounding signal based on adaptive reference cancellation[D]. Changchun: College of Instrumentation and Electrical Engineering, Jilin University, 2013. [本文引用:1]
[4]	Perttu N, Wattanasen K, Phommasone K, et al. Characterization of aquifers in the Vientiance Basin, Laos, using magnetic resonance sounding and vertical electrical sounding[J]. Journal of Applied Geophysics, 2011, 73(3): 207-220. [本文引用:1]
[5]	Plata J, Rubio F. MRS experiments in a noisy area of a detrital aquifer in the south of Spain[J]. Journal of Applied Geophysics, 2002, 50(1-2): 83-94. [本文引用:1]
[6]	Jiang C D, Lin J, Duan Q M, et al. Statistical stacking and adaptive notch filter to remove high-level electromagnetic noise from MRS measurements[J]. Near Surface Geophysics, 2011, 9(5): 459-468. [本文引用:1]
[7]	Walsh D O. Multi-channel surface NMR instrumentation and software for 1D/2D groundwater investigations[J]. Journal of Applied Geophysics, 2008, 66(3-4): 140-150. [本文引用:2]
[8]	田宝凤, 林君, 段清明, 等. 基于参考线圈和变步长自适应的磁共振信号噪声压制方法[J]. 地球物理学报, 2012, 55(7): 2462-2472. Tian Bao-feng, Lin Jun, Duan Qing-ming, et al. Variable step adaptive noise cancellation algorithm for magnetic resonance sounding signal with a reference coil[J]. Chinese Journal of Geophysics, 2012, 55(7): 2462-2472. [本文引用:2]
[9]	李明阳, 柏鹏, 王徐华, 等. 一种基于迭代最小二乘法的精确同步方法[J]. 电子与信息学报, 2013, 35(4): 832-837. Li Ming-yang, Bai Peng, Wang Xu-hua, et al. A precise synchronization method based on iterative least square algorithm[J]. Journal of Electronics & Information Technology, 2013, 35(4): 832-837. [本文引用:1]
[10]	余峰. 宋公仆, 程晶晶, 等. 核磁共振测井回波信号噪声抑制设计[J]. 仪表技术与传感器, 2014(2): 105-107. Yu Feng, Song Gong-pu, Cheng Jing-jing, et al. Design of noise reduction in NMR well logging[J]. Instrument Technique and Sensor, 2014(2): 105-107. [本文引用:1]
[11]	Dalgaard E, Auken E, Larsen J J. Adaptive noise cancelling of multichannel magnetic resonance sounding signals[J]. Geophysical Journal International, 2012, 191(1): 88-100. [本文引用:1]
[12]	Zhang Xiu-ling, Zhang Shao-yu, ZhaoWen-bao, et al. Flatness intelligent controlvia improved least squares support vector regression algorithm[J]. Journal of Central South University of Technology, 2013(3): 688-695. [本文引用:1]
[13]	万玲, 林婷婷, 林君, 等. 基于自适应遗传算法的MRS-TEM联合反演方法研究[J]. 地球物理学报, 2013, 56(11): 3728-3740. Wan Ling, Lin Ting-ting, Lin Jun, et al. Joint inversion of MRS and TEM data based on adaptive genetic algorithm[J]. Chinese Journal of Geophysics, 2013, 56(11): 3728-3740. [本文引用:1]
[14]	Lin Jun, Lin Ting-ting, Ji Yan-ju, et al. Non-invasive characterization of water-bearing strata using a combination of geophysical techniques[J]. Journal of Applied Geophysics, 2013, 91: 49-65. [本文引用:1]
[15]	王中兴, 荣亮亮, 林君, 等. 基于4倍频采样的数字正交FID信号检测技术[J]. 数据采集与处理, 2010, 25(5): 626-630. Wang Zhong-xing, Rong Liang-liang, Lin Jun, et al. FID signal detection based on DLIA sampled by quadruple lamor frequency[J]. Journal of Data Acquisition & Processing, 2010, 25(5): 626-630. [本文引用:1]
[16]	刘长伟. 高分辨率自然伽马测井仪器研制[D]. 杭州: 浙江大学智能系统与控制研究所, 2011. Liu Chang-wei. The research and development of high-resolution natural gamma logging tool[D]. Hangzhou: Institute of Cyber-Systems and Control , Zhejiang University, 2011. [本文引用:1]

2003

0.0

... 0 引言地面核磁共振(Magnetic resonance sounding,MRS)技术是目前最为直接的探测地下水的地球物理方法,得到了广泛的应用^[1,2] ...

2003

0.0

... 0 引言地面核磁共振(Magnetic resonance sounding,MRS)技术是目前最为直接的探测地下水的地球物理方法,得到了广泛的应用^[1,2] ...

2013

0.0

. 2013, :-

Processing method of full-wave magnetic resonance sounding signal based on adaptive reference cancellation

基于自适应参考对消的磁共振全波信号处理方法研究[D]

Hao Hui-cui.

郝荟萃

人类赖以生存的重要资源之一就是水，现在我国主要存在淡水资源紧缺和由地下水引起的地质灾害频发两大问题。能够准确、便捷地确定地下水信息对于人类环境的发展具有重要意义。目前世界上已有的地下水资源探测方法中，磁共振探测方法（MRS）是最直接、最无损的物探方法，该技术通过探测地下水中氢质子产生的核磁共振响应实现对地下水的探测，并且探测结果具有定量和解唯一性等优点。然而，MRS信号极其微弱，对电磁噪声敏感成为该方法应用的主要局限，从而导致成分复杂的噪声干扰被高灵敏度的接收系统采集，信噪比降低，影响反演结果的准确性，因而如何进行噪声滤除提取有效信号变得至关重要。针对磁共振地下水探测的全波信号在工频谐波干扰、自然噪声以及偶发尖峰噪声等强噪声干扰下难以获得有效信号的瓶颈，研究基于多通道自适应对消的噪声抑制方法。引入参考线圈，建立带参考通道的90度移相自适应噪声对消（ANC）系统，依变步长手段，实现不同信噪比下探测通道与参考通道相关噪声的抵消。采用数字正交算法将消噪后的全波信号分解为两个正交分量，然后结合自相关函数和最小一乘非线性拟合法在去除非相关噪声的同时实现初始振幅和弛豫时间特征参数的提取。最后，通过室内外实测数据验证消噪方法的有效性。本文的研究将解决强电磁干扰下MRS信号难以有效提取问题，提供一种切实可行的噪声抑制算法，拓展仪器使用范围，为我国水资源勘查与评价提供技术支持。

... 目前JLMRS仪器数据处理软件中采用的数据滤波方法有自适应滤波法、FIR低通滤波法和滑动平均滤波法等^[3,4,5,6] ...

2011

0.0

... 目前JLMRS仪器数据处理软件中采用的数据滤波方法有自适应滤波法、FIR低通滤波法和滑动平均滤波法等^[3,4,5,6] ...

2002

0.0

... 目前JLMRS仪器数据处理软件中采用的数据滤波方法有自适应滤波法、FIR低通滤波法和滑动平均滤波法等^[3,4,5,6] ...

2011

0.0

... 目前JLMRS仪器数据处理软件中采用的数据滤波方法有自适应滤波法、FIR低通滤波法和滑动平均滤波法等^[3,4,5,6] ...

2008

0.0

... 自适应滤波和FIR低通滤波方法均存在一定局限性,当信号与噪声干扰频率相近时会造成有用信号的失真^[7,8] ...

... 目前滑动平均滤波法中对于数据权值的选取是采用中间值最大,向前向后递减的方式,常规的选择是三角形分布,但是三角形分布的权值只是根据一般规律给出,并不精确^[7,8,9] ...

2012

0.0

. 2012, 55(7):2462-2472 DOI:doi:10.6038/j.issn.0001-5733.2012.07.030

Variable step adaptive noise cancellation algorithm for magnetic resonance sounding signal with a reference coil

基于参考线圈和变步长自适应的磁共振信号噪声压制方法

Tian Bao-feng , Lin Jun , Duan Qing-ming

田宝凤, 林君, 段清明

Due to the high sensitivity of magnetic resonance sounding (MRS) instrument for groundwater exploration, the nV-level MRS signal received from the instrument is susceptible to interference of high industrial frequency harmonics, which leads to accuracy decrease in signal parameter extraction and influences the inversion result. To solve this problem, a 900 phase-shift adaptive noise cancellation system with reference coil for MRS full wave signal, based on the principle of correlation cancellation, is designed in this paper. The distance of reference coil away from the detection coil is theoretically calculated, and the algorithm of variable step adaptive noise cancellation is presented. The simulation results show that with different signal amplitudes and signal to noise ratios (SNR), adopting the adaptive noise cancellation system and variable step algorithm can increase SNR to 5.94dB or above, while the fitting error of initial amplitude and relaxation time is within 2.8%, when industrial frequency harmonics are not in coincidence with the signal frequency. However, when they are in coincidence, SNR can reach 5dB or above and the fitting error of initial amplitude and relaxation time is within 10%. The result of the variable step adaptive noise cancellation algorithm meets the requirement of practical application. Processing of field measured signals further proved the effectiveness of this algorithm.

核磁共振地下水探测仪的灵敏度高,接收到的纳伏级磁共振探测信号极易受到强工频谐波噪声的干扰,导致信号特征参数提取的准确度降低,影响反演解释的水文地质参数结果.为了解决这一难题,基于相关抵消的原理,针对全波磁共振信号,设计带有参考线圈的90°移相自适应噪声抵消系统,理论计算了参考线圈相对于探测线圈的距离,提出变步长LMS算法进行噪声压制.仿真结果表明,在不同的信号强度及不同的信噪比下,当信号与工频谐波干扰频谱不重合时,采用设计的自适应噪声抵消系统和变步长算法,信噪比可以提高到5.94 dB以上,初始振幅、弛豫时间特征参数的拟合误差在2.8%以内;当信号与工频谐波干扰频谱重合时,采用双向自适应滤波算法,信噪比可以达到5dB以上,初始振幅、弛豫时间特征参数的拟合误差在10%以内,可以满足实际应用的要求;实测数据处理进一步证明了方法的有效性.

... 自适应滤波和FIR低通滤波方法均存在一定局限性,当信号与噪声干扰频率相近时会造成有用信号的失真^[7,8] ...

2013

0.0

. 2013, 35(4):832-837 DOI:doi:10.3724/SP.J.1146.2012.01047

A precise synchronization method based on iterative least square algorithm

一种基于迭代最小二乘法的精确同步方法

Li Ming-yang , Bai Peng , Wang Xu-hua

李明阳, 柏鹏, 王徐华

Precise synchronization can be achieved by fitting phase discrimination curve exploiting Least Squares (LS). However, this method not only has very high requirement of coarse synchronization, but also can not counteract frequency- offset effectively. It is analyzed and proved that the measured value of LS is between zero and real value as coarse synchronization error is between the earlier and later chip. Accordingly a precise synchronization method based on iterative least squares is proposed and a modulus of split correlation strategy is also introduced in this paper to counteract frequency-offset. Theoretical analysis shows that this method can outstandingly eliminate influence of noise as well as frequency-offset with short segments. Besides its strong anti frequency-offset and noise capability, the proposed method still has very high measurement precision as the error of coarse synchronization covers the earlier and later half chip according to simulation results.

最小二乘拟合鉴相曲线的方法可以实现精确同步，但其对粗同步要求苛刻且不能有效对抗频偏。该文通过分析证明当粗同步误差在前后各半个码片周期内时，最小二乘法的测量值介于零和实际值之间。根据该特性提出基于迭代最小二乘法的精确同步方法，并引入分段相关取模策略，以达到抗频偏效果。理论分析表明该方法能够有效消除噪声的影响，并且在分段长度不大的情况下具有很强的抗频偏能力。仿真结果表明该方法具有很强的抗频偏和抗噪声能力，并且在粗同步误差覆盖前后半个码片范围时依然具有很高的测量精度。

2014

0.0

... 本文针对现有滑动平均滤波方法(以下称为三角形滑动平均法)中权值选取的不足^[10,11,12],提出了一种更为精确的权值确定方法#cod#x02014 ...

2012

0.0

... 本文针对现有滑动平均滤波方法(以下称为三角形滑动平均法)中权值选取的不足^[10,11,12],提出了一种更为精确的权值确定方法#cod#x02014 ...

2013

0.0

... 本文针对现有滑动平均滤波方法(以下称为三角形滑动平均法)中权值选取的不足^[10,11,12],提出了一种更为精确的权值确定方法#cod#x02014 ...

2013

0.0

. 2013, 56(11):3728-3740 DOI:doi:10.6038/cjg20131114

Joint inversion of MRS and TEM data based on adaptive genetic algorithm

基于自适应遗传算法的MRS-TEM联合反演方法研究

Wan Ling , Lin Ting-ting , Lin Jun

万玲, 林婷婷, 林君

The method of Magnetic Resonance Sounding (MRS) provides a new technology to determine subsurface water qualitatively and quantitatively, which has received much concern of geophysicists. The traditional inversion of MRS uses homogeneous half-space models and ignores effects of resistivity distribution on inversion results. Based on the MRS theory in the multi-layer earth model, we developed a new scheme for joint inversion of MRS data and Transient Electromagnetic (TEM) data. By correcting MRS inversion with resistivity in real time, the accuracy of inversion result was improved greatly. The Adaptive Genetic Algorithm (AGA) was applied. By adaptively adjusting the probability of crossover and mutation, AGA has not only avoided the premature convergence of GA but also has obtained the global optimal solution. Studies with synthetic data show that the MRS-TEM joint inversion scheme can obtain the aquifer structure accurately even 10% noise applied. Compared with the traditional MRS inversion scheme, the advantage of this new approach is obvious. By applying this method to filed data processing, and with the good inversion result, we have verified the the applicability of AGA and the practical significance of MRS-TEM joint inversion scheme.

地面磁共振法(MRS)因具有定性、定量分析地下水能力,而备受关注.传统磁共振地层含水量反演多采用均匀半空间模型,忽略电阻率分布信息对结果的影响.针对这一问题,本文基于多层电介质中磁共振响应理论,提出MRS与瞬变电磁(TEM)联合反演方法,通过电阻率分布信息对含水量反演过程的实时修正,提高了解释结果的准确度.反演算法采用自适应遗传算法(AGA)进行,基于繁殖规则,动态调整交叉概率和变异概率,解决了标准遗传算法易未成熟收敛而难以得到全局最优解问题.模型数据表明,含噪10%情况下,联合反演仍能较准确地反映地下含水单元模型结构,对比MRS单独反演优势明显.同时,内蒙古白旗野外观测数据联合反演结果与钻井资料基本一致,充分验证了AGA反演算法的实用性及MRS-TEM联合反演的实际意义.

... 1 数据处理过程核磁共振野外采集到的数据含有大量噪声,如果不进行消噪处理,则不能准确提取信号的特征参数^[13,14] ...

2013

0.0

... 1 数据处理过程核磁共振野外采集到的数据含有大量噪声,如果不进行消噪处理,则不能准确提取信号的特征参数^[13,14] ...

2010

0.0

. 2010, 25(5):626-630 DOI:doi:10.3969/j.issn.1004-9037.2010.05.016

FID signal detection based on DLIA sampled by quadruple lamor frequency

基于4倍频采样的数字正交FID信号检测技术

Wang Zhong-xing , Rong Liang-liang , Lin Jun

王中兴, 荣亮亮, 林君

提出了基于4倍Lamor频率采样的数字正交锁相放大技术提取包络信号,该技术是根据开关型正交矢量锁定放大器的基本原理和三角函数的特征,通过4倍Lamor频率采样和数字叠加的方法,实现了信号正交与低通滤波功能。该数字正交方法较模拟正交法的优点是能够提高信号的信噪比,且电路设计简单。利用该法所设计的地面核磁共振找水仪采集系统在探寻地下水源中已得到验证与应用,在叠加次数仅为NUMIS系统1/2时,其信噪比至少提高0.5倍。该方法提高了仪器的工作效率和对信号参数的提取精度。

... 核磁共振地下水检测技术中采用4倍频采样的数字正交技术来获得包络信号^[15] ...

2011

0.0

... 最小二乘滑动平均法对噪声有较强的适应能力,适应于随机噪声和尖峰噪声,最小二乘滑动平均法可以采用不同的数据点个数和不同次方对信号进行拟合,拟合阶数越高,其平滑曲线与实测数据拟合得越好,曲线越平滑,消噪效果更为理想,信号信噪比提高更多^[16] ...