基于阶梯波参考信号的改进型正交锁定放大

引用本文

周逢道, 丁凯来, 曾新森, 薛开昶, 孙彩堂. 基于阶梯波参考信号的改进型正交锁定放大.吉林大学学报:工学版, 2016, 46(3): 996-1003
ZHOU Feng-dao, DING Kai-lai, ZENG Xin-sen, XUE Kai-chang, SUN Cai-tang. Improved orthogonal lock-in amplification based on step wave reference signal. Journal of Jilin University Engineering and Technology Edition, 2016, 46(3): 996-1003 复制到剪切板

Permissions

基于阶梯波参考信号的改进型正交锁定放大

周逢道^1,², 丁凯来¹, 曾新森¹, 薛开昶¹, 孙彩堂^1,²

1.吉林大学仪器科学与电气工程学院,长春 130061

2.吉林大学国家地球物理探测仪器工程技术研究中心,长春 130061

通讯作者:孙彩堂(1975-),男,副教授,博士.研究方向:数据处理与可视化.E-mail:sunct@jlu.edu.cn

作者简介:周逢道(1970-),男,教授,博士.研究方向:电磁探测技术及仪器.E-mail:zhoufd@jlu.edu.cn

基金:国家潜在油气资源(油页岩勘探开发利用)产学研用合作创新项目(OSR-02); 吉林省科技厅发展计划重点项目(20100349)

摘要

对以阶梯波作为参考信号的正交锁定放大的探测精度进行了建模分析,基于硬件简单原则给出了以阶梯波作为参考信号的正交锁定放大信号检测方法的实现策略。综合考虑参考波形的失真度与采样率之间的关系,对比分析了基于面积等效法和特定谐波消去法的阶梯波合成方法。根据阶梯波参考信号对采集电路相位精度的要求及待检测信号的周期性,提出了匹配采样技术。实测结果表明:采用现场可编程门阵列(Field programmable gate array, FPGA)实现所提出的正交锁定放大,方法简单、硬件要求低、可用于识别不同异常体。改进后方法的误差为0.7%~7%,与以方波为参考信号的正交锁定放大相比,提高了探测精度。

关键词: 信息处理技术; 近地表; 正交锁定放大; 阶梯波

中图分类号:TH763.1 文献标志码:A 文章编号:1671-5497(2016)03-0996-08

Improved orthogonal lock-in amplification based on step wave reference signal

ZHOU Feng-dao^1,², DING Kai-lai¹, ZENG Xin-sen¹, XUE Kai-chang¹, SUN Cai-tang^1,²

1.College of Instrumentation and Electrical Engineering, Jilin University, Changchun 130061, China

2.National Geophysical Exploration Equipment Engineering Research Center, Jilin University,Changchun 130061, China

Abstract

The detection accuracy of the step wave reference orthogonal lock-in amplification is modeled and analyzed, and the implementation strategy based the principle of using simple hardware is presented. Considering the relationship between the frequency waveform distortion and the sampling rate, the synthesis strategies of step wave based on equivalent area method and selected harmonic elimination method are comparatively analyzed. According to the phase accuracy requirement of step wave reference signal acquisition and the periodicity of the signal to be tested, a matching sampling technique is proposed. Experiments results show that the proposed orthogonal lock-in amplification can achieved by Field Programmable Gate Array (FPGA), and the method is simple and has low hardware requirement, can be used to identify different anomaly bodies. The error of the improved method is 0.7% to 7.0%. Compared with the square wave reference orthogonal lock-in amplification, the detection accuracy is improved by the new method.

Keyword: information processing technology; near-surface; orthogonal lock-in amplification; step wave

Show Figures

0 引言

近地表电磁探测是指在电磁波一次场的激励下, 通过采集由地下异常所产生的二次场, 获取地下介质电磁特性的方法, 被广泛应用于地下管线检测、工程质量监测和考古勘测等领域^[1]。近地表电磁探测中, 低频部分数据反映深层地下结构信息, 而高频部分数据反映浅层地下结构信息, 一般频率范围为1~40 kHz, 频率近似按照对数等间隔分布, 每10倍频程中分布着3~10个频率点。同时, 为了提高野外工作效率, 仪器应尽可能轻便、低功耗并具有一定的实时处理能力^[2]。因此, 对能满足上述要求的数据检测方法进行研究具有较高的实际应用价值。

在近地表电磁探测中, 方波激励源与正弦波激励源相比具有如下优点^{[3, 4, 5, 6, 7]}:①正弦波发射一般采用正弦脉冲宽度调制(Sinusoidal pulse width modulation, SPWM)技术, 调制过程引入交调失真, 导致发射波形随机度大、探测精度低, 而方波发射时不需要调制; ②产生方波时发射电路只需要工作在发射频率, 而产生正弦波时一般需要工作在发射频率的数倍以上, 发射方波具有低的功率管损耗; ③在相同的母线电压等级下, 方波的基波幅度是合成正弦波的4/π 倍, 方波能量更高。

由于采用方波作为一次场激励源, 给常规正交锁定放大技术带来了不便^{[8, 9, 10, 11]}。常规正交锁定放大中的参考信号一般采用正弦波或方波。若选用正弦波作为参考信号, 不可避免地要用乘法运算实现正交锁定放大中的相敏检测(Phase sensitive detection, PSD), 通常需要基于电脑进行运算, 具有高的硬件功耗及成本; 若选用方波作为参考信号, PSD可以通过电子开关实现^[12], 故功耗低、成本低。但在方波激励源的作用下, 因接收信号含有与参考信号频率一致的谐波成份, 故具有较大的检测误差, 虽然可以采用选频带通滤波器抑制接收信号中的谐波成份, 但带通滤波器的中心频率要时刻匹配检测频率, 难以实现。

本文提出了一种采用阶梯波逼近正弦参考信号的方法实现了正交锁定放大。因阶梯参考信号与方波参考信号相比, 具有低的谐波成份, 故精度高于方波参考的正交锁定放大。可以采用在现场可编程门阵列(Field programmable gate array, FPGA)内部对数据进行移位的方式实现阶梯波参考PSD运算, 故不需要做乘法运算, 具有较低的功耗及硬件成本。

1 正交锁定放大模型

1.1 正交锁定放大原理

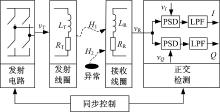
图1为近地表电磁探测的正交锁定放大原理。发射电路向发射线圈发送方波激励信号v_T:

$\begin{matrix} v_{T} = \overset{\infty}{\sum_{k = 1, 3, 5, \dots}} \frac{4 A}{kπ} \sin (kωt) \end{matrix}$ (1)

式中:A表示双极性方波的幅值。

发射线圈产生一次激励场H₁并作用于地下异常体, 感应产生二次场H₂, 因此, H₂包含了地下信息。由发射线圈直接耦合至接收线圈的一次场H₁和感应二次场H₂在接收线圈上产生感应电压v_R, 因为发射线圈、地下介质和接收线圈可以认为是线性时不变系统, 故v_R可以用式(2)表示:

$\begin{matrix} v_{R} = \overset{\infty}{\sum_{k = 1, 3, 5, \dots}} a_{Rk} \sin (kωt + θ_{Rk}) \end{matrix}$ (2)

式中:a_Rk为第k次频率成份对应的幅度; θ _Rk为相对于发射波形, 第k次频率成份的相移。

v_R经正交锁定放大得到同相分量I和正交分量Q。正交参考信号v_I和v_Q通过同步控制与v_T保持同步, 对于周期性的参考信号, v_I和v_Q分别如式(3)(4)所示:

$v_{I} = \overset{\infty}{\sum_{i = 1, 3, 5, \dots}} a_{IQi} \sin (iωt)$ (3)

$v_{Q} = \overset{\infty}{\sum_{i = 1, 3, 5, \dots}} a_{IQi} \sin (iωt - \frac{π}{2} i)$ (4)

式中:a_IQi表示v_I和v_Q中第i次频率成份对应的幅度。

v_I与v_T同相, v_Q比v_I滞后π /2。正交锁定放大中PSD等价于乘法运算; 低通滤波器(Low pass filter, LPF), 用于获取直流分量。I、Q分别为v_R与v_I、v_Q乘积的直流分量。I和Q分别如式(5)和(6)所示:

$I = \frac{a_{IQ 1} a_{R 1}}{2} \sin θ_{R 1} + \overset{\infty}{\sum_{i = k = 1, 3, 5, \dots}} \frac{a_{IQi} a_{Rk}}{2} \sin θ_{Rk}$ (5)

$Q = \frac{a_{IQ 1} a_{R 1}}{2} \cos θ_{R 1} + \overset{\infty}{\sum_{i = k = 1, 3, 5, \dots}} \frac{a_{IQi} a_{Rk}}{2} \sin (θ_{Rk} + \frac{π}{2} i)$ (6)

当按式(7)(8)取基波幅度a_R1和相移θ _R1时, 式(5)(6)中等号右侧第1项即为精确成份, 第2项为误差成份。

$a_{R 1} = \frac{2}{a_{IQ 1}} \cdot \sqrt[]{I^{2} + Q^{2}}$ (7)

$θ_{R 1} = \arctan (\frac{I}{Q})$ (8)

因此, 减小式(3)(4)中i≠ 1的频率成分能减小式(5)(6)中的误差项, 进而提高正交锁定放大的精度。减小式(3)(4)中i≠ 1的频率成分可以转换为降低参考信号的失真度。

	Figure Option View Download New Window
	图1 电磁探测的正交锁定放大原理Fig.1 Orthogonal lock-in amplification principle of electromagnetic prospecting

1.2 阶梯波参考的PSD

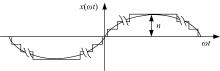
为了降低参考信号v_I和v_Q的失真度, 可采用图2所示的阶梯波x(ω t)逼近正弦波。

	Figure Option View Download New Window
	图2 阶梯波的正弦逼近原理Fig.2 Sinusoidal approximation principle of step wave

	Figure Option View Download New Window
	图3 阶梯波的PSD原理Fig.3 PSD principle of step wave

采用阶梯波参考作PSD的原理图如图3所示。图3中v_R(m)为经模数转换器(Analog-to-digital converter, ADC)采样后的离散化接收信号, 数据以二进制的补码形式表示; x(ω t)为阶梯波参考信号, 设阶梯级数为n, 阶梯幅值步进为1。当一个接收信号的采样点v_R(m)到来时, 首先判断其对应阶梯波的哪一段, 并取出相应段的幅值绝对值|x(ω t)|, 以二进制数D_h, …, D₁D₀表示。当D_h, …, D₁D₀中的第l(l=0, 1, …, n)位为1时, 将v_R(m)左移l位实现v_R(m)与2^l的乘积, 并将移位结果保存。按照相同的方法处理所有D_h, …, D₁D₀中为1的位, 将移位后保存的结果全部累加, 当x(ω t)为负时, 可通过将移位后的结果逐位取反, 然后加1的方式实现取相反数的运算; 当x(ω t)为0时, 将v_R(m)置零。通过这种方法即可完成一个采样点的阶梯波PSD计算。

由于阶梯波参考信号通过拟合正弦波的方式实现, 故失真度低于方波, 精度高于方波。由于阶梯波参考信号与接收信号进行PSD运算时, 可以通过移位累加的方式实现, 故硬件要求及功耗低于正弦波参考信号。

2 阶梯波参考信号的合成

阶梯波参考信号的失真度与电平切换的相角有直接关系, 通常采用特定谐波消去法^{[13, 14]}和等效面积法^{[15, 16]}确定各相角。由于这两种方法主要应用于电力电子领域, 与本文的应用背景及关注点有较大的不同, 故这一节将针对正交锁定放大这一特殊目的进行分析。

2.1 阶梯波失真度分析模型

图4为阶梯波的合成原理, 设所需合成的阶梯波x(ω t)幅值为n, 共有n级阶梯, 可由图4(b)(c)(d)所示的幅值为1的矩形波叠加得到。为了分析各级阶梯波x₁(ω t), x₂(ω t), …, x_n(ω t)的频率成分, 将它们进行傅里叶级数展开, 展开式如(9)所示:

$\begin{matrix} \{\begin{matrix} x_{j} (ωt) = \overset{\infty}{\sum_{i = 1, 3, 5, \dots}} a_{ij} \sin (iωt) \\ a_{ij} = \frac{4}{iπ} \cos (i θ_{j}), j = 1, 2, \dots, n \end{matrix} \end{matrix}$ (9)

根据叠加定理, 所合成的阶梯波x(ω t)的频率成分可由各级阶梯波的展开式相对应的频率成分叠加得到, 如式(10)所示:

$\begin{matrix} \{\begin{matrix} x (ωt) = \overset{n}{\sum_{j = 1}} x_{j} (ωt) = \overset{\infty}{\sum_{i = 1, 3, 5, \dots}} A_{i} \sin (iωt) \\ A_{i} = \frac{4}{iπ} \overset{n}{\sum_{j = 1}} \cos (i θ_{j}) \end{matrix} \end{matrix}$ (10)

	Figure Option View Download New Window
	图4 阶梯波的合成原理Fig.4 Synthesis principle of step wave

由式(10)可知各次频率成分的幅度A_i。结合式(10)及帕斯瓦尔定理, 总谐波失真度(Total harmonic distortion, THD)可用式(11)表示:

$\begin{matrix} \begin{matrix} THD = \frac{\sqrt[]{\overset{\infty}{\sum_{i = 3, 5, 7, \dots}} {(A_{i} / \sqrt[]{2})}^{2}}}{A_{1} / \sqrt[]{2}} = \\ \frac{\sqrt[]{RM S^{2} - {(A_{1} / \sqrt[]{2})}^{2}}}{A_{1} / \sqrt[]{2}} \end{matrix} \end{matrix}$ (11)

式中:RMS为x(ω t)的有效值:

$\begin{matrix} RMS = \sqrt[]{\frac{1}{2 π} \int_{-}^{π} x^{2} (ωt) dωt} \end{matrix}$

由式(9)~(11)可知, x₁(ω t), x₂(ω t), …, x_n(ω t)的相位角θ ₁, θ ₂, …, θ _n直接影响THD。

2.2 特定谐波消去法合成的阶梯波

由式(10)可知, 当i=3, 5, 7, …时, 各次谐波成分的幅度A_i与i成反比。因此, 对于具有n个阶梯的阶梯波, 可以通过控制θ ₁, θ ₂, …, θ _n使如式(10)所示的谐波分量A₃, A₅, …, A₂_n-₁为零。根据这一原理, 可以采用式(12)所示方程求取θ ₁, θ ₂, …, θ _n:

$\begin{matrix} \{\begin{matrix} A_{1} = \frac{4}{π} \overset{n}{\sum_{j = 1}} \cos (θ_{j}) = n \\ A_{3} = \frac{4}{3 π} \overset{n}{\sum_{j = 1}} \cos (3 θ_{j}) = 0 \\ A_{5} = \frac{4}{5 π} \overset{n}{\sum_{j = 1}} \cos (5 θ_{j}) = 0 \\ ︙ \\ A_{2 n - 1} = \frac{4}{(2 n - 1) π} \overset{n}{\sum_{j = 1}} \cos [(2 n - 1) θ_{j}] = 0 \\ 0 < θ_{1} < θ_{2} < \dots < θ_{n} < π / 2 \end{matrix} \end{matrix}$ (12)

由式(12)可知, 虽然方程中等式个数与未知数的个数相等, 但θ ₁, θ ₂, …, θ _n是与三角函数相关的隐函数, 难以精确求解, 故采用计算机进行迭代计算。表1和表2分别为n=1~4时的相位角、频率成份值及THD。表2中, f₀表示基波的频率, 幅值做了归一化处理, 即除以阶数n。表4~表7中幅度值也做了归一化。

表1 特定谐波消去法的相位角(° ) Table 1 Phase angles of selected harmonic elimination(° )

表2 特定谐波消去法的频率成分及THD Table 2 Frequency components and THD of selected harmonic elimination

由表2可知, 特定谐波消去法能将3, 5, …, 2n-1次谐波精确消去。

2.3 等效面积法合成的阶梯波

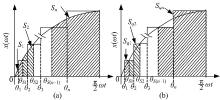
在电力电子领域的SPWM中, 通过使矩形单元的面积与正弦波单元的面积相等来使矩形阶梯波的低频成份与正弦波接近。借鉴这一理论, 可以通过图5所示方法来合成阶梯波。图5(a)为正弦波单元S₁, S₂, …, S_n的划分, S₁、S₂, …, S_n以θ _S₁, θ _S₂, …, θ _Sn作为各正弦波单元的划分, θ _Sj表示nsinθ _Sj=j(j=1, 2, …, n)时对应的相角; 图5(b)为矩形单元S_q₁、S_q₂, …, S_qn的划分。令S_j=S_qj相当于:

$\int_{0}^{θ_{1}} n \sin (ωt) dωt = \int_{θ_{1}}^{θ_{S 1}} [1 - nsin (ωt)] dωt$ (13a)

$\int_{θ_{S (j - 1)}}^{θ_{j}} [nsin (ωt) - (j - 1)] dωt = \int_{θ_{j}}^{{θ_{S}}_{j}} [j - nsin (ωt)] dωt$ (13b)

$\int_{θ_{S (n - 1)}}^{θ_{n}} [nsin (ωt) - (n - 1)] dωt = \int_{θ_{n}}^{\frac{π}{2}} [n - nsin (ωt)] dωt$ (13c)

式中:j=2, 3, …, n-1; θ _S₁, θ _S₂, …, θ _S₍_n-₁₎=sin^-¹(1/n), sin^-¹(2/n), …, sin^-¹[(n-1)/n]。

	Figure Option View Download New Window
	图5 等效面积法原理Fig.5 Principle of equivalent area

根据式(13a)(13b)(13c)获取阶梯波的相位角θ ₁, θ ₂, …, θ _n。

表3和表4分别为n=1~5时的相位角、频率成份值及THD。

表3 等效面积法的相位角 Table 3 Phase angles of equivalent area

表4 等效面积法的频率成分及THD Table 4 Frequency components and THD of equivalent area

2.4 阶梯波合成方法的比较

表5为单位幅值方波的主要频率成分及THD, 将表5与表2、表4对比可知, 阶梯波的谐波及THD显著低于方波。

表5 方波的频率成分及THD Table 5 Frequency components and THD of square wave

对比表2和表4可知, 在相同阶梯数n下, 虽然特定谐波消去能精确消去奇次谐波, 但其THD仍低于等效面积法。同时, 特定谐波消去的相角有分布极近的情况, 如n=3时θ ₁=19.86° 、θ ₂=20.24° , 其对采样频率有过高的要求。

在实际应用中, 受采样频率的限制, 实际可实现的相位精度一般比表1和表3中数据低得多。因此, 表6给出了n=4的阶梯波, 单个相角依次偏差+3° 时两种方法的THD。

表6 相位偏差对特定谐波消去法和等效面积法THD的影响 Table 6 Effect of phase deviation in selected harmonic elimination and equivalent area

表6中, THD₁、THD₂分别为特定谐波消去法和等效面积法在相位偏差时的THD。由表6与表2、表4对比可知:n=4, 某相位角偏差为+3° 时, THD₁误差为-0.0091~+0.0110, THD₂误差为+0.0048~+0.0053, 等效面积法受相位精度的影响较低。

综合表2、表4和表6的比较结果, 等效面积法合成的阶梯波更适合所提出的正交锁定放大。

综合计算结果及工程应用的可行性, 当n=3~5时, 阶梯波的相位角可近似取表7所示的值, 其THD与表4相比差别不大。需特别注意:获取I和Q应除以阶梯波的基波幅值, 阶梯波的基波幅值(即表7中1f₀)不是1。

表7 工程近似阶梯波参数 Table 7 Parameters of engineering approximation step wave

3 匹配采样技术

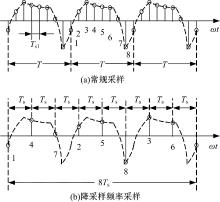
在数据采集过程中, 采样频率越高, 数据对二次场信号描述越细致, 与阶梯波相角匹配得越准确, 但是采用过高的采样频率会对硬件电路提出更高要求。当采用图6所示的降采样频率原理后, 可以用相对低的采样频率实现较高采样频率的效果。对于图6(a)所示的时域信号, 它的周期为T, 当要保证一个周期内采集到8个点时, 对于常规技术, 采样间隔T_s=(1/8)T, 即采样频率为信号频率的8倍。然而, 当取T_s=(3/8)T时, 按图6(b)所示方法, 则可以在3个信号周期T内重构一个周期的8个点。显然, 图6(b)用常规技术1/3倍的采样频率重构了相同相位精度的周期信号。

该原理可以定义为:设希望将一个周期为T的信号进行N点采样, 当取K为一个不能被N整除的质数, 采样周期T_s=(K/N)T时, 在K个信号周期T内可重构N个相位不同的采样点, 采样频率可以比常规技术低K倍。

	Figure Option View Download New Window
	图6 降采样频率原理Fig.6 Principle of sampling rate reduction

4 试验结果

在图7所示的硬件平台上进行试验。采用ALTERA公司的EP3C40Q240C8系列FPGA, 用于实现对发射电路和ADC采集的同步控制以及n=4的阶梯波正交锁定放大, 在采样间隔即可完成运算, 节约了探测时间。上位机用于进行传统的正弦波和方波参考的正交锁定放大。USB模块CY7C68013用于将FPGA运算结果传输到上位机, 便于在上位机中进行本文方法与传统方法的结果对比。

	Figure Option View Download New Window
	图7 硬件平台的结构框图Fig.7 Structure diagram of hardware platform

4.1 采样结果

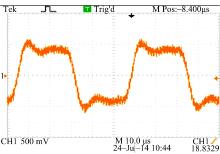
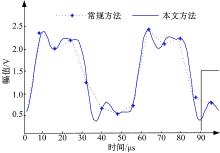
将接收线圈上的感应信号v_R适当放大后, 采用泰克TDS1012C示波器获取的波形图如图8所示。在相同采样率下, 采用本文所述采样技术和常规采样技术对v_R进行采样, 获得的波形分别如图9中实线和虚线所示。将图9中波形与图8中示波器波形比较可知, 本文所提出的降采样频率技术能更好地体现波形细节, 具有更高的相位精度。

	Figure Option View Download New Window
	图8 示波器波形Fig.8 Waveform in oscilloscope

	Figure Option View Download New Window
	图9 本文方法和常规方法的采样波形Fig.9 Sampling waveforms using the proposed method and conventional method

4.2 金属异常探测结果

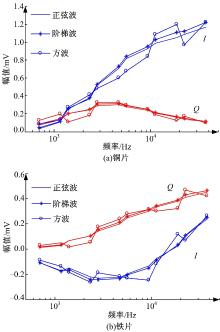
对两个大小相同的异常体进行探测实验, 一个为圆形铜片, 属于非铁磁性材料, 另一个为圆形铁片, 属于磁性材料。采用正弦波、方波及本文所述的阶梯波作为参考信号进行正交锁定放大, 对于铜片和铁片, 获取I、Q曲线分别如图10(a)(b)所示。

	Figure Option View Download New Window
	图10 铜片和铁片的正交锁定放大结果Fig.10 Orthogonal lock-in amplification results of copper and iron plate

将方波、阶梯波、正弦波的测试结果作对比可知, 采用方波参考的探测结果在正弦波参考的探测结果两侧大幅跳动, 而以阶梯波参考的结果较为接近于以正弦波参考的探测结果。对比图10(a)和图10(b)可知, 铜片和铁片具有不同的I、Q分量特性, 阶梯波的I和Q与正弦波的I和Q走势一致, 故本文所提出的正交锁定放大技术可用于近地表电磁探测。

表8给出了图10(a)(b)中阶梯波探测结果误差最大的一条曲线中的数值, 即图10(a)中铜片的I分量值, 用于定量分析方波和阶梯波参考下正交锁定放大的误差。表中的方波误差和阶梯波误差均以正弦波参考下的数值为标准求取。

表8 铜片的I分量 Table 8 I of copper plate

由表8可知:在本文所述阶梯波参考下, I分量的误差为0.7%~7.0%, 远低于方波参考下的误差-14.3%~+18.2%。

5 结束语

提出了基于阶梯波参考的正交检测方法。论述了阶梯波合成原理, 推导了阶梯波谐波表达式, 用特定谐波消去法和等面积法分别确定了阶梯波各级阶梯的相角, 并对比了两种方法所合成的阶梯波的频率成分及THD。采用匹配采样方法更细致地还原了信号波形, 以便与阶梯波进行更准确的运算。试验结果表明:所提出的正交锁定放大方法中的阶梯波相角更适合用等面积法求出, 阶梯波与接收信号的PSD运算可通过在FPGA内部用移位累加来实现, 无需通过乘法器进行运算, 实现方法简单、具有低的硬件要求、精度高于方波正交锁定放大, 可用于识别不同异常体。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	周逢道, 王金玉, 唐红忠, 等. 近地表电磁探测多频数字驱动信号产生技术[J]. 吉林大学学报: 工学版, 2013, 43(3): 682-687. Zhou Feng-dao, Wang Jin-yu, Tang Hong-zhong, et al. Multi-frequency digital drive signal generation technology in near surface electromagnetic detection domain[J]. Journal of Jilin University (Engineering and Technology Edition), 2013, 43(3): 682-687. [本文引用:1]
[2]	张文秀, 林君, 刘立超, 等. 分布式电磁探测宽频数据采集系统设计与实现[J]. 吉林大学学报: 工学版, 2012, 42(6): 1426-1431. Zhang Wen-xiu, Lin Jun, Liu Li-chao, et al. Design and implementation of broadband data acquisition system for distributed electromagnetic exploration[J]. Journal of Jilin University(Engineering and Technology Edition), 2012, 42(6): 1426-1431. [本文引用:1]
[3]	薛开昶, 董威, 林君, 等. 逆m伪随机相位PWM逆变器的EMI峰值抑制方法[J]. 吉林大学学报: 工学版, 2013, 43(6): 1589-1595. Xue Kai-chang, Dong Wei, Lin Jun, et al. Suppression method of inverse m sequence rand om phase PWM inverter’s EMI peak[J]. Journal of Jilin University (Engineering and Technology Edition), 2013, 43(6): 1589-1595. [本文引用:1]
[4]	Zitoun A, Beheim L, Huez R, et al. Smart electrom-agnetic sensor for buried conductive targets identi-cation[J]. IEEE Sensors Journal, 2006, 6(6): 1580-1591. [本文引用:1]
[5]	Svatos J, Vedral J, Fexa P. Metal detector excited by frequency-swept signal[J]. Metrology and Measurement Systems, 2011, 18(1): 57-67. [本文引用:1]
[6]	Ramachand ran G, Gader P D, Wilson J N. GRANMA: Gradient angle model algorithm on wideband EMI data for land -mine detection[J]. Geoscience and Remote Sensing Letters, 2010, 7(3): 535-539. [本文引用:1]
[7]	Shubitidze F, Fernand ez J P, Barrowes B E, et al. The orthonormalized volume magnetic source model for discrimination of unexploded ordnance[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(8): 4658-4670. [本文引用:1]
[8]	罗海军, 何为, 徐征, 等. 基于同步检波的单通道磁感应成像技术研究[J]. 仪器仪表学报, 2012, 44(4): 899-904. Luo Hai-jun, He Wei, Xu Zheng, et al. Study on single-channel magnetic induction tomography technique based on synchronous detection[J]. Chinese Journal of Scientific Instrument, 2012, 44(4): 899-904. [本文引用:1]
[9]	Aguirre J, Garcia R D, Medrano N, et al. Square-signal-based algorithm for analog lock-in amplifiers[J]. IEEE Transactions on Industrial Electronics, 2014, 61(10): 5590-5598. [本文引用:1]
[10]	Qin J H, Huang Z M, Ge Y J, et al. Tand em demodulation lock-in amplifier based on digital signal processor for dualmodulated spectroscopy[J]. Review of Scientific Instruments, 2009, 80(3): 033112. [本文引用:1]
[11]	Yang Y, Huang L, Lu Z L, et al. AC voltage reference using the fundamental of DAC stepwise-approximated sine waves[J]. IEEE Transactions on Instrumentation and Measurement, 2014, 63(2): 473-478. [本文引用:1]
[12]	高晋占. 微弱信号检测[M]. 2版, 北京: 清华大学出版社, 2011: 171-214. [本文引用:1]
[13]	Suresh Y, Pand a A K. Research on a cascaded multi-level inverter by employing three-phase transformers[J]. IET Power Electronics, 2012, 5(5): 561-570. [本文引用:1]
[14]	Young C M, Wu S F. Selective harmonic elimination in multi-level inverter with zig-zag connection transformers[J]. IET Power Electronics, 2014, 7(4): 876-885. [本文引用:1]
[15]	Zhang Y, Zou Y P, Wang C Z, et al. A novel modulation technology for multilevel inverter based on equivalent area[C]//The 33rd Annual Conference of the IEEE Industrial Electronics Society, Taipei, Taiwan, 2007: 2115-2118. [本文引用:1]
[16]	Hua C C, Wu C W, Chuang C W. Control of low-distortion 27-level cascade inverter with three H-bridge inverter modules[C]//IEEE International Conference on Industrial Technology, Bombay, India, 2006: 1844-1849. [本文引用:1]

2013

0.0

. 2013, 43(3):682-687 DOI:doi:10.7964/jdxbgxb201303021

Multi-frequency digital drive signal generation technology in near surface electromagnetic detection domain

近地表电磁探测多频数字驱动信号产生技术

Zhou Feng-dao , Wang Jin-yu , Tang Hong-zhong

周逢道, 王金玉, 唐红忠

To meet the requirements of electromagnetic sounding for emission in the near-surface frequency domain, a System on a Programmable Chip (SOPC) was built using Field Programmable Gate Array (FPGA) as the hardware control platform. The SOPC was based on the unipolar and frequency multiplication Sinusoidal Pulse Width Modulation (SPWM). Verilog was used to realize multi-frequency digital SPWM algorithm, generate the multi-frequency digital drive signal. This signal has a small frequency interval and low Total Harmonic Distortion (THD). It can overcome the defects of other methods, such as the fixed frequency interval and complex system structure of pseudo random method, the over-dependence on load coil and complex algorithm of the bit-stream method. Theoretical simulation and experiment results verify the effectiveness of the method.

针对近地表频率域电磁探测对发射信号的要求,以单极性倍频正弦脉宽调制技术(Sinusoidal pulse width modulation,SPWM)为基础,利用现场可编程门阵列(Field-programmable gate array,FPGA)作为硬件平台,构建了基于嵌入式NiosII软核的片上系统SOPC(System-on-a-programmable-chip);采用硬件描述语言(Verilog)实现多频SPWM的数字算法,产生频率间隔小、谐波失真(THD)低的多频数字驱动信号,克服了伪随机法频率间隔固定、系统结构复杂、位流法过分依赖负载线圈、算法复杂的缺点.最后,通过理论仿真和试验验证了本文方法的优越性.

... 0 引言近地表电磁探测是指在电磁波一次场的激励下,通过采集由地下异常所产生的二次场,获取地下介质电磁特性的方法,被广泛应用于地下管线检测、工程质量监测和考古勘测等领域^[1] ...

2012

0.0

. 2012, 42(6):1426-1431

Design and implementation of broadband data acquisition system for distributed electromagnetic exploration

分布式电磁探测宽频数据采集系统设计与实现

Zhang Wen-xiu , Lin Jun , Liu Li-chao

张文秀, 林君, 刘立超

摘　要：将地球物理勘探中广泛应用于地震数据采集的分布式采集技术引入电磁探测仪器,针对被测电磁场信号宽频带、大动态范围、强噪声干扰的特点,通过设计低噪声的模拟信号调理电路,采用24位Δ-Σ结构模数转换器（Analog-to-digital,ADC）和现场可编程门阵列（Fieldprogrammable gate array,FPGA）构建了高性能的数据采集系统。利用微控制器及其外围功能模块实现了数据采集系统的工作流程控制、数据存储和传输。主要技术指标测试和水槽模型及野外勘探对比试验结果表明：该系统性能先进,测量准确,能够满足分布式电磁探测数据采集的需求。

... 同时,为了提高野外工作效率,仪器应尽可能轻便、低功耗并具有一定的实时处理能力^[2] ...

2013

0.0

. 2013, 43(6):1589-1595 DOI:doi:10.7964/jdxbgxb201306025

Suppression method of inverse m sequence random phase PWM inverter#cod#x02019;s EMI peak

逆m伪随机相位PWM逆变器的EMI峰值抑制方法

Xue Kai-chang , Dong Wei , Lin Jun

薛开昶, 董威, 林君

对逆m序列伪随机的产生和随机相位脉冲宽度调制(RPPWM)的原理进行了论述,推导出了逆m序列的频谱表达式和RPPWM的主要波形.并采用等效频谱分析模型,避开对非线性比较器的直接建模,降低了分析难度,得到了 RPPWM波形频谱的解析表达式.通过对比方波RPPWM和逆m序列RPPWM的波形频谱表达式,从理论上证明了逆m序列RPP-WM具有较优的电磁兼容 (EMC)特性.实验结果表明,在奇数次开关频率附近,逆m序列RPPWM具有较好的电磁干扰(EMI)峰值抑制效果;逆m序列RPPWM与已有随机频率脉冲宽度调制(RFPWM)结合具有良好的应用前景.

... 在近地表电磁探测中,方波激励源与正弦波激励源相比具有如下优点^[3,4,5,6,7]:①正弦波发射一般采用正弦脉冲宽度调制(Sinusoidal pulse width modulation,SPWM)技术,调制过程引入交调失真,导致发射波形随机度大、探测精度低,而方波发射时不需要调制 ...

2006

0.0

2011

0.0

2010

0.0

2014

0.0

2012

0.0

. 2012, 44(4):899-904 DOI:doi:10.3969/j.issn.0254-3087.2012.04.027

Study on single-channel magnetic induction tomography technique based on synchronous detection

基于同步检波的单通道磁感应成像技术研究

Luo Hai-jun , He Wei , Xu Zheng

罗海军, 何为, 徐征

磁感应成像在医学领域的应用,由于生物组织的电导率非常小,需要一种测量相位精度高的系统才能满足应用需要。描述了一种基于同步检波的单通道磁感应测量系统,来测量微小相位变化。系统使用模拟开关代替模拟乘法电路,减少直流漂移,增加电路的动态范围。电路中引入了模拟的相移电路,使参考信号和与检测信号相位正交,提高相位测量的灵敏度。研究了单通道系统的稳定度和灵敏度,通过实测电路,该测量系统在1 min内的相位漂移0.001 5°,在1 h内的相位漂移0.006°;并给出电导率变化相应相位变化关系。

... 由于采用方波作为一次场激励源,给常规正交锁定放大技术带来了不便^[8,9,10,11] ...

2014

0.0

... 由于采用方波作为一次场激励源,给常规正交锁定放大技术带来了不便^[8,9,10,11] ...

2009

0.0

... 由于采用方波作为一次场激励源,给常规正交锁定放大技术带来了不便^[8,9,10,11] ...

2014

0.0

... 由于采用方波作为一次场激励源,给常规正交锁定放大技术带来了不便^[8,9,10,11] ...

2011

0.0

... 若选用方波作为参考信号,PSD可以通过电子开关实现^[12],故功耗低、成本低 ...

2012

0.0

... 2 阶梯波参考信号的合成阶梯波参考信号的失真度与电平切换的相角有直接关系,通常采用特定谐波消去法^[13,14]和等效面积法^[15,16]确定各相角 ...

2014

0.0

... 2 阶梯波参考信号的合成阶梯波参考信号的失真度与电平切换的相角有直接关系,通常采用特定谐波消去法^[13,14]和等效面积法^[15,16]确定各相角 ...

2007

0.0

... 2 阶梯波参考信号的合成阶梯波参考信号的失真度与电平切换的相角有直接关系,通常采用特定谐波消去法^[13,14]和等效面积法^[15,16]确定各相角 ...

2006

0.0

... 2 阶梯波参考信号的合成阶梯波参考信号的失真度与电平切换的相角有直接关系,通常采用特定谐波消去法^[13,14]和等效面积法^[15,16]确定各相角 ...