基于<em> H</em><sub>∞</sub>鲁棒SUKF算法的永磁同步电机转速观测器设计

引用本文

赵彬, 郭孔辉, 许男, 杨一洋. 基于 H_∞鲁棒SUKF算法的永磁同步电机转速观测器设计 .吉林大学学报:工学版, 2016, 46(4): 1017-1022
ZHAO Bin, GUO Kong-hui, XU Nan, YANG Yi-yang. Speed observer design for permanent magnet synchronous motor based on H_∞ robust SUKF algorithm . Journal of Jilin University Engineering and Technology Edition, 2016, 46(4): 1017-1022 复制到剪切板

Permissions

基于 H_∞鲁棒SUKF算法的永磁同步电机转速观测器设计

赵彬^1,², 郭孔辉¹, 许男¹, 杨一洋¹

1.吉林大学汽车仿真与控制国家重点实验室,长春130022

2.长春工业大学电气与电子工程学院, 长春 130012

通讯作者：许男(1988-),男,讲师,博士.研究方向:汽车系统动力学与控制.E-mail:xu.nan0612@gmail.com

作者简介:赵彬(1983-),男,博士研究生.研究方向:汽车系统动力学与控制,智能控制.E-mail:zhao_bin@mail.ccut.edu.cn

基金:“973”国家重点基础研究发展计划项目(2011CB711200)

摘要

为了解决永磁同步电机定子电阻变化对速度观测的影响,利用 α-β坐标系下永磁同步电机非线性系统模型,引入 H_∞鲁棒滤波算法增强观测器鲁棒性。为了解决sigma点计算量大的问题,采用超球体单形采样方法,提出一种新的非线性滤波器。最后设计了 H_∞鲁棒球形无迹卡尔曼滤波观测器对永磁同步电机转速进行状态观测。当永磁同步电机定子电阻变化时,对比分析了 H_∞鲁棒球形无迹卡尔曼滤波器与无迹卡尔曼滤波器、球形无迹卡尔曼滤波器在相同系统噪声和量测噪声时电机转速误差方差。 H_∞鲁棒球形卡尔曼滤波器的转速误差方差接近7 rad/min,明显小于后两者观测器观测值(40、20 rad/min)。

关键词: 车辆工程; 转速观测; 非线性滤波; 永磁同步电机

中图分类号:U41 文献标志码:A 文章编号:1671-5497(2016)04-1017-06

Speed observer design for permanent magnet synchronous motor based on H_∞ robust SUKF algorithm

ZHAO Bin^1,², GUO Kong-hui¹, XU Nan¹, YANG Yi-yang¹

1.State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130022, China

2.College of Electrical and Electronic Engineering,Changchun University of Technology, Changchun 130012, China

Abstract

In order to solve the influence of stator resistance variation of permanent magnet synchronous motor on velocity measurement, by using a nonlinear system model of permanent magnet synchronous motor in α-β coordinate, the H_∞ robust filtering algorithm is introduced to enhance the robustness of the observer. To solve problem of large calculating number of sigma points, a new nonlinear filter is proposed using the method of single sampling of the sphere. A H_∞ robust spherical unscented Kalman filter observer is designed to observe the velocity state of the permanent magnet synchronous motor. When the permanent magnet synchronous motor stator resistance changes, the motor velocity error variances of the H_∞ robust spherical unscented Kalman filter, unscented Kalman filter and spherical unscented Kalman filter are compared and analyzed under the same system noise and measurement noise. The speed error variance of the H_∞ robust spherical unscented Kalman filter observer is close to 7 rad/min, which is much less than that of the other two observers, which are close to 40 rad/min and 20 rad/min respectively.

Keyword: vehicle engineering; speed observation; nonlinear filter; permanent magnet synchronous motor (PMSM)

Show Figures

0 引言

永磁同步电机(PMSM)^[1]转速观测状态方程常采用电流模型或者磁链模型, 二者都具有较强的非线性, 观测器的设计通常采用扩展卡尔曼滤波器或滑膜变结构进行估计^[2]。文献[3]介绍了卡尔曼滤波算法的特点, 文献[4, 5, 6]对卡尔曼滤波算法在PMSM转速观测器中应用做了详细介绍。但是由于扩展卡尔曼滤波器是通过线性化处理来实现非线性滤波, 计算时需对原非线性系统Taylor展开, 并忽略高阶项, 得到局部近似的线性系统, 达到最小方差意义上的次最优估计, 此时如果高阶项无法忽略, 就会产生高阶截断误差, 降低估计精度; 同时扩展卡尔曼滤波器要求对原系统求取雅可比矩阵, 在实际使用时, 有些模型很难求得雅可比矩阵^[7], 降低了使用范围。无迹卡尔曼滤波算法用无迹变换逼近非线性分布, 使非线性统计计算精度至少达到2阶, 提高计算精度。然而该方法需要计算 $\begin{matrix} 2 n + 1 \end{matrix}$ 个 $\begin{matrix} sigma \end{matrix}$ 点, 计算量大, 计算周期长。为了降低 $\begin{matrix} sigma \end{matrix}$ 采样点, 减小计算量, 采用球形无迹变换替换无迹变换, 使采样点降到 $\begin{matrix} n + 2 \end{matrix}$ 个。

为了克服参数变化对观测值影响, 增加系统鲁棒性能, 本文将球形无迹变换(ST)^[8]、无迹卡尔曼滤波器(UKF)^[9]与非线性 $\begin{matrix} H_{\infty} \end{matrix}$ 鲁棒滤波器结合起来形成性能更为优良的非线性 $\begin{matrix} H_{\infty} \end{matrix}$ 鲁棒球形无迹卡尔曼滤波器(HSUKF), 既可以实现对非线性系统进行观测, 又能增强系统鲁棒性并抑制异常观测值的影响。

1 $\begin{matrix} H_{\infty} \end{matrix}$ 滤波基本原理及其模型

1.1 非线性 $\begin{matrix} H_{\infty} \end{matrix}$ 滤波基本原理

假设标准的线性离散系统:

$\begin{matrix} x_{k + 1} = F_{k} x_{k} + w_{k}, y_{k} = H_{k} x_{k} + v_{k} \end{matrix}$

式中: $\begin{matrix} F_{k} \end{matrix}$ 为系统状态矩阵; $\begin{matrix} H_{k} \end{matrix}$ 为量测矩阵; $\begin{matrix} w_{k} ~ (0, Q_{k}); v_{k} ~ (0, R_{k}) 。 \end{matrix}$

定义代价函数:

$\begin{matrix} \begin{matrix} J = \\ \frac{\overset{N}{\sum_{k = 1}} ‖ z_{k} - {\hat{z}}_{k} ‖_{S_{k}}^{2}}{‖ x_{0} - {\hat{x}}_{0} ‖_{P_{0}^{- 1}}^{2} + \overset{N}{\sum_{k = 1}} (‖ w_{k} ‖_{Q_{k}^{- 1}}^{2} + ‖ v_{k} ‖_{R_{k}^{- 1}}^{2})} (1) \end{matrix} \end{matrix}$

式中: $\begin{matrix} z_{k} = L_{k} x_{k}, \end{matrix}$ 其中 $\begin{matrix} L_{k} \end{matrix}$ 为自定义非奇异矩阵, 一般设为单位矩阵; $\begin{matrix} x_{0} \end{matrix}$ 为系统初始化状态; $\begin{matrix} {\hat{x}}_{0} \end{matrix}$ 为对应的初始化估计值, 其方差为 $\begin{matrix} P_{0}; S_{k} \end{matrix}$ 为自定义对称正定矩阵, 一般设为单位矩阵; 定义 $\begin{matrix} ‖ x ‖_{A}^{2} = x^{T} Ax, \end{matrix}$ 代价函数所示项据此类推。

$\begin{matrix} H_{\infty} \end{matrix}$ 滤波问题就是寻找一个 $\begin{matrix} {\hat{x}}_{k} \end{matrix}$ 使 $\begin{matrix} J < 1 / θ, θ \end{matrix}$ 为指定的性能边界, 问题解变为极小极大问题, $\begin{matrix} J^{*} = \min_{{\hat{x}}_{k}} \max_{w_{k}, v_{k}, x_{0}} J, \end{matrix}$ 通常情况下, $\begin{matrix} H_{\infty} \end{matrix}$ 滤波问题可以通过次优迭代算法求解到解析形式的解, 即满足 $\begin{matrix} {(P_{k}^{- 1} + {H^{T}}_{k} R_{k}^{- 1} H_{k} - θ {\bar{S}}_{k})}^{- 1} \end{matrix}$ 是正定的, $\begin{matrix} {\bar{S}}_{k} = {L^{T}}_{k} S_{k} L_{k}, P_{k} \end{matrix}$ 为状态向量的协方差阵。在 $\begin{matrix} H_{\infty} \end{matrix}$ 滤波中, 性能边界 $\begin{matrix} θ \end{matrix}$ 越小, 系统鲁棒性越强; 性能边界 $\begin{matrix} θ \end{matrix}$ 越大, $\begin{matrix} H_{\infty} \end{matrix}$ 滤波的特性越接近标准卡尔曼滤波。

1.2 非线性 $\begin{matrix} H_{\infty} \end{matrix}$ 滤波器模型

球形无迹卡尔曼滤波器是线性的, 为了将 $\begin{matrix} H_{\infty} \end{matrix}$ 鲁棒滤波器应用到球形无迹卡尔曼滤波器中, 对协方差阵递推的黎卡提方差进行转换。转换后的 $\begin{matrix} H_{\infty} \end{matrix}$ 鲁棒控制协方差阵可以写成:

$\begin{matrix} \begin{matrix} P_{k} = P_{k | k - 1} - [P_{X_{k} | Y_{k}} P_{k | k - 1}] \cdot \\ [\begin{matrix} P_{Y_{k}} - R_{k} + I & {P^{T}}_{X_{k} | Y_{k}} \\ P_{X_{k} | Y_{k}} & P_{k | k - 1} - θ^{2} I \end{matrix}] \cdot [\begin{matrix} {P^{T}}_{X_{k} | Y_{k}} \\ {P^{T}}_{k | k - 1} \end{matrix}] (2) \end{matrix} \end{matrix}$

2 UKF算法流程

为了降低非线性系统线性化带来的误差, 采用无迹卡尔曼滤波算法, 相比非线性系统线性化方法, 该算法具有更小的线性化误差。无迹卡尔曼滤波算法步骤如下:

(1)初始化滤波器

$\begin{matrix} \begin{matrix} x_{0} & = E (x_{0}) (3) \\ P_{0} & = E [(x_{0} - {\hat{x}}_{0}) {(x_{0} - {\hat{x}}_{0})}^{T}] (4) \end{matrix} \end{matrix}$

(2)时间更新

假设系统由 $\begin{matrix} n \end{matrix}$ 个状态变量构成, 按照对称采样的方法, 得到共 $\begin{matrix} 2 n + 1 \end{matrix}$ 个 $\begin{matrix} sigma \end{matrix}$ 点作为采样点, 记作 $\begin{matrix} χ_{i, k - 1} (i = 0, 1, \dots, 2 n) 。 \end{matrix}$ 变换原则为:

$\begin{matrix} \begin{matrix} χ_{0, k - 1} & = x_{k - 1 |k - 1} (5) \\ χ_{i, k - 1} & = x_{k - 1 |k - 1} + {(\sqrt[]{(n + λ) P_{k - 1 |k - 1}})}_{i} (6) \\ i = 1, 2, \dots, n \\ χ_{i, k - 1} & = x_{k - 1 |k - 1} - {(\sqrt[]{(n + λ) P_{k - 1 |k - 1}})}_{i} (7) \\ i = n + 1, n + 2, \dots, 2 n \end{matrix} \end{matrix}$

式中: $\begin{matrix} {(\sqrt[]{(n + λ) P_{k - 1 |k - 1}})}_{i} \end{matrix}$ 为矩阵平方根的第 $\begin{matrix} i \end{matrix}$ 列; 参数 $\begin{matrix} λ \end{matrix}$ 为影响因子, $\begin{matrix} λ = α^{2} (n + k) - n, \end{matrix}$ 参数 $\begin{matrix} α \end{matrix}$ 决定 $\begin{matrix} sigma \end{matrix}$ 点围绕状态均值的分布情况, 通常 $\begin{matrix} α \end{matrix}$ 取为[0.0001, 1]之间的正数, 用来控制高阶非线性量对均值的影响, 其中 $\begin{matrix} sigma \end{matrix}$ 点越接近所估计状态的均值, 高阶非线性影响越小。参数 $\begin{matrix} k \end{matrix}$ 为二级影响因子, 在参数估计中为 $\begin{matrix} 3 - n, \end{matrix}$ 而在状态估计中为0。

(3)在计算得到 $\begin{matrix} χ_{i, k - 1} \end{matrix}$ 后, 将该点集带入非线性函数 $\begin{matrix} f (\cdot) \end{matrix}$ 做适当非线性变换, 表示为:

$\begin{matrix} χ_{i, k | k - 1}^{*} = f (χ_{i, k - 1}, u_{k - 1}) \end{matrix}$ (8)

(4)状态变量的预估协方差值和预估状态值计算由加权平均法得到。权值具体计算方法为:

$\begin{matrix} \begin{matrix} W_{0}^{(c)} = λ / (n + λ) + 1 - α^{2} + β (9) \\ W_{0}^{(m)} = λ / (n + λ) (10) \\ W_{i}^{(c)} = W_{i}^{(m)} = 0.5 / (n + λ) i = 1, 2, \dots, 2 n (11) \end{matrix} \end{matrix}$

式中: $\begin{matrix} W_{i}^{(m)} \end{matrix}$ 为状态预估统计权值; $\begin{matrix} W_{i}^{(c)} \end{matrix}$ 为协方差预估统计权值; $\begin{matrix} β \end{matrix}$ 为误差采样因子, 对于状态预估和更新预估均值属于高斯分布来说, $\begin{matrix} β = 2 \end{matrix}$ 为最优采样值。按照式(9)(10)(11)计算权值完毕后, 依照下式计算状态均值的预估值 $\begin{matrix} {\hat{x}}_{k | k - 1} \end{matrix}$ 和协方差的预估值 $\begin{matrix} P_{k | k - 1} \end{matrix}$ :

$\begin{matrix} \begin{matrix} {\hat{x}}_{k | k - 1} = \overset{2 n}{\sum_{i = 0}} W_{i}^{(m)} χ_{i, k | k - 1}^{*} (12) \\ P_{k | k - 1} = \\ \overset{2 n}{\sum_{i = 0}} W_{i}^{(c)} [(χ_{i, k | k - 1}^{*} - {\hat{x}}_{k | k - 1}) (χ_{i, k | k - 1}^{*} - {\hat{x}}_{k | k - 1})^{T}] + Q (13) \end{matrix} \end{matrix}$

(5)对系统的输出方程进行 $\begin{matrix} sigma \end{matrix}$ 点集变换, 得到系统输出 $\begin{matrix} Y_{k} 。 \end{matrix}$ 与初始化 $\begin{matrix} χ_{i, k - 1} \end{matrix}$ 一样, 预测量测值和它的估计协方差都由预估系统的 $\begin{matrix} sigma \end{matrix}$ 点集 $\begin{matrix} χ_{i, k |k - 1}^{*} \end{matrix}$ 产生, 若把系统状态方程的噪声考虑在内, 则 $\begin{matrix} χ_{i, k |k - 1} \end{matrix}$ 可表示为:

$\begin{matrix} \begin{matrix} χ_{i, k | k - 1} = \\ [\begin{matrix} χ_{i, k | k - 1}^{*} & χ_{i, k | k - 1}^{*} + λ \sqrt[]{Q} & χ_{i, k | k - 1}^{*} - λ \sqrt[]{Q} \end{matrix}] (14) \end{matrix} \end{matrix}$

可以通过量测函数得到输出量的预估:

$\begin{matrix} Y_{i, k | k - 1} = h (χ_{i, k | k - 1}) (15) \end{matrix}$

同时, 预估观测值及其方差、协方差分别为:

$\begin{matrix} \begin{matrix} {\hat{Y}}_{k |k - 1} = \overset{2 n}{\sum_{i = 0}} W_{i}^{(m)} Y_{i, k |k - 1} (16) \\ P_{Y_{k}} = \overset{2 n}{\sum_{i = 0}} W_{i}^{(c)} [(Y_{i, k | k - 1} - \\ {\hat{Y}}_{k | k - 1}) {(Y_{i, k | k - 1} - {\hat{Y}}_{k | k - 1})}^{T}] + R (17) \\ P_{X_{k} | Y_{k}} = \\ \overset{2 n}{\sum_{i = 0}} W_{i}^{(c)} [(χ_{i, k | k - 1}^{*} - {\hat{X}}_{k | k - 1}) {(Y_{i, k | k - 1} - {\hat{Y}}_{k | k - 1})}^{T}] (18) \end{matrix} \end{matrix}$

(6)按下式更新增益、均值和协方差:

$\begin{matrix} \begin{matrix} K_{k |k} & = P_{X_{k} |Y_{k}} P_{Y_{k}}^{- 1} (19) \\ {\hat{x}}_{k | k} & = {\hat{x}}_{k | k - 1} + K_{k |k} (Y_{k} - {\hat{Y}}_{k | k - 1}) (20) \\ P_{k} & = P_{k |k - 1} - K_{k |k} P_{Y_{k}} {K^{T}}_{k |k - 1} (21) \end{matrix} \end{matrix}$

式中: $\begin{matrix} K_{k |k} \end{matrix}$ 为 $\begin{matrix} Kalman \end{matrix}$ 增益; $\begin{matrix} Y_{k} - {\hat{Y}}_{k | k - 1} \end{matrix}$ 为系统的更新值。

通过式(20)(21), 可以得出当前时刻系统状态变量和状态变量协方差的估计值。至此UKF算法完成当前时刻状态变量的一次更新, 输出状态 $\begin{matrix} {\hat{x}}_{k | k}, \end{matrix}$ 然后返回步骤(1)进行下一时刻系统状态的估计。

3 球形无迹变换

根据无迹变换定义, 无迹变换需要 $\begin{matrix} 2 n + 1 \end{matrix}$ 个 $\begin{matrix} sigma \end{matrix}$ 点, 实际应用时计算量大, 降低了计算速度, 球形无迹变换通过重新布置 $\begin{matrix} sigma \end{matrix}$ 点, 获得更好的数值稳定性和计算速度。球形无迹变换算法如下:

(1)选择权系数 $\begin{matrix} w^{(0)} \in [0, 1) \end{matrix}$

(2)其余的权系数为

$\begin{matrix} w^{(i)} = \frac{1 - w^{(0)}}{n + 1} i = 1, 2, \dots, n + 1 (22) \end{matrix}$

(3)初始化一元向量

$\begin{matrix} σ_{1}^{(1)} = \frac{- 1}{\sqrt[]{2 w^{(1)}}}, σ_{2}^{(1)} = \frac{1}{\sqrt[]{2 w^{(1)}}} (23) \end{matrix}$

对于 $\begin{matrix} j = 2, 3, \dots, n, \end{matrix}$ 按照下式递推获得向量 $\begin{matrix} σ : \end{matrix}$

$\begin{matrix} σ_{i}^{(j)} = \{\begin{matrix} \begin{matrix} [\begin{matrix} σ_{0}^{(j - 1)} \\ 0 \end{matrix}], i = 0 \end{matrix} \\ \begin{matrix} [\begin{matrix} σ_{i}^{(j - 1)} \\ \frac{- 1}{\sqrt[]{j (j + 1) w^{(1)}}} \end{matrix}], i = 1, 2, \dots, j \end{matrix} \\ [\begin{matrix} 0_{j - 1} \\ \frac{j}{\sqrt[]{j (j + 1) w^{(1)}}} \end{matrix}], i = j + 1 \end{matrix} (24) \end{matrix}$

式中: $\begin{matrix} 0_{j} \end{matrix}$ 是包含 $\begin{matrix} j \end{matrix}$ 个零的列向量。

(4) 球形无迹变换sigma点为:

$\begin{matrix} x^{(i)} = \bar{x} + \sqrt[]{P} σ_{i}^{(n)}, i = 0, L, n + 1 (25) \end{matrix}$

根据球形无迹变换 $\begin{matrix} sigma \end{matrix}$ 点替换无迹变换 $\begin{matrix} χ_{i, k - 1}, χ_{i, k | k - 1} 。 \end{matrix}$

4 H_∞鲁棒球形无迹卡尔曼滤波观测器实现

H_∞鲁棒球形无迹卡尔曼滤波器具体实现方法如下:

(1)根据式(3)(4)初始化滤波器, 初始化过程噪声和量测噪声方差 $\begin{matrix} Q 、 R, \end{matrix}$ 根据式(22)~(24)选择权系数并初始化一元向量。

(2)按照式(25)计算 $\begin{matrix} x^{(i)} (i = 0, L, n + 1) \end{matrix}$ 即计算 $\begin{matrix} χ_{i, k - 1}, \end{matrix}$ 把该点集带入式(8)做非线性变换, 然后按照式(9)~(13)计算状态均值的预估值 $\begin{matrix} {\hat{x}}_{k | k - 1} \end{matrix}$ 和协方差的预估值 $\begin{matrix} P_{k | k - 1}, \end{matrix}$ 按照式(14)~(18)计算输出量的预估 $\begin{matrix} Y_{i, k | k - 1} 、 \end{matrix}$ 预估观测值 $\begin{matrix} {\hat{Y}}_{k |k - 1} \end{matrix}$ 及其方差 $\begin{matrix} P_{Y_{k}} 、 \end{matrix}$ 协方差 $\begin{matrix} P_{X_{k} | Y_{k}} 。 \end{matrix}$

(3)最后通过式(19)(20)计算 $\begin{matrix} Kalman \end{matrix}$ 增益 $\begin{matrix} K_{k |k} \end{matrix}$ 和更新均值 $\begin{matrix} {\hat{x}}_{k | k}, \end{matrix}$ 带入式(2)计算协方差阵 $\begin{matrix} P_{k}, \end{matrix}$ 返回式(25)迭代。

5 $\begin{matrix} α - β \end{matrix}$ 坐标系下永磁同步电机模型

5.1 电机模型

本文基于隐极式永磁同步电机 $\begin{matrix} α - β \end{matrix}$ 轴(两相静止坐标系)设计 $\begin{matrix} H_{\infty} \end{matrix}$ 鲁棒球形无迹卡尔曼观测器, 建立以定子电流 $\begin{matrix} i_{α} 和 i_{β} 、 \end{matrix}$ 转速 $\begin{matrix} ω_{r} \end{matrix}$ 和转子位置角 $\begin{matrix} θ_{r} \end{matrix}$ 为状态变量的非线性状态方程, 以定子电压为输入变量的测量方程, 观测器的输出为转速 $\begin{matrix} ω_{r} 。 \end{matrix}$ 隐极式永磁同步电机数学模型可以表示为:

$\begin{matrix} \begin{matrix} \{\begin{matrix} \overset{\cdot}{x} = f (x) + Bu + w \\ y = h (x) + v \end{matrix} (26) \\ 式中 : \\ x = {[\begin{matrix} i_{α} & i_{β} & ω_{r} & θ_{r} \end{matrix}]}^{T}; u = {[\begin{matrix} u_{α} & u_{β} \end{matrix}]}^{T}; \\ f (x) = [\begin{matrix} f_{1} \\ f_{2} \\ f_{3} \\ f_{4} \end{matrix}] = [\begin{matrix} - \frac{R_{s}}{L_{s}} i_{α} + \frac{ψ_{f}}{L_{s}} ω_{r} \sin θ_{r} \\ - \frac{R_{s}}{L_{s}} i_{β} - \frac{ψ_{f}}{L_{s}} ω_{r} \sin θ_{r} \\ 0 \\ ω_{r} \end{matrix}]; \\ B = [\begin{matrix} \frac{1}{L_{s}} & 0 \\ 0 & \frac{1}{L_{s}} \\ 0 & 0 \\ 0 & 0 \end{matrix}]; h (x) = [\begin{matrix} i_{α} \\ i_{β} \end{matrix}] \end{matrix} \end{matrix}$

式中: $\begin{matrix} x \end{matrix}$ 为状态变量; $\begin{matrix} u \end{matrix}$ 为输入变量; $\begin{matrix} f (x) \end{matrix}$ 为非线性状态矩阵; $\begin{matrix} w \end{matrix}$ 为系统噪声; $\begin{matrix} v \end{matrix}$ 为测量噪声; $\begin{matrix} u_{α} 、 u_{β} \end{matrix}$ 分别为定子电压在 $\begin{matrix} α - β \end{matrix}$ 轴的分量; $\begin{matrix} R_{s} \end{matrix}$ 为定子电阻; $\begin{matrix} L_{s} \end{matrix}$ 为永磁体等效电感。

5.2 控制系统结构框图

图1为状态观测器和永磁同步电机直接转矩控制结构图, 系统采用双闭环调速系统, 其中外环为转速环(ASR), 内环为电流环(ACR)。设定电机转速信号 $\begin{matrix} ω_{r}^{*} \end{matrix}$ 与反馈转速信号 $\begin{matrix} ω_{r} \end{matrix}$ 的差值通过ASR得到参考转矩信号 $\begin{matrix} T_{e}^{*}, \end{matrix}$ 该参考转矩信号与 $\begin{matrix} α - β \end{matrix}$ 轴下解算的电机实际转矩信号 $\begin{matrix} T_{e} \end{matrix}$ 的差值通过ACR得到DTC开关表, 驱动电机运行。

	Figure Option View Download New Window
	图1 状态观测器和永磁同步电机直接转矩控制结构图Fig.1 State observer and direct torque control of per-manent magnet synchronous motor structure

6 仿真分析

6.1 系统初始化

仿真中初始状态 $\begin{matrix} x_{0} = E [x_{0}] = {[0, 0, 0, 0]}^{T}, \end{matrix}$ 初始状态估计 $\begin{matrix} {\hat{x}}_{0} = E [{\hat{x}}_{0}] = {[0.1, 0.1, 1, 0.1]}^{T}, \end{matrix}$ 初始化方差 $\begin{matrix} P_{0} = E [(x_{0} - {\hat{x}}_{0}) (x_{0} - {\hat{x}}_{0})^{T}] = diag [1 \times 10^{- 2}, 1 \times 10^{- 2}, 1 \times 10^{- 2}, 1 \times 10^{- 2}] 。 \end{matrix}$ 假设系统过程噪声和量测噪声为零均值高斯白噪声 $\begin{matrix} w~ (0, Q_{k}), v~ (0, R_{k}), \end{matrix}$ 协方差阵分别为 $\begin{matrix} Q = diag [q_{i_{α}}, q_{i_{β}}, q_{ω_{r}}, q_{θ_{r}}], R = diag [r_{ω_{r}}, r_{θ_{r}}] 。 \end{matrix}$

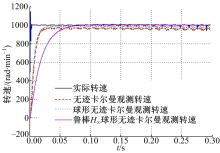
假定无迹卡尔曼滤波器、球形无迹卡尔曼滤波器与 $\begin{matrix} H_{\infty} \end{matrix}$ 鲁棒球形无迹卡尔曼滤波器仿真条件相同, 定子电阻真实值R_s=1.3 Ω , 量测值存在偏差为 $\begin{matrix} \hat{R} \end{matrix}$ _s=1.4 Ω , 定子电感L_s=0.000 835 H, 转子磁链ψ _f=0.175 Wb, 3种曼滤波器过程噪声和量测噪声协方差阵为 $\begin{matrix} Q = diag [1 \times 10^{- 3}, 1 \times 10^{- 3}, 1 \times 10^{- 3}, 1 \times 10^{- 3}], R = diag [1 \times 10^{- 3}, 1 \times 10^{- 3}] 。 \end{matrix}$

6.2 仿真结果

电机实际转速曲线、无迹卡尔曼滤波器、球形无迹卡尔曼滤波器和 $\begin{matrix} H_{\infty} \end{matrix}$ 鲁棒球形无迹卡尔曼转速曲线如图2~图4所示, 其中图2、图3为实际转速曲线及3种滤波器局部稳态波形曲线, 图4为转速误差曲线。

	Figure Option View Download New Window
	图2 转速观测曲线Fig.2 Speed observation curve

	Figure Option View Download New Window
	图3 局部稳态波形曲线Fig.3 Partial steady wave curve

	Figure Option View Download New Window
	图4 转速误差曲线Fig.4 Speed error curve

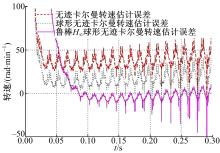
从图2~图4可以看出, 系统设定转速为1000 rad/min, 达到稳态值时, 实际转速存在波动, 分析原因是直接转矩控制依赖定子电阻, 定子电阻的量测值与真实值存在误差, 故转速波动。同时, 无迹卡尔曼滤波器和球形无迹卡尔曼滤波器在稳态时观测转速均出现较大振荡, 系统误差曲线表明二者的观测误差较大, 而 $\begin{matrix} H_{\infty} \end{matrix}$ 鲁棒球形无迹卡尔曼滤波器在稳态时转速振荡比前两者明显小很多, 稳态误差曲线的误差很小, $\begin{matrix} H_{\infty} \end{matrix}$ 鲁棒球形无迹卡尔曼滤波器的观测误差非常近似实际转速, 有非常好的观测效果。系统在定子电阻变化情况下, 观测器仍然可以保证较好的观测性能。在初始阶段无迹卡尔曼滤波器和球形无迹卡尔曼滤波器收敛得较快, 在系统稳态值时误差均方根值分别为40.6011、19.9747, 而 $\begin{matrix} H_{\infty} \end{matrix}$ 鲁棒球形无迹卡尔曼滤波器收敛较比二者慢(7.0619), 分析误差均方根值, 时间段取值范围t=[0.15 0.3]。

在电机实际运行时, 定子电阻随温度变化而变化, 为了验证 $\begin{matrix} H_{\infty} \end{matrix}$ 鲁棒球形无迹卡尔曼滤波器的非线性处理能力和观测器的鲁棒性, 图5给出不同边界性能的转速误差曲线, 表1给出不同性能边界 $\begin{matrix} θ \end{matrix}$ 的系统误差均方根值表。

	Figure Option View Download New Window
	图5 不同边界性能的转速误差曲线Fig.5 Speed error curve of different boundary properties

表1 不同性能边界θ 误差均方根值 Table 1 Performance of different boundary error RMS

$\begin{matrix} θ \end{matrix}$ 值	速度均方根误差	$\begin{matrix} θ \end{matrix}$ 值	速度均方根误差
2	—	0.3	8.154
10	—	0.5	11.128
0.001	7.062	0.7	17.995
0.2	7.494	1	43.162

表1 不同性能边界θ 误差均方根值 Table 1 Performance of different boundary error RMS

从表1可以看出, 在 $\begin{matrix} θ > 1 \end{matrix}$ 时, 系统不能正常运行, 究其原因是系统协方差阵失去正定性, 在 $\begin{matrix} θ \in (0, 1), \end{matrix}$ 转速观测误差均方根植较小, 边界范围越小, 系统鲁棒性越强, 速度均方根误差越小, 边界范围越大, 系统鲁棒性越弱, 速度均方根误差越大。当 $\begin{matrix} θ = 1 \end{matrix}$ 观测值接近无迹卡尔曼滤波器。

7 结论

(1) $\begin{matrix} H_{\infty} \end{matrix}$ 鲁棒球形无迹卡尔曼滤波器能较好解决永磁同步电机转速非线性模型的状态观测问题。

(2) $\begin{matrix} H_{\infty} \end{matrix}$ 鲁棒球形无迹卡尔曼滤波器相比于无迹卡尔曼滤波器、球形无迹卡尔曼滤波器对转速观测误差较小, 系统误差均方值也较小, 可以提高非线性系统观测性能。在性能边界较小时, 可以提高系统鲁棒性。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	宋舒, 龚建国, 林薇, 等. 纯电动汽车用永磁同步电机空间矢量控制系统建模与仿真[J]. 武汉理工大学学报, 2012, 34(4): 118-122, 140. Song Shu, Gong Jian-guo, Lin Wei, et al. Modeling and simulation of space vector control system for pure electric vehicle driven by permanent magnet synchronous motor[J]. Journal of Wuhan University of Technology, 2012, 34(4): 118-122, 140. [本文引用:1]
[2]	王高林, 杨荣峰, 于泳, 等. 内置式永磁同步电机无位置传感器控制[J]. 中国电机工程学报, 2010, 30(30): 93-98. Wang Gao-lin, Yang Rong-feng, Yu Yong, et al. Position sensorless control for interior permanent magnet synchronous motor[J]. Proceedings of the CSEE, 2010, 30(30): 93-98. [本文引用:1]
[3]	Simon D. Optimal State Estimation: Kalman, H Infinity, and Nonlinear Approaches[M]. New York: John Wiley & Sons, 2006. [本文引用:1]
[4]	肖曦, 王伟华, 吕志鹏. 一种基于增量式卡尔曼滤波器的PMSM转速滤波算法[J]. 电机与控制学报, 2014, 18(10): 104-111. Xiao Xi, Wang Wei-hua, Lyu Zhi-peng. Filtering algorithm of speed for PMSM based on incremental Kalman filter[J]. Electric Machines and Control, 2014, 18(10): 104-111. [本文引用:1]
[5]	曲智勇, 姚郁, 韩俊伟. 基于改进型平方根UKF算法的永磁同步电机状态估计[J]. 电机与控制学报, 2009, 12(3): 452-457. Qu Zhi-yong, Yao Yu, Han Jun-wei. State estimation of permanent magnet synchronous motor using modified square root UKF algorithm[J]. Electric Machines and Control, 2009, 12(3): 452-457. [本文引用:1]
[6]	郑泽东, 李永东, Fadel Maurice. 基于EKF的PMSM无机械传感器矢量控制[J]. 清华大学学报: 自然科学版, 2009, 58(10): 1585-1588. Zheng Ze-dong, Li Yong-dong, Fadel Maurice. PMSM mechanical sensor-less vector control based on extended Kalman filter[J]. Journal of Tsinghua University (Science and Technology), 2009, 58(10): 1585-1588. [本文引用:1]
[7]	Julier S J, Uhlmann J K. Unscented filtering and nonlinear estimation[J]. Proceedings of the IEEE, 2004, 92(3): 401-422. [本文引用:1]
[8]	杨萌, 郝燕玲, 高伟. 基于SSUKF的粒子滤波算法研究[J]. 哈尔滨工程大学学报, 2010, 32(5): 601-606. Yang Meng, Hao Yan-ling, Gao Wei. A particle filter algorithm based on a spherical simplex unscented Kalman filter[J]. Journal of Harbin Engineering University, 2010, 32(5): 601-606. [本文引用:1]
[9]	Julier S J, Uhlmann J K. New extension of the Kalman filter to nonlinear systems[C]∥AeroSense International Society for Optics and Photonics, Orland o, 1997: 182-193. [本文引用:1]

2012

0.0

. 2012, 34(4):118-122,140 DOI:doi:10.3963/j.issn.1671-4431.2012.04.026

Modeling and simulation of space vector control system for pure electric vehicle driven by permanent magnet synchronous motor

纯电动汽车用永磁同步电机空间矢量控制系统建模与仿真

Song Shu , Gong Jian-guo , Lin Wei

宋舒, 龚建国, 林薇

在分析小型纯电动汽车动力学方程和永磁同步电机PMSM数学模型的基础上,建立PMSM驱动汽车的数学模型,并利用空间矢量脉宽调制技术和模糊PID控制算法设计了车速电流双闭环控制系统,以驱动汽车变速运行.在Matlab 7.6/Simulink环境下搭建了纯电动汽车车速-电流双闭环控制系统动态仿真模型,依据行驶需求对电动汽车在某档位的车速与转矩进行了仿真分析,并对控制策略进行了静、动态性能验证.仿真结果表明:该系统具有响应速度快、精度高、抗干扰能力强等优点,为实际纯电动汽车驱动控制系统的分析与设计提供了新的思路.

... 0 引言永磁同步电机(PMSM)^[1]转速观测状态方程常采用电流模型或者磁链模型,二者都具有较强的非线性,观测器的设计通常采用扩展卡尔曼滤波器或滑膜变结构进行估计^[2] ...

2010

0.0

. 2010, 30(30):93-98 DOI:doi:10.3969/j.issn.1673-6540.2009.09.005

Position sensorless control for interior permanent magnet synchronous motor

内置式永磁同步电机无位置传感器控制

Wang Gao-lin , Yang Rong-feng , Yu Yong

王高林, 杨荣峰, 于泳

A hybrid observer was proposed for position sensorless vector controlled interior permanent magnet synchronous motor (IPMSM) to achieve wide speed range operation. The observer combined sliding-mode observer with high frequency voltage signal injection. Sliding-mode observer based on extended electromotive force of IPMSM was designed. Digital filter and software phase locked loop (PLL) for signal injection were analyzed. Transient control method was proposed to ensure tracking synchronization of the PLL. To resolve starting problem of IPMSM, practical initial position estimation was adopted. High frequency voltage signal was injected to obtain magnet pole position. Then voltage pulse vectors were injected to identify magnet polarity. Experimental results demonstrate the feasibility of the control strategy by a position sensorless IPMSM vector controlled system.

针对无位置传感器内置式永磁同步电机(interior permanent magnet synchronous motor，IPMSM)矢量控制系统，通过将滑模观测器和高频电压信号注入法相结合，提出一种可实现在宽调速范围获取准确转子位置信息的混合观测方案。设计基于扩展反电动势模型的滑模观测器，对高频信号注入的滤波器和软件锁相环进行研究，并给出混合观测器的切换控制方法，以保证切换过程锁相环跟踪的同步性。针对无传感器IPMSM系统起动困难的问题，研究了一种初始位置估计方法，先注入高频信号检测磁极位置，再注入脉冲电压矢量来判断极性。最后通过IPMSM无位置传感器矢量控制系统验证了该控制策略的有效性。

2006

0.0

... 文献[3]介绍了卡尔曼滤波算法的特点,文献[4,5,6]对卡尔曼滤波算法在PMSM转速观测器中应用做了详细介绍 ...

2014

0.0

. 2014, 18(10):104-111 DOI:doi:10.3969/j.issn.1007-449X.2014.10.016

Filtering algorithm of speed for PMSM based on incremental Kalman filter

一种基于增量式卡尔曼滤波器的PMSM转速滤波算法

Xiao Xi , Wang Wei-hua , Lyu Zhi-peng.

肖曦, 王伟华, 吕志鹏

为了滤除永磁同步电机转子转速测量环节存在的量化误差等噪声,提出一种基于增量式卡尔曼滤波器的转子转速滤波算法。该算法通过两个相邻周期的离散运动方程相减的方式消除负载转矩项,根据卡尔曼滤波器原理,推导出基于增量式卡尔曼滤波器的永磁同步电机转子转速滤波算法,并与低通滤波器的滤波效果进行比较分析。研究表明,基于增量式卡尔曼滤波器的滤波算法可以在不带来延时的前提下有效滤除转速测量噪声,并且计算负荷显著减少,对电机参数依赖度低。仿真和实验结果验证了所提算法的有效性。

... 文献[3]介绍了卡尔曼滤波算法的特点,文献[4,5,6]对卡尔曼滤波算法在PMSM转速观测器中应用做了详细介绍 ...

2009

0.0

. 2009, 12(3):452-457 DOI:doi:10.3969/j.issn.1007-449X.2009.03.026

State estimation of permanent magnet synchronous motor using modified square root UKF algorithm

基于改进型平方根UKF算法的永磁同步电机状态估计

Qu Zhi-yong , Yao Yu , Han Jun-wei.

曲智勇, 姚郁, 韩俊伟

针对永磁同步电机驱动系统的状态估计问题,提出一种改进型平方根UKF(SRUKF)的状态估计算法.为避免增加sigma点带来的计算量大问题,依据UT变换理论,采用超球体单形采样方法,使得sigma点的数量减少,从而在与SRUKF算法估计精度相当的情况下,计算量大大减少.考虑系统的非线性,采用SRUKF估计方法研究系统的状态估计问题,避免了扩展卡尔曼滤波(EKF)产生的线性化误差.同时在滤波过程中采用Cholesky和QR分解,以协方差平方根阵代替协方差阵参加迭代运算,有效地避免了滤波器的发散,提高了滤波算法的收敛速度和稳定性.仿真表明,与EKF、SRUKF估计方法相比,该方法能减少估计过程中的计算量,提高估计精度.

... 文献[3]介绍了卡尔曼滤波算法的特点,文献[4,5,6]对卡尔曼滤波算法在PMSM转速观测器中应用做了详细介绍 ...

2009

0.0

. 2009, 58(10):1585-1588

PMSM mechanical sensor-less vector control based on extended Kalman filter

基于EKF的PMSM无机械传感器矢量控制

Zheng Ze-dong , Li Yong-dong , Fadel Maurice.

郑泽东, 李永东

摘　要：为了准确估计永磁同步电机（PMSM）的转子位置和转速，并实现无机械传感器矢量控制，提出了一种基于扩展Kalman滤波器（EKF）的转子位置和转速观测器，适合于求解永磁同步电机的非线性方程。观测器状态方程采用转子磁链定向的同步旋转坐标系下的电压方程，电感等参数为常数，可以应用于凸极机和隐极机。对扩展Kalman滤波器进行了算法简化，使它可以实用化。把负载转矩作为状态变量，观测器可以同时观测负载转矩，并把观测转矩用作前馈补偿，提高了系统的动态性能。通过实验验证了系统的性能。

... 文献[3]介绍了卡尔曼滤波算法的特点,文献[4,5,6]对卡尔曼滤波算法在PMSM转速观测器中应用做了详细介绍 ...

2004

0.0

... 同时扩展卡尔曼滤波器要求对原系统求取雅可比矩阵,在实际使用时,有些模型很难求得雅可比矩阵^[7],降低了使用范围 ...

2010

0.0

. 2010, 32(5):601-606 DOI:doi:10.3969/j.issn.1006-7043.2010.05.010

A particle filter algorithm based on a spherical simplex unscented Kalman filter

基于SSUKF的粒子滤波算法研究

Yang Meng , Hao Yan-ling , Gao Wei.

杨萌, 郝燕玲, 高伟

针对粒子滤波的退化现象、样本贫化问题以及标准无迹粒子滤波(UPF)算法计算量偏大的缺陷,利用基于超球面采样变换(SSUT)的UKF算法产生重要性概率密度函数,与序贯重要性再采样(SIR)结合,并引入粒子群优化,形成一种新的粒子滤波算法.对称分布UT变换的sigma点为2n+1个,而SSUT变换为n+2个.新算法利用SSUT变换减少了采样点的个数,通过混合建议分布进一步减少了计算量,使计算效率得到了明显的改善.仿真结果表明,该算法滤波精度优于扩展卡尔曼粒子滤波,而与标准UPF相当,计算效率明显高于标准UPF算法.

... 为了克服参数变化对观测值影响,增加系统鲁棒性能,本文将球形无迹变换(ST)^[8]、无迹卡尔曼滤波器(UKF)^[9]与非线性 H∞鲁棒滤波器结合起来形成性能更为优良的非线性 H∞鲁棒球形无迹卡尔曼滤波器(HSUKF),既可以实现对非线性系统进行观测,又能增强系统鲁棒性并抑制异常观测值的影响 ...

1997

0.0