汽车自适应巡航线性参变间距控制算法

引用本文

高振海, 严伟, 李红建, 王大志, 王林. 汽车自适应巡航线性参变间距控制算法.吉林大学学报:工学版, 2016, 46(4): 1023-1029
GAO Zhen-hai, YAN Wei, LI Hong-jian, WANG Da-zhi, WANG Lin. Design of linear parametrically varying headway control algorithm for ACC vehicles. Journal of Jilin University Engineering and Technology Edition, 2016, 46(4): 1023-1029 复制到剪切板

Permissions

汽车自适应巡航线性参变间距控制算法

高振海¹, 严伟¹, 李红建², 王大志³, 王林³

1.吉林大学汽车仿真与控制国家重点实验室,长春 130022

2.中国第一汽车集团公司技术中心,长春 130011

3.上海汽车集团股份有限公司安全工程与虚拟技术部,上海 200041

作者简介:高振海(1973-),男,教授,博士生导师.研究方向:车辆动力学控制,驾驶员操作行为及智能交通系统.E-mail:gaozh@jlu.edu.cn

基金:吉林省科技引导计划项目(20130413058GH); 上海市科学技术委员会项目(13QB1402300); 高等学校博士学科点专项科研基金项目(20120061110028)

摘要

为满足驾驶员对汽车自适应巡航控制系统的个性化安全车间距设计的需求,采用 H_∞理论设计了线性参变间距控制算法。考虑到驾驶员自主设定车头时距带来的控制系统动态不确定性问题,采用线性参变模型描述本车与前车间的相对运动学特性,并通过加速度限值抑制了控制输入饱和且改善了乘坐舒适性。基于 H_∞控制理论并根据时距动态变化实现了对控制器参数的实时调整和汽车纵向动力学的非线性控制。典型仿真工况及其与动态面控制算法的性能对比性分析表明,本文算法可实现驾驶员对车头时距的个性化设定,同时也避免了时距和车辆状态离散变化甚至跳变带来的瞬态跟随性能恶化。

关键词: 车辆工程; 自适应巡航控制; 车头时距模型; 线性参变间距控制; 控制输入饱和; 驾驶员

中图分类号:U461 文献标志码:A 文章编号:1671-5497(2016)04-1023-07

Design of linear parametrically varying headway control algorithm for ACC vehicles

GAO Zhen-hai¹, YAN Wei¹, LI Hong-jian², WANG Da-zhi³, WANG Lin³

1.State Key Laboratory of Automotive Simulation and Control,Jilin University,Changchun 130022,China

2.Research and Development Center, China FAW Group Corporation,Changchun 130011,China

3.Department of Safefy Engineering & Virtual Technology, SAIC Motor Corporation Limited, Shanghai 200041,China

Abstract

An individual linear parametrically varying headway control algorithm is designed based on H_∞ concept for Adaptive Cruise Control (ACC) systems. The relative kinematics between the host vehicle and the preceding vehicle is represented using a linear parametrically varying model considering the uncertainty owing to the time gap set by drivers dynamically. The longitudinal acceleration is restrained under control input saturation and the passenger comfort is improved。 Furthermore, the controller gains are tuned in real time according to the dynamic time gap based on H_∞ concept and the nonlinear longitudinal dynamics controller is designed. Finally, the designed algorithm is validated under a typical condition and compared with the existing Dynamic Surface Controller (DSC). The results show that the individual setting of the time gap is achieved via the linear parametrically varying headway control algorithm, the deterioration of transient following performance for the sake of discrete variation of the time gap and automotive states is avoided.

Keyword: vehicle engineering; adaptive cruise control; constant time headway model; linear parametrically varying headway control; control input saturation; driver

Show Figures

0 引言

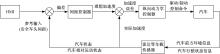
汽车自适应巡航控制(Adaptive cruise control, ACC)是在现有产品车型上业已装配的汽车驱动和制动主动控制系统基础上, 基于加装的雷达等车载传感器探测本车与其行驶车道上的前方它车等有效目标之间的相对距离、速度等相对运动状态, 并考虑本车加速驱动和减速制动极限能力、驾驶员对安全性、舒适性及燃油经济性等多性能指标的协调权衡等因素, 建立的以保持安全车头间距为目标、以本车与行驶车道内的前方目标车相对运动状态为输入、以本车期望纵向加速度或速度为输出的系统控制器, 最终向汽车驱动和制动主动控制系统提供预期控制指令且依靠其执行机构实现精确跟随控制^[1]。

如何开发安全车头间距控制器是ACC系统设计的关键问题, 研究人员相继提出基于固定时间间隔或距离间隔等车头间距特征值的定常时距(Constant time headway, CTH)^[2]、定常距离^[3]、定常安全因子间距策略^[4]及二阶时距策略^[5]等安全车头间距策略。以上研究(也是目前市场上产品车型选配的ACC系统的主流技术路线)大多是事先确定出几个可供驾驶员选择的车头时距或车头间距等参数且允许驾驶员通过ACC人机交互界面(Human machine interface, HMI)在这些固化好的参数中选择出一个最适合其驾驶行为个性的参数。汽车厂家在设计研发阶段也是根据该固定参数调校出效果良好的ACC车头间距控制器。

近年来, 伴随着汽车产品设计越来越强调驾驶体验感, 固定参数的车头间距控制策略难以更好地适应不同驾驶员操控行为的个性化需求, 也限制了驾乘人员对ACC产品的心理接受程度。为此, 研究人员提出驾驶员可以根据其个性化操控特点而动态调整时距的研究构想。由此引发的新技术问题是由于无法提前预知驾驶员对车头间距的动态设定值, 因此要求车头间距控制器可实时在线调整控制参数^[6]。Baek等^[7]应用含有输入整形滤波器的动态面控制(Dynamic surface control, DSC)算法设计了速度控制器和距离控制器。

本文针对驾驶员自行动态设定车头间距带来的控制器实时参数调整问题, 首先采用线性参变(Linear parametrically varying, LPV)模型描述本车与前方目标车之间的相对速度和距离误差依赖于时距参数的线性变化特性, 并考虑到汽车的驱动和制动极限能力, 通过加速度限值抑制了控制输入饱和; 然后, 针对驾驶员动态调整时距参数引起的以上模型参数时变问题, 基于鲁棒控制理论建立了LPV间距控制算法, 实现了根据车头时距动态变化来实时调节控制器参数, 避免了车头时距和车辆状态离散变化甚至跳变带来的瞬态跟随性能恶化问题; 最后, 进行了典型工况下的算法仿真分析, 并与DSC算法进行了控制性能的对比分析。

1 线性参变(LPV)模型

1.1 车间运动学关系及其状态方程描述

ACC系统的总体框图如图1所示, 本文的核心部分是设计间距控制器, 在这之前需要建立面向控制器设计的模型, 即本车与前方目标车的相对运动学关系模型— — LPV模型, 可以利用相对速度、相对距离及两车各自的运动状态来描述, 其车间运动学状态方程如下:

$\begin{matrix} \overset{\cdot}{x} (t) = Ax (t) + Ew (t) + Bu (t) \end{matrix}$ (1)

式中: $\begin{matrix} x (t) = {[\begin{matrix} Δd & Δv & a_{f} \end{matrix}]}^{T}, a_{f} 是本车加速度; u (t) = a_{des}; w (t) = a_{p}, a_{p} \end{matrix}$ 是目标车加速度;

$\begin{matrix} A = [\begin{matrix} 0 & 1 & - t_{g} \\ 0 & 0 & - 1 \\ 0 & 0 & - \frac{1}{T} \end{matrix}]; B = [\begin{matrix} 0 \\ 0 \\ \frac{1}{T} \end{matrix}]; E = [\begin{matrix} 0 \\ 1 \\ 0 \end{matrix}] 。 \end{matrix}$

式中: $\begin{matrix} Δd = d - d_{des} \end{matrix}$ 为车头间距误差, 其中, $\begin{matrix} d \end{matrix}$ 为实际车头间距, $\begin{matrix} d_{des} \end{matrix}$ 为期望车头间距, 即:

$\begin{matrix} d_{des} = t_{g} v_{f} + d_{0} \end{matrix}$ (2)

式中: $\begin{matrix} t_{g} \end{matrix}$ 和 $\begin{matrix} d_{0} \end{matrix}$ 分别为车头时距和车间最小安全距离; $\begin{matrix} v_{f} \end{matrix}$ 是ACC车速度。

令 $\begin{matrix} Δv = v_{p} - v_{f} \end{matrix}$ 为相对速度, 其中, $\begin{matrix} v_{p} \end{matrix}$ 是目标车速度。

通常情况下, 考虑到汽车纵向动力学响应延迟, 即 $\begin{matrix} a_{f} \end{matrix}$ 跟踪期望纵向加速度 $\begin{matrix} a_{des} \end{matrix}$ 存在一定滞后, 采用如下的一阶惯性环节描述二者的关系^[2]:

$\begin{matrix} {\overset{\cdot}{a}}_{f} = \frac{1}{T} (- a_{f} + a_{des}) \end{matrix}$ (3)

式中: $\begin{matrix} T \end{matrix}$ 是汽车纵向动力学的延迟, 本文中T=0.45 s。

	Figure Option View Download New Window
	图1 ACC系统总体框图Fig.1 Block diagram of ACC systems

1.2 带输入饱和约束的车间LPV模型

以上的状态空间方程实质上是建立了一个描述本车与目标车之间的相对速度和距离误差依赖于时距参数线性变化的车间相对运动学线性模型。当采用定常时距控制时, $\begin{matrix} t_{g} \end{matrix}$ 为一常数, 式(1)是一个线性定常系统。而当允许驾驶员动态调整时距时, $\begin{matrix} t_{g} \end{matrix}$ 即为一时变参数, 从而导致车间相对运动状态空间的动态不确定性。

考虑到驾驶员在线调整时距参数带来的车间相对运动学模型参数时变性, 本文在前述的车间运动学状态方程基础上, 进一步引入LPV模型来描述基于动态不确定性时距参数的车间相对运动状态^[8]。

LPV模型通常定义为^[9]:

$\begin{matrix} \overset{\cdot}{x} (t) = A (ρ) x (t) + B (ρ) u (t) \end{matrix}$

式中: $\begin{matrix} ρ \end{matrix}$ 为外部可测参数。该模型与线性定常系统模型的区别在于其系统矩阵线性依赖于参数 $\begin{matrix} ρ, \end{matrix}$ 即LPV模型的动态特性依赖于参数 $\begin{matrix} ρ 。 \end{matrix}$ 从而可以更好地描述非线性系统或时变系统的动态性能。

根据车间相对运动状态及式(1)描述, 可以建立基于动态不确定性时距参数的车间LPV模型如下:

$\begin{matrix} \overset{\cdot}{x} (t) = A (t_{g}) x (t) + Ew (t) + Bu (t) \end{matrix}$ (4)

式中:矩阵 $\begin{matrix} A (t_{g}) \end{matrix}$ 依赖于时距 $\begin{matrix} t_{g}, \end{matrix}$ 而 $\begin{matrix} t_{g} \end{matrix}$ 是不同驾驶员根据自身喜好在 $\begin{matrix} Θ = [t_{gmin}, t_{gmax}] \end{matrix}$ 内动态设定的参数, $\begin{matrix} t_{gmin} = 1 s, t_{gmax} = 2.5 s 。 \end{matrix}$ 根据 $\begin{matrix} t_{g} \end{matrix}$ 的上、下界将 $\begin{matrix} A (t_{g}) \end{matrix}$ 描述为线性组合的形式, 即:

$\begin{matrix} A (t_{g}) = \overset{2}{\sum_{i = 1}} h_{i} A_{i} \end{matrix}$

式中: $\begin{matrix} \begin{matrix} A_{1} = [\begin{matrix} 0 & 1 & - 1 \\ 0 & 0 & - 1 \\ 0 & 0 & - \frac{1}{T} \end{matrix}]; A_{2} = [\begin{matrix} 0 & 1 & - 2.5 \\ 0 & 0 & - 1 \\ 0 & 0 & - \frac{1}{T} \end{matrix}]; \\ h_{1} = \frac{t_{gmax} - t_{g}}{t_{gmax} - t_{gmin}}; h_{2} = \frac{t_{g} - t_{gmin}}{t_{gmax} - t_{gmin}}; h_{i} > 0, i = 1, 2, h_{1} + h_{2} = 1 。 \end{matrix} \end{matrix}$

同时, 考虑到汽车自身驱动和制动系统的纵向运动学性能约束, 本文在LPV模型中引入的汽车纵向加速度限值抑制了控制输入饱和, 降低了汽车纵向运动对驾驶员乘坐舒适性的影响^[10]。

$\begin{matrix} sat (u (t)) \end{matrix}$ 是引入的输入饱和约束项, 其具体形式如下^[11]:

$\begin{matrix} sat (u (t)) = \{\begin{matrix} u_{\min}, u (t) \leq u_{\min} \\ u (t), u_{\min} < u (t) \leq u_{\max} \\ u_{\max}, u (t) > u_{\max} \end{matrix} \end{matrix}$

式中: $\begin{matrix} u_{\min} \leq u (t) \leq u_{\max}, u_{\max} \end{matrix}$ 和 $\begin{matrix} u_{\min} \end{matrix}$ 分别为舒适性期望纵向加速度的上、下界。为了简化设计, 令 $\begin{matrix} u_{\max} = - u_{\min} 。 \end{matrix}$ 由于纵向加速度在[-2.5, 2.5] m/s²内可以保证乘坐舒适性^[12], 本文中设定u_max=2.5 m/s²。

考虑到时距的时变性以及汽车的驱动和制动极限能力, 对期望纵向加速度加以舒适性约束, 引入约束后的公式如下:

$\begin{matrix} \overset{\cdot}{x} (t) = A (t_{g}) x (t) + Ew (t) + Bsat (u (t)) \end{matrix}$ (5)

由于 $\begin{matrix} ‖ sat (u (t)) - \frac{1 + ε}{2} u (t) ‖ \leq \frac{1 - ε}{2} ‖ u (t) ‖, 0 < ε < 1, 有 u_{\min} / ε \leq u (t) \leq u_{\max} / ε 。 \end{matrix}$

综上所述, 最终建立的基于LPV模型和带输入饱和约束的车间运动学状态方程如下:

$\begin{matrix} \begin{matrix} \overset{\cdot}{x} (t) = A (t_{g}) x (t) + \frac{1 + ε}{2} Bu (t) + Ew (t) + \\ B (sat (u (t)) - \frac{1 + ε}{2} u (t)) \end{matrix} \end{matrix}$ (6)

2 基于

\begin{matrix} H_{\infty} \end{matrix}

理论的ACC算法设计

前述建立的描述本车与目标车相对运动学关系的LPV模型依赖于时距 $\begin{matrix} t_{g}, \end{matrix}$ 是一个非线性的含有控制饱和的模型, 无法利用线性控制理论得到满意的控制性能。同时, 目标车运动状态的变化也相当于对该模型加入了一个外部干扰。

针对以上问题, 本文基于 $\begin{matrix} H_{\infty} \end{matrix}$ 控制技术, 建立了基于Lyapunov函数方法的车间LPV模型的 $\begin{matrix} H_{\infty} \end{matrix}$ 间距控制算法。

2.1 问题描述

LPV间距控制器形式如下:

$\begin{matrix} \begin{matrix} u (t) = K (t_{g}) x (t) (7) \\ 其中 : \\ K (t_{g}) = \overset{2}{\sum_{j = 1}} h_{j} K_{j} = [\begin{matrix} k_{1} (t_{g}) & k_{2} (t_{g}) & k_{3} (t_{g}) \end{matrix}], \end{matrix} \end{matrix}$

是待设计的控制器增益。 $\begin{matrix} h_{1} \end{matrix}$ 和 $\begin{matrix} h_{2} \end{matrix}$ 是 $\begin{matrix} t_{g} \end{matrix}$ 的线性函数, 因此 $\begin{matrix} k_{i} (t_{g}) (i = 1, 2, 3) \end{matrix}$ 是 $\begin{matrix} t_{g} \end{matrix}$ 的线性函数。

结合式(6)(7)得到闭环系统:

$\begin{matrix} \{\begin{matrix} \overset{\cdot}{x} (t) = \tilde{A} (t_{g}) x (t) + Ew (t) + \\ B (sat (u (t)) - \frac{1 + ε}{2} K (t_{g}) x (t)) \\ z (t) = Cx (t) \end{matrix} (8) \end{matrix}$

式中: $\begin{matrix} \tilde{A} (t_{g}) = A (t_{g}) + \frac{1 + ε}{2} BK (t_{g}); z (t) \end{matrix}$ 是受调输出; $\begin{matrix} C = I_{3}, \end{matrix}$ 其中 $\begin{matrix} I_{3} \end{matrix}$ 表示3维单位矩阵。

设计如(7)形式的LPV控制器, 闭环系统(8)必须满足以下性质^[13]:①在外部干扰为0时, 闭环系统(8)是渐近稳定的; ②初始状态为0, 外部干扰不为0时, 受调输出对于外部干扰有一个给定的干扰抑制水平 $\begin{matrix} γ \end{matrix}$ , 即:

$\begin{matrix} ‖ z (t) ‖ \leq γ ‖ w (t) ‖ (9) \end{matrix}$

通过如上推导, 本文将ACC系统时距动态变化情况下间距控制算法转化为一个LPV $\begin{matrix} H_{\infty} \end{matrix}$ 控制算法的设计问题。

2.2 LPV间距控制算法设计

基于Lyapunov函数方法设计了面向车间LPV模型的LPV $\begin{matrix} H_{\infty} \end{matrix}$ 间距控制算法。

定义公共Lyapunov函数 $\begin{matrix} V (x (t)) = x^{T} (t) Px (t), P = P^{T} > 0 。 \end{matrix}$ 利用二次稳定性理论, 可以得到 $\begin{matrix} H_{\infty} \end{matrix}$ 控制算法存在的充分条件为^{[11, 13]}。

$\begin{matrix} [\begin{matrix} {\tilde{A}}^{T} (t_{g}) P + P \tilde{A} (t_{g}) + α & PE & C^{T} \\ * & - γ I_{1} & 0 \\ * & * & - I_{3} \end{matrix}] < 0 \end{matrix}$ (10)

式中: $\begin{matrix} α = PB B^{T} P + b^{2} K^{T} (t_{g}) K (t_{g}) 。 \end{matrix}$

定义 $\begin{matrix} Q = P^{- 1}, Y_{i} = K_{i} Q (i = 1, 2), \end{matrix}$ 对式(10)同时左乘和右乘 $\begin{matrix} diag \{\begin{matrix} Q & I_{1} & I_{3} \end{matrix}\}, \end{matrix}$ 利用Schur补的性质得到式(11)^[13]:

$\begin{matrix} \begin{matrix} [\begin{matrix} A_{i} Q + aB Y_{i} + Q {A^{T}}_{i} + a {Y^{T}}_{i} B^{T} & E & Q C^{T} & B & b {Y^{T}}_{i} \\ * & - γ I_{1} & 0 & 0 & 0 \\ * & * & - I_{3} & 0 & 0 \\ * & * & * & - I_{1} & 0 \\ * & * & * & * & - I_{1} \end{matrix}] < 0, \\ i = 1, 2 (11) \end{matrix} \end{matrix}$

另外, 由 $\begin{matrix} |u (t)| = |K (t_{g}) x (t)| \leq u_{\max} / ε \end{matrix}$ 可得到:

$\begin{matrix} [\begin{matrix} c & Y_{i} \\ * & Q \end{matrix}] > 0, i = 1, 2 \end{matrix}$ (12)

式中: $\begin{matrix} a = \frac{1 + ε}{2}, b = \frac{1 - ε}{2}, c = {(\frac{u_{\max}}{ε})}^{2} 。 \end{matrix}$

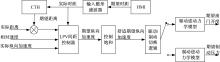
若式(11)与式(12)有解, 那么闭环系统是渐近稳定的而且外部干扰 $\begin{matrix} w \end{matrix}$ 到受调输出 $\begin{matrix} z \end{matrix}$ 有一个给定的 $\begin{matrix} H_{\infty} \end{matrix}$ 干扰抑制水平 $\begin{matrix} γ \end{matrix}$ 。

2.3 纵向动力学控制算法设计

如图2所示, 纵向动力学控制器包括三个部分:驱动控制器、制动控制器以及二者间的切换逻辑^[14]。为了有效补偿汽车纵向动力学的强非线性、强不确定性以及时变性等特性, 设计了驱动和制动系统的逆纵向动力学模型。

同时, 考虑到驾驶员对时距的随机输入导致的系统振荡问题, 采用了一个输入整形滤波器处理驾驶员动态设定的时距, 得到光滑的期望距离作为参考输入(见图2)。

	Figure Option View Download New Window
	图2 LPV间距控制算法Fig.2 LPV headway controller

2.3.1 驱动控制算法

假设忽略发动机和轮胎惯量, 而且液力变矩器锁死, 汽车的力平衡方程为^[15]:

$\begin{matrix} m a_{f} = F_{d} - F_{r} - F_{a} - F_{g} - F_{b} \end{matrix}$ (13)

式中: $\begin{matrix} m \end{matrix}$ 为汽车质量; $\begin{matrix} F_{b} 为路面作用于汽车的制动力。 F_{d} 、 F_{r} 、 F_{a} 、 F_{g} \end{matrix}$ 分别为汽车的驱动力、滚动阻力、空气阻力及坡度阻力。

汽车驱动力计算公式如下:

$\begin{matrix} F_{d} = \frac{T_{tq} i_{g} i_{0} η_{T}}{r} \end{matrix}$

式中: $\begin{matrix} T_{tq} \end{matrix}$ 为发动机转矩; $\begin{matrix} i_{g} \end{matrix}$ 为变速器的传动比; $\begin{matrix} i_{0} \end{matrix}$ 为主减速器的传动比; $\begin{matrix} η_{T} \end{matrix}$ 为的传动系的机械效率。本文采用了一个简化的依赖于发动机转速 $\begin{matrix} n \end{matrix}$ 和油门开度 $\begin{matrix} δ \end{matrix}$ 的经验发动机模型, 即 $\begin{matrix} T_{tq} = T_{e, map} (δ, n) 。 \end{matrix}$

滚动阻力计算公式如下:

$\begin{matrix} F_{r} = mgfcosα \end{matrix}$

式中: $\begin{matrix} f \end{matrix}$ 为滚动阻力系数; $\begin{matrix} g \end{matrix}$ 为重力加速度; $\begin{matrix} α \end{matrix}$ 为坡道角。

空气阻力计算公式如下:

$\begin{matrix} F_{a} = \frac{1}{2} C_{D} Aρ u_{r}^{2} \end{matrix}$

式中: $\begin{matrix} C_{D} \end{matrix}$ 为空气阻力系数; $\begin{matrix} A \end{matrix}$ 为迎风面积; $\begin{matrix} ρ \end{matrix}$ 为空气密度; $\begin{matrix} u_{r} \end{matrix}$ 为相对速度, 无风情况下 $\begin{matrix} u_{r} = v_{f} 。 \end{matrix}$

坡度阻力计算公式如下:

$\begin{matrix} F_{g} = mgsinα \end{matrix}$

驱动控制算法为驱动逆动力学模型, 即已知期望纵向加速度求解油门开度。求解式(13)得到期望发动机转矩 $\begin{matrix} T_{tqdes} \end{matrix}$ 后, 通过逆运算 $\begin{matrix} δ_{des} = T_{e, map}^{- 1} (T_{tqdes}, n) \end{matrix}$ 即可得到期望油门开度δ _des。

2.3.2 制动控制算法

若汽车切换为制动刹车控制, 则节气门开度为0, 式(13)简化为:

$\begin{matrix} m a_{f} = - F_{r} - F_{a} - F_{g} - F_{b} \end{matrix}$ (14)

在不超过路面最大制动力的条件下, 制动力和制动压力可以近似视为线性关系:

$\begin{matrix} F_{b} = K_{b} p_{b} \end{matrix}$ (15)

式中: $\begin{matrix} K_{b} \end{matrix}$ 为常数, 可通过汽车动力学性能确定。

根据期望纵向加速度, 通过求解式(14)和式(15)即可得到期望制动压力p_bdes。

2.3.3 驱动/制动切换逻辑

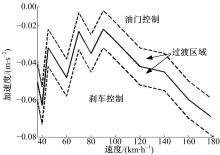
设定节气门开度为0, 在不同速度下测量汽车的最大减速度。在最大减速度-速度曲线的两侧设置一定宽度的过渡区域以改善乘坐舒适性和汽车零部件的可靠性。本文将该宽度设定为0.02 m/s²(该值可以根据实际汽车性能进行精确标定, 也体现出驾驶员自身对驱动和制动性能的了解及乘坐舒适性的考虑)。图3即为建立的驱动、制动与驱动/制动切换逻辑曲线图。

	Figure Option View Download New Window
	图3 驱动/制动切换逻辑曲线Fig.3 Switching logic curves of throttle and brake

3 仿真实验

为验证本文LPV算法在时距动态变化情况下保持安全车间距的可行性和有效性, 设计了跟随控制工况并进行了仿真分析。其中, 在汽车动力学仿真软件Carsim中搭建某国产乘用车的动力学模型, 在控制仿真软件Matlab/Simulink中搭建LPV间距控制算法以及纵向动力学控制算法。同时, 也与DSC算法^[7]进行了性能对比分析。

具体仿真工况设置如下:ACC车初始速度为25 m/s, 前方25 m处有一辆以22 m/s速度行驶的目标车; 在10 s, 前车开始减速, 直到12 m/s。时距变化曲线如图4(a)所示。

	Figure Option View Download New Window
	图4 仿真结果Fig.4 Simulation results

从图4(a)看出, 0~30 s为无驾驶员干预阶段, 30~100 s为车头时距调节阶段。由图4(b)和4(c)看出, 两种算法的车头间距和速度曲线几乎重合, 车头间距和ACC车速度分别渐进收敛到期望车头间距和目标车速度。与DSC算法相比, LPV算法的状态超调量较小。

在无驾驶员干预阶段(见图4(d)), 两种算法的加速度曲线几乎相同。但DSC算法的加速度和油门开度在ACC车加速时发生震荡, 势必会加速油门执行机构的磨损(见图4(e))。

在车头时距调节阶段, 30 s、50 s和70 s, 车头时距调大, 期望车头间距瞬时增大(见图4(b)), 而前车速度不变。由图4(c)可见, ACC车须先减速然后加速到与目标车相同速度以增加车头间距。车头时距调节过程中, LPV算法的ACC车速度最大变化量分别为5.36、4.85和4.55 km/h, 而DSC算法的ACC车速度最大变化量分别为7.06、5.68和4.98 km/h。由图4(d)可见, 与LPV相比, DSC的最大加速度和减速度均较大, 而且存在一定程度震荡, 降低了乘坐舒适性。由图4(e)可知, DSC的油门开度震荡较强, 而LPV的油门开度无震荡。由图4(f)可知, DSC的制动压力在时距调节中达到6 MPa, 而LPV的制动压力最大值分别为0.4、0.27和0.23 MPa。

4 结论

(1)LPV车头间距控制算法实现了根据车头时距动态变化来实时调节控制器参数, 从而满足了不同驾驶员对于期望距离的需求。

(2)在车头时距动态变化过程中, LPV算法的加速度和油门开度变化比较平滑, 有效抑制了控制震荡。

(3)由于引入了输入饱和约束, LPV算法的制动压力最大值分别为0.4、0.27和0.23 MPa, 控制算法在实际的可执行机构上容易实现, 且可延长制动执行机构寿命。

(4)在后续工作中, 将进一步分析驾驶员对汽车纵向速度控制的行为特性, 并在现有的ACC系统设计中引入更多驾驶员个性化因素, 以进一步提供电控系统的人性化程度和乘员接受性。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Rajamani R. Vehicle Dynamics and Control[M]. New York: Springer, 2012: 141-170. [本文引用:1]
[2]	Vibhor L, William B, Garrard L, et al. Model predictive control of transitional maneuvers for adaptive cruise control vehicles[J]. IEEE Transactions on Vehicular Technology, 2004, 53(5): 1573-1585. [本文引用:2]
[3]	Morag D. Operating policies for personal rapid transit[R]. U. S. : DOT Urban Mass Transit Administration, 1974. [本文引用:1]
[4]	Yi K, Moon I, Kwon Y. A vehicle-to-vehicle distance control algorithm for stop-and -go cruise control[C]∥IEEE Intelligent Transportation Systems Conference, Oakland , USA, 2001: 478-482. [本文引用:1]
[5]	Zhou J, Peng H. Range policy of adaptive cruise control vehicles for improved flow stability and string stability[J]. IEEE Transactions on Intelligent Transportation Systems, 2005, 6(2): 229-237. [本文引用:2]
[6]	Bifulco G L, Pariota L, Simonelli F, et al. Development and testing of a fully adaptive cruise control system[J]. Transportation Research Part C, 2013, 29: 156-170. [本文引用:1]
[7]	Baek W, Song B. Design and validation of a longitudinal velocity and distance controller via hardware-in-the-loop simulation[J]. International Journal of Automotive Technology, 2009, 10(1): 95-102. [本文引用:2]
[8]	Mohammadpour J, Scherer C W. Control of Linear Parameter Varying Systems with Applications[M]. New York: Springer, 2012. [本文引用:1]
[9]	Olivier S, Peter G, Jozsef B. Robust Control and Linear Parameter Varying Approaches: Application to Vehicle Dynamics[M]. Berlin: Springer, 2013. [本文引用:1]
[10]	Li S E, Li K, Wang J. Economy-oriented vehicle adaptive cruise control with coordinating multiple objectives function[J]. Vehicle System Dynamics, 2013, 59(1): 1-17, . [本文引用:1]
[11]	Tseng C S, Chen B S. H_∞ fuzzy control design for nonlinear systems subject to actuator saturation[C]∥IEEE International Conference on Fuzzy Systems, Vancouver, BC, Canada, 2006: 783-788. [本文引用:2]
[12]	Yi K, Chung J. Nonlinear brake control for vehicle CW/CA systems[J]. IEEE/ASME Trans Mechatron, 2001, 6(1): 17-25. [本文引用:1]
[13]	俞立. 鲁棒控制-线性矩阵不等式处理方法[M]. 北京: 清华大学出版社, 2002. [本文引用:3]
[14]	Moon S, Yi K. Human driving data-based design of a vehicle adaptive cruise control algorithm[J]. Vehicle System Dynamics, 2008, 46(8): 661-690. [本文引用:1]
[15]	余志生. 汽车理论[M]. 5版. 北京: 机械工业出版社, 2009. [本文引用:1]

2012

0.0

... 0 引言汽车自适应巡航控制(Adaptive cruise control,ACC)是在现有产品车型上业已装配的汽车驱动和制动主动控制系统基础上,基于加装的雷达等车载传感器探测本车与其行驶车道上的前方它车等有效目标之间的相对距离、速度等相对运动状态,并考虑本车加速驱动和减速制动极限能力、驾驶员对安全性、舒适性及燃油经济性等多性能指标的协调权衡等因素,建立的以保持安全车头间距为目标、以本车与行驶车道内的前方目标车相对运动状态为输入、以本车期望纵向加速度或速度为输出的系统控制器,最终向汽车驱动和制动主动控制系统提供预期控制指令且依靠其执行机构实现精确跟随控制^[1] ...

2004

0.0

... 如何开发安全车头间距控制器是ACC系统设计的关键问题,研究人员相继提出基于固定时间间隔或距离间隔等车头间距特征值的定常时距(Constant time headway,CTH)^[2]、定常距离^[3]、定常安全因子间距策略^[4]及二阶时距策略^[5]等安全车头间距策略 ...

... 通常情况下,考虑到汽车纵向动力学响应延迟,即 af跟踪期望纵向加速度 ades存在一定滞后,采用如下的一阶惯性环节描述二者的关系^[2]: ...

1974

0.0

2001

0.0

2005

0.0

... 5] m/s²内可以保证乘坐舒适性^[12],本文中设定u_max=2 ...

2013

0.0

... 由此引发的新技术问题是由于无法提前预知驾驶员对车头间距的动态设定值,因此要求车头间距控制器可实时在线调整控制参数^[6] ...

2009

0.0

... Baek等^[7]应用含有输入整形滤波器的动态面控制(Dynamic surface control,DSC)算法设计了速度控制器和距离控制器 ...

... 同时,也与DSC算法^[7]进行了性能对比分析 ...

2012

0.0

... 考虑到驾驶员在线调整时距参数带来的车间相对运动学模型参数时变性,本文在前述的车间运动学状态方程基础上,进一步引入LPV模型来描述基于动态不确定性时距参数的车间相对运动状态^[8] ...

2013

0.0

... LPV模型通常定义为^[9]: ...

2013

0.0

... 同时,考虑到汽车自身驱动和制动系统的纵向运动学性能约束,本文在LPV模型中引入的汽车纵向加速度限值抑制了控制输入饱和,降低了汽车纵向运动对驾驶员乘坐舒适性的影响^[10] ...

2006

0.0

... sat(u(t))是引入的输入饱和约束项,其具体形式如下^[11]: ...

... 利用二次稳定性理论,可以得到 H∞控制算法存在的充分条件为^[11,13] ...

2001

0.0

... 5] m/s²内可以保证乘坐舒适性^[12],本文中设定u_max=2 ...

2002

0.0

... 设计如(7)形式的LPV控制器,闭环系统(8)必须满足以下性质^[13]:①在外部干扰为0时,闭环系统(8)是渐近稳定的 ...

... 利用二次稳定性理论,可以得到 H∞控制算法存在的充分条件为^[11,13] ...

... 定义 Q=P-1,Yi=KiQ(i=1,2),对式(10)同时左乘和右乘 diagQI1I3,利用Schur补的性质得到式(11)^[13]: ...

2008

0.0

... 3 纵向动力学控制算法设计如图2所示,纵向动力学控制器包括三个部分:驱动控制器、制动控制器以及二者间的切换逻辑^[14] ...

2009

0.0

... 假设忽略发动机和轮胎惯量,而且液力变矩器锁死,汽车的力平衡方程为^[15]: ...