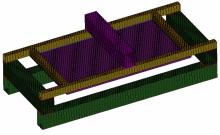
根据本文建立的侧窗玻璃简化模型, 在有限元分析软件中建立相应有限元模型。有限元分析中, 由于壳单元可较好地表达受力情况, 保证计算精度^[7], 故对简化模型中的窗框梁部分采用壳单元离散。由于侧翻过程是一个动态仿真过程, 要在Dyna软件中完成, 侧翻中钢化玻璃会发生断裂。在软件中实体单元能较好地模拟断裂失效过程, 所以模型中粘接剂和钢化玻璃采用实体单元建立。由于本文研究粘接式玻璃对于侧翻过程的影响, 在研究中要保证玻璃断裂而其他因素不变。故在确定玻璃尺寸时, 需经过反复试算, 保证玻璃断裂为单一影响因素, 消除粘接胶开裂等其他因素的影响, 确定最终的模型尺寸, 如图1所示。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 侧窗玻璃有限元模型Fig.1 Finite element model of side window

客车侧翻碰撞是短暂的动态过程, 很难准确加载模拟侧翻时的受力。根据钢化玻璃的失效特性, 低应变时的破坏应力要低于高应变时的破坏应力, 故在试验中采取准静态加载方式。由于要模拟车窗玻璃在侧翻碰撞过程中的失效有多种存在形式, 而本文研究的是玻璃在失效过程中的破碎。因此在试件加载过程中, 为防止应力集中现象, 载荷不直接施加于玻璃上, 而是施加在玻璃上方的加载横梁上, 载荷通过窗框变形经过粘接剂作用于玻璃上, 使玻璃发生断裂失效。

根据多次计算和模型修改, 保证了侧翻过程中玻璃断裂为单一变量, 最终建模模型采用305 mm× 520 mm× 5 mm的钢化玻璃尺寸; 采用20 mm× 20 mm× 1.5 mm的Q235钢管作为窗框尺寸; 支座采用50 mm× 50 mm× 2 mm的钢管焊接而成; 粘接剂的粘接厚度为3 mm; 粘接宽度为16.5 mm。有限元仿真结果如图2所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 窗框有限元模型仿真结果Fig.2 Simulation result of window frame finite element model

通过模拟加载7000 N的最大载荷可以看出, 窗框框架部分达到屈服极限, 但并未断裂, 粘结剂也未开裂, 在仿真结果中也可看出玻璃上的高应力部分, 在试验部分中在此处粘贴应变片。

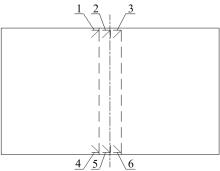
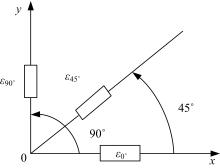
根据上述有限元分析结果, 设计试验测定钢化玻璃的强度极限。按图2所示仿真模型进行建模, 试件加工完成后, 在钢化玻璃上标出加载横梁安放位置。同时在加载横梁上对应的玻璃处选取6个点贴上三角应变花, 位置如图3所示。直角应变花的原理如图4所示。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 应变花位置示意图Fig.3 Location diagram of strain rosette

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 直角应变花原理图Fig.4 Schematic diagram of right-angle strain rosette

为模拟准静态加载过程, 试验应用WDW3100微机控制电子万能试验机, 应用试验机的压缩空间对试件进行加载。将窗框支架放在万能试验机压缩空间中部, 窗框模型置于支架上, 并根据划线位置安放加载横梁, 调节各部分位置, 将屏蔽线连接到静态应变仪上, 并连接温度补偿电阻, 应用万能试验机加载。试验载荷从3000 N开始, 每次增加100 N, 直至钢化玻璃断裂。通过实际加载可知, 在试验载荷增加到5800 N至5900 N时, 钢化玻璃断裂失效。

通过试验中6个应变花测得的第一主应力数据如表1所示, 由于在测试和贴片过程中存在误差, 由6个测试点的平均值估算钢化玻璃断裂极限。

表1

Table 1

表1(Table 1)

表1 应变花第一主应力数据 Table 1 Major principle stress data of strain rosette MPa 序 号 应变 花1 应变 花2 应变 花3 应变 花4 应变 花5 应变 花6 应力平 均值 1 37.3 33.5 31.8 30.7 32.1 35.2 33.4 2 38.1 35.9 33.5 31.3 34.7 36.4 35.0 3 39.4 36.9 34.8 32.2 35.2 37.7 36.0 4 40.6 38.8 36.2 33.0 37.8 38.8 37.5 5 42.0 39.1 37.6 34.2 38.1 40.4 38.6 6 43.1 41.1 39.1 35.3 40.2 41.7 40.1 7 44.6 42.8 40.5 36.5 41.9 43.3 41.6 8 45.8 45.0 42.2 37.9 43.8 44.9 43.3 9 48.9 46.5 44.3 39.8 45.0 47.0 45.3 10 51.3 48.6 46.5 41.8 47.1 49.4 47.4 11 53.7 50.4 48.9 44.0 49.0 51.9 49.6 12 56.2 53.9 51.8 46.6 52.4 54.7 52.6 13 60.0 57.0 54.8 49.6 55.6 58.0 55.8 14 63.2 61.5 58.3 52.8 60.6 61.5 59.6 15 67.5 66.0 62.5 56.6 64.5 65.6 63.8 16 72.0 69.4 66.8 60.9 68.9 70.0 68.0 17 77.5 75.1 71.9 65.9 75.4 75.1 73.5 18 83.2 80.2 77.7 71.5 79.5 80.9 78.8 19 87.6 87.2 84.0 77.8 86.6 87.2 85.1 20 97.0 95.1 91.0 84.4 94.2 94.2 92.6 21 104.0 102.7 98.2 91.7 101.9 101.6 100.0 22 110.5 107.5 103.4 99.0 106.6 108.0 105.8 23 118.5 115.7 111.4 107.5 114.5 115.2 113.8 24 127.0 124.9 120.6 116.6 123.1 123.8 122.7 25 136.6 134.9 130.1 126.4 133.9 133.1 132.5 26 145.9 143.9 139.9 136.4 142.3 142.4 141.8 27 155.9 154.0 149.8 146.7 152.3 152.6 151.9 28 166.9 165.0 160.9 158.3 164.0 163.1 163.0 29 183.1 183.0 178.2 175.6 181.9 179.6 180.2

表1 应变花第一主应力数据 Table 1 Major principle stress data of strain rosette MPa

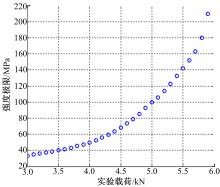
由于通过静态应变仪只能测得玻璃断裂前一点的应力值, 因此通过数值计算软件Matlab根据已知数据, 模拟在玻璃断裂时的应力值, 如图5所示。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 Matlab试验数据拟合曲线Fig.5 Fitting curve of data from Matlab

根据编写的程序求得钢化玻璃的强度极限为210.0553 MPa, 近似取210 MPa作为试验值。将该强度极限作为客车侧翻中粘接玻璃的断裂极限

乘员空间是客车中乘客活动的区域, 为保障乘客安全, 分析侧翻过程中车窗玻璃的断裂强度极限对乘客空间变形的影响很重要。在客车侧翻碰撞过程中, 底架部分的变形较少^[9], 其主要变形存在于侧围和顶盖部分。

模拟试验中为了定量测量车窗玻璃对乘客空间的影响, 采用乘员活动空间对角线的长度变化作为判定依据。选取非碰撞侧地板梁上表面最外端一点与车窗上边梁与车窗立柱的相交点, 两点在 YZ平面上, 分别量取有、无玻璃的车身段模型在侧翻过程中玻璃破碎时的乘员空间对角线长度, 如图6和图7所示。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 有玻璃的车身段对角线长度示意图Fig.6 Diagonal length of body secti on with window

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 无玻璃的车身段对角线长度示意图Fig.7 Diagonal length of body section with none window

对两种模型结果进行对比, 结果如表2所示。从表2可知, 钢化玻璃对抵抗乘员空间变形起到的作用较小。由于在客车侧翻碰撞中, 当钢化玻璃达到其自身的断裂极限时玻璃边缘发生破裂, 随即整块玻璃断裂, 钢化玻璃不能起到承载的作用, 因此有、无侧窗玻璃对乘员空间的影响较小。

表2

Table 2

表2(Table 2)

表2 两种模型乘员空间对角线长度统计表 Table 2 Statistical table of living space diagonal length in two models 车身段模型 原对角线 长度/m 变形后对角线 长度/m 变形量 /m 无玻璃 2.96 2.882 0.078 有玻璃 2.96 2.886 0.074

表2 两种模型乘员空间对角线长度统计表 Table 2 Statistical table of living space diagonal length in two models

侧翻过程中, 由于车体发生接触碰撞, 车身主要杆件的形变能是评价车身性能的重要指标。在前文仿真模拟中, 有玻璃的车身段模型在0.02 s时玻璃就发生断裂。分别统计两种模型主要杆件的形变能, 如表3所示。

表3

Table 3

表3(Table 3)

表3 两种模型主要杆件的形变能 Table 3 Main bars’ deformation energy in two models 杆件部位 形变能/J 无玻璃模型 有玻璃模型 窗立柱 345 276 窗框下边梁 144 142 窗框上边梁 74 64 顶盖纵梁 245 257 顶盖横梁 680 697 侧围立柱 191 193 侧围斜撑 30 53 牛腿 56 53

表3 两种模型主要杆件的形变能 Table 3 Main bars’ deformation energy in two models

通过数据统计可得, 两种模型在吸收主要杆件形变能方面都很接近。比较窗立柱的形变能可知, 有玻璃模型吸能量较小, 说明钢化玻璃在断裂时能有效分担窗立柱的形变能。此外, 在侧围斜撑和顶盖部位, 有玻璃模型比无玻璃模型吸收能量较多。

前、后风挡玻璃可能对侧翻有较大影响, 由于前、后风挡玻璃采用夹层玻璃^[10], 在仿真过程中难以模拟, 本文篇幅有限, 未做讨论。