基于状态观测器的机敏约束阻尼板模态控制

引用本文

王攀, 鲁俊, 邓兆祥, 廖海辰, 王正亚, 阳小光. 基于状态观测器的机敏约束阻尼板模态控制.吉林大学学报:工学版, 2016, 46(4): 1057-1064
WANG Pan, LU Jun, DENG Zhao-xiang, LIAO Hai-chen, WANG Zheng-ya, YANG Xiao-guang. Modal control of smart constrained layer damping plate based on state observer. Journal of Jilin University Engineering and Technology Edition, 2016, 46(4): 1057-1064 复制到剪切板

Permissions

基于状态观测器的机敏约束阻尼板模态控制

王攀¹, 鲁俊¹, 邓兆祥^1,², 廖海辰¹, 王正亚¹, 阳小光¹

1.重庆大学汽车工程学院,重庆 400044

2.重庆大学机械传动国家重点实验室,重庆 400044

作者简介:王攀(1977-),男,副教授,博士.研究方向:车辆NVH控制,车辆系统动力学控制.E-mail:wangpan@cqu.edu.cn

基金:“863”国家高技术研究发展计划项目(2012AA111803); 中央高校基本科研业务费专项资金项目(CDJZR12110006)

摘要

以对边约束板结构为研究对象,研究了压电机敏约束阻尼技术的振动主动控制问题。基于压电本构关系、GHM阻尼模型和模态理论建立了模态主动控制模型。考虑到模态坐标在工程实际中无法由物理传感器直接测量,基于分离定理进行了模态状态观测器设计,并结合非耦合模态控制法与最优二次型控制进行了振动主动控制器设计。搭建了硬件在环实验平台,在不同外扰激励下开展了振动主动控制实验研究。结果表明,采用带有观测器的模态控制器,对板结构的振动主动控制能取得很好效果:当外界激励为复杂周期信号时,振动响应幅值衰减近60%;当外界激励为随机白噪声时,振动响应的均方根值减少9.48%。

关键词: 车辆工程; 机敏约束层阻尼; 振动主动控制; 模态控制; 状态观测器

中图分类号:U463 文献标志码:A 文章编号:1671-5497(2016)04-1057-08

Modal control of smart constrained layer damping plate based on state observer

WANG Pan¹, LU Jun¹, DENG Zhao-xiang^1,², LIAO Hai-chen¹, WANG Zheng-ya¹, YANG Xiao-guang¹

1.College of Automotive Engineering, Chongqing University, Chongqing 400044, China

2.State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044, China

Abstract

The vibration active control of piezoelectric smart constrained layer damping technology was researched with a clamped-clamped plate structure. The modal active control model was established based on piezoelectric constitutive relation, GHM damping model and modal theory. The modal state observer was designed based on separation theorem since the modal coordinates can not be directly acquired by physical sensor in engineering practice. An active vibration controller was also designed using non-coupling modal control and quadratic optimal control. Experiments of hardware in the loop and active vibration control were carried out under different external disturbance excitations. Results show that, using modal controller with an observer, good effect of active control of the plate vibration can be obtained. When the external excitation is complicated periodic signal, the vibration response amplitude attenuates to nearly 60%. When the external excitation is random white noise, the root mean square value of the vibration response reduces by 9.48%.

Keyword: vehicle engineering; smart constrained layer damping; active vibration control; modal control; state observer

Show Figures

0 引言

传统的约束阻尼技术属于被动减振技术, 可有效降低中高频振动, 但对低频振动控制效果欠佳^{[1, 2]}。主动控制技术具有较强的环境适应能力和抑制低频振动的能力^[3], 但安全性和可靠性得不到保证。产生于20世纪90年代的机敏约束层阻尼(Smart constrained layer damping, SCLD)技术结合了约束阻尼技术与主动阻尼控制技术的双重优势, 已被众多学者证明是结构振动噪声控制领域一种非常有效的减振降噪手段^{[4, 5, 6]}。机敏约束阻尼结构因为具有附加质量小, 响应速度快, 以及在很宽的频率范围内都保持较高的阻尼特性, 特别是对低频振动具有良好控制效果, 近年来一直是国内外振动控制的一个研究热点^{[6, 7, 8]}, 可广泛应用于航空航天、船舶、机械和汽车等领域。

机敏约束阻尼的核心在于压电约束层的主动控制。目前应用于机敏约束层阻尼结构的控制算法主要有PID控制^[9]、鲁棒控制^[10]、最优控制^[11]、自适应控制^[7]等。控制算法多局限于理论上的探索或者过于复杂不适合工程应用。模态控制因为具有计算简单、效率高、易于实时控制等优点, 是振动控制领域中常用的一种控制方法^[12], 然而应用于机敏约束层阻尼技术的研究却很少^{[13, 14]}, 而且模态控制属于全状态反馈控制, 存在全状态反馈困难, 无法直接应用到工程实践中。

本文以局部覆盖SCLD结构的对边约束板为研究对象, 基于压电本构关系建立了模态主动控制模型, 为解决全状态反馈困难, 设计了带状态观测器的主动控制器, 并开展了硬件在环控制实验研究。在不同外扰激励下, 取得了良好振动控制效果。

1 有限元动力学模型

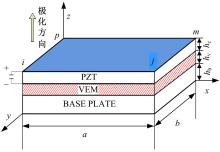
图1为SCLD的典型配置结构。SCLD结构自上而下分为三层, 分别是压电约束层、粘弹性层和基层。其中压电约束层为机敏压电陶瓷, 也是振动主动控制的动力源。当结构振动时, 阻尼层发生剪切变形, 同时传感元件感知结构振动, 然后通过反馈控制器基于逆压电效应, 主动调节机敏压电约束层拉伸或压缩, 使阻尼层的剪切变形进一步加强, 从而实现结构的主动振动控制。

有限元建模中, 其假设满足文献[10, 15, 16]提及的假设条件。利用有限元法将板离散为多个矩形单元。图2为SCLD结构二维4节点单元图, SCLD单元长度为a;宽度为b;每个单元含4个节点;每个节点有7个自由度,分别为压电约束层面内x向及y向位移、基层面对x向及y向位移、结构沿z向的横向位移以及单元中面绕x轴和绕y 轴的转角。

	Figure Option View Download New Window
	图1 典型的SCLD结构Fig.1 Typical structure of SCLD

	Figure Option View Download New Window
	图2 SCLD 矩形单元Fig.2 SCLD rectangular element

设板单元节点 $\begin{matrix} i \end{matrix}$ 的7自由度位移矢量为:

$\begin{matrix} \begin{matrix} \{Δ_{i}\} = {[\begin{matrix} {u^{e}}_{ci} & {v^{e}}_{ci} & {u^{e}}_{bi} & {v^{e}}_{bi} & {w^{e}}_{i} & {w^{e}}_{xi} & {w^{e}}_{yi} \end{matrix}]}^{T}, \\ i = 1, 2, 3, 4 \end{matrix} \end{matrix}$

则单元的节点位移向量为:

$\begin{matrix} \{U^{(e)}\} = {\{\begin{matrix} Δ_{1} & Δ_{2} & Δ_{3} & Δ_{4} \end{matrix}\}}^{T} \end{matrix}$

根据节点位移模式的帕斯卡准则, 假设形函数为:

$\begin{matrix} \{\begin{matrix} u_{c} = a_{1} + a_{2} x + a_{3} y + a_{4} xy; \\ v_{c} = a_{5} + a_{6} x + a_{7} y + a_{8} xy; \\ u_{b} = a_{9} + a_{10} x + a_{11} y + a_{12} xy; \\ v_{b} = a_{13} + a_{14} x + a_{15} y + a_{16} xy; \\ w = b_{1} + b_{2} x + b_{3} y + b_{4} x^{2} + b_{5} xy + b_{6} y^{2} + \\ b_{7} x^{3} + b_{8} x^{2} y + b_{9} x y^{2} + b_{10} y^{3} + b_{11} x^{3} y + \\ b_{12} x y^{3}; \\ w_{x} = \frac{\partial w}{\partial y}; w_{y} = - \frac{\partial w}{\partial x} \end{matrix} \end{matrix}$ 通过单元节点坐标求解方程后, 则该单元任一点的位移可表示为:

$\begin{matrix} {\{\begin{matrix} u_{c} & v_{c} & u_{b} & v_{b} & w & w_{x} & w_{y} \end{matrix}\}}^{T} = N^{T} \{U^{(e)}\} (1) \end{matrix}$

式中: $\begin{matrix} \begin{matrix} N = \\ [N_{uc}] [N_{vc}] [N_{ub}] [N_{vb}] [N_{w}] [N_{wx}] [N_{wy}], \end{matrix} \end{matrix}$ 分别为7个自由度位移场函数对应的形函数矩阵。

1.1 压电单元的本构关系及作动

当应力和电场同时存在时, 三维状态下压电材料的力学耦合本构方程为:

$\begin{matrix} \begin{matrix} [\begin{matrix} ε_{x} \\ ε_{y} \\ ε_{z} \\ γ_{xz} \\ γ_{yz} \\ γ_{xy} \end{matrix}] = [\begin{matrix} S_{11}^{E} & S_{12}^{E} & S_{13}^{E} & S_{14}^{E} & S_{15}^{E} & S_{16}^{E} \\ S_{21}^{E} & S_{22}^{E} & S_{23}^{E} & S_{24}^{E} & S_{25}^{E} & S_{26}^{E} \\ S_{31}^{E} & S_{32}^{E} & S_{33}^{E} & S_{34}^{E} & S_{35}^{E} & S_{36}^{E} \\ S_{41}^{E} & S_{42}^{E} & S_{43}^{E} & S_{44}^{E} & S_{45}^{E} & S_{46}^{E} \\ S_{51}^{E} & S_{52}^{E} & S_{53}^{E} & S_{54}^{E} & S_{55}^{E} & S_{56}^{E} \\ S_{61}^{E} & S_{62}^{E} & S_{63}^{E} & S_{64}^{E} & S_{65}^{E} & S_{66}^{E} \end{matrix}] \times \\ [\begin{matrix} σ_{x} \\ σ_{y} \\ σ_{z} \\ τ_{xz} \\ τ_{yz} \\ τ_{xy} \end{matrix}] + [\begin{matrix} d_{11} & d_{21} & d_{31} \\ d_{12} & d_{22} & d_{32} \\ d_{13} & d_{23} & d_{33} \\ d_{14} & d_{24} & d_{34} \\ d_{15} & d_{25} & d_{35} \\ d_{16} & d_{26} & d_{36} \end{matrix}] [\begin{matrix} E_{x} \\ E_{y} \\ E_{z} \end{matrix}] (2) \end{matrix} \end{matrix}$

式中: $\begin{matrix} S_{ij}^{E} \end{matrix}$ 为电场强度为零时弹性柔顺系数; $\begin{matrix} d_{ij} \end{matrix}$ 为压电应变常数, 下角标1, 2, …, 6分别对应坐标中 $\begin{matrix} x, y, z, xz, yz, x y \end{matrix}$ 方向; $\begin{matrix} σ 、 τ \end{matrix}$ 分别为压电材料的正应力矢量与剪切应力矢量; $\begin{matrix} E \end{matrix}$ 为外加电场强度。

对于薄片状压电材料, 其厚度方向( $\begin{matrix} z \end{matrix}$ 向)为极化方向, 如图2所示, 在上下表面施加正负极电压时, 将产生 $\begin{matrix} x - y \end{matrix}$ 平面内的应力。当压电片力学自由时, 式(2)可简化得到如下二维的本构方程:

$\begin{matrix} \begin{matrix} [\begin{matrix} ε_{x} \\ ε_{y} \\ γ_{xy} \end{matrix}] = [\begin{matrix} d_{11} & d_{21} & d_{31} \\ d_{12} & d_{22} & d_{32} \\ d_{16} & d_{26} & d_{36} \end{matrix}] [\begin{matrix} E_{x} \\ E_{y} \\ E_{z} \end{matrix}] = \\ [\begin{matrix} 0 & 0 & d_{31} \\ 0 & 0 & d_{32} \\ 0 & 0 & 0 \end{matrix}] [\begin{matrix} 0 \\ 0 \\ E_{z} \end{matrix}] = [\begin{matrix} d_{31} \\ d_{32} \\ 0 \end{matrix}] E_{z} (3) \end{matrix} \end{matrix}$

在二维状态下, 压电片在无外加电压下的应力应变关系满足平面应力问题的应力应变关系

$\begin{matrix} [\begin{matrix} σ_{x} \\ σ_{y} \\ τ_{xy} \end{matrix}] = \frac{E}{1 - μ^{2}} [\begin{matrix} 1 & μ & 0 \\ μ & 1 & 0 \\ 0 & 0 & \frac{1 - μ}{2} \end{matrix}] [\begin{matrix} ε_{x} \\ ε_{y} \\ γ_{xy} \end{matrix}] (4) \end{matrix}$

将式(3)带入式(4), 可得到压电层仅在控制电压作用下产生的压电驱动应力为

$\begin{matrix} \begin{matrix} [\begin{matrix} σ_{cx} \\ σ_{cy} \\ τ_{cxy} \end{matrix}] = D_{c} [\begin{matrix} d_{31} \\ d_{32} \\ 0 \end{matrix}] \frac{V_{c} (t)}{h_{c}}, \\ D_{c} = \frac{E_{z}}{1 - μ_{c}^{2}} [\begin{matrix} 1 & μ_{c} & 0 \\ μ_{c} & 1 & 0 \\ 0 & 0 & \frac{1 - μ_{c}}{2} \end{matrix}] (5) \end{matrix} \end{matrix}$

式中: $\begin{matrix} E_{z} \end{matrix}$ 为沿压电片厚度方向的电场强度, $\begin{matrix} E_{z} = V_{c} (t) / h_{c}, 其中 V_{c} (t) \end{matrix}$ 为压电片驱动电压, $\begin{matrix} h_{c} \end{matrix}$ 为压电层厚度; $\begin{matrix} d_{31} \end{matrix}$ 与 $\begin{matrix} d_{32} \end{matrix}$ 为压电应变常数; $\begin{matrix} D_{c} \end{matrix}$ 为压电层的弹性常数矩阵; $\begin{matrix} μ_{c} 、 E_{c} \end{matrix}$ 分别为压电层的泊松比和弹性模量, $\begin{matrix} E_{c} = C_{11}^{E} = 1 / S_{11}^{E}, C_{11}^{E} 、 S_{11}^{E} \end{matrix}$ 分别为压电材料在电场场强度为零时的弹性刚度和弹性柔顺系数。

根据经典板壳理论, 考虑各层之间的位移协调关系, 单元变形后约束层内任意点分别在 $\begin{matrix} x 向和 y \end{matrix}$ 向的位移为:

$\begin{matrix} \begin{matrix} U_{c} = u_{c} - z \frac{\partial w}{\partial x}, V_{c} = v_{c} - z \frac{\partial w}{\partial y} (6) \\ - h_{c} / 2 \leq z \leq h_{c} / 2 \end{matrix} \end{matrix}$

式中: $\begin{matrix} u_{c} 、 v_{c} \end{matrix}$ 分别为约束层内该点在 $\begin{matrix} x 、 y \end{matrix}$ 向的面内位移; $\begin{matrix} z \end{matrix}$ 为该点距约束层中面的距离; $\begin{matrix} w \end{matrix}$ 为挠度。

约束层中该点在 $\begin{matrix} x 向和 y \end{matrix}$ 向的正应变为:

$\begin{matrix} \{\begin{matrix} ε_{cx} = \frac{\partial U_{c}}{\partial x} = \frac{\partial u_{c}}{\partial x} - z \frac{\partial^{2} w}{\partial x^{2}} \\ ε_{cy} = \frac{\partial V_{c}}{\partial y} = \frac{\partial v_{c}}{\partial y} - z \frac{\partial^{2} w}{\partial y^{2}} \end{matrix} (7) \end{matrix}$

该点在面内的剪应变为:

$\begin{matrix} γ_{cxy} = \frac{\partial U_{c}}{\partial y} + \frac{\partial V_{c}}{\partial x} = \frac{\partial u_{c}}{\partial y} - z \frac{\partial^{2} w}{\partial x \partial y} + \frac{\partial v_{c}}{\partial x} - z \frac{\partial^{2} w}{\partial x \partial y} (8) \end{matrix}$

结合式(7)(8), 则压电约束层内任意一点的应变为

$\begin{matrix} ε_{c} = \{\begin{matrix} ε_{cx} \\ ε_{cy} \\ γ_{cxy} \end{matrix}\} = \{\begin{matrix} \frac{\partial u_{c}}{\partial x} - z \frac{\partial^{2} w}{\partial x^{2}} \\ \frac{\partial v_{c}}{\partial y} - z \frac{\partial^{2} w}{\partial y^{2}} \\ \frac{\partial u_{c}}{\partial y} + \frac{\partial v_{c}}{\partial x} - 2 z \frac{\partial^{2} w}{\partial x \partial y} \end{matrix}\} = ε_{c 1} + ε_{c 2} (9) \end{matrix}$

式中: $\begin{matrix} ε_{c 1} 、 ε_{c 2} \end{matrix}$ 分别表示弹性位移的应变和弹性弯曲的应变。

根据弹性力学板壳理论, 外加电压时由面内位移引起的应变做功为:

$\begin{matrix} W_{cf} = \frac{1}{2} \int_{v} {ε^{T}}_{c 1} σ_{c}) dv = {\{U^{(e)}\}}^{T} F_{c} (10) \end{matrix}$

代入式(5)(9)以及相应的形函数矩阵(1)后, 可得压电单元广义力为:

$\begin{matrix} F_{c} = \frac{1}{2} V_{c} (t) \int_{0}^{a} \int_{0}^{b} {[\begin{matrix} N_{uc, x} \\ N_{vc, y} \\ N_{uc, y} + N_{vc, x} \end{matrix}]}^{T} D_{c} [\begin{matrix} d_{31} \\ d_{32} \\ 0 \end{matrix}] dxdy (11) \end{matrix}$

同理, 外加电压时由横向位移引起的应变做功为:

$\begin{matrix} W_{cm} = \frac{1}{2} \int_{v} {ε^{T}}_{c 2} σ_{c}) dv = {\{U^{(e)}\}}^{T} M_{c} (12) \end{matrix}$

压电单元广义力矩为:

$\begin{matrix} M_{c} = \frac{1}{4} V_{c} (t) h_{c} \int_{0}^{a} \int_{0}^{b} {[\begin{matrix} N_{w, xx} \\ N_{w, yy} \\ 2 N_{w, xy} \end{matrix}]}^{T} D_{c} [\begin{matrix} d_{31} \\ d_{32} \\ 0 \end{matrix}] dxdy (13) \end{matrix}$

1.2 有限元动力学方程

在给出节点位移模式和形函数矩阵后, 利用能量原理可分别得到板单元各层的单元质量矩阵和单元刚度矩阵以及粘弹性层的剪切刚度矩阵。由于粘弹性材料特性随温度和频率变化, 为避免反复迭代求解, 将GHM模型^{[17, 18]}引入系统动力学方程。按照有限元的单元组集方法, 并考虑边界约束条件后, 可到结构总动力学方程。为了降低动力学模型维数, 通过物理空间动力缩聚技术^[19]可以得到:

$\begin{matrix} M \overset{\cdot \cdot}{X} + D \overset{\cdot}{X} + KX = F_{c} + F_{d} (14) \end{matrix}$

式中: $\begin{matrix} M \end{matrix}$ 为质量矩阵; $\begin{matrix} D \end{matrix}$ 为阻尼矩阵; $\begin{matrix} K \end{matrix}$ 为刚度矩阵; $\begin{matrix} F_{d} \end{matrix}$ 为激振器扰动力向量; $\begin{matrix} F_{c} \end{matrix}$ 为压电层的主动控制力向量; $\begin{matrix} X \end{matrix}$ 为只包含主自由度( $\begin{matrix} z 向的横向位移, 约束层面内 x 向及 y \end{matrix}$ 向位移)的位移向量。

2 模态控制模型

由于SCLD结构中含有粘弹性阻尼材料, 式(14)中阻尼属于非比例阻尼, 阻尼矩阵不满足对角化条件, 即复模态矢量不具备关于 $\begin{matrix} M 、 K 、 C \end{matrix}$ 加权正交性, 因此需要在状态空间中构造相应的模态空间。

受控下机敏约束阻尼结构的状态方程为

$\begin{matrix} \begin{matrix} \{\begin{matrix} \overset{\cdot}{Y} = \tilde{A} Y + {\tilde{B}}_{c} V + {\tilde{B}}_{d} f \\ Z = \tilde{C} Y \end{matrix} (15) \\ \tilde{A} = [\begin{matrix} 0 & I \\ - M^{- 1} K & - M^{- 1} D \end{matrix}]; {\tilde{B}}_{c} = [\begin{matrix} 0 \\ M^{- 1} F_{c} \end{matrix}]; \\ {\tilde{B}}_{d} = [\begin{matrix} 0 \\ M^{- 1} F_{d} \end{matrix}]; Y = [\begin{matrix} X \\ \overset{\cdot}{X} \end{matrix}] \end{matrix} \end{matrix}$

式中: $\begin{matrix} \tilde{A} \end{matrix}$ 为结构的系统动力学矩阵; $\begin{matrix} {\tilde{B}}_{c} 、 {\tilde{B}}_{d} \end{matrix}$ 分别为压电控制力和激振器扰动力的分布矩阵; $\begin{matrix} \tilde{C} \end{matrix}$ 为传感器输出矩阵; $\begin{matrix} V \end{matrix}$ 为压电片的驱动电压; $\begin{matrix} f \end{matrix}$ 为激振器扰动力。

设模态振型矩阵为 $\begin{matrix} Ψ, \end{matrix}$ 系统物理坐标下的状态向量由模态坐标下的状态向量表示为:

$\begin{matrix} Y = Ψ \tilde{ξ} = \overset{n}{\sum_{i = 1}} Φ_{i} {\tilde{ξ}}_{i} (16) \end{matrix}$

把式(16)带入状态方程(15)可得:

$\begin{matrix} \{\begin{matrix} \overset{\cdot}{\tilde{ξ}} = Λ \tilde{ξ} + Ψ^{- 1} {\tilde{B}}_{c} V + Ψ^{- 1} {\tilde{B}}_{d} f \\ Z = \tilde{C} Ψ \tilde{ξ} \end{matrix} (17) \end{matrix}$

式中: $\begin{matrix} Λ = {(Ψ)}^{- 1} \tilde{A} Ψ = diag [λ_{1} λ_{1}^{*} \dots \dots λ_{i} λ_{i}^{*}], Ψ = [\begin{matrix} φ'_{1} & φ_{1}^{'*} & \dots & \dots & φ'_{n} & φ_{n}^{'*} \end{matrix}], λ_{i} \end{matrix}$ 与 $\begin{matrix} λ_{i}^{*} \end{matrix}$ 为状态方程的第 $\begin{matrix} i \end{matrix}$ 阶共轭复特征值, $\begin{matrix} \begin{matrix} φ'_{i} = [\begin{matrix} φ_{i} \\ φ_{i} λ_{i} \end{matrix}], \\ φ_{i}^{'*} = [\begin{matrix} φ_{i}^{*} φ_{i}^{*} λ_{i}^{*} \end{matrix}], φ_{i} 、 φ_{i}^{*} \end{matrix} \end{matrix}$ 为复模态矢量。

通过线性变换后, 一个 $\begin{matrix} 2 n 维系统转化为 n \end{matrix}$ 个独立的二维共轭子系统, 且每一个二维系统是通过两个共轭子系统组成。不难发现, 式(17)各系数矩阵都为复数矩阵, 如果对复数状态方程进行主动控制器设计还会得到一个复增益矩阵, 使得控制器设计困难^[12]。

文献[20, 21]指出, 复参数的状态空间模型可以用一个等价的实参数状态空间模型表示。设实参数空间的状态向量 $\begin{matrix} ξ \end{matrix}$ 满足:

$\begin{matrix} ξ = T \tilde{ξ} (18) \end{matrix}$

其中复数空间到实数空间的变化矩阵 $\begin{matrix} T \end{matrix}$ 为:

$\begin{matrix} \begin{matrix} T = \\ [\begin{matrix} - i / 2 Im (λ_{1}) & i / 2 Im (λ_{1}) & \dots & 0 & 0 \\ \frac{1}{2} - \frac{i}{2} γ_{1} & \frac{1}{2} + \frac{i}{2} γ_{1} & \dots & 0 & 0 \\ ︙ & ︙ & ︙ & ︙ \\ 0 & 0 & \dots & - i / 2 Im (λ_{n}) & i / 2 Im (λ_{n}) \\ 0 & 0 & \dots & \frac{1}{2} - \frac{i}{2} γ_{n} & \frac{1}{2} + \frac{i}{2} γ_{n} \end{matrix}] \end{matrix} \end{matrix}$

式中: $\begin{matrix} γ_{1} = (Re (λ_{1}) / Im (λ_{1})), γ_{n} = (Re (λ_{n}) / Im (λ_{n})) 。 \end{matrix}$

则实数系数的状态空间方程为:

$\begin{matrix} \begin{matrix} \{\begin{matrix} \overset{\cdot}{ξ} = Aξ + B_{c} V + B_{d} f \\ Z = Cξ \end{matrix} (19) \\ 式中 : \\ A = TΛ T^{- 1} = \\ [\begin{matrix} 0 & 1 & \dots & 0 & 0 \\ - {|λ_{1}|}^{2} & 2 Re (λ_{1}) & \dots & 0 & 0 \\ ︙ & ︙ & ︙ & ︙ \\ 0 & 0 & \dots & 0 & 0 \\ 0 & 0 & \dots & - {|λ_{n}|}^{2} & 2 Re (λ_{n}) \end{matrix}] \\ B_{c} = T Ψ^{- 1} {\tilde{B}}_{c} = [\begin{matrix} Im (ψ_{1}) / Im (λ_{1}) \\ Re (ψ_{1}) + Im (ψ_{1}) Re (λ_{1}) / Im (λ_{1}) \\ ︙ \\ Im (ψ_{n}) / I m (λ_{n}) \\ Re (ψ_{n}) + Im (ψ_{n}) Re (λ_{n}) / Im (λ_{n}) \end{matrix}] \\ B_{d} = T Ψ^{- 1} {\tilde{B}}_{d} = [\begin{matrix} Im (φ_{1}) / Im (λ_{1}) \\ Re (φ_{1}) + Im (φ_{1}) Re (λ_{1}) / Im (λ_{1}) \\ ︙ \\ Im (φ_{n}) / Im (λ_{n}) \\ Re (φ_{n}) + Im (φ_{n}) Re (λ_{n}) / Im (λ_{n}) \end{matrix}] \end{matrix} \end{matrix}$

$\begin{matrix} C = \tilde{C} Ψ T^{- 1} = {[\begin{matrix} - 2 [Re (ψ_{1}) Re (λ_{1}) + Im (ψ_{1})] \\ 2 Re (ψ_{1}) \\ ︙ \\ - 2 [Re (ψ_{n}) Re (λ_{n}) + Im (ψ_{n})] \\ 2 Re (ψ_{n}) \end{matrix}]}^{T} \end{matrix}$

通过变换后, 复数系数的状态方程矩阵全部转换为实数系数的状态方程矩阵, 式(19)仍由 $\begin{matrix} n \end{matrix}$ 个独立的系统组成, 系统矩阵 $\begin{matrix} A \end{matrix}$ 为对角阵, 包含 $\begin{matrix} n \end{matrix}$ 对共轭特征值, 状态变量 $\begin{matrix} ξ \end{matrix}$ 表示为模态位移和模态速度, $\begin{matrix} B_{c} 、 C \end{matrix}$ 中元素的大小分别代表对应模态的可控性和可观性。

根据模态展开定理, 模态坐标下的总响应可通过各阶模态叠加求得。然而, 在实际振动中特别是柔性结构, 往往是某一个或少量的低阶主模态对整个系统的性能起着主要作用, 振动主动控制也主要是消耗这些主模态的振动能量。将模态状态矢量 $\begin{matrix} ξ \end{matrix}$ 分为主模态和剩余模态。在不考虑系统外部干扰时, 式(19)可写成:

$\begin{matrix} \{\begin{matrix} [\begin{matrix} {\overset{\cdot}{ξ}}_{s} \\ {\overset{\cdot}{ξ}}_{r} \end{matrix}] = [\begin{matrix} A_{s} \\ A_{r} \end{matrix}] [\begin{matrix} ξ_{s} \\ ξ_{r} \end{matrix}] + [\begin{matrix} B_{s} \\ B_{r} \end{matrix}] [\begin{matrix} V_{s} & V_{r} \end{matrix}] \\ Z = [\begin{matrix} C_{s} & C_{r} \end{matrix}] [\begin{matrix} ξ_{s} \\ ξ_{r} \end{matrix}] \end{matrix} (20) \end{matrix}$

式中:下角s表示主模态; 下角r表示剩余模态。

3 带观测器的主动控制器设计

3.1 LQR控制

通过状态方程下的模态解耦, 每一阶模态各自独立, 因此可以针对某一阶模态进行单独控制。假设式(20)中的第 $\begin{matrix} i \end{matrix}$ 阶主模态在控制电压下的状态方程为

$\begin{matrix} \{\begin{matrix} {\overset{\cdot}{ξ}}_{i} = A_{i} ξ_{i} + B_{i} V_{i} \\ Z_{i} = C_{i} ξ_{i} \end{matrix} (21) \end{matrix}$

第 $\begin{matrix} i \end{matrix}$ 阶模态的性能指标可以表示为

$\begin{matrix} J (u) = \frac{1}{2} \int_{t_{0}}^{t_{f}} {Z_{i}}^{T} Q_{i} Z_{i} + {V_{i}}^{T} R_{i} V_{i}) dt (22) \end{matrix}$

式中: $\begin{matrix} Z_{i} \end{matrix}$ 为第 $\begin{matrix} i \end{matrix}$ 阶模态的输出响应; $\begin{matrix} V_{i} \end{matrix}$ 为第 $\begin{matrix} i \end{matrix}$ 阶模态的控制电压; $\begin{matrix} Q_{i} \end{matrix}$ 为输出向量权矩阵, $\begin{matrix} Q_{i} \end{matrix}$ 中元素越大, 振动抑制水平越强; $\begin{matrix} R_{i} \end{matrix}$ 为控制电压权矩阵, $\begin{matrix} R_{i} \end{matrix}$ 中元素越大, 控制电压越小。

压电材料的控制电压可表示为:

$\begin{matrix} \begin{matrix} V_{i} & = - G_{i} [\begin{matrix} ξ_{i} \\ {\overset{\cdot}{ξ}}_{i} \end{matrix}] (23) \\ G_{i} & = - {R_{i}}^{- 1} {B_{i}}^{T} P_{i} (24) \end{matrix} \end{matrix}$

其中 $\begin{matrix} P \end{matrix}$ 满足如下二阶黎卡提方程:

$\begin{matrix} P_{i} A_{i} + {A_{i}}^{T} P_{i} - P_{i} B_{i} {R_{i}}^{- 1} {B_{i}}^{T} P_{i} + Q_{i} = 0 \end{matrix}$

闭环系统方程为

$\begin{matrix} ξ_{i} = (A_{i} - B_{i} G_{i}) ξ_{i} (25) \end{matrix}$

3.2 观测器设计

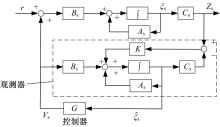
线性二次型最优控制实质是一种最优状态反馈, 实现模态控制的关键是获得被控模态的状态矢量, 然而在实际测量中传感器只能得到位移、速度或者加速度等信号。为实现状态反馈, 本文利用状态观测器估计系统的模态状态矢量, 以实现模态控制。基于观测器和状态反馈的分离特性, 状态反馈矩阵 $\begin{matrix} G \end{matrix}$ 和观测器反馈增益矩阵 $\begin{matrix} K \end{matrix}$ 可以独立设计。带状态观测器的反馈系统设计如图3所示。

	Figure Option View Download New Window
	图3 带状态观测器的反馈系统Fig.3 Feedback system with state observer

闭环状态观测器的状态方程为:

$\begin{matrix} {\overset{\cdot}{\hat{ξ}}}_{s} = (A_{s} - K C_{s}) {\hat{ξ}}_{s} + B_{s} V_{s} + K Z_{s} (26) \end{matrix}$

式中: $\begin{matrix} {\hat{ξ}}_{s} \end{matrix}$ 为系统原状态 $\begin{matrix} ξ_{s} \end{matrix}$ 的观测值; $\begin{matrix} C_{s} {\hat{ξ}}_{s} \end{matrix}$ 为观测输出; $\begin{matrix} K \end{matrix}$ 为观测器增益矩阵, 用来对包含测量输出 $\begin{matrix} Z_{s} \end{matrix}$ 与估计输出 $\begin{matrix} C_{s} {\hat{ξ}}_{s} \end{matrix}$ 之间差值进行加权修正。

设观测误差 $\begin{matrix} e = ξ_{s} - {\hat{ξ}}_{s}, \end{matrix}$ 结合式(20)与式(26)可得误差方程:

$\begin{matrix} \begin{matrix} \overset{\cdot}{e} = (A_{s} - K C_{s}) e (27) \\ 其解为 \\ e (t) = e^{(A_{s} - K C_{s})} e (0) (28) \end{matrix} \end{matrix}$

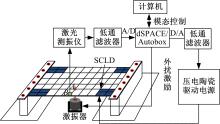
由式(28)可知, 通过观测器增益矩阵 $\begin{matrix} K \end{matrix}$ 不断对模型输出进行修正, 只要 $\begin{matrix} Re λ_{s} (A_{s} - K C_{s}) < 0, \end{matrix}$ 当 $\begin{matrix} t \to \infty \end{matrix}$ 时, 观测误差 $\begin{matrix} e (t) \to 0, \end{matrix}$ 即观测值等于真实值。观测误差趋于零的速度取决于观测器系统矩阵 $\begin{matrix} (A_{s} - K C_{s}) \end{matrix}$ 在复平面左半平面的极点。如果要使观测器在尽可能短的时间内跟踪上真实状态, 观测器在复平面左半平面的极点应该尽量远离虚轴。但是, 实际系统总存在噪声, 如果观测器极点配置得过于远离虚轴, 则很容易放大测量噪声。因此, 观测器极点位置的选择应是快速响应和减少干扰噪声的一个折中, 既要考虑 $\begin{matrix} {\hat{ξ}}_{s} \end{matrix}$ 趋于 $\begin{matrix} ξ_{s} \end{matrix}$ 的速度, 又要照顾到观测器的通频带, 使整个系统具有一定的抗干扰能力。一般, 观测器的极点实部位置选在控制器极点实部位置的3~5倍处^{[22, 23]}。

4 硬件在环实验

以局部覆盖SCLD结构的对边固支板为实验对象, 结构如图4所示。

	Figure Option View Download New Window
	图4 主动控制实验系统Fig.4 Active vibration control experiment system

各层几何和物理参数描述如下:基层(通过实验修正后的参数)为6061铝合金板, 长× 宽× 高为0.4 m× 0.27 m× 0.0025 m, 密度为2800 kg/m³, 弹性模量为55 GPa, 泊松比为0.25; 压电层为PLS-51型压电陶瓷, 厚度为0.001 m, 密度为7500 kg/m³, 柔顺系数为15.9× 10^-12 m²/N, 泊松比为0.36, 压电应变系数为200× 10^-12 C/N; 粘弹性层由ZN-1型粘弹性阻尼材料组成, 厚度为0.001 m, 密度为1250 kg/m³, 泊松比为0.3。

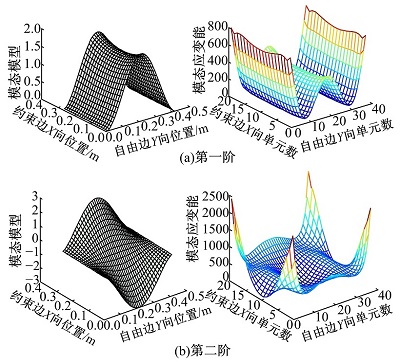
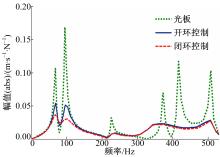
由模态实验发现, 光板的前4阶固有频率分别为74、107、211、256 Hz。在20~150 Hz的低频范围内, 响应峰值频率点主要集中在前两阶模态(一阶弯曲, 二阶扭转)。图5为研究对象的前两阶模态振型与应变能三维分布图。在不同的模态频率下, 模态变形剧烈的区域分布在不同的位置。由于压电片主要通过产生应力来抑制板的振动, 因此本文将压电片覆盖在前两阶模态应变能最大位置, 即两端约束根部位置。

	Figure Option View Download New Window
	图5 前两阶模态振型与模态应变能分布图Fig.5 The first two orders modal shape and mode strain energy

由于SCLD结构的主动控制目标是控制结构的低频振动, 且激振频率较低, 初始位移向量包含高阶固有振型的成分较少, 因此少数低阶弹性模态成为结构的主要模态。本文主动控制模型只包含前两阶主模态, 控制器维数为4× 4。硬件在环实验具体布置如图4所示。实验中, 为充分激励出前两阶模态, 使模态控制模型具有较大的可观、可控性, 将小型激振器和非接触式激光速度传感器位置放在第三阶与第四阶模态节线上, 并对速度传感信号进行二阶Butterworth带通滤波, 以减少传感信号中剩余模态分量和干扰信号的影响。根据控制器和观测器的分离特性, 控制器与观测器设计相互独立, 取最优加权矩阵 $\begin{matrix} Q_{i} = α_{i} {C_{i}}^{T} C_{i}, R_{i} = βI, \end{matrix}$ 前两阶模态 $\begin{matrix} α = 1 \times 10^{8}, β = 1 \times 10^{- 4} 。 \end{matrix}$ 为实现全状态反馈, 采用极点配置法将状态观测器的极点配置在闭环系统的左边, 以使观测器能够快速估计出系统的模态状态变量。观测器的极点位置与系统控制前后的极点分布, 如表1所示。图6为光板、机敏约束阻尼板(开环与闭环控制)的频响曲线对比。

表1 观测器与系统极点 Table 1 Poles of observer and controller

	Figure Option View Download New Window
	图6 控制前后频响函数曲线对比Fig.6 FRF before and after control

以小型激振器为外扰激励, 分别在机敏约束阻尼板前两阶固有频率正弦叠加的复杂周期信号与20~150 Hz随机白噪声激励下, 得到实验控制前后的时域响应曲线如图7和图8所示。

	Figure Option View Download New Window
	图7 复杂周期信号激励下, 控制前、后速度响应曲线Fig.7 Velocity response before and after control under complex periodic signal excitation

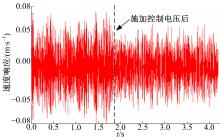	Figure Option View Download New Window
	图8 高斯白噪声信号激励下, 控制前、后速度响应曲线Fig.8 Velocity response before and after control under gauss white noise excitation

由图7和图8的实验结果可知, 通过施加主动控制电压后, 复杂周期信号激励下振动响应幅值衰减了近60%, 控制效果十分明显; 即使在随机白噪声信号激励下, 闭环控制后的随机响应均方根值也降低了9.48%, 证明了本文控制方法的有效性。而且在两种外扰激励下, 压电片驱动电压都低于压电陶瓷驱动电源的最大电压150 V, 控制电压较小。

5 结论

(1)通过本文的控制方法, 在复杂周期信号激励下振动响应幅值能降低近60%; 随机激励下振动响应均方根值能降低9.48%, 控制效果明显, 且需要控制的能量较小, 可满足工程实际应用要求。

(2)将状态观测器与模态模型相结合, 可以较好地解决模态控制的全状态反馈困难问题, 具有一定的工程应用前景。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Khalfi B, Rose A. Influence of partial constrained layer damping on the bending wave propagation in an impacted viscoelastic sand wich[J]. International Journal of Solids and Structures, 2013, 50(25-26): 4133-4144. [本文引用:1]
[2]	Ansari M, Khajepour A, Esmailzadeh E. Application of level set method to optimal vibration control of plate structures[J]. Journal of Sound and Vibration, 2013, 332(4): 687-700. [本文引用:1]
[3]	Wu D, Liang L, Bing P, et al. Experimental study and numerical simulation of active vibration control of a highly flexible beam using piezoelectric[J]. Aerospace Science and Technology, 2014, 37: 10-19. [本文引用:1]
[4]	Kumar R S, Ray M C. Active control of geometrically nonlinear vibrations of doubly curved smart sand wich shells using 1-3 piezoelectric composites[J]. Composite Structures, 2013, 105: 173-187. [本文引用:1]
[5]	Vasques C, Moreira R, Rodrigues J D. Viscoelastic damping technologies-part I: modeling and finite element implementation[J]. Journal of Advanced Research in Mechanical Engineering, 2010, 1(2): 96-110. [本文引用:1]
[6]	Kumar N, Singh S P. Vibration and damping characteristics of beams with active constrained layer treatments under parametric variations[J]. Materials and Design, 2009, 30(10): 4162-4174. [本文引用:2]
[7]	Cao Y, Deng Z, Wang P. A mechanics model and active control for smart constrained layer damping structure[J]. Applied Mechanics and Materials, 2012, 184-185: 767-773. [本文引用:2]
[8]	Kumar N, Singh S P. Vibration control of curved panel using smart damping[J]. Mechanical Systems and Signal Processing, 2012, 30: 232-247. [本文引用:1]
[9]	郑玲, 王宜, 谢熔炉. 主动约束层阻尼结构的振动控制[J]. 重庆大学学报, 2010, 33(2): 1-7. Zheng Ling, Wang Yi, Xie Rong-lu. Vibration control of active constrained layer damping structure[J]. Journal of Chongqing University, 2010, 33(2): 1-7. [本文引用:1]
[10]	Liu T, Hua H, Zhang Z. Robust control of plate vibration via active constrained layer damping[J]. Thin-walled Structures, 2004, 42(3): 427-448. [本文引用:1]
[11]	Baz A, Ro J. Optimum design and control of active constrained layer damping[J]. Journal of Mechanical Design, 1995, 117(B): 135-144. [本文引用:1]
[12]	顾仲权, 马扣根, 陈卫东. 振动主动控制[M]. 北京: 国防工业出版社, 1998. [本文引用:2]
[13]	Balamurugan V, Narayanan S. Finite element formulation and active vibration control study on beams using smart constrained layer damping (SCLD) treatment[J]. Journal of Sound and Vibration, 2002, 249(2): 227-250. [本文引用:1]
[14]	Chantalakhana C, Stanway R. Active constrained layer damping of clamped-clamped plate vibrations[J]. Journal of Sound and Vibration, 2001, 241(5): 755-777. [本文引用:1]
[15]	曹友强, 邓兆祥, 王攀, 等. 机敏约束层阻尼减振板耦合系统有限元模型[J]. 重庆大学学报, 2012, 35(10): 9-16. Cao You-qiang, Deng Zhao-xiang, Wang Pan, et al. Finite element model of coupled systems for vibration reduction plates with smart constrained layer damping[J]. Journal of Chongqing University, 2012, 35(10): 9-16. [本文引用:1]
[16]	Shi Y, Hua H, Sol H. The finite element analysis and experimental study of beams with active constrained layer damping treatments[J]. Journal of Sound and Vibration, 2004, 278(1-2): 343-363. [本文引用:1]
[17]	Golla D F, Hughes P C. Dynamics of viscoelastic structures a time-domain finite element formulation[J]. Applied Mechanics, 1985, 52: 897-907. [本文引用:1]
[18]	Mctavish D J, Hughes P C. Modeling of linear viscoelastic space structures[J]. Vibration and Acoustics, 1993, 115(1): 103-110. [本文引用:1]
[19]	罗虹, 李军, 曹友强, 等. 有限元模型动力缩聚中主副自由度选取方法[J]. 机械设计, 2010, 27(12): 11-14. Luo Hong, Li Jun, Cao You-qiang, et al. Methods for selecting the master and slave degrees of freedom in dynamic condensation technique of finite element models[J]. Journal of Machinical Design, 2010, 27(12): 11-14. [本文引用:1]
[20]	Trindade M A. Reduced-order finite element models of viscoelastically damped beams through internal variables projection[J]. Journal of Vibration and Acoustics, 2006, 128(4): 501-508. [本文引用:1]
[21]	Bouc R, Friot E. Contrôle optimal par retroaction du rayonnement d'une plaque munie de capteurs et d'actionneurs piézo-électriques non colocalisés[C]∥The 2eme Colloque GDR Vibroacoustique, Marseille, France, 1996: 229-248. [本文引用:1]
[22]	Katsuhiko Ogata. 现代控制工程[M]. 卢伯英, 于海勋, 译. 北京: 电子工业出版社, 2007. [本文引用:1]
[23]	张嗣瀛, 高立群. 现代控制理论[M]. 北京: 清华大学出版社, 2006. [本文引用:1]

2013

0.0

... 0 引言传统的约束阻尼技术属于被动减振技术,可有效降低中高频振动,但对低频振动控制效果欠佳^[1,2] ...

2013

0.0

... 0 引言传统的约束阻尼技术属于被动减振技术,可有效降低中高频振动,但对低频振动控制效果欠佳^[1,2] ...

2014

0.0

... 主动控制技术具有较强的环境适应能力和抑制低频振动的能力^[3],但安全性和可靠性得不到保证 ...

2013

0.0

... 产生于20世纪90年代的机敏约束层阻尼(Smart constrained layer damping,SCLD)技术结合了约束阻尼技术与主动阻尼控制技术的双重优势,已被众多学者证明是结构振动噪声控制领域一种非常有效的减振降噪手段^[4,5,6] ...

2010

0.0

2009

0.0

... 机敏约束阻尼结构因为具有附加质量小,响应速度快,以及在很宽的频率范围内都保持较高的阻尼特性,特别是对低频振动具有良好控制效果,近年来一直是国内外振动控制的一个研究热点^[6,7,8],可广泛应用于航空航天、船舶、机械和汽车等领域 ...

2012

0.0

... 目前应用于机敏约束层阻尼结构的控制算法主要有PID控制^[9]、鲁棒控制^[10]、最优控制^[11]、自适应控制^[7]等 ...

2012

0.0

2010

0.0

. 2010, 33(2):1-7 DOI:doi:10.11835/j.issn.1000-582x.2010.02.001

Vibration control of active constrained layer damping structure

主动约束层阻尼结构的振动控制

Zheng Ling , Wang Yi , Xie Rong-lu.

郑玲, 王宜, 谢熔炉

摘　要：基于弹性、粘弹性和压电材料的本构关系，利用Hamilton原理，推导了主动约束层阻尼板的有限元动力学模型。结合压电材料的机电耦合特性，采用自感电压的位移和速度反馈，对主动约束层阻尼板进行了闭环振动控制，研究了不同控制增益条件下，主动约束层阻尼板的动态特性。研究结果表明：采用自感电压的比例、微分反馈控制，能有效控制约束层阻尼板的振动，增大振动能量耗散，尤其对频率共振峰有明显抑制作用。由于该方法结构简单，容易实现，有很好的工程应用前景。

... 目前应用于机敏约束层阻尼结构的控制算法主要有PID控制^[9]、鲁棒控制^[10]、最优控制^[11]、自适应控制^[7]等 ...

2004

0.0

... 目前应用于机敏约束层阻尼结构的控制算法主要有PID控制^[9]、鲁棒控制^[10]、最优控制^[11]、自适应控制^[7]等 ...

1995

0.0

... 目前应用于机敏约束层阻尼结构的控制算法主要有PID控制^[9]、鲁棒控制^[10]、最优控制^[11]、自适应控制^[7]等 ...

1998

0.0

... 模态控制因为具有计算简单、效率高、易于实时控制等优点,是振动控制领域中常用的一种控制方法^[12],然而应用于机敏约束层阻尼技术的研究却很少^[13,14],而且模态控制属于全状态反馈控制,存在全状态反馈困难,无法直接应用到工程实践中 ...

... 不难发现,式(17)各系数矩阵都为复数矩阵,如果对复数状态方程进行主动控制器设计还会得到一个复增益矩阵,使得控制器设计困难^[12] ...

2002

0.0

2001

0.0

2012

0.0

. 2012, 35(10):9-16 DOI:doi:10.11835/j.issn.1000-582x.2012.10.002

Finite element model of coupled systems for vibration reduction plates with smart constrained layer damping

机敏约束层阻尼减振板耦合系统有限元模型

Cao You-qiang , Deng Zhao-xiang , Wang Pan

曹友强, 邓兆祥, 王攀

摘　要：针对机敏约束层阻尼减振板结构,考虑到粘接层、压电层、阻尼层、基层结构的耦合运动及位移协调关系,结合压电学理论、有限元理论以及粘弹性材料阻尼性能的滞弹性位移场模型,建立了耦合系统的有限元动力模型,该模型可适用于含SCLD结构的任意复杂系统的振动建模研究。以局部覆盖SCLD结构的对边约束钢板为研究对象,进行了结构动力学参数理论计算、ANSYS模态分析与模态实验研究,结果表明：理论分析与实验结果及ANSYS分析能较好吻合,充分证明了建模方法的有效性。

2004

0.0

1985

0.0

... 由于粘弹性材料特性随温度和频率变化,为避免反复迭代求解,将GHM模型^[17,18]引入系统动力学方程 ...

1993

0.0

... 由于粘弹性材料特性随温度和频率变化,为避免反复迭代求解,将GHM模型^[17,18]引入系统动力学方程 ...

2010

0.0

. 2010, 27(12):11-14

Methods for selecting the master and slave degrees of freedom in dynamic condensation technique of finite element models

有限元模型动力缩聚中主副自由度选取方法

Luo Hong , Li Jun , Cao You-qiang

罗虹, 李军, 曹友强

对有限元模型动力缩聚中主、副自由度的选取提出了2种方法.针对单层悬臂板的有限元数学模型,在分别用高精度动力缩聚法和加速动力缩聚法进行降阶处理过程中,对2种主、副自由度的选取方法进行了研究分析.归纳出了这两种选取方法的特点及适用范围,为动力缩聚法的实际应用提供了参考.

... 为了降低动力学模型维数,通过物理空间动力缩聚技术^[19]可以得到: ...

2006

0.0

1996

0.0

2007

0.0

... 一般,观测器的极点实部位置选在控制器极点实部位置的3~5倍处^[22,23] ...

2006

0.0

... 一般,观测器的极点实部位置选在控制器极点实部位置的3~5倍处^[22,23] ...