轨道车辆转向架一系悬挂的三向刚度直接关系到转向架及车辆的动力学性能^{[1, 2]}。横向刚度、纵向横向刚度、纵向刚度影响车辆的黏着性能、蛇形稳定性及曲线通过性能; 垂向刚度影响车辆抗倾覆性能、轮重减载性能和垂向稳定性^{[3, 4]}。在设计中, 刚度参数往往以理论计算为参考, 但在生产中, 刚度参数的获取仅靠理论计算远远不够, 零部件质量、相互装配关系等都对其有不同的影响, 必须采取试验的方法进行测定。因此, 转向架一系悬挂三向刚度的测定成为转向架设计生产成功与否的关键。

针对转向架一系悬挂刚度的测定, 欧美国家进行了较早的研究并开发了一系列试验设备, 德国Windhoff公司开发的转向架综合性能自动测试试验台可以对一系悬挂的垂向刚度进行测定; 瑞士NENCKI公司和德国西门子公司也先后开发了相关测试试验台, 但这些试验台都只能进行静态测试, 无法实现动态模拟。近年来随着我国轨道交通的迅猛发展, 国内机构开展了大量的研究工作, 左国兵等^[5]针对转向架一系悬挂采用的金属-橡胶复合锥形弹簧总结了一套比较合理的试验和数据处理方法; 李志强等^[6]针对某型转向架一系悬挂采用的轴箱弹簧进行了分析试验。但是, 这些研究工作都是针对一系悬挂中的弹簧单件进行的试验, 不能代表装备状态下一系悬挂的实际刚度参数。西南交通大学研发的转向架悬挂三向参数测定台以及齐齐哈尔车辆厂研发的转向架参数试验台可以实现装备条件下的刚度参数测定, 但是难以将转向架一系悬挂与二系悬挂分离开来分别测定^{[7, 8]}。作者所在课题组研发了一种新型的转向架试验台, 能实现单独转向架装备状态下一系悬挂、二系悬挂的三向动、静态刚度以及整车落成状态下悬挂参数的测定, 解决了转向架装备状态下悬挂系统刚度参数的测定难题^[9]。作者在课题组前期研究基础上, 针对轨道车辆转向架一系悬挂, 提出了一种三向动、静态刚度测定实验方法。

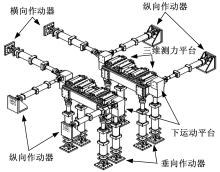
作为一种多功能的轨道车辆参数检测专用设备, 转向架试验台能够实现转向架装备条件下及整车落成状态下悬挂参数的动、静态刚度测定, 并可以实现对车辆实际线路运行工况的模拟, 试验台具有3个独立的6自由度运动平台, 上运动平台用于模拟车体加载及转向架二系悬挂刚度测定, 在转向架一系悬挂系统刚度测定试验中, 只需要其下部两个平行安置的运动平台。图1为转向架试验台下运动平台, 每个运动平台联接有一个横向作动器、2个纵向作动器、4个垂向作动器共7个作动器, 7个作动器协同动作, 实现运动平台在6个自由度的独立或者耦合运动。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 转向架试验台下运动平台Fig.1 Lower motion platform of bogie test bench

每个下运动平台上各安装有平行布置的两台三维测力平台, 三维测力平台将轮对固定安装到下运动平台并测定轮对受力, 测力过程中, 三维测力平台内部安装的4个测力传感器受力, 由传感器应变片的变形将力信号转化为电信号, 测力传感器并联安装, 因此三维测力平台的输出为4个传感器的信号平均值。三维测力平台分别测量横、纵、垂三个方向的作用力, 并消除各个方向作用力之间的耦合作用。

试验过程中, 转向架试验台下运动平台带动轮对沿某方向运动, 同时, 三维测力平台及位移测量系统实时测量悬挂在此方向上的力和位移, 进而完成刚度测定。

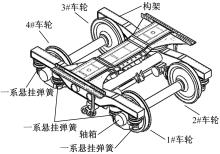
如图2所示, 被测转向架为某型地铁拖车转向架, 其一系悬挂系统结构比较简单, 构架和轴箱之间分别在靠近构架端部和远离构架端部处, 采用两个结构相同的一系悬挂弹簧并列连接, 在1#车轮、2#车轮、3#车轮和4#车轮处分别对应有1#一系悬挂、2#一系悬挂、3#一系悬挂和4#一系悬挂。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 被测地铁转向架Fig.2 Tested metro bogie

一系悬挂弹簧采用锥形金属橡胶弹簧, 锥形金属橡胶弹簧是金属与橡胶叠层硫化粘合而成的整体构件, 兼具金属材料和橡胶材料的优良性能, 广泛应用于地铁及低速轨道车辆转向架的一系悬挂系统中。

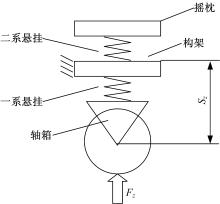
一系悬挂位于转向架构架和轴箱之间, 因此, 必须测量构架和轴箱的相对位移和对应的力值, 计算刚度值。图3为转向架一系悬挂垂向刚度测定原理, 构架固定, 对轮对施加垂向位移, 测量轮对所受垂向力 FZ,以及所对应的轮对轴箱和构架的垂向相对位移Δ S_Z, 得到一系悬挂的垂向刚度为:

μZ=FZ/ΔSZ1

同理, 对轮对施加横向位移和纵向位移, 分别测量轮对所受横向力、纵向力以及对应轮对轴箱与构架的横向相对位移、纵向相对位移, 可以得到转向架一系悬挂的横向刚度和纵向刚度。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 转向架一系悬挂垂向刚度测定原理Fig.3 Principle of primary suspension’ s vertical stiffness testing

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 刚度测定试验中转向架的装夹Fig.4 Clamping of tested bogie in stiffness testing

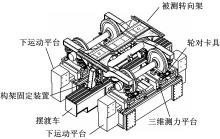
图4为刚度测定试验中被测转向架的装夹, 一系悬挂刚度测定试验中, 将转向架构架通过构架固定装置固定到静止不动的摆渡车上表面, 转向架轮对通过轮对卡具固定到下运动平台上的三维测力平台上表面, 通过下运动平台3个方向的运动带动轮对运动, 用激光位移传感器测量轴箱相对于构架的三向相对位移, 利用三维测力平台测量相对应的轮对受力, 即一系悬挂弹簧的三向受力, 计算得到刚度值。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 垂向刚度测定试验中位移传感器的布置Fig.5 Arrangement of displacement sensor in vertical stiffness testing

图5为垂向刚度测定试验中位移传感器的布置, 激光位移传感器的底座安装在位移传感器支承管上, 发射激光束垂直照射轮对轴箱的水平面, 由于位移传感器支承管固定连接到试验台地基上, 激光位移传感器测量的是轴箱相对于地基的位移, 而转向架构架相对于地基是静止不动的, 因此, 激光位移传感器的测量值同时也是转向架轮对轴箱与构架的垂向相对位移。同样的方法, 可以用激光位移传感器测量轮对轴箱与构架的横向和纵向相对位移。

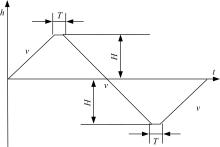
在转向架一系悬挂静态刚度测定试验中, 运动平台施加的运动波形为梯形波。图6为静态刚度测定试验中运动平台位移h的时域波形,运动平台以垂直向上为正方向,正向以速度v匀速运动至正向振幅H,停顿时间T后,以速度v反向运动至反向振幅H,停顿时间T后,以速度v 正向运动直至零位, 完成一个梯形波运动周期。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 静态刚度测定平台运动波形Fig.6 Platform movement waveform in static stiffness testing

由于一系悬挂在横、纵、垂三个方向上的结构以及允许变形量的差异, 不同方向静态刚度的测定试验选取不同的运动振幅 H, 运动速度v均取0.5 mm/s, 以保证试验近似于静态测定, 去除一系悬挂的动态特性对静态刚度测定的影响, 表1为静态刚度测定运动波形参数。

表1

Table 1

表1(Table 1)

表1 静态刚度测定运动波形参数 Table 1 Motion waveform parameters in static stiffness testing 测定项目 振幅H /mm 速度v /(mm· s-1) 时间间隔 T/s 横向静态刚度 3 0.5 1 纵向静态刚度 4 0.5 1 垂向静态刚度 10 0.5 1

表1 静态刚度测定运动波形参数 Table 1 Motion waveform parameters in static stiffness testing

以垂向静态刚度测定为例, 运动平台以梯形波垂向往复运动多个循环, 通过三维测力平台和激光位移传感器实时测量各个车轮的垂向受力和各个车轮处轮对轴箱与构架的相对垂向位移。图7为1#车轮处三维测力平台的垂向力时域曲线和1#车轮轴箱的垂向位移时域曲线。运动平台以梯形波运动时, 三维测力平台和激光位移传感器测量值同样以梯形波同步变化。

图7

Fig.7

	Figure Option ViewDownloadNew Window
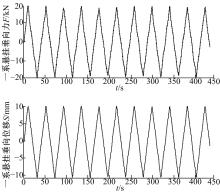	图7 垂向静态刚度测定试验中力与位移的时域曲线Fig.7 Time-domain curve of force and displacement in vertical static stiffness testing

对试验数据等时分割, 分别计算单个运动周期的静态刚度, 求平均值作为试验测定的静态刚度值。图8为选取的某个单运动周期的F-S曲线,横坐标为一系悬挂垂向位移S,纵坐标为一系悬挂垂向力F虚线为试验数据, 实线为对试验数据的线性拟合直线, 其斜率为1.67, 即求得本运动循环一系悬挂的静态垂向刚度为1.67 kN/mm。

图8

Fig.8

	Figure Option ViewDownloadNew Window
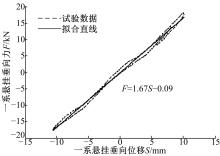	图8 垂向静态刚度测定试验中单运动周期的F-S曲线Fig.8 F-S curve during one single cycle in vertical static stiffness testing

表2为本次试验(共10个运动循环)的静态刚度测定计算值, 各循环计算值相差很小, 表明试验的重复性较好, 1#一系悬挂静态垂向刚度取平均值1.68 kN/mm。

表2

Table 2

表2(Table 2)

表2 静态刚度测定计算值 Table 2 Vertical static stiffness testing results 序号 一系静态垂向刚度计算值/(kN· mm-1) 1 1.70 2 1.68 3 1.67 4 1.68 5 1.68 6 1.68 7 1.68 8 1.68 9 1.67 10 1.67 平均值 1.68

表2 静态刚度测定计算值 Table 2 Vertical static stiffness testing results

依据类似的试验测定及数据处理方法, 得到被测转向架4个轮对处一系悬挂的横向、纵向、垂向3个方向的静态刚度, 并与转向架设计部门提供的设计值做对比。表3为一系悬挂静态刚度测定计算值, 4个轮对处一系悬挂3个方向的静态刚度计算值与设计值的相对误差均小于设计部门所要求的10%的允许误差, 说明被测转向架一系悬挂满足设计要求; 4个轮对处一系悬挂横向静态刚度计算值和垂向静态刚度相互间差别不大, 但是1#轮对处一系悬挂纵向静态刚度计算值(7.42 kN/mm)与2#轮对处一系悬挂纵向静态刚度计算值(8.45 kN/mm)差别较大, 说明被测转向架1#轮对和2#轮对处的两处一系悬挂选用的弹簧质量或者安装尺寸有明显不同, 应该重新安装调校, 使得被测转向架的一系悬挂的各向刚度分布更为均匀。

表3

Table 3

表3(Table 3)

表3 一系悬挂静态刚度测定值 Table 3 Primary suspension’ s vertical static stiffness testing results 数据类型 一系悬挂 1# 2# 3# 4# 静态横向刚度 /(kN· mm-1) 设计值 4.80 4.80 4.80 4.80 计算值 4.67 4.45 4.55 4.37 误差/% 2.71 7.29 5.21 1.88 静态纵向刚度 /(kN· mm-1) 设计值 7.80 7.80 7.80 7.80 计算值 7.42 8.45 7.64 7.44 误差/% 4.87 8.33 2.05 4.62 静态垂向刚度 /(kN· mm-1) 设计值 1.60 1.60 1.60 1.60 计算值 1.68 1.72 1.70 1.74 误差/% 5.00 7.80 5.81 8.88

表3 一系悬挂静态刚度测定值 Table 3 Primary suspension’ s vertical static stiffness testing results

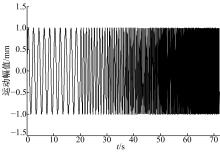
转向架一系悬挂动态刚度测定试验与静态刚度测定试验的试验方法及传感器布置方式相同, 同样由下运动平台施加运动, 测量运动过程中一系悬挂的各向受力和对应的轴箱与构架的相对位移来计算动态刚度, 不同之处在于运动波形为阶梯状变频的正弦波。图9为动态刚度测定试验中运动平台的运动波形, 正弦波振幅为1 mm, 频率为0.5~10 Hz, 频率间隔为0.5 Hz, 每频率下持续运动10个循环。

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 动态刚度测定平台运动波形Fig.9 Platform movement waveform in dynamic stiffness testing

图10

Fig.10

	Figure Option ViewDownloadNew Window
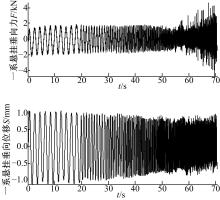	图10 垂向动态刚度测定试验中力与位移的时域曲线Fig.10 Time-domain curve of force and displacement in vertical stiffness testing

以垂向动态刚度测定为例。图10为1#车轮处三维测力平台的垂向力测量值和1#车轮轴箱的垂向位移测量值。下运动平台以正弦波运动时, 三维测力平台和激光位移传感器测量值同步变化, 在低频阶段, 二者的变化遵循正弦波形且振幅保持稳定, 随着频率增加, 垂向力测量值的振幅先减小再增加, 垂向位移的振幅持续减小, 垂向力和垂向位移的高频波形中都夹杂了不规律的成分, 导致波形混乱, 这与试验台以及三维测力平台的动态工作特性有关, 进行刚度计算时应该适当地进行滤波处理, 去除干扰成分。

类似地, 通过绘制运动循环 F-S曲线并拟合求斜率的方法求得不同频率下的动态刚度值。

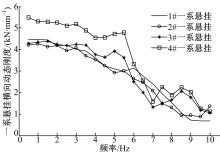
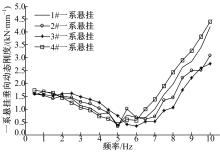
图11为不同频率下一系悬挂横向动态刚度测定值, 随着频率的增加, 动态刚度值总体上降低, 1#一系悬挂和2#一系悬挂的动态刚度基本上随着频率增加而持续降低; 3#一系悬挂和4#一系悬挂的动态刚度则在频率约为5.5 Hz和8.5 Hz均有波动; 1#一系悬挂和2#一系悬挂处于同一条轮对; 3#一系悬挂和4#一系悬挂处于同一条轮对, 这种不同轮对动态刚度的不同是由于轮轴和轴箱的横向装配差异造成的, 应该对被测转向架一系悬挂的横向装配关系进行调校。

图11

Fig.11

	Figure Option ViewDownloadNew Window
	图11 一系悬挂横向动态刚度测定值Fig.11 Primary suspension’ s horizontal dynamic stiffness testing results

图12

Fig.12

	Figure Option ViewDownloadNew Window
	图12 一系悬挂纵向动态刚度测定值Fig.12 Primary suspension’ s longitudinal dynamic stiffness testing results

图12为不同频率下一系悬挂纵向动态刚度测定值, 随着频率的增加, 动态刚度值降低, 并且4个位置的一系悬挂动态刚度变化趋势类似, 说明被测转向架一系悬挂的纵向装配关系是相同的。

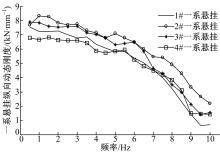
图13为不同频率下一系悬挂垂向动态刚度测定值, 随着频率的增加, 相应动态刚度值先降低, 在5.5 Hz左右达到波谷, 然后持续上升, 并且4个位置的一系悬挂动态刚度变化趋势类似, 说明被测转向架一系悬挂的垂向装配关系是相同的。

图13

Fig.13

	Figure Option ViewDownloadNew Window
	图13 一系悬挂垂向动态刚度测定值Fig.13 Primary suspension’ s vertical dynamic stiffness testing results

基于转向架试验台, 提出了转向架一系悬挂三向动、静态刚度的测定方法。针对某地铁拖车转向架完成了测定试验, 并对试验结果进行了分析:4个轮对处一系悬挂的静态刚度测定值与设计值的相对误差均小于设计部门所要求的10%的允许误差; 一系悬挂的横向、纵向和垂向动态刚度值随着频率分别呈现降低、降低和先降后增的总体趋势。本文试验方法可以满足轨道车辆转向架一系悬挂动、静态刚度的测定要求, 为转向架设计和制造提供必要的试验依据。