基于应变监测的连续梁支承差异沉降识别

引用本文

王少杰, 徐赵东, 李舒, 王凯洋,Dyke Shirley J. 基于应变监测的连续梁支承差异沉降识别.吉林大学学报:工学版, 2016, 46(4): 1090-1096
WANG Shao-jie, XU Zhao-dong, LI Shu, WANG Kai-yang, Dyke Shirley J. Differential settlement identification of pier for continuous beam based on strain monitoring. Journal of Jilin University Engineering and Technology Edition, 2016, 46(4): 1090-1096 复制到剪切板

Permissions

基于应变监测的连续梁支承差异沉降识别

王少杰^1,², 徐赵东³, 李舒¹, 王凯洋¹,Dyke Shirley J²

1.东南大学混凝土及预应力混凝土结构教育部重点实验室,南京 210096

2.普渡大学土木工程学院,美国西拉斐特 47907

3.南京东瑞减震控制科技有限公司,南京 210033

通讯作者：徐赵东(1975-),男,教授,博士生导师.研究方向:结构健康监测,结构抗震及减振.E-mail:zhdxu@163.com

作者简介:王少杰(1985-),男,博士研究生.研究方向:结构检测、监测与车桥耦合振动.E-mail:tumuwsj@163.com

基金:江苏省杰出青年基金项目(BK20140025); 江苏省自然科学基金项目(BK20151092); 科技部中青年科技创新领军人才项目; 江苏省普通高校研究生科研创新计划项目(CXLX13_102,CXZZ12_0108); 中央高校基本科研业务费专项资金项目(3205004907)

摘要

首先,运用基本力学原理,以三跨相等连续梁为对象,推导了梁体应变改变量与支承差异沉降量之间的解析式;并以某刚性轻轨桥为例,证明了微小支承差异沉降导致的应变改变量是可测的。其次,通过三跨不等连续梁模型试验,采用顶升方法模拟差异沉降,深入分析了梁底应变改变量与顶升量之间的关系,同时验证了FBG新型传感器的优越性能。再次,推导了与试验模型对应的梁底应变改变量与桥墩差异沉降之间的关系式,对两种模式(边墩顶升、中墩顶升)在不同差异沉降下的理论解与试验测试结果进行比较分析,结果表明二者吻合程度较高。最后,对识别基本流程与策略作了简要叙述。

关键词: 结构工程; 应变; 差异沉降; 连续梁; 模型试验

中图分类号:TU997 文献标志码:A 文章编号:1671-5497(2016)04-1090-07

Differential settlement identification of pier for continuous beam based on strain monitoring

WANG Shao-jie^1,², XU Zhao-dong³, LI Shu¹, WANG Kai-yang¹, Dyke Shirley J²

1.Key Laboratory of Concrete and Prestressed Concrete Structures of Ministry of Education, Southeast University, Nanjing 210096, China

2.School of Civil Engineering, Purdue University, West Lafayette 47907, USA

3.Nanjing Dongrui Damping Control Technology Co.,Ltd.,Nanjing 210033,China

Abstract

Based on measured strain data, a method of differential settlement identification of piers for continuous beam is proposed using theoretical and experimental analysis. First, the analytical formula with respect to the Variation of Strain Value (VSV) of the beam and the differential settlement identification of piers is derived by employing a three-equal-span continuous beam for instance. Also it is proved that the VSV result from minor differential settlement of piers is measureable in the case of a certain rigid light railway bridge. Second, the relationship between the VSV obtained from the bottom of the beam and the upright rectification value is analyzed using a three-unequal-span continuous beam for verification, where the settlement is simulated using the upright rectification method. Meanwhile, the performance of the new type Fiber Bragg Grating (FBG) sensors is demonstrated as well. Third, for the experimental model, the expression of the relationship between the VSV on the bottom of the beam and the differential settlement of the piers is derived, which reflects a well consistency between theoretical and experimental results in both cases (differential settlement of side pier and mid pier) under the condition of various degrees of differential settlement. Finally, the identification procedure and strategy are briefly clarified.

Keyword: structure engineering; strain; differential settlement; continuous beam; model experiment

Show Figures

0 引言

连续梁因整体性好、跨越能力强等优点, 被广泛应用于道路桥梁、铁路桥梁等工程领域。地面沉降、墩台周边堆卸载、车辆循环荷载等均可能导致支承(桥墩、桥台)产生差异性沉降^[1]。支承差异沉降不仅影响桥梁线形变化, 而且影响连续梁截面内力变化, 过大沉降将导致桥梁结构自身破坏, 甚至危及行车安全^{[2, 3, 4]}。

常用的支承沉降观测方法主要包括百分表、精密水准仪等人工观测方法和GPS、光电成像等自动监测方法^[5]。伴随着技术的进步, 尤其是桥梁健康监测系统的推广应用, 桥梁线形、梁体应变等指标通常是健康监测系统的必测指标^{[6, 7]}, 获取线形所需位移传感器的布设是技术难点, 试图从连续梁桥受力特性出发, 建立梁体应变改变量与桥梁线形间的关系显得尤为必要。近年来, 光纤传感技术作为学术研究热点取得许多创新性成果, 长标距FBG传感技术很好地解决了混凝土梁桥的动静态应变监测、温度监测等^{[8, 9, 10]}。文献[11]从受弯构件基本原理出发, 推导了梁体挠曲线方程与应变间的理论关系式。文献[12]利用B样条函数和大变形理论, 将输油管道简化为梁, 推导了基于应变的管道变形计算方法。上述方法研究重点均是梁体挠曲线测试。作者所在课题组前期开展了基于分布式光纤应变传感技术的改进共轭梁法监测梁体变形的研究^[13], 虽然突破了传统共轭梁法不适用于支承沉降情况, 但是仍没能实现对支承差异沉降的识别, 而是将支承差异沉降作为已知量用于梁体变形监测。

本文首先以等跨连续梁为对象, 采用基本力学原理推导梁体应变改变量与支承差异沉降量之间关系的解析式, 从理论上证明二者间存在显著关系。其次, 采用更具普适性的不等跨连续梁开展模型试验研究, 分析了应变监测数据与支承差异沉降之间的关系, 并与理论解比较。最后, 提出了基于应变监测的连续梁支承差异沉降识别策略及基本流程。

1 本文方法

1.1 梁体应变改变量与支承差异沉降量之间关系解析式

1.1.1 边支座沉降

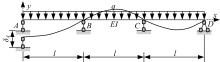
图1为等跨连续梁在边支座产生差异沉降时对应的计算模型。其中, 梁跨度为l;截面抗弯刚度为EI;各跨所受均布线荷载为q;左侧支座A的竖向变形量为δ_A 。坐标系原点位于支座A处,以水平向右为x轴正方向,表示截面位置坐标;以竖直向上为y轴正方向, 正值表示支座被顶起, 负值表示支座产生沉降。

	Figure Option View Download New Window
	图1 边支座沉降计算模型Fig.1 Computing model for settlement of side pier

选取支座 $\begin{matrix} B 、 C \end{matrix}$ 对应的截面转角作为基本未知量, 列出各跨杆端弯矩方程, 根据位移法基本原理和结点平衡方程, 可求解截面转角, 进而可以得到各支座竖向支承反力为:

$\begin{matrix} \{\begin{matrix} F_{A} = \frac{2}{5} ql + \frac{8 EI}{5 l^{3}} δ_{A}, F_{B} = \frac{11}{10} ql - \frac{18 EI}{5 l^{3}} δ_{A} \\ F_{C} = \frac{11}{10} ql + \frac{12 EI}{5 l^{3}} δ_{A}, F_{D} = \frac{2}{5} ql - \frac{2 EI}{5 l^{3}} δ_{A} \end{matrix} (1) \end{matrix}$

水平 $\begin{matrix} x \end{matrix}$ 轴代表连续梁的截面位置, 各跨弯矩方程可采用分段函数表示为:

$\begin{matrix} \{\begin{matrix} M_{AB} (x) = - \frac{q}{2} x^{2} + (\frac{2}{5} ql + \frac{8 EI}{5 l^{3}} δ_{A}) x \\ (0 \leq x < l) \\ M_{BC} (x) = - \frac{q}{2} x^{2} + (\frac{3}{2} ql - \frac{2 EI}{l^{3}} δ_{A}) x + \\ (\frac{18 EI}{5 l^{2}} δ_{A} - \frac{11}{10} q l^{2}) (l \leq x < 2 l) \\ M_{CD} (x) = - \frac{q}{2} x^{2} + (\frac{13}{5} ql + \frac{2 EI}{5 l^{3}} δ_{A}) x - \\ (\frac{6 EI}{5 l^{2}} δ_{A} + \frac{33}{10} q l^{2}) (2 l \leq x \leq 3 l) \end{matrix} (2) \end{matrix}$

根据式(2), 可求出由于边墩产生差异沉降 $\begin{matrix} δ_{A} \end{matrix}$ 所导致的各跨截面弯矩变化方程为:

$\begin{matrix} \{\begin{matrix} Δ M_{AB} = \frac{8 EIx}{5 l^{3}} δ_{A} (0 \leq x < l) \\ Δ M_{BC} = (\frac{18 EI}{5 l^{2}} - \frac{2 EIx}{l^{3}}) δ_{A} (l \leq x < 2 l) \\ Δ M_{CD} = (- \frac{6 EI}{5 l^{2}} + \frac{2 EIx}{5 l^{3}}) δ_{A} (2 l \leq x \leq 3 l) \end{matrix} (3) \end{matrix}$

进而, 根据受弯构件的基本原理(见式(4))可得各跨对应的梁体应变改变量 $\begin{matrix} Δε \end{matrix}$ 与边墩差异沉降量 $\begin{matrix} δ_{A} \end{matrix}$ 之间的解析表达式如式(5)所示:

$\begin{matrix} \begin{matrix} ε = \frac{y}{ρ} = \frac{My}{E I_{z}} (4) \\ \{\begin{matrix} Δ ε_{AB} = \frac{8 x}{5 l^{3}} y δ_{A} (0 \leq x < l) \\ Δ ε_{BC} = (\frac{18}{5 l^{2}} - \frac{2 x}{l^{3}}) y δ_{A} (l \leq x < 2 l) \\ Δ ε_{CD} = (- \frac{6}{5 l^{2}} + \frac{2 x}{5 l^{3}}) y δ_{A} (2 l \leq x \leq 3 l) \end{matrix} (5) \end{matrix} \end{matrix}$

式中: $\begin{matrix} y \end{matrix}$ 为截面形心至梁底或应变测点的距离。

1.1.2 中间支座沉降

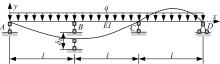
图2为等跨连续梁在中间支座产生差异沉降时对应的计算模型。图2中, 支座B竖向变形量为δ_B,其余参数和坐标系的规定与边墩沉降工况相同。

	Figure Option View Download New Window
	图2 中间支座沉降计算模型Fig.2 Computing model for settlement of mid pier

按照推导边支座沉降工况时采用的相同原理和方法, 可以得到各支座对应的反力、各跨弯矩方程及弯矩变化方程, 也可得出式(6)所示各跨应变改变量 $\begin{matrix} Δε \end{matrix}$ 与中墩差异沉降量 $\begin{matrix} δ_{B} \end{matrix}$ 之间的解析表达式:

$\begin{matrix} \{\begin{matrix} Δ ε_{AB} = - \frac{18 x}{5 l^{3}} y δ_{B} (0 \leq x < l) \\ Δ ε_{BC} = (- \frac{48}{5 l^{2}} + \frac{6 x}{l^{3}}) y δ_{B} (l \leq x < 2 l) \\ Δ ε_{CD} = (\frac{36}{5 l^{2}} - \frac{12 x}{5 l^{3}}) y δ_{B} (2 l \leq x \leq 3 l) \end{matrix} (6) \end{matrix}$

对等跨连续梁上述两种工况的理论推导表明, 支承差异沉降量与应变改变量在各跨均存在线性映射关系。对于某确定截面, 伴随差异沉降量增加, 应变改变量增大, 这为开展基于应变监测的连续梁支承差异沉降识别理论和试验研究奠定了基础。

1.2 案例分析

以某地铁轻轨线路为工程背景, 该工程中高架桥采用等跨连续梁布置, 跨度l=30 m。截面形式为图3所示箱型截面, 其中梁体顶宽9.3 m; 底宽4.0 m; 梁高1.7 m; 截面面积A=4.63 m²; 截面形心距离梁底距离为1.1 m, 即式(5)(6)中y=1.1 m。

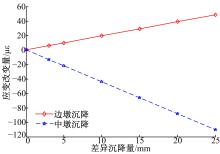
	Figure Option View Download New Window
	图3 箱梁截面尺寸图Fig.3 Box girder cross section dimension

通过分析式(5)(6)可知, 在支座A、B发生沉降时,B支座所在梁的截面应变改变量最大, 即x=30 m处对应截面。将上述已知信息代入式(5)(6)中, 可分别得到边支座 A、B发生沉降时,BA、中间支座B在不同差异沉降量情况下B支座所在梁的截面应该改变量, 变化趋势如图4所示。

	Figure Option View Download New Window
	图4 应变改变量与差异沉降量关系图Fig.4 Relationship between variation of strain and settlement

以微小差异沉降量3 mm为例, 边墩沉降、中墩沉降对应的应变改变量分别为5.87 μ ε 、13.2 μ ε , 表明因支承微小差异沉降导致的相应截面应变改变量完全可测, 采用一般精度的应变采集传感器即可满足工程需求, 且伴随沉降量的增大, 应变改变量呈线性增长。

2 三跨连续梁支承差异沉降试验

2.1 方案设计及模型制作

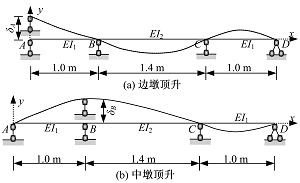
为验证基于应变监测的连续梁支承差异沉降识别方法的有效性, 增强研究问题的普适性, 设计如图5所示的三跨(1.0 m+1.4 m+1.0 m)连续梁模型试验。模型采用Q235级钢制作, 模型截面宽0.5 m; 全长3.6 m; 板厚7.5 mm, 支座与桥墩之间采用专门加工而成的销栓连接, 可实现支座在顺桥向自由转动, 但不能移动。模型共布置了FBG、电阻应变片两种19个应变采集传感器, 其中FBG传感器标距为200 mm, 在支座左右两侧各预留100 mm施测空间, 其余均满跨顺次布设, 两个边跨各布置4个FBG传感器, 中间跨布置6个FBG传感器。为验证FBG传感器采集应变数据的有效性, 在中间跨还按照200 mm间距采用点式方式布置了5个电阻式应变片, 各传感器的具体编号和布设位置详见图5。

	Figure Option View Download New Window
	图5 模型尺寸与传感器布置Fig.5 Model dimension and sensor location

图6为加工制作的且已布设监测元件的待测试试验模型, 试验时, 边支座差异沉降采用厚度为7.5 mm的钢板分三层加高垫在 $\begin{matrix} A \end{matrix}$ 墩下部, 中间支座差异沉降采用厚度为6 mm的钢板分三层加高垫在 $\begin{matrix} B \end{matrix}$ 墩下部, 共两种模式, 6种工况。

	Figure Option View Download New Window
	图6 试验模型Fig.6 Experimental model

2.2 试验结果

图7为FBG、电阻应变片两种应变传感器测试结果及其对比, 数据采集过程中FBG-1传感器失效, 数据丢失。图中数据标签编号规则是短线左侧代表传感器类型, 短线右侧代表对应墩台顶升量。图7(a)为边墩 $\begin{matrix} A \end{matrix}$ 分别顶升7.5、15.0、22.5 mm时两种传感器对应的应变测试结果, 即应变改变量, 从 $\begin{matrix} BC \end{matrix}$ 跨可看出, 在顶升各阶段两种传感器测试结果曲线均近乎重合, R-1号传感器应变微小波动是由于点式传感器自身局限性造成的; 中墩 $\begin{matrix} B \end{matrix}$ 分别顶升6、12、18 mm时, 两种传感器对应的测试结果亦表现出高度吻合。这一比较分析不仅验证了FBG新型应变采集传感器性能的优越性, 而且保证了所采集应变数据的质量。从全局角度分析FBG应变数据, 可明显看出, 不同顶升量在各跨对应的应变改变量均近似呈线性分布特征, 与理论解析式(5)(6)相一致。

	Figure Option View Download New Window
	图7 传感器检测结果比较Fig.7 Result comparison of sensor test

3 试验结果与解析解的对比分析

3.1 试验模型梁底应变改变量与差异沉降量之间关系解析式

式(5)(6)的推导表明, 应变改变量与外荷载无关, 仅与差异沉降量有关。因此, 边墩、中墩差异沉降时试验模型对应的计算简图分别如图8(a)(b)所示, 采用前文推导等跨连续梁梁体应变改变量与支承差异沉降量之间关系解析式对应的方法, 求解支座反力、弯矩方程及弯矩变化方程, 进而推导梁底应变改变量与差异沉降量之间关系的解析式。

为便于求解, 采用代数量予以推导计算, 其中弹性模型E=2.0× 10⁵ N/mm², 其余参量按前文已知条件取值。针对边墩 $\begin{matrix} A \end{matrix}$ 顶升, 推导得到各跨梁底应变改变量与顶升量(即支承差异沉降量, 以正值输入)之间关系的解析式为:

$\begin{matrix} \begin{matrix} Δ ε_{AB} = 5.12 δ_{A} x (0 \leq x < 1.0) \\ Δ ε_{BC} = - 4.73 δ_{A} x + 9.85 δ_{A} (1.0 \leq x < 2.4) \\ Δ ε_{CD} = 1.5 δ_{A} x - 5.08 δ_{A} (2.4 \leq x \leq 3.4) \end{matrix} \end{matrix}$

针对中墩 $\begin{matrix} B \end{matrix}$ 顶升, 各跨梁底应变改变量与顶升量之间关系的解析式为:

$\begin{matrix} \begin{matrix} Δ ε_{AB} = - 11.21 δ_{B} x (0 \leq x < 1.0) \\ Δ ε_{BC} = 13.89 δ_{B} x - 25.1 δ_{B} (1.0 \leq x < 2.4) \\ Δ ε_{CD} = 8.24 δ_{B} x + 28.02 δ_{B} (2.4 \leq x \leq 3.4) \end{matrix} \end{matrix}$

	Figure Option View Download New Window
	图8 试验模型的计算简图Fig.8 Computing model for experimental model

3.2 结果对比分析

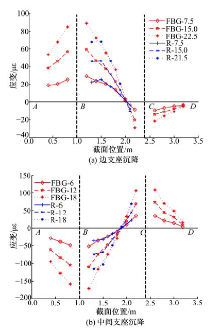
图9为FBG传感器采集应变与理论解析解应变的比较分析, 其中(a)~(c)为边墩顶升工况, (d)~(f)为中墩顶升工况。通过(a)~(c)与(d)~(f)的对比分析不难发现, 各跨应变符号刚好相反, 反弯点均位于中间跨。边墩顶升时, 反弯点左侧梁底应变为拉应变、右侧为压应变; 中墩顶升时, 反弯点左侧梁底应变为压应变、右侧为拉应变, 这为基于应变符号判断沉降支承位置提供了便捷方法。由于中间桥墩所受约束作用大于边墩所受约束作用, 因此, 在发生相同顶升量时, 同一截面位置的应变改变量中墩变形模式大于边墩变形模式, 即用于识别连续梁桥差异沉降的应变传感器应优先布置在中间支承所在区域对应梁的截面。从全局角度分析可知, 两种模式对应的6种工况, 各跨试验采集应变数据与理论解析解变化趋势相同, 数值大致相等, 二者吻合程度高, 通过试验研究进一步证明了本文基于应变识别连续梁支承差异沉降的可行性。

	Figure Option View Download New Window
	图9 FBG应变与解析解对比Fig.9 Comparison between FBG-strain and analytical solution

3.3 基于应变监测的支承差异沉降识别流程

首先, 应结合连续梁受力特点, 科学制定监测方案, 以识别支承差异沉降为目的的应变传感器应主要布置在中间各支承所在区域对应的梁截面底部, 同时做好沉降观测点的埋设和初始高程的测量。其次, 根据应变测试结果, 根据同一温度情况下应变改变量的变化规律, 初步判断支承是否有差异沉降发生。第三, 通过初步判别如发现有支承存在差异沉降可能, 应深入细致分析, 对差异沉降位置进行精确定位。第四, 通过理论推导建立应变改变量与支承差异沉降量之间的函数关系式, 并结合预先埋设的沉降观测点和观测成果, 对建立的函数关系式做修正, 以提高后续识别精度。

需要说明的是, 基于应变监测的连续梁支承差异沉降识别理论与方法是对现有沉降观测手段的有力补充, 与传统观测方法不是一种简单的取代关系, 而是互为补充, 可降低现有观测工作量, 提高识别效率。

4 结论

(1)以三跨相等的连续梁为研究对象, 运用基本力学原理, 构建了基于应变的等跨连续梁支承差异沉降识别理论; 并以某箱型截面刚性轻轨桥为例, 证明支承微小差异沉降导致的梁体截面应变改变量是完全可测和可识别的。

(2)通过三跨不相等的连续梁模型试验, 借助两种应变采集传感器, 验证了FBG新型传感器的优良性能; 通过顶升方法模拟沉降, 深入分析了边墩顶升、中墩顶升两种模式6种工况下各跨梁底应变改变量与支承差异沉降量之间的关系。

(3)以提取模型试验的计算简图为基础, 分别推导了试验模型边墩、中墩差异沉降下梁底应变改变量与桥墩差异沉降量之间的关系式; 两种模式在不同差异沉降下的理论解与试验测试结果的比较分析均表明, 二者在趋势和数值上吻合良好; 最后, 对基于应变的连续梁支承差异沉降识别基本流程和策略作了简要叙述。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	李国和, 孙树礼, 许再良, 等. 地面沉降对高速铁路桥梁工程的影响及对策[J]. 铁道工程学报, 2008, 24(4): 37-41, 61. Li Guo-he, Sun Shu-li, Xu Zai-liang, et al. The influence of land subsidence on the bridge of high-speed railway and its engineering countermeasures[J]. Journal of Railway Engineering Society, 2008, 24(4): 37-41, 61. [本文引用:1]
[2]	邹振华. 不均匀沉降对大跨连续梁及轨道结构影响分析[J]. 铁道工程学报, 2014, 30(3): 61-65. Zou Zhen-hua. Effects analysis of differential settlementon on long-span continuous bridge and ballastless track structure[J]. Journal of Railway Engineering Society, 2014, 30(3): 61-65. [本文引用:1]
[3]	王昆鹏, 夏禾, 郭薇薇, 等. 桥墩不均匀沉降对高速列车运行安全影响研究[J]. 振动与冲击, 2014, 33(6): 137-142, 155. Wang Kun-peng, Xia He, Guo Wei-wei, et al. Influence of uneven settlement of bridge piers on running safely of high-speed trains[J]. Journal of Vibration and Shock, 2014, 33(6): 137-142, 155. [本文引用:1]
[4]	Yau J D. Response of a train moving on multi-span railway bridges undergoing ground settlement[J]. Engineering Structures, 2009, 31(9): 2115-2122. [本文引用:1]
[5]	宋彦君. 梁式桥监测中的应变-位移转换技术及裂缝损伤识别方法研究[D]. 长春: 吉林大学交通学院, 2012. Song Yan-jun. Research on the crack identification method and strain-deflection transferring technology in beam bridge monitoring[D]. Changchun: College of Transportation, Jilin University, 2012. [本文引用:1]
[6]	李惠, 欧进萍. 斜拉桥结构健康监测系统的设计与实现(Ⅱ): 系统实现[J]. 土木工程学报, 2006, 39(4): 45-53. Li Hui, Ou Jin-ping. Design and implementation of health monitoring systems for cable-stayed bridges(Ⅱ): implementations[J]. China Civil Engineering Journal, 2006, 39(4): 45-53. [本文引用:1]
[7]	凌同华, 张胜, 李升冉, 等. 邻近隧道施工既有桥桩变形控制及注浆加固方案优化[J]. 中南大学学报: 自然科学版, 2014, 45(7): 2394-2400. Ling Tong-hua, Zhang Sheng, Li Sheng-ran, et al. Controlling of existing bridge piles deformation induced by adjacent tunneling and scheme of optimizing grouting reinforcement[J]. Journal of Central South University (Science and Technology), 2014, 45(7): 2394-2400. [本文引用:1]
[8]	Moyo P, Brownjohn J M W, Suresh R, et al. Development of fiber Bragg grating sensors for monitoring civil infrastructure[J]. Engineering Structures, 2005, 27(12): 1828-1834. [本文引用:1]
[9]	Cumunel G, Delepine-Lesoille S, Argoul P. Long-gage optical fiber extensometers for dynamic evaluation of structures[J]. Sensors and Actuators A: Physical, 2012, 184(3): 1-15. [本文引用:1]
[10]	李爱群, 周广东. 光纤Bragg光栅传感器测试技术研究进展与展望(I): 应变、温度测试[J]. 东南大学学报: 自然科学版, 2009, 39(6): 1298-1306. Li Ai-qun, Zhou Guang-dong. Progress and prospect of fiber Bragg grating sensors measurement technology (I): strain and temperature measurement[J]. Journal of Southeast University (Science and Technology), 2009, 39(6): 1298-1306. [本文引用:1]
[11]	徐辉, 任伟新. 基于光纤光栅传感器的桥梁挠曲线测试[C]∥第16届全国结构工程学术会议论文集, 北京, 2007: 407-410. [本文引用:1]
[12]	毅力琦, 丁克勤, 钱才富. 基于应变的长输管道变形计算方法研究[J]. 固体力学学报, 2011, 32(S1): 310-313. Yi Li-qi, Ding Ke-qin, Qian Cai-fu. Research on calculation method of long-distance pipeline's deformation based on strain[J]. Chinese Journal of Solid Mechanics, 2011, 32(S1): 310-313. [本文引用:1]
[13]	沈圣, 吴智深, 杨才千, 等. 基于分布式光纤应变传感技术的改进共轭梁法监测结构变形分布研究[J]. 土木工程学报, 2010, 43(7): 63-70. Shen Sheng, Wu Zhi-shen, Yang Cai-qian, et al. An improved conjugated beam method for structural deformation monitoring based on distributed optical fiber strain sensing technique[J]. China Civil Engineering Journal, 2010, 43(7): 63-70. [本文引用:1]

2008

0.0

. 2008, 24(4):37-41, 61 DOI:doi:10.3969/j.issn.1006-2106.2008.04.010

The influence of land subsidence on the bridge of high-speed railway and its engineering countermeasures

地面沉降对高速铁路桥梁工程的影响及对策

Li Guo-he , Sun Shu-li , Xu Zai-liang

李国和, 孙树礼, 许再良

研究目的:研究地面沉降在不同区域及不同发展阶段对不同结构类型桥梁的影响,提出适宜的防治对策与工程措施,供高速铁路勘测、设计及施工参考.研究结论:在抽水井附近及地面沉降的中心区域,不均匀沉降较为严重,对桥梁结构变形影响较大;在地面沉降的扩展区域内,地面沉降引起地层和桥体变形主要是竖向变形,虽然下沉量相对较大,但对桥梁结构变形的影响却不大;在地面沉降区内,表现为平缓的下沉,对高速铁路桥梁工程影响不大,但局部地段出现差异沉降较大的地段.因此在铁路工程建设中应合理选址,优化桥梁布置及结构形式,优先采用简支结构,并采取适宜的工程措施来增强铁路工程本身对地面沉降的适应性.

... 地面沉降、墩台周边堆卸载、车辆循环荷载等均可能导致支承(桥墩、桥台)产生差异性沉降^[1] ...

2014

0.0

. 2014, 30(3):61-65 DOI:doi:10.3969/j.issn.1006-2106.2014.03.011

Effects analysis of differential settlementon on long-span continuous bridge and ballastless track structure

不均匀沉降对大跨连续梁及轨道结构影响分析

Zou Zhen-hua.

邹振华

研究目的:本文结合某高速铁路大跨度无砟轨道桥梁不均匀沉降工程实例,分析墩台发生不均匀沉降工况下,桥梁结构及桥上无砟轨道受力情况,并对结构安全性和适应性进行综合分析,最后根据沉降值范围,提出相应的处理方案及建议。论文旨在通过针对性研究,对今后大跨连续梁不均匀沉降的整治处理提供参考。研究结论:通过计算分析得出:(1)大跨连续梁不均匀沉降值超过现行设计规范一定范围时,对墩台受力影响较小,对连续梁主梁及轨道受力影响可控;(2)现行规范应适当放宽对大跨连续梁不均匀沉降的限值,有利于在设计阶段从源头上既保证结构安全又节约建设成本;(3)对较大的不均匀沉降应及时采取措施进行综合整治;(4)该研究成果可应用于铁路大跨连续梁因软土地基、地下水位变化等因素引起的墩台不均匀沉降整治。

... 支承差异沉降不仅影响桥梁线形变化,而且影响连续梁截面内力变化,过大沉降将导致桥梁结构自身破坏,甚至危及行车安全^[2,3,4] ...

2014

0.0

. 2014, 33(6):137-142, 155

Influence of uneven settlement of bridge piers on running safely of high-speed trains

桥墩不均匀沉降对高速列车运行安全影响研究

Wang Kun-peng , Xia He , Guo Wei-wei

王昆鹏, 夏禾, 郭薇薇

The piles of bridge built on soft clay foundation produce additional settlement due to cyclic loading of moving trains, which affects the operation safety of the train. Dynamic model of vehicle-bridge system and settlement model of pile foundation-soil system are established. Reaction force induced by the moving vehicle is got from dynamic model, firstly, which is taken as excavation of settlement model to study the train-induced cumulative settlement. Then, the additional track irregularity induced by settlement pier is overlaid to original track irregularity, and consider the influence of the vertical centrifugal force induced by settlement pier, which influences on running safety of train is studied by dynamic model. Calculation is performed with German ICE3 train running on the 32 m three-span simple-supported beam. The calculated results show that most cumulative settlement occurs in the range of 10 m below the pile bottom. Relative camber of the bridge induced by adjacent pile settlement is more dangerous to running safety of the train, because the train bears vertical centrifugal force in the direction opposite to the settlement direction, when it runs on the bridges with camber.

... 支承差异沉降不仅影响桥梁线形变化,而且影响连续梁截面内力变化,过大沉降将导致桥梁结构自身破坏,甚至危及行车安全^[2,3,4] ...

2009

0.0

... 支承差异沉降不仅影响桥梁线形变化,而且影响连续梁截面内力变化,过大沉降将导致桥梁结构自身破坏,甚至危及行车安全^[2,3,4] ...

2012

0.0

. 2012, :-

Research on the crack identification method and strain-deflection transferring technology in beam bridge monitoring

梁式桥监测中的应变-位移转换技术及裂缝损伤识别方法研究

Song Yan-jun.

宋彦君

桥梁是道路交通的咽喉，桥梁的通行能力直接决定着整个道路的通行能力。施工质量、材料老化以及交通荷载的增长等因素可能会导致桥梁的使用状态退化或不满足交通荷载增长的需求。在这种情况下，如果不对桥梁进行有效的监测，准确掌握桥梁的使用状态信息，很可能会导致桥塌车毁的交通事故，对人民的生命和财产造成极大地伤害。因此，桥梁监测是一项十分有意义的工作。所谓桥梁监测就是采用预埋等方式在桥梁结构中布置一些监测仪器，实时采集桥梁的不同响应，根据响应对桥梁结构的使用状态进行判定。桥梁的监测参数一般包括位移、应变、变位、温度、动力响应等，而其中位移是一个容易精确测量的重要参数。并且位移可以同桥梁的刚度建立内在联系，因此桥梁结构的位移监测备受人们的青睐。当桥梁跨越江、河、山涧等障碍物，或跨越城市道路时，由于不能布设固定支架，传统的接触式位移测量方法存在无法安装的困难，并且位移测量装置存在人为损坏的风险。而采用可以固定于桥梁上的静力位移测试设备（例如静力水准仪等），又不能实时采集桥梁的动态位移信息。面对这种困境，如何实时获得桥梁结构的位移信息是一个十分有意义的研究课题。对于梁式桥而言，桥梁结构的应变与位移存在一定的内在联系，通过应变的实时监测数据来获取位移信息是可行的。对于混凝土梁式桥，实测应变中包含了混凝土的徐变、收缩、温度、恒载以及活载等引起的应变。如果想要获得活载引起的桥梁结构位移响应，则需要实测到活载引起的桥梁应变。在混凝土梁式桥的监测中，实测应变包含了徐变、荷载等多种因素引起的应变。因此，如何从监测应变中对各种因素引起的应变进行分离是十分必要的。裂缝是混凝土梁式桥最为典型的病害之一，裂缝对桥梁结构的耐久性、强度和稳定性都存在一定的影响。因此，准确的掌握裂缝信息，从而采取适当的维修和加固措施对于确保桥梁的安全通行是十分必要的。引起混凝土梁式桥出现裂缝的因素很多，例如荷载、温度变化、收缩、地基础变形、钢筋锈蚀、冻胀、施工材料质量以及施工工艺质量等都会引起裂缝。混凝土梁式桥中的裂缝一般存在两个特点：（1）隐蔽性，包括裂缝早起的隐蔽性和出现在隐蔽部位的裂缝隐蔽性；（2）数量多，对于使用一段时间的老桥，裂缝数量可能会很多。如果采用传统的无损检测方法，则势必要浪费大量的人力和物力，并且难以发现隐蔽部位的裂缝病害。研究表明，桥梁结构的动力参数对裂缝存在一定的敏感性。如何通过动力参数的变化来准确的识别出裂缝损伤是桥梁工程领域一个十分重要的研究方向。本文依托863国家高科技研究发展计划项目“季节冻土区大范围道路灾害参数监测与辨识预警系统研究（2009AA11Z104）”，针对梁式桥监测中的应变-位移转换技术及裂缝损伤识别方法进行研究，主要开展了以下研究工作： 1、从位移和应变的基本定义出发，通过建立二者的内在联系，来形成基于应变计的梁式桥位移动态测量方法。本方法无需任何位移测量仪器，只利用已有的应变数据，便能实时地分析出桥梁位移，并能形成位移的动力响应。分别对简支梁和连续梁进行了数值模拟分析，模拟分析结果表明，采用本文方法形成的简支梁和连续梁位移静力响应和动力响应精度均较高，在应变数值混有1%随机误差的情况下位移的静力响应和动力响应的误差小于5%。 2、对徐变机理、徐变理论和徐变预测模式进行深入研究的基础上，采用有限元方法与递归方法相结合，形成了基于有限元方法的徐变效应分离两层次递归算法，该算法可以实现徐变效应引起的应变和外荷载引起应变的分离。以长春市东风大街立交桥为工程依托，对本文提出的徐变效应分离算法进行了验证。实践结果表明，本文提出的徐变效应分离算法是可行的和有效的。 3、对基于伯努利梁模型及基于有限元方法的带裂缝工作的简支梁模态参数理论分析模型进行了分析。基于理论分析模型计算了多种裂缝损伤工况下简支梁的模态参数，分析了裂缝宽度和裂缝高度等参数对简支梁模态参数的影响规律。并且对比了这两种理论计算模型的特点。 4、以多片简支梁桥为研究对象，采用基于模态柔度差曲率及优化支持向量机的分步识别法（PSO-SVM）实现其损伤位置及程度的识别。该方法首先通过模态柔度差曲率指标实现结构的损伤定位；其次通过粒子群优化支持向量机实现结构的损伤程度识别。以一座五片简支T梁桥的数值模拟结果来说明本文方法的识别精度和有效性。数值模拟结果表明，PSO-SVM可以准确的实现多片简支梁桥的单位置及多位置损伤定位；对裂缝深度的识别精度较高，最大相对误差为4.13%。

... 常用的支承沉降观测方法主要包括百分表、精密水准仪等人工观测方法和GPS、光电成像等自动监测方法^[5] ...

2006

0.0

... 伴随着技术的进步,尤其是桥梁健康监测系统的推广应用,桥梁线形、梁体应变等指标通常是健康监测系统的必测指标^[6,7],获取线形所需位移传感器的布设是技术难点,试图从连续梁桥受力特性出发,建立梁体应变改变量与桥梁线形间的关系显得尤为必要 ...

2014

0.0

. 2014, 45(7):2394-2400

Controlling of existing bridge piles deformation induced by adjacent tunneling and scheme of optimizing grouting reinforcement

邻近隧道施工既有桥桩变形控制及注浆加固方案优化

Ling Tong-hua , Zhang Sheng , Li Sheng-ran

凌同华, 张胜, 李升冉

为了分析隧道在已有桥桩附近施工时对桥桩产生的影响,依托深圳市葵坝路隧道下穿高速公路桥梁段,采用三维有限差分法研究隧道动态施工引起的地表沉降以及桥梁桩基变形的规律,将数值模拟结果与现场监测结果进行对比分析,验证本文方法的正确性和有效性。为了进一步得到控制地表沉降和桥桩变形的最优注浆加固方案,通过改变注浆范围提出不进行注浆加固、原注浆加固以及优化后的注浆加固3种方案,并对这3种加固方案下地表沉降和桥桩变形进行对比分析。研究结果表明:优化后的注浆加固方案不但能够有效控制地表沉降和桥桩位移,而且能减小注浆范围,是最佳注浆加固方案。

2005

0.0

... 近年来,光纤传感技术作为学术研究热点取得许多创新性成果,长标距FBG传感技术很好地解决了混凝土梁桥的动静态应变监测、温度监测等^[8,9,10] ...

2012

0.0

... 近年来,光纤传感技术作为学术研究热点取得许多创新性成果,长标距FBG传感技术很好地解决了混凝土梁桥的动静态应变监测、温度监测等^[8,9,10] ...

2009

0.0

. 2009, 39(6):1298-1306 DOI:doi:10.3969/j.issn.1001-0505.2009.06.041

Progress and prospect of fiber Bragg grating sensors measurement technology (I): strain and temperature measurement

光纤Bragg光栅传感器测试技术研究进展与展望(I): 应变、温度测试

Li Ai-qun , Zhou Guang-dong.

李爱群, 周广东

摘　要：综述了土木工程中用于结构应变和温度测试的各种光纤Bragg光栅传感器的研究现状,对其存在的问题进行了分析并指出其发展方向.从传感器制作方面分类介绍了管式、基片式和嵌入式封装应变传感器,增敏型和不受应变干扰的温度传感器,应变和温度同时测量传感器的最新成果.并概括了各种传感器的基本原理,总结了其优点和不足.通过对光纤光栅传感器特点和土木工程结构测试需求的综合分析,指出光纤光栅传感器在混凝土中的埋入技术及光纤光栅传感器的实用性、在结构中的优化布置、耐久性和长期稳定性等问题还需要进一步研究.

... 近年来,光纤传感技术作为学术研究热点取得许多创新性成果,长标距FBG传感技术很好地解决了混凝土梁桥的动静态应变监测、温度监测等^[8,9,10] ...

2007

0.0

. 2007, :407-410

基于光纤光栅传感器的桥梁挠曲线测试

徐辉, 任伟新

本文提出了基于光纤光栅(FBG)应变传感器的桥梁挠曲线测试方法,详细阐述了其原理、算法,以及实施过程,推导了相应的公式,实验验证表明该方法具有很高的精度。

... 文献[11]从受弯构件基本原理出发,推导了梁体挠曲线方程与应变间的理论关系式 ...

2011

0.0

. 2011, 32(S1):310-313

Research on calculation method of long-distance pipeline's deformation based on strain

基于应变的长输管道变形计算方法研究

Yi Li-qi , Ding Ke-qin , Qian Cai-fu.

毅力琦, 丁克勤, 钱才富

论文提出了基于应变分析的管道变形计算方法.将管道看作梁,考虑轴线伸长的情况,根据梁大变形问题的几何方程建立应变与位移的关系,利用同一截面的不同位置及同一母线上不同位置的应变值,采用数值计算的方法通过应变与位移的关系式求解得到梁的变形量.

... 文献[12]利用B样条函数和大变形理论,将输油管道简化为梁,推导了基于应变的管道变形计算方法 ...

2010

0.0

. 2010, 43(7):63-70

An improved conjugated beam method for structural deformation monitoring based on distributed optical fiber strain sensing technique

基于分布式光纤应变传感技术的改进共轭梁法监测结构变形分布研究

Shen Sheng , Wu Zhi-shen , Yang Cai-qian

沈圣, 吴智深, 杨才千

摘　要：工程结构的变形分布是识别结构损伤累积的一个重要手段和指标,但通过现有各种＂点式＂传感技术还难以全面准确监测结构变形分布。本文基于PPP-BOTDA分布式应变测量技术,提出一种适用于监测简支结构和多跨连续结构变形分布的改进共轭梁法。首先针对传统共轭梁法无法监测由支座沉降产生结构变形的缺点进行改进,使之适用于荷载与支座沉降同时作用的情况。根据本文方法得到的结构变形分布与应变分布呈显式线性关系,与荷载及截面刚度条件无关。理论分析与试验结果均表明,由本文方法得到的某跨结构变形监测精度仅由该跨应变测量误差控制,与其它跨应变测量误差无关,这就限制了应变测量误差的影响范围并保证结构变形的准确监测。

... 作者所在课题组前期开展了基于分布式光纤应变传感技术的改进共轭梁法监测梁体变形的研究^[13],虽然突破了传统共轭梁法不适用于支承沉降情况,但是仍没能实现对支承差异沉降的识别,而是将支承差异沉降作为已知量用于梁体变形监测 ...