混沌粒子群算法优化最小二乘支持向量机的混凝土强度预测

引用本文

张静, 刘向东. 混沌粒子群算法优化最小二乘支持向量机的混凝土强度预测.吉林大学学报:工学版, 2016, 46(4): 1097-1102
ZHANG Jing, LIU Xiang-dong. Prediction of concrete strength based on least square support vector machine optimized by chaotic particle swarm optimization. Journal of Jilin University Engineering and Technology Edition, 2016, 46(4): 1097-1102 复制到剪切板

Permissions

混沌粒子群算法优化最小二乘支持向量机的混凝土强度预测

张静^1,², 刘向东¹

1.内蒙古工业大学材料科学与工程学院,呼和浩特 010051

2.内蒙古建筑职业技术学院机电与暖通工程分院,呼和浩特 010070

刘向东(1966-),男,教授,博士.研究方向:材料工程.E-mail:zj601187@163.com

作者简介:张静(1983-),女,副教授,博士研究生.研究方向:建筑材料.E-mail:zhangjing@126.com

基金:国家自然科学基金项目(51164023); 国家教育部新世纪优秀人才支持计划项目(NCET-13-0847); 内蒙古自治区教育厅项目(NJZC13344)

摘要

为了获得更理想的混凝土强度预测结果,提出一种混沌粒子群算法优化最小二乘支持向量机(LSSVM)的混凝土强度预测模型。首先采集混凝土强度数据,并进行归一化处理。然后采用LSSVM对混凝土强度与影响因子之间的变化关系进行建模,并采用混沌粒子群算法搜索最优LSSVM参数。最后采用具体混凝土强度预测实例对其性能进行分析。结果表明,本文模型可以准确描述混凝土强度与影响因子间的变化关系,提高了混凝土强度预测精度,具有一定的实际应用价值。

关键词: 土木工程; 混凝土强度; 最小二乘支持向量机; 混沌粒子群算法; 通用性测试

中图分类号:TU528 文献标志码:A 文章编号:1671-5497(2016)04-1097-06

Prediction of concrete strength based on least square support vector machine optimized by chaotic particle swarm optimization

ZHANG Jing^1,², LIU Xiang-dong¹

1.School of Materials Science and Engineering, Inner Mongolia University of Technology, Hohhot 010051, China

2.Department of Electromechanical and Heating Ventilation Engineering, Inner Mongola Technical College of Construction, Hohhot 010070,China

Abstract

In order to obtain precise prediction of concrete strength, a prediction model of concrete strength is proposed, which is based on Least Square Support Vector Machine (LSSVM) optimized by Chaotic Particle Swarm Optimization (CPSO). First, the data of concrete strength are collected and normalized. Second, LSSVM is used to model the relationship between the concrete strength and the impact factors, and CPSO algorithm is applied to search the optimal parameters of LSSVM. Finally, the prediction performance is analyzed on the concrete strength data. Results show that the proposed model can accurately describe the relationship between the concrete strength and the impact factors, and improve the prediction accuracy of the concrete strength. This model has certain practical value.

Keyword: civil engineering; concrete strength; least squares support vector machine(LSSVM); chaotic particle swarm optimization(CPSO) algorithm; general test

Show Figures

0 引言

针对混凝土强度的预测问题, 国内外学者提出许多有效的预测模型^{[1, 2, 3]}。最原始预测模型主要为多元线性回归分析, 其假设混凝土强度与影响因素之间是一种线性关系, 建模速度快、易实现^[4], 但影响混凝土强度的因素十分复杂, 且各种因素之间互相作用, 导致混凝土强度与其影响因素之间是一种复杂的非线性关系, 而多元线性回归分析模型无法描述混凝土强度的非线性变化特点, 预测精度低、实际应用范围比较窄^{[5, 6, 7]}。随后, 出现了基于非线性理论的混凝土强度预测模型, 如神经网络、支持向量机等机器学习算法^{[8, 9, 10, 11, 12]}, 它们不需要知道处理问题的精确函数, 就可以较好地拟合混凝土强度与影响因素之间的关系, 混凝土强度的预测精度得到了提高, 成为当前主要的研究方向。

最小二乘支持向量机(Least squares support vector machine, LSSVM)不仅克服了神经网络的不足和继承了支持向量机的优点, 而且加快了训练速度, 解决了支持向量机建模效率低的缺陷^[13], 为了获得更加理想的混凝土强度预测结果, 提出了一种基于混沌粒子群(Chaotic particle swarm optimization, CPSO)算法优化最小二乘支持向量机的混凝土强度预测模型, 并通过具体应用实例测试证明了该模型的可行性。

1 最小二乘支持向量机和混沌粒子群算法

1.1 最小二乘支持向量机

最小二乘支持向量机对标准支持向量机进行了简化, 降低了计算复杂度, 加快了学习速度, 更加适合于混凝土强度预测建模。设收集的混凝土强度样本为: $\begin{matrix} {x_{i}, y_{i}}_{i = 1}^{l}, x_{i} \in R^{n} 为第 i \end{matrix}$ 个混凝土强度样本的影响因子, $\begin{matrix} y_{i} \in R^{n} 为第 i \end{matrix}$ 个样本混凝土强度的期望输出值, LSSVM的线性回归函数为:

$\begin{matrix} f (x) = ω^{T} \cdot φ (x) + b (1) \end{matrix}$

式中: $\begin{matrix} φ (x) \end{matrix}$ 为映射函数; ω为权值向量;b 为偏置向量。

根据结构风险最小化原理, LSSVM的回归优化目标可以表示为:

$\begin{matrix} \begin{matrix} \min_{ω, b, ξ} J (ω, ξ) = \frac{1}{2} ω^{T} ω + \frac{γ}{2} \overset{n}{\sum_{i = 1}} ξ_{i}^{2} \\ s.t. y_{i} [ω^{T} φ (x) + b] = 1 - ξ_{i} (2) \\ i = 1, 2, \dots, l \end{matrix} \end{matrix}$

式中: $\begin{matrix} ξ_{i} \end{matrix}$ 为误差变量; $\begin{matrix} γ \end{matrix}$ 为调整参数。

引入Lagrange乘子 $\begin{matrix} α_{i} \end{matrix}$ 对LSSVM回归过程进行优化, 可以得到:

$\begin{matrix} \begin{matrix} L (ω, b, ξ, α) = \\ J (ω, ξ) - \overset{l}{\sum_{i = 1}} (α_{i} {y_{i} [ω^{T} φ (x_{i}) - b]} - 1 + ξ_{i}) (3) \end{matrix} \end{matrix}$

根据Karush-Kuhn-Tucker(KKT)条件, 可以得到:

$\begin{matrix} \frac{\partial L}{\partial ω} = 0, \frac{\partial L}{\partial b} = 0, \frac{\partial L}{\partial ξ_{i}} = 0, \frac{\partial L}{\partial α_{i}} = 0 (4) \end{matrix}$

消去 $\begin{matrix} ξ_{i} \end{matrix}$ 和 $\begin{matrix} ω \end{matrix}$ 后, 即有:

$\begin{matrix} [\begin{matrix} 0 & Q^{T} \\ Q & K + γ^{- 1} I \end{matrix}] [\begin{matrix} b \\ A \end{matrix}] = [\begin{matrix} 0 \\ Y \end{matrix}] (5) \end{matrix}$

式中: $\begin{matrix} Q = {[1 \dots 1]}^{T}; A = [a_{1} \dots a_{l}]^{T} 。 \end{matrix}$

对于非线性回归问题, 根据Mercer条件采用核函数转化成为线性回归问题, 核函数定义如下:

$\begin{matrix} k (x_{k}, x_{h}) = φ (x_{k})^{T} φ (x_{h}) (6) \end{matrix}$

本文选择径向基核函数, 其定义如下:

$\begin{matrix} k (x, x_{i}) = \exp (- \frac{| x - x_{i} |^{2}}{σ^{2}}) (7) \end{matrix}$

式中: $\begin{matrix} σ \end{matrix}$ 为核函数宽度。

这样式(5)变为:

$\begin{matrix} \begin{matrix} [\begin{matrix} 0 & y_{1} & \dots & y_{l} \\ y_{1} & y_{1} y_{1} k (x_{1}, x_{1}) + γ^{- 1} & \dots & y_{1} y_{1} k (x_{1}, x_{l}) \\ ︙ & ︙ & ︙ \\ y_{1} & y_{1} y_{1} k (x_{l}, x_{l}) l & \dots & y_{l} y_{l} k (x_{l}, x_{l}) + γ^{- 1} \end{matrix}] \times \\ [\begin{matrix} b \\ a_{1} \\ ⋮ \\ a \end{matrix}] = [\begin{matrix} 0 \\ 1 \\ ⋮ \\ 1 \end{matrix}] (8) \end{matrix} \end{matrix}$

LSSSVM的预测模型为:

$\begin{matrix} f (x) = \overset{l}{\sum_{i = 1}} α_{i} k (x, x_{i}) + b (9) \end{matrix}$

1.2 混沌粒子群优化算法

设粒子i的飞行速度和位置分别为v_i=(v_i1,v_i2,…,v_iD )^T 和x_i=( x_i1,x_i2,…, x _iD ) ^T,粒子i和种群的历史最优位置分别为p_i=(p_i1, p _i2,…, p _iD)和p_g=(p_g1,p_g2,…, p _gD),在第t次迭代过程中, 粒子位置和速度更新方式为:

$\begin{matrix} \begin{matrix} V_{id} (t + 1) = ω V_{id} (t) + c_{1} r_{1} (p_{id} - X_{id} (t)) + \\ c_{2} r_{2} (p_{gd} - X_{id} (t)) (10) \\ X_{id} (t + 1) = X_{id} (t) + V_{id} (t + 1) (11) \end{matrix} \end{matrix}$

式中: $\begin{matrix} c_{1} 、 c_{2} 为加速系数; ω \end{matrix}$ 为惯性权值, 其定义如下:

$\begin{matrix} ω = ω_{\max} - \frac{iter}{ite r_{\max}} (ω_{\max} - ω_{\min}) (12) \end{matrix}$

式中: $\begin{matrix} ω_{\max} \end{matrix}$ 和 $\begin{matrix} ω_{\min} \end{matrix}$ 分别为最大和最小的惯性权值^[14]。iter为当前迭代次数;iter_max为最大迭代次数。

在基本粒子群优化(PSO)算法中, 如果一个粒子得到了一个局部最优解, 粒子群中的其他粒子飞向该局部最优解聚集, 易导致整个粒子群陷入局部最优解, 难以找到问题的全局最优解。混粒子群算法(CPSO)将混沌系统的随机性和遍历性引入到基本粒子群优化算法, 对粒子群的历史最优解进行混沌处理, 帮助粒子群跳出局部最优解, 寻优能力更强^[14]。

2 CPSO-LSSVM的混凝土强度预测模型

2.1 混凝土强度预测模型的参数优化

分析LSSVM的工作原理可以发现, 建立精度高的混凝土强度预测模型必须获得LSSVM参数γ 和σ 的最优值、γ 和σ 参数两者之间相互联系, 因此是一种组合、带约束的优化问题, 混凝土强度预测模型的LSSVM参数优化数学模型可以定义如下:

$\begin{matrix} \begin{matrix} minf (γ, σ) = \\ \frac{1}{N_{A}} \overset{N_{A}}{\sum_{j = 1}} (y_{j} - y_{j}^{*})^{2} + \frac{1}{N_{B}} \overset{N_{B}}{\sum_{j = 1}} (y_{j} - y_{j}^{*})^{2} \\ s.t. \{\begin{matrix} γ \in [γ_{\min}, γ_{\max}] \\ σ \in [σ_{\min}, σ_{\max}] \end{matrix} (13) \end{matrix} \end{matrix}$

式中: $\begin{matrix} y_{i} \end{matrix}$ 和 $\begin{matrix} {\hat{y}}_{i} 分别为第 i \end{matrix}$ 个混凝土强度的实际值和预测(拟合)值; $\begin{matrix} N_{A} \end{matrix}$ 和 $\begin{matrix} N_{B} \end{matrix}$ 分别为训练样本和验证样本数。

2.2 LSSVM参数的粒子编码

在实际应用过程中, CPSO算法首先通过编码方式与待解决的问题进行关联, 因此LSSVM参数与 $\begin{matrix} γ 和 σ \end{matrix}$ 相对应, 其采用实数编码方式, 具体如图1所示。

	Figure Option View Download New Window
	图1 粒子与LSSVM参数对应关系Fig.1 Relationship between particle and LSSVM parameters

2.3 适应度函数

在混凝土强度建模和预测过程中, CPSO算法的目标是降低混凝土强度预测误差, 因此粒子群的适应度函数定义如下:

$\begin{matrix} \begin{matrix} f (x) = \sqrt[]{\frac{1}{N_{A}} \overset{N_{A}}{\sum_{j = 1}} (y_{j} - y_{j}^{*})^{2}} + \\ \sqrt[]{\frac{1}{N_{B}} \overset{N_{B}}{\sum_{j = 1}} (y_{j} - y_{j}^{*})^{2}} (14) \end{matrix} \end{matrix}$

2.4 CPSO-LSSVM的混凝土强度预测流程

(1)对具体混凝土类型的强度进行多次实验, 收集影响因子和混凝土的强度值。

(2)设置LSSVM参数 $\begin{matrix} γ 和 σ \end{matrix}$ 的范围, 并根据参数范围随机生成初始粒子群。

(3)一个粒子位置向量与LSSVM参数 $\begin{matrix} γ 和 σ \end{matrix}$ 相对应, 根据式(14)计算每一个粒子的适应度值, 并进行排序, 将适应度值最小的粒子位置设置为种群的历史最优位置。

(4)更新粒子的位置和速度, 产生新一代粒子群, 与个体和粒子群的历史最优位置进行比较, 确定个体和粒子群的历史最优位置。

(5)对粒子群的历史最优位置进行混沌处理。

(6)若满足终止条件, 则LSSVM参数寻优停止, 不然计算新一代粒子群的适应度值, 返回步骤(4)继续搜索LSSVM参数。

(7)将粒子群最优位置进行反编码, 根据找到的最优LSSVM参数, 对混凝土强度训练样本进行学习, 建立预测模型, 对验证样本进行预测, 并对预测结果进行分析。

综上所知, 基于CPSO-LSSVM的混凝土强度建模和预测流程如图2所示。

	Figure Option View Download New Window
	图2 混凝土强度预测模型的工作流程Fig.2 Flow chart of concrete strength prediction model

3 CPSO-LSSVM在混凝土强度预测中的应用

3.1 数据源

实验环境为:Intel酷睿i5 4590 CPU; 金士顿DDR3 1600 8 GB内存; Windows 8操作系统; Matlab 2012R编程工具。选择标准数据库中的Concrete compressive strength数据集作为实验对象, 其包括1030个样本, 每一样本有8个影响因子, 即LSSVM的输入向量; 1个期望输出值(混凝土强度), 即LSSVM的输出向量。随机选择200个样本数据组成训练集, 建立混凝土强度预测模型, 并检验CPSO-LSSVM对混凝土强度的拟合性能, 随机选择100个样本作为验证集, 检验混凝土强度预测模型的泛化推广能力。

3.2 样本的预处理

混凝土强度影响因子的意义各异, 它们值之间的绝对误差大, 会对LSSVM的训练过程产生不利影响, 降低建模的效率, 为此对混凝土强度样本进行归一化处理, 具体为:

$\begin{matrix} x' (i) = \frac{x (i) - \min (x (i))}{\max (x (i) - \min (i))} (15) \end{matrix}$

式中:max(· )和min(· )分别表示混凝土强度的最大和最小值。

3.3 结果及分析

3.3.1 CPSO-LSSVM的混凝土强度拟合性能

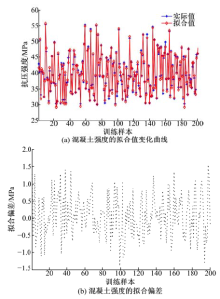
将归一化处理后的混凝土强度训练集输入到LSSVM进行训练, 采用粒子群算法优化LSSVM参数, 得到最优参数分别为:γ =450.815, σ =8.749, 从而建立混凝土强度预测模型, 并对训练集进行拟合, 得到混凝土强度拟合结果如图3所示。

从图3可以看出, CPSO-LSSVM的混凝土强度拟合值与混凝土强度实际值十分接近, 它们之间偏差十分小, 混凝土强度的拟合结果表明, CPSO-LSSVM能够有效拟合混凝土强度与其影响因子之间的非线性变化关系, 拟合精度高达98%以上, 可以满足混凝土强度的拟合精度要求。

	Figure Option View Download New Window
	图3 CPSO-LSSVM的混凝土强度拟合性能Fig.3 Fitting performance of CPSO-LSSVM for concrete strength

3.3.2 CPSO-LSSVM的混凝土强度泛化性能

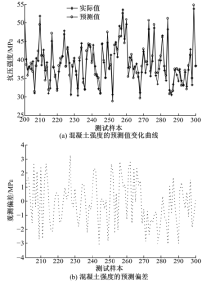
在实际应用中, 混凝土预测模型的泛化能力也是一种关键的评价指标, 对混凝土强度验证集的预测结果如图4所示。

	Figure Option View Download New Window
	图4 CPSO-LSSVM的混凝土强度泛化性能Fig.4 Generalization performance of CPSO-LSSVM for concrete strength

从图4可以看出, CPSO-LSSVM的混凝土强度验证集的预测结果变化曲线与实际值的变化曲线相似, 预测偏差变化幅度小, 验证集的预测结果表明, 本文将LSSVM引入到复杂多变的混凝土强度建模及预测中, 建立的模型可以准确反映混凝土强度与其影响因子之间的非线性变化趋势, 克服了传统模型的缺陷, 通过引入混沌粒子群算法优化LSSVM的参数, 有效解决了LSSVM参数优化的难题, 混凝土强度的预测精度高达95%以上, 说明CPSO-LSSVM的混凝土预测模型具有较好的泛化能力。

3.3.3 与当前经典模型的性能对比

为了进一步验证CPSO-LSSVM的混凝土强度预测模型, 选择当前经典混凝土强度预测模型进行参照实验, 它们具体为:多元线性回归(MLR)模型、BP神经网络(BPNN)、RBF神经网络(RBFNN)^[15]、支持向量机(SVM)^[16], 采用拟合精度和预测精度对性能进行衡量, 所有模型的拟合精度和预测精度如表1所示。

表1 CPSO-LSSVM与经典模型的性能对比 Table 1 Performance comparison of CPSO-LSSVM and classical models

对表1的结果进行分析可知:

(1)在所有模型中, MRL的拟合精度和预测精度最低, 这是主要是因为MRL是一种线性建模方法, 不能反映混凝土强度与其影响因子之间的非线性变化趋势, 混凝土强度的预测误差大。

(2)相对于MRL模型, BPNN和RBFNN的混凝土强度的拟合精度和预测精度得到大幅提高, 这主要是由于BPNN和RBFNN具有自适应学习能力, 可以逼近混凝土强度与影响因子之间的变化关系, 提高了混凝土强度的预测精度, 但是由于BPNN和RBFNN均基于经验风险最大化原理, 有个别样本预测误差比较大, 出现了“ 过拟合” 现象, 预测结果不稳定、不可靠。

(3)CPSO-LSSVM模型的拟合精度和预测精度最高, 预测误差要小于对照模型, 主要是由于LSSVM是一种基于结构风险最小原则的机器学习算法, 解决了泛化性能和学习效率之间的矛盾, 比SVM的建模时间大幅度减少, 克服了当前经典模型的不足, 是一种可行、精度高的混凝土强度预测和建模工具。

3.3.4 通用性测试

为了全面分析CPSO-LSSVM的性能, 采用多种类型的混凝土进行通用性测试, 结果如表2所示。从表2可知, 对于所有类型混凝土的强度, CPSO-LSSVM的平均拟合精度高达98%以上, 平均预测精度为95%上, 实验结果表明, CPSO-LSSVM是一种通用性能较好的混凝土强度预测模型, 为其他非线性预测问题提供一种建模思路。

表2 CPSO-LSSVM对其他类型混凝土强度预测 Table 2 Prediction of other types concrete strength based on CPSO-LSSVM

4 结束语

混凝土强度预测是当前的一个研究热点, 为此, 本文提出一种基于CPSO-LSSVM的混凝土强度预测模型。首先采用CPSO算法选择LSSVM参数, 然后挖掘混凝土强度与其影响因子之间的变化关系, 最后采用多个具体混凝土强度数据对其性能进行实证检验。结果表明, 本文模型的混凝土强度拟合和预测结果具有很高的精度, 有一定的实际应用价值。本文建模时没有考虑混凝土强度影响因子对预测结果的贡献, 如何确定每一个混凝土强度影响因子权重, 以建立精度更高的混凝土强度预测模型是下一步将要研究的问题。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Limbachiya M C, Leelawat T, Dhir R K. Use of recycled concrete aggregate in high-strength concrete[J]. Material and Structure, 2000, 33(9): 574-580. [本文引用:1]
[2]	陆克芬, 方崇, 张春乐. 非参数投影寻踪回归在粉煤灰混凝土强度测中的应用[J]. 计算机工程与设计, 2010, 31(6): 1394-1396. Lu Ke-fen, Fang Cong, Zhang Chun-le. Nonparametric projection pursuit regression and its application of strength prediction about fly as concrete[J]. Computer Engineering and Design, 2010, 31(6): 1394-1396. [本文引用:1]
[3]	张英姿, 范颖芳, 赵颖华. 受盐酸腐蚀混凝土抗压强度的灰色预测模型[J]. 建筑材料学报, 2007, 10(4): 397-401. Zhang Ying-zi, Fan Ying-fang, Zhao Ying-hua. Grey prediction model for compressive strength of concrete corroded by hydrochloric acid[J]. Journal of Building Materials, 2007, 10(4): 397-401. [本文引用:1]
[4]	王江荣. 基于模拟退火的粒子群算法优化的二次回归在混凝土抗压强度预测中的应用[J]. 工程质量, 2013, 31(12): 32-35. Wang Jiang-rong. Quadratic regression based on optimization algorithm of simulated annealing particle group theory application in the concrete compressive strength prediction[J]. Construction Quality, 2013, 31(12): 32-35. [本文引用:1]
[5]	高峰, 郝奇亮. 基于MATLAB7. 2 神经网络工具箱的混凝土抗压强度预测[J]. 山西大同大学学报: 自然科学版, 2012, 28(6): 60-63. Gao Feng, Hao Qi-liang. Concrete compression strength prediction based on Matlab 7. 2 neural Network toolbox[J]. Journal of Shanxi Datong University (Natural Science), 2012, 28(6): 60-63. [本文引用:1]
[6]	徐国强, 苏幼坡, 韩佃利, 等. 基于BP 神经网络的绿色混凝土抗压强度预测模型[J]. 混凝土, 2013(2): 33-35. Xu Guo-qiang, Su You-po, Han Dian-li, et al. Prediction model of green concrete compressive strength based on BP neural network[J]. Concrete, 2013(2): 33-35. [本文引用:1]
[7]	黄庆时, 郑建岚, 罗素蓉. 人工神经网络在自密实混凝土抗压强度预测中的应用[J]. 福州大学学报: 自然科学版, 2007, 35(1): 100-104. Huang Qing-shi, Zheng Jian-lan, Luo Su-rong. Application of artificial neural networks for prediction of self-compacting concrete strength[J]. Journal of Fuzhou University (Natural Science), 2007, 35(1): 100-104. [本文引用:1]
[8]	李红, 彭涛. 基于BP、RBF 神经网络混凝土抗压强度预测[J]. 武汉理工大学学报, 2009, 31(8): 33-36. Li Hong, Peng Tao. Prediction of concrete compress strength based on BP and RBF neural network theories[J]. Journal of Wuhan University of Technology, 2009, 31(8): 33-36. [本文引用:1]
[9]	马清秀. 基于支持向量机的水泥抗压强度预测[J]. 公路与汽运, 2009(3): 93-95. Ma Qing-xiu. Prediction of concrete strength based on support vector machine[J]. Highways and Automotive Applications, 2009(3): 93-95. [本文引用:1]
[10]	王江荣. 基于小波分析的神经网络在混凝土测强曲线拟合中的应用[J]. 工程质量, 2011, 29(12): 63-65. Wang Jiang-rong. Neural network application of concrete strength test curve fitting based on small wave analysis[J]. Construction Quality, 2011, 29(12): 63-65. [本文引用:1]
[11]	何晓凤, 周红标. 基于GA-BP 的混凝土抗压强度预测研究[J]. 淮阴工学院学报, 2011, 20(3): 21-25. He Xiao-feng, Zhou Hong-biao. Prediction of concrete compressive strength based on GA-BP[J]. Journal of Huaiyin Institute of Technology, 2011, 20(3): 21-25. [本文引用:1]
[12]	陈斌, 郭雪莽, 刘国华. 基于粗糙集(RS)和支持向量机(SVM)的混凝土性能预测实证研究[J]. 水力发电学报, 2011, 30(6): 251-257. Chen Bin, Guo Xue-mang, Liu Guo-hua. Prediction of concrete properties based on rough sets and support vector machine method[J]. Journal of Hydroelectric Engineering, 2011, 30(6): 251-257. [本文引用:1]
[13]	张鹤, 宁作君. 基于LS-SVM的混凝土断裂参数回归与预测[J]. 混凝土, 2012(6): 17-19. Zhang He, Ning Zuo-jun. Data regression and forecast of concrete fracture by LS-SVM[J]. Concrete, 2012 (6): 17-19. [本文引用:1]
[14]	龙文, 梁昔明, 龙祖强, 等. PSO-LSSVM灰色组合模型在地下水埋深预测中的应用[J]. 系统工程理论与实践, 2013, 33(1): 243-248. Long Wen, Liang Xi-ming, Long Zu-qiang, et al. LSSVM grey combined forecasting model based on PSO and its application in groundwater dynamic prediction[J]. Systems Engineering—Theory and Practice, 2013, 33(1): 243-248. [本文引用:2]
[15]	王晓伟. 基于RBF网络的混凝土抗压强度的预测[J]. 筑路机械与施工机械化, 2006(10): 23-26. Wang Xiao-wei. Prediction of concrete compressive strength based on RBF neural network[J]. Pavement Machinery and Construction Technology, 2006(10): 23-26. [本文引用:1]
[16]	龚珍, 卜小波, 吴浩. 基于PSO-SVM的混凝土抗压强度预测模型[J]. 混凝土, 2013(12): 11-13. Gong Zhen, Pu Xiao-bo, Wu Hao. Concrete compressive strength test based on vector machine optimized by particle swarm optimization algorithm[J]. Concrete, 2013(12): 11-13. [本文引用:1]

2000

0.0

... 0 引言针对混凝土强度的预测问题,国内外学者提出许多有效的预测模型^[1,2,3] ...

2010

0.0

. 2010, 31(6):1394-1396

Nonparametric projection pursuit regression and its application of strength prediction about fly as concrete

非参数投影寻踪回归在粉煤灰混凝土强度测中的应用

Lu Ke-fen , Fang Cong , Zhang Chun-le.

陆克芬, 方崇, 张春乐

为了进一步优化粉煤灰混凝土配合比设计,改进混凝土施工工艺,提高混凝土质量.针对粉煤灰混凝土强度与其影响因素之间复杂的非线性关系,通过对影响粉煤灰混凝土强度的主要因素进行分析,提出了基于投影寻踪回归分析的粉煤灰混凝土强度预测模型,用单纯形优化算法确定最佳投影方向,并在Matlab环境下编写了相应的计算程序.利用某工程粉煤灰混凝土配合比的实测数据,进行粉煤灰混凝土强度的预测.实验结果表明,该方法具有较高的拟合度和良好的预测精度,满足工程实际要求. Abstract： In order to further optimize mix proportion design of fly ash concrete, improve the construction technology and the quality of concrete, according to the complex non-linear relationship between fly ash concrete strength and its influencing factors and analyzing the main factors of affect the strength of fly ash concrete, a prediction model based on the projection pursuit regression analysis for the strength of fly ash concrete is proposed, the best projection direction is found using the simplex optimization algorithm, and the corre-sponding calculation program is compiled under the Matlab. The strength of fly ash concrete will be predicted by the use of relevant data measured. It shows that this method has a high fit, good prediction accuracy, and applicable to practical engineering.

... 0 引言针对混凝土强度的预测问题,国内外学者提出许多有效的预测模型^[1,2,3] ...

2007

0.0

. 2007, 10(4):397-401 DOI:doi:10.3969/j.issn.1007-9629.2007.04.004

Grey prediction model for compressive strength of concrete corroded by hydrochloric acid

受盐酸腐蚀混凝土抗压强度的灰色预测模型

Zhang Ying-zi , Fan Ying-fang , Zhao Ying-hua.

张英姿, 范颖芳, 赵颖华

基于受盐酸腐蚀混凝土抗压强度的试验研究,采用灰色系统理论建立了单变量的一阶灰色预测模型GM(1,1),对受盐酸腐蚀混凝土的抗压强度进行预测,并将预测值与试验值进行了比较.研究表明,灰色预测模型的预测结果与试验结果吻合较好;这种模型简便易行,能够有效地预测受腐蚀混凝土的抗压强度.

... 0 引言针对混凝土强度的预测问题,国内外学者提出许多有效的预测模型^[1,2,3] ...

2013

0.0

. 2013, 31(12):32-35 DOI:doi:10.3969/j.issn.1671-3702.2013.12.008

Quadratic regression based on optimization algorithm of simulated annealing particle group theory application in the concrete compressive strength prediction

基于模拟退火的粒子群算法优化的二次回归在混凝土抗压强度预测中的应用

Wang Jiang-rong.

王江荣

混凝土抗压强度与其影响因素之间存在着很强的非线性关系,精确预测混凝土抗压强度对提高工程质量和施工进度等具有重要意义.为了提高预测值的精确度,建立了二次回归预测模型,利用基于模拟退火的粒子群算法对模型系数进行了优化和求解.实例仿真表明这种经智能算法优化后的二次回归预测模型优于传统神经网络预测模型,预测精度得到了较大提高.

... 最原始预测模型主要为多元线性回归分析,其假设混凝土强度与影响因素之间是一种线性关系,建模速度快、易实现^[4],但影响混凝土强度的因素十分复杂,且各种因素之间互相作用,导致混凝土强度与其影响因素之间是一种复杂的非线性关系,而多元线性回归分析模型无法描述混凝土强度的非线性变化特点,预测精度低、实际应用范围比较窄^[5,6,7] ...

2012

0.0

. 2012, 28(6):60-63 DOI:doi:10.3969/j.issn.1674-0874.2012.06.021

Concrete compression strength prediction based on Matlab 7.2 neural Network toolbox

基于MATLAB7.2 神经网络工具箱的混凝土抗压强度预测

Gao Feng , Hao Qi-liang.

高峰, 郝奇亮

为最大限度地利用回弹法和超声波法混凝土抗压强度非破损检测试验数据,应用通用数学软件Matlab7.2神经网络工具箱中的BP人工神经网络(BP-ANN)算法,通过优化网络结构和隐层节点数量建立了拓扑结构为 2-10-1的BP-ANN模型；将其充分训练后,用于混凝土抗压强度预测.分析结果表明,混凝土抗压强度预测值与实测值的误差小于5.0％,能够满足工程需要；BP-ANN预测能力较强,具有一定的工程应用价值.

0.0

. , 2013(2):33-35 DOI:doi:10.3969/j.issn.1002-3550.2013.02.009

基于BP 神经网络的绿色混凝土抗压强度预测模型

Xu Guo-qiang , Su You-po , Han Dian-li

徐国强, 苏幼坡, 韩佃利

与普通混凝土相比,绿色混凝土具有成分复杂的特点,为了在多因素作用下更为准确地预测绿色混凝土的抗压强度,在分析三层BP神经网络原理的基础上,选择影响绿色混凝土抗压强度的7个指标,以66个抗压强度试验为示例,建立了三层BP神经网络抗压强度预测模型。验证样本的训练结果表明,该模型能够较准确地快速预测绿色混凝土的抗压强度,并通过对各指标的权重计算,确定了影响绿色混凝土抗压强度的主要因素。

2007

0.0

. 2007, 35(1):100-104 DOI:doi:10.3969/j.issn.1000-2243.2007.01.022

Application of artificial neural networks for prediction of self-compacting concrete strength

人工神经网络在自密实混凝土抗压强度预测中的应用

Huang Qing-shi , Zheng Jian-lan , Luo Su-rong.

黄庆时, 郑建岚, 罗素蓉

针对传统BP神经网络的不足, 采用不同改进算法的网络模型对自密实混凝土抗压强度预测进行了详细的分析.研究表明:采用变梯度算法的模型M1、P-B复位算法的模型M2、拟牛顿算法的模型M3以及LM算法的模型M4,这4种模型均成功地建立了自密实混凝土强度的非线性关系,可用于其强度预测;通过用MATLAB编写程序,为解决BP网络隐层节点数的不确定性提供了一种较为方便的途径.

2009

0.0

. 2009, 31(8):33-36

Prediction of concrete compress strength based on BP and RBF neural network theories

基于BP、RBF 神经网络混凝土抗压强度预测

Li Hong , Peng Tao.

李红, 彭涛

为了预测混凝土的抗压强度,在分析BP、RBF神经网络原理的基础上,提出用BP、RBF神经网络模拟混凝土抗压强度与搅拌机各主要影响参数间关系的方法。根据搅拌机的实际工作状况,分别建立了4维输入向量、1维输出向量的BP、RBF神经网络模型,通过19组试验,验证了2种模型的可靠性。结果表明,实测结果与预测结果相接近,该2种神经网络模型能较准确地快速预测混凝土抗压强度。

... 随后,出现了基于非线性理论的混凝土强度预测模型,如神经网络、支持向量机等机器学习算法^{[8,9,10,11,12]},它们不需要知道处理问题的精确函数,就可以较好地拟合混凝土强度与影响因素之间的关系,混凝土强度的预测精度得到了提高,成为当前主要的研究方向 ...

0.0

. , 2009(3):93-95 DOI:doi:10.3969/j.issn.1671-2668.2009.03.029

Prediction of concrete strength based on support vector machine

基于支持向量机的水泥抗压强度预测

Ma Qing-xiu.

马清秀

利用支持向量机结构简单、学习性能出色和较强的推广性等优点,通过对已有实例样本的学习,建立了水泥28 d抗压强度与其各影响因素之间的高度非线性映射关系,然后用样本学到的新关系预测新的水泥抗压强度,并将预测结果与传统回归分析、神经网络预测结果进行了对比.研究表明,与传统的方法相比,支持向量机方法精度较高、相对误差小,为预测水泥28 d抗压强度提供了一条新途径.

2011

0.0

. 2011, 29(12):63-65 DOI:doi:10.3969/j.issn.1671-3702.2011.12.014

Neural network application of concrete strength test curve fitting based on small wave analysis

基于小波分析的神经网络在混凝土测强曲线拟合中的应用

Wang Jiang-rong.

王江荣

摘　要：将小波母函数嵌入人工神经网络的神经元形成紧致型小波神经网络，将此种网络用于混凝土非破损检测的测强曲线拟合和预测，提升了纯粹的BP神经网络的拟合和预测精度，效果远胜于最小二乘拟合和预测。通过一个算例对小波神经网络的高精准性和非性线逼近能力进行了验证，对实验数据进行了统计分析，结论表明小波神经网络优于BP神经网络。

2011

0.0

. 2011, 20(3):21-25 DOI:doi:10.3969/j.issn.1009-7961.2011.03.005

Prediction of concrete compressive strength based on GA-BP

基于GA-BP 的混凝土抗压强度预测研究

He Xiao-feng , Zhou Hong-biao.

何晓凤, 周红标

研究如何利用BP神经网络建立多因子混凝土抗压强度BP预测模型。针对BP网络收敛速度慢和难以获得全局最优的缺点,提出利用遗传算法优化BP神经网络初始权值和阈值,建立混合GA-BP预测模型。模型以每立方混凝土中水泥、高炉矿渣粉、粉煤灰、水、减水剂、粗集料和细集料的含量以及置放天数作为输入参数,混凝土抗压强度值作为输出参数。用UCI数据库中的Concrete Compressive Strength数据集进行仿真测试。结果表明：BP模型平均相对误差为7.24%,GA-BP模型平均相对误差为4.51%。实验结果证明,GA优化后的BP网络更能准确地预测混凝土抗压强度,从而为混凝土质量评价提供指导,具有重要的实用价值。 Abstract： This research makes use of BP nerve network to create multi-factor concrete compression strength BP prediction model.Genetic algorithm（GA） is used to optimize the initial weights and threshold value of the neural network based on the inherent local minimum problem of NN and the good global convergence and global search ability of GA.The model uses cement,blast furnace slag,fly ash,water,super plasticizer,coarse aggregate,fine aggregate and age as the model input parameters,and concrete compressive strength as the model output parameter.Concrete Compressive Strength data in UCI data bank is used for imitating test.The results show that the average predicted error of GA-BP model is only 4.51%,less than 7.24% of BP model.Through test verification the excellent BP network after turning can even accurately predict concrete compression strength,which has great practical value and can provide instruction for concrete mass appraisal.

2011

0.0

. 2011, 30(6):251-257

Prediction of concrete properties based on rough sets and support vector machine method

基于粗糙集(RS)和支持向量机(SVM)的混凝土性能预测实证研究

Chen Bin , Guo Xue-mang , Liu Guo-hua.

陈斌, 郭雪莽, 刘国华

针对多元胶凝体系混凝土的性能预测问题,以各种原材料用量及其质量指标为预测自变量,以混凝土初始坍落度和7天、28天抗压强度为预测因变量,先采用粗糙集（RS）方法约简自变量组合,后采用支持向量机回归（SVR）模型建立混凝土性能预测模型。通过单掺粉煤灰集169组配合比、复掺粉煤灰和矿粉集135组配合比的2/3样本拟合、1/3样本预测实验,表明该模型预测精度明显优于线性回归,稳定性优于BP人工神经网络。进一步的自变量敏感性分析表明,RS-SVM模型能准确地反映混凝土性能对原材料变化的依赖性,总体性能最优。

2012

0.0

. 2012, 2012(6):17-19 DOI:doi:10.3969/j.issn.1002-3550.2012.06.006

Data regression and forecast of concrete fracture by LS-SVM

基于LS-SVM的混凝土断裂参数回归与预测

Zhang He , Ning Zuo-jun.

张鹤, 宁作君

摘　要：选择最小二乘支持向量机对混凝土测量中存在的大样本数据进行回归分析以及预测。研究表明：利用LS-SVM模型进行混凝土测量当中存在的大样本数据回归分析具有精度高,速度快等优点。模型不需建立方程式,修改容易,可处理被干扰的数据,具有较强的概括性。利用LS-SVM对冻融作用下的混凝土的断裂韧度进行回归分析以及断裂预测,模型较好的反映了断裂韧度的下降趋势。

... 最小二乘支持向量机(Least squares support vector machine,LSSVM)不仅克服了神经网络的不足和继承了支持向量机的优点,而且加快了训练速度,解决了支持向量机建模效率低的缺陷^[13],为了获得更加理想的混凝土强度预测结果,提出了一种基于混沌粒子群(Chaotic particle swarm optimization,CPSO)算法优化最小二乘支持向量机的混凝土强度预测模型,并通过具体应用实例测试证明了该模型的可行性 ...

2013

0.0

. 2013, 33(1):243-248 DOI:doi:10.3969/j.issn.1000-6788.2013.01.031

LSSVM grey combined forecasting model based on PSO and its application in groundwater dynamic prediction

PSO-LSSVM灰色组合模型在地下水埋深预测中的应用

Long Wen , Liang Xi-ming , Long Zu-qiang

龙文, 梁昔明, 龙祖强

To solve the problems of the uncertain parameters of LSSVM and the low forecasting precision of single method, the learning algorithm of grey least squares support vector machines combined forecasting model optimized by particle swarm algorithm is proposed. Optimize two parameters of LSSVM model study by particle swarm algorithm's abilities of the fast convergence and whole optimization. It can escape from the blindness of man-made choice. First, the combinational results of initial forecasts are put as the input and the corresponding actual values are put as the output of LSSVM. Then we can get combinational model of the grey and the least squares support vector machine based on particle swarm algorithm by training it. The proposed combinational model can enhance the efficiency and the capability of forecasting. Actual data from 1985 to 2006 of area in Sanjiang plain is taken as the sample data. A combinational model based on PSO-LSSVM and GM(1,1) model is proposed. Predict precision of the model is examined by two ways, and the results show that it is more precise than the other methods.

针对LSSVM参数难以确定和单一方法预测精度不高的问题, 提出一种基于粒子群优化LSSVM灰色组合预测模型的学习方法. 利用粒子群算法的收敛速度快和全局优化能力, 优化LSSVM模型的惩罚因子和核函数参数. 避免了人为选择参数的盲目性. 在同一时刻利用不同长度序列的灰色预测方法对历史数据进行初步预测, 将初步预测结果的组合作为LSSVM的输入, 该时刻的实际值作为输出, 进行训练建立灰色LSSVM组合预测模型, 提高了模型的推广预测能力. 选取三江平原某地区1985年至2006年地下水埋深实测数据, 建立PSO-LSSVM组合预测模型. 通过两种方式对模型进行检验, 与其他模型相比, 该组合模型具有较高的预测精度.

... 式中: ωmax和 ωmin分别为最大和最小的惯性权值^[14] ...

... 混粒子群算法(CPSO)将混沌系统的随机性和遍历性引入到基本粒子群优化算法,对粒子群的历史最优解进行混沌处理,帮助粒子群跳出局部最优解,寻优能力更强^[14] ...

0.0

. , 2006(10):23-26 DOI:doi:10.3969/j.issn.1000-033X.2006.10.011

Prediction of concrete compressive strength based on RBF neural network

基于RBF网络的混凝土抗压强度的预测

Wang Xiao-wei.

王晓伟

为了预测混凝土的抗压强度,在分析RBF神经网络原理的基础上提出了用RBF神经网络模拟抗压强度与各影响因素间关系的方法.根据搅拌机的实际工作状况,建立了4个输入节点、1个输出节点的RBF神经网络模型,通过19组试验,验证了模型的可靠性.结果表明,实测结果与预测结果相接近,RBF神经网络模型是一种较准确的快速预测混凝土抗压强度的方法.

... 为了进一步验证CPSO-LSSVM的混凝土强度预测模型,选择当前经典混凝土强度预测模型进行参照实验,它们具体为:多元线性回归(MLR)模型、BP神经网络(BPNN)、RBF神经网络(RBFNN)^[15]、支持向量机(SVM)^[16],采用拟合精度和预测精度对性能进行衡量,所有模型的拟合精度和预测精度如表1所示 ...

0.0

. , 2013(12):11-13 DOI:doi:10.3969/j.issn.1002-3550.2013.12.004

Concrete compressive strength test based on vector machine optimized by particle swarm optimization algorithm

基于PSO-SVM的混凝土抗压强度预测模型

Gong Zhen , Pu Xiao-bo , Wu Hao

龚珍, 卜小波, 吴浩

为了在多因素作用下更准确的预测混凝土的抗压强度,在分析SVM模型的基础上,建立了基于PSO-SVM的混凝土抗压预测模型。该模型采用粒子群算法对支持向量机的参数进行优化选择, 提高了支持向量机的预测能力,并对已知的具体算例进行了研究分析。研究结果表明:该方法科学可行,并具有很好的精度。