斜盘式轴向柱塞泵加速模型

引用本文

赵存然, 刘伟, 姜继海, 邵辉, 田勇. 斜盘式轴向柱塞泵加速模型.吉林大学学报:工学版, 2016, 46(4): 1124-1129
ZHAO Cun-ran, LIU Wei, JIANG Ji-hai, SHAO Hui, TIAN Yong. Accelerated model of swash-plate axial piston pump. Journal of Jilin University Engineering and Technology Edition, 2016, 46(4): 1124-1129 复制到剪切板

Permissions

斜盘式轴向柱塞泵加速模型

赵存然¹, 刘伟¹, 姜继海¹, 邵辉², 田勇²

1.哈尔滨工业大学机电工程学院,哈尔滨 150001

2.沈阳中之杰流体控制系统有限公司,沈阳 110122

作者简介:赵存然(1983-),男,博士研究生.研究方向:加速可靠性试验.E-mail:zhaocunran@163.com

基金:国家自然科学基金项目(51275123); “十二五”国家科技支撑计划项目(2014BAF08B06)

摘要

针对斜盘式轴向柱塞泵多故障失效模式的特点,首先利用失效模式、影响和关键性分析(FMEA)方法识别柱塞泵中各组件单元的失效模式及影响,在此基础上通过分析影响失效率的应力因素,针对柱塞泵加速寿命试验(ALT)应力施加形式,建立了简化后的斜盘式轴向柱塞泵失效率模型,得到了斜盘式轴向柱塞泵的加速模型。

关键词: 流体传动与控制; 斜盘式轴向柱塞泵; 加速寿命试验; 失效率; 加速模型

中图分类号:TG156 文献标志码:A 文章编号:1671-5497(2016)04-1124-06

Accelerated model of swash-plate axial piston pump

ZHAO Cun-ran¹, LIU Wei¹, JIANG Ji-hai¹, SHAO Hui², TIAN Yong²

1.College of Mechatronics Engineering, Harbin Institute of Technology, Harbin 150001,China

2.Shenyang Hero Fluid Control System Co., Ltd., Shenyang 110122, China

Abstract

In light of the characteristics of the swash-plate axial piston pump with multiple failure modes, first, the Failure Modes, Effects and Criticality Analysis (FMEA) method is employed to identify the failure mode and effect of each component in a piston pump. Then, on the basis of the analysis of the stress factors that impact the failure rate, a simplified failure rate model of the swash-plate axial piston pump was set up according to the two forms of stresses applied in the Accelerated Life Test (ALT). Finally, an accelerated model of the swash-plate axial piston pump was obtained.

Keyword: turn and control of fluid; swash-plate axial piston pump; accelerated life test(ALT); failure rate; accelerated model

Show Figures

0 引言

斜盘式轴向柱塞泵(下文简称柱塞泵)为液压系统提供动力。柱塞泵具有工作压力高、功率密度大、效率高、使用寿命较长等优点。但柱塞泵一旦出现问题, 将会影响到整个液压系统的正常运行, 从而给企业造成重大损失^[1]。因此, 通过试验方法对柱塞泵进行可靠性试验, 找出产品失效故障模式和薄弱环节, 进而分析失效机理, 提出改进设计方法和改善加工工艺, 对于提高斜盘式轴向柱塞泵的可靠性水平和市场竞争力具有重要意义。

利用加速寿命试验分析柱塞泵的可靠性时, 建立柱塞泵的加速模型是首要和关键性环节。在目前国内外柱塞泵可靠性寿命试验研究中, 许耀明等^[2]在研究XB型斜盘式柱塞泵磨损强化试验时, 通过分析材料体积磨损量磨损特性, 提出了以压力p和速度v作为双应力的逆幂律模型。与其类似, Jung等^[3]在实施柱塞泵的加载压力为周期循环的加速寿命试验时, 以金属疲劳失效的S-N曲线为理论依据^[4], 提出了与文献中[2]形式相同的加速模型。王少萍等^[5]以ZB-34M斜盘式轴向柱塞泵为研究对象, 以文献[6]结果为参考依据, 同样以压力 p和速度v作为交叉加速应力, 但是建立了不同的逆幂律模型。同时, 王少萍等^[7]以某型航空泵为研究对象, 以压力p、速度v和温度T综合应力为加速应力, 提出了融合逆幂律和阿伦尼斯的模型。

上述文献在研究过程中主要存在以下几个问题:①将柱塞泵视为由单失效机理引起的失效, 例如, 文献[2]中柱塞泵失效模式是由于轻微耗损磨损引起的; 文献[3]中柱塞泵失效模式是由于应力疲劳磨损引起的。②文献[2]和[4]中加速寿命试验样本量太少, 分析方法又是基于最大似然估计, 无法确保模型正确性。③文献[3]和[5]中提供了强化验证的理论和方法, 而没有试验数据支撑理论的正确性。

基于以上问题, 本文将柱塞泵视为多故障整机, 从柱塞泵失效率角度着手进行研究, 最后近似得到柱塞泵加速模型。

1 柱塞泵FMEA方法

斜盘式轴向柱塞泵由多个元件组成, 不同元件的不同失效模式都可能会导致柱塞泵失效, 在制定柱塞泵加速寿命试验(Accelerated life test, ALT)之前, 首先利用失效模式、影响和关键性分析方法(Failure mode and effects analysis, FMEA)识别柱塞泵中各组件、单元的各种失效模式及影响, 在此基础上更进一步分析失效影响的关键性。

表1中仅列举了柱塞泵的主要失效模式^{[8, 9, 10, 11]}, 并没有考虑诸如安装方法错误、维修不及时、材料热处理等工艺缺陷、油液使用不当、液压系统设计缺陷等容易造成柱塞泵失效的故障模式。失效模式的“ 严重程度” 按照缩短柱塞泵寿命的程度和造成安全事故的隐患从轻到重分为:较小、一般、关键、灾害。不同失效模式的“ 失效率” 按照发生的可能性从高到低分为:经常、有一定可能、偶尔、短时间几乎不可能、几乎不可能。

试验时当柱塞泵发生失效, 需要对柱塞泵的失效机理和失效原因进行分析。导致柱塞泵失效的应力在试验中经常被作为加速应力, 表1中给出了导致相应失效模式的应力或应力组合种类。表1中, 输出流量不足或者根本没有输出流量的原因均会导致压力升不上去或者根本无法升压, 重点应检查配流盘端面的磨损和拉伤情况。

2 柱塞泵失效率模型

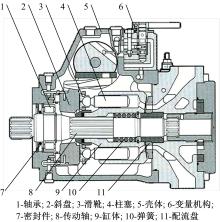
斜盘式轴向柱塞泵是由多个元件组成的复杂系统, 如图1所示。

滑靴副、柱塞副、配流副是斜盘式轴向柱塞泵中的关键部件, 对液压泵的容积效率、机械效率、温升、摩擦、磨损、工作可靠性及使用寿命均有很大影响^[1]。粘着磨损在摩擦副中经常发生, 在柱塞泵的早期研制中, 粘着磨损往往是泵早期报废的重要原因之一; 而在柱塞泵检验合格投入市场后, 随时间积累因粘着磨损造成的磨损量下降导致泵容积效率和机械效率下降^[12]往往是柱塞泵失效的主要原因。除了三大摩擦副外, 柱塞泵中的滚动轴承, 由于转速高、负载重, 也往往是泵可靠性中的薄弱环节。

	Figure Option View Download New Window
	图1 A4VG斜盘式轴向柱塞泵Fig.1 A4VG swash-plate axial piston pump

如果将柱塞泵视为一个串联系统, 每个元件为系统单元, 假设柱塞泵有 $\begin{matrix} n \end{matrix}$ 种失效模式, 每个单元的任何一种失效模式均能引起元件的失效, 那么柱塞泵的失效时间为:

$\begin{matrix} η = \min {η_{1}, \dots, η_{i}, \dots, η_{n}} (1) \end{matrix}$

式中: η为柱塞泵失效时间;η_i 为第i个失效原因引起的失效时间。

柱塞泵的失效率为各单元失效率之和^[11]:

$\begin{matrix} \begin{matrix} λ_{tot .} = λ_{SE} + λ_{SH} + λ_{BE} + λ_{CA} + \\ (λ_{FD} \cdot C_{TLF} \cdot C_{PS} \cdot C_{C}) (2) \end{matrix} \end{matrix}$

表1 斜盘式轴向柱塞泵FMEA表 Table 1 FMEA table of swash-plate axial piston pump

失效模式	具体症状	严重程度	失效率	失效原因	解决方法
输出流量不足或者根本没有输出流量	柱塞泵定心弹簧折断	一般	偶尔	弹簧受疲劳应力所致载荷& 速度	选择性能优异的泵轴定心弹簧
	配流副结合面擦伤出现沟槽甚至黏着咬死	轻者一般, 重者灾害	几乎不可能	①轴承磨损产生径向力, 引起柱塞卡死 ②结合面间进入污物 ③过载或材料强度弱载荷& 速度& 污染物	①更换成长寿命轴承 ②重新评估材料硬度和纹理特征, 优化材料特性
	柱塞副结合面擦伤出现轴向通槽甚至粘着咬死	轻者一般, 重者灾害	几乎不可能	①柱塞副承受较大的侧向力 ②结合面间进入污物 ③过载或材料强度弱载荷& 速度& 污染物	重新评估材料硬度和纹理特征, 优化材料特性
	滑靴副结合面擦伤甚至粘着咬死	轻者一般, 重者灾害	几乎不可能	①结合面间进入污物 ②过载或材料强度弱载荷& 速度& 污染物	重新评估材料硬度和纹理特征, 优化材料特性
压力升不上去或者根本无法升压	控制变量特性的弹簧折断	一般	偶尔	弹簧受疲劳应力载荷& 速度	更换弹簧或优化液压系统设计
压力升不上去或者根本无法升压	限位调节螺钉松动	一般	偶尔	限位调节螺钉在使用过程中因振动而松动载荷& 速度	优化锁紧方案
噪声大, 压力波动大	松靴	轻者一般, 重者灾害	偶尔或者短时间内几乎不可能	①长期运行过程中逐步形成 ②滑靴内球面表面加工粗糙度太高不可控	改变单元结构工艺设计
	单元金属颗粒剥落	关键	有一定可能	气穴现象温度	重新优化设计泵结构
	轴转动不平稳	关键	有一定可能	①密封件磨损泄漏 ②轴承磨损	选择高性能密封材料和轴承
泵发热, 油热温升过高	摩擦副结合面擦伤或磨损程度严重	一般	几乎不可能	因摩擦副结合面磨损和擦伤导致泄漏的能量转化成的热能不可控	重新评估材料硬度和纹理特征, 优化材料特性
	摩擦副结合面擦伤或磨损程度严重	一般	几乎不可能	因摩擦副擦伤导致机械摩擦力变大产生的热能不可控	重新评估材料硬度和纹理特征, 优化材料特性
	泵轴承磨损	关键	有一定可能	因轴承磨损使传动力矩增大产生的热能载荷& 速度	更换长寿命轴承
泵内泄漏量大	摩擦副结合面磨损严重	一般	短时间内几乎不可能	摩擦副使用一段时间后因磨损造成配合间隙过大不可控	重新评估材料硬度和纹理特征, 优化材料特性
	定心弹簧疲劳或折断	一般	偶尔	定心弹簧因疲劳失效或折断对缸体没有压抑作用, 缸体浮动距离增大载荷& 速度	分析原因, 选择性能优异弹簧或者优化泵结构
	轴承磨损	关键	有一定可能	缸体与配流盘之间产生楔形间隙, 吸油腔与压油腔产生沟通载荷& 速度	更换长寿命轴承

表1 斜盘式轴向柱塞泵FMEA表 Table 1 FMEA table of swash-plate axial piston pump

式中: $\begin{matrix} λ_{tot .} \end{matrix}$ 为柱塞泵失效率; $\begin{matrix} λ_{SE} \end{matrix}$ 为柱塞泵中密封件失效率; $\begin{matrix} λ_{SH} \end{matrix}$ 为柱塞泵轴失效率; $\begin{matrix} λ_{BE} \end{matrix}$ 为柱塞泵中轴承失效率; $\begin{matrix} λ_{CA} \end{matrix}$ 为柱塞泵壳体失效率; $\begin{matrix} λ_{FD} \end{matrix}$ 为柱塞泵流体驱动器失效率; $\begin{matrix} C_{TLF} \end{matrix}$ 为柱塞泵轴向载荷影响因子; $\begin{matrix} C_{PS} \end{matrix}$ 为柱塞泵运行转速影响因子; $\begin{matrix} C_{C} \end{matrix}$ 为柱塞泵污染物影响因子。

需要说明的是, 流体驱动器根据文献[11]定义, 指的是机械能转化为液压能的实现装置。对斜盘式柱塞泵而言, 指的是柱塞泵摩擦副及其辅助元件。

与其他单元相比, 柱塞泵泵轴和壳体通常具有更高的可靠性, 研究表明^[11], 球轴承和密封件失效率分别是传动轴失效率的8倍和3倍。柱塞泵壳体的平均寿命为一般可以达到密封件的5倍甚至10倍。

从理论上讲, 当进行完加速寿命试验时, 需要拆开柱塞泵, 检查柱塞泵失效部位, 分析失效机理, 通常可以假设柱塞泵某个部位先发生失效, 然后根据文献[11]相应元件经验模型进行分析建模。而实际上, 柱塞泵失效往往可能是由多个失效模式引起的。比如, 柱塞泵泄漏量增大可能是由摩擦副磨损、定心弹簧疲劳、轴承磨损任何一种失效模式或者组合引起的。此时, 利用上面的失效率公式计算柱塞泵失效率, 不仅与“ 将柱塞泵视为一个串联系统” 假设相违背, 同时实施过程将会变得非常复杂。比如, 根据文献[11], 轴承失效率为:

$\begin{matrix} λ_{BE} = \frac{2 \times 10^{5}}{L_{10}} C_{v} C_{t} C_{SF} (3) \end{matrix}$

式中: $\begin{matrix} L_{10} \end{matrix}$ 为轴承90%可靠度寿命; $\begin{matrix} C_{v} \end{matrix}$ 为润滑油影响因子; $\begin{matrix} C_{t} \end{matrix}$ 为轴承温度影响因子; $\begin{matrix} C_{SF} \end{matrix}$ 为工作状况影响因子。

可见, 仅是为了确定轴承失效率, 除了轴承固有参数 $\begin{matrix} L_{10} \end{matrix}$ 外, 还需要估算3个参数。所以, 为了更方便分析都有哪些因素并且这些因素如何影响柱塞泵的失效率和寿命, 有必要建立一个更简便有效的失效率公式:

$\begin{matrix} λ_{tot .} = λ_{BASE .} C_{LO} C_{PS} C_{TLF} C_{T} C_{C} C_{v} C_{t} C_{SF} (4) \end{matrix}$

式中: $\begin{matrix} λ_{BASE .} \end{matrix}$ 为柱塞泵基本失效率, 由柱塞泵失效数据决定, 为常数; $\begin{matrix} C_{LO} \end{matrix}$ 为载荷影响因子; $\begin{matrix} C_{T} \end{matrix}$ 为温度影响因子。

本文将基于简化后的式(4)展开讨论。式(4)主要考虑了载荷、转速、流量、温度、油液润滑特性、工况对柱塞泵失效率的影响, 易知柱塞泵失效部位重点考查了轴承、摩擦副组件。从表1对柱塞泵的FMEA结果看, 这样考虑也是合乎实际情况的。在实际柱塞泵加速寿命试验后, 根据实际情况, 需要对式(4)中的参数合理取值。现在参考文献[11], 得到柱塞泵的具体失效率模型。

2.1 影响因子表达式

载荷影响因子可以用下式描述:

$\begin{matrix} C_{LO} = k_{1} {(\frac{p_{o}}{p_{\max}})}^{m_{1}} (5) \end{matrix}$

式中: $\begin{matrix} k_{1} 、 m_{1} \end{matrix}$ 为常数; $\begin{matrix} p_{o} \end{matrix}$ 为柱塞泵运行时工作压力; $\begin{matrix} p_{\max} \end{matrix}$ 为柱塞泵指定最高工作压力。

速度影响因子可以用下式描述:

$\begin{matrix} C_{PS} = k_{2} {(\frac{n_{o}}{n_{\max}})}^{m_{2}} (6) \end{matrix}$

式中: $\begin{matrix} k_{2} 、 m_{2} \end{matrix}$ 为常数; $\begin{matrix} n_{o} \end{matrix}$ 为柱塞泵运行时轴转速; $\begin{matrix} n_{\max} \end{matrix}$ 为柱塞泵设计最高转速。

轴向载荷影响因子可以用下式^[11]描述:

$\begin{matrix} C_{TLF} = k_{3} + k_{4} (\frac{q_{o}}{q_{\max}}) (7) \end{matrix}$

式中: $\begin{matrix} k_{3} 、 k_{4} \end{matrix}$ 为常数; $\begin{matrix} q_{o} \end{matrix}$ 为柱塞泵运行时出口流量; $\begin{matrix} q_{\max} \end{matrix}$ 为柱塞泵设计最大流量。根据文献[11], $\begin{matrix} k_{3} \end{matrix}$ 建议取0.8, $\begin{matrix} k_{4} \end{matrix}$ 建议取1.1。

当柱塞泵在稳定压力和转速下加速试验时, 式(7)可以近似变形为:

$\begin{matrix} C_{TLF} = k_{3} + k_{4} (\frac{n_{o}}{n_{\max}}) (8) \end{matrix}$

当柱塞泵做惯性循环加速试验时, 因为此时柱塞泵受到的冲击力明显大于横向载荷, 所以省略此项。

温度影响因子可以用下式描述:

$\begin{matrix} C_{T} = {(\frac{T_{o}}{T_{\max}})}^{m_{3}} (9) \end{matrix}$

式中: $\begin{matrix} m_{3} \end{matrix}$ 为常数; $\begin{matrix} T_{o} \end{matrix}$ 为柱塞泵运行时油液温度; $\begin{matrix} T_{\max} \end{matrix}$ 为柱塞泵允许最高工作油温。

污染物影响因子可以用下式^[11]描述:

$\begin{matrix} C_{C} = 0.6 + 0.5 F_{AC} (10) \end{matrix}$

式中: $\begin{matrix} F_{AC} \end{matrix}$ 为过滤器尺寸。

润滑油影响因子可以用下式^[11]描述:

$\begin{matrix} C_{υ} = {(\frac{υ_{sp}}{υ_{o}})}^{0.54} (11) \end{matrix}$

式中: $\begin{matrix} υ_{sp} \end{matrix}$ 为指定润滑油黏度; $\begin{matrix} υ_{o} \end{matrix}$ 为柱塞泵使用润滑油黏度。

轴承温度影响因子可以用下式^[11]描述:

$\begin{matrix} C_{t} = \{\begin{matrix} 1, & C_{t} < 183 ℃ \\ {(\frac{T_{o}}{183})}^{3}, & C_{t} \geq 183 ℃ \end{matrix} (12) \end{matrix}$

工作状况影响因子参考值见表2^[11]。

表2 工作状况影响因子 Table 2 Impact factor of working condition

工作状态	$\begin{matrix} C_{SF} \end{matrix}$
平稳运行, 无冲击	1.0~1.2
正常运行	1.2~1.5
伴随冲击和振动	1.5~3.0

表2 工作状况影响因子 Table 2 Impact factor of working condition

2.2 柱塞泵失效率表达式

针对柱塞泵可靠性高、寿命长的特点, 使用单应力在短时间内很难获得充分的失效数据。在许多情况下, 元件的寿命取决于几个应力同时运行, 对于室外产品来说, 多应力代表了一个真实的现场环境。由于温度、油液黏度及添加剂、污染度因素在进行柱塞泵寿命试验时控制其有规律变化实际操作难度很大, 同时考虑到一个合格的液压系统必须满足液压油液工作温度和清洁度的要求, 所以利用压力和转速作为双敏感应力进行柱塞泵寿命试验是有效的且从技术上容易实现, 同时也更接近柱塞泵的真实工作状况。

假设柱塞泵加速寿命试验时, 作为工作介质的液压油型号选择正确, 油液温度变化范围控制在± 3℃, 并确保油液黏度位于最佳工作范围内。同时, 油液清洁度指标可以满足柱塞泵正常工作。

(1)当柱塞泵做稳定状态加速试验时, 柱塞泵失效率为:

$\begin{matrix} \begin{matrix} λ_{tot .} = λ_{BASE .} [k_{1} {(\frac{p_{o}}{p_{\max}})}^{m_{1}}] \cdot [0.8 + 1.1 (\frac{q_{o}}{q_{\max}})] \cdot \\ [k_{2} {(\frac{n_{o}}{n_{\max}})}^{m_{2}}] (13) \end{matrix} \end{matrix}$

将常数项合并, 化简得:

$\begin{matrix} λ_{tot .} = k {(\frac{p_{o}}{p_{\max}})}^{m_{1}} \cdot [0.8 + 1.1 (\frac{n_{o}}{n_{\max}})] \cdot {(\frac{n_{o}}{n_{\max}})}^{m_{2}} (14) \end{matrix}$

(2)当柱塞泵做惯性循环加速试验时, 柱塞泵失效率为:

$\begin{matrix} λ_{tot .} = λ_{BASE .} [k_{1} {(\frac{p_{o}}{p_{\max}})}^{m_{1}}] \cdot [k_{2} {(\frac{n_{o}}{n_{\max}})}^{m_{2}}] (15) \end{matrix}$

将常数项合并, 化简得:

$\begin{matrix} λ_{tot .} = k {(\frac{p_{o}}{p_{\max}})}^{m_{1}} \cdot {(\frac{n_{o}}{n_{\max}})}^{m_{2}} (16) \end{matrix}$

3 柱塞泵加速模型

威布尔分布是由最弱环节模型导出的, 即一个整体的任何部分失效则整体就失效, 机械中的疲劳强度、疲劳寿命、磨损寿命、腐蚀寿命大多服从威布尔分布^[13]。为了得到柱塞泵加速模型, 假设柱塞泵在正常工作阶段失效, 此时, 柱塞泵的失效率为常数, 柱塞泵的平均失效时间(假设柱塞泵故障产品单元的修理时间忽略不计)与失效率互成倒数。从而可以得到:

当柱塞泵做稳定状态加速试验时, 柱塞泵加速模型为:

$\begin{matrix} \begin{matrix} η = \frac{1}{k {(\frac{p_{o}}{p_{\max}})}^{m_{1}} \cdot [0.8 + 1.1 (\frac{n_{o}}{n_{\max}})] \cdot {(\frac{n_{o}}{n_{\max}})}^{m_{2}}} = \\ l {(\frac{p_{\max}}{p_{o}})}^{m_{1}} \cdot \frac{1}{0.8 + 1.1 (\frac{n_{o}}{n_{\max}})} \cdot {(\frac{n_{\max}}{n_{o}})}^{m_{2}} (17) \end{matrix} \end{matrix}$

当柱塞泵做惯性循环加速试验时, 柱塞泵加速模型为:

$\begin{matrix} η = \frac{1}{k {(\frac{p_{o}}{p_{\max}})}^{m_{1}} \cdot {(\frac{n_{o}}{n_{\max}})}^{m_{2}}} = l {(\frac{p_{\max}}{p_{o}})}^{m_{1}} \cdot {(\frac{n_{\max}}{n_{o}})}^{m_{2}} (18) \end{matrix}$

式中: $\begin{matrix} l \end{matrix}$ 为常数。

4 结束语

将斜盘式轴向柱塞泵视为串联系统, 从分析其失效率角度入手, 推导得到了斜盘式轴向柱塞泵加速模型。这种分析方法对存在多故障模式包括突发性失效和退化性失效模式并存的大多数机械产品(服从威布尔分布)都适应。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	李壮云. 液压元件与系统[M]. 北京: 机械工业出版社, 2012. [本文引用:2]
[2]	孙毅刚, 许耀铭. 液压元件可靠性试验的基本方法[J]. 哈尔滨工业大学学报, 1992, 24(5): 96-99. Sun Yi-gang, Xu Yao-ming. The basic methods of reliability tests of hydraulic components[J]. Journal of Harbin Institute of Technology, 1992, 24(5): 96-99. [本文引用:2]
[3]	Jung Dong-soo, Kim Hyoung-eui. Development of accelerated life test method of hydraulic pump[J]. Key Engineering Materials, 2006, 326-328: 1861-1864. [本文引用:1]
[4]	Bannantine J A, Comer J J, Hand rock J L. Fundamentals of Fatigue Analysis[M]. Upper Saddle River: Prentice-Hall, 1990. [本文引用:1]
[5]	王少萍, 李沛琼, 王占林. 双应力加速模型的建立及参数估计[J]. 航空学报, 1994, 15(2): 236-241. Wang Shao-ping, Li Pei-qiong, Wang Zhan-lin. The double-stress accelerated model establishment and parameters estimation[J]. Chinese Journal of Aeronautics, 1994, 15(2): 236-241. [本文引用:1]
[6]	B·M·莫尔辛, Г·Г·萨莫洛夫. 王伯良(译). 轴向柱塞泵加速试验的方法[DB/OL]. [2014-09-30]. http://www.cqvip.com/read/read.aspx?id=171946. [本文引用:1]
[7]	Wang Shao-ping, Shi Jian. Accelerated life testing under variable synthetic stresses for hydraulic pump[J]. Materials Science Forum, 2006, 505-507: 1165-1170. [本文引用:1]
[8]	Tan L, Zhu B S, Cao S L, et al. Cavitation flow simulation for a centrifugal pump at a low flow rate[J]. Chinese Science Bulletin, 2013, 58(8): 949-952. [本文引用:1]
[9]	Luo X W, Wei W, Ji B, et al. Comparison of cavitation prediction for a centrifugal pump with or without volute casing[J]. Journal of Mechanical Science and Technology, 2013, 27(6): 1643-1648. [本文引用:1]
[10]	Du Jun, Wang Shao-ping, Zhang Hai-yan. Layered clustering multi-fault diagnosis for hydraulic piston pump[J]. Mechanical Systems and Signal Processing, 2013, 36(2): 487-504. [本文引用:1]
[11]	Surface N. Hand book of Reliability Prediction Procedures for Mechanical Equipment[M]. Dan Neck: Naval Surface Warfare Center (NSWC), 2009. [本文引用:8]
[12]	Hydraulic fluid power components-assessment of reliability by testing[R]. National Fluild Power Association(NFPA), 2007. [本文引用:1]
[13]	茆诗松, 汤阴才, 王玲玲. 可靠性统计[M]. 北京: 高等教育出版社, 2008. [本文引用:1]

2012

0.0

... 但柱塞泵一旦出现问题,将会影响到整个液压系统的正常运行,从而给企业造成重大损失^[1] ...

... 滑靴副、柱塞副、配流副是斜盘式轴向柱塞泵中的关键部件,对液压泵的容积效率、机械效率、温升、摩擦、磨损、工作可靠性及使用寿命均有很大影响^[1] ...

1992

0.0

. 1992, 24(5):96-99

The basic methods of reliability tests of hydraulic components

液压元件可靠性试验的基本方法

Sun Yi-gang , Xu Yao-ming.

孙毅刚, 许耀铭

描述了适合于不同要求下的液压元件可靠性试验方法,包括部件疲劳、部件磨损、整机序贯寿命和整机磨损四种可靠性试验方法。

... 在目前国内外柱塞泵可靠性寿命试验研究中,许耀明等^[2]在研究XB型斜盘式柱塞泵磨损强化试验时,通过分析材料体积磨损量磨损特性,提出了以压力 p和速度v作为双应力的逆幂律模型 ...

... 与其类似,Jung等^[3]在实施柱塞泵的加载压力为周期循环的加速寿命试验时,以金属疲劳失效的S-N曲线为理论依据^[4],提出了与文献中[2]形式相同的加速模型 ...

2006

0.0

1990

0.0

1994

0.0

. 1994, 15(2):236-241

The double-stress accelerated model establishment and parameters estimation

双应力加速模型的建立及参数估计

Wang Shao-ping , Li Pei-qiong , Wang Zhan-lin.

王少萍, 李沛琼, 王占林

This paper suggests a new method of aceelerated life testing, which uses a double-stress power law model for Weibull distribution,and gives the corresponding method of parameter estimation. The double-stress accelerated model is suitable for any stress accelerated except temperature in life testing of mechanical components.Compared with the model of con-stant single stress accelerated,the model not only can reduce testing time but suits for any stress spectra.By using this model,the service life and reliability for high reliable components can be es-timnted.From the test data of hydraulic pump, the results are satisfactory.

建立了威布尔分布下的双应力加速模型并给出了相应的参数估计方法。利用这种模型进行机械产品的加速寿命试验,具有试验时间短、适用于任意变动载荷等特点,是高可靠性产品寿命评估和可靠性分析的一种新方法。

... 王少萍等^[5]以ZB-34M斜盘式轴向柱塞泵为研究对象,以文献[6]结果为参考依据,同样以压力 p和速度v作为交叉加速应力,但是建立了不同的逆幂律模型 ...

2014

0.0

2006

0.0

... 同时,王少萍等^[7]以某型航空泵为研究对象,以压力 p、速度v和温度T综合应力为加速应力,提出了融合逆幂律和阿伦尼斯的模型 ...

2013

0.0

... 表1中仅列举了柱塞泵的主要失效模式^[8,9,10,11],并没有考虑诸如安装方法错误、维修不及时、材料热处理等工艺缺陷、油液使用不当、液压系统设计缺陷等容易造成柱塞泵失效的故障模式 ...

2013

0.0

2013

0.0

... 柱塞泵的失效率为各单元失效率之和^[11]: ...

... 与其他单元相比,柱塞泵泵轴和壳体通常具有更高的可靠性,研究表明^[11],球轴承和密封件失效率分别是传动轴失效率的8倍和3倍 ...

... 轴向载荷影响因子可以用下式^[11]描述: ...

... 污染物影响因子可以用下式^[11]描述: ...

... 润滑油影响因子可以用下式^[11]描述: ...

... 轴承温度影响因子可以用下式^[11]描述: ...

... 工作状况影响因子参考值见表2^[11] ...

0.0

... 而在柱塞泵检验合格投入市场后,随时间积累因粘着磨损造成的磨损量下降导致泵容积效率和机械效率下降^[12]往往是柱塞泵失效的主要原因 ...

2008

0.0

... 3 柱塞泵加速模型威布尔分布是由最弱环节模型导出的,即一个整体的任何部分失效则整体就失效,机械中的疲劳强度、疲劳寿命、磨损寿命、腐蚀寿命大多服从威布尔分布^[13] ...