基于BEM理论的兆瓦级风力机叶片设计及其气动性能

引用本文

袁哲, 周茜茜, 刘春宝, 马文星, 徐志轩. 基于BEM理论的兆瓦级风力机叶片设计及其气动性能.吉林大学学报:工学版, 2016, 46(4): 1142-1148
YUAN Zhe, ZHOU Qian-qian, LIU Chun-bao, MA Wen-xing, XU Zhi-xuan. Blade design and aerodynamics of MW wind turbine based on BEM theory. Journal of Jilin University Engineering and Technology Edition, 2016, 46(4): 1142-1148 复制到剪切板

Permissions

基于BEM理论的兆瓦级风力机叶片设计及其气动性能

袁哲, 周茜茜, 刘春宝, 马文星, 徐志轩

吉林大学机械科学与工程学院,长春 130022

通讯作者：刘春宝(1980-),男,副教授,博士.研究方向:液力传动与自动变速.E-mail:liuanbc@126.com

作者简介:袁哲(1984-),男,工程师,博士.研究方向:液力传动与自动变速.E-mail:yuanzhe@jlu.edu.cn

基金:吉林省科技发展计划项目(201205095)

摘要

根据风力机设计标准,在考虑叶尖损失和升阻力等影响因素的条件下,采用BEM理论设计了2 MW桨距控制型风力机叶片。为验证所开发风力机叶片的气动性能,对风力机模型进行全三维CFD数值模拟。模拟结果表明,该叶片静压强、绕流特性、湍流强度等符合叶片气动特性规律,满足设计要求。叶片展向的升阻系数与二维升阻系数对比结果表明,全三维的数值模拟能更准确地反映叶片绕流的气动特性。

关键词: 流体传动与控制; 兆瓦级风力机叶片; 气动特性; 三维CFD数值模拟; 绕流流场

中图分类号:TK81 文献标志码:A 文章编号:1671-5497(2016)04-1142-07

Blade design and aerodynamics of MW wind turbine based on BEM theory

YUAN Zhe, ZHOU Qian-qian, LIU Chun-bao, MA Wen-xing, XU Zhi-xuan

College of Mechanical Science and Engineering, Jilin University, Changchun 130022,China

Abstract

According the design standard of wind turbine and considering the influence of tip loss and lift-drag and other factors, Blade Element Momentum (BEM) theory was used to design the blade on a 2MW pitch-control wind turbine to meet the design requirements. To validate the aerodynamic performance of the designed wind turbine blade, full 3D numerical simulation is conducted. Simulation results show that the static pressure, flow characteristics and turbulence intensity are in accordance with the blade aerodynamic characteristics and meet the design requirements. Comparison of the blade spanwise lift-drag coefficients with the 2D results suggests that full 3D numerical simulation can more accurately reflect the aerodynamic performance.

Keyword: fluid power transmission and control; MW wind turbine blade; aerodynamic performance; three-dimensional CFD numerical simulation; circle flow field

Show Figures

0 引言

风力机是捕获风能并进行能量转化的重要元件。风轮气动性能计算是风力机风轮设计的重要环节, 它为叶片气动设计提供性能评价和反馈^[1]。风洞试验能比较准确地控制实验条件, 而且受气候条件和时间的影响小, 但是该方法成本高、周期长, 且大尺寸的风力机叶片气动试验条件很难满足。因此, 发展数值模拟技术, 研究全尺度的风力机叶片的气动性能势在必行。长期以来, 很多研究者一直利用程序法对风力机气动性能展开预测^{[2, 3, 4]}。该方法思路简单, 但没有考虑到雷诺数对升阻比的影响, 影响了求解结果的准确性。随着计算流体动力学(Computational fluid dynamics, CFD)的发展, 很多研究者开始利用CFD方法对风力机进行数值模拟计算, 并展开气动优化设计^{[5, 6, 7]}。相对程序法而言, CFD方法思路较为简洁、运算周期短、成本低。Sezer-Uzol和Long^[8]借助有限元体积求解器PUMA2, 利用旋转、非结构化网格, 对NREL的第六代风机风轮进行了在不同风速和偏航角下的CFD模拟, 模拟结果与实验数据表现出非常好的一致性; Nikolaou等^[9]采用CFD方法对6种不同的典型翼型做了数值模拟, 研究发现, 在小攻角下, 计算所得的翼型升阻系数与实验结果吻合较好, 而在大攻角下, 计算较难收敛, 且计算结果不够准确。

本文充分考虑到叶尖损失和升阻力等影响因素, 根据风力机设计标准, 采用动量叶素(Blade element momentum, BEM)理论, 建立较准确的风力机叶片模型。为使计算结果更准确, 采用CFD通用网格交界面技术处理交界面, 可保证旋转域和静止域在公共边界上的数据传递。

1 叶片设计

1.1 BEM理论

将叶片沿展向分成若干个微元, 每个微元称为一个叶素, 叶素理论是从叶素附近流动来分析叶片上的受力和功能交换。这里假设每个微元之间没有干扰, 作用在每个叶素上的力仅由叶素的翼型升阻特性来决定, 叶素本身可以看成一个二元翼型, 这时, 将作用在每个叶素上的力和力矩沿展向积分, 就可以求得作用在风轮上的力和力矩, 如式(1)(2)所示:

$\begin{matrix} \begin{matrix} δ F_{L} = \frac{1}{2} ρ W^{2} C C_{L} dr (1) \\ δ F_{D} = \frac{1}{2} ρ W^{2} C C_{D} dr (2) \end{matrix} \end{matrix}$

式中:ρ 、W、C、C_L、C_D分别为任一叶素上的气流密度、气流相对速度、弦长、升力系数、阻力系数; dr为任一微元的长度,其中r为叶片截面到转动中心的距离;δF_L、δF_D 分别为作用在任一叶素上的气动升力和气动阻力^[10]。

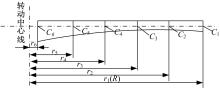
动量理论描述的是作用在风轮上的力与来流速度的关系, 如图1所示。该理论主要用来衡量有多少动能转换成机械能。在风轮扫略面内半径 $\begin{matrix} r \end{matrix}$ 处取一个圆环微元, 应用动量定理, 求得作用在微元上的推力:

$\begin{matrix} dT = m (V_{1} - V_{2}) = 4 πρr V_{1}^{2} (1 - a) adr (3) \end{matrix}$

式中: $\begin{matrix} V_{1} \end{matrix}$ 为距离风力机一定距离的上游风速, m/s; V₂为离风轮远处的下游风速, m/s; $\begin{matrix} a \end{matrix}$ 为轴向干扰因子。

	Figure Option View Download New Window
	图1 风轮扫掠面上微元体Fig.1 Element swept by wind turbine

将动量理论与叶素理论相结合得:

$\begin{matrix} \frac{NC C_{L}}{r} = \frac{8 πa}{1 - a} \cdot \frac{si n^{2} ϕ}{co s^{2} ϕ} (4) \end{matrix}$

式中: N为风力机的叶片数;ϕ为入流角。

采用Prandt1叶尖损失理论来预测风力机叶轮的叶尖气动损失, 公式如下:

$\begin{matrix} f (μ) = \frac{2}{π} co s^{- 1} [e^{- [((N / 2) (1 - μ) / μ) \sqrt[]{1 + (λ π^{2}) / (1 - α^{2})}]}] (5) \end{matrix}$

式中:μ 为黏性系数, 它的值与叶素所在的位置有关, 从轮毂处的μ =0.005逐渐增加至叶尖处的μ =1^[11]。

考虑升阻力影响以后的BEM理论如下:

$\begin{matrix} \begin{matrix} \frac{af}{1 - a} = \frac{σ_{r}}{4 si n^{2} ϕ} (C_{X} - \frac{σ_{r}}{4 si n^{2} ϕ} C_{y}^{2}) \frac{1 - a}{1 - af} (6) \\ \begin{matrix} \frac{a' f}{1 + a'} & = \frac{σ_{r} C_{Y}}{4 sinϕcosϕ} \cdot \frac{1 - a}{1 - af} (7) \\ C_{X} & = C_{L} \cos ϕ + C_{D} sinϕ (8) \\ C_{Y} & = C_{L} sinϕ + C_{D} cosϕ (9) \end{matrix} \end{matrix} \end{matrix}$

式中: $\begin{matrix} a' \end{matrix}$ 为切向干扰因子; σ _r为叶片的实积比; C_L、C_D为叶片的升、阻力系数。

应用以上考虑叶尖损失和升、阻力等影响因素的动量叶素理论对风力机叶片进行设计。

1.2 设计要素

风力机的设计要素如图2所示。额定功率给定为2 MW, 根据“ JB/T 10300-2001风力发电机组设计要求” , 确定风力机为三叶片桨距控制变桨变速型。

	Figure Option View Download New Window
	图2 设计要素Fig.2 Design elements

1.3 设计结果

本文采用三叶片风力机, 也就是 B=3;风轮半径为R满足:

$\begin{matrix} R = \sqrt[]{\frac{P}{k c_{a} c_{t} v^{3} ηπ}} (10) \end{matrix}$

式中: k为换算系数;c_a 为空气密度海拔高度系数;c_t 为空气密度湿度系数;η为全效率。

根据“ JB/T10194-2000” , 风能利用系数C_P满足:

$\begin{matrix} C_{P} = \frac{P}{0.5 ρS V_{1}^{3}} (11) \end{matrix}$

式中: $\begin{matrix} S \end{matrix}$ 为风轮扫风面积, m²。

叶尖速比 $\begin{matrix} λ \end{matrix}$ 被定义为:

$\begin{matrix} λ = \frac{2 πRn}{60 V} (12) \end{matrix}$

通过对以上各要素的设计计算, 得到风力机整体设计参数如下:额定功率P=2 MW; 风能利用系数C_P=0.5; 风轮半径R=37 m; 额定转速n=23 r/min; 额定风速v=12 m/s; 切入风速v_in=3.5 m/s; 切出风速v_out=25 m/s; 叶尖速比λ =7; 风轮叶片数B=3。

为使叶片具有较好空气动力学特性, 从转动中心到叶尖不同半径处的叶片弦长计算简图如图3所示, 计算公式如下:

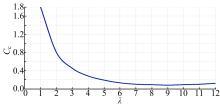
$\begin{matrix} C_{i} = \frac{r_{i} C_{c}}{C_{L} B} (13) \end{matrix}$

式中:C_c为叶片形状参数, 可由图4查得; C_L由翼型确定。

叶片各截面设有扭角

$\begin{matrix} θ_{i} = φ_{i} - α_{m} (14) \end{matrix}$

式中: $\begin{matrix} φ_{i} 为 r_{i} 处对应的相对迎风角; α_{m} \end{matrix}$ 为叶片的平均迎风角。

在叶片设计中, 不同截面分别选用了4种翼型:①FX77-W-343; ②NACA4418; ③NACA4415; ④NACA4412。叶片平面如图5所示, 图中数字代表上述对应翼型。

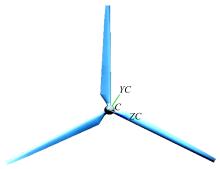
通过三维绘图软件建立风力机几何模型, 如图6所示。

	Figure Option View Download New Window
	图3 叶片弦长计算简图Fig.3 Blade chord length calculation simple diagram

	Figure Option View Download New Window
	图4 叶尖速比λ 与叶片形状参数的关系曲线Fig.4 Relation curve between blade tip speed ratio and leaf shape parameter

	Figure Option View Download New Window
	图5 叶片平面图Fig.5 Blade floor plan

	Figure Option View Download New Window
	图6 风轮几何模型Fig.6 Wind wheel geometry model

2 气动性能计算方法

2.1 控制方程组

由于风力机叶片大, 旋转速度低, 对周围流体温度影响不大, 可忽略其对流体密度的影响。于是流体运动的控制方程包括质量方程和动量守恒方程。直角坐标系下定常不可压流体的Reynolds时均控制方程可表示为如下形式:

$\begin{matrix} \frac{\partial u_{i}}{\partial x_{i}} = 0 (15) \end{matrix}$

$\begin{matrix} ρ \frac{\partial}{\partial x_{j}} (u_{i} u_{j}) = \frac{\partial p}{\partial x_{i}} + \frac{\partial}{\partial x_{i}} (μ \frac{\partial u_{i}}{\partial x}) + \frac{\partial τ_{ij}}{\partial x_{j}} (16) \end{matrix}$

式中: $\begin{matrix} u_{i} 、 u_{j} (i, j = 1, 2, 3) 是各时均速度分量; x_{i} 、 x_{j} (i, j = 1, 2, 3) 为各坐标分量; p 是流体时均压力; ρ 表示空气的密度; τ_{ij} \end{matrix}$ 代表雷诺应力, 需要通过湍流模型求得^[12]。

湍流模型采用工程上广泛使用的k-ε SST二阶模型^[13]:

$\begin{matrix} τ_{ij} = μ_{t} (\frac{\partial u_{i}}{\partial x_{j}} + \frac{\partial y_{j}}{\partial x_{i}}) - \frac{2}{3} ρk δ_{ij} (17) \end{matrix}$

式中: $\begin{matrix} μ_{t} \end{matrix}$ 为流体的湍流黏度, 满足:

$\begin{matrix} μ_{t} = 0.09 ρ k^{2} / ε (18) \end{matrix}$

2.2 计算域选取

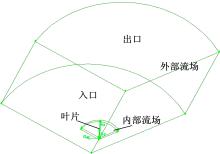
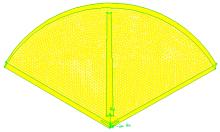
由于风力机本身旋转, 其将带动周围流体旋转, 包围风轮的旋转流场区域视为旋转域, 远离风力机的区域可视为静止流域, 本文称作外部流域, 两域的接触面即为内部交界面。相对应的控制方程将采用静止和旋转相对坐标系下的不可压缩流体Reynolds时均方程。周期性边界条件用来解决物理模型和所期待的流动解具有周期性重复的问题^[14]。由于风轮流场具备周期性, 为节约计算资源, 仅对一个叶片进行模拟, 采用旋转型周期边界条件。如图7所示, 该三叶片模型旋转型周期边界关于旋转对称几何外形的相邻对称面之间的角度为120° 。

2.3 网格划分

网格形式有多种, 六面体网格计算结果较精确, 但对模型要求较高; 四面体网格计算量较大, 但对于复杂曲面的适应性较好, 基本可以适用于任意复杂的几何形状。因此内部流域采取非结构化四面体网格, 在叶片处形状较复杂, 设置为尺寸较小的网格并局部加密, 采用Sizing Function方案, 实现从叶片表面到内流域边界处网格由精细到粗糙的平稳过渡; 外部流域形状较规格, 因此采用六面体网格, 如图8和图9所示。

	Figure Option View Download New Window
	图7 流场区域划分Fig.7 Divided flow field

	Figure Option View Download New Window
	图8 内流域网格Fig.8 Internal grid in flow field

	Figure Option View Download New Window
	图9 外流域网格Fig.9 External grid in flow field

为了接近实际工况, 同时考虑计算的准确性和计算时间, 采用CFD方法进行数值模拟, 空间离散格式选择高精度(二阶离散格式), 湍流模型选择为SST(剪切应力运输) k-ε模型,即在近壁面处使用k-ω模型,在边界层外部使用k-ε模型, 在边界层内则混合使用这两种模型, 同时增加了横向耗散导数项, 在湍流黏度定义中考虑了湍流剪切应力的运输过程, 因此模型适应范围更广、适用性更强。

分别针对旋转域和静止域进行边界条件设置。其中, 参考压力设为一个标准大气压, 流场入口设为速度入口条件, 流场出口设为出流条件, 周期边界面设为旋转周期边界。整体网格数为200万, 计算300步左右时收敛, 用时4 h左右, 计算周期较短。

3 计算结果分析

3.1 静态压强分布

设定风速为11.5 m/s, 转子速度为15 r/min。图10(a)、(b)分别是叶片迎风面静压强和背风面静压强。

	Figure Option View Download New Window
	图10 迎风面、背风面静压强Fig.10 Static pressure in windward and leeward

风力机叶片的迎风面由于来流流动受到阻滞导致风速迅速下降, 大部分动压转换成静压, 故迎风面压强基本为正压, 叶片表面风压达到整个流场的最大值。这与一般结构的表面压强分布相符。迎风面中间处压强大于前、后缘处, 这正是流线型翼型的特质。由图10可以明显看出叶根处压力较叶尖处压力大, 由此可以推测叶尖处风速较叶根处大。迎风面正压是由气流流动速度的降低导致静压转成动压而形成的; 叶片背风面处正好相反, 接近背风面的风速随着叶片的转动而迅速增加, 产生漩涡。风速的增加导致背风区域负压增多, 其在叶尖处的负压值最大, 使叶片旋转。

3.2 截面绕流

图11为 $\begin{matrix} r / R = 0.2 、 0.5 和 0.7 \end{matrix}$ 三个截面处的速度矢量图, 单位为m/s。

	Figure Option View Download New Window
	图11 叶片不同截面处的速度矢量图Fig.11 Velocity vector at different sections

就单个叶片来看:风速由迎风面流向背风面。迎风面整体趋势为风速较高, 原因是由于叶片的阻碍作用, 迎风面积减小导致前缘处风速急剧增大; 沿着翼型流动, 风速由前缘到后缘逐渐减小, 因此背风面整体趋势为风速较低。

对比各个截面处的速度矢量图可知:绕流随翼型延展向向叶尖移动, 且风速越来越大。在叶片周围的空气流动没有形成明显的涡流状况, 仅在某些部位例如叶片的根部以及前缘部分存在很不明显的紊流, 这对叶片性能的影响可忽略不计。在叶片的后缘处, 空气流没有发生分离, 这充分说明了叶片周围空气流动的稳定性。因叶片尺寸的关系, 叶片两端的流速差别也越来越大。

3.3 湍流强度

湍流强度是描述风速随时间和空间变化的程度, 反映脉动风速的相对强度, 是描述大气湍流运动特性的最重要的特征量。图12(a)、(b)、(c)分别是 $\begin{matrix} r / R = 0.2 、 0.5 和 0.7 \end{matrix}$ 三个截面处的湍流云图, 单位为m/s。

从图12可知, 气体接触迎风面后流向发生变化, 绕叶片流动, 翼型周围湍流强度较低, 这与相应截面处的绕流分析吻合; 湍流主要发生在风轮旋转时叶片的后缘部分, 且分别从前、后缘处沿风向逐渐扩大, 湍流强度也围绕翼型由叶根到叶尖处不断增大。由此可以看出叶尖处容易失速。

	Figure Option View Download New Window
	图12 不同截面处湍流强度图Fig.12 Turbulence intensity at different section

3.4 截面升阻系数分布

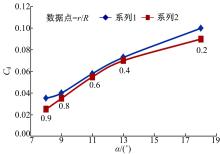
为分析三维模型中各截面升阻力特性, 本文取r/R=0.2、0.4、0.6、0.8、0.9处截面的翼型升阻力系数, 与相同条件下相应翼型二维数值模拟结果作对比分析, 如图13、图14所示。

	Figure Option View Download New Window
	图13 升力系数对比Fig.13 C_l Comparison

	Figure Option View Download New Window
	图14 阻力系数对比Fig.14 C_d Comparison

在r/R=0.2截面处, 三维升力系数较二维小, 阻力系数较二维大, 两者差异均在10%左右; 在r/R=0.4、0.6截面处可以看出, 三维计算与二维计算的升阻力之间的差异逐渐减小; 在r/R=0.8处, 三维升力系数陡然下降, 到r/R=0.9截面处明显升力系数相差较大, 而阻力系数相差很小。从总体上看, 叶根到叶尖的截面升力系数逐渐减小, 整体趋势为三维升力系数较二维小, 与二维的差距由大变小后又增大。靠近叶根处升力系数小、阻力系数偏大的主要原因可能是轮毂对叶片产生的影响; 在叶尖附近, 三维升力系数的骤减明显是由叶尖失速引起的。由此可以得出结论:相比于二维数值模拟, 三维数值模拟结果反映了轮毂以及叶尖失速等对升、阻力系数的影响, 因此更准确, 更具有参考价值。

4 结束语

本文根据风力机设计标准, 在充分考虑叶尖损失和升、阻力等影响因素的基础上, 采用BEM理论设计2 MW桨距控制型风力机叶片。对所设计的风力机模型进行了全三维CFD数值模拟, 计算周期短。对其气动特性进行了分析, 结果表明, 该叶片静压强、绕流特性、湍流强度等较符合叶片气动特性规律, 满足设计要求。通过叶片展向的升、阻系数与二维升、阻系数对比分析, 进一步说明了相比于简单的二维数值模拟, 全三维的数值模拟能更准确地反映叶片绕流的气动特性。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	何显富, 卢霞, 杨跃进, 等. 风力机设计、制造与运行[M]. 北京: 化学工业出版社, 2009. [本文引用:1]
[2]	胡丹梅, 张志超, 孙凯, 等. 风力机叶片流固耦合计算分析[J]. 中国电机工程学报, 2013, 33(17): 98-104. Hu Dan-mei, Zhang Zhi-chao, Sun Kai, et al. Computational analysis of wind turbine blades based on fluid-structure interaction[J]. Proceedings of the CSEE, 2013, 33(17): 98-104. [本文引用:1]
[3]	路宽. 基于数值模拟和风洞试验的垂直轴风力机性能研究[D]. 哈尔滨: 哈尔滨工业大学机电工程学院, 2012. Lu Kuan. Research on performance of vertical axis wind turbine based on numerical simulation and wind tunnel test[D]. Harbin: School of Mechatronics Engineering, Harbin Institute of Technology, 2012. [本文引用:1]
[4]	王菲, 吕剑虹, 王刚. 翼型厚度对风力机叶片翼型气动特性的影响[J]. 流体机械, 2011, 39(12): 5-9. Wang Fei, Lv Jian-hong, Wang Gang. Effects of airfoil thickness on airfoil aerodynamic characteristics[J]. Fluid Machinery, 2011, 39(12): 5-9. [本文引用:1]
[5]	Abdelsalam A M, Boopathi K, Gomathinayagam S, et al. Experimental and numerical studies on the wake behavior of a horizontal axis wind turbine[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2014, 128(5): 54-65. [本文引用:1]
[6]	Kim B, Kim W, Lee S, et al. Developement and verification of a performance based optimal design software for wind turbine blades[J]. Renewable Energy, 2013, 54(6): 166-172. [本文引用:1]
[7]	Diego C, Escárpita A A, Hugo E, et al. Numerical validation of a finite element thin-walled beam model of a composite wind turbine blade[J]. Wind Energy, 2012, 15(2): 203-223. [本文引用:1]
[8]	Sezer-Uzol N, Long L N. 3-D time-accurate CFD simulations of wind turbine rotor flow fields[C]∥AIAA Paper, 2006-0394. [本文引用:1]
[9]	Nikolaou I G, Politis E S, Chaviaropoulos P K. Modelling the flow around airfoils equipped with vortex generators using a modified 2D Navier-Stokes solver[J]. Journal of Solar Energy Engineering, 2005, 127(2): 223-233. [本文引用:1]
[10]	Bazilevs Y, Hsu M C, Kiendl J, et al. 3D simulation of wind turbine rotors at full scale. Part II: Fluid-structure interaction modeling with composite blades[J]. International Journal for Numerical Methods in Fluids, 2011, 65(1-3): 236-253. [本文引用:1]
[11]	Li Y, Paik K J, Xing T, et al. Dynamic overset CFD simulations of wind turbine aerodynamics[J]. Renewable Energy, 2012, 37(1): 285-298. [本文引用:1]
[12]	Shen X, Zhu X, Du Z. Wind turbine aerodynamics and loads control in wind shear flow[J]. Energy, 2011, 36(3): 1424-1434. [本文引用:1]
[13]	钟伟, 王同光. SST湍流模型参数校正对风力机CFD模拟的改进[J]. 太阳能学报, 2014, 35(9): 1743-1748. Zhong Wei, Wang Tong-guang. Improvement of CFD simulations for wind turbines by calibrating a closure constant of SST turbulence model[J]. Acta Energiae Solaris Sinica, 2014, 35(9): 1743-1748. [本文引用:1]
[14]	周茜茜. MW级风力机叶片气动特性及流固耦合特性研究[D]. 长春: 吉林大学机械科学与工程学院, 2015. Zhou Qian-qian. Study on aerodynamic and fluid-structure interaction characteristics of MW wind turbine blade[D]. Changchun: College of Mechanical Science and Engineering, Jilin University, 2015. [本文引用:1]

2009

0.0

... 风轮气动性能计算是风力机风轮设计的重要环节,它为叶片气动设计提供性能评价和反馈^[1] ...

2013

0.0

. 2013, 33(17):98-104

Computational analysis of wind turbine blades based on fluid-structure interaction

风力机叶片流固耦合计算分析

Hu Dan-mei , Zhang Zhi-chao , Sun Kai

胡丹梅, 张志超, 孙凯

The analysis of blade deformation and vibration under fluid-structure interaction is of great significance for the security of large wind turbine. Fluid-structure interaction computation analysis was carried out on the blade of a 5MW offshore wind turbine under NREL using the k - ω SST model and sliding meshes. The results show that blade deformation will occur on flap-wise direction, edge-wise direction and torsional direction under the rated wind speed fluid-structure interaction effect, and the deformation increases approaching to the blade tip with non-linear distribution. The area of stress concentration is likely to occur in the middle of the blade. The average aerodynamic force with fluid-structure interaction being taken into account is slightly higher than that without consideration of it. Aerodynamic attack angle and torque of blade increase under fluid-structure interaction. The increase of attack angle is the main reason for the increase of torque.

流固耦合条件下风力机的叶片变形及振动分析对大型风力机的安全具有重要意义。采用 k - ω SST紊流模型和滑移网格技术，对美国国家可再生能源实验室5MW海上风力机叶片进行了流固耦合计算分析。结果表明：叶片在额定风速流固耦合作用下会发生挥舞方向、摆振方向变形和扭转变形，越接近叶梢，叶片变形就越大而且变形呈非线性分布，而在叶片中段容易出现应力集中区；考虑叶片流固耦合作用时叶片所受到的持续平均气动力略大于未考虑叶片流固耦合作用时的情况；叶片流固耦合作用使叶片气动攻角、扭矩增大；而叶片攻角增大是导致叶片扭矩增大的主要原因。

... 长期以来,很多研究者一直利用程序法对风力机气动性能展开预测^[2,3,4] ...

2012

0.0

. 2012, :-

Research on performance of vertical axis wind turbine based on numerical simulation and wind tunnel test

基于数值模拟和风洞试验的垂直轴风力机性能研究

Lu Kuan.

路宽

近年来,人们大力发展可再生的绿色能源,以部分替代高污染的传统能源,利用清洁能源风能发电的风力发电机因此得到了快速的发展。垂直轴风力发电机由于结构简单、任意风向下都可以发电、启动力矩大、成本低,在小型风力发电领域获得了广泛的应用。但垂直轴风力机风能利用系数较低的,这个不足限制了它的发展。　　为了提升阻力型垂直轴风力机的性能,本文对一种垂直轴风力机的性能进行了研究,并从改变导流板数目、增加风力机段数等方面改进了其性能。论文首先阐述了风力机的基本理论和相关概念,并对阻力型垂直轴风机的平均功率计算公式进行了推导,根据公...

... 长期以来,很多研究者一直利用程序法对风力机气动性能展开预测^[2,3,4] ...

2011

0.0

... 长期以来,很多研究者一直利用程序法对风力机气动性能展开预测^[2,3,4] ...

2014

0.0

... 随着计算流体动力学(Computational fluid dynamics,CFD)的发展,很多研究者开始利用CFD方法对风力机进行数值模拟计算,并展开气动优化设计^[5,6,7] ...

2013

0.0

... 随着计算流体动力学(Computational fluid dynamics,CFD)的发展,很多研究者开始利用CFD方法对风力机进行数值模拟计算,并展开气动优化设计^[5,6,7] ...

2012

0.0

... 随着计算流体动力学(Computational fluid dynamics,CFD)的发展,很多研究者开始利用CFD方法对风力机进行数值模拟计算,并展开气动优化设计^[5,6,7] ...

0.0

... Sezer-Uzol和Long^[8]借助有限元体积求解器PUMA2,利用旋转、非结构化网格,对NREL的第六代风机风轮进行了在不同风速和偏航角下的CFD模拟,模拟结果与实验数据表现出非常好的一致性 ...

2005

0.0

... Nikolaou等^[9]采用CFD方法对6种不同的典型翼型做了数值模拟,研究发现,在小攻角下,计算所得的翼型升阻系数与实验结果吻合较好,而在大攻角下,计算较难收敛,且计算结果不够准确 ...

2011

0.0

... δFL、δFD分别为作用在任一叶素上的气动升力和气动阻力^[10] ...

2012

0.0

... =1^[11] ...

2011

0.0

... τij代表雷诺应力,需要通过湍流模型求得^[12] ...

2014

0.0

. 2014, 35(9):1743-1748

Improvement of CFD simulations for wind turbines by calibrating a closure constant of SST turbulence model

SST湍流模型参数校正对风力机CFD模拟的改进

Zhong Wei , Wang Tong-guang.

钟伟, 王同光

以NREL PhaseⅥ叶片为对象,基于RANS方法开展CFD数值模拟研究,发展了先在二维翼型上校正湍流模型封闭常数然后用于三维旋转叶片数值模拟的方法.将在S809翼型上校正出的SST湍流模型封闭常数β*的最佳数值用于NREL PhaseⅥ叶片的数值模拟,可显著提高该叶片在失速状态下气动力的数值模拟准确程度.

... SST二阶模型^[13]: ...

2015

0.0

. 2015, :-

Study on aerodynamic and fluid-structure interaction characteristics of MW wind turbine blade

MW级风力机叶片气动特性及流固耦合特性研究

Zhou Qian-qian.

周茜茜

随着世界性能源危机日益加剧，环境污染日趋严重，推进新能源和可再生能源的开发利用已是大势所趋。风能具有就地可取、分布广、无污染、可再生等优点，已成为新能源发展的重要方向。风力发电有着广阔的发展前景，在世界各地得到迅速发展。风力发电对于调整能源结构、降低环境污染、缓解能源危机等方面有着非常重要的意义。叶片是风力机的关键零部件，叶片的翼型、结构形式直接影响风力机的性能。叶片设计是一个复杂的多目标优化过程。理想的叶片不仅能获得良好的气动性能和较高的能量转换效率，还能使风电机组的整体性能得到改善。因此本文结合吉林省科技厅科技发展计划项目“基于HPC的兆瓦级风力机系统动力学仿真模拟研究（201205095）”，选取风力机的功率为2MW，对其展开气动结构设计与性能研究。主要研究内容和结论有以下几点。 1.采用动量叶素理论设计法对风力机叶片参数进行计算，并应用粒子群算法对参数进行优化。优化后的风力机有较好的启动性能，弦长和扭角更加合理，年发电量增加了5.97%。利用空间坐标转化法，将各截面翼型坐标转化为空间三维坐标，建立风力机叶片的空间三维模型，为叶片气动特性分析奠定基础。 2.翼型的气动特性对风力机整机的性能具有决定性的影响。对优化后叶片所选用的典型翼型NACA4415进行数值模拟，得到该翼型在额定风速下的气动特性。此外，还研究了雷诺数、相对弯度和相对厚度等因素对翼型气动性能的影响。 3.采用周期性边界条件，利用Fluent软件对单叶片三维流场数值仿真，得到叶片迎风面、背风面的压力分布和r/R=0.2、0.5、0.7三个截面下的空气流速及湍流动能分布图。分析了迎风面和背风面压力形成机理。研究了空气流速与湍流动能沿叶片展向的分布规律。研究结果表明空气流速和湍流动能随r/R的增大而增大。空气流经过叶片后没有明显分离和漩涡，表明叶片周围气流比较稳定。湍流动能强度围绕翼型由叶根到叶尖处不断增大，这是叶尖处容易失速的原因。以上结论表明，本文所设计的叶片有较好的气动特性。 4.采用流固耦合方法研究了风力机整机模型的气动特性以及动力学特性。先用CFX软件计算整机模型气动特性，再将气动特性载荷加载到固体风力机上，实现单向流固耦合。主要分析额定风速下叶片振动频率、振型以及形变，研究叶片变形与载荷分布相互影响机理。对风力机模型无预应力状态下静力学特性也进行了分析。计算结果表明所设计的风力机在流固耦合作用下不容易发生共振，验证了设计的合理性。

... 周期性边界条件用来解决物理模型和所期待的流动解具有周期性重复的问题^[14] ...