基于虚拟梯度材料的螺栓结合面建模方法

引用本文

廖静平, 张建富, 郁鼎文, 冯平法. 基于虚拟梯度材料的螺栓结合面建模方法.吉林大学学报:工学版, 2016, 46(4): 1149-1155
LIAO Jing-ping, ZHANG Jian-fu, YU Ding-wen, FENG Ping-fa. Modeling method of bolted joint interface based on gradient virtual materials. Journal of Jilin University Engineering and Technology Edition, 2016, 46(4): 1149-1155 复制到剪切板

Permissions

基于虚拟梯度材料的螺栓结合面建模方法

廖静平^1,², 张建富^1,², 郁鼎文^1,², 冯平法^1,²

1.清华大学机械工程系, 北京100084

2. 清华大学精密超精密制造装备及控制北京市重点实验室,北京100084

通讯作者：张建富(1975-),男,副教授,博士.研究方向:高效精密加工工艺与装备.E-mail:zhjf@tsinghua.edu.cn

作者简介:廖静平(1989-),男,博士研究生.研究方向:TBM刀盘结构设计分析.E-mail:woshiliao1989@163.com

基金:“973”国家重点基础研究发展计划项目(2013CB035402)

摘要

为准确分析螺栓连接件的动态性能,提出了一种基于虚拟梯度材料的螺栓结合面建模方法。将螺栓连接结合部等效为一种局部的虚拟梯度材料,虚拟梯度材料与被连接件皆为固定连接。通过有限元方法获得了螺栓连接结合面的接触压强分布情况,在此基础上,应用胡克定律,推导了虚拟梯度材料的弹性常量与径向位置之间的关系。采用分层法建立了基于虚拟梯度材料的螺栓结合面有限元分析模型,分别获取了固结、传统虚拟材料与虚拟梯度材料结合面表征下试件的理论模态,并开展模态实验,从振型和固有频率两方面进行了对比分析,验证了本文虚拟梯度材料建模方法的有效性。结果表明:虚拟梯度材料模型的模态与实验模态的前6阶振型一致,前6阶固有频率的相对误差数值都在10%以内,建模精度高。

关键词: 机械学; 螺栓结合面; 面压分布; 虚拟梯度材料; 模态分析

中图分类号:TH113.1 文献标志码:A 文章编号:1671-5497(2016)04-1149-07

Modeling method of bolted joint interface based on gradient virtual materials

LIAO Jing-ping^1,², ZHANG Jian-fu^1,², YU Ding-wen^1,², FENG Ping-fa^1,²

1.Department of Mechanical Engineering, Tsinghua University, Beijing 100084,China

2.Beijing Key Laboratory of Precision/Ultra-precision Manufacturing Equipments and Control, Tsinghua University,Beijing 100084,China

Abstract

To improve the modeling precision of bolted joints, a new modeling method based on gradient virtual materials was proposed. First, the contact pressure distribution on bolted joint interface was obtained through interpolating and revising the contact interface force. Then, the analytical expressions of the elastic modulus and shear modulus were derived for gradient virtual material according to Hooke Law. By using a layering method, the analytical formulas of the gradient virtual material was inserted into finite element software to construct the interface model. Qualitative comparison of similar mode and quantitative comparison of corresponding natural frequency were carried out between the simulation and experimental results. It is shown that the first six order vibration shapes of the gradient virtual material models are consistent with experimental results. The modeling precision of the gradient virtual material model is much better than that of traditional virtual material model.

Keyword: mechanics; bolted joint; contact pressure distribution; gradient virtual material; modal analysis

Show Figures

0 引言

螺栓连接广泛应用于工程结构中, 螺栓连接的效果与被连接件结合面之间的压强分布密切相关^[1]。此外, 研究表明螺栓连接件结合面压强直接影响结合面的动静态特性^{[2, 3]}。当前很多学者在研究螺栓结合面建模时, 基于小结合面假设(均匀受力), 忽略了实际压强分布的不均匀性, 当结合面尺度较大时, 难以建立准确的螺栓结合部模型^[4]。

目前, 对于螺栓连接件结合面压强分布的研究主要采用实验的方法^{[5, 6, 7]}。实验结果都表明螺栓连接件结合面间压强呈非均匀分布, 压强主要集中在螺栓连接件附近, 在远离螺栓连接件处压强几乎为零。螺栓结合部的建模方法对机械结构的设计与分析至关重要, 国内外研究人员对此做了大量的工作。Kim等^[8]对比了螺栓结合部的几种有限元建模方法, 并指出接触单元法的建模精度最高。田红亮等^{[9, 10]}指出, 常用的弹簧阻尼法存在建模前无法准确给定弹簧阻尼单元的数量和位置、法向与切向特性相互独立等不足, 并依据赫兹接触理论和分形几何理论提出了结合部的各向同性虚拟材料的建模方法, 顾及了结合部法向与切向特性的相互影响。石坤等^[11]基于GW接触模型和赫兹接触理论, 由单位面积刚度推导了结合部等效虚拟材料参数。传统的虚拟材料法虽具有一定的建模精度, 但是该方法没有考虑螺栓分布对模型精度的影响, 在静动态特性分析方面仍存在较大的误差。

基于此, 本文提出了螺栓连接件结合面的虚拟梯度材料建模方法, 考虑了螺栓分布的影响。在采用有限元法获得螺栓连接件结合面压强分布的基础上, 根据材料力学的胡克定律, 推导了虚拟梯度材料的弹性常量与径向位置之间的关系。最后, 通过有限元仿真和实验, 比较了两者的模态(相似振型定性比较, 相应的固有频率定量比较), 验证了虚拟梯度材料建模方法的有效性。

1 结合面压强分布的表征及拟合

1.1 结合面压强分布的表征

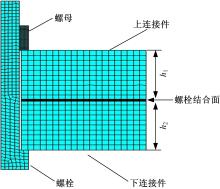
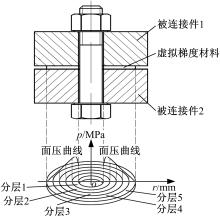
为了减小边界的影响, 被连接件的尺寸应远大于螺栓的作用范围。为简化计算, 采用轴对称模型, 忽略螺纹部分的建模。建立如图1所示的螺栓连接件二维轴对称有限元模型。其中被连接件、螺栓与螺母采用Plane182单元进行网格划分, 被连接件与螺母之间、被连接件之间以及被连接件与螺栓头之间, 采用接触单元Contac172和Targe169模拟接触行为。采用Prets179预紧单元和Psmesh命令模拟螺栓的预紧力。被连接件材料为45号钢, 被连接件厚度h₁=h₂=10 mm, M6螺栓预紧, 中等装配精度, 预紧力为14 kN。

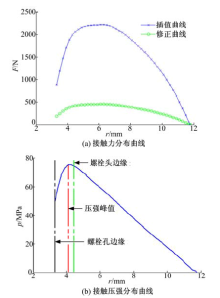
	Figure Option View Download New Window
	图1 螺栓连接件有限元模型Fig.1 Finite element model of bolted joint

提取被连接件接触面各接触节点的初始接触力, 对节点初始接触力进行插值以提高表征精度, 为使插值后曲线总压力等于螺栓预紧力, 按比例缩小插值曲线以完成修正。求取修正后径向各区间的平均压强, 由于插值区间较小, 因而可用平均压强的分布曲线来近似被连接件结合面处压强的径向分布曲线, 如图2所示。文献[12]采用类似的方法对螺钉连接固定结合面压强进行了仿真表征, 并通过实验验证了该方法的有效性。由图2可以看出, 压强峰值并不出现在螺栓孔边缘处, 而是在螺栓孔边缘和螺栓头边缘之间, 这说明压强峰值同时受到螺栓孔边缘和螺栓头边缘的影响。这一现象与文献[13]中的实验结论一致。

	Figure Option View Download New Window
	图2 接触力及压强的仿真曲线Fig.2 Simulation curves of contact force and pressure

1.2 结合面压强分布曲线的拟合及修正

为了便于对仿真数据进行量化处理, 采用四次多项式对螺栓结合面的压强分布曲线进行拟合。拟合公式为:

$\begin{matrix} P_{n} (r) = c_{1} r^{4} + c_{2} r^{3} + c_{3} r^{2} + c_{4} r + c_{5} (1) \end{matrix}$

式中:r为径向位置; c₁~c₅为常数。

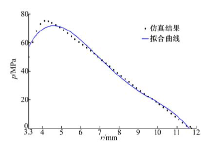
在95%置信度下, 采用线性最小二乘法对结合面接触范围内的压强仿真结果进行曲线拟合, 如图3所示。曲线的拟合度如下:R²=0.9919; 标准差为2.279。

	Figure Option View Download New Window
	图3 结合面压强的曲线拟合Fig.3 Fitting curve of interface contact pressure

为了保证压强拟合曲线在最大接触半径处为零, 且拟合曲线在接触面积下的积分与螺栓预紧力相等, 需要对拟合曲线进行修正。拟合曲线的修正分两步进行:①从拟合曲线中减去一个常数, 以使最大接触半径处的压强值为零; ②将拟合曲线乘以一个常数, 保证接触面积下的曲线积分等于螺栓预紧力。拟合曲线修正后的压强分布式如下:

$\begin{matrix} \begin{matrix} P_{n} (r) = - 0.097878 r^{4} + 3.2388 r^{3} - 38.891 r^{2} + \\ 189.98 r - 251.11 (2) \end{matrix} \end{matrix}$

2 结合面虚拟梯度材料力学模型

有别于传统的虚拟材料模型, 本文基于螺栓结合面接触压强分布的不均匀性, 提出了一种虚拟梯度材料模型来描述螺栓结合面的刚度特性。假设由实验或者理论计算得到了均匀压力作用下的单位面积结合面的法向动刚度K_n和切向动刚度K_τ为:

$\begin{matrix} \begin{matrix} K_{n} = α_{n} \cdot P_{n}^{β_{n}} (3) \\ K_{τ} = α_{τ} \cdot P_{n}^{β_{τ}} (4) \end{matrix} \end{matrix}$

式中:α _n、β _n为结合部法向特性参数; α _τ、β _τ为结合部切向特性参数, 它们与结合面的材料、润滑方式、加工方法、表面粗糙度等因素有关; P_n为结合面的接触压强。

根据材料力学中的胡克定律, 有:

$\begin{matrix} K = \frac{F}{Δh} = \frac{ES}{h} (5) \end{matrix}$

式中:K为虚拟材料层的总刚度; Δ h、h分别为虚拟材料层的法向变形量和初始厚度; F为虚拟材料层受力; E为虚拟材料层的弹性模量; S为虚拟材料层的面积。由式(3)(5)可得虚拟材料层的弹性模量与径向位置之间的关系式如下:

$\begin{matrix} E (r) = K_{n} \cdot S \cdot h / S = α_{n} \cdot P_{n} {(r)}^{β_{n}} \cdot h (6) \end{matrix}$

同理, 可得虚拟材料切变模量与径向位置之间的关系式为:

$\begin{matrix} G (r) = K_{τ} \cdot S \cdot h / S = α_{τ} \cdot P_{n} {(r)}^{β_{τ}} \cdot h (7) \end{matrix}$

式中:G(r)为虚拟材料层的切变模量。

根据弹性模量E、泊松比μ 和切变模量G三个弹性常量之间的关系可以确定虚拟材料泊松比μ 。常用各向同性材料的泊松比为-1.0~0.5, 有限元软件也只允许输入此范围内的泊松比数值, 而由式(6)(7)确定的虚拟材料泊松比μ 一般不在此范围内, 因此将各向同性的虚拟材料转换成正交各向异性的等效虚拟材料^[14]。正交各向异性虚拟材料层的法向对应结合面法向刚度K_n的方向; 切向对应结合面切向刚度K_τ的方向; 其他参数使用结合面的等效弹性模量、等效切变模量; 泊松比可取为实际材料的泊松比。对于虚拟材料层的厚度h常取为1 mm, 虚拟材料层的密度可取为被连接件材料的平均密度。

3 仿真及实验验证

3.1 试件的设计

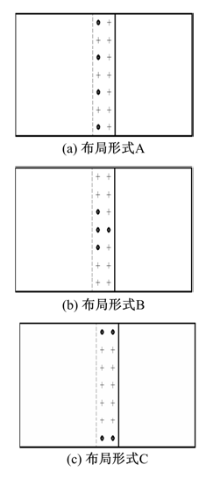
为了验证本文建模方法的正确性, 设计了如图4所示的3种不同螺栓布局形式的试验件。试验件由两块45号钢的薄板搭接而成, 薄板的尺寸为260 mm× 210 mm× 10 mm。两板由4个12.9级的M6螺栓以不同的分布形式进行连接, 螺栓预紧力矩为16.8 N· m。结合面尺寸为210 mm× 60 mm。

	Figure Option View Download New Window
	图4 3种螺栓布局示意图Fig.4 Schematic diagram of bolts distribution

两薄板之间的结合面状况为:钢-钢, 磨削, Ra=0.8, 无油。根据文献[15]中的实验数据, 单位面积结合面上的法向动刚度和切向动刚度公式分别为:

$\begin{matrix} \begin{matrix} K_{n} = 3.262540 P_{n}^{0.604} (8) \\ K_{τ} = 0.268894 P_{n}^{0.48} (9) \end{matrix} \end{matrix}$

式中:K_n、K_τ的单位为MPa/μ m; P_n的单位为MPa。

3.2 试件模态的仿真及实验

(1)仿真模型

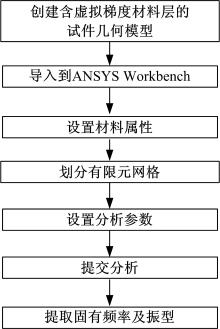
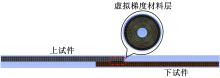
对于梯度材料结构, 可采用分层法建立其有限元分析模型。将梯度材料划分成若干层, 每层的材料参数不相同, 但同一层的材料参数为常数。在此基础上, 每层按照常规的有限元网格划分方法, 建立有限元求解模型。当划分的层数越多, 材料参数的变化越接近连续变化, 模型的求解结果也就越接近理论解析解。考虑计算的效率, 将本文中的虚拟梯度材料层均匀划分成5层。在每个连接螺栓周围建立如图5所示的虚拟梯度材料模型, 其中每层虚拟材料的压强取为每层的平均接触压强。对于多螺栓组合的情况, 可以看作是单个螺栓作用下压强分布的线性叠加。有限元分析的流程如图6所示, 在ANSYS Workbench15.0中建立试件的有限元分析模型, 如图7所示。

	Figure Option View Download New Window
	图5 虚拟梯度材料分层模型Fig.5 Layering model of gradient virtual material

	Figure Option View Download New Window
	图6 模型有限元分析流程图Fig.6 Flow chart of finite element analysis of structure

	Figure Option View Download New Window
	图7 试件的有限元模型Fig.7 Finite element model of the structure

(2)实验原理及方法

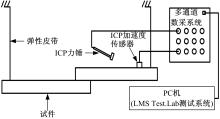
根据图8所示的原理图搭建试件模态测试平台。在模态测试过程中, LMS SCADAS III多通道数据采集系统获取和处理动态测试数据, LMS Test.Lab 10A振动测试和分析系统可同时获取试件输入输出之间的动态响应。冲击力锤的灵敏度为2.23 N/V; 非线性度小于1%; 共振频率大于22 kHz。加速度传感器的灵敏度为10.2 mV/(m· s^-2); 共振频率大于25 kHz; 非线性度小于1%。试件采用弹性皮带悬挂的方式模拟自由边界, 以锤击法测量试件的模态, 如图9所示。

	Figure Option View Download New Window
	图8 实验原理图Fig.8 Schematic diagram of test

	Figure Option View Download New Window
	图9 实验测试现场图Fig.9 Modal test of bolted structure

建立40个节点的试件测试模型并依次进行敲击, 加速度传感器获取试件在不同敲击点下的振动情况, 进而可由LMS Test.Lab机械振动测试系统计算相应点间的频响函数关系, 最后, 通过频响函数的幅频曲线、相频曲线可确定试件的各阶固有频率和振型。图10为螺栓分布形式A的试件实测幅频特性曲线。

(3)结果对比及讨论

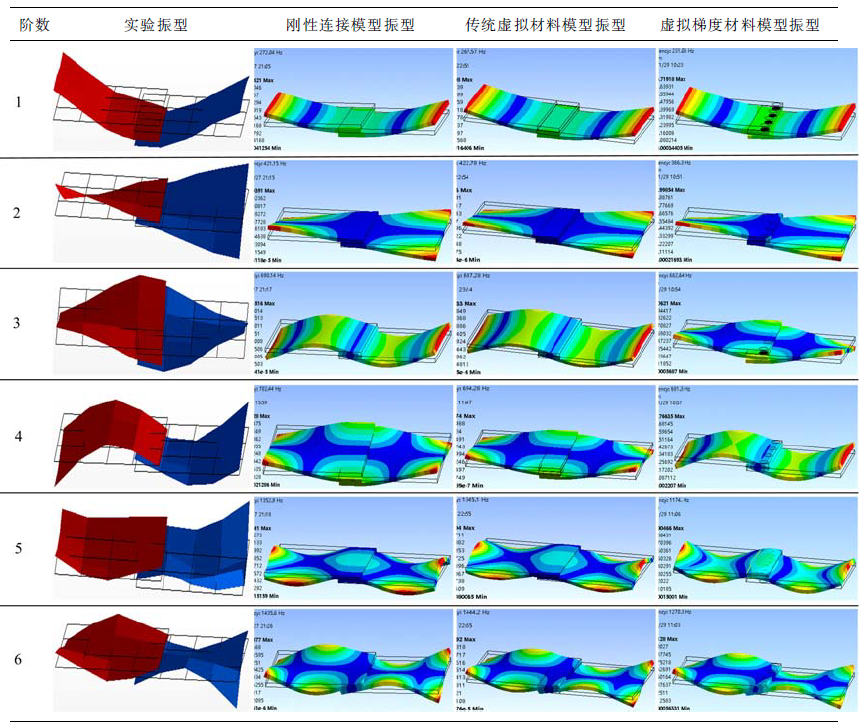
	Figure Option View Download New Window
	图10 螺栓分布形式A的试件特性曲线Fig.10 Measured characteristic curve of structure

根据“ 相似振型定性比较, 相应固有频率定量比较” 的原则, 比较3种理论仿真模型模态与实验辨识模态。限于篇幅, 仅以螺栓分布形式A为例, 比较仿真与实验的振型, 如表1所示, 其中刚性连接模型将结合部直接固连, 即在有限元软件中设置为Bonded接触。在螺栓分布形式A下, 实验的前6阶振型与虚拟梯度材料的前6阶振型皆一一对应, 刚性连接模型、传统虚拟材料模型的第3和4阶振型与实验的第3和4阶振型错位。

在3种不同螺栓布局形式下, 3种理论仿真固有频率与实验辨识固有频率(简称固频)的比较见表2。在3种螺栓布局形式下, 刚性连接模型的前6阶固有频率皆大于实验的前6阶固有频率, 说明在实际中应该考虑结合部的影响。此外, 3种螺栓布局形式下的实验前6阶固有频率各不相同, 这表明在虚拟材料建模时不能忽视螺栓分布的影响。本文虚拟梯度材料建模方法考虑了螺栓分布的影响, 总体来看, 在3种螺栓分布形式下, 虚拟梯度材料模型的前6阶固有频率的相对误差数值都在10%之内, 且对于结构分析中常关心的前3阶固有频率, 虚拟梯度材料建模法的精度要明显优于传统虚拟材料法。

表1 3种仿真模型振型与实验振型的比较 Table 1 Comparison among three theoretical models’ vibration shapes and experimental results

表2 3种理论模型固有频率与实验固有频率的比较 Table 2 Comparison of three theoretical models’ natural frequencies with experimental results

4 结论

(1)螺栓连接件结合面接触压强呈非均匀分布, 压强峰值并不在螺栓孔边缘, 而是出现在螺栓孔边缘与螺栓头边缘之间, 这说明压强峰值同时受到了螺栓孔边缘和螺栓头边缘的影响。

(2)根据材料力学胡克定律, 推导了螺栓结合面虚拟梯度材料弹性常量与径向位置之间的函数关系, 并在此基础上提出了螺栓结合面的虚拟梯度材料建模法, 该建模方法考虑了螺栓分布对模型精度的影响。

(3)通过模态实验和仿真分析, 根据“ 相似振型定性比较, 相应固有频率定量比较” 的原则, 比较了实验模态与虚拟梯度材料模型模态。虚拟梯度材料模型的前6阶振型与实验前6阶振型皆一一对应, 虚拟梯度材料模型的前6阶固有频率的相对误差数值都在10%之内, 对于结构分析中常关心的前3阶固有频率, 虚拟梯度材料法的建模精度要优于传统虚拟材料法。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Marshall M B, Zainal I, Lewis R. Influence of the interfacial pressure distribution on loosening of bolted joints[J]. Strain, 2011, 47(2): 65-78. [本文引用:1]
[2]	Wang Lei, Liu Hai-tao, Zhang Jun, et al. Analysis and modeling for flexible joint interfaces under micro and macro scale[J]. Precision Engineering, 2013, 37(4): 817-824. [本文引用:1]
[3]	蔡力钢, 郝宇, 郭铁能, 等. 螺栓结合面法向静态刚度特性提取方法研究[J]. 振动与冲击, 2014, 33(16): 18-23. Cai Li-gang, Hao Yu, Guo Tie-neng, et al. Method of extracting normal static stiffness of bolted joint interfaces[J]. Journal of Vibration and Shock, 2014, 33(16): 18-23. [本文引用:1]
[4]	蔡力钢, 王锋, 李玲, 等. 栓接结合部动态特性研究进展[J]. 机械工程学报, 2013, 49(9): 158-168. Cai Li-gang, Wang Feng, Li Ling, et al. Review on dynamic properties of bolted joints[J]. Journal of Mechanical Engineering, 2013, 49(9): 158-168. [本文引用:1]
[5]	Pau M, Baldi A, Leban B. Visualization of contact areas in bolted joints using ultrasonic waves[J]. Experimental Techniques, 2008, 32(4): 49-53. [本文引用:1]
[6]	Mantelli M, Milanez F H, Pereira E, et al. Statistical model for pressure distribution of bolted joints[J]. Journal of Thermophysics and Heat Transfer, 2010, 24(2): 432-437. [本文引用:1]
[7]	Stephen J T, Marshall M B, Lewis R. An investigation into contact pressure distribution in bolted joints[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2014, 228(18): 3405-3418. [本文引用:1]
[8]	Kim J, Yoon J C, Kang B S. Finite element analysis and modeling of structure with bolted joints[J]. Applied Mathematical Modeling, 2007, 31(5): 895-911. [本文引用:1]
[9]	田红亮, 刘芙蓉, 方子帆, 等. 引入各向同性虚拟材料的固定结合部模型[J]. 振动工程学报, 2013, 26(4): 561-573. Tian Hong-liang, Liu Fu-rong, Fang Zi-fan, et al. Immovable joint surface's model using isotropic virtual material[J]. Journal of Vibration Engineering, 2013, 26(4): 561-573. [本文引用:1]
[10]	Tian Hong-liang, Li Bin, Liu Hong-qi, et al. A new method of virtual material hypothesis-based dynamic modeling on fixed joint interface in machine tools[J]. International Journal of Machine Tools and Manufacture, 2011, 51(3): 239-249. [本文引用:1]
[11]	石坤, 宋俐, 师俊平. 机械结合部等效材料参数建立与试验[J]. 农业机械学报, 2014, 45(2): 297-301. Shi Kun, Song Li, Shi Jun-ping. Establishment and experiment of mechanical joint equivalent material properties[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(2): 297-301. [本文引用:1]
[12]	王磊, 杜瑞, 金涛, 等. 螺钉连接固定结合面匹配设计研究[J]. 西安交通大学学报, 2013, 47(7): 62-67. Wang Lei, Du Rui, Jin Tao, et al. Matching design for bolted joints based by effective contact radius maximization[J]. Journal of Xi'an Jiaotong University, 2013, 47(7): 62-67. [本文引用:1]
[13]	Marshall M B, Lewis R, Dwyer-Joyce R S. Characterisation of contact pressure distribution in bolted joints[J]. Strain, 2006, 42(1): 31-43. [本文引用:1]
[14]	王书亭, 李杰, 刘涛, 等. 机械固定结合面刚度特性建模[J]. 华中科技大学学报: 自然科学版, 2011, 39(8): 1-5. Wang Shu-ting, Li Jie, Liu Tao, et al. Interfacial stiffness characteristic modeling of mechanical fixed joints[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2011, 39(8): 1-5. [本文引用:1]
[15]	张学良. 机械结合面动态特性及应用[M]. 北京: 中国科学技术出版社, 2002. [本文引用:1]

2011

0.0

... 0 引言螺栓连接广泛应用于工程结构中,螺栓连接的效果与被连接件结合面之间的压强分布密切相关^[1] ...

2013

0.0

... 此外,研究表明螺栓连接件结合面压强直接影响结合面的动静态特性^[2,3] ...

2014

0.0

. 2014, 33(16):18-23 DOI:doi:10.13465/j.cnki.jvs.2014.16.004

Method of extracting normal static stiffness of bolted joint interfaces

螺栓结合面法向静态刚度特性提取方法研究

Cai Li-gang , Hao Yu , Guo Tie-neng

蔡力钢, 郝宇, 郭铁能

Joint interfaces static stiffness is closely related to connection mode、the bolted member stiffness and the joint part stiffness, it is very difficult to measure and calculate Joint interfaces static stiffness directly. Taking bolted joint interfaces as research objects, this paper establish a method of extracting normal static stiffness of bolted joint interfaces. First through the way of combination of the normal static stretching experiment and data processing, the joint part stiffness will be obtained. Then this paper performed optimizations to theoretical analysis for bolted member stiffness, and formed the refined analytic formula. Exploiting relationships among joint interfaces static stiffness、the bolted member stiffness and the joint part stiffness quite efficiently, we can extract normal static stiffness of bolted joint interfaces from the whole bolted joint part stiffness. In accordance with the above analysis the results, the nonlinear characteristic curve of normal static stiffness of bolted joint interfaces corresponding to effective contact pressure，can be extracted exactly. This paper provided a new way to the in-depth study about Joint interfaces static stiffness.

针对结合面静态刚度与联接方式、被联接段刚度、结合部刚度密切相关，直接测量、计算结合面静态刚度具有较大困难问题，以螺栓结合面为研究对象，建立螺栓结合面法向静态刚度特性提取方法。通过法向静态拉伸实验与数据分析结合方式，获得结合部刚度；通过优化计算螺栓结合面被联接段刚度，建立被联接段刚度精化解析公式；依托螺栓结合面刚度、被联结件刚度、结合部刚度三者间串联倒数关系，将螺栓结合面法向静态接触刚度从螺栓结合部整体静态刚度中分离；形成确定螺栓结合面有效作用面积方法，完整提取螺栓结合面面压的螺栓结合面法向静态接触刚度非线性特性曲线，为结合面接触刚度深入研究提供新方法。

... 此外,研究表明螺栓连接件结合面压强直接影响结合面的动静态特性^[2,3] ...

2013

0.0

. 2013, 49(9):158-168 DOI:doi:10.3901/JME.2013.09.158

Review on dynamic properties of bolted joints

栓接结合部动态特性研究进展

Cai Li-gang , Wang Feng , Li Ling

蔡力钢, 王锋, 李玲

栓接结合部是机床中最为典型的一种结合部形式,其影响因素众多,作用机理极其复杂,直接影响机床的整体性能,研究其动静态特性对整机的创新设计和自主研发具有重要意义.在过去三十多年时间里,众多学者开展栓接结合部特性研究,进一步明确了其内部机理和主要影响因素,但真正建立其本构模型、获取通用性数据仍存在困难,因此,有必要对现有研究成果进行系统分析和深入总结.早期研究是从栓接结合部等效线性化特性开展,近些年来其非线性特性越来越受到重视,这是由栓接结合部具有强非线性特性的本质决定的.以这两种研究思路为脉络,从栓接结合部的基础试验及理论研究、物理模型建立及参数辨识和工程应用展开综述,比较各研究提出的假设及其优缺点,总结研究所存在的不足,并对未来研究趋势进行展望.

... 当前很多学者在研究螺栓结合面建模时,基于小结合面假设(均匀受力),忽略了实际压强分布的不均匀性,当结合面尺度较大时,难以建立准确的螺栓结合部模型^[4] ...

2008

0.0

... 目前,对于螺栓连接件结合面压强分布的研究主要采用实验的方法^[5,6,7] ...

2010

0.0

... 目前,对于螺栓连接件结合面压强分布的研究主要采用实验的方法^[5,6,7] ...

2014

0.0

... 目前,对于螺栓连接件结合面压强分布的研究主要采用实验的方法^[5,6,7] ...

2007

0.0

... Kim等^[8]对比了螺栓结合部的几种有限元建模方法,并指出接触单元法的建模精度最高 ...

2013

0.0

. 2013, 26(4):561-573 DOI:doi:10.3969/j.issn.1004-4523.2013.04.013

Immovable joint surface's model using isotropic virtual material

引入各向同性虚拟材料的固定结合部模型

Tian Hong-liang , Liu Fu-rong , Fang Zi-fan

田红亮, 刘芙蓉, 方子帆

摘　要：为提高整机的建模精度,提出利用各向同性虚拟材料假设的机床固定结合部动力学建模的解析法.将固定结合部的两个接触面的微观接触部分假设为一种虚拟的各向同性材料,虚拟材料与固定结合部两侧的零件皆为固定连接.通过增加一个元件可将含结合部的复杂部件等效为不含结合部的简单零件,达到将复杂的固定结合部问题简单化的目的.考虑固定结合部法向和切向特性的相互影响,应用赫兹接触理论和分形几何理论推导虚拟材料弹性模量、泊松比、厚度、密度等参数的解析解.将虚拟材料参数的解析解导入到有限元软件中,可获得整机的理论模态.对实验试件的理论模态与实验模态进行比较（相似振型定性比较,相应的固有频率定量比较）.比较结果表明：理论模态与实验模态的前6阶振型一致,理论模态与实验模态前6阶固有频率的相对误差在-8.1％～8.1％之间.验证虚拟材料参数解析解的有效性,虚拟材料模型可为计算机数控机床固定结合部的精确动力学建模提供一定的理论基础.

... 田红亮等^[9,10]指出,常用的弹簧阻尼法存在建模前无法准确给定弹簧阻尼单元的数量和位置、法向与切向特性相互独立等不足,并依据赫兹接触理论和分形几何理论提出了结合部的各向同性虚拟材料的建模方法,顾及了结合部法向与切向特性的相互影响 ...

2011

0.0

2014

0.0

. 2014, 45(2):297-301 DOI:doi:10.6041/j.issn.1000-1298.2014.02.049

Establishment and experiment of mechanical joint equivalent material properties

机械结合部等效材料参数建立与试验

Shi Kun , Song Li , Shi Jun-ping.

石坤, 宋俐, 师俊平

In order to improve the commonality of research findings in the mechanical joint properties, the equivalent material properties of the mechanical joints were proposed. Based on GW contact model and Hertz-Mindilin contact theory, the Young’s modulus and the Poisson’s ratio of the equivalent material properties were deduced by the stiffness per unit area in the joint, which was obtained by the experiment. A bolted structure was taken as the example. The deformation of the structure was measured and analyzed under the different loads, which including the deformation of the structure’s joints. The comparison between the results of calculation and experiment validated the feasibility and effectiveness of the equivalent materical properties of the mechanical joints.

针对目前机械结合部特性研究成果通用性差的问题，提出了一种机械结合部等效材料参数模型。基于GW接触模型和Hertz Mindilin接触理论，由机械结合部试验获得的结合部单位面积刚度，推导出机械结合部等效材料参数——弹性模量和泊松比。以螺栓连接的机械结构为研究对象，对不同载荷作用下结构变形进行了数值分析，并将分析结果与试验测量结果进行了比较，验证了机械结合部等效材料参数的可行性和准确性。

... 石坤等^[11]基于GW接触模型和赫兹接触理论,由单位面积刚度推导了结合部等效虚拟材料参数 ...

2013

0.0

. 2013, 47(7):62-67 DOI:doi:10.7652/xjtuxb201307012

Matching design for bolted joints based by effective contact radius maximization

螺钉连接固定结合面匹配设计研究

Wang Lei , Du Rui , Jin Tao

王磊, 杜瑞, 金涛

为改善机床固定结合面的实际接触状态,对螺钉结合面压强分布的影响参数及影响规律进行了研究.通过建立的单螺钉连接结合面接触分析模型,获得了结合面的接触压强分布.通过改变结合面的设计参数,来实现螺钉有效影响半径、有效连接区域的最大化,得到了被连接件厚度与螺钉直径的匹配关系,以及相邻螺钉的最大间距.采用压强沿连接孔径向的高斯型分布曲线,对结合面压强分布规律进行了参数化表征和分析,分析结果表明:预紧力的增大可使压强值呈线性增大,但不改变压强分布趋势及分布范围;被连接件厚度的增加使压强分布由集中向均化分布过渡,但效果则逐步减弱;当螺钉直径增大时,结合面压强分布半径增大,当径向距离为螺钉直径的0.8倍时,压强最大.

2006

0.0

2011

0.0

. 2011, 39(8):1-5

Interfacial stiffness characteristic modeling of mechanical fixed joints

机械固定结合面刚度特性建模

Wang Shu-ting , Li Jie , Liu Tao

王书亭, 李杰, 刘涛

摘　要：针对机械结合面G-W接触模型和M-B接触模型存在的不足,基于分形理论,提出一种能描述2粗糙面接触的配对几何粗糙特性的法向刚度力学模型.该模型在几何尺寸上独立,给出了结合面面压与刚度的解析解,能有效求解结合面配对接触的法向刚度.根据应变能相等的原则,把结合面法向刚度和切向刚度折合成连续体的材料属性,建立了描述结合面特性的虚拟材料模型,试验证明了该方法的有效性.

... 一般不在此范围内,因此将各向同性的虚拟材料转换成正交各向异性的等效虚拟材料^[14] ...

2002

0.0