硬涂层复合结构非线性刚度及阻尼辨识

引用本文

孙伟, 李健, 贾师. 硬涂层复合结构非线性刚度及阻尼辨识.吉林大学学报:工学版, 2016, 46(4): 1156-1162
SUN Wei, LI Jian, JIA Shi. Identification of nonlinear stiffness and damping for hard-coating composite structure. Journal of Jilin University Engineering and Technology Edition, 2016, 46(4): 1156-1162 复制到剪切板

Permissions

硬涂层复合结构非线性刚度及阻尼辨识

孙伟, 李健, 贾师

东北大学机械工程与自动化学院,沈阳 110819

作者简介:孙伟(1975-), 男, 副教授,博士生导师.研究方向:机械系统动力学及振动控制.E-mail:weisun@mail.neu.edu.cn

基金:国家自然科学基金项目(51375079)

摘要

针对硬涂层复合结构共振衰减的时域响应,研究了基于Hilbert变换辨识硬涂层复合结构的非线性刚度及阻尼的方法。首先,确定了硬涂层复合结构共振状态下自由衰减的运动方程,进而推导了辨识该复合结构非线性刚度及阻尼参数的原理性公式;其次,用数值算例证明了辨识算法的正确性;然后,提出了将辨识算法应用于硬涂层复合结构非线性刚度及阻尼参数辨识的流程;最后,进行了实验验证,辨识出单面涂敷NiCrAlY+YSZ硬涂层的悬臂钛板非线性刚度及阻尼参数,并与未涂层试件进行了比对。结果表明,涂覆硬涂层后钛板的刚度非线性增强,阻尼增大,硬涂层具有减振效果。

关键词: 机械学; 硬涂层; 复合结构; 非线性刚度及阻尼; 参数辨识; Hilbert变换

中图分类号:TB535 文献标志码:A 文章编号:1671-5497(2016)04-1156-07

Identification of nonlinear stiffness and damping for hard-coating composite structure

SUN Wei, LI Jian, JIA Shi

School of Mechanical Engineering and Automation, Northeastern University, Shenyang 110819, China

Abstract

Based on the resonance decay response of time domain, a method to identify the nonlinear stiffness and damping was proposed using Hilbert transform. First, the free decay motion equation of the hard-coating composite structure under resonance status was determined and the formulas to identify nonlinear stiffness and damping parameters were derived. A numerical example was used to verify the correctness of the proposed identification algorithm. Then, the procedure of identifying the above parameters was presented. Finally, a titanium plate coated with NiCrAIY + YSZ hard coating was chosen as a study case, the nonlinear stiffness and damping parameters of the composite plate were identified and compared with the results of uncoated plate. It is shown that the hard coating can enhance the nonlinearity and increasing the damping of the structure, thus, improving the effect of vibration reduction.

Keyword: mechanics; hard coating; composite structure; nonlinear stiffness and damping; parameter identification; Hilbert transform

Show Figures

0 引言

硬涂层是指用金属或陶瓷制成的涂层材料, 由于硬涂层可以在高温、高腐蚀环境对薄壳结构进行减振, 因而近年来受到了越来越广泛的关注^{[1, 2, 3]}。硬涂层材料具有非线性特点, 其杨氏模量及耗因子都会随着系统激励幅度的不同而发生改变^{[4, 5]}。正因为硬涂层材料具有上述特点, 致使涂敷硬涂层的复合结构表现出变刚度及变阻尼的非线性振动特性。

有效辨识出这些非线性刚度及阻尼参数是硬涂层复合结构动力学分析以及硬涂层减振有效性评价的基础, 但是目前还没有提出有效的辨识算法来实现这一目标。Hilbert变换广泛应用于结构动力学特性参数的识别, 例如, 赵岩等^[6]建立了基于扭摆法的时变转动惯量测量模型, 提出了基于Hilbert变换辨识时变转动惯量计算方法。Feldman^{[7, 8]}推导了基于Hilbert变换和经验模态分解(Empirical mode decomposition, EMD)辨识动力学系统振动特性参数的方法。由此可以推断, Hilbert变换技术也可应用于硬涂层复合结构非线性刚度及阻尼参数的辨识。

本文针对硬涂层复合结构共振衰减的时域响应, 研究基于Hilbert变换辨识涂层复合结构非线性刚度和阻尼参数的方法。首先, 确定了硬涂层复合结构共振状态下自由衰减的运动方程, 进而推导了辨识该复合结构非线性刚度及阻尼参数的原理性公式; 其次, 用数值算例证明了辨识算法的正确性; 然后, 提出了将辨识算法应用于硬涂层复合结构非线性刚度及阻尼参数辨识的流程; 最后, 进行了实验验证, 辨识出单面涂敷NiCrAlY+YSZ硬涂层悬臂钛板的非线性刚度及阻尼参数, 并与未涂层薄板进行了比对。

1 非线性刚度及阻尼辨识原理

结构处于共振状态时, 当各阶模态耦合不严重时, 其动力学特性可由单一模态来确定^[9]。当切断激振力时, 由于存在阻尼, 结构上某点的响应信号会逐渐衰减。对于硬涂层复合结构, 由于其刚度及阻尼参数均随着系统的振幅而发生改变, 因而对于这一衰减过程, 可以认为复合结构的刚度及阻尼随着时间发生改变。这样, 可将上述过程用如下单自由度方程来描述:

$\begin{matrix} m \overset{\cdot \cdot}{q} (t) + c (t) \overset{\cdot}{q} (t) + k (t) q (t) = 0 (1) \end{matrix}$

式中: 为复合结构的模态质量c(t)和k(t)分别表示硬涂层复合结构的时变模态阻尼及刚度q(t); 为对应模态坐标的振动衰减响应。以下基于Hilbert变换技术推导辨识非线性刚度及阻尼的辨识公式。

对衰减响应信号 $\begin{matrix} q (t) \end{matrix}$ 进行Hilbert变换, 变换表达式可记为:

$\begin{matrix} \tilde{q} (t) = H [q (t)] = \frac{1}{π} \int_{-}^{\infty} \frac{q (τ)}{t - τ} dτ (2) \end{matrix}$

式中:H(· )表示Hilbert变换; $\begin{matrix} \tilde{q} (t) 是变换后的 q (t) 。 \end{matrix}$

由变换后的信号和原始衰减响应信号组成分析信号, 表达为:

$\begin{matrix} Q (t) = q (t) + j \tilde{q} (t) (3) \end{matrix}$

则分析信号 $\begin{matrix} Q (t) \end{matrix}$ 的包络线A(t)和瞬时相位可分别表示为Ψ(t):

$\begin{matrix} \begin{matrix} A (t) = \sqrt[]{q^{2} (t) + {\tilde{q}}^{2} (t)} (4) \\ Ψ (t) = \arctan [\tilde{q} (t) / q (t)] (5) \end{matrix} \end{matrix}$

对瞬时相位 $\begin{matrix} Ψ (t), \end{matrix}$ 求导数可得即时频率即ω(t):

$\begin{matrix} Ψ' (t) = ω (t) (6) \end{matrix}$

对式(1)进行Hilbert变换, 可以得到:

$\begin{matrix} m \overset{\cdot \cdot}{\tilde{q}} (t) + c (t) \overset{\cdot}{\tilde{q}} (t) + k (t) \tilde{q} (t) = 0 (7) \end{matrix}$

需要说明的是在进行Hilbert变换时, 这里假设时变阻尼 $\begin{matrix} c (t) \end{matrix}$ 和时变刚度稳k(t)定改变, 在变换过程中认为是常数, 即:

$\begin{matrix} \begin{matrix} H [c (t) \overset{\cdot}{q} (t)] = c (t) H [\overset{\cdot}{q} (t)] = c (t) \overset{\cdot}{\tilde{q}} (t) (8) \\ H [k (t) q (t)] = k (t) H [q (t)] = k (t) \tilde{q} (t) (9) \end{matrix} \end{matrix}$

将式(7)两端乘以j加到式(1), 可得到用分析信号表达的运动方程, 即:

$\begin{matrix} m \overset{\cdot \cdot}{Q} (t) + c (t) \overset{\cdot}{Q} (t) + k (t) Q (t) = 0 (10) \end{matrix}$

利用式(3)(4)(5), 可将式(10)中分析信号一阶及二阶导数 $\begin{matrix} \overset{\cdot}{Q} 、 \overset{\cdot \cdot}{Q} 用包络线 A (t) 和即时频率 ω (t) \end{matrix}$ 来表达, 即:

$\begin{matrix} \begin{matrix} \overset{\cdot}{Q} (t) = Q (t) [\frac{\overset{\cdot}{A} (t)}{A (t)} + jω (t)] (11) \\ \overset{\cdot \cdot}{Q} (t) = Q (t) [\frac{\overset{\cdot \cdot}{A} (t)}{A (t)} - ω^{2} (t) + 2 j \frac{\overset{\cdot}{A} (t) ω (t)}{A (t)} + j \overset{\cdot}{ω} (t)] (12) \end{matrix} \end{matrix}$

将式(11)(12)代入到式(10), 并整理得:

$\begin{matrix} \begin{matrix} m \frac{\overset{\cdot \cdot}{A} (t)}{A (t)} - m ω^{2} (t) + k (t) + c (t) \frac{\overset{\cdot}{A} (t)}{A (t)} + \\ j [2 m \frac{\overset{\cdot}{A} (t)}{A (t)} + m \overset{\cdot}{ω} (t) + c (t) ω (t)] = 0 (13) \end{matrix} \end{matrix}$

令方程(13)的实部和虚部都等于零, 可获得非线性阻尼及非线性刚度的表达式分别如下:

$\begin{matrix} \begin{matrix} c (t) = - m [2 \frac{\overset{\cdot}{A} (t)}{A (t)} + \frac{\overset{\cdot}{ω} (t)}{ω (t)}] (14) \\ k (t) = m [ω^{2} (t) - \frac{\overset{\cdot \cdot}{A} (t)}{A (t)} + 2 \frac{{\overset{\cdot}{A}}^{2} (t)}{A^{2} (t)} + \frac{\overset{\cdot}{ω} (t)}{ω (t)} \frac{\overset{\cdot}{A} (t)}{A (t)}] (15) \end{matrix} \end{matrix}$

需要说明的是上述刚度及阻尼辨识原理主要适用于具有低模态密度的结构系统, 即各模态之间耦合效应小, 因而可用单自由度方程来描述某一阶次的运动状态。如果结构具有密集频率特性, 模态耦合严重, 则所提出的辨识方法失效。

2 数值算例

以下用数值算例校验辨识算法的正确性, 设时变刚度(单位:N/m)及阻尼(单位:(N· s)/m)的表达式分别为 $\begin{matrix} k (t) = 1000 - 100 t, c (t) = 0.5 + 0.2 t, \end{matrix}$ 系统的质量m=1 kg。

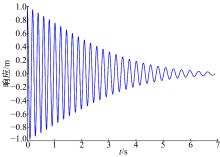首先, 利用Newton Raphson法, 并设初始条件为 $\begin{matrix} q_{0} = 1, {\overset{\cdot}{q}}_{0} = 0, {\overset{\cdot \cdot}{q}}_{0} = 0,, \end{matrix}$ 计算出系统的振动响应如q(t)图1所示。

	Figure Option View Download New Window
	图1 数值计算获得的原系统振动衰减响应Fig.1 Vibration decay response of original system obtained by numerical calculation

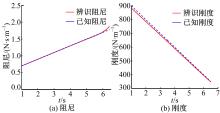
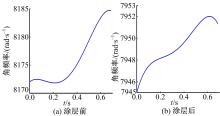
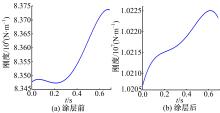
进一步对q(t)进行Hilbert变换, 并获得包络线A(t)和即时频率ω(t),如图2所示。最后利用式(14)(15)辨识得出系统的时变刚度和时变阻尼, 辨识结果与已知值的对比见图3。

从图3可以看出, 最终辨识的时变刚度及阻尼与预设值差距不大, 从而证明了上述辨识算法的正确性。

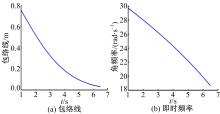	Figure Option View Download New Window
	图2 响应信号的Hilbert变换后获得的包络线A(t)和即时频率ω (t)Fig.2 Envelope A(t) and instant frequency ω (t) obtained by Hilbert transform of response signal

	Figure Option View Download New Window
	图3 辨识结果与已知值的对比Fig.3 Comparison between identification results and known values

3 非线性刚度及阻尼辨识流程

按照辨识算法, 测试硬涂层复合结构非线性刚度及阻尼, 可参照如下流程进行。

(1)测试硬涂层复合结构件的共振衰减响应

在找到硬涂层复合结构各阶共振频率的前提下, 利用稳态激励装置(例如电磁振动台)以共振频率作为激振频率激励复合结构件, 待达到稳态振动后, 切断激励装置, 记录衰减位移响应。

(2)计算拾振点位置处的模态质量

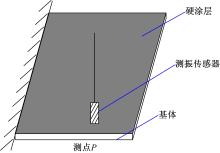
不同的拾振点对应结构的模态质量不同, 需要利用结构件的模态振型计算出该拾振点处的模态质量。对于单面全部涂敷硬涂层的悬臂板(见图4), 可以认为涂层前后模态振型没有改变。按照双向梁函数法悬臂薄板的振型函数可表示为^[10]:

$\begin{matrix} W_{n} (x, y) = \overset{p}{\sum_{i = 1}} \overset{q}{\sum_{j = 1}} α_{ij} X_{i} (x) Y_{j} (y) (16) \end{matrix}$

式中: $\begin{matrix} α_{ij} (i = 1, 2, \dots, p; j = 1, 2, \dots, q) 是与激振力幅相关的待定系数; X_{i} (x) 是一端固定、一端自由梁的第 i 阶模态函数; Y_{j} (y) 是两端自由梁的第 j 阶模态函数; p 、 q 为各自模态所考虑的最大阶次; n 为薄板振型的阶次。利用该振型函数可获得悬臂薄板任一位置处 (对应拾振点) 的模态质量 m_{n} (x, y), \end{matrix}$ 求解式为:

$\begin{matrix} m_{n} (x, y) = \underset{S}{\int \int} (ρ_{d} H_{d} + ρ_{c} H_{c}) W_{n}^{2} (x, y) dxdy (17) \end{matrix}$

式中: S为薄板的面积;ρ_d 、ρ_c分别为基体和硬涂层的密度;H_d 、H_c 分别为基体和硬涂层的厚度。

	Figure Option View Download New Window
	图4 拾振点模态质量提取示意图Fig.4 Schematic diagram of getting modal mass

(3)对获取的振动响应进行EMD分解

Hilbert变换需要信号在任意时刻具有单频性, 而测试获得的信号在某一时刻不能完全保证处于单一频率, 因而需要对原始信号进行EMD分解。此外, 对原始测得的信号进行EMD分解也能用于判断测得的衰减响应是否为共振衰减响应, 因为实践发现结构件的共振与非共振衰减响应经EMD分解后存在明显的差异。例如, 图5为对硬涂层板共振及非共振响应进行EMD分解获得的响应信号, 可发现由共振响应EMD分解后得到的是单一频率的主体信号和一些振动很小的扰乱信号, 而由非共振响应EMD分解后得到的是多个频率的振动信号。

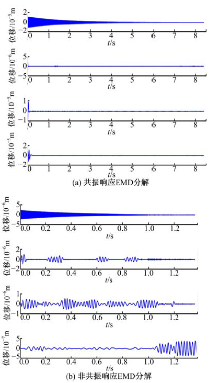	Figure Option View Download New Window
	图5 硬涂层薄板共振及非共振衰减响应EMD分解Fig.5 EMD decomposition of resonant and non-resonant decay response for hard-coating thin plate

(4)获得模态坐标下的振动响应

可按照模态理论将真实坐标下的响应变换为模态坐标下的响应。同样以硬涂层板为例, 变换公式为:

$\begin{matrix} q (t) = y_{x_{p}, y_{p}} (t) / W_{n} (x, y) (18) \end{matrix}$

式中: $\begin{matrix} y_{x_{p}, y_{p}} (t) \end{matrix}$ 为硬涂层薄板测点P处的振动响应。

(5)进行Hilbert变换, 获取 $\begin{matrix} A (t), ω (t) \end{matrix}$

对模态坐标下的振动响应 $\begin{matrix} q (t) \end{matrix}$ 进行Hilbert变换, 进一步利用式(4)和式(6)获得包络线 $\begin{matrix} A (t) 和即时频率 ω (t) 。 \end{matrix}$

(6)带入公式获得时变刚度及阻尼

将获得包络线A(t)和即时频率ω(t)带入到式(14)(15)则可获得被测硬涂层复合结构的非线性阻尼及刚度。

需要说明的是, 上述非线性刚度及阻尼辨识流程同样也适用于未涂层结构。受到夹持边界条件的影响, 未涂层结构也会产生上述变刚度及变阻尼的非线性现象, 只是非线性的程度会有所减弱。

4 实验验证

4.1 涂层前后钛板共振衰减响应测试

以未涂层的和单面涂敷NiCrAlY+YSZ硬涂层的悬臂钛板为研究对象, 来检验本文方法的可行性, 同时对比涂层前后薄板动力学参数的变化。具体试验件见图6, 硬涂层及薄板的材料及相关尺寸见表1。需要说明的是, 硬涂层材料的杨氏模量不是一个固定值, 其大小随激励幅度的不同而改变, 表1中给定值是参照文献[11]给出的大致范围。

	Figure Option View Download New Window
	图6 涂层前后的钛板Fig.6 Uncoated and coated titanium plate

表1 硬涂层及薄板的材料及相关尺寸参数 Table 1 Material parameters and dimension of hard coating and thin plate

所组配的实验系统见图7, 板以悬臂的方式固定在夹具上(夹持区为20 mm), 测试装置包括:金盾EM-1000F振动台、LMS SCADAS采集前端、金盾EM-1000F电磁振动台和Polytec PLD-100激光测振仪等。

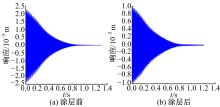
	Figure Option View Download New Window
	图7 硬涂层板振动测试现场图Fig.7 Vibration test scene of hard-coating plate

这里以在1.5 g激励下的钛板第6阶共振特性为例对本文算法进行验证。经扫频测试, 未涂层钛板第6阶的固有频率为1297.88 Hz, 涂层后第6阶的固有频率为1262.25 Hz。分别按以上固有频率定频激励涂层前后的钛板, 待达到稳定后切掉激励源, 获得的共振状态的自由振动衰减响应见图8。

	Figure Option View Download New Window
	图8 薄板的共振衰减响应Fig.8 Resonant decay response of thin plate

4.2 非线性阻尼及刚度辨识

按照第3节所述的流程辨识该硬涂层薄板的时变刚度及阻尼。其中对应于拾振点处(x=0.029 m, y=0.041 m), 由式(17)计算的涂层前第6阶的模态质量为0.1250 kg, 涂层后的模态质量为0.1617 kg。根据式(18), 指定点处模态坐标与真实坐标之间变换系数为-0.9266。

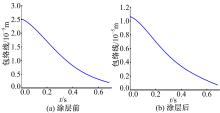
首先对测得的共振衰减响应信号进行EMD分解, 提取主体信号。进而用获得的变换系数将真实坐标下的响应变换为模态坐标下的响应。然后, 对模态坐标响应进行Hilbert变换, 利用式(4)和式(5), 识别出复合结构的包络线和即时频率, 分别见图9和图10。

	Figure Option View Download New Window
	图9 辨识得到的包络线Fig.9 Envelope obtained by identification

	Figure Option View Download New Window
	图10 辨识得到的即时频率Fig.10 Instant frequency obtained by identification

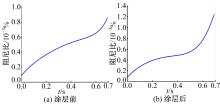
最后由式(14)和式(15)辨识出硬涂层薄板的非线性阻尼和刚度, 由测得的阻尼可进一步得出模态阻尼比, 分别如图11和图12所示。

	Figure Option View Download New Window
	图11 辨识得到的刚度Fig.11 Stiffness obtained by identification

	Figure Option View Download New Window
	图12 辨识得到的阻尼比Fig.12 Damping ratio obtained by identification

从测试结果可以看出, 从0.3 s以后, 辨识结果发散, 结果的可信度降低。发散的原因主要来自于测试获得的时域信号在高响应幅度时信噪比高, 而在低响应幅度时容易受到外界因素(例如电磁噪声)干扰而使信噪比降低。低信噪比信号将失去原始结构的力学信息, 导致辨识结果发散。因而后续需要进一步研究低响应幅度时, 针对时域衰减信号的降噪技术。

大约在0~0.3 s的时间范围内, 结果较为稳定, 可以反应出一定的规律, 因而本文的测试也具有一定的意义。对比涂层前后0~0.3 s时间范围内钛板的刚度及阻尼参数变化情况可以看出:①未涂层板在这一时间段内刚度和即时频率基本不变, 而涂层板的刚度和即时频率发生显著变化, 具体为随响应幅度的减小而快速增大; ②未涂层板和涂层板在这一时间段内的阻尼都发生变化, 表明阻尼与响应幅度相关, 此外涂层板的阻尼大于未涂层板的阻尼。

以上现象说明, 涂覆硬涂层后钛板的刚度非线性增强, 阻尼增大, 硬涂层具有减振效果。实际上, 从共振衰减响应(见图8)中也可以看出, 硬涂层具有减振效果, 涂层后共振响应的幅值显著降低。

5 结论

(1)将硬涂层复合结构简化为单自由度分析模型, 并基于Hilbert变换可辨识出硬涂层复合结构的非线性刚度及阻尼。基于本文提出的辨识流程, 可有效测试出涂层前后钛板的时变刚度和时变阻尼。

(2)辨识算法对信号的信噪比要求较高, 对于本文所研究的实例, 在0.3 s以后的数据结果发散, 可信度降低。因而后续需要进一步研究低响应幅度时, 针对时域衰减信号的降噪技术。

(3)对比钛板涂覆NiCrAlY+YSZ硬涂层前后的时变刚度和时变阻尼的变化可以看出:硬涂层使钛板的刚度非线性增强, 阻尼增大, 并有效抑制了复合结构的共振响应。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Blackwell C, Palazotto A, George T J, et al. The evaluation of the damping characteristics of a hard coating on titanium[J]. Shock and Vibration, 2007, 14(1): 37-51. [本文引用:1]
[2]	Ivancic F, Palazotto A. Experimental considerations for determining the damping coefficients of hard coatings[J]. Journal of Aerospace Engineering, 2005, 18(1): 8-17. [本文引用:1]
[3]	Du G Y, Ba D C, Tan Z, et al. Vibration damping performance of ZrTiN coating deposited by arc ion plating on TC4 Titanium alloy[J]. Surface and Coatings Technology, 2013, 229: 172-175. [本文引用:1]
[4]	Patsias S, Saxton C, Shipton M. Hard damping coatings: an experimental procedure for extraction of damping characteristics and modulus of elasticity[J]. Materials Science and Engineering: A, 2004, 370(1): 412-416. [本文引用:1]
[5]	Reed S A, Palazotto A N, Baker W P. An experimental technique for the evaluation of strain dependent material properties of hard coatings[J]. Shock and Vibration, 2008, 15(6): 697-712. [本文引用:1]
[6]	赵岩, 张晓琳, 王军, 等. 基于Hilbert 变换的时变转动惯量测量研究[J]. 机械工程学报, 2012, 48(20): 21-26. Zhao Yan, Zhang Xiao-lin, Wang Jun, et al. Measurement of time-varying moment of inertia based on hilbert transform[J]. Journal of Mechanical Engineering, 2012, 48(20): 21-26 [本文引用:1]
[7]	Feldman M. Considering high harmonics for identification of non-linear systems by Hilbert transform[J]. Mechanical Systems and Signal Processing, 2007, 21(2): 943-958. [本文引用:1]
[8]	Feldman M. Hilbert transform methods for nonparametric identification of nonlinear time varying vibration systems[J]. Mechanical Systems and Signal Processing, 2014, 47(1-2): 66-77. [本文引用:1]
[9]	Illaire H, Kropp W, Mace B. A phenomenological model of active constrained layers[J]. Journal of Sound and Vibration, 2005, 285(1): 281-302. [本文引用:1]
[10]	曹志远. 板壳振动理论[M]. 北京: 中国铁道出版社, 1989. [本文引用:1]
[11]	Pearson L E. Vibration analysis of commercial thermal barrier coatings[R]. Wright-patterson AFB OH: Air Force Institute of Technology, School of Engineering and Management, 2008. [本文引用:1]

2007

0.0

... 0 引言硬涂层是指用金属或陶瓷制成的涂层材料,由于硬涂层可以在高温、高腐蚀环境对薄壳结构进行减振,因而近年来受到了越来越广泛的关注^[1,2,3] ...

2005

0.0

2013

0.0

2004

0.0

... 硬涂层材料具有非线性特点,其杨氏模量及耗因子都会随着系统激励幅度的不同而发生改变^[4,5] ...

2008

0.0

... 硬涂层材料具有非线性特点,其杨氏模量及耗因子都会随着系统激励幅度的不同而发生改变^[4,5] ...

2012

0.0

. 2012, 48(20):21-26 DOI:doi:10.3901/JME.2012.20.022

Measurement of time-varying moment of inertia based on hilbert transform

基于Hilbert 变换的时变转动惯量测量研究

Zhao Yan , Zhang Xiao-lin , Wang Jun

赵岩, 张晓琳, 王军

摘　要：针对时变转动惯量测量的问题,建立基于扭摆法的时变转动惯量测量模型,提出基于Hilbert变换的时变转动惯量计算方法。根据分析动力学的原理,利用第二类拉格朗日方程建立基于时变转动惯量的单自由度扭摆运动方程。对物体的角位移信号进行Hilbert变换并构造解析信号。利用角位移信号的瞬时角频率和包络信号计算扭摆运动的瞬时无阻尼固有频率。根据瞬时无阻尼固有频率求出物体的转动惯量。利用基于气浮转台的扭摆系统,对转动惯量线性变化的试验样件进行转动惯量测量。由于测量系统采用气浮转台,因此,消除机械摩擦力对转动惯量测量的影响。试验结果表明,试验样件的转动惯量测量值的相对误差小于0.5%,从而验证基于Hilbert变换的时变转动惯量测量方法的有效性。

... Hilbert变换广泛应用于结构动力学特性参数的识别,例如,赵岩等^[6]建立了基于扭摆法的时变转动惯量测量模型,提出了基于Hilbert变换辨识时变转动惯量计算方法 ...

2007

0.0

... Feldman^[7,8]推导了基于Hilbert变换和经验模态分解(Empirical mode decomposition,EMD)辨识动力学系统振动特性参数的方法 ...

2014

0.0

... Feldman^[7,8]推导了基于Hilbert变换和经验模态分解(Empirical mode decomposition,EMD)辨识动力学系统振动特性参数的方法 ...

2005

0.0

... 1 非线性刚度及阻尼辨识原理结构处于共振状态时,当各阶模态耦合不严重时,其动力学特性可由单一模态来确定^[9] ...

1989

0.0

... 按照双向梁函数法悬臂薄板的振型函数可表示为^[10]: ...

2008

0.0