制动盘材料和结构对滑动摩擦系统热弹性失稳的影响

引用本文

夏德茂, 奚鹰, 华滨滨, 周亚红, 左建勇. 制动盘材料和结构对滑动摩擦系统热弹性失稳的影响.吉林大学学报:工学版, 2016, 46(4): 1163-1174
XIA De-mao, XI Ying, HUA Bin-bin, ZHOU Ya-hong, ZUO Jian-yong. Effect of geometry and material properties of brake disc on thermoelastic instability of sliding frictional system. Journal of Jilin University Engineering and Technology Edition, 2016, 46(4): 1163-1174 复制到剪切板

Permissions

制动盘材料和结构对滑动摩擦系统热弹性失稳的影响

夏德茂¹, 奚鹰¹, 华滨滨¹, 周亚红¹, 左建勇²

1.同济大学机械与能源工程学院,上海 201804

2.同济大学铁道与城市轨道交通研究院,上海 201804

通讯作者：奚鹰(1957-),男,教授,博士生导师.研究方向:大型复杂机械系统关键技术及理论.E-mail:yingxi@tongji.edu.cn

作者简介:夏德茂(1986-),男,博士研究生.研究方向:摩擦制动器热力耦合及理论.E-mail:xiademaonihao@163.com

基金:国家留学基金项目(201406260074); 国家自然科学基金项目(61004077)

摘要

建立了滑动摩擦系统热弹性失稳的数学模型,并推导了不同热点模式对应的临界速度表达式。分析了摩擦副的厚度和滑动层材料的热物理特性参数对摩擦系统热弹性失稳的影响。结果表明:滑动摩擦系统更易出现反对称分布的热点模式;增加摩擦层厚度,减小滑动层厚度、热传导系数、弹性模量以及热膨胀系数均可以提高标志滑动摩擦系统进入热弹性失稳状态所需的最低临界速度,而滑动层比热容对系统的稳定性几乎没有影响。

关键词: 机械设计; 扰动增长系数; 热弹性失稳; 最低临界速度; 扰动频率; 热点

中图分类号:TH117 文献标志码:A 文章编号:1671-5497(2016)04-1163-12

Effect of geometry and material properties of brake disc on thermoelastic instability of sliding frictional system

XIA De-mao¹, XI Ying¹, HUA Bin-bin¹, ZHOU Ya-hong¹, ZUO Jian-yong²

1.School of Mechanical Engineering, Tongji University, Shanghai 201804,China

2.Institute of Railway and Urban Mass Transit, Tongji University, Shanghai 201804, China

Abstract

First, a mathematical model related to the thermoelastic instability was established, and the critical speeds of two different types of distribution of hot spots were derived. Then the effects of the thickness of the brake pair and thermal-physical properties of the sliding layer on the stability of the sliding frictional systems were analyzed and compared. Results show that, the sliding frictional system is more vulnerable to have dissymmetrical mode of hot spots. The minimum critical speed, which denotes the threshold of thermoelastic instability of the sliding frictional system, can be enhanced by increasing the thickness of the frictional layer and decreasing thickness, thermal conductivity, thermal expansion coefficient and elastic modulus of the sliding layer. However, the specific heat of the sliding layer almost has no influence on the stability of the sliding frictional system.

Keyword: mechanical design; growth rate of perturbation; thermoelastic instability; minimum critical speed; wave number; hot spot

Show Figures

0 引言

当两个弹性体在外力作用下处于相对滑动状态时, 因表面粗糙度、磨损、结构变化及其他因素的影响, 弹性体内的温升效应呈非均匀分布, 导致摩擦面发生非均匀热弹性变形, 改变了接触面间的压力分布及其连续性。反过来, 不均匀的热弹性变形又会进一步加剧接触压力的非均匀分布^{[1, 2]}。在摩擦热、热弹性变形、热应力及弹性接触的相互耦合作用下, 当两弹性体的相对滑动速度足够高时, 反馈过程将变得不稳定, 易在摩擦面的局部区域形成温度和应力的集中, 最终形成热点, 该热力耦合过程被称为热弹性不稳定(Thermo-Elastic Instability, TEI)^{[3, 4, 5, 6]}。针对此问题, Burton和Dow等^{[7, 8, 9]}首先提出扰动分析法, 研究了2个垂直于二维坐标的平面在相对滑动时的准静态解。此后, 许多学者在Burton^[7]的研究基础上展开试验测试^{[10, 11, 12]}, 发现由解析法确定的临界速度要比试验值高, 分析原因可能是由于其TEI模型中并未考虑滑动层有限厚度的影响。为评价该因素的作用, Barber等^[13]研究了一有限厚度滑动层在两块具有无限厚度的摩擦层内相对滑动时的汽车制动器TEI问题, 并对不同热点分布模式下的TEI失稳临界条件进行了求解, 得到的结果与试验测试值较接近。此后, Du等^[14]采用有限元方法将TEI问题离散为一系列求解特征值的问题。Yi等^{[15, 16, 17, 18, 19]}在Du^[14]的研究基础上, 使用傅立叶降阶法将求解TEI失稳的临界条件转化为仅与扰动增长系数和扰动频率相关的特征值问题, 并讨论了摩擦片有限周向接触弧长带来的影响。Painer和Majcherczak等^{[20, 21]}通过测试将盘面热点分为粗糙凸点型、梯度型、形变型、焦点型和区域型5种。Kasem和Kumar等^{[22, 23]}则通过试验指出:热点最初会出现在制动盘的外边缘, 随后逐渐向内径方向发展, 高温区域与低温区域的温差近700 ° C。

在传统摩擦制动器和离合器的设计过程中, 如何从结构设计和材料选择上来避免TEI问题的出现一直是工程设计人员关注的焦点。本文采用扰动分析法建立摩擦制动器TEI失稳模型, 研究了摩擦副的结构以及滑动层材料的热物理特性参数的影响, 得到了避免滑动摩擦系统出现TEI失稳的方法, 可为其他类似滑动摩擦系统的设计提供一定的参考。

1 TEI理论模型

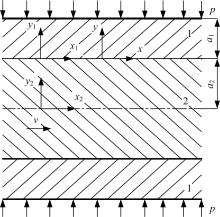
在工程实际应用中, 最常见的滑动摩擦系统主要有汽车变速箱中的离合器、鼓式制动器、高速列车的盘式制动器以及飞机多盘片制动器等。以火车盘式制动器为例, 组成摩擦副的零件主要有摩擦层闸片、与闸片联接的钢背以及滑动层制动盘。为不失一般性, 建立了如图1所示的滑动摩擦系统的TEI数学模型。

	Figure Option View Download New Window
	图1 滑动摩擦系统TEI数学模型Fig.1 Mathematical model of sliding frictional system

图1中, 摩擦层闸片1在均匀压力 $\begin{matrix} p 的作用下贴紧滑动层制动盘 2 。假设摩擦层和滑动层的运动速度为 v_{i} (i = 1, 2), 且滑动层以恒定速度 v (v > 0) 沿 x 轴正方向运动。 a_{1} 和 a_{2} 分别为摩擦层和滑动层的厚度; (x_{i}, y_{i}) 为层 i 的静态坐标系, 其中, (x_{1}, y_{1}) 固定在滑动摩擦面上, (x_{2}, y_{2}) 固定在滑动层 2 的中分面上; (x, y) \end{matrix}$ 为全局坐标系。显然, 各坐标系之间存在如下关系:

$\begin{matrix} y = y_{1} = y_{2} - a_{2} (1) \end{matrix}$

Burton和Dow等^{[7, 8, 9]}通过研究指出:当滑动层和摩擦层之间的相对滑动速度达到某一临界值时,摩擦面间的均匀接触压力p会出现不稳定的余弦扰动并随时间t呈指数增长, 可将其记为:

$\begin{matrix} p = p_{0} \cdot \exp (bt) \cdot \cos (mx) (2) \end{matrix}$

式中: p为接触压力的扰动形式;p₀为接触压力的扰动幅值;b为扰动增长系数;t为时间;m为扰动频率, 并注意到:

$\begin{matrix} \exp (jmx) = \cos (mx) + jsin (mx) (3) \end{matrix}$

式中:j为虚数单位, j=(-1)^0.5。

将式(3)代入式(2)化简后并取实数部分可得到:

$\begin{matrix} p = p_{0} \cdot Re \{\exp (bt + jmx)\} (4) \end{matrix}$

式中:Re(· )为取实数。

从式(4)中可看出:当b<0时,系统处于稳定状态;当b>0时,系统处于不稳定扰动;当b=0时, 系统处于TEI失稳的临界状态^{[1, 2, 3, 4, 12, 13]}。

假设扰动在坐标系 (x_i,y_i)内沿x轴方向的速度分别为c_i,其与速度v_i )的关系为:

1.1 温度场扰动

依据热传导理论, 在滑动摩擦过程中, 摩擦副的温度场扰动应满足二维瞬态热传导方程, 即:

$\begin{matrix} \begin{matrix} \frac{\partial^{2} T_{i}}{\partial {x_{i}}^{2}} + \frac{\partial^{2} T_{i}}{\partial {y_{i}}^{2}} = \frac{1}{k_{i}} \frac{\partial T_{i}}{\partial t} (i = 1, 2) (7) \\ k_{i} = \frac{K_{i}}{ρ_{i} c_{pi}} (8) \end{matrix} \end{matrix}$

式中: $\begin{matrix} T_{i} 、 k_{i} 、 K_{i} 、 ρ_{i} 和 c_{pi} 分别为层 i \end{matrix}$ 的温度场扰动、热扩散系数、热传导系数、密度和比热容。

若将摩擦副的温度场扰动形式记为:

$\begin{matrix} T_{i} (x_{i}, y_{i}, t) = Θ_{i} (y_{i}) \cdot \exp [bt + jm (x_{i} - c_{i} t)] (9) \end{matrix}$

式中: $\begin{matrix} Θ_{i} (y_{i}) 为关于 y_{i} \end{matrix}$ 的未知函数。

将式(9)代入方程(7), 依据高等数学知识, 通过求解 $\begin{matrix} Θ_{i} (y_{i} \end{matrix}$ )可得到其形式为:

$\begin{matrix} Θ_{i} (y_{i}) = n_{i 1} \exp (δ_{i} y_{i}) + n_{i 2} \exp (- δ_{i} y_{i}) (10) \end{matrix}$

$\begin{matrix} δ_{i} = ξ_{i} + j η_{i} = \sqrt[]{(m^{2} + \frac{b}{k_{i}}) - j (\frac{m c_{i}}{k_{i}})} (11) \end{matrix}$

式中: $\begin{matrix} ξ_{i} 和 η_{i} 分别为式 (11) 中的实数和虚数部分, 且 ξ_{i} > 0; n_{i 1} 和 n_{i 2} \end{matrix}$ 为未知常数。

为求解式(10)中4个未知常数 $\begin{matrix} n_{i 1} 和 n_{i 2} (i = 1, 2), \end{matrix}$ 摩擦副温度场扰动应满足以下热边界条件:

(1)若热点在滑动层的两个摩擦面上呈对称分布^[13], 则在滑动层的中分面上有:

$\begin{matrix} q_{y_{2}} = - K_{2} {\frac{\partial T_{2}}{\partial y_{2}}|}_{y_{2} = 0} = 0 (12) \end{matrix}$

式中: $\begin{matrix} q_{y_{2}} \end{matrix}$ 为滑动层吸收的热载荷。

(2)若热点在滑动层的两个摩擦面上呈反对称分布^[13], 则在滑动层的中分面上有:

$\begin{matrix} {T_{2}|}_{y_{2} = 0} = 0 (13) \end{matrix}$

(3)由于摩擦层闸片的刚度要远小于与其联接的钢背。因此, 文中假设摩擦层在 $\begin{matrix} y_{1} = a_{1} \end{matrix}$ 处的温度场扰动为0, 即:

$\begin{matrix} {T_{1}|}_{y_{1} = a_{1}} = 0 (14) \end{matrix}$

(4)摩擦面上, 对应接触点温度扰动连续, 则有:

$\begin{matrix} {T_{1}|}_{y_{1} = 0} = T_{0} = {T_{2}|}_{y_{2} = a_{2}} (15) \end{matrix}$

式中:T₀为任意常数。

将式(12)~式(15)分别代入式(9), 通过代数运算可确定4个未知常数 $\begin{matrix} n_{i 1} 和 n_{i 2} (i = 1, 2), \end{matrix}$ 并进一步可得到不同热点分布模式下, 摩擦层和滑动层的温度场扰动形式分别为:

对称模式:

$\begin{matrix} \{\begin{matrix} T_{1} (x_{1}, y_{1}, t) = T_{0} \frac{g' (δ_{1} (a_{1} - y_{1}))}{g' (δ_{1} a_{1})} \cdot \\ Re \{\exp [bt + jm (x_{1} - c_{1} t)]\} \\ T_{2} (x_{2}, y_{2}, t) = T_{0} \frac{g (δ_{2} y_{2})}{g (δ_{2} a_{2})} \cdot \\ Re \{\exp [bt + jm (x_{2} - c_{2} t)]\} \end{matrix} (16) \end{matrix}$

反对称模式:

$\begin{matrix} \{\begin{matrix} T_{1} (x_{1}, y_{1}, t) = T_{0} \frac{g (δ_{1} (a_{1} - y_{1}))}{g (δ_{1} a_{1})} \cdot \\ Re \{\exp [bt + jm (x_{1} - c_{1} t)]\} \\ T_{2} (x_{2}, y_{2}, t) = T_{0} \frac{g (δ_{2} y_{2})}{g (δ_{2} a_{2})} \cdot \\ Re \{\exp [bt + jm (x_{2} - c_{2} t)]\} \end{matrix} (17) \end{matrix}$

式中:当热点为对称分布模式时, g(· )=cosh; 当热点为反对称分布模式时, g(· )=sinh。

1.2 热弹性应力和位移

依据弹性理论, 由位移表示的二维热弹性平衡微分方程如式(18)所示, 即:

$\begin{matrix} \begin{matrix} \{\begin{matrix} μ_{i} \nabla^{2} u_{x} + (μ_{i} + κ_{i}) \frac{\partial ε_{v}}{\partial x} - \frac{α_{i} E_{i}}{1 - 2 ν_{i}} \frac{\partial T_{i}}{\partial x} = 0 \\ μ_{i} \nabla^{2} u_{y} + (μ_{i} + κ_{i}) \frac{\partial ε_{v}}{\partial y} - \frac{α_{i} E_{i}}{1 - 2 ν_{i}} \frac{\partial T_{i}}{\partial y} = 0 \end{matrix} (18) \\ κ_{i} = \frac{E_{i} ν_{i}}{(1 + ν_{i}) (1 - 2 ν_{i})} (19) \end{matrix} \end{matrix}$

式中: $\begin{matrix} u_{x} 、 u_{y} 分别为 x 、 y 方向位移分量; μ_{i} 为材料的剪切模量; ε_{v} 为总应变, ε_{v} = ε_{x} + ε_{y}; ν_{i} 为材料的泊松比; α_{i} 为线性膨胀系数; κ_{i} \end{matrix}$ 为拉梅常数。

根据高等数学知识, 方程(18)的解可由两部分组成:一是求出该方程的任意一组特解; 二是找出其任意一组齐次解; 最后将这两组解相加, 并让总的位移和热应力满足相应的热边界条件即可。为了找出方程的一组特解, 引入位移势函数 $\begin{matrix} ψ_{i}, \end{matrix}$ 且其须满足下式:

$\begin{matrix} \nabla^{2} ψ_{i} = 2 μ_{i} α_{i} \frac{1 + ν_{i}}{1 - ν_{i}} T_{i} (20) \end{matrix}$

将温度场扰动式(16)(17)代入式(20), 可得到不同热点分布模式下, 满足热弹性平衡微分方程(18)的一组特解分别为:

对称模式:

$\begin{matrix} \begin{matrix} \{\begin{matrix} ψ_{1} (x_{1}, y_{1}, t) = \frac{β_{1} T_{0}}{{δ_{1}}^{2} - m^{2}} \frac{g' (δ_{1} (a_{1} - y_{1}))}{g' (δ_{1} a_{1})} \cdot \\ Re \{\exp [bt + jm (x_{1} - c_{1} t)]\} \\ ψ_{2} (x_{2}, y_{2}, t) = \frac{β_{2} T_{0}}{{δ_{2}}^{2} - m^{2}} \frac{g (δ_{2} y_{2})}{g (δ_{2} a_{2})} \cdot \\ Re \{\exp [bt + jm (x_{2} - c_{2} t)]\} \end{matrix} (21) \\ β_{i} = 2 μ_{i} α_{i} \frac{1 + ν_{i}}{1 - ν_{i}} (22) \end{matrix} \end{matrix}$

反对称模式:

$\begin{matrix} \{\begin{matrix} ψ_{1} (x_{1}, y_{1}, t) = \frac{β_{1} T_{0}}{{δ_{1}}^{2} - m^{2}} \frac{g (δ_{1} (a_{1} - y_{1}))}{g (δ_{1} a_{1})} \cdot \\ Re \{\exp [bt + jm (x_{1} - c_{1} t)]\} \\ ψ_{2} (x_{2}, y_{2}, t) = \frac{β_{2} T_{0}}{{δ_{2}}^{2} - m^{2}} \frac{g (δ_{2} y_{2})}{g (δ_{2} a_{2})} \cdot \\ Re \{\exp [bt + jm (x_{2} - c_{2} t)]\} \end{matrix} (23) \end{matrix}$

为避免出现当 $\begin{matrix} δ = m \end{matrix}$ 时, 式(21)和式(23)的分母出现奇异性, 文中对其做一定的修改, 如式(24)和式(25)所示, 即:

对称模式:

$\begin{matrix} \{\begin{matrix} ψ_{1} (x_{1}, y_{1}, t) = \\ \frac{β_{1} T_{0}}{δ_{1}^{2} - m^{2}} [\frac{g' (δ_{1} (a_{1} - y_{1}))}{g' (δ_{1} a_{1})} - \frac{g' (m y_{1})}{g' (m a_{1})}] \cdot \\ Re \{\exp [bt + jm (x_{1} - c_{1} t)]\} \\ ψ_{2} (x_{2}, y_{2}, t) = \\ \frac{β_{2} T_{0}}{δ_{2}^{2} - m^{2}} [\frac{g (δ_{2} y_{2})}{g (δ_{2} a_{2})} - \frac{g (m y_{2})}{g (m a_{2})}] \cdot \\ Re \{\exp [bt + jm (x_{2} - c_{2} t)]\} \end{matrix} (24) \end{matrix}$

反对称模式:

$\begin{matrix} \{\begin{matrix} ψ_{1} (x_{1}, y_{1}, t) = \\ \frac{β_{1} T_{0}}{δ_{1}^{2} - m^{2}} [\frac{g (δ_{1} (a_{1} - y_{1}))}{g (δ_{1} a_{1})} - \frac{g (m y_{1})}{g (m a_{1})}] \cdot \\ Re \{e xp [bt + jm (x_{1} - c_{1} t)]\} \\ ψ_{2} (x_{2}, y_{2}, t) = \\ \frac{β_{2} T_{0}}{δ_{2}^{2} - m^{2}} [\frac{g (δ_{2} y_{2})}{g (δ_{2} a_{2})} - \frac{g (m y_{2})}{g (m a_{2})}] \cdot \\ Re \{\exp [bt + jm (x_{2} - c_{2} t)]\} \end{matrix} (25) \end{matrix}$

则由热弹性平衡微分方程(18)的特解 $\begin{matrix} ψ_{i} \end{matrix}$ 引起的热弹性变形和热应力分别为:

$\begin{matrix} \{\begin{matrix} _{g}^{} u_{x_{i}} = \frac{1}{2 μ_{i}} \frac{\partial ψ_{i}}{\partial x},_{g}^{} u_{y_{i}} = \frac{1}{2 μ_{i}} \frac{\partial ψ_{i}}{\partial y} \\ _{g}^{} σ_{y y_{i}} = - \frac{\partial^{2} ψ_{i}}{\partial x^{2}},_{g}^{} σ_{x y_{i}} = \frac{\partial^{2} ψ_{i}}{\partial x \partial y} \end{matrix} (26) \end{matrix}$

式中: $\begin{matrix} σ \end{matrix}$ 为热应力。

二维热弹性平衡方程(18)的齐次特解可由Green和Zerna等^[24]温解的A和D的形式相加得到。这里引入4个调和函数 $\begin{matrix} χ_{i} 、 φ_{i} 、 τ_{i} 和 ω_{i}, \end{matrix}$ 且其均须满足式(27), 即:

$\begin{matrix} \nabla^{2} χ_{i} = \nabla^{2} φ_{i} = \nabla^{2} τ_{i} = \nabla^{2} ω_{i} = 0 (27) \end{matrix}$

为计算简便, 文中所取的4个调和函数的形式如式(28)所示, 即:

$\begin{matrix} \{\begin{matrix} χ_{i} = A_{i} T_{0} \exp (bt - m y_{i} + jmx) \\ φ_{i} = B_{i} T_{0} \frac{\cos h (m y_{i})}{\cos h (m a_{i})} \exp (bt + jmx) \\ τ_{i} = C_{i} T_{0} \exp (bt + m y_{i} + jmx) \\ ω_{i} = D_{i} T_{0} \frac{\sin h (m y_{i})}{\sin h (m a_{i})} \exp (bt + jmx) \end{matrix} (28) \end{matrix}$

式中: $\begin{matrix} A_{i} 、 B_{i} 、 C_{i} 和 D_{i} \end{matrix}$ 为未知常数。

根据式(27)(28), 由热弹性平衡微分方程的齐次解, 即调和函数 $\begin{matrix} χ_{i} 、 φ_{i} 、 τ_{i} 和 ω_{i} \end{matrix}$ 所引起的热弹性变形和热应力分别为:

$\begin{matrix} \{\begin{matrix} _{p}^{} u_{x_{i}} = \frac{1}{2 μ_{i}} (\frac{\partial χ_{i}}{\partial x} + \frac{\partial φ_{i}}{\partial x} + y_{i} \frac{\partial τ_{i}}{\partial x} + y_{i} \frac{\partial ω_{i}}{\partial x}) \\ _{p}^{} u_{y_{i}} = \frac{1}{2 μ_{i}} [\frac{\partial χ_{i}}{\partial y} + \frac{\partial φ_{i}}{\partial y} + y_{i} \frac{\partial τ_{i}}{\partial y} - (3 - 4 ν_{i}) τ_{i} + \\ y_{i} \frac{\partial ω_{i}}{\partial y} - (3 - 4 ν_{i}) ω_{i}] \\ _{p}^{} σ_{y y_{i}} = y_{i} \frac{\partial^{2} τ_{i}}{\partial y^{2}} - 2 (1 - ν_{i}) \frac{\partial τ_{i}}{\partial y} + y_{i} \frac{\partial^{2} ω_{i}}{\partial y^{2}} - \\ 2 (1 - ν_{i}) \frac{\partial ω_{i}}{\partial y} - \frac{\partial^{2} χ_{i}}{\partial x^{2}} - \frac{\partial^{2} φ_{i}}{\partial x^{2}} \\ _{p}^{} σ_{x y_{i}} = \frac{\partial^{2} χ_{i}}{\partial x \partial y} + \frac{\partial^{2} φ_{i}}{\partial x \partial y} + y_{i} \frac{\partial^{2} τ_{i}}{\partial x \partial y} - (1 - 2 ν_{i}) \frac{\partial τ_{i}}{\partial x} + \\ y_{i} \frac{\partial^{2} ω_{i}}{\partial x \partial y} - (1 - 2 ν_{i}) \frac{\partial ω_{i}}{\partial x} \end{matrix} (29) \end{matrix}$

在方程(18)的特解和齐次通解确定后, 分别将式(24)(25)代入式(26), 式(28)代入式(29), 便可得到总的热弹性变形和应力分别为:

$\begin{matrix} \{\begin{matrix} u_{x_{i}} =_{g}^{} u_{x_{i}} +_{p}^{} u_{x_{i}}, u_{y_{i}} =_{g}^{} u_{y_{i}} +_{p}^{} u_{y_{i}} \\ σ_{y y_{i}} =_{g}^{} σ_{y y_{i}} +_{p}^{} σ_{y y_{i}}, σ_{x y_{i}} =_{g}^{} σ_{x y_{i}} +_{p}^{} σ_{x y_{i}} \end{matrix} (30) \end{matrix}$

在确定了总的热弹性位移和热应力后, 令其满足热边界条件式(31)~式(34), 便可分别求出4个调和函数中的8个未知常数 $\begin{matrix} A_{i} 、 B_{i} 、 C_{i} 和 D_{i} (i = 1, 2) 。 \end{matrix}$

(1)在滑动摩擦面(y=0)上有:

$\begin{matrix} \{\begin{matrix} u_{y_{1}} = u_{y_{2}}, σ_{y y_{1}} = σ_{y y_{2}} \\ σ_{x y_{1}} = σ_{x y_{2}}, σ_{x y_{1}} = f σ_{y y_{1}} \end{matrix} (31) \end{matrix}$

式中: $\begin{matrix} f \end{matrix}$ 为摩擦因数。

(2)当热点呈反对称分布, 在滑动层的中分面(y₂=0)上有^[13]:

$\begin{matrix} u_{x_{2}} = 0, σ_{y y_{2}} = 0 (32) \end{matrix}$

(3)当热点呈对称分布, 在滑动层的中分面(y₂=0)上有^[13]:

$\begin{matrix} u_{y_{2}} = 0, σ_{x y_{2}} = 0 (33) \end{matrix}$

(4)与钢背连接的摩擦层背面处(y₁=a₁), 有:

$\begin{matrix} u_{x_{1}} = 0, u_{y_{1}} = 0 (34) \end{matrix}$

待未知常数 $\begin{matrix} A_{i} 、 B_{i} 、 C_{i} 和 D_{i} 确定后, 即可根据在滑动摩擦面上的边界条件式 (35) 来确定式 (4) 中接触压力 p 的扰动幅值 p_{0}, \end{matrix}$ 即:

$\begin{matrix} \begin{matrix} p_{0} \cdot Re \{\exp (bt + jmx)\} = - σ_{y y_{2}} = \\ \frac{\partial^{2} ψ_{2}}{\partial x^{2}} + \frac{\partial^{2} χ_{2}}{\partial x^{2}} + \frac{\partial^{2} φ_{2}}{\partial x^{2}} - a_{2} \frac{\partial^{2} τ_{2}}{\partial y^{2}} + 2 (1 - \\ ν_{2}) \frac{\partial τ_{2}}{\partial y} - a_{2} \frac{\partial^{2} ω_{2}}{\partial y^{2}} + 2 (1 - ν_{2}) \frac{\partial ω_{2}}{\partial y} (35) \end{matrix} \end{matrix}$

1.3 热特征平衡方程

依据能量守恒原理, 滑动摩擦面上被层吸收的热载荷之和应等于摩擦因数f、滑动速度v和接触压力p三者的乘积, 忽略在滑动摩擦过程中, 由空气引起的对流换热和辐射换热带来的影响^[25], 则有式(36)成立, 即:

$\begin{matrix} q_{y_{1}} + q_{y_{2}} = {K_{2} \frac{\partial T_{2}}{\partial y}|}_{y = 0} {- K_{1} \frac{\partial T_{1}}{\partial y}|}_{y = 0} = fvp (36) \end{matrix}$

式中: $\begin{matrix} q_{yi} \end{matrix}$ 为热流密度。

将式(16)(17)和式(35)分别代入式(36), 并令扰动增长系数b=0, 即可得到不同热点分布模式下, 临界速度v_cr的表达式分别为:

$\begin{matrix} \begin{matrix} v_{cr} = [K_{1} δ_{1} \frac{g (δ_{1} a_{1})}{g' (δ_{1} a_{1})} + K_{2} δ_{2} \frac{g' (δ_{2} a_{2})}{g (δ_{2} a_{2})}] \frac{1}{f p_{0}} (对称) (37) \\ v_{cr} = [K_{1} δ_{1} \frac{g' (δ_{1} a_{1})}{g (δ_{1} a_{1})} + K_{2} δ_{2} \frac{g' (δ_{2} a_{2})}{g (δ_{2} a_{2})}] \frac{1}{f p_{0}} (反对称) (38) \end{matrix} \end{matrix}$

2 结果及分析

以国内某条快速城市轨道交通车辆所装备的基础盘形制动单元中的摩擦副^[26]为研究对象, 室温下, 其滑动层制动盘和摩擦层闸片的热物理特性参数和结构参数分别如表1和表2所示。注意到式(37)和式(38)是关于5个未知变量m、v、c₁、c₂和b的非线性方程组。为了求解该方程, 可令式(37)和式(38)中的实数和虚数部分分别相等, 加上式(6)和b=0, 若已知其余4个未知变量中的任意一个, 代入表1和表2中的参数, 则其余未知变量便可通过数值编程求出。

表1 摩擦副材料热物理特性参数 Table 1 Thermo-physical properties of brake pair

材料属性	摩擦层	滑动层
弹性模量E/GPa	2.2	105.0
密度ρ /(kg· m^-3)	1590	7220
比热容c_pi/[J· (kg· K)^-1]	900	503
传热系数K/[W· (m· K)^-1]	12.00	42.38
泊松比 $\begin{matrix} ν \end{matrix}$	0.25	0.30
热膨胀系数α × 10^-6/K^-1	10.00	4.39
摩擦因数 $\begin{matrix} f \end{matrix}$	0.32	0.32

表1 摩擦副材料热物理特性参数 Table 1 Thermo-physical properties of brake pair

表2 摩擦副结构参数 Table 2 Geometry parameters of brake pair

层 $\begin{matrix} i \end{matrix}$	内半径r₁/mm	外半径r₂/mm	厚度a_i/mm
闸片	185	310	10
制动盘	175	320	15

表2 摩擦副结构参数 Table 2 Geometry parameters of brake pair

作者已在文献[27]中给出了不同热点分布模式下, 滑动摩擦副系统的临界速度随扰动频率的变化曲线。但由于在理论推导过程中较文献[27]有所改变, 且本文旨在探讨摩擦副的结构及滑动层制动盘的材料参数对滑动摩擦系统进入热弹性失稳状态所需最低临界速度的影响。因此, 为便于后续讨论和分析, 本文仍给出了不同热点分布模式下临界速度v_cr随扰动频率 $\begin{matrix} m \end{matrix}$ 的变化关系, 如图2所示。从图2可以看出, 在loglog坐标系中, 随着扰动频率 $\begin{matrix} m \end{matrix}$ 的增加, 不同热点分布模式对应的临界速度v_cr均呈先减小后增大的变化规律。每条曲线下方为TEI稳定区, 反之为失稳区。显然, 在满足制动性能要求的前提下, 应尽可能保证摩擦系统的相对滑动速度位于TEI稳定区域内。 A点和B点分别是热点呈对称和反对称分布模式下, 系统发生TEI失稳现象所需的最低临界速度, 即v_crmin, 对应的扰动频率被称为临界扰动频率, 即m_cr。显然, v_crmin(A)要远大于v_crmin(B), m_cr(A)也大于m_cr(B)。图中C点和D点为反对称分布模式下, 临界速度变化曲线上具有相同的临界速度v_cr, 但扰动频率m不同的两点。比较B、C和D三点可知:临界速度v_cr(C)=v_cr(D)> v_crmin(B), 但扰动频率m(D)>m_cr(B)>m(C) 作者在文献[27]中也已给出了图2中B、C和D三点所对应的扰动增长系数随滑动速度的变化关系,并得出临界扰动频率m_cr(B)为系统的主扰动, 且在不同扰动频率具有相同临界速度的前提下, 扰动频率越低, 扰动增长系数越小, 对系统发生热弹性失稳的影响也就越小。但针对文献[27]中的图3, 这里需要进一步指出的是:在临界扰动频率的左侧和相同滑动速度的前提下, 扰动增长系数随扰动频率的增大而逐渐增大, 而在临界扰动频率的右侧, 变化规律正好相反。这表明:对于特定的滑动摩擦副, 若其要发生热弹性失稳现象, 理论上在滑动层制动盘的摩擦面上更容易观测到 $\begin{matrix} m_{cr} = m (B) \end{matrix}$ 对应的热点数目。

	Figure Option View Download New Window
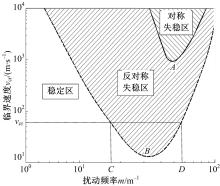	图2 不同热点分布模式下v_cr与m的关系Fig.2 Relationship between v_cr and m at two different types of distribution of hot spots

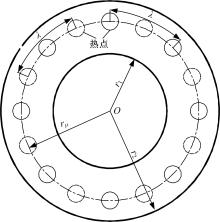
若以滑动层制动盘为研究对象, 图3给出了热点在制动盘的两个摩擦面上呈反对称分布模式时的示意图, 分别用实线和虚线表示。图3中: $\begin{matrix} r_{1} 、 r_{2} 和 r_{μ} 分别为制动盘的内半径、外半径以及当量摩擦半径; λ 为相邻热点之间的波长。假设 N = 8 (N 须为整数) 个热点均匀分布在制动盘摩擦面的当量摩擦半径 {r_{μ}}^{[28]} 的圆周方向上。显然, 扰动频率 m 、热点数 N 、波长 λ 以及当量摩擦半径 r_{μ} 存在式 (39) ~ 式 (41) 的关系。可以看出, 扰动频率 m 会随热点数 N 的增加而增大, 但波长 λ \end{matrix}$ 却要减小。结合图2和图3可得出:在相同激励条件下, 滑动摩擦系统更易出现热点呈反对称分布模式的TEI失稳问题, 该结论也可在文献[9, 12, 15, 27]中得到验证。此外, 不同热点分布模式下, 最低临界速度v_crmin对应的热点数 $\begin{matrix} N 也不同, 显然 N (A) > N (B) 。 \end{matrix}$

$\begin{matrix} \begin{matrix} m & = N / r_{μ} (39) \\ λ & = 2 π r_{μ} / N (40) \\ r_{μ} & = \frac{2 (r_{2}^{3} - r_{1}^{3})}{3 (r_{2}^{2} - r_{1}^{2})} (41) \end{matrix} \end{matrix}$

文献[28]和[29]通过研究指出:随扰动频率 $\begin{matrix} m \end{matrix}$ 变化的临界速度v_cr曲线上的最低点是判断摩擦副系统发生TEI失稳现象难易的主要标准, 且v_crmin越小, 摩擦副系统的稳定性越差, 在滑动摩擦过程中更容易出现局部高温而失效。因此, 有必要研究摩擦副的几何结构和材料热物理特性参数的改变对v_crmin的影响。作者在文献[27]中已讨论了摩擦副厚度及热物理特性参数对同一扰动频率所对应的临界速度的影响, 而式(37)和式(38)确定的临界速度v_cr又是摩擦副厚度及热物理特性参数的函数, 但由于热点主要出现在滑动层制动盘的摩擦面上。因此, 本文将分别研究上述参数的改变对最低临界速度v_crmin的影响, 并与文献[27]中得到的在相同热点数 $\begin{matrix} N \end{matrix}$ 的前提下, 摩擦副结构及材料的热物理特性参数对临界速度的影响进行比较。

	Figure Option View Download New Window
	图3 制动盘热点呈反对称分布示意图Fig.3 Antisymmetric type of hot spots on disc's surface

2.1 结构参数对v_crmin的影响

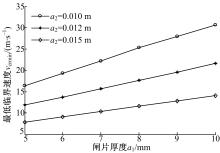
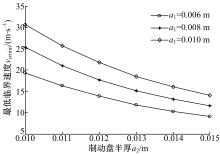
若分别改变摩擦副的厚度 $\begin{matrix} a_{1} 和 a_{2}, \end{matrix}$ 可得到滑动摩擦系统的最低临界速度v_crmin的变化规律分别如图4和图5以及表3所示。从图4中可看出, 对于同一摩擦层厚度a₁, 最低临界速度v_crmin随滑动层厚度a₂的增加反而逐渐减小。从表3中可知, 当a₂=0.012 m时, v_crmin随a₁从0.008 m时的17.63 m/s增加至0.01 m时的21.59 m/s, 增幅为22.46%, 但对于a₁=0.01 m, 当a₂从0.01 m增加至0.015 m时, v_crmin却由30.67 m/s下降至14.08 m/s, 降幅达到了54.09%。

从图5中可看出, 若a₂保持不变, 最低临界速度v_crmin则随摩擦层厚度a₁的增加而增大, 引起该现象的原因具体可参考文献[27]。从表3中可看出, 若a₁=0.01 m, v_crmin从a₂=0.01 m时的30.67 m/s降低至a₂=0.012 m时的21.59 m/s, 降幅为29.61%, 但当a₂=0.012 m时, v_crmin从a₁=0.01 m时的21.59 m/s下降至a₁=0.005 m时的11.87 m/s, 降幅则达到了45.02%。可见, 增加a₂不能提高系统的最低临界速度v_crmin。

	Figure Option View Download New Window
	图4 不同摩擦层a₁和v_crmin随a₂的变化关系Fig.4 Variation of v_crmin as a function of a₂ for different values of a₁

	Figure Option View Download New Window
	图5 不同滑动层a₂和v_crmin随a₁的变化关系Fig.5 Variation of v_crmin as a function of a₁ for different values of a₂

通过比较图4和5可知, a₁和a₂的变化对系统最低临界速度v_crmin的影响规律正好相反。为了分析该原因, 图6和图7分别给出了图4和图5中对应的由不同a₁和a₂组成的滑动摩擦系统的临界速度v_cr随扰动频率 $\begin{matrix} m \end{matrix}$ 的变化曲线。从图6中可以看出, 若保证滑动层厚度a₂=0.015 m不变, 随着摩擦层厚度a₁的增加, 摩擦副系统的最低临界速度v_crmin逐渐增大, 但对应的临界扰动频率m_cr逐渐减小, 且当扰动频率m< 20 m^-1时, 不同摩擦层厚度a₁对应的临界速度v_cr基本重合。而从图7中可以看出, 若保持a₁=0.01 m不变, 最低临界速度v_crmin则随a₂的增加而逐渐减小, 且对应的临界扰动频率m_cr也逐渐降低。上述结果表明:在滑动摩擦系统的设计过程中, 可以通过增加摩擦层厚度以及减小滑动层厚度来提高最低临界速度v_crmin, 但如前文所述, 增加摩擦层厚度a₁不仅增加制造成本, 也会增加列车的簧下质量, 而降低滑动层厚度a₂虽可以节约成本, 但又会降低其热容量。因此, 合理选择摩擦副的结构参数对其发生热弹性失稳起着重要的影响作用。

表3 不同摩擦副厚度比对应的v_crmin Table 3 Minimum critical speed corresponding to different thickness ratio

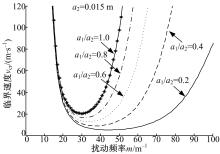	Figure Option View Download New Window
	图6 不同厚度比a₁/a₂下v_cr与m的关系Fig.6 Relationship between v_cr and m for different values of thickness ratio a₁/a₂

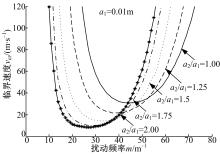	Figure Option View Download New Window
	图7 不同厚度比a₂/a₁下v_cr与m的关系Fig.7 Relationship between v_cr and m for different values of thickness ratio a₂/a₁

此外, 从图7中可看出, 当扰动频率m约大于55 m^-1时, 随着滑动层厚度a₂的增加, 不同扰动频率所对应的临界速度呈逐渐增大的变化趋势; 当扰动频率m约为25~55 m^-1时, 临界速度随扰动频率没有明确的变化规律; 而当m约小于25 m^-1时, 滑动层越厚, 同一扰动频率所对应的临界速度越小, 系统越不稳定。而文献[27]中得到的不同滑动层厚度与摩擦片组成的滑动摩擦系统的扰动增长系数将随滑动层厚度的增加而增大的结论是基于扰动频率m=60 m^-1得到的。因此, 可以得出:滑动层制动盘厚度的增加会引起最低临界速度的减小, 但其对临界速度的影响要取决于具体扰动频率值。

2.2 滑动层材料参数对v_crmin的影响

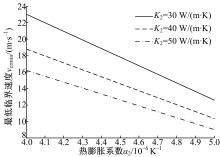
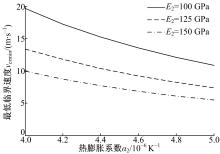
图8给出了不同滑动层制动盘传热系数K₂对应的最低临界速度v_crmin随热膨胀系数α ₂的变化规律。从图8可看出, 随着α ₂的增加, 不同K₂对应的v_crmin均呈线性减小的变化规律。分析原因主要是由于热膨胀系数是指物体单位温度变化所导致的体积变化, 是表征材料发生热应变能力的参数。在等量温升的条件下, 制动盘热膨胀系数越高, 则由温升引起的热弹性变形也就越大, 加剧了滑动摩擦面间压力和温度场分布的不均匀性, 进而使系统的稳定性逐渐降低。当α ₂=4× 10^-6 K^-1时, v_crmin从K₂=30 W/(m· K)时的23.05 m/s降低至K₂=40 W/(m· K)时的18.86 m/s, 降幅为18.18%。这表明:滑动摩擦系统的TEI稳定性会随制动盘传热系数的增大逐渐降低。传热系数是指热流密度与温度梯度的比值, 是表征材料传导热量能力的参数。如式(42)所示, 若假设摩擦层闸片和滑动层制动盘的热膨胀系数和比热容以及摩擦层闸片的传热系数保持不变, 则因摩擦生热而进入滑动层制动盘的热载荷会随其传热系数的增大而增大, 进而会引起温升效应和摩擦面上温度梯度的增加, 从而加剧热弹性变形, 在相同的激励条件下, 提高了热点产生的可能性。

$\begin{matrix} γ = \frac{\sqrt[]{K_{2} ρ_{2} c_{p 2}}}{\sqrt[]{K_{2} ρ_{2} c_{p 2}} + \sqrt[]{K_{1} ρ_{1} c_{p 1}}} (42) \end{matrix}$

	Figure Option View Download New Window
	图8 不同滑动层K₂和v_crmin随α ₂的变化曲线Fig.8 Relationship between $\begin{matrix} {v_{cr}}_{\min} \end{matrix}$ and α ₂ for different values of K₂

	Figure Option View Download New Window
	图9 不同滑动层E₂和v_crmin随K₂的变化曲线Fig.9 Relationship between v_crmin and K₂ for different values of E₂

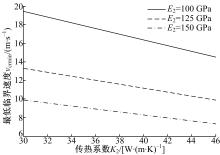
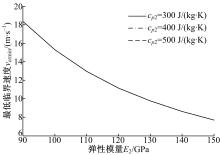
图9给出了不同制动盘弹性模量E₂, 最低临界速度v_crmin随传热系数K₂的变化关系。从图9可以看出, 不同E₂对应的v_crmin随K₂的减小而逐渐线性增加, 该结论与图8一致, 即v_crmin随K₂的增大而逐渐减小。当E₂=100 GPa时, 随着K₂从46 W/(m· K)降低至30 W/(m· K), v_crmin则从14.64 m/s提高到19.53 m/s, 增幅为33.4%。而当K₂=42 W/(m· K), E₂从100 GPa逐渐增加至125 GPa, 最终至150 GPa时, 对应v_crmin分别为15.53 m/s、10.5 m/s和7.68 m/s, 降幅分别为32.39%和29.61%。这表明当制动盘弹性模量E₂增加至一定值时, 对滑动摩擦系统发生TEI失稳的影响程度在逐渐减小。材料的弹性模量是指变形阶段应力与应变的正比例系数, 是表征其抵抗弹性变形能力大小的参数。弹性模量越大, 使材料发生一定弹性变形的应力也越大, 进而增强了由温度梯度引起的热应力场的非均匀分布, 导致系统的稳定性随制动盘弹性模量的增大而逐渐降低。

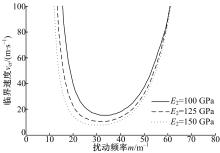
图10给出了当K₂=42.38 W/(m· K)时, 保持其他参数不变, 不同制动盘弹性模量E₂对应的临界速度v_cr随空间扰动频率m的变化曲线。从图10可以看出, 当空间扰动频率m< 55 m^-1时, 随着弹性模量E₂增大, 最低临界速度v_crmin逐渐减小, 且对应的空间扰动频率值m_cr越小。此外, 不同空间扰动频率对应的临界速度随制动盘弹性模量的增大而逐渐减小。但当空间扰动频率m> 60 m^-1时, 临界速度基本重合。这表明, 对于特定的滑动摩擦系统, 当空间扰动频率m达到一定值时, 制动盘弹性模型E₂对系统的热弹性失稳几乎没有影响。作者在文献[27]中给出了图2中反对称热点分布模式, 且在临界扰动频率右侧, 滑动层制动盘弹性模量对同一扰动频率所对应的临界速度的变化关系, 发现临界速度随制动盘弹性模量的增大改变较小。结合图9和10可知, 滑动层弹性模量的改变对最低临界速度以及同一热点数对应的临界速度的影响较为复杂。

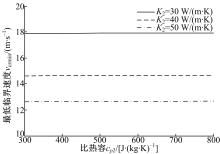
	Figure Option View Download New Window
	图10 不同滑动层E₂和v_cr随m的变化关系Fig.10 Relationship between v_cr and m for different values of E₂

若改变制动盘的传热系数K₂, 滑动摩擦系统的最低临界速度v_crmin随比热容c_p₂的变化关系如图11所示。从图11可以看出, 不同K₂对应的v_crmin随c_p₂几乎不变。可见, 增加制动盘比热容c_p₂对系统TEI稳定性几乎没有影响。分析原因主要是由于:如式(42)所示, 滑动摩擦过程中进入制动盘的热载荷会随其比热容c_p₂的增大而提高, 增强了制动盘的摩擦面以及 $\begin{matrix} y \end{matrix}$ 轴方向上的温升效应和温度梯度, 降低了系统的稳定性, 最低临界速度理应降低。但由于制动盘的传热系数和密度要大于闸片, 参考表1中的数据, 当制动盘的比热容由503 J/(kg· K)增加至903 J/(kg· K)时, 由式(42)确定的被其吸收的热载荷比例由0.75增加至0.8, 增量仅有6.67%。因此, 引起制动盘温升效应的该变量较小。此外根据比热容的自身定义, 如式(43)所示, 为单位质量的物质, 在其吸收(温度升高)或释放(温度降低)的热量与质量和温差乘积之比。若已知被制动盘吸收的热量Q₂、质量m₂以及初始温度T_c保持不变, 若增大制动盘的比热容, 则温差就要减小, 即制动盘比热容的增大反而会引起末温度T_m的降低。正是由于上述两个原因的相反作用而导致制动盘比热容的改变对系统发生TEI失稳几乎没有影响。

$\begin{matrix} c_{p_{2}} = \frac{Q_{2}}{m_{2} (T_{m} - T_{c})} (43) \end{matrix}$

式中:Q₂、m₂、T_m和T_c分别为被制动盘吸收的热载荷、质量、末温度和初始温度。

	Figure Option View Download New Window
	图11 不同滑动层K₂和v_crmin随c_p₂的变化曲线Fig.11 Relationship between $\begin{matrix} {v_{cr}}_{\min} \end{matrix}$ and c_p₂ for different values of K₂

图12给出了不同制动盘比热容c_p₂, 最低临界速度v_crmin随弹性模量E₂的变化曲线。从图12可以看出, 随着E₂的增加, v_crmin逐渐减小。结合图9和图10可以得出, 制动盘材料弹性模量越大, 最低临界速度值越小, 系统稳定性越差。

	Figure Option View Download New Window
	图12 不同滑动层c_p₂和v_crmin随E₂的变化曲线Fig.12 Relationship between $\begin{matrix} {v_{cr}}_{\min} \end{matrix}$ and E₂ for different values of c_p₂

	Figure Option View Download New Window
	图13 不同滑动层c_p₂和v_crmin随α ₂的变化曲线Fig.13 Relationship between v_crmin and α ₂ for different values of c_p₂

从图13可知, 随着α ₂的增加, 不同c_p₂和E₂对应的v_crmin均近似呈线性减小。随着c_p₂的增加, 最低临界速度保持不变。当c_p₂=500 J/(kg· K)时, v_crmin从α ₂=5× 10^-6K^-1时的10.02 m/s增加至α ₂=4× 1 $\begin{matrix} {0^{- 6}}^{} \end{matrix}$ K^-1时的18.13 m/s, 增幅为44.73%。从图14中可知, 不同E₂对应的v_crmin随α ₂呈线性变化的斜率随E₂呈逐渐增加的趋势。当α ₂=5× 1 $\begin{matrix} {0^{- 6}}^{} \end{matrix}$ K^-1时, v_crmin则从E₂=100 GPa时的10.94 m/s减小至E₂=150 GPa时的5.44 m/s, 降幅为50.27%。结合图5~图9可知, 制动盘弹性模量越小、热膨胀系数越低、导热系数越小, 滑动摩擦系统越趋于稳定, 而比热容的改变对滑动摩擦系统的热弹性失稳没有影响。

比较图4~图14, 假设若分别单独给摩擦层厚度 $\begin{matrix} a_{1} 、滑动层厚度 a_{2} 、热传导系数 K_{2} 、 \end{matrix}$ 比热容c_p₂、弹性模量E₂以及热膨胀系数α ₂相同的增量(+25%), 其余参数如表1和表2保持不变, 则对

应的最低临界速度及变化如表4所示。可以看出, 在各参数具有相同增量的前提下, 影响滑动摩擦系统TEI稳定性的最大因素为滑动层热膨胀系数, 其次为滑动层的厚度和弹性模量, 摩擦层厚度和滑动层的传热系数的改变对最低临界速度的影响为中等, 而滑动层比热容的改变几乎不会影响系统的稳定性。与文献[27]相比较可知:滑动层材料的传热系数和热膨胀系数对标志系统进入热弹性失稳所需的最低临界速度以及同一扰动频率所对应的临界速度具有相同的影响作用。滑动层制动盘的厚度对临界速度的影响要取决于具体扰动频率值, 且滑动摩擦系统的稳定性会因其厚度的减小而逐渐提高。增加滑动层材料的弹性模量, 对同一扰动频率所对应的临界速度影响较小, 但最低临界速度值却逐渐减小。虽滑动层比热容对两者均无影响, 但引起该现象的具体原因请以本文中的解释为参考。

	Figure Option View Download New Window
	图14 不同滑动层E₂和v_crmin随α ₂的变化曲线Fig.14 Relationship between v_crmin and α ₂ for different values of E₂

表4 结构和材料的热物理特性参数对最低临界速度的影响比较 Table 4 Comparison of effect from geometrical and thermo-physical properties on minimum critical speed

3 结论

(1)在文献[27]的基础上, 进一步改进了不同热点分布模式下临界速度表达式的推导过程, 发现滑动摩擦系统在摩擦运动过程中, 更容易在滑动层的两摩擦面上出现呈反对称分布的热点模式, 且临界扰动频率越大, 系统越不稳定。

(2)摩擦层和滑动层厚度的改变对最低临界速度的变化具有相反的作用。随着摩擦层厚度的增加, 最低临界速度值增大。

(3)减小滑动层的传热系数、热膨胀系数以及弹性模量均可以提高最低临界速度, 但比热容的改变对滑动摩擦系统的稳定性几乎没有影响。

(4)针对滑动层, 影响滑动摩擦系统热弹性失稳的最大因素为热膨胀系数, 其后次依次为厚度、弹性模量、传热系数和比热容。

(5)本文建立的二维热弹性失稳数学模型是基于摩擦层和滑动层均为圆周轴对称结构。实际铁路和路面车辆上所装备的盘式制动器中的闸片和制动盘在制动过程中为间歇接触, 即闸片不具有圆周轴对称结构, 对于此类滑动接触模型, 文中并没有考虑。但文中得到的结论仍可为车辆离合器、飞机多盘片等摩擦制动器的设计提供一定的借鉴。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	孟德建, 张立军, 阮丞, 等. 摩擦引起的制动器热点问题综述[J]. 同济大学学报: 自然科学版, 2014, 42(8): 1203-1210. Meng De-jian, Zhang Li-jun, Ruan Cheng, et al. Literature survey of friction-induced hot spots in brakes[J]. Journal of Tongji University(Natural Science), 2014, 42(8): 1203-1210. [本文引用:2]
[2]	Du S. Thermoelastic effects in automotive brakes[D]. Ann Arbor: University of Michigan, 1997. [本文引用:2]
[3]	Al-Shabibi A M. Transient solution of a thermoelastic instability problem using a reduced order model [D]. Ann Arbor: University of Michigan, 2002. [本文引用:2]
[4]	Davis C L, Krousgrill C M, Sadeghi F. Effect of temperature on thermoelastic instability in thin disks[J]. ASME J Tribol, 2002, 124(3): 429-437. [本文引用:2]
[5]	Joachim-Ajao D, Barber J R. Effect of material properties in certain thermoelastic contact problems[J]. J Appl Mech-T, 1998, 65(4): 889-893. [本文引用:1]
[6]	Liu Y, Jang Y H, Barber J R. Finite element implementation of an eigenfunction solution for the contact pressure variation due to wear[J]. Wear, 2014, 309(1): 134-138. [本文引用:1]
[7]	Dow R A, Burton R A. Thermoelastic instability of sliding contact in the absence of wear[J]. Wear, 1972, 19(3): 315-328. [本文引用:3]
[8]	Burton R A, Nerlikar V, Kilaparti S R. Thermoelastic instability in a seal-like configuration[J]. Wear, 1973, 24(2): 177-188. [本文引用:2]
[9]	Dow T A. Thermoelastic effects in brakes[J]. Wear, 1980, 59(1): 213-221. [本文引用:2]
[10]	Lee K, Barber J R. An experimental investigation of frictionally-excited thermoelastic instability in automotive disk brakes under a drag brake application[J]. ASME J Tribol, 1994, 116(3): 409-414. [本文引用:1]
[11]	Byon C, Choo K, Kim S J. Experimental and analytical study on chip hot spot temperature[J]. Int J Heat Mass Transfer, 2011, 54(9): 2066-2072. [本文引用:1]
[12]	Lee K. Frictionally-excited thermoelastic instability in automotive disk brakes[D]. Ann Arbor: University of Michigan, 1993. [本文引用:2]
[13]	Lee K, Barber J R. Frictionally excited thermoelastic instability in automotive disk brakes[J]. ASME J Tribol, 1993, 115(4): 607-614. [本文引用:6]
[14]	Du S, Zagrodzki P, Barber J R, et al. Finite element analysis of frictionally excited thermoelastic instability[J]. J Therm Stresses, 1997, 20(2): 185-201. [本文引用:2]
[15]	Yi Y B, Barber J R, Zagrodzki P. Eigenvalue solution of thermoelastic instability problems using Fourier reduction[J]. Proc Roy Soc, 2000, 456(2003): 2799-2821. [本文引用:1]
[16]	Lee K. Frictionally excited thermoelastic instability in automotive drum brakes[J]. ASME J Tribol, 2000, 122(4): 849-855. [本文引用:1]
[17]	Ayala J R R, Lee K, Rahman M, et al. Effect of intermittent contact on the stability of thermoelastic sliding contact[J]. ASME J Tribol, 1996, 118(1): 102-108. [本文引用:1]
[18]	Hartsock D L, Fash J W. Effect of pad/caliper stiffness, pad thickness, and pad length on thermoelastic instability in disk brakes[J]. ASME J Tribol, 2000, 122(3): 511-518. [本文引用:1]
[19]	Geijselaers H J M, Koning A J E. Finite element analysis of thermoelastic instability with intermittent contact[J]. ASME J Tribol, 2000, 122(1): 42-46. [本文引用:1]
[20]	Painer S, Dufrénoy P, Weichert D. An experimental investigation of hot spots in railway disc brakes[J]. Wear, 2004, 256(7): 764-773. [本文引用:1]
[21]	Majcherczak D, Dufrénoy P, Berthier Y. Tribological, thermal and mechanical coupling aspects of the dry sliding contact[J]. Tribol Int, 2007, 40(5): 8340-8343. [本文引用:1]
[22]	Kasem H, Brunel J F, Dufrénoy P, et al. Thermal levels and subsurface damage induced by the occurrence of hot spots during high-energy braking[J]. Wear, 2011, 270(5): 355-364. [本文引用:1]
[23]	Kumar M, Boidin X, Desplanques Y, et al. Influence of various metallic fillers in friction materials on hot-spot appearance during stop braking[J]. Wear, 2011, 270(5): 371-381. [本文引用:1]
[24]	Green A E, Zerna W. Theoretical Elasticity[M]. Oxford: Oxford University Press, 1968. [本文引用:1]
[25]	Yi Y B, Bendawi A. Effect of convective cooling on frictionally excited thermoelastic instability[J]. Wear, 2012, 296(1): 583-589. [本文引用:1]
[26]	夏德茂, 奚鹰, 华滨滨, 等. RZS盘式制动器制动倍率的研究(续)[J]. 中国机械工程, 2015, 26(16): 2244-2248. Xia De-mao, Xi Ying, Hua Bin-bin, et al. Study on braking rate of disc brake unit RZS(Continue)[J]. China Mechanical Engineering, 2015, 26(16): 2244-2248. [本文引用:1]
[27]	夏德茂, 奚鹰, 朱文翔, 等. 二维轴对称摩擦制动器瞬态热弹性失稳的研究[J]. 机械工程学报, 2015, 51(20): 144-155. Xia De-mao, Xi Ying, Zhu Wen-xiang, et al. Transient frictionally excited thermoelastic instability analysis of two dimensional axisymmetric friction brake[J]. Journal of Mechanical Engineering, 2015, 51(20): 144-155. [本文引用:1]
[28]	马彪, 赵家昕, 李和言, 等. 离合器结构参数对其热弹性不稳定性的影响[J]. 吉林大学学报: 工学版, 2014, 44(4): 933-938. Ma Biao, Zhao Jia-xin, Li He-yan, et al. Effect of clutches' structural parameters on thermoelastic instability[J]. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(4): 933-938. [本文引用:1]
[29]	Decuzzi P, Demelio G. The effect of material properties on the thermoelastic stability of sliding systems[J]. Wear, 2002, 252(3): 311-321. [本文引用:1]

2014

0.0

. 2014, 42(8):1203-1210 DOI:doi:10.3969/j.issn.0253-374x.2014.08.009

Literature survey of friction-induced hot spots in brakes

摩擦引起的制动器热点问题综述

Meng De-jian , Zhang Li-jun , Ruan Cheng

孟德建, 张立军, 阮丞

Brake hot spot due to friction is a worldwide forefront and complicated technical problem in brake research and development. Based on many studies on hot spot both at home and abroad in last two decades, the research progresses of experimental study and theoretical analysis are reviewed systematically, and the limitations of current theories are analyzed deeply. The unsolved and ambiguous problems of hot spots are presented, and the main research directions in future are proposed.

基于国内外近20年来关于制动器摩擦热点的大量文献，系统评述了试验研究和理论分析方面的研究进展，深入分析了既有理论的缺陷，提出了制动器热点研究存在的悬疑问题，进而对未来制动器热点研究的重点方向提出了建议.

... 反过来,不均匀的热弹性变形又会进一步加剧接触压力的非均匀分布^[1,2] ...

... 当b=0时,系统处于TEI失稳的临界状态^{[1,2,3,4,12,13]} ...

1997

0.0

... 反过来,不均匀的热弹性变形又会进一步加剧接触压力的非均匀分布^[1,2] ...

... 当b=0时,系统处于TEI失稳的临界状态^{[1,2,3,4,12,13]} ...

2002

0.0

... 在摩擦热、热弹性变形、热应力及弹性接触的相互耦合作用下,当两弹性体的相对滑动速度足够高时,反馈过程将变得不稳定,易在摩擦面的局部区域形成温度和应力的集中,最终形成热点,该热力耦合过程被称为热弹性不稳定(Thermo-Elastic Instability,TEI)^[3,4,5,6] ...

... 当b=0时,系统处于TEI失稳的临界状态^{[1,2,3,4,12,13]} ...

2002

0.0

... 当b=0时,系统处于TEI失稳的临界状态^{[1,2,3,4,12,13]} ...

1998

0.0

2014

0.0

1972

0.0

... 针对此问题,Burton和Dow等^[7,8,9]首先提出扰动分析法,研究了2个垂直于二维坐标的平面在相对滑动时的准静态解 ...

... 此后,许多学者在Burton^[7]的研究基础上展开试验测试^[10,11,12],发现由解析法确定的临界速度要比试验值高,分析原因可能是由于其TEI模型中并未考虑滑动层有限厚度的影响 ...

... Burton和Dow等^[7,8,9]通过研究指出:当滑动层和摩擦层之间的相对滑动速度 v达到某一临界值时,摩擦面间的均匀接触压力p会出现不稳定的余弦扰动,并随时间t呈指数增长,可将其记为: ...

1973

0.0

... 针对此问题,Burton和Dow等^[7,8,9]首先提出扰动分析法,研究了2个垂直于二维坐标的平面在相对滑动时的准静态解 ...

1980

0.0

... 针对此问题,Burton和Dow等^[7,8,9]首先提出扰动分析法,研究了2个垂直于二维坐标的平面在相对滑动时的准静态解 ...

1994

0.0

2011

0.0

1993

0.0

... 当b=0时,系统处于TEI失稳的临界状态^{[1,2,3,4,12,13]} ...

1993

0.0

... 为评价该因素的作用,Barber等^[13]研究了一有限厚度滑动层在两块具有无限厚度的摩擦层内相对滑动时的汽车制动器TEI问题,并对不同热点分布模式下的TEI失稳临界条件进行了求解,得到的结果与试验测试值较接近 ...

... 当b=0时,系统处于TEI失稳的临界状态^{[1,2,3,4,12,13]} ...

... (1)若热点在滑动层的两个摩擦面上呈对称分布^[13],则在滑动层的中分面上有: ...

... (2)若热点在滑动层的两个摩擦面上呈反对称分布^[13],则在滑动层的中分面上有: ...

... (2)当热点呈反对称分布,在滑动层的中分面(y₂=0)上有^[13]: ...

... (3)当热点呈对称分布,在滑动层的中分面(y₂=0)上有^[13]: ...

1997

0.0

... 此后,Du等^[14]采用有限元方法将TEI问题离散为一系列求解特征值的问题 ...

... Yi等^{[15,16,17,18,19]}在Du^[14]的研究基础上,使用傅立叶降阶法将求解TEI失稳的临界条件转化为仅与扰动增长系数和扰动频率相关的特征值问题,并讨论了摩擦片有限周向接触弧长带来的影响 ...

2000

0.0

2000

0.0

1996

0.0

2000

0.0

2000

0.0

2004

0.0

... Painer和Majcherczak等^[20,21]通过测试将盘面热点分为粗糙凸点型、梯度型、形变型、焦点型和区域型5种 ...

2007

0.0

... Painer和Majcherczak等^[20,21]通过测试将盘面热点分为粗糙凸点型、梯度型、形变型、焦点型和区域型5种 ...

2011

0.0

... Kasem和Kumar等^[22,23]则通过试验指出:热点最初会出现在制动盘的外边缘,随后逐渐向内径方向发展,高温区域与低温区域的温差近700 #cod#x000b0 ...

2011

0.0

... Kasem和Kumar等^[22,23]则通过试验指出:热点最初会出现在制动盘的外边缘,随后逐渐向内径方向发展,高温区域与低温区域的温差近700 #cod#x000b0 ...

1968

0.0

... 二维热弹性平衡方程(18)的齐次特解可由Green和Zerna等^[24]温解的A和D的形式相加得到 ...

2012

0.0

... 3 热特征平衡方程依据能量守恒原理,滑动摩擦面上被层 i吸收的热载荷之和应等于摩擦因数f、滑动速度v和接触压力p三者的乘积,忽略在滑动摩擦过程中,由空气引起的对流换热和辐射换热带来的影响^[25],则有式(36)成立,即: ...

2015

0.0

. 2015, 26(16):2244-2248 DOI:doi:10.3969/j.issn.1004132X.2015.16.020

Study on braking rate of disc brake unit RZS(Continue)

RZS盘式制动器制动倍率的研究(续)

Xia De-mao , Xi Ying , Hua Bin-bin

夏德茂, 奚鹰, 华滨滨

Firstly,according to the working principles of the braking unit RZS,the kinematic diagram was built up.Then,the DOF of RZS with and without the brake disc was analyzed and compared.The braking rate and its change rules were calculated and analyzed respectively under two conditions:the pad clearance was equal to the setting value and another the pad clearance was reset after braking operation.It is found that:the braking rate of RZS meets the design requirements and there is a linear relationship between the increment of the self-adjustment mechanism and the amount of the pad's 　wear.During the entire service life of the pad, the braking rate of RZS barely changes.

依据RZS盘式制动器的工作原理，建立了其机构运动简图；计算和比较了该机构在有无制动盘情况下的自由度；考虑闸调机构伸长量的影响，研究了该制动器在闸片间隙等于设定值和闸片间隙补偿后制动倍率的变化情况。研究结果表明：RZS盘式制动器的制动倍率符合工程设计要求；闸调机构的伸长量与闸片磨损量存在线性变化关系；在闸片的整个服役周期内，制动倍率几乎不变。

... 2 结果及分析以国内某条快速城市轨道交通车辆所装备的基础盘形制动单元中的摩擦副^[26]为研究对象,室温下,其滑动层制动盘和摩擦层闸片的热物理特性参数和结构参数分别如表1和表2所示 ...

2015

0.0

. 2015, 51(20):144-155 DOI:doi:10.3901/JME.2015.20.144

Transient frictionally excited thermoelastic instability analysis of two dimensional axisymmetric friction brake

二维轴对称摩擦制动器瞬态热弹性失稳的研究

Xia De-mao , Xi Ying , Zhu Wen-xiang

夏德茂, 奚鹰, 朱文翔

提出考虑摩擦层闸片厚度的影响，建立二维轴对称摩擦制动器热弹性失稳的数学模型。基于扰动分析法，推导摩擦副的温度场扰动以及不同热点分布模式下的热特征平衡方程。研究临界速度和扰动增长系数的变化规律。计算摩擦面瞬态名义温度随制动时间的变化关系。分析和比较不同摩擦副厚度比、热导率、弹性模量、比热容以及热膨胀系数对系统稳定性的影响。结果表明，当热点呈反对称分布时，系统发生热弹性失稳时所需的最低临界速度远低于对称分布模式，临界速度随扰动频率的增加呈先减小后增加的变化趋势。不同扰动频率对应的扰动增长系数随滑动速度近似呈线性增加，最低临界扰动频率对应的扰动增长系数最大。当扰动频率低于临界扰动值时，温度随扰动频率的增加而增加，反之，则降低。增加摩擦副的厚度、摩擦层闸片的热导率和比热容以及减小滑动层制动盘的热导率和热膨胀系数和摩擦层闸片的弹性模量均可以提高滑动摩擦系统的稳定性。

... 而文献[27]中得到的不同滑动层厚度与摩擦片组成的滑动摩擦系统的扰动增长系数将随滑动层厚度的增加而增大的结论是基于扰动频率m=60 m^-1得到的 ...

2014

0.0

. 2014, 44(4):933-938 DOI:doi:10.13229/j.cnki.jdxbgxb201404006

Effect of clutches' structural parameters on thermoelastic instability

离合器结构参数对其热弹性不稳定性的影响

Ma Biao , Zhao Jia-xin , Li He-yan

马彪, 赵家昕, 李和言

摘　要：应用热弹性不稳定性（TEI）理论研究离合器接合过程中的局部高温区产生的原因与发展规律。通过有限元建模的方法建立了离合器接合过程三维有限元模型，并求解不同频率扰动对应的增长系数。研究发现：减小离合器半径尺寸、增大摩擦片厚度可以提高系统热弹性稳定性；离合器内外径比值小于0．6时，减小内外径比值有利于提高稳定性；离合器对偶片半厚度小于2mm时，减小对偶片厚度有利于提高稳定性。

2002

0.0