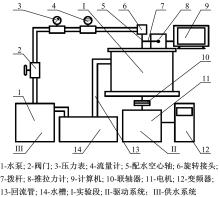
本射流减阻测试平台以同轴圆筒旋转黏度计测量原理为设计基础^[11], 为保证流场稳定性、避免二次流产生^[12], 选用外旋立式方案作为实验段核心结构, 其装置如图1所示。具体性能参数如下:总体尺寸为1700 mm(长)× 560 mm(宽)× 1030 mm(高); 电机转速范围为0~3000 r/min, 能够模拟的主流场流速范围约为5~9 m/s; 流量控制范围为0~6.3 m³/h, 控制精度为0.01 m³/h; 阻力测量范围为0~10 N, 测量精度为0.01 N。

测试平台结构方案如图2所示, 工作原理如下:测试平台主要分为三部分, 即实验段、供水系统及驱动系统。驱动系统主要依靠立式三相异步电动机作为转筒动力源, 并通过变频器调节电机输出轴转速; 实验段内部装有一组同心圆筒, 外筒与电机主轴通过联轴器相接, 从而获取旋转动力; 筒内流体在其旋转作用带动下, 以某一固定角速度绕筒轴线旋转。由于内筒处于静止状态, 其壁面将与外部运动的流体产生相对运动, 在流体黏性作用下, 内筒壁会受到一定的黏性摩擦阻力, 该阻力由装置上端的拨杆传递至HP-10数显推拉力计, 数据可在与之配套的测试系统中得到可视化反馈。供水系统主要承担了测试平台的射流提供及流场水源补给任务, 通过水泵从水槽中获取实验流体, 经管路所连接的阀门、流量计、压力表、旋转接头以及配水空心轴送至内筒, 由筒壁射流孔喷出, 实现射流功能。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 测试平台Fig.1 Photo of experimental platform

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 测试平台结构方案Fig.2 Structural concept of testing platform

本测试平台供水线路方案如图3所示, 具体供水过程如下:供水槽中的实验流体受水泵抽吸作用, 将流经流量调节阀a和b, 结合压力表和流量计控制阀门, 以实现管路中单位时间供水量的动态调节。一部分实验流体经阀b流至实验段, 在压力作用下, 由内筒壁面各射流孔喷出, 实现样件表面射流功能; 而多余流体则通过阀a沿分流排水管回流至储水槽, 完成部分流体的循环过程。筒间流体在外筒高速旋转作用下形成稳定的流场, 而单位时间内由筒壁射流孔排出的流体则作为附加流体, 沿压力调节盘中间的圆形孔排至外环道。外环道连有主排水管, 用以排出上述额外流体, 保证实验段流场容量恒定, 实现主循环过程。测试平台下端接有副排水管, 目的是防止外筒在高速旋转过程中产生轻微泄漏现象, 致使小部分流体滞留在腔体内部无法挥发, 导致锈蚀现象发生。在设计过程中, 将主排水管、副排水管及分流排水管出口置于储水槽液面上方, 方便流体自由出流, 防止由于出口处存在压力导致实验段流体发生存积。储水槽中流体沿整流板流至供水槽, 进而为实验流场提供水源补给。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 供水线路方案Fig.3 Scheme of water supply lines

(1)基本假设

为便于建模及仿真, 需对流场环境做出相应假设如下:①内外筒保持严格同心旋转, 忽略偏心对仿真结果造成的影响; ②筒壁表面无滑移; ③筒间流场无轴向流动; ④实验流体均一, 且不可压缩; ⑤系统恒温, 忽略温度变化对流体黏性系数产生的影响。

(2)数值计算方法

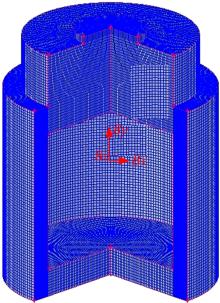
以实验段结构特征为基础, 建立仿真简化模型。鉴于内外筒间流场处于绕轴高速旋转状态, 为保证计算精度, 采用多连域O型网格划分方式。受实验工况所限, 近壁区流体速度梯度变化较大, 因而在近壁处采用高质量贴体网格, 其第一个网格点距内壁0.05 mm, 比例因子取1.2, 网格点数为15。模型网格划分情况如图4所示, 网格单元共计572 945个。由于旋转出口处易发生回流, 为便于计算收敛, 将模型上端出口定义为压力出口。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 总体网格划分情况Fig.4 Overall meshes of computational domain

选择基于压力的求解器; 采用隐式求解方式; 针对实验段流场高雷诺数特性, 选用重组化群 k-ε湍流模型, 结合增强壁面函数法, 用以获得较为准确的壁面模拟效果。

(1)流体体积分数分布

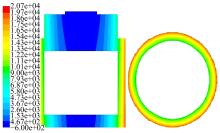
结合前文仿真模型, 以外筒转速2000 r/min为例, 对射流减阻测试平台实验段流场进行分析, 其流体体积分数分布云图(单位:%)如图5所示。图5中内筒壁面完全被实验流体所包裹, 符合所需流场环境, 而上端开口处液体与空气形成的自由液面几乎呈竖直圆柱面, 且半径与上端开口孔径相同, 具有较强规律性。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 实验段流体体积分数云图Fig.5 Contour of fluid volume fraction for experimental section

(2)径向压强分布

以外筒转速2000 r/min为例, 其实验段筒间环流运动压强分布云图(单位:Pa)如图6所示。图6中实验段中心区域压强相对较低, 而越靠近外筒壁面压强值越高。在内外筒间隙内的压强梯度沿径向方向变化较为平缓, 且在环形流场内同一圆柱面上各点压强值相等, 与轴向位置无关。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 湍流状态下环流运动压强分布云图Fig.6 Contour of circulation flow pressure in turbulence

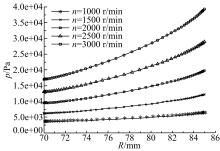
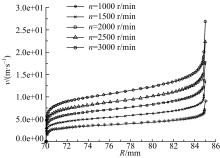
基于以上结论, 取筒间径向流场作为研究对象, 令外筒转速分别等于1000、1500、2000、2500、3000 r/min, 获得不同转速条件下筒间压强分布曲线, 如图7所示, 其中 R表示流场内任意一个流体质点所处的半径位置, R∈ (72, 85)mm。由图7可知, 筒间流场压强沿径向近似呈线性分布, 数值增长速度较为平稳, 能为阻力测试实验提供良好的压强环境。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 不同转速下径向压强分布曲线Fig.7 Curves of radial pressure in different rotating speed

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 湍流状态下环流运动速度分布云图Fig.8 Contour of circulation flow velocity in turbulence

(3)径向速度分布

图8为当外筒转速n=2000 r/min时实验段筒间环流运动速度分布云图(单位:m/s)。由图8可知, 处于实验段中心区域的各流体质点速度几乎为零, 而沿径向方向速度变化梯度较为明显。处于内外筒间隙内大部分流场区域速度云图颜色较为近似, 速度变化不明显, 而在近壁面处的小区域范围内出现速度突变现象, 其中内筒近壁区流体速度趋于零, 而外筒近壁区流体速度与外筒线速度相同, 并且上述运动规律与流体质点所处的轴向位置无关。

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 不同转速下径向速度分布曲线Fig.9 Curves of radial velocity in different rotating speed

基于以上结论, 取筒间径向流场作为研究对象, 令外筒转速分别等于1000、1500、2000、2500、3000 r/min, 获得不同转速条件下径向速度分布曲线, 如图9所示。由图9可知, 在内筒壁面70 mm及外筒壁面85 mm两处近壁区域流体速度下降梯度十分明显, 呈陡降趋势, 而处于中间占据大部分空间区域的各流体周向速度曲线则变化较为均匀, 呈现出近似水平状态, 此现象称之为速差极化现象, 此时, 筒间流场与平板流场情况近似, 适宜作为实验流场予以使用。

在外旋立式流场中, 径向压力梯度和离心力保持平衡, 即有:

1ρdpdr=Vφ2r=ω2r1

式中:ω=v_φ/r为流体单元绕旋转轴旋转的角速度; ρ为流体密度。

同时, 在远离壁面的无黏流体中, 流体单元的角动量 ωr2保持为常数。当半径为 r',旋转角速度为 ωr'的流体单元在扰动的作用下, 向外运动到半径为 r″时, 其角速度变成:

ωr″=ωr'r'r″22

受到的离心力为:

ωr″2r″=ωr'2r'4r″3=ωr'2r'r'r″33

由于在外旋情况下, 流体单元角速度随半径的增大而提高, 因而角速度与半径平方的乘积亦随半径的增大而提高, 即 d(ωr2)/dr> 0。此时, 该处流场的压力梯度将大于流体单元的离心力, 即:

1ρ∂P∂rr″=ωr'2r'> ωr″2r″=ωr'2r'r'r″34或|ωr″r″2> ωr'r'2|(5)

因此, 在压力梯度的作用下流体单元会回到原来的位置, 从而保证了流体的稳定性。

本实验拟定以表面减阻率来对样件的减阻效果进行评估, 即将射流特性表面所受到的流体黏性摩擦阻力与光滑无射流表面所受阻力进行对比, 以获得不同射流表面减阻率。令 FJ表示具有射流特性样件表面所受黏性摩擦阻力, FS表示无射流光滑表面所受黏性摩擦阻力, 则减阻率 η计算公式为:

η=FJ-FSFS×100%(6)

本实验分别将具有竖式和横式矩形射流孔样件的减阻结果与仿真结果进行对照, 从而验证测试平台的可行性。选择型号为SDR13.6的聚乙烯塑料PE管作为样件材料, 其外径为140 mm、壁厚为10.3 mm, 公称压力为0.8 MPa, 表面粗糙度μ =0.009, 截取样件筒高100 mm, 总质量约为0.43 kg。为保证射流过程中内筒沿径向方向受力均衡, 本实验样件采用沿周向均布四列, 沿壁面母线每列均布5个尺寸相同的射流孔的布置方式。

第一类孔形为竖式矩形孔, 样件实物图如图10(a)所示, 其沿样件周向长度为a,轴向长度为b,其中a≤b,令a=2 mm为定值, 分别取b等于2、4、6、8、10 mm。实验过程中, 第一类孔形采用代号a2bi表示,其中i指代轴向长度b的尺寸。第二类孔形为横式矩形孔, 样件实物图如图10(b)所示, 其沿样件周向长度为 c,轴向长度为d,其中c≥d,令d=2 mm为定值, 分别取c等于2、4、6、8、10 mm。在实验过程中, 第二类孔采用代号cjd2表示,其中j指代周向长度c的尺寸。

图10

Fig.10

	Figure Option ViewDownloadNew Window
	图10 两类孔形样件实物图Fig.10 Experimental samples with two kinds of jet hole shapes

仿生射流减阻特性研究结果表明, 影响样件表面阻力的因素除射流孔排布方式外还包括主流场速度(外筒转速)、射流速度、孔形尺寸。在排布方式相同的情况下, 拟定外筒转速为1500、2000、2500、3000 r/min, 射流速度为0.5、1.0、1.5、2.0、2.5 m/s。实验过程中, 分别测量不同转速下两种样件在不同射流速度下所受流体黏性摩擦阻力, 结合式(6), 计算并评估处于不同工况下射流表面的减阻效果。

根据实验方案分别对样件进行实验, 当外筒转速为1500、2000、2500、3000 r/min时无射流光滑表面样件受力测量值分别为1.73、2.82、4.08、5.71 N。采用前文两类样件完成阻力测试实验, 结合公式(6), 求得在不同外界条件下两类射流表面的减阻率, 根据减阻率数据绘制其变化规律曲线如图11、12所示。

图11为第一类孔形下五组实验样件在转速一定条件下减阻率随射流速度改变而变化的曲线。由11图可知, 第一类孔形下各实验样件表面减阻率随外筒转速及射流速度变化较为明显, 且在转速及射流速度一定的情况下, 具有 a2b10射流孔的实验样件表面具有最好的减阻效果, 且当外筒转速为3000 r/min、射流速度为2.5 m/s时, 该类型射流孔减阻率达到最大值, 为12.78%。

图11

Fig.11

	Figure Option ViewDownloadNew Window
	图11 不同射流速度下第一类样件减阻率曲线图Fig.11 Drag reduction rate curves of first-kind samples in different jet velocity

图12为第二类孔形下5组实验样件在转速一定条件下减阻率随射流速度改变而变化的曲线。由图12可知, 第二类孔形下各实验样件表面减阻率随外筒转速及射流速度变化较为平缓。当外筒转速为3000 r/min、射流速度为2.0 m/s时, 具有 c2d2射流孔的实验样件表面获得最大减阻率, 最大值为6.83%, 与第一类孔形减阻效果相比较弱。

图12

Fig.12

	Figure Option ViewDownloadNew Window
	图12 不同射流速度下第二类孔形减阻率曲线图Fig.12 Drag reduction rate curves of second-kind samples in different jet velocity

此外, 通过将以上实验数据与此前仿真结果进行对比, 发现其二者减阻效果趋势相同, 且各曲线峰值近似, 因此可以证明本文所建立的外旋立式射流减阻测试平台能够较好地满足仿生射流减阻测试实验的要求, 其能够在模拟多种主流场速度的前提下完成对具有各类射流孔形样件的阻力测试任务。