考虑载荷大小变化次序的球轴承寿命修正模型

引用本文

关健, 王黎钦. 考虑载荷大小变化次序的球轴承寿命修正模型.吉林大学学报:工学版, 2016, 46(4): 1182-1189
GUAN Jian, WANG Li-qin. Modified life model of ball bearing considering load changing sequence. Journal of Jilin University Engineering and Technology Edition, 2016, 46(4): 1182-1189 复制到剪切板

Permissions

考虑载荷大小变化次序的球轴承寿命修正模型

关健, 王黎钦

哈尔滨工业大学机电工程学院,哈尔滨 150001

王黎钦(1964-),男, 教授, 通讯作者：博士生导师.研究方向:摩擦学及其控制技术.E-mail:lqwanghit@gmail.com

作者简介:关健(1989-), 男, 博士研究生.研究方向:摩擦学及其控制技术.E-mail:j.guan@hit.edu.cn

基金:“973”国家重点基础研究发展计划项目 (2013CB632305); 国家自然科学基金项目(51375108)

摘要

为建立考虑载荷大小变化次序的球轴承疲劳寿命模型,在Miner理论和改进的Lundberg-Palmgren理论的基础上,引入了一种新的疲劳损伤累积理论,并考虑了材料疲劳极限应力对寿命的影响。以深沟球轴承6205为例,采用高速滚动轴承性能预测分析软件中的拟动力学计算模块,分析了等效载荷法和修正寿命模型中载荷类型、载荷均值、载荷振幅、载荷频率、转速等因素对寿命的影响规律。计算结果表明:相比于等效载荷法,修正的寿命模型能更全面地反映上述5种因素对轴承疲劳寿命的影响程度。

关键词: 机械设计; 循环变载荷; 球轴承; 加载次序效应; 疲劳极限; 等效载荷法; 寿命修正模型

中图分类号:TH133.33 文献标志码:A 文章编号:1671-5497(2016)04-1182-08

Modified life model of ball bearing considering load changing sequence

GUAN Jian, WANG Li-qin

School of Mechatronics Engineering, Harbin Institute of Technology, Harbin 150001, China

Abstract

In order to establish bearing fatigue life model considering the effect of load sequence, a new fatigue damage accumulation theory and material fatigue limit stress were introduced based on the Miner theory and improved L-P theory. Taking deep-groove bearing 6205 as an example, the effects of load type, mean load, load amplitude, load frequency and rolling speed on bearing life were analyzed by combining bearing quasi dynamic calculation software. The results show that, comparing to equivalent load method, the modified life model can fully reflect the effects of the above mentioned five factors. The effect of load sequence is also considered in this modified life model.

Keyword: mechanical design; pulsating load; ball bearing; effect of load sequence; fatigue limit; equivalent load method; modified life model

Show Figures

0 引言

现代航天技术的发展要求滚动轴承能够在高速、重载等苛刻条件下长时间运转, 对滚动轴承的性能、寿命和可靠性提出了更高的要求^[1]。目前在一些机械装备, 如列车、偏心轮冲床、轧机甚至航天、航空发动机上的轴承, 需要承受循环载荷^[2]。在这种情况下, 疲劳损伤成为轴承的主要失效形式, 对机械元件和装备的使用寿命都有很大的影响^[3]。在早期, 威布尔将滚动轴承疲劳寿命分布情况用数学表达式描述出来, 即威布尔分布^[4]。在此基础上, 瑞典科学家Lundberg和Palmgren提出了经典的Lundberg-Palmgren理论(以下简称L-P理论), 并给出了包含失效概率、最大剪切应力 $\begin{matrix} τ 、 \end{matrix}$ 最大剪应力发生深度 $\begin{matrix} Z_{0} 、 \end{matrix}$ 受力体积 $\begin{matrix} V \end{matrix}$ 和应力循环次数 $\begin{matrix} N \end{matrix}$ 的经验关系式^[5]。

国际标准ISO281/1-2007对原始的L-P理论公式进行了修正和简化, 得到了基于轴承额定动载荷和当量动载荷的计算公式^[6], 并沿用至今。哈尔滨工业大学的冷钢^[7]在L-P理论和Ioannides-Harris理论的基础上, 考虑了游隙、温度、过盈、润滑和污染等因素的影响, 得到了复杂工况下滚动轴承的寿命算法。这些寿命模型可以计算静载荷下轴承的疲劳寿命, 当载荷呈周期性变化时, 一般通过Miner理论对变载荷进行等效处理^[8]。

因为Miner理论并未考虑到载荷次序效应的影响, 所以其计算结果不是十分准确。Kwofie和Rahbar^[9]提出了一个考虑载荷作用次序效应的疲劳累积损伤公式, 在Miner理论基础上引入了损伤累积的修正系数, 经过试验验证, 其相比于Miner公式更接近试验结果。

本文首先通过拟动力学软件计算了各个接触点在一个周期内承载的变化, 得到接触载荷的表达式。然后在改进的L-P理论基础上建立了球轴承的修正寿命模型, 模型中考虑了载荷大小变化次序效应和材料疲劳极限应力的影响, 最终计算和比较了等效载荷法和修正寿命模型中各因素对球轴承疲劳寿命的影响。

1 球轴承基本额定寿命算法

1.1 滚道接触点寿命

改进的L-P寿命公式^[10]不仅考虑了滚动体寿命对轴承寿命的影响, 同时也考虑了不同方位角上球与内外圈接触角的不同, 计算结果更加接近真实轴承寿命值。根据额定动载荷理论, 对于点接触的向心球轴承, 滚动体与滚道间的基本额定动载荷为:

$\begin{matrix} \begin{matrix} Q_{cnj} = \\ 98.1 {(\frac{f_{n}}{2 f_{n} - 1})}^{0.41} \frac{{(1 \mp γ_{nj})}^{1.39}}{{(1 \pm γ_{nj})}^{\frac{1}{3}}} {(\frac{D}{d_{m}})}^{0.3} D^{1.8} Z^{- \frac{1}{3}} (1) \end{matrix} \end{matrix}$

式中: $\begin{matrix} n = (μ, v), \end{matrix}$ 分别对应内圈和外圈; $\begin{matrix} f_{n} \end{matrix}$ 为内(外)滚道的沟曲率系数; $\begin{matrix} D \end{matrix}$ 为球直径, mm; $\begin{matrix} d_{m} \end{matrix}$ 为流动轴承节圆直径, mm; $\begin{matrix} Z \end{matrix}$ 为滚动体个数; $\begin{matrix} γ_{nj} = Dcos α_{nj} / d_{m}, α_{nj} \end{matrix}$ 为球与内(外)滚道接触角。

对于内圈和外圈, 每个接触点的寿命为:

$\begin{matrix} L_{nj} = {(\frac{Q_{cnj}}{Q_{nj}})}^{3} (2) \end{matrix}$

式中: $\begin{matrix} Q_{nj} \end{matrix}$ 为滚动体与内(外)圈接触载荷, N。

1.2 滚动体接触点寿命

球的基本额定动载荷为:

$\begin{matrix} \begin{matrix} Q_{Bnj} = 77.9 {(\frac{2 f_{n}}{2 f_{n} - 1})}^{0.41} (1 \mp \\ γ_{nj})^{1.69} \frac{D^{1.8}}{{(\cos α_{nj})}^{0.3}} (3) \end{matrix} \end{matrix}$

与计算滚道接触点的寿命计算方法相同, 球与内(外)滚道的寿命为:

$\begin{matrix} L_{Bnj} = {(\frac{Q_{Bnj}}{Q_{nj}})}^{3} (4) \end{matrix}$

利用式(4)计算球的寿命时, 球的寿命是以球自身的转数计的, 而实际的轴承寿命是以旋转套圈的转数计的, 因此需要将球的寿命转化为以旋转套圈计。对于不计滑动的轴承转动, 通过几何关系计算, 可得内圈每转一周球的转数为:

$\begin{matrix} N = \frac{d_{m}}{2 D} (1 - {γ_{nj}}^{2}) (5) \end{matrix}$

综合内外滚道和球的寿命, 可以得到球轴承的整体寿命为:

$\begin{matrix} \begin{matrix} L = (\frac{1}{Z} (\overset{Z}{\sum_{j = 1}} {L_{μj}}^{- e} + \overset{Z}{\sum_{j = 1}} {L_{vj}}^{- e}) + \\ \overset{Z}{\sum_{j = 1}} {(\frac{L_{Bμj}}{N_{μ}})}^{- e} + \overset{Z}{\sum_{j = 1}} {(\frac{L_{Bvj}}{N_{v}})}^{- e})^{- \frac{1}{e}} (6) \end{matrix} \end{matrix}$

2 循环变载荷作用下轴承内部的载荷分布

滚动轴承内部的载荷分布是计算球轴承疲劳寿命的基础。载荷分布情况与初始游隙、温度、过盈量和轴承钢材料等因素都有关。在循环变载荷工况下, 球-滚道接触载荷呈周期性变化, 采用修正寿命模型计算轴承疲劳寿命时, 需要得到一个载荷周期内承载滚动体与滚道接触载荷的表达式。通过高速滚动轴承性能预测分析软件^[11]来计算滚动轴承内部的载荷分布。崔立^[11]在博士论文中使用Gupta滚动轴承动力学典型算例^[12]进行理论验证、采用高速滚动轴承实验台架进行实验验证, 证明软件准确可靠。

以正弦波载荷为例, 分析滚动轴承内部载荷变化情况。正弦载荷的表达式为:

$\begin{matrix} F = 3000 + 1000 \sin (2 πt) (7) \end{matrix}$

根据式(7)计算了轴承内部载荷分布, 建立了滚动体-滚道接触载荷的三维分布图, 如图1所示。从图1可以看出, 由于的轴承游隙为正, 承载的滚动体个数为5。每个滚动体与滚道的接触负荷呈正弦变化趋势, 并且接触负荷以与径向载荷方向平行的轴承中心线为轴对称分布。

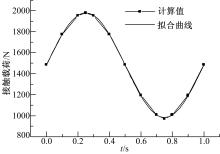
	Figure Option View Download New Window
	图1 球轴承内部载荷分布Fig.1 Load distribution of ball bearing

进一步研究单个滚动体的承载情况。从上述计算结果中提取出承载最大滚动体的接触载荷。可以看出, 外加径向载荷值约为滚动体-滚道接触载荷的2倍, 证明该滚动体承载了大部分的载荷, 因此也最容易失效。

对该滚动体在一个载荷周期的载荷进行曲线拟合, 如图2所示。拟合后的曲线与计算得到的结果非常接近, 可以认为滚动体-滚道接触载荷是呈正弦变化的。该滚动体接触载荷的表达式为:

$\begin{matrix} Q = 1481.5 + 498.2 \sin (2 πt) (8) \end{matrix}$

	Figure Option View Download New Window
	图2 正弦波载荷下单个滚动体承载的拟合情况Fig.2 Fitting curve of single rolling element under sine wave load

3 球轴承疲劳寿命修正模型

3.1 考虑载荷作用次序效应的寿命修正模型

疲劳损伤累积理论一般分为线性损伤累积理论和非线性损伤累积理论^[13]两类。在工程实际中, Miner线性损伤理论累积应用最广泛。Miner损伤累积公式如式(9)所示^[14], 当损伤累积值达到1时, 材料发生疲劳破坏。但其未考虑到载荷作用次序效应的影响, 所以并不能很好地体现疲劳累积损伤规律, 在循环变载荷作用下计算结果存在一定偏差。

$\begin{matrix} D = \frac{n_{1}}{N_{1}} + \frac{n_{2}}{N_{2}} + \dots + \frac{n_{i}}{N_{i}} (9) \end{matrix}$

式中: $\begin{matrix} n_{i} \end{matrix}$ 为材料在载荷 $\begin{matrix} σ_{i} \end{matrix}$ 下的循环次数; $\begin{matrix} N_{i} \end{matrix}$ 为材料在载荷水平 $\begin{matrix} σ_{i} \end{matrix}$ 下达到疲劳的循环次数, 即疲劳寿命。

3.1.1 考虑载荷大小变化次序的寿命修正模型

文献[9]中提出的考虑载荷作用次序效应的疲劳累积损伤公式如式(10)所示:

$\begin{matrix} D = \sum \frac{n_{i}}{N_{i}} \frac{\ln (N_{i})}{\ln (N_{1})} (10) \end{matrix}$

式中: $\begin{matrix} N_{i} \end{matrix}$ 为材料在载荷 $\begin{matrix} σ_{i} \end{matrix}$ 作用下的疲劳寿命; $\begin{matrix} N_{1} \end{matrix}$ 为材料在初始载荷 $\begin{matrix} σ_{1} \end{matrix}$ 作用下的疲劳寿命; $\begin{matrix} n_{i} \end{matrix}$ 为材料在载荷 $\begin{matrix} σ_{i} \end{matrix}$ 作用下的循环次数。

当损伤累积值达到1时, 接触点发生疲劳失效。该模型引入了考虑载荷作用次序效应的修正系数 $\begin{matrix} \ln (N_{i}) / \ln (N_{1}), \end{matrix}$ 且经过试验验证, 该模型更加接近试验得到的结果。

当疲劳载荷谱不是用若干级载荷范围水平的组合表示, 而是用相应于一定时期内的连续载荷函数表示时, 根据式(10)可以将损伤累积公式以积分的形式表达, 那么一个接触点在一个载荷周期内的损伤累积值为:

$\begin{matrix} ΔD = \int_{0}^{1} \frac{\ln (N_{t})}{N_{t} \ln (N_{0})} dt (11) \end{matrix}$

式中: $\begin{matrix} f \end{matrix}$ 为载荷频率; $\begin{matrix} N_{t} \end{matrix}$ 为接触点在任意载荷作用下的疲劳寿命, 是时间 $\begin{matrix} t \end{matrix}$ 的函数; $\begin{matrix} N_{0} \end{matrix}$ 为接触点在一个载荷周期初始时刻的载荷作用下的疲劳寿命, 为常数。

每个接触点在循环变载荷作用下直至失效, 当损伤值达到1时, 可以得到:

$\begin{matrix} D = L_{nj} f \int_{0}^{1} \frac{\ln (N_{t})}{N_{t} \ln (N_{0})} dt = 1 (12) \end{matrix}$

式中: $\begin{matrix} L_{nj} \end{matrix}$ 为接触点的疲劳寿命, 此处单位为s; $\begin{matrix} L_{nj} f \end{matrix}$ 为循环变载荷作用次数。

滚道接触点的疲劳寿命为:

$\begin{matrix} L_{nj} = \frac{1}{f \int_{0}^{1} \frac{\ln (N_{t})}{N_{t} \ln (N_{0})} dt} (13) \end{matrix}$

式中: $\begin{matrix} N_{t} = {(Q_{cnj} / Q_{nj})}^{3} \times 10^{6} \times 60 \times f / n, N_{0} = {(Q_{cnj} / Q_{nj} (0))}^{3} \times 10^{6} \times 60 \times f / n, \end{matrix}$ 其中, $\begin{matrix} {(Q_{cnj} / Q_{nj})}^{3} \end{matrix}$ 为接触点在载荷 $\begin{matrix} Q_{nj} \end{matrix}$ 作用下的疲劳寿命, $\begin{matrix} Q_{nj} 是时间 t 的函数; {(Q_{cnj} / Q_{nj} (0))}^{3} \end{matrix}$ 为滚道接触点在载荷 $\begin{matrix} Q_{nj} (0) \end{matrix}$ 作用下的疲劳寿命, $\begin{matrix} Q_{nj} (0) \end{matrix}$ 为 $\begin{matrix} Q_{nj} \end{matrix}$ 在初始时刻的载荷值。

轴承的寿命通常是以百万转作为单位的, 由式(13)可以进一步得到:

$\begin{matrix} \begin{matrix} L_{nj} = \\ \frac{1}{f \int_{0}^{1} \frac{{Q_{nj}}^{3}}{{Q_{cnj}}^{3}} \frac{\ln ({(Q_{cnj} / Q_{nj})}^{3} \times 10^{6} \times 60 \times f / n)}{\ln ({(Q_{cnj} / Q_{nj} (0))}^{3} \times 10^{6} \times 60 \times f / n)} dt} (14) \end{matrix} \end{matrix}$

式中: $\begin{matrix} L_{nj} \end{matrix}$ 的单位为 $\begin{matrix} 10^{6} r 。 \end{matrix}$

球的寿命计算方法与内外套圈相同, 考虑到滚动体与套圈的转数比, 得到滚动体接触点的疲劳寿命为:

$\begin{matrix} \begin{matrix} L_{Bnj} = \\ \frac{1}{f \int_{0}^{1} \frac{{Q_{nj}}^{3} N}{{Q_{Bnj}}^{3}} \frac{\ln ((Q_{Bnj} / Q_{nj})^{3} \times 10^{6} \times 60 \times f / (nN))}{\ln ((Q_{Bnj} / Q_{nj} {(0))}^{3} \times 10^{6} \times 60 \times f / (nN))} dt} (15) \end{matrix} \end{matrix}$

式中: $\begin{matrix} N \end{matrix}$ 为转数比, 由式(5)可以得到。

由式(1)~(6)、(14)(15)可以得到球轴承整体疲劳寿命。

式(14)(15)可以计算接触点在任意变载荷作用下的疲劳寿命, 应用于航空、航天等工况比较复杂的领域中。最常见的循环变载荷有3种, 正弦波、锯齿波和方波。3种循环变载荷的表达式分别为:

$\begin{matrix} \begin{matrix} Q_{nj} = a_{nj} + b_{nj} \sin (2 πft) (16) \\ \{\begin{matrix} Q_{nj} = a_{nj} + 4 b_{nj} ft, 0 \leq t \leq 0.25 / f \\ Q_{nj} = a_{nj} + 2 b_{nj} - 4 b_{nj} ft, 0.25 / f \leq t \leq 0.75 / f \\ Q_{nj} = a_{nj} - 4 b_{nj} + 4 b_{nj} ft, 0.75 / f \leq t \leq 1 / f \end{matrix} (17) \\ \{\begin{matrix} Q_{nj} = a_{nj} + b_{nj}, 0 \leq t \leq 0.5 / f \\ Q_{nj} = a_{nj} - b_{nj}, 0.5 f \leq t \leq 1 / f \end{matrix} (18) \end{matrix} \end{matrix}$

式中: $\begin{matrix} a_{nj} \end{matrix}$ 为载荷均值, N; $\begin{matrix} b_{nj} \end{matrix}$ 为载荷振幅, N; $\begin{matrix} t \end{matrix}$ 为时间。

将不同载荷表达式分别代入式(14)(15), 即可得到不同载荷作用下球轴承接触点的疲劳寿命。

3.1.2 两级循环变载荷下球轴承寿命修正模型

轴承在实际运转过程中, 载荷的频率、均值和幅值均可能发生变化, 不同级数的载荷下损伤累积值也不相同^[15]。在两级循环变载荷作用下, 得到接触点在两级循环变载荷作用下的损伤值分别为:

$\begin{matrix} \begin{matrix} D_{1} = {L_{nj}}^{(1)} f_{1} \int_{0}^{1} \frac{\ln ({N_{t}}^{(1)})}{{N_{t}}^{(1)} \ln (N_{0})} dt (19) \\ D_{2} = {L_{nj}}^{(2)} f_{2} \int_{0}^{1} \frac{\ln ({N_{t}}^{(2)})}{{N_{t}}^{(2)} \ln (N_{0})} dt (20) \end{matrix} \end{matrix}$

当损伤累计值达到1时, 接触点发生疲劳失效:

$\begin{matrix} D_{1} + D_{2} = 1 (21) \end{matrix}$

接触点的疲劳寿命可以表示为:

$\begin{matrix} L_{nj} = {L_{nj}}^{(1)} + {L_{nj}}^{(2)} (22) \end{matrix}$

3.1.3 多级循环变载荷下球轴承寿命修正模型

多级加载下寿命的计算方法与两级加载相同, 接触点在第 $\begin{matrix} m \end{matrix}$ 级循环变载荷作用下的损伤为:

$\begin{matrix} D_{m} = {L_{nj}}^{(m)} f_{m} \int_{0}^{1} \frac{\ln ({N_{t}}^{(m)})}{{N_{t}}^{(m)} \ln (N_{0})} dt (23) \end{matrix}$

同样当损伤累计值达到1时, 接触点发生疲劳失效:

$\begin{matrix} D_{1} + D_{2} + \dots + D_{m} = 1 (24) \end{matrix}$

接触点的疲劳寿命为:

$\begin{matrix} L_{nj} = {L_{nj}}^{(1)} + {L_{nj}}^{(2)} + \dots + {L_{nj}}^{(m)} (25) \end{matrix}$

3.2 考虑材料疲劳极限的寿命修正模型

Ioannides-Harris^[16]理论认为, 当接触区域所承受的应力小于材料疲劳极限应力时, 材料不发生疲劳失效; 当接触区域所承受的应力大于材料疲劳极限应力时, 材料会发生疲劳失效。对于循环变载荷, 当接触应力高于材料疲劳极限时, 发生损伤累积; 反之, 不会发生损伤累积。这样, 就将材料的疲劳极限应力引入到修正疲劳寿命模型中。

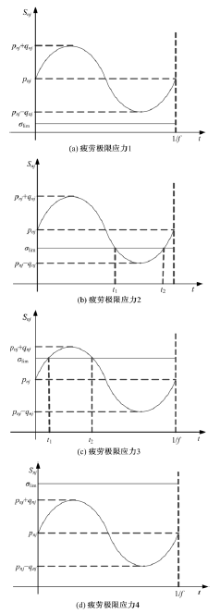
以正弦波载荷为例分析材料的疲劳极限应力对疲劳寿命的影响。随着材料疲劳极限应力的变化分为4种情况进行讨论, 如图3所示。

(1) $\begin{matrix} σ_{\lim} \leq p_{nj} - q_{nj} \end{matrix}$

如图3(a)所示, 在一个载荷周期中, 每个时间点的载荷对接触点都会造成损伤累积, 根据疲劳累积损伤理论, 接触点的疲劳寿命与式(14)相同。

	Figure Option View Download New Window
	图3 疲劳极限应力与接触应力关系Fig.3 Different situations between contact stress and fatigue limit stress

(2) $\begin{matrix} p_{nj} - q_{nj} < σ_{\lim} \leq p_{nj} \end{matrix}$

如图3(b)所示, 在一个载荷周期内, 时间段 $\begin{matrix} [0, t_{1}] 和 [t_{2}, 1 / f] \end{matrix}$ 内的载荷对接触点会造成疲劳损伤累积, 接触点的疲劳寿命为:

$\begin{matrix} \begin{matrix} L_{nj} = \\ 1 / f \{\int_{0}^{t_{1}} \frac{{Q_{nj}}^{3} \ln ({(\frac{Q_{cnj}}{Q_{nj}})}^{3} \times 10^{6} \times 60 \times f / n)}{{Q_{cnj}}^{3} \ln ({(\frac{Q_{cnj}}{Q_{nj} (0)})}^{3} \times 10^{6} \times 60 \times f / n)} dt + \\ \int_{t_{2}}^{1} \frac{{Q_{nj}}^{3} \ln ({(\frac{Q_{cnj}}{Q_{nj}})}^{3} \times 10^{6} \times 60 \times f / n)}{{Q_{cnj}}^{3} \ln ({(\frac{Q_{cnj}}{Q_{nj} (0)})}^{3} \times 10^{6} \times 60 \times f / n)} dt\} (26) \end{matrix} \end{matrix}$

式(26)中的 $\begin{matrix} t_{1} \end{matrix}$ 和 $\begin{matrix} t_{2} \end{matrix}$ 可由式(27)得到。

$\begin{matrix} \begin{matrix} S_{nj} = p_{nj} + q_{nj} \sin (2 πft) = σ_{\lim} (27) \\ 解得 : \\ \{\begin{matrix} t_{1} = \frac{1}{2 f} - \frac{1}{2 πf} \arcsin (\frac{σ_{\lim} - p_{nj}}{q_{nj}}) \\ t_{2} = \frac{1}{f} + \frac{1}{2 πf} \arcsin (\frac{σ_{\lim} - p_{nj}}{q_{nj}}) \end{matrix} \end{matrix} \end{matrix}$

(3) $\begin{matrix} p_{nj} < σ_{\lim} \leq p_{nj} + q_{nj} \end{matrix}$

如图3(c)所示, 在一个载荷周期内, 时间段 $\begin{matrix} [t_{1}, t_{2}] \end{matrix}$ 内的载荷对接触点会造成疲劳损伤累积, 接触点的疲劳寿命为:

$\begin{matrix} \begin{matrix} L_{nj} = \\ \frac{1}{f \int_{t_{1}}^{t_{2}} \frac{{Q_{nj}}^{3} \ln ({(\frac{Q_{cnj}}{Q_{nj}})}^{3} \times 10^{6} \times 60 \times f / n)}{{Q_{cnj}}^{3} \ln ({(\frac{Q_{cnj}}{Q_{nj} (0)})}^{3} \times 10^{6} \times 60 \times f / n)} dt} (28) \end{matrix} \end{matrix}$

根据式(27)可以得到:

$\begin{matrix} t_{1} = \frac{1}{2 πf} \arcsin (\frac{σ_{\lim} - p_{nj}}{q_{nj}}) \end{matrix}$

$\begin{matrix} t_{2} = \frac{1}{2 f} - \frac{1}{2 πf} \arcsin (\frac{σ_{\lim} - p_{nj}}{q_{nj}}) \end{matrix}$

(4) $\begin{matrix} p_{nj} + q_{n j} < σ_{\lim} \end{matrix}$

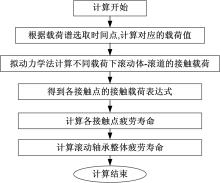
如图3(d)所示, 在一个载荷周期内, 载荷不会对接触点造成损伤累积, 此时, 就出现了接触点不发生疲劳的现象, 从宏观来看, 就是滚动轴承的无限长寿命。球轴承疲劳寿命的计算流程图如图4所示。

	Figure Option View Download New Window
	图4 滚动轴承疲劳寿命计算流程Fig.4 Calculation procedure for fatigue life of rolling bearing

4 计算结果及讨论

基于上述球轴承寿命修正模型, 通过Matlab开发了寿命计算程序。以深沟球轴承6205为例, 结合拟动力学软件, 研究了循环变载荷工况下载荷类型、载荷均值、载荷幅值、载荷频率和转速对轴承寿命的影响, 并与等效载荷算法进行了比较。6205轴承的参数为:内径为25 mm; 外径为52 mm; 节圆直径为38.5 mm; 球直径为7.968 mm; 球数为9; 轴承钢材料为GCr15; 弹性模量为205 GPa; 泊松比为0.3; 疲劳极限应力为684 MPa; 转速为5000 r/min。润滑方式为油润滑, 润滑油选用航空润滑油4050。下面将在考虑疲劳极限应力的情况下研究上述5种因素对轴承疲劳寿命的影响。

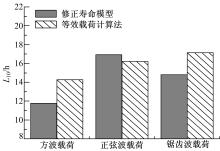
	Figure Option View Download New Window
	图5 载荷类型对轴承疲劳寿命的影响Fig.5 Effect of load type for bearing’ s fatigue life

图5为3种循环变载荷(方波载荷、正弦波载荷、锯齿波载荷)下轴承的疲劳寿命。载荷均值为3000 N; 载荷振幅为1000 N; 载荷频率为1 Hz。采用等效载荷法进行计算时, 得到的等效载荷值从大到小依次为:方波载荷、正弦波载荷、锯齿波载荷。所以方波载荷作用下轴承寿命最小, 锯齿波载荷作用下轴承寿命最大。通过修正模型计算得到正弦波载荷作用下轴承寿命最大, 方波载荷作用下轴承寿命最小。相比于等效载荷法, 正弦波载荷作用下的寿命值增加了4.5%; 方波载荷作用下的寿命值减小了17.4%; 锯齿波载荷作用下的寿命值减小了13.6%。修正的寿命模型相比于Miner公式考虑到了加载次序的影响, 反映出了不同加载类型下轴承寿命的变化规律。相比于方波载荷高-低的加载方式和锯齿波载荷“ 尖峰” 加载方式, 正弦波载荷波动(大小变化次序效应)相对比较平稳, 所以计算得到的寿命值最大。

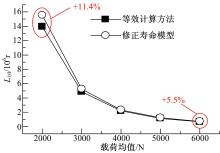
图6为正弦波载荷作用下由两种寿命计算方法得到的轴承寿命随载荷均值的变化情况。随着载荷均值增大, 两种方法计算得到的轴承疲劳寿命都减小, 变化趋势相同, 且相同载荷下, 修正模型计算得到的寿命值大于等效载荷计算得到的寿命值。载荷均值为2000 N时, 寿命值增大了11.4%; 载荷均值为6000 N时, 寿命值只增大了5.5%。这是因为随着载荷均值增大, 振幅的影响变小, 载荷均值起主导作用。因此在载荷均值比较小的情况下使用修正寿命模型时修正的比例较大。

	Figure Option View Download New Window
	图6 载荷均值对轴承疲劳寿命的影响Fig.6 Effect of mean load for bearing’ s fatigue life

	Figure Option View Download New Window
	图7 载荷振幅对轴承疲劳寿命的影响Fig.7 Effect of load amplitude for bearing’ s fatigue life

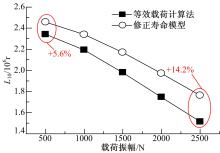
当循环变载荷振幅增大时, 每个滚动体承受的载荷幅值也增大, 这就导致了接触点的损伤累积速度加快。图7为均值4000 N、频率1 Hz的正弦波载荷作用下疲劳寿命随振幅的变化情况。可以看出, 采用等效载荷法得到的寿命值小于采用修正寿命计算法得到的寿命值。同时, 随着振幅值的增大, 修正寿命计算方法与等效载荷法得到的寿命偏差大, 当振幅值达到2500 N时, 修正寿命计算方法的寿命呈增大的趋势, 原因是随着载荷阶数的增加寿命相比于等效载荷法增加了14.2%, 随着振幅值的增大, 加载次序效应更加显著。

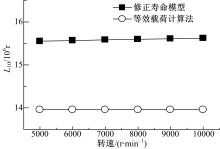
对循环变载荷进行等效计算时, 即使频率发生变化, 得到的等效载荷值也不发生变化。所以在等效载荷法中, 频率对轴承寿命是没有影响的。实际上载荷频率会影响材料的疲劳损伤累积。图8为正弦波载荷下频率对寿命的影响情况。采用修正模型计算时, 随着载荷频率增大, 轴承疲劳寿命减小, 当频率大于50 Hz时, 频率对轴承寿命的影响就很小了。

	Figure Option View Download New Window
	图8 载荷频率对轴承疲劳寿命的影响Fig.8 Effect of load frequency for bearing’ s fatigue life

采用修正模型进行计算时, 随着转速提高, 轴承的寿命(10⁶ r)呈增大的趋势, 但是幅度较小, 如图9所示。

	Figure Option View Download New Window
	图9 转速对轴承疲劳寿命的影响Fig.9 Effect of rolling speed for bearing’ s fatigue life

从图5中可以看出, 在3种载荷中, 方波载荷对球轴承的寿命影响最大, 方波载荷的表征量包括载荷次序(高-低, 低-高)和载荷阶数。图10反映了载荷次序和载荷阶数对轴承疲劳寿命的影响。

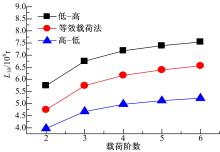	Figure Option View Download New Window
	图10 载荷阶数和加载次序对轴承寿命的影响Fig.10 Effect of load sequence and order for bearing’ s fatigue life under square-wave load

从图中可以看出, 随着载荷阶数的增加, 轴承的疲劳寿命呈增大的趋势, 原因是随着载荷阶数的增加, 大载荷的影响变小, 材料的疲劳损伤减小。相同阶数下, 高-低加载次序下轴承疲劳寿命< 等效载荷法疲劳寿命< 低-高加载次序下轴承疲劳寿命, 说明高-低加载次序对轴承疲劳寿命的影响比较显著, 原因在于当首先施加高载荷时, 接触区局部产生较高的应力集中, 造成了更多的损伤, 接下来低载荷会加剧损伤程度, 加载次序会直接影响接触点的疲劳寿命。从式(16)也可以看出, 施加高-低载荷时的 $\begin{matrix} Q_{nj} (0) \end{matrix}$ 值相比于施加低-高载荷的 $\begin{matrix} Q_{nj} (0) \end{matrix}$ 值更大, 导致计算得到的 $\begin{matrix} L_{nj} \end{matrix}$ 和 $\begin{matrix} L_{Bnj} \end{matrix}$ 较小。

5 结论

(1)首先基于拟动力学软件计算了循环变载荷作用下球轴承6205内部的载荷分布情况, 通过对滚动体-滚道接触载荷进行拟合, 认为每个接触点的接触载荷是呈正弦变化, 得到了接触载荷的表达式。

(2)基于改进的L-P理论和材料疲劳累积损伤理论, 建立了滚动轴承修正的疲劳寿命模型。与等效载荷计算方法相比, 该模型考虑了变载荷作用下载荷大小变化次序的影响。

(3)在循环变载荷工况下, 载荷类型、载荷均值、载荷振幅、载荷频率和转速都会对轴承疲劳寿命有不同程度的影响。等效载荷计算方法中频率和转速对轴承寿命是没有影响的, 在修正模型中通过引入了疲劳损伤累积的修正系数, 可以反映载荷频率和转速对轴承寿命的影响。可以通过选择合适的工况参数(如减小载荷均值、振幅、频率或提高轴承转速), 来提高球轴承的疲劳寿命(10⁶r)。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	彭波. 高速脉动重载滚动轴承工作特性仿真分析[D]. 哈尔滨: 哈尔滨工业大学机电工程学院, 2007. Peng Bo. Simulation analysis on working characteristics of high-speed rolling bearings under high pulsating load[D]. Harbin: School of Mechatronics Engineering, Harbin Institute of Technology, 2007. [本文引用:1]
[2]	卢黎明. 循环载荷冲击下滚滑轴承的振动特性[J]. 机械工程学报, 2013, 49(5): 39-46. Lu Li-ming. Vibration characteristics of rolling-sliding blend bearing under the impact of cyclic loading[J]. Journal of Mechanical Engineering, 2013, 49(5): 39-46. [本文引用:1]
[3]	Yuan Rong, Li Hai-qing, Huang Hong-zhong, et al. A new non-linear continuum damage mechanics model for fatigue life prediction under variable loading[J]. Mechanika, 2013, 19(5): 506-511. [本文引用:1]
[4]	Weibull W. Efficient method for estimating fatigue life distribution of rolling bearings[M]∥ Bidwell J B, Rolling Contact Phenomena, New York: Elsevier, 1962: 252-265. [本文引用:1]
[5]	Lundberg G, Palmgren A. Dynamic capacity of rolling bearings[J]. Journal of Applied Mechanics-Transactions of the ASME, 1949, 16(2): 165-172. [本文引用:1]
[6]	International Organization for Stand ardization. ISO 281-2007: Roiling bearings dynamic load ratings and rating life[S]. Switzer Land , 2007. [本文引用:1]
[7]	冷钢. 复合工况下高速滚动轴承的寿命和可靠性预测[D]. 哈尔滨: 哈尔滨工业大学机电工程学院, 2012. Leng Gang. Prediction on life and reliability of high speed rolling bearings in complex operating conditions[D]. Harbin: School of Mechatronics Engineering, Harbin Institute of Technology, 2012. [本文引用:1]
[8]	Weppert Gmb H, Co K G. FAG Rolling Bearings: Catalogue WL41 520EA[M]. Schweinfurt: Springer, 1995: 31-33. [本文引用:1]
[9]	Kwofie S, Rahbar N. A fatigue driving stress approach to damage and life prediction under variable amplitude loading[J]. International Journal of Damage Mechanics, 2012, 22(3): 393-404. [本文引用:1]
[10]	Harris T A. Rolling Bearing Anaysis[M]. 5th ed. New York: John Wiley&Sons, Inc, 2007: 165-236. [本文引用:1]
[11]	崔立. 航空发动机高速滚动轴承及转子系统的动态性能研究[D]. 哈尔滨: 哈尔滨工业大学机电工程学院, 2008. Cui Li. Research on dynamic performances of high-speed rolling bearing and rotor system of aeroengine[D]. Harbin: School of Mechatronics Engineering, Harbin Institute of Technology, 2008. [本文引用:2]
[12]	Gupta P K. Dynamic of rolling-element bearings part III: ball bearing analysis[J]. Trans of ASME, 1979, 101(3): 312-318. [本文引用:1]
[13]	Aid A, Amrouche A, Bouiadjra B B, et al. Fatigue life prediction under variable loading based on a new damage model[J]. Materials and Design, 2011, 32(1): 183-191. [本文引用:1]
[14]	Miner M A. Cumulative damage in fatigue[J]. Journal of Applied Mechanics, 1945, 12(3): 159-164. [本文引用:1]
[15]	Shang De-guang, Yao Wei-xing. A nonlinear damage cumulative model for uniaxial fatigue[J]. International Journal of Fatigue, 1999, 21(2): 187-194. [本文引用:1]
[16]	Ioannides E, Harris T. A new fatigue life model for rolling bearings[J]. ASME Trans J Tribol, 1985, 107(3): 367-377. [本文引用:1]

2007

0.0

. 2007, :-

Simulation analysis on working characteristics of high-speed rolling bearings under high pulsating load[D]. Harbin: School of Mechatronics Engineering,

高速脉动重载滚动轴承工作特性仿真分析

Peng Bo.

彭波

滚动轴承是各种机械中广泛应用的重要基础部件。现代工业的发展要求滚动轴承工作在重载、高速、高温等苛刻工况下,对滚动轴承的性能、寿命和可靠性提出了更高的要求。要确定滚动轴承在工程应用中的实际效果,必须充分了解它们在实际工况下的工作性能。在实际研究中,仿真分析是获得滚动轴承在其工作条件下各项工作性能数据的一种有效方法。本文建立了角接触球轴承和圆柱滚子轴承在外圈旋转、内圈静止工作时的拟静力学分析模型。两类轴承的径向载荷均作用于外圈上,角接触球轴承同时有轴向载荷的作用。在分析模型中,考虑了滚动轴承高速运转下产生的离心力和陀螺力矩、各轴承元件间的相互作用、弹性流体动力润滑作用以及轴承游隙的影响。以对两类滚动轴承进行静力分析得到的静态载荷分布和接触变形结果为初始值,使用Newton-Raphson法求解拟静力学模型非线性方程组。在角接触球轴承拟静力学模型求解中,建立了未知量的约束条件,能够保证非线性方程组求解正确和快速收敛。在圆柱滚子轴承拟静力学模型中,动态载荷分布的方程组和轴承元件角速度的方程组分别求解,求解结果互为已知参数,保证了求解结果的准确性和精度要求。分析了高速滚动轴承的工作特性,主要包角接触球轴承接触角和接触变形变化、轴承的最大接触应力变化、摩擦功率损耗、高速轴承元件附加动态载荷、角接触球轴承微区滑移特性、圆柱滚子轴承的打滑、轴承的润滑性能和变载荷损伤累积疲劳寿命。本文采用VB和Matlab语言编制了滚动轴承工作特性仿真分析软件。以两种类型共六个规格的滚动轴承为载体验算软件,对它们在高速、脉动重载工况下的工作特性进行仿真分析。利用该软件得到的仿真分析数据,为优化滚动轴承的结构和性能提供了数值依据。

... 0 引言现代航天技术的发展要求滚动轴承能够在高速、重载等苛刻条件下长时间运转,对滚动轴承的性能、寿命和可靠性提出了更高的要求^[1] ...

2013

0.0

. 2013, 49(5):39-46 DOI:doi:10.3901/JME.2013.05.039

Vibration characteristics of rolling-sliding blend bearing under the impact of cyclic loading

循环载荷冲击下滚滑轴承的振动特性

Lu Li-ming.

卢黎明

摘　要：在深入研究其结构和工作机理的基础上，建立一种新型轴承的振动物理模型，运用振动力学的相关理论，建立其数学模型，通过数学模型，得出其固有振动的特征方程及特征解：由系统的固有振动方程得出伴随矩阵，由伴随矩阵求出其主振型，由主振型得出主质量矩阵，由主质量矩阵得出正则振型矩阵，最后得到该新型轴承系统的稳态响应表达式。通过稳态响应表达式分析系统的振型及振幅，并通过计算和试验分析了影响系统振幅的一些因素。研究结果表明：系统的主振型为内圈在X和Y方向上作同为正向或同为负向振动和内圈在X和Y方向上作正负相反方向振动两种，新型轴承产生共振的影响因素为内圈质量、滚子个数、内圈旋转位置、滚子的横向刚度、滑块与内外圈之间的油楔刚度，当这些因素以一定方式结合且其值等于激振频率时，系统将产生共振，新型轴承产生振动的振幅在内圈转动过程中无变化、与其滚子个数及滚子横向刚度大小成反比。

... 目前在一些机械装备,如列车、偏心轮冲床、轧机甚至航天、航空发动机上的轴承,需要承受循环载荷^[2] ...

2013

0.0

... 在这种情况下,疲劳损伤成为轴承的主要失效形式,对机械元件和装备的使用寿命都有很大的影响^[3] ...

1962

0.0

... 在早期,威布尔将滚动轴承疲劳寿命分布情况用数学表达式描述出来,即威布尔分布^[4] ...

1949

0.0

... 在此基础上,瑞典科学家Lundberg和Palmgren提出了经典的Lundberg-Palmgren理论(以下简称L-P理论),并给出了包含失效概率、最大剪切应力 τ、最大剪应力发生深度 Z0、受力体积 V和应力循环次数 N的经验关系式^[5] ...

2007

0.0

... 国际标准ISO281/1-2007对原始的L-P理论公式进行了修正和简化,得到了基于轴承额定动载荷和当量动载荷的计算公式^[6],并沿用至今 ...

2012

0.0

. 2012, :-

Prediction on life and reliability of high speed rolling bearings in complex operating conditions

复合工况下高速滚动轴承的寿命和可靠性预测

Leng Gang.

冷钢

滚动轴承在航空航天及轨道交通等工况苛刻与可靠度要求极高的领域均有着广泛的应用，是传动部分的关键零部件。对选用轴承的寿命预测过大，一旦轴承提前失效，将导致传动部分甚至整个系统发生严重的故障。轴承的寿命估计过小，致使过早更换轴承，拆装过程会大大增加维护成本。本课题研究了工况对轴承寿命的影响，并提出了复合工况与高可靠度条件下轴承寿命的修正计算方法。传统的ISO寿命计算方法，只能针对常用内部几何结构的轴承，在一般可靠度要求下，计算仅受轴向力与径向力的滚动轴承疲劳寿命。该方法利用基于经验选取的修正系数，针对材料及工作条件进行修正，不但修正的精确度不够，同时也无法考虑弯矩、装配、温度等对轴承寿命的影响。本文首先对多种基本额定寿命的计算公式进行分析与比较，确定利用Harris改进的L-P基本额定寿命计算公式作为基础，讨论轴承内部载荷分布与滚动体寿命对轴承整体寿命的影响，得到一次修正计算方法。在基于次表层疲劳起源的L-P理论基础上，从轴承内部载荷分布与套圈周向应力的角度，研究了过盈配合、初始游隙、弯矩、温度及残余应力对次表层最大剪应力的影响，进一步研究它们对疲劳寿命的影响，形成了能够精确计算工况影响的基于轴承内部载荷分布的二次修正计算方法。在以考虑轴承内部载荷分布的一次修正算法和考虑部分工况影响的二次修正算法的基础上，结合基于I-H理论的ISO281-2007寿命修正计算方法，考虑接触区域表层产生的应力及材料疲劳极限对轴承寿命的影响，针对润滑、污染、高可靠度及轴承超长寿命现象进行修正，得到最终的复合工况与高可靠度条件下滚动轴承寿命修正计算方法，并利用VB与Matlab联合开发出计算软件。

... 哈尔滨工业大学的冷钢^[7]在L-P理论和Ioannides-Harris理论的基础上,考虑了游隙、温度、过盈、润滑和污染等因素的影响,得到了复杂工况下滚动轴承的寿命算法 ...

1995

0.0

... 这些寿命模型可以计算静载荷下轴承的疲劳寿命,当载荷呈周期性变化时,一般通过Miner理论对变载荷进行等效处理^[8] ...

2012

0.0

... Kwofie和Rahbar^[9]提出了一个考虑载荷作用次序效应的疲劳累积损伤公式,在Miner理论基础上引入了损伤累积的修正系数,经过试验验证,其相比于Miner公式更接近试验结果 ...

2007

0.0

... 1 滚道接触点寿命改进的L-P寿命公式^[10]不仅考虑了滚动体寿命对轴承寿命的影响,同时也考虑了不同方位角上球与内外圈接触角的不同,计算结果更加接近真实轴承寿命值 ...

2008

0.0

. 2008, :-

Research on dynamic performances of high-speed rolling bearing and rotor system of aeroengine

航空发动机高速滚动轴承及转子系统的动态性能研究

Cui Li.

崔立

滚动轴承作为航空发动机转子系统广泛采用的一种支承，其动态力学特性对转子系统的动力特性有重要的影响，随着航空发动机的性能不断提高，这种影响更为显著。因此，为了优化和提升现有发动机的动态性能，满足新一代先进航空发动机的研制需要，进行高速滚动轴承及其转子系统动态性能的研究十分必要。本文围绕航空发动机高速滚动轴承及其支承的转子系统，建立了滚动轴承的拟动力学分析模型、滚动轴承-转子系统的动特性和非线性振动模型，分析了不同工况参数和轴承结构参数对滚动轴承及转子系统动特性的影响，开发了分析程序，在现有的高速轴承台架上进行了高...

... 通过高速滚动轴承性能预测分析软件^[11]来计算滚动轴承内部的载荷分布 ...

... 崔立^[11]在博士论文中使用Gupta滚动轴承动力学典型算例^[12]进行理论验证、采用高速滚动轴承实验台架进行实验验证,证明软件准确可靠 ...

1979

0.0

... 崔立^[11]在博士论文中使用Gupta滚动轴承动力学典型算例^[12]进行理论验证、采用高速滚动轴承实验台架进行实验验证,证明软件准确可靠 ...

2011

0.0

... 1 考虑载荷作用次序效应的寿命修正模型疲劳损伤累积理论一般分为线性损伤累积理论和非线性损伤累积理论^[13]两类 ...

1945

0.0

... Miner损伤累积公式如式(9)所示^[14],当损伤累积值达到1时,材料发生疲劳破坏 ...

1999

0.0

... 轴承在实际运转过程中,载荷的频率、均值和幅值均可能发生变化,不同级数的载荷下损伤累积值也不相同^[15] ...

1985

0.0

... 2 考虑材料疲劳极限的寿命修正模型Ioannides-Harris^[16]理论认为,当接触区域所承受的应力小于材料疲劳极限应力时,材料不发生疲劳失效 ...